Abstract
Scheduling of megaprojects is very challenging because of typical characteristics, such as expected long project durations, many activities with multiple modes, scarce resources, and investment decisions. Furthermore, each megaproject has additional specific characteristics to be considered. Since the number of nuclear dismantling projects is expected to increase considerably worldwide in the coming decades, we use this type of megaproject as an application case in this paper. Therefore, we consider the specific characteristics of constrained renewable and non-renewable resources, multiple modes, precedence relations with and without no-wait condition, and a cost minimisation objective. To reliably plan at minimum costs considering all relevant characteristics, scheduling methods can be applied. But the extensive literature review conducted did not reveal a scheduling method considering the special characteristics of nuclear dismantling projects. Consequently, we introduce a novel scheduling problem referred to as the nuclear dismantling project scheduling problem. Furthermore, we developed and implemented an effective metaheuristic to obtain feasible schedules for projects with about 300 activities. We tested our approach with real-life data of three different nuclear dismantling projects in Germany. On average, it took less than a second to find an initial feasible solution for our samples. This solution could be further improved using metaheuristic procedures and exact optimisation techniques such as mixed-integer programming and constraint programming. The computational study shows that utilising exact optimisation techniques is beneficial compared to standard metaheuristics. The main result is the development of an initial solution finding procedure and an adaptive large neighbourhood search with iterative destroy and recreate operations that is competitive with state-of-the-art methods of related problems. The described problem and findings can be transferred to other megaprojects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Megaprojects denote the biggest investment boom in human history with an assessed total global spending of US$6 to US$9 trillion annually, or 8% of the total global gross domestic product (GDP) (Flyvbjerg 2014). The dismantling of nuclear facilities (in this paper, the term “nuclear facilities” includes both nuclear power plants and research reactors) is a special application case of megaprojects with expected durations of about 10 to 15 years and costs of about 0.3 to 1.3 billion euros per facility (European Commission 2016b). The International Energy Agency (IEA) forecasts that until 2040, about 200 nuclear reactors in various nuclear facilities worldwide will have to be decommissioned and dismantled (IEA 2014). Especially the EU, the USA, Russia, and Japan will have the highest numbers of nuclear dismantling projects (IEA 2014; Volk et al. 2019). In its Nuclear Illustrative Programme, the European Commission estimates that more than 50 nuclear reactors will be decommissioned in the EU until 2025 (European Commission 2016a). Because of the huge amount of investment in the future (Volk et al. 2019) and the specific project characteristics, the dismantling of nuclear facilities is used as an application case in this paper to be solved. In particular, we develop a scheduling problem and a methodology to solve the problem. However, the developed mathematical model and the methodology can be adapted to the requirements of other application cases and thus can be transferred to other megaprojects.
By the end of 2018, about 17 nuclear reactors worldwide were fully dismantled (WNA 2017). The project duration and project costs of completed nuclear dismantling projects most commonly deviate significantly from the original dismantling plans (NEA 2016). The reasons for such deviations are, on the one hand, long-lasting and costly approval procedures and, on the other hand, insufficient planning due to manual planning, errors, misestimation, unexpected events. Since activities and resources have to be approved by a legal authority, project scheduling is required to be very detailed, and hence, operational planning is needed. Changes in planning after receipt of a legal approval must again be approved, which again causes high costs, takes much time, and thus may lead to project delays.
Since there are only few completed nuclear dismantling projects, only very little scheduling and estimation experience is available so far. Consequently, uncertainties in the planning and execution prevail. To avoid replanning and the necessity of new legal approvals, uncertainties should be considered in project planning. Furthermore, an effective and efficient operational planning is crucial. Such an operational planning has to calculate schedules in a sufficient degree of detail for practitioners within short computation times considering the large number of activities, activity modes, and scarce resources of such a megaproject. Additionally, specific constraints, such as legal or technical specifications, time lags, or overhead expenses, have to be considered in project scheduling. The goal of the dismantling companies is to dismantle the nuclear facilities at minimum costs taking safety and security into account. To minimise errors in the planning and to compile a reliable planning at minimum costs, scheduling methods can be applied.
A general overview of different scheduling methods is given in Sect. 2. To be able to use these scheduling methods for certain application cases, adaptions are often necessary. In a literature review of related approaches conducted in Sect. 2, we show that for operational scheduling of nuclear dismantling projects, optimising scheduling methods and project scheduling software considering the specific characteristics of multiple modes, constrained renewable and non-renewable resources, precedence relations with and without no-wait condition, and a cost minimisation objective are lacking. Therefore, the aim of this paper is to define the problem formally and to implement and test a metaheuristic framework for its solution. Four steps are required. In the first step, relevant and necessary data for scheduling of a sample project are compiled, and the scheduling goal with its influencing parameters is explained in Sect. 3. In the second step, with the help of these scheduling requirements in this particular case, the related mathematical model is derived (also Sect. 3). To obtain an adequate mathematical model for this scheduling problem, we adapt and extend the multi-mode resource investment problem (MRIP) considering the constraints of the application case. We introduce a novel project scheduling problem called the nuclear dismantling project scheduling problem (NDPSP). In the third step, for tackling this problem, we propose necessary adaptations of a metaheuristic framework which is described in Sect. 4. In the fourth and last step, we apply, test, and validate the algorithm with several data samples of real-life projects with up to 300 activities. Different instances of these real-life projects and computational results using the algorithm are presented in Sect. 5. Finally, Sect. 6 gives a critical appraisal and concludes the findings of this paper.
2 Literature review
In Sect. 2.1, we first present a literature review on existing project scheduling software. The specific characteristics of nuclear dismantling projects are not considered using available project scheduling software (see Sect. 2.1). To identify an appropriate scheduling method, we present a literature review on existing scheduling methods for the application case of nuclear dismantling projects in Sect. 2.2. As shown in Sect. 2.2, scheduling in this application case has been subject to several shortcomings so far. To identify an appropriate scheduling method for the application case “dismantling of a nuclear facility”, we present a literature overview of existing scheduling methods in Sect. 2.3.
2.1 Project scheduling software
For the planning of projects, different software is available. In this paper, we focus on project scheduling software for the dismantling of nuclear facilities as an example for project scheduling of megaprojects. The scheduling goal is to identify a schedule at minimum costs taking safety and security into account. However, current approaches in practice are based on manual planning and experience, or, if experience is lacking, speculation. Such approaches are often error-prone and most commonly lead to deviations from the respective plans. Mostly, only software to visualise the schedule, such as MS Project, Primavera, or Cora Calcom, which is based on MS Access and MS Project, is applied and scheduling is done by engineers and qualified people manually without support by optimisation methods.
An extensive literature review did not reveal a software applying optimising methods. Only the report of the Co-ordination Network on Decommissioning of Nuclear Installations (CND) of the Research and Technological Development (RTD) of the European Commission recommends using the critical path method as an optimising scheduling method. Furthermore, MS Project, Primavera P6, Cora Calcom, or CERREX is used as planning software for nuclear dismantling projects.
MS Project is a software of Microsoft that can visualise schedules linking it with the resources needed. Nevertheless, costs are only considered using resources and are not completely included in the planning. The main shortcoming is the absence of an optimising method. Primavera P6 of Oracle is comparable to MS Project. It is only able to visualise schedules, but not able to optimise them. Cora Calcom is a software of the company Siempelkamp that consists of the two modules: “Cora” and “Calcom”. Cora (Component Registration and Analysis) is a database implemented in MS Access or Oracle Database that helps to structure the project and to estimate inventory and masses of a dismantling project. Based on the information of Cora, the module Calcom (Calculation and Cost Management) helps to schedule the project including a resource and cost planning. Nevertheless, all these plannings have to be done manually. The International Atomic Energy Agency (IAEA) provides the MS Excel-based calculation software CERREX (Cost Estimate for Research Reactor in Excel) for the cost planning of nuclear research reactors. With the help of this software, the whole dismantling project is structured by several dismantling steps. The planner has to enter information for each step and CERREX sums up the total project dismantling costs. An optimising scheduling method is missing, too. Consequently, a manual scheduling is necessary.
2.2 Project scheduling of nuclear facility dismantling
Scheduling methods for the application case “dismantling of a nuclear facility” are very rare because many adaptations of existing approaches are necessary (Bartels 2009). Bartels (2009) used a resource-constrained project scheduling problem with discounted cash flows (RCPSPDC) and extended it by cumulative resources and two modes. Furthermore, Bartels (2009) adapted the objective function to minimise the total project costs. Cumulative resources are used to describe buffer stocks for nuclear wastes. The two modes represent either the execution of an activity by own staff or by external staff. To minimise the total project costs, costs for own staff as well as for external staff are considered and discounted by a discount rate. For solving the problem, Bartels (2009) extended an enumeration algorithm provided by De Reyck and Herroelen (1998). Bartels’ scheduling model has several shortcomings. He only considers two modes which concern the execution of activities with own or external staff. A differentiation of modes, such as the use of different alternative machines, is not considered. In this context, Bartels (2009) minimises only the costs related with these two modes. Variable costs of the use of different machines, procurement costs, and indirect overhead costs, such as post-operational costs, are not considered. Furthermore, in his approach, Bartels (2009) modelled cumulative resources using two kinds of activities: either storing or removal activities. For each storing activity, a corresponding removal activity must exist. This is not realistic since two or more removal activities can have the same amount of pieces/material as one or more storing activity/activities and vice versa. Also, a major shortcoming is planning with time slices of three months which is not an operational planning procedure satisfying the requirements for legal approvals of nuclear facilities.
Apart from the methodology introduced by Bartels (2009), to the authors’ knowledge no scheduling method for nuclear dismantling projects exists. Only Yanagihara et al. (2012) and Iguchi et al. (2004) considered nuclear dismantling project planning in their research. They use the programme evaluation and review technique (PERT) to schedule nuclear dismantling projects and exposure times of staff. However, further details on how the scheduling method and the underlying algorithms work are missing in their publications.
The scheduling of nuclear dismantling projects is especially challenging because of the project-scale process requiring many resources, such as specific machinery or diverse qualified staff, expected durations of about 10 to 15 years, and a budget per reactor/unit that amounts to about 0.3 to 1.3 billion euros (European Commission 2016b). The main goal of nuclear dismantling projects is dismantling at minimum costs considering safety, security, and resources, the latter being partly constrained. To avoid cost increases because of misestimation or unexpected events, uncertainties should be considered in operational project planning. Herroelen and Leus (2005) compare different methods for schedule generation under uncertainty. Stochastic project scheduling aims at scheduling project activities with uncertain durations but does not use a baseline schedule and rather uses scheduling policies or scheduling strategies that make decisions at decision points during project execution (Herroelen and Leus 2005). Since a baseline schedule has to be submitted to the authorities for a legal approval before project execution, stochastic scheduling is not applicable for this application case. Reactive scheduling uses a baseline schedule, but with no anticipation of variability (Herroelen and Leus 2005). In the case of unexpected events, the baseline schedule has to be revised or reoptimised. Since the procedures for new legal approvals are long-lasting and costly, replanning or plan adaptions should be avoided. Consequently, reactive scheduling is also not applicable for this application case. Instead, an ex ante stable schedule should be identified. Therefore, Herroelen and Leus (2005) recommend using proactive and robust scheduling. “This approach may use information about the particular variability characteristics (for example probability distributions for activity durations) [...]” (Herroelen and Leus 2005, p. 291). To identify an ex ante stable schedule Herroelen and Leus (2005) recommend to apply sensitivity analysis. For the application case of nuclear dismantling projects, the application of sensitivity analysis is suitable to identify an ex ante stable schedule for a given project. Therefore, different potential scenarios are simulated, optimised, and compared regarding their robustness. However, an effective scheduling method to calculate a schedule at minimum costs for a deterministic scenario is lacking. Consequently, in this paper we focus on the development of such a deterministic scheduling method that deals with the specific requirements of nuclear dismantling projects and thus with the specific requirements of megaprojects. An example how to simulate different scenarios is given in Sect. 5.1.
2.3 General project scheduling approaches
In the field of project scheduling, Möhring (1984) distinguishes between problems of scarce resources and problems of scarce time. In the former, known as resource-constrained project scheduling problems (RCPSP), the amount of resources is fixed and the goal is to find the shortest possible schedule. Problems of scarce time, however, are determined by a due date that has to be respected. Their goal is minimisation of the costs of the resources that are allocated to the project. In the literature, such problems are called resource investment problems (RIP) or resource availability cost problems (RACP). These terms were first introduced by Möhring (1984).
The resource-constrained project scheduling problem (RCPSP) and its extensions have received a lot of attention in literature. Especially for the multi-mode extension, where activities can be performed in different modes, many different heuristic, e.g. Geiger (2017), and exact procedures, e.g. Schnell and Hartl (2017), have been proposed in the recent years. For a broad overview of the existing work concerning the MRCPSP, we refer to Mika et al. (2015). Another extension of the RCPSP is the RCPSP/max, where more advanced precedence constraints are introduced. They are also called generalised precedence constraints or time windows, and with them, it is possible to define minimum and maximum time lags between the start of two activities. Schnell and Hartl (2016) present an exact approach to the multi-mode extension of the RCPSP/max, applying a combination of constraint programming (CP) and Boolean satisfiability solving (SAT) techniques.
Since our primary concern related to project scheduling of nuclear dismantling projects is the minimisation of costs, the resource investment problem is more applicable to our purposes. The amount of resources is not fixed, and project duration plays only a secondary role. For an overview of the existing exact and heuristic procedures for the basic RIP, we refer to Rodrigues and Yamashita (2015) and van Peteghem and Vanhoucke (2015), respectively. Most recently, Kreter et al. (2018) have investigated different mixed-integer programming (MIP) and CP formulations for the RIP, and Zhu et al. (2017) proposed an effective heuristic procedure.
Shadrokh and Kianfar (2007) propose an extension of the RIP where they allow exceeding the project’s due date, but penalise this in the objective function. A multi-mode extension of the RIP, called MRIP, was firstly introduced by Hsu and Kim (2005). They propose a heuristic that combines two priority criteria for this new problem setting, where each activity can be processed in different modes that differ in both duration and resource requirements.
Another similar project scheduling problem is the resource levelling problem (RLP), where activities also require resources and have to respect precedence relations. However, here, the goal is to level or smoothen the resource utilisation over the course of the project. Different types of objective functions are considered. The most common ones as well as exact and heuristic procedures for RLP are presented by Rieck and Zimmermann (2015) and Christodoulou et al. (2015).
The software project scheduling problem (SPSP) is also closely related to the RCPSP and our setting. Employees are the single resource in this problem and can have different skills that are needed to perform project tasks (cf. Alba and Chicano (2007)). Like in our problem, it is hard to predict the optimal project duration and resource usage in the SPSP. However, the objective in the SPSP is minimising two conflicting goals at the same time: the project duration and the project costs that are associated with employee costs. For a literature overview of the SPSP, we refer to Vega-Velázquez et al. (2018).
Most of the existing project scheduling methods mentioned above were only tested on small- to medium-sized project instances with 10 to 30 activities per project. The literature available on larger, practical-sized instances is scarce. The authors van Peteghem and Vanhoucke (2014) present a benchmark library with up to 100 activities per project for the MRCPSP. For the single-mode resource investment problem, Kreter et al. (2018) investigate their proposed methods on project instances with a maximum of 500 activities, but their procedure is not suited (yet) for the multi-mode setting we desire.
While many of the above problems possess useful properties to model the task of dismantling a nuclear facility, none can capture its challenges completely, yet. However, by adding a special form of generalised precedence constraints to the MRIP and adjusting the objective function, it is possible to model our application case more accurately and provide additional decision support on resource investments/procurement to project managers. Therefore, we propose a novel kind of project scheduling problem in the next section (Sect. 3).
3 Problem description
3.1 Definition
The main goal of nuclear dismantling projects is dismantling at minimum costs in line with national safety and security guidelines as well as the consideration of (partly) constrained resources. Project costs in nuclear dismantling projects particularly arise from
-
1.
procurement costs, which are different for different resources, such as machines, and arise for any procurement,
-
2.
direct, variable costs, which only occur when activities are executed due to the use of resources, e.g. because of wear, abrasion, or electricity needed, and
-
3.
post-operational costs, which are indirect costs and occur independently of the execution of activities, e.g. due to the operation of ventilation systems, cleaning systems, security services, fire protection, or general safety protection that have to be maintained 24/7 to guarantee safety and security.
In particular, the post-operational costs that may amount to three up to five million euro per month significantly influence the total project costs (cf. Klasen and Seizer (2015)). Some activities reduce the amount of post-operational costs, e.g. when ventilation or cleaning systems are removed. However, this can only be done when it is technically safe and reasonable. Furthermore, the post-operational costs may also increase after the completion of specific activities, e.g. when additional ventilation or cleaning systems are installed.
Since procurement costs, variable costs, and post-operational costs should be minimised, influences on these costs should be considered in planning. Procurement costs depend on the number of machines that have to be bought for project execution. Variable costs arise from the execution of activities. In some cases, activities can be executed in different modes, e.g. with own or external staff (cf. Bartels (2009)). However, the execution of activities also may be done using different techniques, such as decontamination by means of a milling machine versus decontamination by means of chemicals. The execution of an activity in different modes may differ in terms of activity duration and direct, variable costs per activity. When an activity mode is shorter than other modes of this activity, the total project duration and, thus, the amount of post-operational costs and maybe also the total project costs might be reduced. However, it has to be considered that in some cases, activities may only be executed earlier when a higher amount of resources will be procured or when more expensive modes of activities are chosen beforehand. Consequently, this trade-off has always to be considered when scheduling nuclear dismantling projects.
Furthermore, a maximum amount of resources is available that can be used at the same time, e.g. due to limited space conditions in the reactor room or supply bottlenecks for nuclear containers. To minimise the total project costs, decision makers have to decide in which mode each activity should be executed considering post-operational costs, procurement costs, direct, variable costs of execution, and scarce resources.
Moreover, the starting times must be determined considering predefined technically induced precedence relations. For example, before removal of the reactor vessel, the vessel head has to be removed (Brusa et al. 2002). In some cases, activities have to be executed successively without the execution of other activities and without any waiting time in between, e.g. when activities contain work with radioactive material. We call these types of successors successors with no-wait condition.
Altogether, the result of scheduling should be a schedule with minimum total project costs that defines the starting times of each activity, the mode of each activity, and the number of each resource type that is needed in total. The total project costs and total project duration can be derived from the resulting schedule. Further limitations are discussed in Sect. 6.
3.2 Mathematical and constraint programming model
Since the existing problems found in the literature do not capture all desired features of the nuclear dismantling megaproject, we suggest a new problem type: the nuclear dismantling project scheduling problem (NDPSP). It is an extension of the MRIP, where we adapt the objective function and add extra constraints. To model successors with a no-wait condition, we use finish-to-start minimum and maximum time lags of 0. They are a special case of “generalised precedence constraints” and are represented in the set \(E^{nw}\). Kreter et al. (2018) propose MIP and CP models for the RIP with generalised precedence constraints.
An instance of the NDPSP consists of the following information:
-
a set of activities A
-
a set of renewable resources \(\mathcal {R}\)
-
a set of non-renewable resources \(\mathcal {R}^n\) as in the
MRCPSP (Mika et al. 2015)
-
a set of modes \(M_i\) for each activity \(i \in A\)
-
a set of precedence relations \(E \subset A \times A\) among the activities
-
a set of no-wait precedence relations \(E^{nw} \subset A \times A\) among the activities
-
durations \(d_{im} \in \mathbb {Z}^+_0\) for each activity i and each mode \(m \in M_i\)
-
resource requirements \(r_{imk} \in \mathbb {Z}^+_0\) for each activity i and each mode \(m \in M_i\) and each resource \(k \in \mathcal {R} \cup \mathcal {R}^n\)
-
resource unit cost factors \(c_k \in \mathbb {Z}^+_0\)
-
resource maximum capacities \(a_k^{\max } \in \mathbb {Z}^+\)
-
activity finish bonus/penalty cost factors \(b_i \in \mathbb {Z}\)
The goal is to determine a processing mode and, thus, the resource requirements and starting time for each activity and, consequently, a resource allocation to the project so that the resulting schedule is resource- and precedence-feasible and the total project costs are minimised. Precedence feasibility is achieved, on the one hand, if for each pair of activities \((i,j) \in E\), the predecessor activity i finishes no later than the start of the successor activity j. This represents precedence relations without no-wait condition. On the other hand, for each pair of activities \((i,j) \in E^{nw}\), there is a minimum and maximum time lag of 0 between the finish of activity i and the start of activity j. These are so-called no-wait precedence relations, where no time lag is allowed between activities. The no-wait precedence relations cannot be modelled/aggregated to one single activity as also mode decisions have to be made for each activity, and resource use among resources would vary.
The schedule is resource-feasible if the amount of allocated resources is at least as high as the amount used by activities. Furthermore, the amount of allocated units of a resource k cannot exceed the upper bound \(a_k^{\max }\). The total project costs consist of resource procurement costs, direct, variable costs per activity, and post-operational costs. The resource costs for resource k are the product of the amount of allocated units of resource k multiplied with the respective resource unit cost factor \(c_k\). The direct, variable costs are modelled as a non-renewable resource and the number of needed non-renewable resource units for each activity differs in each mode. The resource unit cost factor of these non-renewable resources is 1. Post-operational costs are incurred by each period the project is not finished. The factor \(b_i \in \mathbb {Z}\) defines how the completion of activity i influences the post-operational costs per period. Hence, at project start, the post-operational costs per period are exactly equal to \(\sum _{i \in A} b_i\) and are increased and decreased in the following periods depending on which activities terminate. For each period where activity i is not completed, post-operational costs \(b_i \ge 0\) occur, and completing the activity reduces the post-operational costs per period. The term \(b_i < 0\) represents a rise in post-operational costs per period since in each period before completion of that activity i, we subtract \(|b_i |\). Depending on the values of \(b_i\), it may occur that the problem is unbounded. With Succ(i), we denote the set of all successor activities of activity i, i.e. \(Succ(i) = \{ j~\in ~A : \exists \text { a path from i{ to}j in graph } G = (A, E \cup ~E^{nw}) \}\). If \(Succ(i) = \emptyset \) and \(b_i< 0\), then the instance is unbounded since the starting and finish time tend towards infinity, the costs approach negative infinity. Furthermore, if there is an activity i with \(b_i < 0 \) and \({\sum _{j \in Succ(i)} b_j < - b_i}\), then the problem is also unbounded. Again, we can delay the finish of activity i and its successors indefinitely and the costs decrease more and more. We assume that the values for \(b_i\) are reasonable and the problem is bounded.
Next, we present a mixed-integer programming formulation for the problem described in the previous subsection. The model uses similar variables and constraints as a time-indexed model for the MRCPSP introduced by Talbot (1982). In this model, we have two types of decision variables. First, there are real-valued decision variables \(a_k\) for each renewable and non-renewable resource k. They determine how many units of resource k are allocated to the project. Second, we introduce binary decision variables \(x_{imt}\) that represent the mode choice and the scheduling decision for all activities. For an activity i, a mode \(m \in M_i\) and a time point \(t \in \{ ES_i, \dots , LS_i \}\), the decision variable \(x_{imt} \) is 1 if and only if activity i is processed in mode m and starts at time point t. Here, \(ES_i\) and \(LS_i\) denote the earliest and latest starting times of the activity, which can either be computed using the critical path method (CPM) introduced by Kelley (1963) or specified in a restrictive way to reduce computational complexity of a MIP (as described in Sect. 4.2).
The objective function (1) minimises, in the first term, the costs of the allocated renewable and non-renewable resources, and the sum of post-operational costs in the second term. The renewable resource costs correspond to the procurement costs while the direct, variable costs per activity are captured by the non-renewable resources. Equation (2) enforces that for each activity exactly one mode and one starting time is chosen. If for activities i and j, the tuple \((i,j) \in E\), then activity i has to be completed before activity j can start. This is modelled by inequality (3), where on the left side of the inequality is the finish time of activity i and on the right side is the starting time of activity j. Similarly, the set \(E^{nw}\) represents no-wait precedence relations among activities, which means that there is a zero time lag between the finish time of activity i and the starting time of activity j. Consequently, j has to start directly after the finishing period of its predecessor i, if \((i,j) \in E^{nw}\). Due to the fact that the finish time of activity i, on the left side of (4), and the starting time of activity j, on the right side of (4), have to be equal, a zero time lag, and thus, no-wait conditions are represented in equation (4).
The next constraints (5)–(8) are concerned with the resources. In constraint (5), we compute the use of the non-renewable resources in the project and set the availability variable \(a_k\) for that resource \(k \in \mathcal {R}^n\) accordingly. For the renewable resources, inequality (6) ensures that for each time period, sufficient units of the respective resource are allocated to the project. With inequality (7), it is possible to introduce an upper bound on how many units of a resource can be allocated to the project, e.g. due to space limitations. Note that in the original problem formulation of the RIP, such limitations were not given.
Finally, (8) and (9) define the real-valued and binary decision variables, respectively.
Note that, unlike in the original problem description of the RIP, there is no due date or deadline constraint. As an upper bound T for the calculation of the latest starting times, we use the sum of the maximal durations of all activities (10).
We assume that the problem is bounded, i.e. there is a reasonable post-operational cost structure, and, hence, there is no reason for considering starting times later than T. For a given solution, we can compute in polynomial time if it is feasible. Hence, the NDPSP is in NP. Furthermore, the NDPSP is also an NP-complete problem since we can construct a polynomial-time reduction from the well-known MRCPSP which is NP-complete. Given an MRCPSP instance, we compile an equivalent NDPSP instance where \(b_{n+1} = 1 \) and \(b_i = 0\) for all \(i \in A \setminus \{n+1\}\). The resource cost factors are all set to 0 and the maximum resource capacities \(a_k^{\max }\) are chosen equal to the resource capacities in the MRCPSP instance. There are no no-wait constraints in the NDPSP instance and all other data, such as precedence constraints and mode, is chosen as in the MRCPSP instance. It is easy to see that they are equivalent.
Next, we also give a CP formulation in (11) - (19) for the problem using the framework of IBM ILOG CP Optimizer (Laborie et al. 2018). It is an adaption of CP formulation of the MRCPSP and utilises so-called interval variables to model the start and end times of the activities. The objective function (11) is similar to the MIP formulation but the end time of activity i is denoted by \(\texttt {endOf}(act[i])\). Here, act[i] is an interval variable that marks the start and end of activity \(i \in A\). We introduce additional interval variables mode[i, m] for each mode \(m \in M_i\) (see (19)). The mode variables get the keyword optional which means that they do not need to be processed. However, with the alternative constraint in (12), we ensure that exactly one of the mode interval variables is processed and the start and end time of the corresponding act[i] interval variable coincide. Hence, each activity is processed in exactly one mode. With (13) and (14), we model the normal as well as the no-wait precedence constraints, respectively. The non-renewable resources are considered in (15) where we sum up the resource consumption of all present (i.e. chosen) modes. To model a renewable resource \(k \in \mathcal {R}\), we use a so-called cumulative function \(renewU\!sage_k\) and the pulse expression in (16). This expression sums up the resource consumption \(r_{imk}\) between the start and end time of the interval variable mode[i, m]. Finally, (17) sets the bounds of the real-valued decision variables that represent the amount of allocated resources like in the MIP model.
To compute a simple lower bound for the problem, we use the following equation:
In Eq. (20), for renewable resources \(k \in \mathcal {R}\), we use as minimum resource consumption \(a_k^{\min }\) with
being the maximum overall minimum activity resource consumptions. For non-renewable resource \(k \in \mathcal {R}^n\), the minimum allocation \(a_k^{\min }\) is the sum over all minimum resource consumptions of the activities, i.e.:
The minimal resource allocations are multiplied with the respective unit resource cost factor in the first sum in (20). The second sum takes into account activities with a positive post-operational cost value \(b_i\) and multiplies them with the earliest finish time of the activity. Finally, in the last sum in (20), activities with negative post-operational cost values are multiplied with their latest finish time in order to reduce costs as much as possible. We will use this lower bound to evaluate our results in Sect. 5.2.
We set up the formulation of the NDPSP displayed in (1)–(9) for different projects of different project sizes (number of activities, modes, resources, etc.) using the MIP solver CPLEX to calculate optimised schedules. But, as described in Sect. 5.2.3, CPLEX needs long computation time or does not even find a feasible schedule for larger projects. Therefore, we adapt an existing metaheuristic to develop a new methodology to solve such problems quicker and to identify optimised schedules for larger projects (see Sect. 4).
4 Methodology
Next, we describe the methodology we used to generate (nearly) optimal solutions to this problem. The proposed approach is divided into two phases. In the first phase, the main goal is to find a feasible solution and improve it by means of a local search procedure. Finding any feasible solution to the project instances at hand can be a difficult task especially because of the no-wait precedence constraints and the resource constraints. We use a multi-start local search (MLS) that applies a parallel schedule generation scheme (PSGS).
In the second phase of the proposed procedure, we use an adaptive large neighbourhood search (ALNS) to further improve the initial solution. Here, large parts of the solution are destroyed by various destroy operators. A recreate operator is used to repair these destroyed parts and obtain a feasible solution that usually has a better objective value. In our implementation, the recreate operator uses exact optimisation techniques to obtain feasible and (sub-)optimal solutions.
4.1 Initial solution generation
Since the ALNS needs a feasible initial solution, we use priority rules and a schedule generation scheme to compute a feasible initial solution. Different rules are used to generate scheduling sequences. The initial solution can then be further improved by a multi-start local search (MLS) procedure. The local search component of the MLS only changes the scheduling sequence and keeps the mode choice. Multi-start methods have been applied to various combinatorial optimisation problems. For an overview of the concept and existing work, we refer to Martí et al. (2013).
In the MLS, we use a parallel schedule generation scheme (PSGS) to construct schedules based on a sequence of strongly connected components \(\pi \) and a mode vector M. We partition the graph \(G = (A, E \cup E^{nw} \cup \overline{E^{nw}} )\) into its maximum set of strongly connected components, also called strong components. Here, the set \(\overline{E^{nw}} = \{ (j,i) : (i,j) \in E^{nw} \} \) contains the backward arc for each no-wait precedence constraint in \(E^{nw}\). We denote the set of strong components with \(\mathcal {C} = \{ C_1, \dots , C_p \}\). A maximum strongly connected component (strong component) \(G_C\) of the graph G is a maximum subgraph \(G_C=(C, A_C)\) induced by the vertex set C such that for two vertices \(i,j \in C\) there is a directed path from i to j and from j to i in \(G_C\). If an activity i is not strongly connected with any other activity j in graph G, then it forms its own singleton subgraph in \(\mathcal {C}\). Note that each strong component \(G_C\) is defined by its vertex set C, and hence, we may also use the term strong component for C.
The reason why we use a parallel schedule generation scheme is that the no-wait precedence relations may require a successor of an activity to start directly after the predecessor activity is finished. Hence, if the starting time of an activity i is set to a specific point of time the starting times of all no-wait successors and predecessors of activity i are also determined. Therefore, we determine the starting times of all activities that belong to the same strong component simultaneously, i.e. in parallel, during the PSGS.
A small example of precedence relations and the resulting strong components is depicted in Fig. 1 and Table 1. There, dotted arcs represent no-wait precedence relations in \(E^{nw}\) and \(\overline{E^{nw}}\) while normal arcs represent the normal precedence relations in E.
We use Tarjan’s algorithm (Tarjan 1972) to compute the strong components of the project in linear time. Given a mode choice for each activity, we can compute minimum start-to-start time lags \(\delta _{ij}\) for all activities in \(i,j \in C\) in a strong component C using a longest path label-correcting algorithm on the strong component (cf. Neumann et al. (2003), Sect. 1.4). A minimum start-to-start time lag \(\delta _{ij}\) defines how large the time difference between the start of two activities i and j has to be, i.e. \(S_j - S_i \ge \delta _{ij}\).
The arc weights for this longest path problem are chosen as follows:
This label correcting algorithm returns a matrix \(\delta \) in \(\mathcal {O}(|C |^3)\). Hence, if we find an activity i with \(\delta _{ii}>0\) the current mode choice is infeasible since the no-wait precedence constraints will be violated for this component. If \(\delta _{ij} + \delta _{ji} = 0\), we know that \(S_j = S_i + \delta _{ij}\) and the start of one activity determines the start of the other.
Next, we explain how the PSGS translates a sequence of strong components \(\pi \) and a mode vector M into a schedule. Algorithm 1 depicts the basic outline of the PSGS. For each activity, the mode vector M determines in which mode the activity is processed, i.e. the mode is not determined during the PSGS, but given as an input parameter. For each activity, we keep track of the earliest and latest starting times. They are initialised with the ones calculated with CPM and are updated whenever a successor or predecessor of an activity is scheduled.
The sequence of components \(\pi \) determines in which order the strong components are scheduled. At iteration s of the PSGS, strong component \(C_{\pi _s}\) is scheduled. When we schedule a component, we choose a starting time for activity \(j^* = \arg \min \{ES_i : i \in C_{\pi _s} \}\) with the lowest earliest starting time and determine the starting times of all other activities \(i \in C_{\pi _s} \setminus \{j^*\}\) by adding the value \(\delta _{j^*i}\), i.e. if \(S_{j^*} = t\), then \(S_i = t + \delta _{j^*i} \). Hence, for activities with no-wait conditions between them, these are fulfilled. However, for activities with some float time, e.g. activity 3 in Fig. 1, we choose the earliest starting time which respects the normal precedence constraints. If this violates the resource constraints, an unscheduling procedure tests later starting times for such activities.
Since our objective function is locally quasiconcave, not all starting times need to be checked as it suffices to check the starting times in the set \(DT(\pi _s)\) (Neumann et al. 2003, Sect. 3.3).
Above, DT is the set of already assigned starting and finish times in the (partial) schedule. Hence, the set \(DT(\pi _s)\) consists of all the relevant time points where the resource use may change. A starting time \(t \in DT(\pi _s)\) is only considered for scheduling if the maximum resource consumption of any resource k does not exceed \(a_k^{\max }\) if the component is scheduled at that time (cf. constraint (7)).
Among the feasible starting times for the strong component in question, we choose the one with the least change in the objective function value \(\varDelta \) when comparing the partial schedules. If a resource infeasibility for time t is encountered, we set the respective cost increase \(\varDelta ^t = \infty \).
Here, the effect on the objective function of activities with a negative cost reduction \(b_i\) value is omitted since it would favour delaying these activities to late finish times. Ties are resolved by selecting the earlier time.
It is possible that the PSGS does not find a feasible schedule for a specific scheduling sequence even if the scheduling sequence itself is precedence-feasible. As explained above, this can happen when the activity durations in the chosen modes produce positive length cycles in a strong component or when the resource demands of the chosen modes exceed the given resource capacity limits. Yet, for the instances at hand, this procedure always found at least one feasible schedule when applying it to different precedence-feasible activity sequences.

For the example depicted by the network in Fig. 1 and the data shown in Table 1, we illustrate the outcome of different sequences of strong components and mode vectors. Note that only activity 3 has 2 modes available. We assume that there is only one renewable resource with unit cost factor \(c_1 = 1\) and no maximum availability limitation. For the component sequence \(\pi ^1 = [0, 1, 2, 3] \) and mode vector \(M^1~=~ [ 1, 1, 1, 1, 1, 1, 1, 1] \), the schedule computed by the PSGS and the resource consumption is depicted in Fig. 2.
At first, the component \(C_0\) containing only dummy activity 0 is scheduled with start and finish at time 0. Next, the component containing activities 1, 2, 3, and 4 is scheduled. No matter which feasible starting times are selected, the change in costs of the partial schedule is the same. Hence, the PSGS schedules the start of activity 1 at time 0 and the other activities in the component according to the zero time lag precedence constraints. It is not possible to update the earliest start time \(ES_7\) of activity 7.
The next component to be scheduled (\(C_2\)) contains activities 5 and 6. For all starting times earlier than 8, the maximum resource use would increase. Hence, the PSGS determines the starting time of activity 5 to be 8 and the one of activity 6 at time 12 such that no extra resource costs occur. We update \(ES_7 := 14\) because of the finish of activity 6. The dummy end activity 7 starts and finishes at time 14. If the positions of component 1 and 2 are reversed, i.e. \(\pi ^2 = [0, 2 ,1 ,3] \), the PSGS obtains the schedule which is depicted in Fig. 3. Since the project finish time of this schedule is greater than before, \(b_7 > 0\), and the amount of used resources is the same, this schedule has higher costs than the one depicted in Fig. 2.
If the mode of activity 3 is changed to 2, i.e. \(M^2 = [ 1, 1, 1, 2, 1, 1, 1, 1]\), we can detect a cycle of positive length in component \(C_1\) while computing the \(\delta _{i,j}\). Since there are no-wait precedence constraints among activities 1 and 2 and activities 2 and 4, the processing duration of activity 3 cannot be greater than the one of activity 2. Because of the precedence constraints among activities 1 and 3 and 3 and 4, activities 3 and 2 need to be executed partly in parallel. Hence, \(M^2\) is an infeasible mode vector.

In Algorithm 2, the pseudocode of the MLS is depicted. The input parameters of the MLS are an overall time limit T and perturbation parameters for the mode vector \(p^M\) and for the component sequence \(p^S\), respectively. First, a mode vector is computed where for each activity the minimum duration is selected. Next, we calculate an initial sequence \(\pi \) of strong components by applying several priority rules. This sequence respects the precedence constraints of the set E: if \((i,j) \in E\) and i and j do not belong to the same component, then the strong component of activity i has to be at an earlier position in the sequence \(\pi \) than the component of activity j. We get a precedence-feasible order in the following way: First, we add the component of the dummy start activity to the sequence. Then, we iteratively select the component with the highest priority value according to the chosen priority rule among the components where all the components containing predecessors with respect to E have already been added to the sequence and add it to the sequence. This is repeated until all strong components are added to the sequence and ties are resolved by choosing the component with the lowest index. We used the following priority rules: minimum LST, minimum LFT, minimum slack, i.e. the difference between the latest and earliest finish time, minimum number of successors, maximum number of successors and maximum rank positional weight (cf. Kolisch (1996)). These rules were traditionally used to obtain activity sequences. Hence, we adapted them such that for example the minimum LST of a component C is defined as the minimum LST of the activities in the component, i.e. \(min_{i \in C} LS_i\). We apply the six rules mentioned above in turn and, together with the mode vector M, we use the PSGS to translate them into a solution candidate. The priority rule that results in the lowest costs is stored in \(\pi \) and kept as starting point for the local search.
Together with the mode vector, we use the PSGS to translate \(\pi \) into the first solution candidate \(c^{b}\). Then, we initialise the mode vector \(M^{b}\) and sequence \(\pi ^{b}\) with M and \(\pi \), respectively. In every iteration of the while loop, we first perturb the current best mode vector and component sequence to obtain \(M^{it}\) and \(\pi ^{it}\). In the mode vector perturbation, we change the chosen mode of a random activity to another one (the total number of changes is random and smaller than or equal to \(p^M \cdot |A |\)). A changed mode vector is only used if it is feasible with respect to the time lags in the components, i.e. \(\delta _{ii} \le 0\) for all activities i. To obtain a perturbed sequence \(\pi ^{it}\), we iteratively delete a random strong component from the sequence and reinsert it at a random but precedence feasible position. This is repeated a random number of times, but at most \(p^S \cdot |\mathcal {C} |\) many times. Then, we translate the current mode vector \(M^{it}\) and the current sequence \(\pi ^{it}\) into a solution candidate with the PSGS. Afterwards, we try to improve this solution candidate with a local search.
In the local search, we exchange the position of two strong components in the sequence. If the exchange meets the precedence constraints as mentioned above, we apply the PSGS to the altered sequence and evaluate the cost value. If a cost improvement is found, we apply the change to the sequence. Hence, we use a first improving move policy. This is repeated until all possible 2-swaps have been checked and have not led to a cost improvement. If an improvement to \(c^{b}\) was obtained, we update \(c^{b}\) as well as \(M^b\) and \(\pi ^b\). In Sect. 5.2.1 we perform experiments to identify suitable parameter choices for the MLS procedure.
4.2 Adaptive large neighbourhood search
Here, we explain how the master algorithm for the second phase of the search is implemented. We basically use the adaptive large neighbourhood search (ALNS) metaheuristic with modifications. The concept of ALNS was introduced by Ropke and Pisinger (2006). It is an extension of the large neighbourhood search (LNS) framework established by Shaw (1997). In the field of project scheduling, the ALNS concept was successfully applied to the MRCPSP by Muller (2011) and Gerhards et al. (2017).
In each iteration of the ALNS, one of several destroy operators is chosen with some defined probability and used to destroy large parts of the current solution. It is then repaired by the use of a mixed-integer programme based on the formulation in (1)–(9) or using the constraint programming formulation in (11)–(19). We do not solve the full MIP or CP, but instead, we limit the number of decision variables present with a parameter \(\texttt {freeVar}\) in the destroy step and solve a subproblem by fixing all other decision variables to the value in the undestroyed solution part. The purpose of reducing the number of decision variables is to be able to solve the MIP or CP in reasonable time. When introducing decision variables for all available modes and starting times for each activity, the MIP or CP is not solvable with current state-of-the-art hardware components for the desired instance sizes due to memory and time limitations. Thus, by limiting the number of decision variables, the MIP or CP becomes solvable. The application of exact optimisation techniques in the recreate step of the ALNS enables us to incorporate complex problem-specific constraints, such as precedence relations with no-wait condition.
In our implementation, instead of changing the probabilities for choosing the destroy and recreate operators, the adaptive part of the ALNS consists of adapting the size of the neighbourhood that is searched. More precisely, if the search has not found a better solution in the current iteration because it has got stuck in a local optimum, for example, we increase the neighbourhood size and the iteration time limit.
The neighbourhood size is defined by the two parameters freeVar and varPerMode. Here, freeVar limits the total number of decision variables in the MP, and varPerMode is an upper bound on the number of decision variables introduced for each mode of an activity. If the search encounters a better solution, the neighbourhood size and the iteration time limit are reset to their initial values. The implementation of the ALNS for the MRCPSP in Gerhards et al. (2017) also uses MIP techniques in the recreate step. However, there the neighbourhood size was only defined by the number of decision variables in the MIP and each activity could start at all possible starting times in the MIP. For the instances at hand, the respective MIP would not be solvable in reasonable time, and hence, we saw the need to limit the number of decision variables per activity. Furthermore, in this implementation, we obtain the schedule directly from the MIP without an additional SGS step. The ALNS implementation in Gerhards et al. (2017) used the MIP to obtain priority values for the activities and then translated them with an SGS into a feasible solution. Since constraint programming solvers have become a powerful tool for resource-constrained project scheduling problems (see e.g. Kreter et al. (2018) for a successful implementation of CP for the RIP), we also implement a CP solver as a recreate operator.
The basic outline of the algorithm is depicted in Algorithm 3. In the next subsections, we will describe in more detail how the destroy operators and the recreate operator work.

As relevant input data for the ALNS, we need a feasible solution candidate \(c^{i}\), a pool of destroy operators D, and probabilities P to select them. Furthermore, we need initial values for the maximum number of decision variables (initFreeVar), for the number of decision variables for each mode (initVarPerMode) as well as for the MIP solver time limit of each iteration (initTimePerIteration). Lastly, the parameters \(\alpha \) and \(\beta \) are used to increase the size of the neighbourhood. In Sect. 5.2.1, we investigate which values for these parameters perform best.
In lines 1–4 of Algorithm 3, we initialise the variable parameters. Here, freeVar and varPerMode are used in the destroy step (see Sect. 4.2.1) as parameters, and timePerIteration is used in the recreate step (see Sect. 4.2.2). Each iteration of the while loop (lines 5–23) can be divided into three parts: The destroy step (line 7), the recreate step (line 8), and the update and adapt step (lines 9–22).
In the destroy step, one of the destroy operators is chosen based on probability values stored in P. This operator destroys specific parts of the current best solution candidate \(c^{b}\). The parts selected for destruction are determined by the type of operator. The number of parts that are chosen and the size of these parts are controlled by the parameters freeVar and varPerMode, respectively. The destruction process is explained in further detail in the next subsection.
The recreate operator sets up either a mixed-integer programme with the mathematical model depicted in (1)–(9) or the constraint programming formulation shown in (11)–(19). But instead of adding all activity decision variables to the model, some of them are fixed according to the current undestroyed solution parts. Only in destroyed parts of the solution, the decision variables are added. Thus, only a subproblem is set up and solved by a generic solver, such as CPLEX or Gurobi. This has the advantage that it is less time- and memory-consuming than solving the full MIP or CP formulation of the problem. With timePerIteration, we limit the computation time of the solver. More information on how the exact optimiser is used is described in Sect. 4.2.2.
If an improving solution candidate is found by the recreate operator, the current best solution candidate is updated (line 10) and we reset the parameters that control the destroy and recreate operators to their initial values (lines 11–13). Otherwise, we adapt the parameters so that a larger neighbourhood is searched. Therefore, the parameter freeVar is increased by factor \(\alpha \) (line 15). Hence, in the destroy step of the next iteration, more parts of the current solution are destroyed. Also, every second iteration, we increase the parameter varPerMode by factor \(\beta \) (lines 16–18) to enlarge the size of the destroyed parts. We extend the time for the MIP or CP solving (lines 19–21) since the neighbourhood that is investigated in the following iteration is larger. We set the time limit to the actual computation time of the current iteration and add one extra second. This is done because we expect a longer computation time for the increased neighbourhood; thus, we need to limit the overall computation time.
4.2.1 Destroy operators
The purpose of the destroy operators in the ALNS is to destroy specific parts of the current solution candidate while the remaining parts of the solution are fixed. In order to do so, we define with the term destroyed candidate a data structure which contains the information about the fixed and destroyed parts of the solution which is used in the recreate step of the ALNS. A destroyed candidate stores lists that contain information about mode indices in which each activity i can be processed. Also, for each activity i, an earliest (\(ES^d_i\)) and latest starting time (\(LS^d_i\)) is stored. A destroy operator d returns a destroyed candidate DC and takes a solution candidate c, the maximum number of decision variables freeVar, and the number of variables per mode varPerMode as input parameters. The corresponding number of decision variables of such a destroyed candidate depends on the number of modes and possible starting times of the chosen activities.
In the destroyed candidate, activities can be classified as either free or fixed activities. We apply two destroy operators that differ in the sequence the activities are selected as free activities. A fixed activity i has only its mode \(m_i\) of the input solution candidate c available for processing, and earliest starting time as well as the latest starting time are set to be the starting times in the schedule of the input solution candidate c. Hence, nothing can change for this activity. For a free activity i, all of its possible mode indices are added to the mode list in the destroyed candidate DC and the earliest and latest starting time (\(ES^d_i\) and \(LS^d_i\), respectively) depend on the starting time \(s_i\) in the solution candidate as well as the parameter varPerMode. Basically, we want to set \(ES^d_i\) and \(LS^d_i\) to such values that they form an interval with the old start \(s_i\) in the middle of it. The size of the interval is not larger than varPerMode, i.e. \(LS^d_i - ES^d_i \le varPerMode\). Hence, we initially set \(ES^d_i := s_i - \frac{varPerMode}{2}\) and \(LS^d_i := s_i + \frac{varPerMode}{2}\). We adjust the borders of the interval if they extend over the earliest or latest starting times calculated by CPM (\(ES_i\) and \(LS_i\), see also 3.2). Hence, if \(ES^d_i < ES_i\), we shift the interval to the right by increasing \(LS^d_i\) by \(ES_i - ES^d_i\) and setting \(ES^d_i = ES_i\). Similarly, if \(LS^d_i > LS_i\), we shift the interval to the left by decreasing \(ES^d_i\) by \(LS^d_i -LS_i\) and setting \(LS^d_i = LS_i\). However, if both cases appear simultaneously, i.e. \(ES^d_i < ES_i\) and \(LS^d_i > LS_i\), we assign the earliest and latest starting times calculated by CPM. After a shift, the old start \(s_i\) may not be in the centre of the interval formed by \(ES^d_i\) and \(LS^d_i\) but it is still contained in the interval.
For each free activity, we can count how many decision variables are added in the recreate step to the MIP. For free activity i, we introduce
decision variables. The destroy operator stops selecting free activities after a certain threshold of decision variables freeVar has been exceeded. All remaining activities are fixed activities. Hence, the sum of decision variables corresponding to a destroyed candidate is calculated as follows and has to be lower than or equal to the parameter freeVar:
In the following, we describe how the two applied operators work.
The first destroy operator we introduce is called destroyTimeInterval (DTI). The main idea is to select activities that are processed in similar time periods. First, a random time period \(t \in \{1, \dots , c^{\max }\}\) is chosen with equal probability. Here, \(c^{\max }\) denotes the makespan of the current schedule and a period t starts at time \(t-1\) and ends at t. We use a time period to identify which activities are selected as free with initial lower bound \(t-1\) and upper bound t. Iteratively, DTI selects free activities that fulfil one of the following criteria:
-
The starting time point of the activity is contained in the time period.
-
The finish time point of the activity is included in the time period.
-
The time period contains both the start time point and the finish time point of the activity.
The activities are selected in increasing order of their indices if more than one activity is eligible for selection. If an activity is selected, we add all activities that belong to the same strong component as free activities since they are linked by no-wait precedence constraints. If the sum of corresponding decision variables does not exceed the parameter freeVar, we increase the original interval. To make more activities eligible for selection in the next iteration, we increase the interval by 5 time units in both directions in order to speed up the selection process. The activity selection and interval enlargement alternation is repeated until either the bound freeVar of corresponding variables is reached or all activities are selected. All activities that have not been selected are fixed activities in the destroyed candidate. Hence, the free activities all have relatively close-by starting or finish time points, and the change of the mode or starting time point of one of them will most likely influence the others.
The second destroy operator, destroyPredecessorsAndSuccessors (DPS), exploits the precedence relations among activities. Iteratively, we select a random strong component \(C \in \mathcal {C}\) that has not been selected before and mark all activities belonging to it as free. Then, we also select all strong components that contain successor activities or predecessor activities of the current component’s activities and mark their activities as free in this order and if they were not marked previously. Furthermore, we also consider transitive successors and predecessors in this selection process, i.e. if \((i,j) \in E\) and \((j,k) \in E\), then k is a transitive successor of i. We repeat this procedure with another random strong component until the limit freeVar is reached or exceeded. Again, all activities that have not been selected are fixed. Here, we want to focus on activities that have precedence relations between them since they often limit the starting or finish time. In the case of the no-wait precedence relations \(E^{nw}\), changing the start of one activity has effects on all activities in the same strong component, and thus, the solver can explore the neighbourhood more effectively if all activities of the strong component are free.
4.2.2 Recreate operator
Next, we present how the recreate operator works. It uses the following input parameters: the current best solution candidate \(c^{b}\), a destroyed candidate DC, and a time limit timePerIteration. The recreate operator returns a feasible solution candidate \(c^{p}\).
It uses the information provided in the destroyed candidate data structure to set up a MIP or a CP. In the MIP case, we use the mathematical formulation presented in (1)–(9) (see Sect. 3.2) but with the mode list from the destroyed candidate. Hence, for the binary decision variables in (9), the set \(M_i\) is adapted, and we also use the adapted earliest and latest starting times \(ES_i^d\) and \(LS_i^d\) instead of the ones calculated by CPM. Thus, for fixed activities, only the decision variable corresponding to the mode and starting time from the current best solution candidate is added to the MIP. For free activities, however, we use all available modes but depending on varPerMode only a subset of the possible starting times. By design of the destroy operators, the total number of decision variables in the MIP is smaller than or equal to the parameter freeVar. Similarly, in the CP case, we setup the formulation presented in (11)–(19). Here, we restrict the earliest start and finish times of the interval decision variables in (18) and remove the mode interval variables displayed in (19) if they are not present in the destroyed candidate.
We use the parameter timePerIteration to limit the running time for solving the MP. This is done to save time that could be wasted by the exact solver by proving the optimality of a solution.
Since by definition of the destroy operators the current best solution candidate \(c^{b}\) is feasible for the constructed MIP or CP, we hand it to the solver for a warmstart. In this way, the MIP or CP solver obtains an upper bound immediately which speeds up the search process. The solution obtained by the solver for the subproblem can be an improvement of the current solution candidate. If the MIP or CP solver does not find an improving solution, this may be due to three reasons:
-
The current solution candidate is already optimal, but we do not know it since the lower bound information of the solver is only for a subproblem and not for the original problem.
-
The current solution candidate is locally optimal for the current neighbourhood defined by the destroyed candidate but a better solution candidate exists in a larger neighbourhood.
-
The solver was not able to find a better solution in the current neighbourhood because the iteration time limit timePerIteration was too small.
The latter two reasons are addressed by the adaptation step of the ALNS, where we increase the size of the neighbourhood and the iteration time limit.
5 Case study
5.1 Real-life projects data
To apply, test, and validate our algorithms, we used data of three nuclear dismantling projects of different sizes. Since worldwide only 17 nuclear facilities have been totally dismantled yet (see Sect. 1), data of three nuclear dismantling projects is a very good sample size. All data of these real-life projects were handed over by companies that are involved in the nuclear dismantling industry.
These real-life projects represent one small-sized project with about 50 activities and 37 renewable resources, one mid-sized project with about 85 activities and 37 renewable resources, and one large-scale project with about 300 activities and 22 renewable resources in Germany. The projects all feature activities with different modes and are described in detail at the end of this subsection after some general information about the uncertainty and the simulation of different scenarios were depicted.
Altogether, the project planning of these projects is subject to the planning requirements described in Sects. 1 and 3.1. Since uncertainty prevails in real-life projects, this has to be considered in project planning. Thus, for each project, we considered uncertainties in activity durations and uncertain sequences of activities to cover as many potential changes during project execution as possible.
Therefore, experts estimated potential activity durations, parameters of the activity duration distribution, activity modes, and potential sequences of activities. By varying activity durations and the sequence of activities, we simulated for each project 200 deterministic instances covering these potential changes. These 200 deterministic instances per project are divided into two sets of 100 instances each. One hundred instances are used as a training set for optimising the parameter setting of the heuristic (see Sect. 5.2.1) and a test set of 100 instances is used for assessing the quality of the algorithm (see Sect. 5.2.2 and Sect. 5.2.3).
The activity durations in real-life projects are either well known, e.g. for standard procedures, or not well known, e.g. when using new techniques or when an unknown intensity of contamination prevails. We modelled well-known activity durations with deterministic values and uncertain activity durations using a beta distribution. With the help of minimum, maximum, and most likely duration values, that are also estimated by experts, we derived the parameters of the beta distribution by combining the PERT formulas for the expected value and the variance with the formulas for the parameters \(\alpha \) and \(\beta \) of the beta distribution.
The sequence of activities in nuclear dismantling projects is most commonly deterministic. However, in some cases, it is uncertain which activities have to be executed, e.g. when it is uncertain whether or not radioactivity is found in some areas. To model the uncertainty of activity sequences, we distinguish between deterministic and stochastic decision points. At a deterministic decision point, all outgoing activities are executed with a probability of 1. However, at stochastic decision points, exactly one outgoing activity among several optional activities is carried out. For each of these optional activities, a probability of execution <1 is allocated where the sum of optional activities’ probabilities at one decision point must be 1. Consequently, in some cases, e.g. when contamination is found, different activities have to be executed as compared to when no contamination was found. Different activities can be executed in either only one or several modes. Furthermore, in some cases, decontamination activities have to be repeated several times to comply with the legal threshold. Because of these reasons, each project has a set of obligatory and a set of optional activities. Altogether, the number of activities and, consequently, the number of possible execution modes may be different in each deterministic instance.
In the following, we briefly describe the data of the instances of each project. The first project is dedicated to the dismantling of a pressurised water reactor (PWR), which is the core unit of a nuclear power plant. Considering every possible activity, it consists of 55 activities without dummy activities and 37 different resources. One of them is a non-renewable resource representing the activity costs and the others are renewable resources. The 200 simulated deterministic instances consist of 47 to 55 activities, 4 to 7 activities can be executed in different modes, 21 to 24 activities have successors without a no-wait condition, and 26 to 31 activities have successors with a no-wait condition.
The second project deals with the dismantling of a boiling water reactor (BWR) and the dismantling of the connected turbine hall. Initially, the project consists of 92 activities and 38 different resources Again, one of them is a non-renewable resource and the others are of the renewable type. After simulation, the 200 deterministic instances consist of 82 to 90 activities. Four to seven activities can be executed in different modes, 66 to 72 activities have successors without a no-wait condition, and 14 to 19 activities have successors with a no-wait condition.
The third project comprises the dismantling of a whole nuclear facility through to the so-called green field. This includes dismantling of the reactor and all its components in the reactor room, the cooling systems including the cooling tower, the turbines, the generator and all components in the turbine hall as well as all further components and building structures. In this sample, 305 activities may be executed and 23 resources can be used in this project. By varying the activity durations and the sequence of activities, 200 deterministic instances were created with 295 to 299 activities, whereof 33 to 37 activities may be executed in several modes, 204 to 206 activities have successors without a no-wait condition, and 100 to 102 activities have successors with a no-wait condition.
5.2 Computational experiments
In order to evaluate the proposed methods, we also implemented an adaption of a simulated annealing (SA) approach with reheating of Józefowska et al. (2001). This metaheuristic procedure was originally used to find solutions for the MRCPSP. To encode a solution, we used the same scheduling sequence and mode vector as in the MLS procedure presented above. However, in the SA metaheuristic the acceptance rule differs and it is possible to accept a worse solution with some probability. A starting solution for the SA was computed by applying the same priority rules that we use in the MLS.
Furthermore, we also adapted the genetic algorithm (GA) of Afshar et al. (2019) which was also proposed for the MRCPSP. To represent a solution, we used the same encoding as with the MLS and the SA procedure. The initial population was generated by applying each of the priority rules presented in Sect. 4.1 as well as random scheduling sequences. We utilised the one-point crossover in our GA implementation. However, the forward backward improvement (FBI, cf. Tormos and Lova (2001)) that is used as local improvement operator does not work in the NDPSP problem setting since the objective function of the NDPSP is not regular. Therefore, we adapted the local improvement procedure of the GA in such a way that the activities are still shifted to the back (front) but not necessarily to the latest (earliest) starting time. Instead, each activity is shifted to its best cost improving starting time. Especially for activities with a negative \(b_i\) value, this results in starting times that improve the overall objective value of a solution. Although this adapted FBI operator is time-consuming, it yielded better results than using the GA without this local improvement operator. Furthermore, we used a 2-tournament system to select the solutions for the next iteration of the GA as in Tormos and Lova (2001).
Before evaluating the proposed MLS and ALNS procedure in long-run experiments with 3 600 seconds of runtime (cf. Sect. 5.2.2), we performed experiments to calibrate the algorithm parameters. This was done to investigate which parameters have yielded the best solution quality. We measured the solution quality as the relative optimality gap. This is the relative deviation of the upper bound \(U\!B\) and a lower bound LB. As a lower bound, we used the term (20) introduced in Sect. 3.2, and as \(U\!B\) we used \(c^{b}\). Hence, the relative gap in percent computes as follows:
A software prototype of the proposed procedure was coded in C\(^\#\). We used IBM ILOG CPLEX 12.8 to solve the MIP and IBM ILOG CP Optimizer 12.8 to solve the CP in the recreate step. All experiments were performed on a PC with 16 GB of RAM and an Intel i7 6700 CPU running at 3.40 GHz.
5.2.1 Calibration of the algorithm parameters
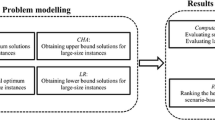
We calibrated the algorithm parameters on a training set consisting of 100 instances for each of the three project types. We used the irace software package of the statistical computing software R to tune the algorithm parameters (cf. López-Ibáñez et al. (2016)). This software package performs iterated racing which is an extension of the iterated F-racing algorithm proposed by Birattari et al. (2010). The parameters of the MLS and ALNS algorithm were calibrated in separate irace experiments. Furthermore, we distinguished between an ALNS using MIP methods (ALNSMIP) and one using CP methods (ALNSCP). For each calibration, we specified the maximum number of experiments, the time limit of a single experiment, and the possible values for each algorithm parameter. Here, it is especially important to balance the portion between total calibration time and gained precision of the estimated parameter values. Therefore, we limited the running time of the single experiments in order to speed up the calibration experiments to lower values than in the long-run experiments in Sect. 5.2.2. The comparison in Sect. 5.2.3 clearly shows that the proposed methodology outperforms a standard MIP solver. Longer calibration experiments would merely further improve the results of the MLS and ALNS.
Note that the MLS procedure always found an optimal solution with \(U\!B = LB\) for the sample PWR project instances after an average running time of 0.62 seconds in the initial experiments. Therefore, we omitted those instances from calibration experiments, but it is still important to see whether other methods can also find optimal solutions for these instances.
For the calibration of the MLS, we set the number of MLS runs to be at most 2 000 and tested different parameters \(p^M \in [0,0.2]\) and \(p^S \in [0,0.5]\) with a running time limit of \(T = 600\) seconds. Higher values for \(p^M\) are not suitable for the instances at hand since only approximately 10% of the activities can be performed in different modes. With \(p^S \le 0.5\), we limited the maximal perturbation of the current best scheduling sequence. The irace calibration run shows that \(p^M = 0.04\) and \(p^S = 0.19\) performs best on the training data. Hence, we use this parameter configuration in the following experiments.
Next, we investigated which parameter values are appropriate for the ALNS. Again, we used the irace software package with the following parameter choices:
-
initFreeVar \(\in [1\,000, 100\,000]\)
-
initVarPerMode \(\in [10,5\,000]\)
-
\(\alpha \in [1,1.5]\)
-
\(\beta \in [1, 1.5] \)
-
initTimePerIteration \(\in [0.1, 10]\)
-
\(P=\{p_1, p_2\}\) with \(p_1 \in [0,1]\), \(p_2 = 1-p_1\)
Here, \(p_1\) and \(p_2\) are the probabilities of selecting the destroy operators DTI and DPS, respectively. For each instance of the training set, we computed an initial solution by applying the MLS with the parameters calibrated above and a running time of 1 second. We set a fixed maximum running time of 600 seconds for each ALNS run in the calibration experiments and performed 2 000 ALNS runs for both the MIP and the CP version. Again, this was done to speed up the calibration process but we expect the calibrated parameters to be appropriate for longer running times of the ALNS as well. The irace experiment results are depicted in Table 2.
To our surprise, the CP-based version can cope with a higher count of decision variables than the MIP. This also results in a larger neighbourhood that is investigated in each iteration. Hence, we expect better results from ALNSCP. Since the parameter \(\texttt {initVarPerMode}\) is chosen rather large, a small value for its adoption rate \(\beta \) is efficient. The destroy operator DTI, which is focusing on specific time intervals in the current schedule, seems to be more efficient for the MIP version, and therefore, it is selected with a higher probability. For the CP version, it is the other way around and the DPS operator is chosen with a higher probability.
The calibration of the SA adaption of Józefowska et al. (2001) results in a cooling factor of 0.83 for the temperature. This factor is used to reduce the probability of choosing a deteriorating solution along the search. For a runtime limit of 600 seconds, the number of reheats is equal to 964. After a reheat, the temperature is reset to its initial value and we adjusted the number of reheats for longer running times accordingly. For the GA, the population size, i.e. the number of solutions generated in each iteration, is set to 262 and the mutation probability is equal to 0.2. This probability controls, how often a random alteration of a population member is performed after the crossover.
5.2.2 Main experiments
The calibration experiments revealed that for the small-sized instances we are able to find optimum solutions in a short time. For the larger instances at hand, however, the performance of the MLS and the ALNS varied depending on the parameter setting. Hence, we performed additional experiments with the best-performing parameter settings found in the previous section. We tested the MLS and the ALNS procedure on the 100 BWR and large project test instances that were not used during the calibration experiments. The running time of the search was increased to a total time of 3 600 seconds in order to investigate the long-term behaviour of the algorithm. In all experiments, we computed an initial solution using the priority rules and the PSGS. For the BWR instances, the minimum LST rule yields the best results for 97 instances and the minimum slack rule for the remaining 3 instances. The average relative gap of the BWR instances after using the priority rules is \(5.78\%\). The minimum LFT rule outperforms all other rules on all large instances with an average relative gap of \(3.88\%\). The average computation time for the priority rule solutions is 0.44 seconds.
To compare the MLS and the ALNS, we used different time allocations for the MLS and the ALNS part of the search. With \(\texttt {MLS}_{x}{} \texttt {ALNS}\), we denote a run where the MLS part of the search is allowed x seconds and the ALNS part uses the remaining time. Table 3 shows the average gap for the tested combinations as well as the SA and GA metaheuristics. We also included a run where we used only the MLS and one experiment where the constraint programming solver is used without the ALNS and no warmstart solution (CP). It is interesting to see that the application of the ALNS improves the results for the BWR instances only slightly. We suspect that those instances, much like the PWR instances, are in fact solved optimally but the lower bound used in our comparison is too weak for these instances. The standalone CP experiment compute an average relative gap of \(0.47\%\) for these instances, but cannot detect optimality. The ALNS approaches and the standalone CP find the same results and simulated annealing and the MLS perform slightly worse.
To our surprise, the standalone MLS outperforms the MIP-based ALNS versions on the large project instances. Shorter running time limits were not successful with ALNSMIP since setting up the time-indexed model required more than 60 seconds for most of the instances.
As expected, the CP-based ALNS performs very well and especially for the shorter run time limits of 60 and 600 seconds. However, for the 3 600 seconds time limit, the standalone CP run achieves slightly better results than ALNSCP. It is interesting to see that the MIP solver is not able to cope with the large project instances. Even setting up the MIP model can take several minutes. The CP solver, on the other hand, sets up the model in a matter of seconds and is even able to achieve high quality results without the ALNS framework. The average relative gap computed with the CP lower bound after one hour of computation is \(1.45\%\) for the large project instances. The SA and the GA metaheuristics are superior to the MLS on both the BWR and the large project instances except for a run time limit of 60 seconds where the MLS achieves slightly better results than the GA. Furthermore, the SA performs better than the GA. However, SA is outperformed by ALNSCP and the standalone constraint programming formulation. Compared to the solutions initially generated with the priority rules, the ALNSCP procedure was able to improve them by \(0.97\%\) for the large instances and by \(0.09\%\) for the BWR instances. On first glance, this may not sound like much, but the absolute improvement is on average \(4.5\cdot 10^6\) monetary units in the case of the large projects. Hence, utilising our proposed method can help save millions.
5.2.3 Evaluation against a MIP solver
To analyse the strength of the methodology presented in Sect. 4, we compare its scheduling results in terms of the objective function value, relative optimality gap, and computation time with the scheduling results using CPLEX solving the NDPSP formulation displayed in (1)–(9) with and without warmstart.
The NDPSP formulation is set up in IBM ILOG Optimization Studio 12.8.0 (CPLEX Studio IDE) and solved using CPLEX (version 12.8.0). For the warmstart, we use the best obtained schedule of the MLS step of the methodology with \(T = 60\), \(p^S=0.19\), and \(p^M=0.04\). Because of the high computational effort solving the NDPSP with CPLEX, all following experiments are performed on a PC with 64 GB of RAM and an Intel i7 4930 CPU running on 12 processors at 3.40 GHz each. For the methodology, we use the parameter settings obtained by the calibration experiments and a total time limit of 3 600 seconds with time allocations as in \(\texttt {MLS}_{1}{} \texttt {ALNSCP}\). For the evaluation, we use the three real-life projects presented in Sect. 5.1.
Table 4 shows the results of the evaluation of the methodology and CPLEX solving the NDPSP with and without warmstart for scenario 1 of each project. We only tested scenario 1 because, on the one hand, it is a representative example and on the other hand calculation with and without warmstart is very time-consuming. For the PWR project, each procedure calculates the same objective function value with a relative optimality gap of 0.00%. But, CPLEX with warmstart needs 163 times and CPLEX without warmstart 388 times longer than the proposed methodology. The complete mixed-integer linear programme has 23 362 decision variables and 37 942 constraints.
The calculation of the BWR project with CPLEX without warmstart crashed after 495 509 seconds. Since the relative optimality gap of 0.37% is already very small and since the computation time is very high compared to the methodology, we refrained from recalculating. For the same reasons we abandoned the calculation of CPLEX with warmstart after 253 753 seconds. This mixed-integer linear programme consists of 77 944 decision variables and 61 028 constraints. The methodology found the best objective function value after 8 seconds. But, since the lower bound is not adapted, only a relative optimality gap of 5.55% was calculated.
Due to the fact that CPLEX without warmstart did not find any schedule for the large project, we abandoned the calculation after 434 532 seconds. The complexity of the calculation becomes obvious by 951 185 decision variables and 98 053 constraints. We abandoned the calculation of CPLEX with warmstart after 83 569 seconds because of the calculated relative optimality gap of close to 0%. Our ALNSCP methodology, however, found an even better solution with a gap of \(2.80\%\) with respect to the simple lower bound. This solution is \(1.4\%\) better than the one found by CPLEX with a warmstart. ALNSCP found the best-known solution after 2 585 seconds.
Altogether, for small- and medium-sized projects the methodology needs less computation time and identifies schedules with the same or less total project costs than CPLEX with or without warmstart. Figures 4 and 5 illustrate the pathway of the calculated key indicators objective function value and relative optimality gap depending on the computation time. Note that the pathway of relative optimality gap for the methodology is not visible in both figures because of the short computation time and the overlying graph representing the objective function value of the methodology in Fig. 5. But since the lower bound is only very vague and is not adapted during the calculation by the methodology, the relative optimality gap can be higher than using CPLEX. This is for example the case for the methodology in Fig. 5. MLS starts with a relative optimality gap of 5.63% which is improved to 5.55%. Nevertheless, time savings by calculating schedules with minimum total project costs are the main advantage of the developed methodology. In particular, for large-scale projects feasible schedules cannot be identified with CPLEX without warmstart. Furthermore, with the proposed methodology feasible schedules with lower objective functions can be identified with less computation times than CPLEX with warmstart.
6 Conclusion
For scheduling and resource allocation, various different scheduling methods are described in the literature. However, for megaprojects special requirements have to be considered, such as expected long project durations, many activities with multiple modes, scarce resources, and investment decisions.
As shown in this paper, the dismantling of nuclear facilities is a growing sector of megaprojects with up to 200 projects until 2040. Consequently, nuclear dismantling projects were used as an application case in this paper to develop a planning method for these specific megaprojects. The findings can be transferred to other megaprojects.
Nuclear dismantling projects have specific characteristics, such as constrained renewable and non-renewable resources, precedence relations with and without no-wait condition, and a cost minimisation objective. An extensive literature review could neither reveal a problem formulation nor a scheduling method considering these characteristics. Hence, we introduced a novel project scheduling problem referred to as the nuclear dismantling project scheduling problem (NDPSP). It contains the desired features for the dismantling of nuclear facilities.
For this novel problem, we developed and implemented an effective algorithm that is able to obtain feasible solutions for projects with about 300 activities and considers the specific characteristics of a nuclear dismantling project. To consider uncertainties and to identify an ex ante stable schedule, the developed algorithm can be used for sensitivity analysis.
In this paper, we also tested and validated the developed algorithm with samples of real-life nuclear facility dismantling projects.
One main result is the development of an initial solution finding procedure and an adaptive large neighbourhood search with iterative destroy and recreate operations that enable project scheduling that was not possible before due to computational limitations of existing algorithms. The adapted parallel schedule generation scheme was able to find feasible solutions very fast, and the proposed combination of multi-start local search and adaptive large neighbourhood search improved them effectively. On average, it took 0.44 seconds to find an initial feasible solution for our test samples with about 300 project activities, and this could be further improved by 0.97% from the initial solution within 3 600 seconds.
Nevertheless, some extensions in future work are possible. To minimise the total project costs, we consider procurement, direct and variable, and post-operational costs. But, we do not consider funding, depreciation, inflation, or exchange rates although this could significantly influence total project costs. The consideration of these constraints is complex because of changing interest rates during such large-scale projects. Furthermore, various individual project conditions, such as funding or contracts with foreign companies, have to be considered. As a further development, post-operational costs could be modelled in more detail. In our algorithms, we assume that the post-operational costs are zero at the end of the project. If we want to consider any possible amount of post-operational costs at the end of a project, the algorithms have to be adapted. Additionally, we only consider finish-to-start precedence relations. By implementing generalised precedence relations, any precedence relation can be implemented. A further development could also consider time-dependent descending capacities of renewable resources. In nuclear dismantling projects, own staff of the nuclear facilities’ operational stage is usually entrusted with the deconstruction project. During project execution, own staff is retiring step by step due to the high average age of staff in nuclear facilities, and new staff is not hired by facility operators. Consequently, the number of own staff decreases during project execution and may lead to external staff hiring, expertise bottlenecks, or project prolongation and thus may affect project scheduling and project cost. Because of the high complexity and thus high computational effort, we skipped these constraints in this paper to be able to calculate a feasible schedule in reasonable time.
As already mentioned, many uncertainties prevail during project execution, and especially in nuclear dismantling projects, because of very little experience, long project durations, and hardly calculable risks. Thus, uncertainties could be integrated or considered in project planning in the future by efficient proactive scheduling methods or concepts. In particular, the comparison of optimised scenarios regarding their robustness while performing sensitivity analysis could be further investigated.
Due to the increasing number of nuclear dismantling projects expected in the coming decades worldwide, the development and further improvement of project scheduling methods are essential for efficient project time and resource management. The developed methods enable planners to quickly calculate and compare initial and alternative project schedules and total project costs for different project risks/uncertainties and scenarios. Moreover, the approach cannot only be applied to nuclear dismantling projects but can also easily be transferred to other projects involving long project durations, many activities with multiple modes, constrained renewable and non-renewable resources, precedence relations with and without no-wait condition, and a cost minimisation objective, such as construction, infrastructure and power plant projects, urban development, and restructuring projects.
References
Afshar, M. R., Shahhosseini, V., & Sebt, M. H. (2019). A genetic algorithm with a new local search method for solving the multimode resource-constrained project scheduling problem. International Journal of Construction Management, pp. 1–9
Alba, E., & Chicano, J. F. (2007). Software project management with GAs. Information Sciences, 177(11), 2380–2401.
Bartels, J. -H. (2009). Anwendung von Methoden der ressourcenbeschränkten Projektplanung mit multiplen Ausführungsmodi in der betriebswirtschaftlichen Praxis: Rückbauplanung für Kernkraftwerke und Versuchsträgerplanung in Automobilentwicklungsprojekten (Application of methods of resource-constrained project scheduling with multiple execution modes in the business-management practice: Dismantling planning for nuclear power plants and experimental vehicle planning in automotive development projects). Gabler Edition Wissenschaft : Produktion und Logistik. Gabler, Wiesbaden.
Birattari, M., Yuan, Z., Balaprakash, P., & Stützle, T. (2010). F-race and iterated f-race: An overview. In T. Bartz-Beielstein, M. Chiarandini, L. Paquete, & M. Preuss (Eds.), Experimental Methods for the Analysis of Optimization Algorithms (pp. 311–336). Berlin: Springer. 978-3-642-02537-2.
Brusa, L., DeSantis, R., Nurden, P. L., Walkden, P., Watson, B. (2002). The decommissioning of the trino nuclear power plant, URL https://www.osti.gov/servlets/purl/829556-bgfnku/native/. Waste Management 2002 Symposium, Tucson, AZ (US), 02/24/2002–02/28/2002.
Christodoulou, S. E., Michaelidou-Kamenou, A., & Ellinas, G. (2015). Heuristic methods for resource leveling problems. In C. Schwindt & J. Zimmermann (Eds.), Handbook on project management and scheduling (Vol. 1, pp. 389–407). Cham: Springer.
De Reyck, B., & Herroelen, W. (1998). A branch-and-bound procedure for the resource-constrained project scheduling problem with generalized precedence relations. European Journal of Operational Research, 111(1), 152–174. https://doi.org/10.1016/S0377-2217(97)00305-6.
European Commission. (2016a). Nuclear illustrative programme: presented under article 40 of the euratom treaty for the opinion of the european economic and social committee, Retrieved November 19, 2018 URL https://ec.europa.eu/transparency/regdoc/rep/1/2016/EN/1-2016-177-EN-F1-1.PDF.
European Commission. (2016b), Nuclear Illustrative Programme presented under Article 40 of the Euratom Treaty for the opinion of the European Economic and Social Committee: Accompanying the document, Retrieved November 19, 2018 URL https://ec.europa.eu/energy/sites/ener/files/documents/1_EN_autre_document_travail_service_part1_v10.pdf.
Flyvbjerg, B. (2014). What you should know about megaprojects and why: An overview. Project Management Journal, 45(2), 6–19. https://doi.org/10.1002/pmj.21409.
Geiger, M. J. (2017). A multi-threaded local search algorithm and computer implementation for the multi-mode, resource-constrained multi-project scheduling problem. European Journal of Operational Research, 256(3), 729–741. https://doi.org/10.1016/j.ejor.2016.07.024.
Gerhards, P., Stürck, C., & Fink, A. (2017). An adaptive large neighborhood search as a matheuristic for the multi-mode resource-constrained project scheduling problem. European Journal of Industrial Engineering, 11(6), 774–791. https://doi.org/10.1504/EJIE.2017.10006713.
Herroelen, W., & Leus, R. (2005). Project scheduling under uncertainty: Survey and research potentials. European Journal of Operational Research, 165(2), 289–306. https://doi.org/10.1016/j.ejor.2004.04.002.
Hsu, C.-C., & Kim, D. S. (2005). A new heuristic for the multi-mode resource investment problem. Journal of the Operational Research Society, 56(4), 406–413. https://doi.org/10.1057/palgrave.jors.2601827.
IEA (2014). World Energy Outlook 2014. International Energy Agency, Paris, ISBN 978-92-64-20805-6.
Iguchi, Y., Kanehira, Y., Tachibana, M., & Johnsen, T. (2004). Development of Decommissioning Engineering Support System (DEXUS) of the Fugen Nuclear Power Station. Journal of Nuclear Science and Technology, 41(3), 367–375. https://doi.org/10.1080/18811248.2004.9715497.
Józefowska, J., Mika, M., Różycki, R., Waligóra, G., & Weglarz, J. (2001). Simulated annealing for multi-mode resource-constrained project scheduling. Annals of Operations Research, 102(1–4), 137–155.
Kelley, J. E. (1963). The critical-path method: Resources planning and scheduling. Industrial Scheduling, 13(1), 347–365.
Klasen, J., & Seizer, B. (2015). Managing complexity of nuclear decommissioning & dismantling projects—an advanced project-management approach, ICOND conference, 18.11.2015, Bonn.
Kolisch, R. (1996). Efficient priority rules for the resource-constrained project scheduling problem. Journal of Operations Management, 14(3), 179–192.
Kreter, S., Schutt, A., Stuckey, P. J., & Zimmermann, J. (2018). Mixed-integer linear programming and constraint programming formulations for solving resource availability cost problems. European Journal of Operational Research, 266(2), 472–486. https://doi.org/10.1016/j.ejor.2017.10.014.
Laborie, P., Rogerie, J., Shaw, P., & Vilím, P. (2018). IBM ILOG CP optimizer for scheduling. Constraints, 23(2), 210–250.
López-Ibáñez, M., Dubois-Lacoste, J., Cáceres, L. P., Birattari, M., & Stützle, T. (2016). The irace package: Iterated racing for automatic algorithm configuration. Operations Research Perspectives, 3, 43–58.
Martí, R., Resende, M. G., & Ribeiro, C. C. (2013). Multi-start methods for combinatorial optimization. European Journal of Operational Research, 226(1), 1–8. https://doi.org/10.1016/j.ejor.2012.10.012.
Mika, M., Waligóra, G., & Weglarz, J. (2015). Overview and state of the art. In C. Schwindt & J. Zimmermann (Eds.), Handbook on Project Management and Scheduling (Vol. 1, pp. 445–490). Cham: Springer.
Möhring, R. H. (1984). Minimizing costs of resource requirements in project networks subject to a fixed completion time. Operations Research, 32(1), 89–120. https://doi.org/10.1287/opre.32.1.89.
Muller, L. F. (2011). An adaptive large neighborhood search algorithm for the multi-mode RCPSP. Technical report, Report 3.2011, Department of Management Engineering, Technical University of Denmark,
NEA. (2016). Costs of decommissioning nuclear power plants. Paris: OECD Publishing.
Neumann, K., Schwindt, C., & Zimmermann, J. (2003). Project scheduling with time windows and scarce resources: Temporal and resource-constrained project scheduling with regular and nonregular objective functions. Berlin: Springer.
Rieck, J., & Zimmermann, J. (2015). Exact methods for resource leveling problems. In C. Schwindt & J. Zimmermann (Eds.), Handbook on project management and scheduling (Vol. 1, pp. 361–387). Cham: Springer.
Rodrigues, S. B., & Yamashita, D. S. (2015). Exact methods for the resource availability cost problem. In C. Schwindt & J. Zimmermann (Eds.), Handbook on project management and scheduling (Vol. 1, pp. 319–338). Cham: Springer.
Ropke, S., & Pisinger, D. (2006). An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transportation Science, 40(4), 455–472. https://doi.org/10.1287/trsc.1050.0135.
Schnell, A., & Hartl, R. F. (2016). On the efficient modeling and solution of the multi-mode resource-constrained project scheduling problem with generalized precedence relations. OR Spectrum, 38(2), 283–303. https://doi.org/10.1007/s00291-015-0419-6.
Schnell, A., & Hartl, R. F. (2017). On the generalization of constraint programming and boolean satisfiability solving techniques to schedule a resource-constrained project consisting of multi-mode jobs. Operations Research Perspectives, 4(1), 1–11. https://doi.org/10.1016/j.orp.2017.01.002.
Shadrokh, S., & Kianfar, F. (2007). A genetic algorithm for resource investment project scheduling problem, tardiness permitted with penalty. European Journal of Operational Research, 181(1), 86–101. https://doi.org/10.1016/j.ejor.2006.03.056.
Shaw, P. (1997). A new local search algorithm providing high quality solutions to vehicle routing problems. Glasgow, Scotland: APES Group: Department of Computer Science, University of Strathclyde Glasgow, Scotland, UK.
Talbot, F. B. (1982). Resource-constrained project scheduling with time-resource tradeoffs: The nonpreemptive case. Management Science, 28(10), 1197–1210. https://doi.org/10.1287/mnsc.28.10.1197.
Tarjan, R. (1972). Depth-first search and linear graph algorithms. SIAM Journal on Computing, 1(2), 146–160.
Tormos, P., & Lova, A. (2001). A competitive heuristic solution technique for resource-constrained project scheduling. Annals of Operations Research, 102(1–4), 65–81.
van Peteghem, V., & Vanhoucke, M. (2014). An experimental investigation of metaheuristics for the multi-mode resource-constrained project scheduling problem on new dataset instances. European Journal of Operational Research, 235(1), 62–72. https://doi.org/10.1016/j.ejor.2013.10.012.
van Peteghem, V., & Vanhoucke, M. (2015). Heuristic methods for the resource availability cost problem. In J. Zimmermann & C. Schwindt (Eds.), Handbook on project management and scheduling (Vol. 1, pp. 339–359). Cham: Springer. ISBN 978-3-319-05443-8.
Vega-Velázquez, M. Á., García-Nájera, A., & Cervantes, H. (2018). A survey on the software project scheduling problem. International Journal of Production Economics, 202, 145–161.
Volk, R., Hübner, F., Hünlich, T., & Schultmann, F. (2019). The future of nuclear decommissioning—a worldwide market potential study. Energy Policy, 124, 226–261. https://doi.org/10.1016/j.enpol.2018.08.014.
WNA. (2017) Decommissioning nuclear facilities, Retrieved November 19, 2018. URL http://world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-wastes/decommissioning-nuclear-facilities.aspx.
Yanagihara, S., Sukegawa, T., & Shiraishi, K. (2012). Development of computer systems for planning and management of reactor decommissioning. Journal of Nuclear Science and Technology, 38(3), 193–202. https://doi.org/10.1080/18811248.2001.9715021.
Zhu, X., Ruiz, R., Li, S., & Li, X. (2017). An effective heuristic for project scheduling with resource availability cost. European Journal of Operational Research, 257(3), 746–762. https://doi.org/10.1016/j.ejor.2016.08.049.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hübner, F., Gerhards, P., Stürck, C. et al. Solving the nuclear dismantling project scheduling problem by combining mixed-integer and constraint programming techniques and metaheuristics. J Sched 24, 269–290 (2021). https://doi.org/10.1007/s10951-021-00682-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-021-00682-x