Abstract
In this paper, we describe new complexity results and approximation algorithms for single-machine scheduling problems with non-renewable resource constraints and the total weighted completion time objective. This problem is hardly studied in the literature. Beyond some complexity results, only a fully polynomial-time approximation scheme (FPTAS) is known for a special case. In this paper, we discuss some polynomially solvable special cases and also show that under very strong assumptions, such as the processing time, the resource consumption and the weight is the same for each job; minimizing the total weighted completion time is still NP-hard. In addition, we also propose a 2-approximation algorithm for this variant and a polynomial-time approximation scheme (PTAS) for the case when the processing time equals the weight for each job, while the resource consumptions are arbitrary.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Non-renewable resources, such as raw material, energy or money, are used in all sectors of production, and depending on the stocking policy, they have varying impact on the preparation of daily and weekly production schedules. Consider for instance the preparation of the weekly schedule of a production line, where some of the raw materials built into the products arrive over the week, and the supplies constrain what can be produced and when. Of course, if all the purchased items were in stock right at the beginning of the week, then the supply arriving during the week would not influence the scheduling decisions, but the drawback is that larger stocks should be kept, which incurs additional costs.
In this paper, we consider single-machine scheduling problems with one additional non-renewable resource. The non-renewable resource has an initial stock and some additional supplies in the future with known supply dates and quantities. A job can only be started if the inventory level of the resource is at least as much as the quantity required by the job. When the job is started, the inventory level is decreased by the required quantity. Therefore, when determining the schedule, one must take into account not only the initial stock level, but also the future supplies. This is an extra constraint in addition to, e.g., job release dates, or sequence-dependent setup times.
More formally, in all problems studied in this paper, there are a single machine, a non-renewable resource, and a finite set of jobs \(\mathcal {J}\). Each job \(j \in \mathcal {J}\) has a processing time \(p_j > 0\), a weight \(w_j \ge 0\), and a resource requirement \(a_j\ge 0\). The resource has an initial supply \(\tilde{b}_1\) available at time \(u_1 = 0\), and additional supplies \(\tilde{b}_\ell \) at supply dates \(u_\ell \) for \(\ell =2,\ldots ,q\). For convenience, we also define \(u_{q+1} = +\infty \). We assume that the supplies are indexed in increasing \(u_\ell \) order, i.e., \(u_\ell < u_{\ell +1}\) for \(\ell =1,\ldots ,q-1\). Let S be a schedule specifying a start time \(S_{j}\) for each job j. It is feasible if (i) the jobs do not overlap in time, and (ii) for each \(\ell =1,\ldots , q\), \(\sum \nolimits _{j : S_j < u_{\ell +1}} a_j \le \sum \nolimits _{\ell '=1}^\ell \tilde{b}_{\ell '}\), i.e., the supply arriving up to \(u_\ell \) covers the demands of those jobs starting before \(u_{\ell +1}\). The objective function is the weighted sum of job completion times, i.e., a feasible schedule of minimum \(\sum \nolimits _{j \in \mathcal {J}} w_{j} C_{j}\) value is sought, where \(C_{j} = S_{j} + p_{j}\). We mention that a feasible schedule exists only if \(\sum \nolimits _{j \in \mathcal {J}} a_{j} \le \sum \nolimits _{\ell =1}^q \tilde{b}_{\ell }\), and more resources are not needed. In fact, without loss of generality we may assume that
-
(i)
\(\sum \nolimits _{j \in \mathcal {J}} a_j = \sum \nolimits _{\ell =1}^q \tilde{b}_\ell \), and
-
(ii)
\(\tilde{b}_q > 0\), i.e., at least one job must start not before \(u_q\).
In the standard \(\alpha |\beta |\gamma \) notation of Graham et al. (1979), we will indicate in the \(\beta \) field by \(nr=1\) that the number of non-renewable resources is 1. In addition, we will constrain the number of supply dates to a constant by \(q=const\). We will use a number of other constraints, which are standard in the scheduling literature.
In this paper, we establish new complexity and approximability results for special cases of \(1|nr=1|\sum w_j C_j\). The special cases are obtained by imposing constraints on the parameters of the jobs. For instance, the constraint \(w_j = p_j\) means that for each job j, its weight equals its processing time, while \(w_j=\lambda p_j\) indicates that \(w_j\) is proportional to \(p_j\), \(\lambda > 0\) which is a common ratio. Furthermore, \(p_j = 1\) or \(p_j = {\bar{p}}\) restricts the processing time of each job to 1 or to some other common constant value \({\bar{p}}\). The new results are summarized in Table 1. As we can see, three special cases can be solved in polynomial time by list scheduling; we identify three new NP-hard variants and propose approximation algorithms in two cases. We emphasize that the 2-approximation algorithm is merely list scheduling using the LPT order, but the analysis of the algorithm is tricky. On the other hand, the polynomial time approximation scheme for \(1|nr=1, w_j = p_j, q=const.| \sum p_j C_j\) is rather involved, and the underlying analysis needs new ideas, which may be used in the analysis of other problems as well.
In Sect. 2, we overview the related literature. In Sect. 3, we generalize list scheduling to our problem and discuss special cases that can be solved optimally with this method. In Sect. 4, we establish the NP-hardness of \(1|nr=1, p_j=1, a_j = w_j | \sum w_j C_j\). In Sect. 5, we present complexity results and a 2-approximation algorithm for the special case with \(p_j = a_j = w_j\). Finally, in Sect. 6 we devise a PTAS for \(1|nr=1,p_j = w_j, q=const.| \sum w_j C_j\).
2 Literature review
Machine scheduling problems with non-renewable resources have been introduced by Carlier (1984) and Slowinski (1984). In Carlier (1984), the computational complexity of several variants with a single machine is established. In particular, it is shown that \(1|nr=1|\sum w_j C_j\) is NP-hard in the strong sense, which is also proved in Gafarov et al. (2011). However, the problem remains NP-hard in the weak sense if \(q=2\) (two supplies), see Kis (2015). In Kis (2015), an FPTAS is devised for the special case \(1|nr=1,q=2|\sum w_j C_j\). Moreover, Gafarov et al. (2011) study a variant of this problem, where each job has processing time 1, and there are n supplies such that \(u_\ell = \ell M\), and \(\tilde{b}_\ell = M\) for \(\ell =1,\ldots ,n\), where \(M = \sum _{j \in \mathcal {J}} a_j / n\) is an integer number, and \(n = |\mathcal {J}|\). Without the non-renewable resource constraint, the problem \(1||\sum w_j C_j\) can be solved optimally in polynomial time by scheduling the jobs in non-increasing \(w_j /p_j\) order, a classical result of Smith (1956).
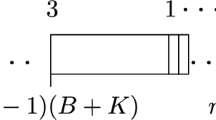
The case \(C^*_{j_1}<S^*_{j_2}\) of Theorem 1 (c). The schedule \(S^*\) is depicted in part (a), where the dashed line indicates two options for the length of \(j_2\). The form of the schedule \(S'\) if \(C'_{j_2}\ge u_\ell \) and if \(C'_{j_2}< u_\ell \) is depicted in part (b) and (c), respectively
There are several results about the complexity and approximability of machine scheduling problems with non-renewable resources and the makespan and the maximum lateness objective, see e.g., Slowinski (1984), Toker et al. (1991), Xie (1997), Grigoriev et al. (2005), Györgyi and Kis (2014, 2015a, b) and Györgyi (2017). For an overview, see Györgyi and Kis (2017). In particular, Slowinski (1984) considers a parallel machine problem with preemptive jobs, and with a single non-renewable resource, which has an initial stock and some additional supplies. It is assumed that the rate of consuming the non-renewable resource is constant during the execution of the jobs. These assumptions led to a polynomial time algorithm for minimizing the makespan. Toker et al. (1991) prove that the single-machine scheduling problem with a single non-renewable resource and the makespan objective reduces to the 2-machine flow shop problem provided that the single non-renewable resource has a unit supply in every time period. In Grigoriev et al. (2005), 2-approximation algorithms are devised for the makespan and the maximum lateness objective (under some additional conditions). In a series of papers Györgyi and Kis (2014, 2015a, b, 2017) and Györgyi (2017), Györgyi and Kis present approximation schemes and inapproximability results for various special cases of single and parallel machine problems with the makespan and the maximum lateness objectives. In Györgyi and Kis (2018), a branch-and-cut algorithm for minimizing the maximum lateness is devised and evaluated.
3 List scheduling
In this section, we discuss polynomially solvable special cases of \(1|nr=1|\sum w_j C_j\). All the algorithms presented below are based on the following extension of the well-known list scheduling method:
-
1.
Sort the jobs according to some total ordering relation. Let \(L=(j_1,\ldots ,j_n)\) be the sequence obtained. Let \(t := 0\), \(\ell := 1\), and \(r := \tilde{b}_1\).
-
2.
For \(i=1\) to n do
-
3.
While \(a_{j_i} > r\) repeat let \(\ell := \ell +1\), \(t := \max \{t,u_\ell \}\), and \(r := r+ \tilde{b}_\ell \). End-while.
-
4.
Schedule \(j_i\) at time t. That is, set \(S_{j_i} := t\), and then \(t := t + p_{j_i}\), \(r:= r-a_{j_i}\).
-
5.
End-for
-
6.
Output S.
In the above algorithm, t represents the time when the next job may be scheduled, and r the resource level before scheduling it. In Step 3, t and r are reset if the resource available after scheduling the previous jobs is not enough to schedule \(j_i\). Notice that in such a case, the supply of more than one period may be needed to increase the available quantity of the resource sufficiently.
The above simple algorithm is a generalization of the well-known algorithm that schedules the jobs in some given order without interruptions.
Theorem 1
All of the following special cases can be solved optimally by list scheduling:
-
(a)
Scheduling the jobs in non-increasing \(w_j\) order is optimal for \(1|nr=1,p_j={\bar{p}}, a_j={\bar{a}}|\sum w_j C_j\).
-
(b)
Scheduling the jobs in non-decreasing \(a_j\) order is optimal for \(1|nr=1,p_j={\bar{p}}, w_j={\bar{w}}|\sum w_j C_j\).
-
(c)
For any \(\lambda > 0\), the LPTFootnote 1 schedule is optimal for \(1|nr=1,a_j={\bar{a}}\), \(w_j = \lambda p_j |\sum w_j C_j\).
Proof
The proof of optimality is left to the reader, except in the last case, that we can verify as follows. Consider any instance of \(1|nr=1,a_j={\bar{a}}\), \(w_j = \lambda p_j |\sum w_j C_j\), and let \(S^*\) be an optimal schedule in which the number of job pairs violating the LPT order is the smallest. Define \(C^*_j := S^*_j + p_j\) for each job j. Suppose that there are at least two jobs that are not in LPT order. Consider the first two such consecutive jobs, say \(j_1\) and \(j_2\), where \(j_1\) is scheduled before \(j_2\), and \(p_{j_1}+K=p_{j_2}\) for some \(K>0\). Let \(S'\) be the schedule where we swap the order of \(j_1\) and \(j_2\). We distinguish two cases.
If \(C^*_{j_1}=S^*_{j_2}\), then \(S'_{j_1} = S^*_{j_1} + p_{j_2}\), \(S'_{j_2} = S^*_{j_1}\), and \(S'_j = S^*_j\) for all \(j \notin \{j_1,j_2\}\). It is easy to verify that \(w_{j_1}(S^*_{j_1}+p_{j_1}) + w_{j_2}(S^*_{j_2} + p_{j_2}) = w_{j_2}(S'_{j_2}+p_{j_2}) + w_{j_1}(S'_{j_1} + p_{j_1})\), and the objective function does not change. Since \(S'\) is feasible, as each job has the same resource requirement, we reached a contradiction with the choice of \(S^*\).
Now suppose \(C^*_{j_1}<S^*_{j_2}\). Hence, there is an \(\ell \) such that \(S^*_{j_2}=u_\ell \). Note that we have \(S'_{j_2}=S^*_{j_1}\), \(S'_{j_1}=\max \{C'_{j_2},u_\ell \}\). Further on we have \(S'_j=S^*_{j}\) for each job j with \(S^*_j<S^*_{j_1}\), and \(S'_j\le S^*_j\) for each job j with \(S^*_j\ge S^*_{j_2}\), see Fig. 1. Notice that only the start time of job \(j_1\) increases after swapping job \(j_1\) and job \(j_2\). To reach a contradiction with the choice of \(S^*\), it is enough to prove that \(w_{j_1}C^*_{j_1}+w_{j_2}C^*_{j_2} \ge w_{j_1} C'_{j_1} +w_{j_2} C'_{j_2}\). Suppose that we have \(u_\ell =S^*_{j_1}+p_{j_1}+L\) where \(L>0\). We have
and
Thus, \(w_{j_1}C^*_{j_1}+w_{j_2}C^*_{j_2}-(w_{j_1}C'_{j_1}+w_{j_2}C'_{j_2})=\lambda (p_{j_1}S^*_{j_1}+(p_{j_1}+K)\cdot (p_{j_1}+L)- p_{j_1}\max \{C'_{j_2},u_\ell \})\). Since \(\max \{C'_{j_2},u_\ell \}=\max \{S^*_{j_1}+p_{j_1}+K,S^*_{j_1}+p_{j_1}+L\}\), thus \(w_{j_1}C^*_{j_1}+w_{j_2}C^*_{j_2} > w_{j_1}C'_{j_1}+w_{j_2}C'_{j_2}\) follows. \(\square \)
4 Problem \(1|nr=1,p_j=1\), \({w_j=\lambda a_j}|\sum w_j C_j\)
Theorem 2
For any \(\lambda > 0\), the problem \(1|nr=1,p_j=1, {w_j = \lambda a_j} | \sum w_j C_j\) is weakly NP-hard even for \(q=2\).
Proof
We reduce the NP-hard PARTITION problem to our scheduling problem. An instance of the former problem is given by a natural number n, and the sizes of n items, \(s_1,\ldots , s_n\), which are nonnegative integer numbers. One has to decide whether the items can be partitioned into two subsets, \(Q_1\) and \(Q_2\), such that \(\sum _{i \in Q_1} s_i = \sum _{i\in Q_2} s_i\). Since all item sizes are integer numbers, the answer is “NO”, unless \(\sum _{i=1}^n s_i =2A\) for some integer A. Therefore, we assume that \(\sum _{i=1}^n s_i\) is an even integer, and let \(A := \sum _{i=1}^n s_i/2\). Let I be an instance of PARTITION, the corresponding instance \(I'\) of \(1|nr=1,p_j=1, {w_j = \lambda a_j} | \sum w_j C_j\) consists of n jobs, and for each item j, the corresponding job has a processing time \(p_j = 1\), \(a_j := s_j\) and \(w_j := \lambda s_j\), where \(\lambda > 0\) is fixed arbitrarily. In addition, there is a single resource with an initial stock of \(\tilde{b}_1 := A\), available at time \(u_1 := 0\), and with one more supply \(\tilde{b}_2 := A\) at time \(u_2 := n^2 A^2\).
We claim that I has a “YES” answer if and only if \(I'\) has a feasible schedule of objective function value at most \(\lambda (n^2 A^3 + 2nA)\). First suppose that I has a partitioning of the items \(Q_1, Q_2\) of equal size. Schedule the jobs corresponding to the items in \(Q_1\) from time 0 on consecutively in decreasing \(w_j\) order, and those in \(Q_2\) from \(u_2\) consecutively in decreasing \(w_j\) order. This schedule is clearly feasible. Suppose \(Q_1 = \{j_1,\ldots ,j_k\}\), and \(w_{j_i} \ge w_{j_{i+1}}\) for \(i=1,\ldots , k-1\), and \(Q_2 = \{j_{k+1},\ldots ,j_n\}\), and \(w_{j_i} \ge w_{j_{i+1}}\) for \(i=k+1,\ldots , n-1\). Then, we compute
Conversely, suppose the scheduling problem admits a feasible schedule S of objective function value at most \(\lambda (n^2 A^3 + 2nA)\). Let \(C_j := S_j+1\) for each job j. Let \(Q_1 = \{ j \ |\ S_j < u_2\}\) and \(Q_2 = \{ j\ |\ S_j \ge u_2\}\). Since S is feasible, the total resource consumption of those jobs in \(Q_1\) is at most A. Indirectly, suppose it is less than A. Then, the total weight of those jobs in \(Q_2\) is at least \({\lambda }(A+1)\). But then we have
which is a contradiction.
Finally, notice that the transformation is of polynomial time complexity, which shows that there is a polynomial reduction from PARTITION to a decision version of the scheduling problem \(1|nr=1,p_j=1, {w_j = \lambda a_j} | \sum w_j C_j\). \(\square \)
5 Problem \(1|nr=1,p_j=a_j=w_j|\sum w_j C_j\)
We start this section by providing a non-trivial expression for the objective function value of an optimal schedule under the condition \(p_j = w_j\) for every job j.
Let S be any feasible schedule for the problem, and let \(C_j = S_j + p_j\) be the completion time of job j in S. Let \(H_\ell \) denote the length of the idle period, if any, in schedule S in the interval \([u_{\ell },u_{\ell +1}]\) and let \(G_\ell =\sum _{\nu =1}^{\ell }H_\nu \) be the total idle time until \(u_{\ell +1}\). Let \(P_\ell \) denote the total working time (when the machine is not idle) in \([u_{\ell },u_{\ell +1}]\), noting that \(u_\ell =\sum _{\nu =1}^{\ell -1} P_\nu +G_{\ell -1}\). See Fig. 2a for an illustration. Using the new notation, we can express the objective function value of S as follows:
a The new notations (\(G_\ell \), \(H_\ell \) and \(P_\ell \)); b Proof of Lemma 1
Lemma 1
If \(p_j = w_j\) for each job j, then the objective function value of any feasible schedule S can be expressed as
Proof
Consider any working period \(B=[u_\ell , t]\) in the schedule S, that is, the machine is idle right before \(u_\ell \) and right after t, and is working contiguously throughout B. Suppose \(t \in (u_{\ell '}, u_{\ell '+1}]\), where \(\ell ' \ge \ell \). Let k be an arbitrary job that is processed in B, see Fig. 2b. We have \(C_k=\sum _{C_j\le C_k}p_j+G_{\ell -1}\); thus, the total weighted completion time of the jobs processed in B is
where the first equation follows from \(\sum _{k : C_k \in B} p_k = \sum _{\nu =\ell }^{\ell '} P_\mu \), and the second from \(G_\nu = G_{\ell -1}\) for each \(\ell \le \mu < \ell '\), since the machine is not idle in the interval B. Since the schedule can be partitioned into working and idle periods, we derive
Finally, the second equation of the statement of the lemma can be derived by using the definition of \(G_\ell \) and by rearranging terms. \(\square \)
Theorem 3
The problem \(1|nr=1, q=2, p_j=a_j=w_j|\sum w_jC_j\) is weakly NP-hard, and \(1|nr=1, p_j=a_j=w_j|\sum w_jC_j\) is strongly NP-hard.
Proof
Recall the definition of the PARTITION problem from the proof of Theorem 2. For proving the weak NP-hardness of \(1|nr=1, q=2, p_j=a_j=w_j|\sum w_jC_j\), we reduce the PARTITION problem to this scheduling problem. For any instance of PARTITION, the corresponding instance of \(1|nr=1, q=2, p_j=a_j=w_j|\sum w_jC_j\) consists of n jobs, one job for each item, and \(p_i = a_i = w_i = s_i\) for each item \(i = 1,\ldots ,n\). There are two supplies, one at \(u_1 = 0\) and the supplied quantity from the single resource is A, and another at \(u_2 = A\) with supplied quantity A. We claim that the PARTITION problem instance has a solution if and only if the corresponding scheduling problem instance has a feasible solution of value at most \(\sum _{j\le k} p_j p_k\). Using Lemma 1, the latter holds if and only if the schedule has no idle time. So, it suffices to prove that the PARTITION problem instance has a solution if and only if the corresponding scheduling problem instance admits a feasible schedule without any idle time. First suppose that the PARTITION problem instance has a “yes” answer, i.e., there is a subset Q of items with \(\sum _{i\in Q} s_i = A\). Schedule the corresponding jobs contiguously in any order in the interval [0, A]. Since \(p_j = a_j\), and the supply at \(u_1 = 0\) is A, this is feasible. Now, schedule the remaining jobs without idle times from \(u_2 = A\). The result is a feasible schedule without idle times. Conversely, suppose there is a feasible schedule without idle times. Then, the machine is working throughout the interval [0, A]. Since the supply at \(u_1 = 0\) is A, the total processing time of the jobs starting before \(u_2 = A\) is A. Let the set Q consist of the items corresponding to these jobs. This yields a feasible solution for the PARTITION problem instance.
For proving the strong NP-hardness of \(1|nr=1, p_j=a_j=w_j|\sum w_jC_j\), we reduce the 3-PARTITION problem to this scheduling problem. Recall that an instance of 3-PARTITION consists of an positive integer t, and 3t items, each having a size \(s_i\), \(i \in \{1,\ldots ,3t\}\), where the item sizes are bounded by polynomial in the input length. It is assumed that \(\sum _{i=1}^{3t} s_i\) is divisible by t, and \(B/4< s_i < B/2\) for each i, where \(B = \sum _{i=1}^{3t} s_i / t\). The question is whether the set of items can be partitioned into t groups \(Q_1,\ldots , Q_t\) such that \(\sum _{i\in Q_\ell } s_i = B\) for \(\ell =1,\ldots ,t\). The corresponding instance of the scheduling problem \(1|nr=1, p_j=a_j=w_j|\sum w_jC_j\) has 3t jobs corresponding to the 3t items with \(p_i = a_i = w_i = s_i\), and \(q = t\) supplies at supply dates \(u_\ell = (\ell -1)B\) with supplied quantities \(b_\ell = B\) for \(\ell =1,\ldots ,q\). The rest of the proof goes along the same lines as in the first part, i.e., we argue that 3-PARTITION has a feasible solution if and only if the corresponding scheduling problem instance has a solution of objective function value \(\sum _{j\le k} p_j p_k\) if and only if there is a feasible schedule without any idle times. \(\square \)
Theorem 4
Scheduling the jobs in LPT order is a 2-approximation algorithm for \(1|nr=1,p_j=a_j=w_j|\sum w_jC_j\).
Proof
The main idea of the following proof is that first we transform the problem data such that the resource supplies are deferred until they are used in a selected optimal schedule, and then we bound the approximation ratio of the LPT schedule. Finally, we observe that the LPT order yields at least as good a schedule with the original problem data as the same job order for the modified problem data.
Let I be any instance of the scheduling problem and fix an optimal schedule \(S^*\) for I. Let \(\mathcal {J}_\ell ^*\) be the set of jobs that start in \([u_\ell ,u_{\ell +1})\) in \(S^*\). Let \(I'\) be a new problem instance derived from I by modifying the supplied quantities (the other problem data do not change): \(b'_1:=\sum _{j\in \mathcal {J}_1^*}a_j\) and for each \(\ell \ge 2\), \(b'_\ell :=\sum _{\nu =1}^\ell \sum _{j\in \mathcal {J}_\nu ^*}a_j-\sum _{\nu =1}^{\ell -1}b'_{\nu }\). \(\square \)
Claim 1
\(I'\) has the following properties:
-
(i)
\(b'_\ell \ge 0\) for each \(\ell = 1,\ldots ,q\),
-
(ii)
\(\sum _{\ell = 1}^q b'_\ell = \sum _{j=1}^n a_j\),
-
(iii)
\(S^*\) is optimal for \(I'\),
-
(iv)
any ordering of the jobs yields at least as good a schedule for I as for \(I'\).
Proof
The first two claims are straightforward consequences of the definitions, while (iii) and (iv) both follow from the fact that in \(I'\) the resource supplies are deferred with respect to I. \(\square \)
From now on we consider \(I'\).
Let \(S^{LPT}\) denote the schedule obtained from the LPT order for problem instance \(I'\), and let \(C^{LPT}_j\) denote the completion time of job j in this schedule. Let \(G_\ell ^{LPT}\) denote the total idle time in \(S^{LPT}\) in \([0, u_{\ell +1}]\) and \(P^{LPT}_\ell \) the total working time (when the machine processes a job) in \([u_\ell ,u_{\ell +1}]\). We have \(u_\ell =\sum _{\nu =1}^{\ell -1}P_{\nu }+ G^{LPT}_{\ell -1}\).
Let us define \(\tilde{P}^{LPT}_\ell \) as follows. If the machine is working just before \(u_\ell \), or idle just after \(u_{\ell }\) in \(S^{LPT}\), then \(\tilde{P}^{LPT}_\ell =0\); otherwise, \(\tilde{P}^{LPT}_\ell \) equals the length of the working period starting at \(u_\ell \) until the first idle period in \(S^{LPT}\), see Fig. 3. Notice that if the machine is working right before and also right after \(u_\ell \), then \(\tilde{P}^{LPT}_\ell = 0\) by definition.
According to Lemma 1, we can express the total weighted processing time of the LPT schedule as follows:
Note that the second equation follows from the fact that if \(\tilde{P}^{LPT}_\ell = 0\), then \(G^{LPT}_{\ell -1} = G^{LPT}_{\ell '-1}\) for the largest \(\ell ' < \ell \) with \(\tilde{P}^{LPT}_{\ell '} > 0\).
In the next claim, we relate (2) to (1). The notations \(P^*_{\ell }\), \(G^*_\ell \) and \(H^*_\ell \) refer to \(P_\ell \), \(G_\ell \) and \(H_\ell \) in case of \(S^*\). Note that \(u_\ell =\sum _{\nu =1}^{\ell -1}P^*_\nu +G^*_{\ell -1}\).
Claim 2
If \(\tilde{P}^{LPT}_\ell > 0\), i.e., the machine is idle just before \(u_\ell \), and a job \(j(\ell )\) is started at \(u_\ell \) in \(S^{LPT}\), then
-
(i)
\(\sum _{\nu =1}^{\ell -1} \tilde{P}^{LPT}_\nu + p_{j(\ell )} > \sum _{\nu =1}^{\ell -1} P^*_\nu \) and \(\sum _{\nu =\ell }^{q} \tilde{P}^{LPT}_\nu < \sum _{\nu =\ell }^{q} P^*_\nu + p_{j(\ell )}\),
-
(ii)
\(G^{LPT}_{\ell -1} < G^*_{\ell -1}+p_{j(\ell )}\).
Proof
If \(\sum _{\nu =1}^{\ell -1} \tilde{P}^{LPT}_\nu + p_{j(\ell )}\le \sum _{\nu =1}^{\ell -1}b_\nu \) were true, then \(j(\ell )\) could be scheduled earlier in \(S^{LPT}\). Thus, we have \(\sum _{\nu =1}^{\ell -1} \tilde{P}^{LPT}_\nu + p_{j(\ell )}> \sum _{\nu =1}^{\ell -1}b_\nu \). Since we have \(\sum _{\nu =1}^{\ell -1} P^*_\nu \le \sum _{\nu =1}^{\ell -1}b_\nu \), (i) follows. The second inequality of (i) follows from \(\sum _{\nu =1}^q \tilde{P}^{LPT}_\nu =\sum _{\nu =1}^q P^*_\nu \). Finally, (ii) follows from \(\sum _{\nu =1}^{\ell -1}\tilde{P}^{LPT}_{\nu }+ G^{LPT}_{\ell -1}=u_\ell =\sum _{\nu =1}^{\ell -1} P_\nu ^*+G^*_{\ell -1}\). \(\square \)
Using (2) and Claim 2 (ii), we derive
where the first inequality follows from Claim 2 (ii), the second from the observation that \(p_{j(\ell )}\) is multiplied by the total processing time of job \(j(\ell )\) and all those jobs following \(j(\ell )\) in the LPT order, and the rest is obtained by rearranging terms.
Since \(\sum _jp_jC_j^*= \sum _{j\le k}p_jp_k+\sum _{\ell =2}^{q} H^*_{\ell -1}\big ( \sum _{\mu =\ell }^q P^*_\mu \big )\) (from Lemma 1), it is enough to prove
Claim 3
Note that \(H^*_{\ell -1}\ne 0\) means the machine is not working before \(u_\ell \) in \(S^*\), \(\sum _{\mu =\ell }^{q} \tilde{P}^{LPT}_{\mu }\) equals the total amount of work after \(u_\ell \) in \(S^{LPT}\), while \(\sum _{\mu =\ell }^q P^*_\mu \) is the same in the optimal schedule \(S^*\).
Proof (of Claim 3)
First we prove the claim for each \(\ell \) such that \(\tilde{P}^{LPT}_\ell \ne 0\). Consider such an \(\ell \). If \(\sum _{\mu =\ell }^q P^*_\mu \) were less than \(p_{j(\ell )}\), then each job with a processing time at least \(p_{j(\ell )}\) would be scheduled before \(u_\ell \) in \(S^*\); thus, \(\sum _{\nu =1}^{\ell -1}b'_\nu \) would be at least the total processing time of these jobs. However, this would mean that \(j(\ell )\) could be scheduled earlier (recall that the machine is idle just before \(u_\ell \) in \(S^{LPT}\)); thus, we have \(\sum _{\mu =\ell }^q P^*_\mu \ge p_{j(\ell )}\). Since \(\tilde{P}^{LPT}_\ell \ne 0\), we can use Claim 2 (i) and we have
Now suppose that \(\tilde{P}^{LPT}_\ell =0\). If \(\sum _{\mu =\ell }^{q} \tilde{P}^{LPT}_{\mu }=0\), then the claim is trivial. Otherwise, let \(\ell '>\ell \) be the smallest index such that \(\tilde{P}^{LPT}_{\ell '}\ne 0\). Since we know that the claim is true for \(\ell '\), we have
and we are ready. \(\square \)
Finally, as we have already noted, the LPT ordering of the jobs yields at least as good a schedule for I as the same job order for \(I'\), and the theorem is proved. \(\square \)
Tight example For any integer \(n\ge 3\) consider the scheduling problem with n jobs, the first \(n-1\) jobs are of unit processing time, while the last job has processing time n. That is, \(p_j = a_j = w_j = 1\) for \(j=1,\ldots ,n-1\), and \(p_n = a_n = w_n = n\) for job n. There are two supplies, one at \(u_1=0\) with supplied quantity \(n-1\), and another at \(u_2 = n^2\) with supplied quantity n. In the optimal schedule, the first \(n-1\) jobs are scheduled from time 0, and the last job is scheduled at time \(n^2\) (at \(u_2\)), see Fig. 4. That is, \(C^*_j = j\) for \(j = 1,\ldots ,n-1\), and \(C^*_n = n^2+n\). The optimal objective function value is
In contrast, in the LPT schedule job n comes first, but it can be scheduled only at time \(u_2 = n^2\), since its demand is n. Hence, \(C^{LPT}_n = n^2+n\), and \(C^{LPT}_j = n^2+n+j\) for \(j=1,\ldots , n-1\). Consequently,
Therefore, the relative error of LPT on these instances is
which tends to 2 as n goes to infinity.
6 PTAS for \(1|nr=1,p_j=w_j, q=const|\sum w_j C_j\)
Now we consider the special case when the number of supply dates is a constant (not part of the input), and at least 3 (for \(q=2\), there is an FPTAS for the general problem \(1|nr=1, q=2|\sum w_j C_j\)Kis 2015), and \(p_j = w_j\) for each job j. Theorem 3 implies that this version is still NP-hard. However, below we describe a PTAS for it.
Let \(P_{\mathrm {sum}}:= \sum _j p_j\) be the total processing time of the jobs. Let \(\varDelta := 1+(\varepsilon /q^2)\). We will guess the total processing time of those jobs starting after \(u_{\ell }\) for \(\ell =2,\ldots ,q\), where a guess is a \(q-1\) dimensional vector of non-increasing numbers \(P^g_2,\ldots , P^g_q\), i.e., \(P^g_\ell \ge P^g_{\ell +1} \ge 1\) for \(\ell =2,\ldots , q-1\), and each \(P^g_{\ell }\) is of the form \(\varDelta ^t\) for some integer \(t \ge 0\) with \(\varDelta ^t \le P_{\mathrm {sum}}\). Also, fix \(P^g_1 := P_{\mathrm {sum}}\). For any guess, define the set of large size jobs\(\mathcal{M}_{\ell } := \{ j\ |\ p_j \ge (\varDelta -1) P^g_{\ell } \}\). Note that \(\mathcal{M}_q \supseteq \mathcal{M}_{q-1} \supseteq \cdots \supseteq \mathcal{M}_1\), since \(P^g_q \le P^g_{q-1} \le \cdots \le P^g_1\). Let \(\mathcal{S}_\ell \) be the complement of \(\mathcal{M}_\ell \), i.e., \(\mathcal{S}_{\ell } := \{ j\ |\ p_j < (\varDelta -1) P^g_{\ell } \}\). Clearly, \(\mathcal{S}_q \subseteq \mathcal{S}_{q-1} \subseteq \cdots \subseteq \mathcal{S}_1\). After these preliminaries, the PTAS for \(1|nr=1,p_j=w_j, q=const|\sum w_j C_j\) consists of the following steps:
-
1.
Consider each possible guess \((P^g_2,\ldots ,P^g_q)\) of the total processing time of those jobs starting after the supply dates \(u_2,\ldots , u_q\), respectively. For each possible guess, define the sets of jobs \(\mathcal{M}_\ell \) and \(\mathcal{S}_\ell \) (see above), and perform the steps 2–5. After processing all the guesses, go to Step 6.
-
2.
For each \(\ell = 1,\ldots , q\), choose at most \(1/(\varDelta -1)\) large size jobs from \(\mathcal{M}_{\ell }\) (since the sets \(\mathcal{M}_{\ell }\) are not disjoint, care must be taken to choose each job at most once). For each possible choice \((T_1,\ldots ,T_q)\) of the large size jobs (where \(T_\ell \subseteq \mathcal{M}_\ell \)), perform steps 3–5. After evaluating all choices, continue with the next guess in Step 1.
-
3.
Determine a schedule of the large jobs. That is, for \(\ell =1,\ldots , q\), schedule the jobs in \(T_{\ell }\) in any order contiguously after \(u_{\ell }\), and after all the previously scheduled jobs.
-
4.
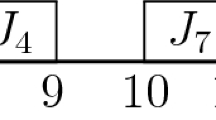
Let \(\mathcal{J}^u_0\) be the set of unscheduled jobs. For \(\ell =q,q-1,\ldots ,1\), repeat the following. In a general step with \(\ell \ge 2\), pick jobs from \(\mathcal{J}^u_{q-\ell } \cap \mathcal{S}_\ell \) in non-increasing \(a_j / p_j\) order until the selected subset \(K_{\ell }\) satisfies \(p(K_{\ell }) + p(T_{\ell }) \ge P^g_\ell - (1/\varDelta )P^g_{\ell +1}\), or no more jobs are left, i.e., \(K_\ell = \mathcal{J}^u_{q-\ell } \cap \mathcal{S}_\ell \). In either case, insert the jobs of \(K_\ell \) in any order after \(u_\ell \) and after all the jobs in \(T_1\cup \cdots \cup T_{\ell -1}\), and before all the jobs in \(T_{\ell } \cup \bigcup _{\ell '=\ell +1}^q (K_{\ell '}\cup T_{\ell '})\) (pushing some of them to the right if necessary). Let \(\mathcal{J}^u_{q-\ell +1} := \mathcal{J}^u_{q-\ell } \backslash K_\ell \) and continue with \(\ell -1\) until \(\ell =1\) or no more unscheduled jobs are left. For \(\ell =1\), just schedule all the remaining jobs from time \(u_1=0\) on (pushing the already scheduled jobs to the right, if necessary). If the complete schedule obtained satisfies the resource constraints, then continue with Step 5, otherwise with the next choice of large size jobs in Step 2. See Fig. 5 for illustration.
-
5.
Compute the objective function value of the complete schedule obtained in step (4) and store this schedule as the best schedule if it is the first feasible schedule or if it is better than the best feasible schedule found so far. Continue with next choice of large size jobs in Step 2.
-
6.
Output the best schedule found in the previous steps.
Theorem 5
The above algorithm is a PTAS for \(1|nr=1, p_j = w_j, q= const|\sum w_j C_j\).
Proof
Let I be any instance of the scheduling problem and \(S^*\) an optimal solution for I. Let \({\hat{P}}^*_\ell \) be the total processing time of those jobs starting after \(u_\ell \) in \(S^*\). Clearly, \({\hat{P}}^*_\ell \ge {\hat{P}}^*_{\ell +1}\) for \(\ell =1,\ldots ,q-1\). Consider the guess \(P^g_2,\ldots ,P^g_q\) in Step 1 of our algorithm such that \({\hat{P}}^*_\ell \le P^g_{\ell } < \varDelta {\hat{P}}^*_\ell \) for each \(\ell =2,\ldots ,q\). Such a guess must exist by the definition of guesses.
For each \(\ell =1,\ldots ,q\), let us partition the set of jobs that start in the interval \([u_\ell , u_\ell +1)\) in the schedule \(S^*\) into subsets \(T^*_\ell \subseteq \mathcal{M}_\ell \) and \(K^*_\ell \subseteq \mathcal{S}_\ell \). Clearly, the sets \(T^*_\ell \) are disjoint, and the cardinality of each \(T^*_\ell \) is at most \(1/(\varDelta -1)\), since \(P^g_\ell \ge P^*_\ell \), and thus each job in \(T^*_\ell \) is of size at least \((\varDelta -1)P^g_\ell \ge (\varDelta -1){\hat{P}}^*_\ell \), while the total size of all the jobs starting after \(u_\ell \) in \(S^*\) is \({\hat{P}}^*_\ell \) by definition. Therefore, the algorithm will enumerate and process the choice \((T^*_1,\ldots ,T^*_q)\) in Step 2. In the rest of the proof, we fix this choice of large jobs. After scheduling them in Step 3, the resulting schedule is like \(S^*\), except that some jobs may be yet unscheduled. Thus, we perform Step 4, and let \(S^A\) be the resulting schedule. In Step 4, the algorithm will find sets of jobs \(K_1,\ldots ,K_q\), and it may well be the case that \(K^*_\ell \ne K_\ell \) for some \(\ell \), but we know that \(\bigcup _{\ell =1}^q K_\ell = \bigcup _{\ell =1}^q K^*_\ell \), since in \(S^*\) and \(S^A\), for each \(\ell \), the same subset \(T^*_\ell \) of \(\mathcal{M}_\ell \) is chosen. We will prove that \(S^A\) is a feasible schedule and that its objective function value is at most \(1+O(\varepsilon )\) times the optimum.
Claim 4
The total processing time of those jobs that start after \(u_\ell \) in \(S^*\) and in \(S^A\), respectively, satisfies the inequalities
Proof
First notice that for each \(\ell = 2,\ldots ,q\), we have \(\cup _{\ell '=\ell }^q K^*_{\ell '} \subseteq \mathcal{S}_\ell \backslash \left( \bigcup _{\ell '=\ell +1}^q T^*_{\ell '} \right) \), since \(K^*_{\ell '} \subseteq \mathcal{S}_{\ell '} \subseteq \mathcal{S}_\ell \) and \(T^*_{\ell '}\cap K^*_{\ell '} = \emptyset \) for \(\ell '\ge \ell \), and similarly, \(\cup _{\ell '=\ell }^q K_{\ell '} \subseteq \mathcal{S}_\ell \backslash \left( \bigcup _{\ell '=\ell +1}^q T^*_{\ell '} \right) \). We prove (3) by induction. Along with (3), we will also prove
where we define \(P^g_{q+1} := 0\). The base case is for \(\ell =q+1\), when all the inequalities trivially hold (we define \({\hat{P}}^*_{q+1} := 0\)). Now suppose that (3) and (4) hold for \(\ell +1\) for some \(\ell \ge 2\), and we verify them for \(\ell \).
First suppose that \(p(K_\ell ) + p(T^*_\ell ) \ge P^g_\ell - (1/\varDelta )P^g_{\ell +1}\). Since \({\hat{P}}^*_\ell - {\hat{P}}^*_{\ell +1}\) equals the total processing time of those jobs that start in the interval \([u_\ell , u_{\ell +1})\) in \(S^*\), and \({\hat{P}}^*_{\ell } \le P^g_\ell < \varDelta {\hat{P}}^*_\ell \), we have
So, the induction hypothesis implies the first inequality in (3). To verify the second one, recall that in Step 4 we stop selecting jobs as soon as \(p(T^*_\ell ) + p(K_\ell )\) exceeds \(P^g_\ell - (1/\varDelta ) P^g_{\ell +1}\), and the processing time of all jobs in \(\mathcal{S}_\ell \) is bounded by \((\varDelta -1) P^g_\ell \), which implies (4) for \(\ell \), since
Using the induction hypothesis, we obtain
A simple calculation shows that \(\varDelta ^2< 1+3(\varepsilon /q^2) < 1+(\varepsilon / q)\) (since \(q \ge 3\) by assumption); therefore, the right-hand side of (6) is less than \((1+(\varepsilon /q)) P^g_\ell + 3(\varepsilon /q^2)\sum _{\ell '=\ell +1}^q P^g_{\ell '} \le (1+ 4 (\varepsilon /q))P^g_\ell \). Since \(P^g_\ell < \varDelta {\hat{P}}^*_\ell \), and \((1+ 4 (\varepsilon /q)) \varDelta < 1+6 (\varepsilon /q)\) (since \(q\ge 3\) by assumption), the second inequality in (3) follows.
Now suppose \(K_\ell = \mathcal {J}^u_{q-\ell } \cap \mathcal{S}_\ell \) and \(p(K_\ell ) + p(T^*_\ell ) < P^g_\ell - (1/\varDelta )P^g_{\ell +1}\) in Step 4 of the algorithm at iteration \(\ell \). Then, we deduce that in \(S^A\), all the small jobs in \(\mathcal{S}_\ell \backslash \left( \bigcup _{\ell '=\ell +1}^q T^*_{\ell '} \right) \) are scheduled after \(u_\ell \) in the iterations \(\ell ,\ldots ,q\), while in \(S^*\), some jobs of \(\mathcal{S}_\ell \backslash \left( \bigcup _{\ell '=\ell +1}^q T^*_{\ell '} \right) \) may be started before \(u_\ell \). Therefore, the first inequality in (3) holds in this case as well. To verify the second inequality in (3), note that since \(p(K_\ell ) + p(T^*_\ell ) < P^g_\ell - (1/\varDelta )P^g_{\ell +1}\) by assumption, (4) follows immediately. Then, using the induction hypothesis, we obtain (6), and then the same argument applies as above. \(\square \)
In order to prove (resource) feasibility, we need some further technical results. To simplify notation, suppose \(\mathcal{S}_1\backslash \bigcup _{\ell =2}^q T^*_\ell = \{1,\ldots ,n_1\}\) and \(a_j / p_j \ge a_{j+1} / p_{j+1}\) for \(1\le j < n_1\), i.e., job j is the jth job in the ordered sequence. Let \(X_t := \{1,\ldots ,t\}\) be the index set of the first \(t\le n_1\) jobs with the largest \(a_j / p_j\) ratio.
Claim 5
There exists a unique \(t \in \{0,\ldots ,n_1\}\) such that
Proof
If \(\bigcup _{\ell '=\ell }^q K_{\ell '}\) is the empty set, then \(t = 0\) will do. Otherwise, let t be the maximum element in \(\bigcup _{\ell '=\ell }^q K_{\ell '}\). Indirectly, suppose there exists some \(t'<t\) such that \(t' \not \in \bigcup _{\ell '=\ell }^q K_{\ell '}\), but \(t'\in \mathcal{S}_\ell \backslash \bigcup _{\ell '=\ell }^q T^*_{\ell '}\). Then, at some iteration in Step 4 of the algorithm, t would be chosen in place of \(t' < t\), which is a contradiction. \(\square \)
Corollary 1
For the job index t defined in Claim 5,
Claim 6
For each \(t=1,\ldots ,n_1\), and \(2\le \ell \le q\), we have
Proof
We proceed by induction, the base case being for \(\ell =q\). Then, \(K_q, K^*_q \subseteq \mathcal{S}_q\). If \(K_q\) is a proper subset of \(\mathcal{S}_q\), then we have \(p(K^*_q) \le p(K_q)\) by (5). Otherwise, \(K_q = \mathcal{S}_q \supseteq K^*_q\), and we have \(p(K^*_q) \le p(K_q)\) in this case, too. For the sake of a contradiction, suppose there exists \(1\le t\le n_1\) such that (8) does not hold. Let t be the smallest such job index. Then, job \(t \in K^*_q \backslash K_q\); otherwise, t could be decreased. Then, \(K_q\) does not contain any job v with \(v > t\); otherwise, before picking v, the algorithm would have picked t. But then
which is a contradiction.
Now assume by induction that (8) holds for \(\ell = k+1\), with \(k\ge 2\), and for all \(1\le t\le n_1\), and we check it for \(\ell =k\). We distinguish two cases.
-
\(K_\ell \subset \mathcal{S}_\ell \backslash \bigcup _{\ell '=\ell +1}^q (T^*_{\ell '} \cup K_{\ell '})\). Then, we have \(p(K^*_\ell ) \le p(K_\ell )\) by (5). For the sake of a contradiction, suppose there exists \(1\le t\le n_1\) such that (8) does not hold. Let t be the smallest such job index. Then, it must be the case that \(t \in (K^*_\ell \cup \cdots \cup K^*_q) \backslash (K_\ell \cup \cdots \cup K_q)\); otherwise, t could be decreased. So suppose \(t \in K^*_{\ell '}\) for some \(\ell \le \ell '\le q\). Then, \(\{t,\ldots ,n_1\} \cap K_\ell = \emptyset \), because if not, then, since \(t \in K^*_{\ell '} \subseteq \mathcal{S}_{\ell '} \subseteq \mathcal{S}_\ell \), the algorithm would have chosen t before picking some \(v \in \{t+1,\ldots ,n_1\} \cap K_\ell \). Consequently, \(K_\ell \subseteq X_{t-1}\). Now we use the induction hypothesis:
$$\begin{aligned} \begin{aligned} \sum _{j\in X_t \cap (K_{\ell }\cup \cdots \cup K_q)} p_j&= \sum _{j \in K_\ell } p_j + \sum _{j\in X_t \cap (K_{\ell +1}\cup \cdots \cup K_q)} p_j \\&\ge \sum _{j \in K_\ell } p_j + \sum _{j\in X_t \cap (K^*_{\ell +1}\cup \cdots \cup K^*_q)} p_j\\&\ge \sum _{j \in K^*_\ell \cap X_t} p_j + \sum _{j\in X_t \cap (K^*_{\ell +1}\cup \cdots \cup K^*_q)} p_j, \end{aligned} \end{aligned}$$where the first equation follows from \(K_\ell \subseteq X_{t-1} \subset X_t\), the first inequality from the induction hypothesis, and the last inequality from the fact that \(p(K_\ell ) \ge p(K^*_\ell )\). However, the derived inequality is just (8) for \(\ell \) and t, a contradiction.
-
\(K_\ell = \mathcal{S}_\ell \backslash \bigcup _{\ell '=\ell +1}^q (T^*_{\ell '} \cup K_{\ell '})\). Since \(\bigcup _{\ell '=\ell }^q K^*_{\ell '} \subseteq \mathcal{S}_\ell \backslash \bigcup _{\ell '=\ell +1}^q T^*_{\ell '}\), we can observe that each \(t \in \mathcal{S}_\ell \backslash \bigcup _{\ell '=\ell +1}^q T^*_{\ell '}\) belongs to one of the sets \(K_{\ell '}\) with \(\ell \le \ell '\le q\), but may not belong to any of the sets \(K^*_{\ell '}\) with \(\ell \le \ell '\le q\). Hence, the claim follows in this case, too. \(\square \)
Corollary 2
For each \(\ell = 2,\ldots ,q\), we have
Now we verify resource feasibility by showing that for each \(\ell =2,\ldots ,q\),
This suffices to prove the feasibility of \(S^A\), because then for each \(\ell = 2,\ldots ,q\), the total resource consumption of those jobs that start after \(u_\ell \) in \(S^A\) is at least as much as that in \(S^*\). Therefore, the total resource consumption of those jobs that start not later than \(u_\ell \) in \(S^A\) cannot be more than that in \(S^*\). Hence, \(S^A\) is a feasible schedule. Let t be the job index defined in Claim 5. Now we compute
where (a), (b) and (d) are obvious, and (c) follows from three observations:
-
(i)
the first terms of the two expressions are the same by Corollary 1,
-
(ii)
the inequality between the second terms follows from
$$\begin{aligned} \max _{j \in {\overline{X}}_t \cap \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '}\right) } \frac{a_j}{p_j} \le \min _{j \in \left( \bigcup _{\ell '=\ell }^q K_{\ell '}\right) \backslash \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '}\right) } \frac{a_j}{p_j}, \end{aligned}$$since the jobs are indexed in non-increasing \(a_j / p_j\) order, and \(\bigcup _{\ell '=\ell }^q K_{\ell '} \subseteq X_t\), and from
-
(iii)
$$\begin{aligned} \sum _{ j \in {\overline{X}}_t\cap \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '}\right) } p_j \le \sum _{ j \in \left( \bigcup _{\ell '=\ell }^q K_{\ell '}\right) \backslash \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '}\right) } p_j, \end{aligned}$$
which can be derived from the inequality of Corollary 2 by subtracting the equation \(\sum _{j\in X_t \cap \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '} \right) }p_j=\sum _{j\in \left( \bigcup _{\ell '=\ell }^q K^*_{\ell '} \right) \cap \left( \bigcup _{\ell '=\ell }^q K_{\ell '} \right) }p_j\) (Corollary 1) from it.
Now we bound the objective function value of \(S^A\). Again, we need a technical result. Let \(H^A_\ell \) denote the idle time in \([u_\ell , u_{\ell +1})\) in the schedule \(S^A\), and \(G^A_\ell \) the total idle time before \(u_{\ell +1}\).
Claim 7
\(H^A_{\ell } \le H^*_\ell + (6\varepsilon /q) {\hat{P}}^*_{\ell +1}\).
Proof
Observe that in \(S^A\) at most \((6\varepsilon /q) {\hat{P}}^*_{\ell +1}\) more work is scheduled after \(u_{\ell +1}\) than in \(S^*\) by inequality (3). Therefore, the total gap in \(S^A\) before \(u_{\ell +1}\) is at most \((6\varepsilon /q) {\hat{P}}^*_{\ell +1}\) more than in \(S^*\), i.e.,
On the other hand, \(G^*_{\ell -1} \le G^A_{\ell -1}\), since in \(S^A\), \(\sum _{\ell '=\ell }^q (p(T^*_{\ell '})+p(K_{\ell '})) \ge {\hat{P}}^*_\ell \) by (3). Now, using the fact that \(G^A_\ell = G^A_{\ell -1} + H^A_\ell \), we obtain
\(\square \)
Now we compute:
It remains to verify the running time of the algorithm. The number of guesses in Step 1 is \(O((\log _{\varDelta } P_{\mathrm {sum}})^q)\) which is bounded by \(O(((q^2/\varepsilon ) \ln P_{\mathrm {sum}})^q)\), which is polynomial in the size of the input. The number of choices in Step 2 is bounded by \(O(n^{q^3/\varepsilon })\). The rest can be done in \(O(n^2)\) time for every guess \((P^g_2,\ldots ,P^g_q)\) and choice of jobs \((T_1,\ldots ,T_q)\). Hence, the total time complexity is polynomial bounded in the size of the input. \(\square \)
7 Final remarks
In this paper, we have established new complexity and approximability results for single-machine scheduling problems with non-renewable resource constraints and the total weighted completion time objective. As it has turned out, list scheduling is a useful tool in solving a number of special cases, and it can also be the basis of designing approximation algorithms.
There are a number of open problems. For instance, what is the complexity of \(1|nr=1,a_j = 1 | \sum C_j\)? Is there a polynomial time approximation algorithm of constant approximation ratio for the problem \(1|nr=1|\sum w_j C_j\)? What is the approximability status of the special case \(1|nr=1, p_j = 1, w_j = a_j|\sum w_j C_j\)?
Notes
Non-increasing \(p_j\) order.
References
Carlier, J. (1984). Problèmes d’ordonnancements à contraintes de ressources: algorithmes et complexité. Thèse d’état. Université Paris 6
Gafarov, E. R., Lazarev, A. A., & Werner, F. (2011). Single machine scheduling problems with financial resource constraints: Some complexity results and properties. Mathematical Social Sciences, 62, 7–13.
Graham, R. L., Lawler, E. L., Lenstra, J. K., & Kan, A. H. G. R. (1979). Optimization and approximation in deterministic sequencing and scheduling: A survey. Annals of Discrete Mathematics, 5, 287–326.
Grigoriev, A., Holthuijsen, M., & van de Klundert, J. (2005). Basic scheduling problems with raw material constraints. Naval Research of Logistics, 52, 527–553.
Györgyi, P. (2017). A PTAS for a resource scheduling problem with arbitrary number of parallel machines. Operations Research Letters, 45, 604–609.
Györgyi, P., & Kis, T. (2014). Approximation schemes for single machine scheduling with non-renewable resource constraints. Journal of Scheduling, 17, 135–144.
Györgyi, P., & Kis, T. (2015). Approximability of scheduling problems with resource consuming jobs. Annals of Operations Research, 235(1), 319–336.
Györgyi, P., & Kis, T. (2015). Reductions between scheduling problems with non-renewable resources and knapsack problems. Theoretical Computer Science, 565, 63–76.
Györgyi, P., & Kis, T. (2017). Approximation schemes for parallel machine scheduling with non-renewable resources. European Journal of Operational Research, 258(1), 113–123.
Györgyi, P., & Kis, T. (2018). Minimizing the maximum lateness on a single machine with raw material constraints by branch-and-cut. Computers & Industrial Engineering, 115, 220–225.
Kis, T. (2015). Approximability of total weighted completion time with resource consuming jobs. Operations Research Letters, 43(6), 595–598.
Slowinski, R. (1984). Preemptive scheduling of independent jobs on parallel machines subject to financial constraints. European Journal of Operational Research, 15, 366–373.
Smith, W. E. (1956). Various optimizers for single-stage production. Naval Research Logistics (NRL), 3(1–2), 59–66.
Toker, A., Kondakci, S., & Erkip, N. (1991). Scheduling under a non-renewable resource constraint. Journal of the Operational Research Society, 42, 811–814.
Xie, J. (1997). Polynomial algorithms for single machine scheduling problems with financial constraints. Operations Research Letters, 21(1), 39–42.
Acknowledgements
Open access funding provided by the MTA Institute for Computer Science and Control (MTA SZTAKI). The authors are grateful to two anonymous referees for constructive comments that helped to improve the paper. This work has been supported by the National Research, Development and Innovation Office—NKFIH, Grant No. K112881, and by the GINOP-2.3.2-15-2016-00002 Grant of the Ministry of National Economy of Hungary.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Györgyi, P., Kis, T. Minimizing total weighted completion time on a single machine subject to non-renewable resource constraints. J Sched 22, 623–634 (2019). https://doi.org/10.1007/s10951-019-00601-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-019-00601-1