Reevaluating soil amplification using multi-spectral HVSR technique in La Chana Neighborhood, Granada, Spain

Abstract

This work presents a thorough reevaluation of soil amplification in the La Chana neighborhood of Granada through a pioneering application of the horizontal-to-vertical spectral ratio technique on seismic noise data using various spectral approaches. The research recycles old seismic noise data recorded at 34 stations with 2 Hz instruments in the year 2010, supplemented with additional measurements recorded with broadband seismometers at nearby locations in the years 2013 and 2017. Initial traditional processing identifies a narrowband dominant frequency around 1.5 Hz, attributed to artificial or anthropogenic sources. To address this, the Maximum Entropy Algorithm was implemented to smooth the spectral response below 1 Hz, and filter out frequency peaks with very narrow spectral bands, while preserving the narrowband frequency around 1.5 Hz in some records. The Thomson Multitaper method further refined the spectral ratio, emphasizing the detection and suppression of narrow frequency bands that may be related to industrial activity. The results demonstrated the reappearance of the 1.5 Hz frequency, but this time without narrow bandwidths, indicating its possible correlation with the natural ground movement. Fundamental periods, ranging from 0.45 s to 0.88 s, suggest a diverse lithological composition, indicating the presence of layers of sands, clays, conglomerates, and carbonates over a basement that represents the main impedance contrast in the area. The multispectral approach surpasses conventional methods in precision and reliability, providing valuable insights for earthquake risk assessment, urban planning, and engineering decisions in seismically active regions.

1 Introduction

The Horizontal-to-Vertical Spectral Ratio (HVSR) method, originally proposed by Nogoshi and Igarashi (1971) and extended by Nakamura (1989, 2000), has become a cornerstone in the field of geophysics for assessing site effects and subsurface properties using ambient noise recordings. This technique, leveraging the simplicity of single-station measurements, offers an efficient and non-intrusive means for estimating a site's fundamental resonant frequency, crucial for understanding seismic site response and soil-structure interaction.

Recent advancements and applications of the HVSR method have broadened its utility beyond traditional site effect studies. The method's adaptation to include recordings from both microtremors and earthquake events, as discussed by Xu and Wang (2021), has enhanced its applicability in site classification, mineral exploration, and the determination of subsurface shear-wave velocity profiles. This evolution underscores HVSR's versatility and its potential for delivering insightful analyses in various geophysical investigations. Supporting this, the findings of Bonnefoy-Claudet et al. (2006) and Molnar et al. (2018) illustrate the method's expanded applications, showcasing its effectiveness in urban areas and its ability to discern the contributions of different seismic wave types to the HVSR signal, thereby enriching our understanding of ambient noise sources.

Notably, the method's theoretical underpinnings have been further elaborated through contributions by researchers like Lermo and Chávez-García (1993), who extended HVSR's application to S-wave recordings, laying a theoretical groundwork that has broadened the method's scope. Concurrently, the incorporation of strong-motion data into HVSR analyses has facilitated detailed site classification efforts, enhancing our comprehension of soil behavior under seismic stress. The comprehensive study by Bonnefoy-Claudet et al. (2006) provides a critical examination of the H/V ratio, addressing the effects of Love waves on microtremor H/V ratios and challenging previous assumptions about ambient noise wavefields, which further illuminates the theoretical complexities inherent in HVSR analysis.

Moreover, the development of web-based applications such as HVSRweb by Vantassel et al. (2021) represents a significant stride towards making HVSR processing more accessible and standardized. Such platforms not only streamline computational processes but also promote research reproducibility and collaboration, echoing the modern demand for openness and transparency in scientific exploration. The research contributions from both Bonnefoy-Claudet et al. (2006) and Molnar et al. (2018) are emblematic of this trend towards digital innovation in geophysics, offering tools and insights that facilitate the broader adoption and application of the HVSR method.

However, the journey of HVSR from its conception to its current state has not been devoid of challenges. The quest for a precise physical interpretation of HVSR results, particularly concerning the nature of ambient-vibration wavefields and source effects, and faced challenges in the identifying nearby frequency peaks and distinguishing between natural and artificial sources, remains a topic of vigorous debate. Despite these issues, the method's cost-effectiveness and the growing repository of high-quality vibration records continue to fuel its popularity and utility across the geophysical research spectrum.

In light of these developments and challenges, this paper aims to reevaluate soil amplification in Granada's La Chana neighborhood, Spain. Integrating HVSR with advanced spectral techniques, such as the Maximum Entropy Method (MEM), initially explained by Burg (1967, 1968, 1975) and then extended by Cadzow (2005), and the Multitaper Spectral Estimation Method (MSEM) developed by Thomson (1982), promises to enhance the precision and reliability of conventional HVSR analyses. By pioneering the application of a multi-spectral approach in analyzing seismic noise, this study not only enriches the body of HVSR research but also underscores the method's growing relevance in addressing intricate geophysical phenomena. This endeavor holds substantial promise for earthquake risk assessment, urban planning, and engineering decision-making in seismically active regions, marking a significant advancement in the field.

2 Geological setting

The Granada Basin (GB) situated in the Betic Cordillera (BC), southern Spain, is a sedimentary basin characterized by late orogenic intramountain basin development, resulting in a complex geological structure. The region is geographically surrounded by various domains of the Betic Cordillera, making it susceptible to high-risk seismic activity and historically experiencing destructive earthquakes. Given its urban areas and potential seismic hazards, is crucial to conduct a comprehensive seismic risk analysis (García-Hernández et al. 1980; Rodríguez-Fernández et al. 1989; Morales et al. 1990, 1997; Ruano et al. 2000; Rodríguez-Fernández and Sanz de Galdeano 2006; Sanz de Galdeano et al. 2003; Agosta et al. 2012; Azañón et al. 2013).

2.1 Granada basin description

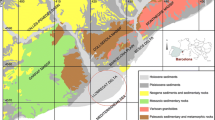
The GB, classified as a Neogene pull-appart basin, has been continuously filled with sedimentary material from the Late Miocene to the Quaternary (Morales et al. 1990). It spans a considerable area, measuring approximately 65 km from east to west and 40 km from north to south (Sanz de Galdeano 2011), as depicted the Fig. 1. The central portion of the basin experiences subsidence, resulting in sedimentary thicknesses of up to 2 km (Morales et al. 1990; Rodríguez-Fernández and Sanz de Galdeano 2006). The oldest sediments found within the basin date back to the Late Miocene, specifically the Tortonian conglomerates, along with calcareous sandstones and marls (Rodríguez-Fernández et al. 1989).

Fig. 1

Geologic map of the Granada Basin, modified from Sanz de Galdeano et al. (2012). The white frame highlights the study zone (La Chana) shown in Fig. (4. The study area is placed within the Betic Cordillera in the lower left image, which depicts the GB as a yellow dot inside a yellow box

The GB's geological evolution was marked by regressive and transgressive events, initiated during the Messinian stage at the end of the Miocene, leading to the deposition of continental sedimentary deposits. This sequence includes conglomerates and sands of the Pinos de Genil Formation (Valverde Palacios 2010), which are overlain by a turbiditic sediment package comprising fine sands. The base of this package features lower evaporites, topped by a thin gypsum layer with lateral facies of lacustrine limestones and fluvio-lacustrine deposits. In the Late Pliocene to the Lower Pleistocene, the basin accommodated conglomerates and sands forming the Alhambra Formation (Valverde Palacios 2010). The red conglomerates in this formation originated from alluvial fans sourced from the Sierra Nevada, displaying facies of sands, silts, and clays, indicative of marine regression events and a continental basin (Lupiani et al. 1997).

The Genil, Beiro, Darro, and Dílar rivers played significant roles in depositing red clays, gravels, sands, and silt–clay intercalations within various sedimentary valleys. Late Pleistocene conglomerates surround the gravels to the south, giving rise to the recent alluvial fans of the Vega Alta, encompassing the Sierras de Huetor and Nevada. In the Holocene, floodplain sediments were deposited over river valleys, resulting from detrital input and forming 250-m-thick layers (Navarro et al. 2010) (Fig. 1). The diverse sedimentary succession and depositional processes within the GB unveil a complex history of geological events that have shaped its unique stratigraphic architecture over time.

2.2 Main fault systems

The central-eastern sector of the GB is characterized by active fault systems (Fig. 2), which contribute to the uplift of its eastern part and the subsidence of its central-western side, because the BC has been subjected to severe tectonic pressures. This process, combined with delaminations and roll-back states (Mancilla et al. 2015), together with differentiated fault movement, have allowed the formation of strike-slip faults, which have generated the basins within the Betic system, such as GB, leading to uplift and subsidence of blocks along these basins (Morales et al. 1990; Pérez-Peña et al. 2015).

Fig. 2

Location map of the most energetic earthquakes that have occurred in the Granada Basin in the last 600 years along with the active (continuous lines) and possibly active (dashed lines) faults (García-Mayordomo et al. 2012; QAFI 2021). The yellow rectangle highlights the study zone shown in Fig. 4

Within this complex tectonic framework, normal faults emerge as the primary neotectonic formations, identifiable through seismic reflection profiles and terrestrial geological observations. These faults, notable for their significant geomorphological features and well-maintained fault scarps, have been previously documentated by other researchers (Morales et al. 1990; Sanz de Galdeano et al. 2003, 2012; Rodríguez-Fernández and Sanz de Galdeano 2006; Pérez-Peña et al. 2015).

The Iberian catalog of fault source models records activity from the Upper Pleistocene to the Holocene era for four specific structures¹(García Mayordomo et al. 2012; QAFI 2021; García-Mayordomo and Martín-Banda 2022): the Atarfe, Pinos Puente, Padul-Niguelas, and Ventas de Zafarraya faults. Of these, the Ventas de Zafarraya fault is distinctly linked to the notable 1884 Andalusian Mw 6.5–6.7 earthquake, which resulted in surface ruptures (Reicherter et al. 2003). While some faults, like the Padul-Niguelas fault, are situated in regions of low recorded seismic activity, others, such as the Atarfe and Pinos Puente faults, are found in areas of higher seismic activity. Nonetheless, the correlation between specific seismic incidents or sequences and these faults remains indeterminate (Lozano et al. 2022). Figure 2 illustrates the distribution of the most significant active faults in the GB, including Obéilar-Pinos Puente, Pinos Puente, El Fargue-Jun, Granada, Belicena-Alhendin, Dilar, Padul, and Padul-Durcal. With all of these faults and the sedimentary basin frame, the area appears to be vulnerable to site effects that could result in increased damages.

3 Material and methods

This study employs a methodology consisting of an analysis of recycled seismic noise data collected from 38 stations in La Chana. This analysis is conducted utilizing the HVSR technique as implemented by the Geopsy code (Wathelet et al. 2020). A Matlab code is then used to conduct a more thorough evaluation of the obtained results using the MEM and MSEM techniques. The integration of various spectral techniques in the analysis of seismic noise could offers a reliable approach to estimate soil amplification. Additionally, this study seeks to identify artificial sources of frequency, such as traffic and industrial activities, that have the potential to be used for data inversion and comparison with geotechnical data.

3.1 Spectral techniques employed

3.1.1 Traditional horizontal-to-vertical spectral ratio method

The HVSR method (Nakamura 1989, 2000) is a standard technique for estimating the fundamental frequency f₀ and amplification factor A₀ of the soil as a spectral transference function of site effects S_m(ω) based on the ratio of the horizontal Hs(ω) and vertical V_S (ω) seismic noise spectral amplitudes of surface waves, as shown Eq. (1). The periodogram or modified periodogram (Welch 1967; Johnson and Long 1999) is used by the Geopsy code as spectral method to calculate the HVSR.

$$Sm(\omega )=\frac{Hs(\omega )}{Vs(\omega )}$$

(1)

The HVSR assumes that seismic noise is composed of both surface waves and body waves, with surface waves dominating at low frequencies, and that the sedimentary layer above the basement is responsible for horizontal rather than vertical movement amplification by site effects. This method is advantageous because it is a non-destructive and cost-effective technique for determining the resonance frequencies of S-waves in the soil that can cause infrastructure damage. Among its limitations are the inability to differentiate between natural and artificial sources of frequencies, and the sensitivity to the quality of seismic noise data (Navarro et al. 2000; Sánchez-Sesma et al. 2011; García-Jerez et al. 2016; Piña-Flores et al. 2016). The technique has numerous applications in geotechnical and earthquake engineering, including site characterization, seismic hazard assessment, and earthquake early warning systems.

3.1.2 Maximun entropy method

The MEM (Burg 1968, 1975) is a method of spectral analysis that is utilized to determine the power spectral density S(f) of a signal using a restricted amount of data. The process utilizes the autocovariance function ρ(k) of the entropy H as a Nyquist frequency f_N limited process, as demonstrated in Eq. (2).

$$H={\int }_{-{f}_{N}}^{+{f}_{N}}log [S(f)] df=\frac{1}{4{f}_{N}}{\int }_{-{f}_{N}}^{+{f}_{N}}log\sum_{k=-\infty }^{\infty }\rho (k{)}^{-i2\pi fk\Delta t}]df$$

(2)

This parametric method produces spectra with greater theoretical resolution than the data utilized. Therefore, the MEM is used to overcome the restricted precision of the Fourier Transform (FT), which is especially beneficial in situations where it is necessary to identify closely spaced peak frequencies.

The solution of this method is obtained by optimizing Lagrange multipliers while ensuring that the function S(f) is aligned with the given autocovariance function ρ(k). Equation (3) assumes that the signal is generated by an autoregressive AR process. This process produces a real, stationary, and non-deterministic value of p-porder for a sampled signal x(n) over time at point n. Consequently, this method increases the amount of data that can be used by predicting the behavior of the autocorrelation function for significant deviations. The system functions as a recursive filter, where each signal sample is derived from the previous p-samples, except for a random error e(n).

$$x(n)=-\sum_{j=1}^{p}{a}_{j}x(n-j)+e(n)$$

(3)

A crucial aspect of this approach involves acquiring the accurate p-value, which is calculated using the Akaike's Information Criteria (AIC) as demonstrated in Eq. (4) (Sörnmo and Laguna 2005; Shiavi 2006).

$$AIC(p)=\text{ln}({\sigma }_{p}^{2})+\frac{2p}{N}$$

(4)

In this scenario, the AIC is used to determine the optimal order (p-order) of the signal. The AIC considers the signal length (N) and the variance (σ_p²) of the sequence error e(n). The MEM has a wide range of uses in signal processing, including speech recognition, image processing, and time series analysis. In the field of geotechnical and earthquake engineering, this technique can be employed as an experimental method alongside other spectral analysis techniques, like the HVSR, to enhance the accuracy and reliability of results. By employing this method, it can help identify the main periods of the soil while reducing the effects of noise and uncertainties in the data.

3.1.3 Multitaper spectral estimation method

The MSEM, developed by Thomson (1982), is a non-parametric technique employed for estimating the power spectral density (PSD) of a signal. The development of this method was motivated by the need to address the limitations of the traditional periodogram approach, which fails to provide a reliable estimate of the PSD for stationary wide-sense processes (Park et al. 1987). The MSEM utilizes a series of orthogonal tapers (cones) that have optimal concentration properties in both frequency and time domains. These tapers are used to modify the spectra and generate a dependable estimate of the PSD. The tapers are designed to have narrow bandwidths and low sidelobes, which leads to a decrease in the variance of the estimate and an improvement in spectrum resolution (Babadi and Brown 2014).

The tapers used in the MSEM are mutually orthogonal, guaranteeing interference-free combination to produce a weighted average of the modified spectra. This method is especially useful when working with brief sequences, diverse spectra, or a wide range of frequencies. Moreover, the MSEM is resistant to extreme values because it employs overlapping windows and can efficiently handle nonstationary signals. In summary, the MSEM provides an enhanced and adaptable method for estimating the PSD of different signals.

In the MSEM method, the tapers used are Discrete Prolate Spheroid Sequences (DPSS), which were first introduced by Slepian (1978). These sequences are derived from the discrete-time continuous frequency concentration problem for all index-limited m-sequences in a series ranging from 0 to N-1. The objective is to identify the m-sequence that exhibits the greatest concentration of energy within a frequency range of [-W,W] (Slepian 1978; Thomson 1982; Percival and Walden 1993; Babadi and Brown 2014).

This approach enables the determination of eigenvalues λ_κ and eigenvectors g_m for a positive semidefinite operator of order N x N. There are N linearly independent real eigencfucntions associated the eigenvalues λ_κ. W is a positive real number that is less than 1/2. If the amplitude of the spectrum becomes null for frequencies where W <|| f ||< 1/2, it is asserted that the sequence is bandwidth-limited by W.

As a result, the eigenvalues λ_κ are positive real numbers, and the corresponding eigenvectors g_m are orthogonal to each other. The λ_κ values in this problem are constrained to be less than or equal to 1, which indicates the level of energy concentration of the sequence. Equation (5) denotes the mathematical problem involving eigenvalues and eigenvectors equation system per each κ = 0,1,2,…, N- 1 (Slepian 1978; Percival and Walden 1993).

$${\lambda }_{k}\left(N,W\right){g}_{n}^{(\kappa )}(N,W)=\sum_{m=0}^{N-1}\frac{sin\left(2\pi W\left(n-m\right)\right)}{\pi \left(n-m\right)}{g}_{m}^{(\kappa )}(N,W); n=\left\{0,\pm 1,\pm 2,\dots \right\}$$

(5)

It is noted that for the case where n equals m, the expression [sin 2πW(n—m)]/π(n—m) assumes a value of 2W. This technique utilizes κ modified spectra, with each spectrum corresponding to a distinct DPSS sequence, per window. The revised spectra are calculated using the κ-th frequency of the DPSS, as described in Eq. (6). The κ-modified spectra are averaged to generate an estimate of the multitaper spectral power density, as shown in Eq. (7).

$${S}_{k}\left(f\right)=\Delta |\sum_{n=0}^{N-1}{g}_{k,n}{x}_{n}{e}^{-i2\pi fn\Delta t}$$

(6)

$${S}^{MT}\left(f\right)=\frac{1}{K}\sum_{k=0}^{K-1}{S}_{k}(f)$$

(7)

The notation g_κ,n represents the data cone for the κ-th direct spectral estimator. S_κ(f) denotes the κ-th self-spectrum. x_n is the discrete signal, and Δt represents the sampling time. S^MT(f) represents the mean of κ-spectra, which enhances the spectral resolution to its maximum capacity. The Multitaper approach is widely used in various fields, such as geophysics, seismology, neuroscience, and signal processing, for tasks like spectral analysis, noise reduction, and feature extraction (Thomson 1982; Percival and Walden 1993; Babadi and Brown 2014).

In certain conditions, the dominant frequency peak of the Horizontal component is considerably greater than the vertical component, which is exceedingly small and near zero. Consequently, the basic modes of HVSR become unstable. Therefore, it can be difficult to establish a relationship between S-waves and HV Rayleigh waves. This challenge, raised from the unstability conditions, can be mitigated by employing a smoothing technique before computing the HV relationship for Rayleigh waves, similar to the procedure used in analyzing seismic noise data. In this way, Konno and Ohmachi (1998), proposed a smothing window function (W_B), shown in Eq. (8), appropiated for this circunstances, which incorporates the bandwidth coefficient (b), frequency (f), and central frequency (f_c).

$${W}_{B}\left(f,{f}_{c}\right)={\left[\frac{sin \left(lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}\right)}{lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}}\right]}^{4}$$

(8)

3.1.3.1 Konno-Omachi bandwidth coefficient

To ascertain the bandwidth coefficient, referred to as the b-value, within the context of the Konno-Ohmachi window W_B, it is imperative to identify the juncture at which the power is halved, as delineated by Eq. (9).

$${\left[\frac{sin \left(lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}\right)}{lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}}\right]}^{4}=\frac{1}{2}$$

(9)

This leads to the simplified form:

$${\left[\frac{sin \left(x\right)}{x}\right]}^{4}=\frac{1}{2}$$

where

$$x=lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}$$

Addressing the equation equation $\frac{\text{sin}\left(x\right)}{x}={\left(\frac{1}{2}\right)}^\frac{1}{4}$ entails engaging with a transcendental equation. Transcendental equations are not solvable through mere algebraic techniques due to their inherent complexity and often requires numerical methods for approximation or graphical analyses for solution visualization. Significantly, the equation lacks a straightforward inverse for direct solution for x. As x approaches 0, the left-hand side of the equation tends towards 1 and exhibits oscillatory behavior with diminishing amplitude as x increases (refer to Fig. 3A).

Fig. 3

(A) Plot of the function ${\left[\frac{sin \left(x\right)}{x}\right]}^{4}$ y the red line idicating the desired result line at ½. (B) Function of bandwidth $b$-parameter in Konno-Ohmachi smoothing. (C) Graphic of b-value across frequencies f (0.1 to 10 Hz) using a central frequency f_c = 1 Hz. (D) Effects of fifferents b-values on the smoothing

Employing the Brent method (Brent 2013), we derive x = -1.002. Given$x=lo{g}_{10}{\left(\frac{f}{{f}_{c}}\right)}^{b}$, we infer$b*lo{g}_{10}\left(\frac{f}{{f}_{c}}\right)=-1.002$. Solving for f/f_c ratio yields$\frac{f}{fc}={10}^{\frac{-1.002}{b}}$. This expression, symbolized by b, showcases a graphical representation (Fig. 3B), approaching unity with increasing b-values. Consequently, excessively high, or low, b-values are inadvisable. For instance, examining potential b-values across frequencies f ranging from 0.1 to 10 Hz with a central frequency f_c of 1 Hz through $b=-1.002/{log}_{10}(f/fc )$​, illustrates that higher b-values might exaggerate smoothing effects, while lower values might understate them, as depicted in Fig. 3C. A pragmatic b-value may be deduced by defining the bandwidth in octaves of the limiting frequency f_h​, representing the f/f_c ratio, where f_h = 10^–1.002/b, leading to the following formulation:

${{f}_{h}}_{i}={10}^{\frac{{\text{log}}_{10}2}{2{n}_{i}}}$, where ${n}_{i}={2}^{i}$ for I = {0, 1, 2, 3}

Consequently, if f_h​ is represented as a vector with values 1.414, 1.189, 1.091, 1.044 for each n_i, equality can be achieved by setting ${10}^{\frac{x}{{b}_{i}}}={10}^{\frac{{\text{log}}_{10}2}{2{n}_{i}}}$. This methodology enables the determination of a vector of b-values through the equation:

$$\frac x{b_i}=\frac{{\text{log}}_{10}2}{2n_i}\Rightarrow bi=\frac{2xn_i}{{\text{log}}_{10}2}\Rightarrow b=\begin{bmatrix}6.657\\\begin{array}{c}13.313\\\begin{array}{c}26.626\\53.252\end{array}\end{array}\end{bmatrix}$$

Furthermore, an optimal b-value should coincide with the ¼ octave bandwidth. Via comprehensive graphical and numerical analysis, a b-value of 27 is discerned, situated between the recommended ranges of 20 and 30 by Konno and Ohmachi (1998). To elucidate the influence of varying b-values (5, 10, 15, 20, 30, and 40) on the smoothing window, a graphical representation is provided (Fig. 3D), employing a central frequency of 1 Hz and examining frequency ranges pertinent to the study, spanning from 1 to 10 Hz and extending beyond to 30 Hz to observe the effects on the smoothing windows. For instance, selecting b = 5 might result in the underestimation of frequencies between 4 and 15 Hz by the smoothing function, whereas b = 40 might inadequately smooth the high frequencies near 10 Hz. Thus, the selected value resides between the curves that depict the values of 20 and 30, giving a moderate equilibrium that are smoothing the narrow high frequencies.

3.2 Data acquisition

This study is founded on a reassessment of 38 seismic noise recordings that were previously gathered from the La Chana neighborhood of Granada in the past decade. This dataset comprises a total of 38 records. It includes 34 records from 2010 (Paton 2010), 2 records from 2013 (Velasco 2013), and an additional 2 records from 2017 obtained from locations near La Chana (Lucas 2017). Figure 4 provides a comprehensive depiction of the spatial arrangement of seismic noise stations.

Fig. 4

Locations of seismic noise records across Granada City. Red circles represent the stations from 2010, green circles indicate the two stations from 2013, and yellow circles denote the two stations from 2017

The data collected in 2010 used a portable digital seismograph with a Geospace HS-1 triaxial sensor with three geophones. The sensor operated at a frequency of 2 Hz. Furthermore, the data acquisition setup included a three-channel SARA SADC20 digitizer. The digitizer possesses a resolution of 24 bits, a sensitivity of 0.24 Volts per count, and a sampling rate of 100 samples per second. Subsequently, seismic noise data from 2013 and 2015 were recorded using a Taurus digital seismic station, coupled with a Nanometrics Trillium Compact 20 s triaxial sensor with a uniform response time of 20 s at 100 Hz, and a frequency of 100 samples per second. The instrumental dynamic response was designed to ensure accurate results within the frequency range of 1–10 Hz.

3.3 Data processing

The workflow used for data from the 2010 campaign was traditional for HVSR, resulting in 26 stable and reliable curves. The raw records from the resulted curves are reprocessed together with more recent records (from the years 2013 and 2017) using the MEM and MSEM methods, as depicted in Fig. 5 and in the following sections.

Fig. 5

General processing flowchart implmented in this study

3.3.1 Treatment of data from 2010 campaign

For this dataset the reprocessing was performed utilizing the Geopsy code (Wathelet et al. 2020). The workflow begins with the import of raw seismic data collected during a 2010 campaign from 34 stations, formatted in Seed. This data is then subjected to bandpass filtering using a Butterworth filter with cutoff frequencies set between 0.1 and 10 Hz, aiming to isolate the frequency range of interest for seismic analysis. Following filtering, the Horizontal to Vertical (HV) module parameters are established, with time windows set to 20 s, 50% overlap, and anti-triggering enabled. Subsequently, Konno-Ohmachi smoothing is applied using a constant value of 40, and Tukey windowing equivalent to 5% of the time window is implemented. The HVSR is calculated based on the processed data, spanning the filtered frequency range from 0.1 to 10 Hz with a logarithmic step and 100 data points. The Geopsy code uses the periodogram or modified periodogram (Welch 1967) as spectral method to calculate the HVSR. Reliability checks are conducted on the resulting HVSR curves according to SESAME (2004) guidelines, resulting in the identification of 33 reliable curves and one unreliable curve. Stability analysis follows, with 26 stable curves of which 6 exhibit clear fequency peaks. This comprehensive workflow ensures the accurate processing and evaluation of seismic noise data to derive meaningful HVSR curves for further analysis and interpretation. The results are summarized in Tables 1 and 2.

Table 1 Summary of reliability conditions of seismic noise recordings for 2010 data

Table 2 Summary of seismic noise records stability and amplitude check for 2010 data

The HV rotate module of the Geopsy program was applied to the 26 reliable and stable curves obtained from the previous stages. This was performed to determine the orientation of the particle motion of the sismic wave to obtain insigth about the seismic sources and propagation paths. The workflow performed was smilar to the previous HVSR standar procedure. First is called again the raw data of the concerning 26 records. This data is then subjected again to a bandpas filtering with cutoff frequencies set between 0.1 and 10 Hz. The HV rotate module parameters are stablished as before, applying again a Konno-Ohmachi smothing and a Tukey windowing. The output results are between 0.1 and 10 Hz with a logaritmic step. The HV rotate were calculated from 0° to 180° every 10°. As result, some azimutal frequencies are centered near 1.5 Hz with two preferencial bandwidth angles, one between 0º and 40º, and the other between 140º and 180º, generating doubts about if this 1.5 Hz are representing the natural frequency of the site.

3.3.2 Reprocessing the dataset from all campaigns

In order to verify the accuracy of previous results and eliminate doubts about the presence of artificial directions caused by an unbalanced instrumental component-or by anthropogenic sources-, two additional records were collected in 2013 (CH1 and CH2 stations) in La Chana and two more in 2017 in nearby areas (RIO and DIV stations). The most recent records, collected using broadband seismometers, have been appended to the preexisting dataset of 26 stable and reliable records obtained in 2010 (refer to Fig. 4). The data from these 30 stations has been analyzed using the MEM and MSEM methods to examine their HVSRs.

The MEM approach initiates by taking into account 30 raw seismic data files from the 2010, 2013, and 2017 expeditions in Seed format. The data is subsequently processed by the North, East, and Vertical components. It is normalized by subtracting the mean and detrended to eliminate any linear trends. A 4th order Butterworth filter is used to apply bandpass filtering to each component, with a frequency range between 0.1 and 10 Hz. The time period is subsequently separated into five distinct parts of the day, referred to as time windows. These time windows are as follows: 00:00–05:00, 05:00–09:00, 09:00–14:00, 14:00–19:00, and 19:00–24:00. A matrix is subsequently generated to symbolize these divisions.

The AR model's optimal order (p) was determined by calculating the AIC for each window and then averaging the AIC outputs. An assessment was conducted on a series of p-orders ranging from 0 to 100. The AR model coefficients and residual variances for each p-order were obtained using the arburg function in MATLAB. The optimal p-order was determined by minimizing or stabilizing the residual variance within the 90% confidence interval, thus ensuring the robustness of the model selection. For each window, the p-order with the lowest variance within the 90% confidence interval was chosen. Afterwards, the power spectrum for all windows was calculated using MATLAB's pburg function, taking into account the specified p-order, a sampling rate of 100 Hz, and a resolution of 2048 samples.

Correlation analysis is performed on time windows to detect any unrelated dataset that may be attributed to artificial causes, such as traffic. Windows are considered related if the correlation between them is 0.8 or higher, and their mean values are then computed. Ultimately, the smoothed spectra undergo HVSR analysis, aiming to detect distinct peaks around 1.5 Hz in most situations and potentially an additional peak around 2.5 Hz in certain cases.

Utilizing the identical raw dataset in seed format as in the prior aproach, the MSEM technique was employed to enhance spectral resolution and depict artificial sources characterized by sharp spectral peaks. Initially, the data is processed and consolidated into a single matrix file comprising three columns, each representing a different component. The MATLAB function pmtm is then utilized to calculate the PSD, setting the time-halfbandwidth product (N_W) to 4. This setting is related with the required tapers (K) from the DPSS (K = 2N_W -1), aiming to achieve an optimal balance between smoothing and resolution. The sample resolution is established at 2048, with a sampling rate of 100 samples per second. Subsequently, a specific function is executed to remove narrow peaks, potentially artifact sources, by setting a threshold of 6 dB. Peaks surpassing this threshold are replaced with the median value between the peak's boundaries. Following this, a Konno-Ohmachi smoothing technique is applied to decrease variance, which requires the calculation of the b parameter associated with the smoothing's bandwidth. The optimal b-value was determined to be 27, with the calculation method detailed previously in Konno-Omachi bandwidth coefficient subsection. Finally, HVSR analysis was conducted, yielding new curves that facilitate identifying the fundamental frequency and dominant period of the soil in La Chana. This resulted in the creation of a map depicting the distribution of periods and frequencies within the study area.

3.4 Statistical analysis

A graphical analysis using boxplots was conducted to statistically compare the fundamental f₀ frequencies and A₀ amplitudes obtained from each method. This analysis aimed to observe the extent of variation in the fundamental frequencies and amplitudes when each method was applied. Subsequently, a correlation analysis was conducted to examine the relationship or similarity between the three data groups. This analysis involved examining the correlation matrix of the fundamental f₀ frequencies and A₀ amplitudes of each approach.

Finally, to assess the impact of the narrowband frequency centered at 1.5 Hz, a bootstrap technique was employed to generate resamplings from frequencies near 1.5 Hz-ranging between 1.4 and 1.6 Hz-for each HVSR method (Traditional, MEM, MSEM). This method does not rely on specific assumptions about the data distribution, making it especially useful for handling restricted data that do not conform to a normal distribution or when sample sizes are small. In our study, the sample sizes were comprised of four observations for the Traditional method, 15 for the MEM, and 11 for the MSEM, forming the original sample space.

From this dataset, 1000 bootstrap samples were produced by selecting observations with replacement. Each bootstrap sample had the same size as the original, yet replacement allowed some observations to recur, while others might not appear at all in a given sample. The median of the filtered frequencies was computed for each sample. This procedure was repeated across all generated samples, resulting in a distribution of estimated medians.

The collection of these medians from multiple bootstrap samples creates a bootstrap distribution for the median. This distribution provides an estimate of the variability and uncertainty of the median frequencies near 1.5 Hz for each HVSR method, thereby facilitating a robust, non-parametric estimation of the median fundamental frequencies for each method. These medians are subsequently utilized to perform a Kruskal–Wallis test, which assesses the presence of significant disparities in the frequency distributions around 1.5 Hz among the different HVSR methods. The null hypothesis posits that the data are not influenced by these types of narrow signals centered at 1.5 Hz. A low p-value from this test would suggest noteworthy distinctions between the groups, indicating an impact of the narrowband frequency on the frequency distributions.

4 Results

4.1 Reability and stability analys for the 2010 dataset

The initial traditional analysis of the seismic noise data from 2010 campaign revealed fundamental frequencies f₀ of approximately 1 Hz, with f₀ peaks reaching around 1.5 Hz. The main amplitude A₀ ranged from 1.6 to 3.9 units. However, due to the limited sensitivity of the instrument, only f₀ higher than 1 Hz are considered as viable outcomes. Therefore, a total of 33 highly reliable HVSR curves are obtained, with the exclusion of the C36 curve after assessing its reliability based on the criteria outlined in the SESAME project (2004) conditions, as illustrated in Table 1

The C36 curve, which was rejected, had a f₀ that is less than the quotient of 10 divided by the window length (lw). Furthermore, the f₀ frequency interval exhibits a higher standard deviation of the A₀ amplitude. Out of the 33 curves that were accepted in the previous reliability analysis, a stability and amplitude analysis was conducted. It was determined that 26 of these curves were stable following the SESAME Project (2004) criteria. Among these stable curves, only 6 showed clear A₀ amplitude peaks at frequencies higher than 1 Hz. The stability analysis is summarized in Table 2. Figure 6 displays the 6 records that exhibit clear peaks (C11, C28, C34, C35, C45, and C47).

Fig. 6

Reliable and stable HVSR curves with clear amplitude peaks, corresponding to HVSR curves of the C11, C28, C34, C35, C45, and C47 records, respectively

The average f₀ frequency is 1.0 Hz ± 0.30 Hz, the average A₀ amplitude is 2.5 units ± 0.38 units if only are considered the 26 raliable and stable curves. Some records, including C28, feature f₀ frequency centered at 1.5 Hz, which is replicated in other HV curves with lower amplitudes.

4.2 HV rotate analysys

The HV rotation plots were generated for the 26 records that demonstrated a degree of stability using the SESAME (2004) criteria. For frequencies greater than 1 Hz, the HV rotate plots display a bandwidth between 1 and 1.5 Hz, indicating a preferential direction from 0° to 40°, and from 120° to 180° azimuth, with A₀ amplitudes of approximately 3 units, indicating a gap between 40° and 120°. Some HV rotate plots depict a narrow band with pronounced directionality around 1.5 Hz (e.g., HV rotate plots of records C15, C19, C25, C26, C28 and C38 shown in Fig. 7). This suggest that the frequency content is not coming from all directions, so it is possible that the frequencies near 1.5 Hz are the result of human activity, such as vehicular traffic, industry, or an instrumental error.

Fig. 7

HV rotate graph of some seismic noise recordsreliable and stable from 2010 data. The black frame higlighs the records identified in the HVSR analysis as clear peaks

Consequently, doubts arise about the veracity of the results, especially for the 1.5 Hz frequency, due to possible errors in the response of the Geospace HS-1 triaxial sensors that may induce some bias in the directionality. To rule out this issue, the effect of 1.5 Hz peak into 2010 data was analyzed by the MEM and MSEM techniques to the 26 stable records, adding broadband records from 2013, and from 2017 (see stations CH1, CH2, RIO, and DIV in Fig. 4).

4.3 MEM and MSEM analysis in HVSR

In order to carry out the MEM, the AIC criteria must have been previously met to estimate the p-order of the AR model, whose mean value was 60; however, the specific p-value was considered for each record due to the varying recording length and number of samples in each case. Thirty HVSR plots were generated using the MEM technique. As an example, the new HVSR curves from several records, along with their values of the AR model, are displayed in Fig. 8.

Fig. 8

Autoregressive model order value according to Akaike's criteria (AIC) for recorded data with clear peaks, and HV curve using the MEM technique for some records (C11, C28, C34, C35, C45, C47, CH2, RIO). The black, red, and blue frames are indicating the data from the 2010, 2013, and 2017 campaigns, respectively

One of the general characteristics is that the HVSR curves have a flat, or smooth, response at frequencies below 1 Hz, thereby resolving the problem of having low spectral frequencies in the vertical component, highlighting the frequencies above 1 Hz, and aiming the identification of the frequency peaks (grouped in Table 3). The fundamental frequencies and amplitudes were computed using their respective mean value and standard deviation.

Table 3 Peaks of fundamental frequencies and amplitudes observed in HVSR curves with MEM technique

The average A₀ amplitude was 2.88 $\pm$ 1.15 units, and the average f₀ frequency was 1.8 Hz $\pm$ 0.54 Hz, as determined by the HVSR curves obtained from MEM. Nonetheless, fundamental f₀ frequencies around 1.5 Hz were obtained again (e.g., stations C15, C16, C19, C21, C27, C28, C29, C34, C37, C38, C44, CH1, DIV and RIO, see Table 3), indicating that the narrow frequency bands previously observed in HV rotate are again recognized with MEM, which affects the HVSR result.

The preceding evidence suggest that the 1.5 Hz peaks are not induced by instruments, supressing any doubt about the instrumental bias in the 2010 data, as this frequency is reproduced in the data collected by broadband seismometers (such as CH2, DIV, and RIO). In some instances, a secondary mean f₁ frequency of 2.75 $\pm$ 0.65 Hz and a secondary average A₁ amplitude of 1.67 $\pm$ 0.34 units were identified.

These secondary f₁ frequencies, or second peaks, being of lower amplitude than the fundamental f₀ frequencies are not highlighted with the MEM, presenting only a cleaner spectral responses centered at f₀. Therefore, Burg’s algorithm concentrates on reproducing the 1.5 Hz peaks when they are present, this being an issue that can be avoided, or at least prevented, with Thomson’s high-resolution multitaper analysis (MSEM). In addition, the results show that the MEM techinique, despite representing very clean spectra, does not allow us to assess the reliability of the results.

Then, the Thomson algorithm (MSEM) was applied to the data previously analized with the MEM method, since theoretically it optimally solves the narrow spectral peaks, such the concerned 1.5 Hz, and allows separating them before the Konno-Ohmachi smoothing and calculating the HVSR. In this way, it was necessary to obtain the b-value parameter (bandwidth coefficient) for Konno-Ohmachi smoothing function. This function requires the power spectrum, represented as a vector, along with the corresponding frequency values, the frequency spectrum boundaries, and the appropriate bandwidth coefficient, as input parameters.

Once the correct b-value was obtained, as were explained on the the methodological section, having the power spectra of each component with the MSEM technique, narrow peaks were suppressed and attenuated, then doing the HVSR and Konno-Ohmachi smoothing, obtaining another 30 new HVSR curves (e.g. C11, C28, C34, C35, C45, C47, CH2, and RIO records in Fig. 9). In the Multitaper power spectrum plots, for each of the three components, clean and smoothed responses are observed (see Fig. 9), where very hardly appear narrow frequency peaks around 1.5 Hz. The results are summarized in the Table 4.

Fig. 9

Power spectrum density Multitaper for C11, C28, C34,C34, C45, C47, CH2, and RIO records by horizontals (East and North) and vertical (Z) components in blue, red, and green color lines, respectively. HVSR for spectrum Multitaper applied to for C11, C28, C34,C34, C45, C47, CH2, and RIO records with Konno-Ohmachi smoothing in ligth-blue color lines

Table 4 Peaks of fundamental frequencies and amplitudes observed on HVSR curves with MSEM technique

The mean f₀ and A₀ obtained from the HVSR analysis using the MSEM approach are 1.88 ± 1.03 Hz and 4.19 ± 1.43 units, respectively. The secondary peak exhibited f₁ and A₁ values of approximately 2.74 Hz and 2.59 units, respectively. Nevertheless, there are still noticeable increases in amplitude at approximately 1.5 Hz due to the fact that the vertical component of the records has a lower spectral content compared to the horizontal components. This causes the HVSR to be amplified, resulting in the persistence of the 1.5 Hz frequency's effect as a clear peak in some records.

4.4 Statistical comparissons

A quantitative comparative analysis of the HVSR is performed by statistical summary in graphical plots for the mean frequencies f₀ and amplitudes A₀ across the different methods employed-traditional, MEM, and MSEM- as shown Fig. 10. Then, the three datasets were correlated, performing a correlation matrix between the mean frequencies and amplitudes as shown in Fig. 11.

Fig. 10

Comparative boxplots for mean frequency (f₀) and amplitude (A₀) by employed HVSR method (traditional, MEM, and MSEM). The outlier values are labeled to show the variability of the data through the different spectral ratio methods

Fig. 11

Correlation matrix between the mean frequency (f₀) and amplitude (A₀) by employed HVSR method (traditional, MEM, and MSEM)

The conventional HVSR concentrates frequencies primarily at 1 Hz, exhibiting average amplitudes of 2.5 units and a median of 2.8 units. This distribution emphasizes both lower frequencies and those in the vicinity of 1.5 Hz. The MEM has caused a change by effectively removing low frequencies, specifically those below 1 Hz. This has led to values that are concentrated around 1.8 Hz as the average, with a median at 1.45 Hz. The average amplitude is 2.88 units, while the median amplitude is 1.88 units. The MSEM exhibits mean frequencies of 1.88 Hz and median frequencies of 1.6 Hz, along with mean and median amplitudes of 4.1 units. The correlations between the fundamental frequencies obtained by each method often exhibit negative values or are close to zero, suggesting that there is no linear association between the employed methods, particularly regarding the observed frequencies. This is logical because the MEM and MSEM have effectively eliminated the low frequencies and narrow bandwidth frequencies that were detected by the traditional method. However, the amplitude relationship between the first two methods improves, but it disappears in the MSEM. This is because the MSEM is more sensitive to amplifications, even though multiple tapers and smoothing procedures are applied.

Bootstrap analysis revealed a statistically deviation from the 1.5 Hz frequency for the last methods (Fig. 12), with 95% confidence intervals for the mean differences not encompassing zero. These findings indicate a discernible influence of the 1.5 Hz frequency on the f₀ values within each HVSR method, rejecting the null hypothesis of no influence of this frequency.

Fig. 12

Mean frequency (f₀) distribution near 1.5 Hz for HVSR method (traditional, MEM, and MSEM)

Comparative analysis through the Kruskal–Wallis test demonstrated significant differences in the f₀ distributions across the three datasets. The p-value obtained was well below the 0.05 threshold, indicating that the variations in f₀ values among the different HVSR methods are not by random chance, thereby underscoring the distinct nature of each method's response to the underlying geophysical processes.

5 Discussions

Comparing the mean values for each of the employed techniques reveals that the results obtained by the original Nakamura's HVSR are not entirely reliable in GB, because the low frequencies have much lower amplitudes in the vertical component compared to the horizontal components, causing frequency peaks below 1 Hz as artifacts; this problem is solved by the application of MEM and MSEM techniques instead the traditional one in the HVSR.

There is a significant qualitative difference in the shape of the HVSR curves depending on the spectral technique used. Thus, it can be argued that MSEM generates more reliable HVSR curves because it can locate narrow spectral peaks more accurately, which allows attenuating them and reducing the effects of anthropogenic sources despite the fact that the standard deviation increases for the values of frequency and amplitude with this method. However, the similarity of frequencies obtained between MEM and MSEM indicates that both methods can help to remove narrow spectral bands that may be associated with anthropogenic activity.

The reason why MSEM is superior to MEM in reducing the anthropogenic peak frequency is because there is frequency replication in certain records, like C28, when using MEM, whereas this narrow bandwidth frequency disappears when using MSEM. To determine if these techniques are effectively replicating 1.5 Hz, a quantitative bootstrap method is performed to evaluate the frequency distribution near 1.5 Hz for strech bandwidths (Fig. 12). This analysis demonstrates that the initial methods exhibit a concentrated distribution of frequencies around 1.5 Hz benchmarck, whereas MEM displays some variability and MSEM deviates the most from this frequency value. However, the mean statistical values do not accurately reflect this outcome.

The findings suggest that the occurrence of frequency peaks at approximately 1.5 Hz (with a fundamental period of T₀ = 0.67 s) does not accurately indicate soil movement when identified using the traditional HVSR method, primarily due to its narrow spectral bands. Paton (2010) indicated that the successions of 1.5 Hz peaks were due to the complexity of the area's geology, possibly because of a basin effect, but not due to soil movement. However, if these spectral peaks reappear in the HVSR analysis after applying the MEM and MSEM on the corresponding spectra, it could indicate actual soil movement. Moreover, these methods are unable to accurately determine whether these frequencies are caused by basin effects or natural soil movements, opening a window for furhter reseach.

Consequently, the HVSR results were classified into zones following the application of the MSEM, where the fundamental frequency of approximately 1.6 Hz with periods ranging from 0.45 s to 0.80 s are repsenting the natural soil movement of studied zone. These periods tend to increase to the north-northeast of the La Chana neighborhood, diminishing their frequency. Similarly, the periods of ground vibration decrease toward the southwest, where the fundamental frequencies increase, as depicted in Fig. 13.

Fig. 13

(A) Distribution of fundamental frequencies obtained from MSEM HVSR. (B) Fundamental periods obtained from MSEM HVSR

In contrast of prior findings (Cheddadi 2001), who obtained periods between 0.2 and 0.5 s, and others who indicated that the shortest periods are concentrated in the central zone of the La Chana neighborhood (Paton 2010), the current results indicate that the shortest periods are concentrated in the western, central, and southern zones. This may be consistent with former geological descriptions (Valverde Palacios 2010; Feriche 2012), who argued that La Chana sits on an old alluvial formation with silty clay lenses beneath carbonates, sands, and gravels. It is inferred that the most hard material is the one with the shortest fundamental periods, possibly due to the presence of carbonates, and the least competent material is the one with the longest fundamental periods, due to the presence of poorly consolidated sands and gravels with underlying clay lenses.

Henceforth, based on the similarity of the periods to those described formerly (Valverde Palacios 2010, Navarro et al. 2011), values between 280 and 330 m/s have been used as reference data for S-wave velocities (V_S), since no data inversion was performed to infer and verify the wave velocities. Consequently, a mean Vs of 310 m/s is assumed.

In addition, if the Rayleigh wave velocity (V_R) is roughly 0.9194 times the V_S (for a Poisson's ratio of 0.25) then V_R is near 285 m/s. Using the simple relation, ${V}_{s}=4\times \frac{H}{T}$, the basin's depth was calculated (Fig. 14B), or pseudo-depth, where V_s is the S-wave velocity, $H$ the sedimentary depth or thickness, and T the fundamental period.

Fig. 14

(A) Distribution of fundamental amplitudes obtained from MSEM HVSR. (B) Pseudo-depth obtained from MSEM HVSR with a mean Vs of 310 m/s

From the preceding, is deduced that basement represent the main seismic impedance constrast, uplifting in areas with low ${T}_{0}$, but to clarify the basement depth accurately, it is necessary to invert the results, generate 1D-velocity profiles from S-wave, and compare these insights with MASW or MSOR to obtain more reliable basement depth results. However, the calculated depth is near to the basement approach made by Rodríguez-Fernández and Sanz de Galdeano (2006) from old seismic reflection profiles.

The ${A}_{0}$ amplification of the fundamental frequency may also help to explain the results, because as ${A}_{0}$ increases around a ${f}_{0}$ frequency, the impedance contrast between the underlying basement and the upper sedimentary column increases, particularly if a high proportion of soft soil is present. The highest ${A}_{0}$ are concentrated in the south-central and west-central regions of La Chana (see Fig. 14A), indicating that there is a greater contrast between the lower rock strata and the overlying soft soil in these areas, which may have a greater effect on the urban settlement, whose structures may resonate with the natural vibration of the soil during a seismic event.

In the south-central zone, where the ${T}_{0}$ is 0.7 s and the ${A}_{0}$ is 6.5, 14-story buildings would enter resonance with a greater amplitude than in other sectors if the equation $T=0.049N$ (Navarro et al. 2004, 2007) is applied, where $N$ is the number of floors. Consequently, for ${f}_{0}$ = 1.5 Hz, ${T}_{0}$ = 0.67 s is obtained, affecting structures with 12 to 14 stories in the event of an earthquake. In contrast, if the situation is evaluated using the equation $T=0.09N$ for buildings with reinforced concrete frames without the assistance of stiffening screens (NCSE 2002), the ratio will be doubled, with 6- and 7-story buildings being significantly affected by ground movements. The lithology corresponds to type III soils composed of sands and silty clays in the form of lenses, with the presence of some conglomerates according with the Spanish Constructive Normative (NCSE 2002).

According to the range of fundamental periods, and comparing the lithology described by Valverde Palacios (2010) and Navarro et al (2011) with the classification of geotechnical sites according to the fundamental periods (Bray and Rodriguez-Marek 1997), the study area corresponds to soft weathered rocks for periods of 0. 45 s (type C-1) with thin layers of soft clays for periods shorter than 0.7 s (type E-1), with the presence of superficial soft rocks associated with periods shorter than 0.5 s (type C-2) and deep stiff rocks for periods between 0.7 s and 0.8 s (type C-3). The possible soft rock layers coincide with the presence of sands and poorly consolidated clasts from the old alluvial formation, the thin clay layers coincide with the clay lenses described above and the stiff rocks such as limestones, increasing the impedance contrast at depth.

6 Conclusion

When performing HVSR, the algorithm used by traditional method to process seismic noise signals recorded with non-wideband instruments could generate unstable or unclear responses, particularly at low frequencies. However, frequency peaks in the 1 to 10 Hz range can be observed, as confirmed by other spectral estimation methods.

There is evidence of a frequency of 1.5 Hz, which is initially associated with industrial activity due to its preferential direction and narrow bandwidth in the HV rotate analysis. Earlier authors have suggested that this is the result of possible basin effects, which is implausible given its directivity, confirming that it is not the result of instrumental errors. Similarly, when applying Burg's algorithm (MEM), its effect persists in the region of La Chana, requiring the application of Thomson's Multitaper algorithm (MSEM) to detect narrow spectral bands associated with impulsive sources of anthropic origin by removing a frequency of 1.5 Hz from each spectral component of the original signals.

However, after applying the HVSR to the power spectra obtained with the MSEM, the frequency of 1.5 Hz reappears but not with a narrow bandwidth as in the other methods, suggesting that although the signal appears randomly in the city of Granada, it may correspond to the soil behavior in the La Chana sector. Therefore, it is advised to continue investigating the origin of this frequency by expanding the study area, but this time with broadband seismometers and on non-working days.

In addition, when comparing the data processing methods, a better result is obtained when performing Thomson's Multitaper spectral approach, since it ensures that the signal in each HV-components does not contain narrow energy peaks, whose origin is obviously from artificial sources, and in turn gives a higher spectral resolution in the final result. Therefore, with the Thomson technique, the HVSR provide a simple way to verify the reliability and stability of the results, as well the identification of clear peaks in comparison with the results obtained by the Maximum Entropy Method and that with the traditional algorithm, which uses the periodogram or modified periodogram (Welch) as spectral method.

The fundamental frequency of La Chana is 1.6 Hz, which corresponds to fundamental periods between 0.45 s and 0.90 s, increasing in the NNE (thereby decreasing its ${f}_{0}$), and decrease in the SSW (increasing ${f}_{0}$). When evaluating the ratio of fundamental periods as a function of the number of building floors proposed by Navarro et al. (2004) for the Granada region, 9-story buildings will be affected for periods of 0.45 s and 18-story buildings will be affected for periods of 0.88 s, highlighting those cases where the amplification is maximum (${A}_{0}$=6.5), whose fundamental period is 0.7 s, impacting 14-story buildings in greater proportion if a major earthquake occurs. Alternatively, if the relationship proposed by NCSE (2002) is evaluated, the affected heights would be half as great.

Similarly, the results are consistent with the lithology described by other authors (Valverde Palacios 2010; Navarro et al. 2011; Feriche 2012), relating the study area to an ancient alluvial formation, corresponding to poorly cohesive soils composed by sands and silty clays in the form of lenses (geotechnical sites type C-1 and E-1, with the possible presence of some conglomerates. Without estimating a model of S-wave velocity, it is not possible to accurately determine the sediments' depth despite the results are near to the basement approach of Rodríguez-Fernández and Sanz de Galdeano (2006). This research, which was developed from earlier seismic noise data, has generated new insights that could be used as another tool to mitigate seismic hazard and vulnerability of structures in urban areas, such as the city of Granada.