1 Introduction

Although reliable prediction of earthquakes is not feasible at present, mitigation strategies can be put in place if the arrival of damaging ground shaking can be known in advance. Earthquake Early Warning (EEW) systems can provide such information and are vital technologies for emergency preparedness and for reducing the effects of secondary hazards following earthquakes (e.g., risk of fire). For the southwestern British Columbia region of Canada, where it is exposed to a high level of seismic hazards from a variety of earthquake types within the continental crust and subducting oceanic plate (Atkinson 2005; Cassidy et al. 2010), Ocean Networks Canada (ONC) (in collaboration with Natural Resources Canada, NRCan), began developing an EEW system in 2015, which has been operational as of April 2023 (Schlesinger et al. 2021; Babaie Mahani et al. 2023). The system detects earthquakes based on rapid identification of P waves and determines epicentral location and magnitude. Alerts are then generated and sent to infrastructure subscribers.

Deployments of the onshore and offshore stations within the ONC EEW system involved a remarkable effort in planning to achieve an adequate spatial densification of telemetered recording sites. This allows for ample stations to be available to quickly detect an earthquake, while at the same time providing redundancy in case of station loss. Ideally, seismic stations used in earthquake monitoring should be placed on bedrock and in quiet areas far from noise sources. However, the network configuration is not uniform as some stations are placed in less ideal locations due to infrastructure or logistical limitations. For example, subsea stations need to be placed near nodes to enable power and internet connections. Land-based stations are not exempted from these limitations, which include recorded waveforms contaminated by natural and anthropogenic noise. Non-ideal circumstances limit the ability to detect seismic phases, which can be obscured within the background noise. The lack of bedrock condition can result in amplification of ground motion and overestimation of vital source parameters such as earthquake magnitude.

In this study, we take a close look at the ONC EEW system to provide detail analysis on earthquake magnitude estimation at each station and study site condition including non-linearity and site dominant frequency. We first explain how earthquake magnitude is determined by the ONC EEW system and provide statistics on magnitude estimates at each station. We then compile earthquake ground motion data, analyze site condition using horizontal-to-vertical spectral ratio (HVSR), and discuss the results.

2 Magnitude estimation by the ONC EEW system

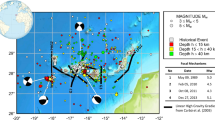
ONC uses both onshore and offshore stations for a source-based regional EEW system in southwestern British Columbia (Fig. 1). All sites (onshore and offshore) are equipped with accelerometers. Global navigation satellite system (GNSS) antennas (onshore) and tiltmeters (offshore) are also collocated with accelerometers at several locations. GNSS data are processed using the Precise Point Positioning (PPP) algorithm provided by the Canadian Geodetic Survey with three instances of the PPP products (in the order of increasing accuracy): broadcast orbit, float, and integer.

Fig. 1
figure 1

Map of southwestern British Columbia showing active tectonic plates, seismicity, and seismic stations of Ocean Networks Canada (ONC) and Natural Resources Canada (NRCan). Stars show the locations of the two earthquakes discussed in Figs. 4 and 5. EP: Explorer Plate, JdFP: Juan de Fuca Plate. Stations shown in Figs. 4 and 5 are labeled on the map as BAMF: Bamfield station, NCBC: Barkley Canyon Upper Slope South station, and BACME: Barkley Canyon Mid-East station

Full size image

The ONC EEW system relies on parametric data (e.g., P-wave arrival times) from each station to associate detections into events. For onshore stations, parametric data are extracted from waveforms on-site (from accelerometer and GNSS) whereas waveforms from offshore stations are transmitted via the power and fiber optic cable that serves the NEPTUNE observatory (Schlesinger et al. 2021), to which the underwater instruments are connected, to a data center in Port Alberni, British Columbia, where parametric data are extracted. Parametric data are then sent to a data center at the University of Victoria (as well as to a secondary data center located 400km away in Kamloops, BC) where they are associated into earthquake parameters (epicenter location, origin time, and magnitude) and alerts.

Parametric data include those obtained by accelerometers only (seismic parameters) and those obtained through combining the accelerometer and GNSS data (seismo-geodetic parameters) via a Kalman filter (Kalman 1960; Schlesinger et al. 2021). Each of the three components of accelerometer and the respective PPP data are passed through the Kalman filter to generate unbiased displacement time series. The general idea of the Kalman filter is to predict a system's behavior from incomplete observations. The problem here is to predict high resolution displacement from acceleration and PPP data which are available at different times and rates from accelerometers and GNSS devices. Double integration from acceleration time series produces bias that would let the integrated signal grow out of bands over time and small errors in the very-low frequency components would be disproportionally amplified. The goal is to force the bias and the low frequency component in the combined displacement time series to largely follow the PPP data while retaining the high-frequency components derived from double integration of the acceleration time series (Rosenberger et al. 2018). Note that at offshore stations, tiltmeters provide acceleration data and are usually used as backups in case data are not available from accelerometers. Seismic parameters include P- and S-wave detection (arrival times), P-wave predominant period, P-wave peak displacement (\({P}_{d}\)), and Japan Meteorological Agency (JMA) intensity amplitude. Seismo-geodetic parameters include P-wave peak displacement (\({P}_{D}\)) and peak ground displacement (\(PGD\)). Here, we only describe \({P}_{d}\), \({P}_{D}\), and \(PGD\) that are used in magnitude determination.

\({P}_{d}\) is calculated from the displacement time series obtained by double integration of acceleration time series and it is the absolute maximum displacement value from the vertical component over a 4 s time window immediately after P-wave detection (Kuyuk and Allen 2013; Rosenberger 2019). Kuyuk and Allen (2013) provided a global relationship between \({P}_{d}\) and earthquake magnitude as:

$${M}_{{P}_{d}}={c}_{0}{log}_{10}\left({P}_{d}\right)+{c}_{1}{log}_{10}\left({R}_{epi}\right)+{c}_{2}$$
(1)

where \({c}_{0}\) = 1.23, \({c}_{1}\)= 1.38, and \({c}_{2}\)= 5.39. In Eq. (1), \({P}_{d}\) is in cm and \({R}_{epi}\) is epicentral distance in km. \({P}_{D}\) and \(PGD\) use the two horizontal components and three components of the unbiased displacement time series, respectively (from each of the available PPP solutions of broadcast orbit, float, and integer) as (Crowell et al. 2013; Rosenberger et al. 2018):

$${P}_{D}={max}_{t=0}^{t=5sec}\sqrt{{d}_{N}{(t)}^{2}+{d}_{E}{(t)}^{2}}$$
(2)
$$PGD={max}_{t=0}^{t=200sec}\sqrt{{d}_{N}{(t)}^{2}+{d}_{E}{(t)}^{2}+{d}_{Z}{(t)}^{2}}$$
(3)

For \({P}_{D}\), the maximum absolute value of P-wave displacement is obtained over 5 s after P-wave detection (Eq. 2). For \(PGD\), the maximum absolute value of displacement is obtained immediately after P-wave detection and is continuously updated over all phases of the seismic signal for 200 s (Eq. 3). In Eqs. (2) and (3), \({d}_{N}(t)\), \({d}_{E}(t)\), and \({d}_{Z}(t)\) are the north, east, and vertical components of unbiased displacement time series for each of the available PPP solutions. Crowell et al. (2013) obtained magnitude scaling relationship using \({P}_{D}\) and \(PGD\) as:

$${M}_{{P}_{D}}=\frac{{log}_{10}\left({P}_{D}\right)+A+C{log}_{10}({R}_{hypo})}{B}$$
(4)
$${M}_{PGD}=\frac{{log}_{10}\left(PGD\right)+D}{E-F{log}_{10}({R}_{hypo})}$$
(5)

where \(A\) = 0.893, \(B\) = 0.562, \(C\) = 1.731, \(D\) = 5.013, \(E\) = 1.219, and \(F\) = 0.178. In Eqs. (4) and (5), \({P}_{D}\) and \(PGD\) are in cm and \({R}_{hypo}\) is hypocentral distance in km. Several studies have shown that \({M}_{{P}_{d}}\) saturates for large earthquakes (> 6 or 7) whereas this problem is solved by using \({M}_{{P}_{D}}\) and \({M}_{PGD}\) (Crowell et al. 2013; Rosenberger et al. 2018; Rosenberger 2019). Using Eqs. (1), (4), and (5), the ONC EEW system calculates magnitude for each station based on available data (\({P}_{d}\), \({P}_{D}, PGD\)) and takes the median value of station magnitudes to assign a magnitude for an event. Note that once an event is created in the system with its initial source parameters, subsequent notifications are generated in case of any change in the source parameters (epicentral location or magnitude) as more data from stations become available.

Figure 2 compares the earthquake magnitudes detected by the ONC EEW system with the values reported by NRCan and United States Geological Survey (USGS). For each event, both the initial and final magnitudes by the ONC EEW system is used for this comparison. In general, it appears that ONC underestimates magnitudes for larger events (> 4) while overestimating smaller events. Similar trends are visible in both the ONC-NRCan and ONC-USGS pairs, although data is scarce for smaller magnitude earthquakes in the ONC-USGS pair, which is expected as the magnitude of completeness is higher in the USGS catalogue than NRCan for this area. Note that the differences between magnitude values determined by the ONC EEW system and those reported by NRCan or USGS are due to several factors. First, ONC, NRcan, and USGS use different seismographic stations to detect earthquakes. Second, while the ONC’s procedure for magnitude determination relies on the first few seconds of P-wave amplitudes, NRCan and USGS use the entire waveform encompassing both the P and S waves. Third, different methodologies are used to measure earthquake magnitude. NRCan and USGS use various magnitude scales such as local magnitude (ML; Richter 1935) or some variations of the moment magnitude (Mw; Hanks and Kanamori 1979) scale compared to the methodologies used by ONC as explained earlier in this section. In Fig. 2, all the magnitudes reported by the ONC EEW system are \({M}_{{P}_{d}}\) (Eq. 1).

Fig. 2
figure 2

Comparison of the magnitudes (initial and final) reported by Ocean Networks Canada’s (ONC) earthquake early warning system with the values reported by Natural Resources Canada (NRCan) and United States Geological Survey (USGS). Dashed lines are the 1:1 line

Full size image

To further investigate magnitude estimations by the ONC EEW system, we download station magnitudes for each event detected by the system. We then calculate the difference between station and event magnitude (station minus event) and take the average of differences over all notifications for each station. By looking at the plot of magnitude differences (Fig. 3) one can identify stations that systematically generate high or low magnitudes. There are several stations with high or low values that are more than or close to 1 unit of magnitude. For example, the SAYW station shows a significantly large positive residual (2 units of magnitude). Note that the number of contributions (bottom panel in Fig. 3) over which magnitude differences are computed varies among stations. For example, although BACND.Z1 shows a large magnitude difference, its average value is only from a few points. Higher number of contributions ensure that the magnitude difference holds statistical significance and that the difference has occurred over a long period of time. Data from Fig. 3 can be used to correct magnitudes for each station as:

$${M}_{c}=M-c$$
(6)

where \({M}_{c}\) is the corrected magnitude and \(c\) is the correction value. A positive value of \(c\) for a station means that it systematically shows higher magnitudes and, therefore, magnitudes should be reduced. On the other hand, if \(c\) is negative, magnitudes should be increased at that station. This is a practical and simple approach to correct for station outliers because of source, path, and site effects and have been used in other regions (e.g., Richter 1935). Table S1 in the electronic supplement of this paper provides correction values for each station.

Fig. 3
figure 3

Average magnitude difference between station and event over all notifications for each ONC EEW station. Error bars show one standard deviation

Full size image

The presented findings in Fig. 3 have important implications for accurate determination of magnitude as this value is one of the most important source parameters that is correlated with severity of shaking. In an EEW system, this parameter (in conjunction with epicentral location) determines the severity of shaking in terms of peak ground motion amplitude or shaking intensity. Therefore, it is important to understand the accuracy of earthquake magnitude as both over- and under-estimation of this parameter leads to generation of false alerts and missing a potentially damaging event, respectively. The effect of systematic high or low magnitude values at some stations is especially significant for events with small number of contributing stations as large outliers would skew the final magnitude towards a high or low value.

3 Site characterization

In general, it is expected that ground motion in the subsurface will differ from ground motion at the surface. As waves propagate toward the surface, they undergo changes due to several factors that modify the frequency and amplitude of the upgoing phases (Shearer and Orcutt 1987; Babaie Mahani and Kao 2018). A practical approach in site response characterization is classification based on the underlying geological materials beneath the site. Sites can be qualitatively grouped into rock/soil based on surface geology of the area or geotechnical boreholes. The most well-known technique for site classification is using the time-averaged shear-wave velocity in the top 30 m of the soil column (VS30). This information is obtained through seismic surveys by taking the sum of the shear-wave travel times within each layer of soil to 30m depth. The National Earthquake Hazard Reduction Program classifies sites based on VS30 as A (VS30 > 1500 m/sec), B (VS30 between 760 and 1500 m/sec), C (VS30 between 360 and 760 m/sec), D (VS30 between 180 and 360 m/sec), E (VS30 < 180 m/sec), and F (special conditions such as peat).

In the absence of data from seismic surveys, proxy measurements have been suggested for site characterization and ground motion amplification, including the reference site method (Borcherdt 1970; Kagami et al. 1982, 1986; Safak 1997), HVSR (Nogoshi and Igarashi 1970, 1971; Nakamura 1989; Field and Jacob 1993; Theodulidis et al. 1996), vertical-to-horizontal spectral ratio (Kim et al. 2016), ground motion inversion (Hartzell 1992), theoretical amplification factors (Boore and Joyner 1997), topographic slope method (Wald and Allen 2007), geology method (Wills and Clahan 2006), geomorphology (Yong et al. 2012; Yong 2016), site dominant frequency (Field and Jacob 1993; Ohmachi et al. 1994; Ghofrani and Atkinson 2014; Hassani and Atkinson 2016; Hassani et al. 2019), and probabilistic methods (Najaftomarei et al. 2020; Mital et al. 2021). In this section, we analyze site response at each seismic station. Using ground motion amplitude data from multiple earthquakes and the HVSR technique, we look at the possibility of non-linear site behavior, especially at offshore sites buried under the ocean floor. We also estimate site dominant frequency and amplification at each station. The HVSR technique, which was first introduced by Nogoshi and Igarashi (1970, 1971) and popularized by Nakamura (1989), has been used extensively due to its simple approach which only needs data from one station. In this approach, amplification at the vertical component is assumed to be minimal, therefore, amplification can be associated with larger ground motion amplitudes on horizontal components (Lermo and Chavez-Garcia 1993).

3.1 Ground motion dataset

We download an earthquake catalogue from NRCan for events with magnitudes ≥ 4 since 2009 for the area between 44 to 58 N and 120 W to 132 W. For each seismic event, three-component waveforms in SAC format are obtained from Incorporated Research Institutions in Seismology (IRIS) (a member of the EarthScope consortium). Recorded waveforms are obtained from ONC and NRCan seismometers and accelerometers, with channel codes BH*, HH*, and HN*. From the NRCan stations, those that locate within a box encompassing Vancouver Island and parts of the mainland are included. Note that while NRCan (network code CN) and ONC’s offshore (network code NV) stations send continuous waveforms to IRIS, data from ONC’s onshore (network code OW) stations are only available as event-based waveforms. Figure 1 shows the location of events and stations used in this study. Not all earthquakes are shown in Fig. 1 as the map is drawn to focus on the location of seismic stations. To ensure data relevance and quality, a distance threshold that varies linearly with earthquake magnitude is employed as:

$${d}_{t}\left(M\right)=a\times {M}^{\prime}+{d}_{min}$$
(7)

where \({d}_{t}\left(M\right)\) is the magnitude-dependent distance threshold, and \({d}_{min}\) is the minimum distance set as 300 km. In Eq. (7), \(a\) is calculated as:

$$a=\frac{{d}_{max}-{d}_{min}}{\mathit{max}\left({M}^{\prime}\right)-min({M}^{\prime})}$$
(8)

where \({d}_{max}\) is maximum distance set as 1000 km, and \({M}^{\prime}\) is normalized magnitude which is calculated as:

$${M}^{\prime}=\frac{M}{min(M)}-1$$
(9)

The time window for each waveform is determined based on seismic wave velocities. The following steps are involved to ensure full capture of seismic phases: 1) P-wave travel time (\({t}_{p}\)) estimation using the P-wave velocity and event-station hypocentral distance as \({t}_{p}=distance/{V}_{p}\), 2) S-wave travel time (\({t}_{s}\)) estimation as \({t}_{s}={t}_{p}\times \frac{{V}_{p}}{{V}_{s}}\), 3). Surface-wave travel time (\({t}_{surface}\)) estimation as \({t}_{surface}={t}_{s}\times \frac{{V}_{s}}{{V}_{surface}}\), 4) P-wave arrival time (\({t}_{{2}_{p}}\)) estimation as \({t}_{{2}_{p}}={t}_{1}+{t}_{p}\), where \({t}_{1}\) is event origin time, 5) beginning of the signal window as \({tw}_{1}={t}_{{2}_{p}}-{t}_{before}\), with \({t}_{before}\) representing the time before P-wave arrival, 6) end of signal window as \({tw}_{2}={t}_{{2}_{p}}+{t}_{after}\), with \({t}_{after}\) calculated as \(\left({t}_{s}-{t}_{p}\right)+\left({t}_{surface}-{t}_{s}\right)+{t}_{sc}\). Here, \({t}_{sc}\) represents the time window for surface and coda waves. In the above calculations, assumptions are made, including a P-wave velocity (\({V}_{p}\)) of 7 km/sec, a \(\frac{{V}_{p}}{{V}_{s}}\) ratio of 1.7, a \(\frac{{V}_{s}}{{V}_{surface}}\) ratio of 1.1, \({t}_{before}\) of 0.5 min, and a \({t}_{sc}\) of 2 min. Instrument response information in RESP format for each waveform is subsequently retrieved from IRIS. To account for potential changes in sensor responses, a time window of 5 h starting from the beginning time of each SAC file is used, thus ensuring accuracy regarding the sensor's response during recording.

The quality of the waveforms is checked to make sure the assumptions made in downloading the waveforms are correct. Samples of waveforms are manually checked to make sure the entire waveforms are captured. Figures 4 and 5 show examples of acceleration time series (filtered using a 4th order bandpass Butterworth filter with corner frequencies of 0.075 and 25 Hz) of two earthquakes that occurred within the continental and oceanic crust, respectively (Fig. 1). The onshore/continental earthquake occurred on November 26, 2022, with Mw of 4.8 whereas the offshore/oceanic earthquake occurred on October 22, 2018, with Mw of 6.5. In each figure, three component data are shown for an onshore (top) and offshore (bottom) station. As can be seen from Figs. 4 and 5, it seems that the event-station path has a significant effect on waveform characteristics, especially the coda portion of the waveforms. For the November 26 earthquake occurred within the North American plate, short coda waves are observed at the onshore station BAMF whereas the recorded waveforms at the offshore station NCBC presents a much longer coda. For the October 22 earthquake within the pacific plate, the recordings at both the onshore and offshore stations (BAMF and BACME, respectively) show a long-period, large-amplitude tail. Testing different filtering options show that this long-period tail is completely removed when the high-pass corner frequency of the band-pass filter increases to 0.5 Hz (we tested filtering with 0.075, 0.1, 0.2, 0.3, 0.4, and 0.5 Hz) making the dominant period of this phase more than 2 s. The long-period, large-amplitude phase at the end can be attributed to the generation of T-phase when seismic waves enter water from ocean floor and propagate either within the low-velocity sound fixing and ranging (SOFAR) channel or by multiple reflections between the ocean floor and ocean surface (Bath and Shahidi 1971; Bullen and Bolt 1985).

Fig. 4
figure 4

Acceleration time series at two onshore (top) and offshore (bottom) stations from the continental crust earthquake on November 26, 2022, with moment magnitude of 4.8. The location of the epicenter and stations are shown in Fig. 1. Distance is epicenteral distance. Waveforms were filtered using a 4th order band pass Butterworth filter with corner frequencies of 0.075 and 25 Hz

Full size image
Fig. 5
figure 5

Acceleration time series at two onshore (top) and offshore (bottom) stations from the oceanic crust earthquake on October 22, 2018, with moment magnitude of 6.5. The location of the epicenter and stations are shown in Fig. 1. Distance is epicenteral distance. Waveforms were filtered using a 4th order band pass Butterworth filter with corner frequencies of 0.075 and 25 Hz

Full size image

Data processing of the waveforms and calculation of ground motion parameters include the following steps: 1) data are detrended and their mean is removed, 2) instrument response is removed based on the Haney et al. (2012) method and acceleration time series are obtained, 3) each time series is filtered using a 4th order band-pass Butterworth filter with corner frequencies of 0.08 and 25 Hz, 4) smoothed Fourier amplitude of acceleration (FACN) and 5% damped response spectral acceleration (RSA) are calculated at 100 log-spaced frequencies between 0.1 and 20 Hz. Note that only FACN is smoothed as damping used in calculating a response spectrum has an incidental smoothing effect (Zhu et al. 2020). In pursuit of attaining the highest possible quality of data, time series are checked based on their signal-to-noise ratio (SNR). SNR is calculated for a noise and signal window of 20 s before and after P-wave arrival with a threshold of 10 for pass/fail. To calculate SNR, signal and noise powers are calculated as \(\sum {S(t)}^{2}\) and \(\sum {N(t)}^{2}\), respectively, and their ratios are obtained in dB as \(10{log}_{10}({~}^{{P}_{S}}\!\left/ \!{~}_{{P}_{N}}\right.)\), where \({P}_{S}\) and \({P}_{N}\) are signal and noise powers, respectively. Using FACN and RSA, HVSR is calculated at each frequency (Eq. 2 in Ghofrani and Atkinson 2014) by dividing the geometric mean of the horizontal component by the vertical component as:

$${log}_{10}\left(HVSR\right)=0.5\left({log}_{10}\left({H}_{1}\right)+{log}_{10}\left({H}_{2}\right)\right)-{log}_{10}(V)$$
(10)

where \({H}_{1}\), \({H}_{2}\), and \(V\) are the horizontal and vertical components of FACN or RSA for each event and station. HVSR for a single station is obtained by taking the average of ratios from all events as:

$${log}_{10}\left(\overline{HVSR}\right)=\frac{\sum_1^N{log}_{10}(HVSR)}N$$
(11)

where \(N\) is the number of earthquakes and \(\overline{HVSR }\) is the average ratio (Eq. 3 in Ghofrani and Atkinson 2014). The smallest number for \(N\) in this study is set at 3 to calculate the average HVSR for a station. Tables S2 and S3 in the electronic supplement of this paper provide the HVSR dataset prepared in this study from FACN and RSA, respectively.

3.2 Non-linear site response

Generally, the response of the medium to seismic waves is linear, meaning that ground motions are amplified when waves travel from "stiff materials" into "soft materials". Under specific situations (existence of soft sediments and very large ground motions), however, the response of the soil column is non-linear, meaning that ground motions (at high frequencies) are de-amplified, with lower amplitudes at soft sediments than at bedrock condition. Nonlinear site effects result in increased damping and reduction in shear wave velocity as input ground motion increases and can be investigated using the spectral ratio techniques (Wen 1994; Wen et al. 1994, 2006). Evidence from ground motion analysis of earthquakes has shown the dependence of non-linearity on input ground motion, either using ground motions from mainshock-aftershock pairs at a single station (Frankel, et al. 2002), or ground motions from a single event at two stations with different site conditions but at similar distances and azimuths to the earthquake using the weak and strong portion of the waveforms (Babaie Mahani and Kazemian 2018).

In this study, we analyze non-linearity by considering HVSR from the weak and strong portion of waveforms (Babaie Mahani and Kazemian 2018). For sites with linear site response behavior, HVSR from the weak and strong portion of waveforms should show similar behavior at high frequencies. However, at sites with non-linear behavior, HVSR from the strong portion of the waveform should decrease with increasing frequency and falling below unity at which the vertical component records higher ground motions than the horizontal components due to de-amplification. We test this hypothesis for several earthquakes. For each event, we calculate HVSR from the weak (pre-event noise or the P-wave portion of the waveforms) and strong shaking portions of the waveforms (mainly the S wave). FACN from weak and strong windows of 20 s are smoothed and the ratios are obtained at 100 frequencies between 0.1 and 20 Hz with filtering applied in the same way as before (between 0.08 and 25 Hz) and HVSR curves are obtained based on Eq. (10). Similarly, HVSR curves from RSA are obtained (without smoothing), which show similar results as the HVSR curves from FACN. Figure 6 shows HVSR (from RSA) at several stations (sorted by their epicentral distance) for the Mw 4.8 November 26, 2022, earthquake (Figs. 1 and 4). At two occasions at 58 km distance from epicenter, HVSR for the strong portion of the waveform has a decreasing trend and falls under unity whereas the weak-motion HVSR remains close to unity or does not fall as much as the strong-motion HVSR. This behavior is seen at two sensors located in Gold River, British Columbia, one belonging to NRCan (station GDR) and the other to the ONC network (station GLRI). The distance between the two sensors is approximately 600 m. No other stations show this trend between the weak and strong HVSR. We also test other events including the October 22, 2018, earthquake with Mw of 6.5 that occurred offshore (Figs. 1 and 5). Although the magnitude of this event is almost twice larger than the November 26, 2022, earthquake, the closest station is at 125 km. Figure 7 shows HVSR (from RSA) for the weak and strong portion of the waveforms for the Mw 6.5 earthquake. As can be seen in Fig. 7, the only evidence of the HVSR from strong shaking falling below unity is seen at the closest station, which troughs at approximately 15 Hz and increase afterwards. However, at this station, the weak-motion HVSR also falls below unity, therefore, it is difficult to ensure whether the high-frequency decrease in the strong-motion HVSR is an indicator of non-linearity at this location.

Fig. 6
figure 6

Horizontal-to-vertical spectral ratio (HVSR) of response spectral acceleration from the weak and strong portion of the waveforms at several stations (with their epicentral distance shown) following the November 26, 2022, earthquake with moment magnitude of 4.8 (Figs. 1 and 4)

Full size image
Fig. 7
figure 7

Horizontal-to-vertical spectral ratio (HVSR) of response spectral acceleration from the weak and strong portion of the waveforms at several stations (with their epicentral distance shown) following the October 22, 2018, earthquake with moment magnitude of 6.5 (Figs. 1 and 5)

Full size image

3.3 Site dominant frequency

Although site classification based on VS30 data has been the standard approach within the seismological and earthquake engineering community for decades, with application in ground motion prediction equations and in building codes (Borcherdt 1994; Dobry et al. 2000; Abrahamson et al. 2008; Kolaj et al. 2023), direct measurements of VS30 are not available for most seismic networks due to the large costs associated with seismic surveys. As a result, techniques have been suggested to estimate VS30 such as using topographic slope or surficial geology (Wills and Clahan 2006; Wald and Allen 2007; Zalachoris and Rathje 2019). HVSR from earthquake and microtremors have also gained attention in characterizing relevant site parameters including site dominant frequency and its peak amplitude (Hassani and Atkinson 2016; Molnar et al. 2017; Hassani et al. 2019).

In this study, for each station with available \({log}_{10}(\overline{HVSR})\) as described by Eq. (11), we obtain site dominant frequency (fpeak) and its peak amplitude (Apeak). Due to the large variability in HVSR data, finding the frequency at which the peak occurs can be difficult since HVSR does not necessarily results in one peak. We follow a similar approach as described in Ghofrani and Atkinson (2014) and Hassani and Atkinson (2016) to determine fpeak and Apeak. This procedure includes: 1) a baseline for amplification is calculated by taking the average value of \({log}_{10}(\overline{HVSR})\) over all frequencies, 2) local maxima on the \({log}_{10}(\overline{HVSR})\) curve are marked, 3) significant peaks are selected from these local maxima as those that are above the baseline (step 1) and with a minimum value of 0.3 (amplification factor of approximately 2), 4) a window is picked manually around significant peaks and fpeak and Apeak are calculated by taking the average of the frequency and amplitude of the significant peaks within the selected window. Figure 8 shows an example of fpeak and Apeak calculation using HVSR from FACN for one station. We use HVSR from both FACN and RSA to calculate fpeak and Apeak for each station and the results are compared in Fig. 9. Although there are differences in the behavior of FACN and RSA (Bora et al. 2016; Stafford et al. 2017; Hassani et al. 2019), there is good agreement in site parameters obtained from the two ground motion types, especially for Apeak. This is important to observe as researchers have used RSA and FACN interchangeably in HVSR studies (Atkinson and Cassidy 2000; Molnar et al. 2004; Ghofrani and Atkinson 2014; Hassani and Atkinson 2016; Farrugia et al. 2018). Tables S4 and S5 in the electronic supplement of this paper provide fpeak and Apeak values from FACN and RSA, respectively.

Fig. 8
figure 8

Estimation of site dominant frequency (fpeak) and its peak (Apeak) using horizontal-to-vertical spectral ratio (HVSR) from Fourier amplitude of acceleration for a seismic station in this study. Vertical dashed lines show the selected window from which significant peaks are used to calculate fpeak and Apeak

Full size image
Fig. 9
figure 9

Comparison of site dominant frequency (fpeak) and its peak (Apeak) obtained from horizontal-to-vertical spectral ratio of Fourier amplitude of acceleration (FACN) and response spectral acceleration (RSA). Dashed lines are the 1:1 line

Full size image

Figure 10 shows the relationship between fpeak and Apeak. Both FACN and RSA show the same decreasing trend in Apeak with increasing fpeak, although the trend does not seem linear. A decreasing amplification with increasing site dominant frequency is expected since higher fpeak values correlate with stiffer site conditions (higher VS30), which in turn correlate with smaller amplification (e.g., Hassani and Atkison 2016). A breakdown of site parameters for the onshore and offshore stations shows an overall similar behavior between the two locations although it seems that offshore sites have higher amplification (Apeak) than onshore stations at some locations (Fig. 11). Overall, offshore sites show fpeak and Apeak in the range of approximately 1.7–6 Hz and 0.4–1.2 (in base-10 log unit), respectively, whereas onshore sites show approximately 1–6 Hz for fpeak and 0.3–0.7 (in base-10 log unit) for Apeak. We also look at the effect of distance in fpeak and Apeak for each station by calculating these values using data in several distance bins. We find no distance dependent trends in these site parameters.

Fig. 10
figure 10

Peak site amplitude (Apeak) versus its frequency (fpeak) obtained from horizontal-to-vertical spectral ratio of Fourier amplitude of acceleration (FACN) and response spectral acceleration (RSA)

Full size image
Fig. 11
figure 11

Boxplots of the site dominant frequency (fpeak) and its peak (Apeak) for onshore and offshore stations based on the horizontal-to-vertical spectral ratio of Fourier amplitude of acceleration (FACN) and response spectral acceleration (RSA)

Full size image

Results from our analysis of site dominant frequency and amplification agree with previous studies for stations on Vancouver Island (e.g., Atkinson and Cassidy 2000; Molnar et al. 2004; Molnar and Cassidy 2006). For stations located in Victoria, British Columbia, Molnar et al. (2004) and Molnar and Cassidy (2006) showed that sites with thin soil layer (< 3 m) do not show significant amplifications below 10 Hz. On the other hand, sites with thick soil layer (> 10 m) amplify ground motions by up to 6 times higher than the sites with bedrock or thin soil site condition at frequencies 2–5 Hz.

4 Magnitude difference and site characteristics

In Section 2, we investigated magnitude estimation by the ONC EEW system and obtained station terms based on the average difference between station and event magnitudes. In Section 3, site response was analyzed using HVSR of FACN and RSA. The systematic behavior in site magnitudes is investigated in this section in connection to site response characteristics of stations. Understanding systematic behaviors in magnitude estimations at individual sites is essential knowledge for accurate determination of earthquake source parameters. For newly developed seismic networks, station terms might not be available as sufficient data must be recorded first. Therefore, existing relationships between station terms and site response characteristics (VS30, fpeak, Apeak) can be used for preliminary estimation of station terms. Using available data from the California Integrated Seismic Network, Yong et al. (2020) analyzed the correlations between site response parameters (VS30 and fpeak) and station component adjustments (dML). They found that there is a positive relationship between VS30 and dML, which implies that greater site amplification (lower VS30) results in smaller dML. Similarly, they observed a positive correlation between fpeak and dML, which implies lower dML values are related to site resonance at depth-dependent frequencies.

Figure 12 shows magnitude difference (as shown in Figure 3) versus fpeak and Apeak obtained from FACN and RSA. Magnitude differences are scattered across both fpeak and Apeak with no obvious trend, although there might be a positive correlation with magnitude differences at larger fpeak and Apeak values.

Fig. 12
figure 12

Magnitude difference (as shown in Fig. 3) versus site dominant frequency (fpeak) and its peak (Apeak) obtained from horizontal-to-vertical spectral ratio of Fourier amplitude of acceleration (FACN) and response spectral acceleration (RSA)

Full size image

5 Conclusion

Analysis of magnitudes calculated by Ocean Networks Canada’s Earthquake Early Warning (ONC EEW) system and site response characterization of onshore and offshore stations were the subjects of this paper. We compared the magnitudes by the ONC EEW system with those reported by Natural Resources Canada (NRCan) and Unites States Geological Survey (USGS). Overall, the ONC EEW system somewhat underestimates magnitudes for larger events (> 4) while overestimating smaller earthquakes compared to NRCan and USGS. We attribute these discrepancies to several factors, including the use of different stations, procedures, and methodologies to detect earthquakes among different agencies. We also looked at systematic magnitude behavior at each station by calculating the average difference between station and event magnitude over many EEW notifications. These differences can be used as station terms to correct future magnitudes from stations with systematic high or low values. Using a rich ground motion amplitude dataset compiled in this study and applying the horizontal-to-vertical spectral ratio method from Fourier amplitude of acceleration (FACN) and response spectral acceleration (RSA), we investigated site characterization through evaluation of non-linear site response behavior and estimation of site dominant frequency (fpeak) and its peak amplitude (Apeak) for each station. Results from FACN and RSA show strong agreement. In general, no strong evidence of non-linearity could be observed at either the onshore or offshore stations considering the magnitude-distance distribution of ground motions in this study. Overall, offshore sites show fpeak and Apeak in the range of approximately 1.7–6 Hz and 0.4–1.2 (in base-10 log unit), respectively, whereas onshore sites show approximately 1–6 Hz for fpeak and 0.3–0.7 (in base-10 log unit) for Apeak.