The 12 October 2021, $M_W$=6.4, Zakros, Crete earthquake

Abstract

We study the strong 12 October 2021, $M_W$=6.4, offshore Zakros, Crete earthquake, and its seismotectonic implications. We obtain a robust location (azimuthal gap equal to 17$^{\circ }$) for the mainshock by combining all freely available local, regional and teleseismic phase arrivals (direct and depth phase arrivals). Based on our location and the spatial distribution of the poor aftershock sequence we parameterise the fault area as a 30 km $\times$ 20 km planar surface, and using three-component strong motion data we calculate slip models for both earthquake nodal planes. Our preferred solution shows a simple, single slip episode on a NE-SW oriented, NW shallow-dipping fault plane, instead of a N-S oriented, almost vertical nodal plane. An anti-correlation of the aftershocks spatial distribution versus the maximum slip ($\sim$ 27 cm) of our model further supports this, although the accuracy of the aftershock hypocentral locations could be somewhat questionable. Coulomb stress changes calculated for both kinematic models do not show substantial differences, as the aftershock seismicity within the first 3 months after the mainshock is distributed along the stress shadow zone and over the stress enhanced areas developed at the southern fault edge, induced by the mainshock. The Kasos island tide gauge record analysis shows a small signal after the earthquake, but it can hardly demonstrate the existence of tsunami waves due to the low signal-to-noise ratio. Tsunami simulations computed for the two nodal planes do not yield conclusive evidence to highlight whether the causative fault plane is NE-SW oriented, NW shallow-dipping plane, or the N-S oriented plane, nevertheless, the power spectrum analysis of the NW shallow-dipping nodal plane matches the spectral peak at 8 s period and is overall closer to the spectrum of the tide gauge record. A USGS Shakemap was also produced with all available local strong motion data and EMSC testimonies. This was also investigated in an effort to document the responsible fault. The overall analysis in this study, slightly suggests a rather westward, shallow-dipping offshore fault zone, being antithetic to the main Zakros almost vertical normal fault which shapes the coast of eastern Crete and is perpendicular to the direction of Ptolemy Trench in this area. This result agrees with seismotectonic and bathymetric evidence which support the existence of approximately N-S trending grabens, east and northeast of Crete.

1 Introduction

On 12 October 2021, at 09:24 UTC, a strong, $M_W$=6.4, earthquake occurred approximately 10 km off the east coast of Crete. The earthquake was widely felt in Crete, Karpathos and Dodecanese islands, causing minor damage in East Crete, especially in older constructions and heritage monuments, with the old church of Saint Nicholas in Xirokampos, Siteia collapsed due to the shaking. No casualties were reported, whilst maximum intensity was observed in Ierapetra (VII, https://accelnet.gein.noa.gr/noa_sites/noa.shakemaps.gr/public/index/128499). Fault plane solutions showed an extensional seismotectonic behaviour and substantial left-lateral slip component (see Table S1 in the supplementary material). The mainshock prompted the Tsunami Service Providers operating in the Eastern Mediterranean to issue local advisory messages (possibility of strong tsunami-induced currents in the nearshore for areas for up to 100 km from the earthquake epicentre). The tide gauge in Kasos, which supports the operations of the Hellenic National Tsunami Warning Center (HL-NTWC, one of the three Tsunami Service Providers operating in the Eastern Mediterranean), picked up what appears to be a very small tsunami. No other tide gauge in the region showed any sea level excitation after the earthquake. Given the noise-level wave amplitudes of the Kasos tide gauge record, tsunami-ongoing messages were not issued by the Tsunami Service Providers, and the authors are not aware of sightings of tsunami waves or currents being reported. Only a small number of aftershocks followed the mainshock, an observation which raises the question whether this is attributed to the lack of aftershock activity as a result of the mainshock being significantly deeper than previously reported (i.e. $\sim$ 10 km, http://bbnet.gein.noa.gr/Events/2021/10/noa2021tzsju_info.html), or due to the sparse seismic station coverage for this highly active part of the South-East Aegean Sea which poses a high threat level regarding earthquakes and the 12 October 2021, $M_W$=6.4, Zakros earthquake tsunami excitation (Papazachos and Papazachou 2003; Ebeling et al. 2012; Kalligeris et al. 2022).

Fig. 1

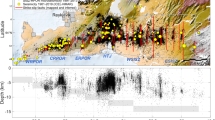
Map of Crete showing the study area (yellow rectangle). The NOA epicentre of the 12 October 2021, $M_W$=6.4, Zakros earthquake is plotted as white star, whereas, moderate to major historical earthquakes (1964–2020), taken from the ISC-EHB dataset (International Seismological Centre 2022a), are shown as circles (see legend for details). Best-fitting double-couple mechanisms of past earthquakes are taken from GCMT (Dziewonski et al. 1981; Ekström et al. 2012). Major trenches of the Hellenic Subduction Zone (HSZ): Ptolemy (Pt.Tr.), Pliny (Pl.Tr.) and Strabo (St.Tr.) are shown in black, and normal faults following Caputo and Pavlides (2013) are shown in orange

The epicentral area is situated north of the Hellenic Subduction Zone (HSZ, see Fig. 1) where a seismically active North–South extended basin is developed between Crete and Karpathos islands (Kreemer and Chamot-Rooke 2004). Compression across the HSZ caused intense crust thickening and the formation of the accretionary wedge, the surface expression of which is the Aegean arc, with Crete and Karpathos being emerged as its main parts. Other parts constitute a sedimentary ridge with an amphitheatric shape approximately 150 km SSE of Crete, bounded by the Strabo trench (St.Tr) from the North. To the East, the deep bathymetry of the Hellenic Trough splits into large parallel to the arc tectonic features, namely, the WSW-ENE trenches of Ptolemy (Pt.Tr), Pliny (Pl.Tr) and Strabo which are deep sea wedge-shaped depressions exhibiting sinistral strike slip faulting (Bohnhoff et al. 2001). Back arc extension gave rise to crust thinning, volcanism and the formation of neotectonic basins within the Aegean Sea (Jolivet et al. 2013). The geotectonic history of Crete reveals a complicated series of tectonic episodes and is considered a tectonic horst signifficantly uplifted during Quaternary (Mouslopoulou et al. 2017). Crete is sharply formed by a system of offshore and inland active WNW-ESE, NNE-SSW and E-W normal fauts (Fassoulas 2001; Caputo et al. 2010) which shape the coastal morphology complexity and bound the neotectonic grabens. Bohnhoff et al. (2005) highlighted the dominance of a sinistral transpression for eastern Crete according to fault mechanisms. The deep Karpathos basin lies on a NNE-SSW strike between Crete and Karpathos islands (Angelier et al. 1982; Kreemer and Chamot-Rooke 2004), whilst Friederich et al. (2014) suggested that the area south of Karpathos is also affected by subduction mechanisms which further exert a subhorizontal pressure and cause the rotation of the compressional axis of the stress field.

So far, there are no published studies regarding the 12 October 2021, $M_W$=6.4, earthquake to our knowledge, possibly due to its low impact. Given the complex tectonic setting of the epicentral area and the poor aftershock sequence following the mainshock, it is not clear which fault was activated during this event. Believing this earthquake deserves to be studied further, thus, we attempt to obtain a more robust location based on all available parametric data on a global scale, and we study the kinematics of the rupture and its associated stress change. Moreover, we perform tsunami simulations to study the Kasos tide gauge record, and we perform a USGS Shakemap in order to investigate the effect of both possible faults.

2 Data and methods

2.1 Parametric phase arrival data and earthquake relocation

In order to relocate the mainshock, we combined all the freely available phase arrival data from the International Seismological Centre (International Seismological Centre 2022b, database last accessed in December 2021). It is worth mentioning that phase arrivals become progressively available over time as they are reported to the ISC by different data providers. For example, at the time of our analysis we used phase arrivals from 951 distinct stations on a global scale, whereas, for any seismic stations in Greece, we used manually picked phase arrivals from 43 distinct seismic stations from the NOA Bulletin (http://bbnet.gein.noa.gr/Events/2021/10/noa2021tzsju_info.html, database last accessed in December 2021).

The procedure we followed is similar to the analysis carried out at the ISC for compiling the ISC Reviewed Bulletin, namely, we followed the IASPEI standards (Storchak et al. 2003) for the phase naming and we used the ISC locator algorithm (Bondár and Storchak 2011) with the 1D, ak135 velocity model (Kennett et al. 1995). Specifically, we used a wide range of seismic phase arrivals from local to teleseismic, including depth phases (e.g. pP, sP) and core reflections (e.g. PcP, ScP) which can contribute to better constraining the focal depth, as well as diffracted seismic phases beyond 100$^{\circ }$ (e.g. $P_{dif}$, $PKP_{df}$). Moreover, as the focal depth may vary from iteration to iteration during the inversion, local/regional phases were allowed to exchange names (i.e. Pb to Pn) if lower time residuals were possible due to these conversions. Nevertheless, we did not allow P phases to become S phases, and vice versa.

2.2 Waveform data and slip inversion

We used three-component strong motion data from five accelerometric stations and one 20-s seismic station (National Observatory of Athens, Institute of Geodynamics, Athens 1975; ITSAK Institute of Engineering Seimology Earthquake Engineering 1981) whose signal was not clipped, at a maximum epicentral distance of approximately 120 km (Fig. S1 in the supplementary material). We removed the mean and the instrument responses from our data, converted the data to displacement and filtered the waveforms from 0.05 Hz to 0.5 Hz. We determined the kinematic slip model of the mainshock based on the method developed by Gallovič et al. (2015) which solves the slip rate function in space and time and is parameterised by overlapping Dirac functions over a grid of subfaults along the fault surface on a 1 km discretisation step, which is sufficient for the shortest wavelength ($\sim$5 km) that corresponds to the maximum frequency of our signal (0.5 Hz). The seismic fault area was determined by both the distribution of the aftershocks and the empirical equations of Wells and Coppersmith (1994) and set to 30 km along strike by 20 km along dip. The seismic source was represented by the Global Centroid Moment Tensor (GCMT, Dziewonski et al. 1981; Ekström et al. 2012), best-fitting double-couple solution, (https://www.globalcmt.org/CMTsearch.html, database last accessed in October 2022) and the Green functions were computed based on the velocity model of Karagianni et al. (2002).

2.3 Coulomb stress change models

In order to study the distribution of the coseismic Coulomb stress changes induced by the occurrence of the mainshock and the association with the detected aftershocks the Coulomb Failure Function criterion (Scholz 2002) was applied. The criterion is known for examining the closeness to failure and the conditions under which failure occurs on rocks. Changes in Coulomb Failure Function Criterion ($\Delta CFF$) depend on changes in shear ($\Delta \tau$) and normal stress ($\Delta \sigma$) resolved onto the earthquake fault plane, given by $\Delta CFF$ = $\Delta \tau$ + $\mu ' \Delta \sigma$. Positive ($\Delta CFF$) values favour future rupture and imply a high likelihood for future earthquake occurrence whereas negative ($\Delta CFF$) values indicate that fault failure is rather prevented. Subsequent earthquakes preferentially occur on locations with positive increments (bright zones) whereas negative values are considered areas of seismic quiescence described as shadow zones. Parameter $\mu '$ is the apparent coefficient of friction associated with the fluid effect on the pore pressure change and ranges between 0.5 and 0.8 for dry materials (Harris 1998). In this case $\mu '$ was considered equal to 0.5 as proposed by many researchers. Source models for large earthquakes approximate the rupture geometry in the sense of a planar rectangular geometric structure, which dips into the brittle part of the crust. Fault geometry is adequately described by the fault plane solution, which serves as an input for stress changes evaluation. Slip is either based on theoretical estimation of an average slip obtained from mathematical equations or according to a produced variable slip model. In this case Coulomb stress changes were accomplished by using Coulomb 3.4 software (Toda et al. 2011).

2.4 Tide gauge record analysis and tsunami modelling

For the analysis of NOA’s tide gauge record in Kasos (26.9217$^{\circ }$E, 35.4188$^{\circ }$N) we used the methodology described by Kalligeris et al. (2022). The original tide gauge record was high-pass filtered using a first-order Butterworth filter with a 90 min cutoff period, generating the residual signal shown in Fig. 2. The residual signal is clearly close to the background noise level (the ratio of the root-mean-square values of the data points two hours after and before the earthquake is just 1.27), making it difficult to clearly distinguish the first-wave arrival of tsunami waves. We used the wavelet package of Torrence and Compo (1998) to examine the spectral progression of the residual signal, before and after the earthquake (Fig. 2c, see Kalligeris et al. (2022) for methodology details).

Fig. 2

(a) The original tide gauge record in Kasos (black line) and the low-pass filter representation of the tide (red line). (b) The residual signal after filtering the tide; the time of the earthquake is denoted through the vertical dashed line. (c) The wavelet power spectrum using the Morlet wavelet. (d) The global wavelet spectrum

Fig. 3

Azimuthal equidistant plots for the 12 October 2021, $M_W$=6.4, Zakros earthquake. The NOA location (black star) is plotted in the centre of each map and the stations reporting local/regional phase arrivals (Pb, Sb, Pg, Sg, Pn, Sn) are shown as red reverse triangles. Great circle paths are colour-coded with respect to ak135 time residuals calculated by fixing the location to the NOA hypocentre

Fig. 4

Same as in Fig. 3 but for stations reporting teleseismic phases (P, S, pP, sP, PP, ScP, $P_{dif}$, $PKP_{df}$)

We employ the Method Of Splitting Tsunamis (MOST, Titov et al. 2016), a fully validated non-linear shallow water code (see Titov et al. (2016) for model applications), to model the tsunamis generated by the two nodal planes of the earthquake’s focal mechanism. The static initial conditions for the two nodal planes, generated by employing the Okada (1985) analytical formulae, are shown in Fig. S2 in the supplementary material. Three nested relief grids of increasing resolution were used for the simulations (Fig. S3 in the supplementary material). The coarsest grid, grid A, of $\sim$ 115 m resolution, was extracted from the EMODNET bathymetry data set and encompasses the tsunami source region, eastern Crete, Kasos and Karpathos. The source of grid B that encompasses the island of Kasos is also EMODNET, with the grid values being interpolated down to $\sim$ 23 m resolution. Grid C of $\sim$ 5.6 m cell size, which covers the harbor of Kasos, was created by digitising the nautical chart of the Hellenic Hydrographic Service and combining it with a 5 m cell-size DTM of the Hellenic Cadastre. It should be noted that according to the EMODNET metadata, the EMODNET gridded bathymetry around the island of Kasos is based on coarse satellite-derived gravity data, sparse bathymetric soundings, and on satellite image-extracted bathymetry mostly in nearshore areas of the island’s northern coast.

2.5 Shakemap computations

For the production of ShakeMaps we used the USGS ShakeMap v4.1 software package (Worden et al. 2020). Available analysed three-component strong motion data from accelerometric stations (National Observatory of Athens, Institute of Geodynamics, Athens 1975; ITSAK Institute of Engineering Seimology Earthquake Engineering 1981) and broad-band and short-period waveforms from seismic stations of the Unified Hellenic Seismic Network received at NOA-IG in real time with not clipped signal, at a maximum epicentral distance of approximately 250 km were used, alongside with available EMSC testimonies. Both fault plane instances were tried using GMICE (Worden et al. 2012) and GMPE (Boore et al. 2020), considering that the focal depth for the specific event is shallow, above 25 km. The Greece Vs30 map available at https://github.com/usgs/earthquake-global_vs30 (last seen May 2023) and produced after Stewart et al. (2014) was also used.

Fig. 5

Map showing the obtained hypocentral location in this study (circle) for the 12 October 2021, $M_W$=6.4, Zakros earthquake against other available locations (stars) from various agencies (GCMT, GFZ, KOERI, INGV, IPGP, NOA, USGS) colour-scaled with depth. Part of the Ptolemy (Pt.Tr.) and Pliny trenches (Pl.Tr.) are shown in black, as well as the Zakros (Zk.F.) and West Kasos (WKas.F.) normal faults (Caputo and Pavlides 2013) are shown in orange

3 Results

3.1 Mainshock relocation

Since the Zakros $M_W$=6.4 mainshock is located offshore the Crete island at the Southern end of the seismic network, the station coverage is sparse and therefore, the hypocentral solution at the NOA Bulletin shows a very large azimuthal gap of 228$^{\circ }$ (http://bbnet.gein.noa.gr/Events/2021/10/noa2021tzsju_info.html). Firstly, we examined the hypocentral solution at the NOA Bulletin against all the reported phase arrivals from the ISC Bulletin, and phase arrivals reported at NOA Bulletin. It is worth mentioning that at the current state the ISC Bulletin has not provided a reviewed solution for the examined earthquake, since their analysis is approximately 48 months behind real time, hence, some phase arrivals may get deprecated or renamed in the ISC Reviewed Bulletin. Figures 3 and 4 display the corresponding phase residual distribution according to the NOA origin time (2021-10-12 09:24:02.70 UTC) and hypocentral solution ($\varphi$ = 34.89$^{\circ }$, $\lambda$ = 26.47$^{\circ }$, h = 10.4 km). In this case the time residuals of the depth phases (pP, sP, ScP) show systematically, high, positive values (> 5 s), suggesting that a deeper focal depth would be more apropriate.

Fig. 6

Same as in Fig. 3 but ak135 time residuals are associated with the hypocentral solution obtained in this study (black star)

Fig. 7

Same as in Fig. 4 but ak135 time residuals are associated with the hypocentral solution obtained in this study (black star)

We then carried out several tests aiming to obtain a free-depth solution, with a balanced distribution of time residuals around zero seconds, and as low as possible time residuals for the crustal and depth phases. We found that not allowing conversions of direct phases (i.e. P, S) to depth phases (pP, sP, pwP) and core reflections (PcP, ScP) provided the most robust free-depth solution (origin time: 2021-10-12 09:24:05.20 UTC, $\varphi$ = 35.09$^{\circ }$, $\lambda$ = 26.38$^{\circ }$, h = 19.9 km, see Fig. 5 for a comparison with locations from other agencies), with the associated azimuthal gap equal to 17$^{\circ }$. The spatial distribution of traveltime residuals for the obtained solution is presented in Fig. 6 for crustal phase arrivals (Pb, Sb, Pn and Sn), and in Fig. 7 for the rest of the reported seismic phases (P, S, pP, sP, PP, ScP, $P_{dif}$, and $PKP_{df}$). Since we have obtained a deeper hypocentre, any Pg and Sg phases in our dataset have now been renamed to Pb and Sb, respectively (Fig. 6). The time residuals of these phase arrivals are still systematically negative, nevertheless, their absolute values are now closer to zero. Moreover, the distribution of positive and negative Pn and Sn time residuals show a characteristic pattern for both the NOA and our locations (mostly positive values for azimuths between the 30$^{\circ }$W and 70$^{\circ }$E), which may be associated with the use of a 1D velocity model in a complex area characterised by high lateral heterogeneities (Hellenic subduction zone). Direct P phases which dominate our dataset are more equally distributed in azimuth around zero seconds than before, whilst they show slightly lower absolute time residuals overall (Fig. 7). The depth estimation is strongly biased by surface reflections, core reflections and depth phases (Engdahl et al. 1998), however in our case there is a deficiency of detected depth phases along with a poor azimuthal coverage. Nevertheless, the obtained depth yielded an overall better fit for these phases too.

3.2 Aftershocks

As mentioned in the Introduction, the 30-days aftershock sequence that followed the $M_W$=6.4 Zakros, Crete earthquake was rather poor. More details on the reasons for this observation will be given in the Discussion section. Hence, the detailed analysis of the aftershock sequence is beyond the scope of this study, nevertheless, it is worth mentioning that a relocation using differential travel times (Waldhauser and Ellsworth 2000) was initially attempted. However, due to the absence of P/S phase arrival pairs from the same stations in many small magnitude aftershocks (most station readings were just first P-phase arrivals), almost only half of the aftershocks were relocated, without improving dramatically their locations overall. Figure S4 in the supplementary material, offers a rough estimate of the quality of the NOA aftershock locations, by showing the difference in arrival times of P/S pairs for each aftershock pair, with respect to their interevent distances. Differential P/S travel time pairs are within ±2 s up to 10 km interevent distance, whereas, larger dispersion is observed for more distant pairs, indicating that the aftershocks are not very well clustered around the mainshock, but rather diffused in space. Moreover, the fact that only a few P/S station readings for each event are available leaves high uncertainty in the depth resolution of the aftershocks determined by NOA. This is not surprising, taking into account that the epicentral area lies outside the station coverage of the HUSN seismological network (e.g. Melis et al. 2023), usually yielding poorly constrained earthquake locations, also characterised by large station azimuthal gaps which are associated with large horizontal and vertical errors (Bondár and Storchak 2011).

Table 1 Input parameters and parametrisation for the kinematic slip inversions described in Section 3.3 based on the NE-SW oriented, shallow-dipping nodal plane

3.3 Kinematic slip model

According to available fault plane solutions (see Table S1 in the supplementary material) the earthquake rupture took place on a normal fault with either NE-SW orientation and a rather shallow-dipping surface to the NW, or an almost vertical fault with N-S orientation. Since neither of these nodal planes align well with any of the known main normal faults in the study area, and the aftershock sequence is rather poor not letting us draw safe conclusions on the tectonics associated with the mainshock, we make the hypothesis that the earthquake possibly activated a not previously mapped fault. Normal faults with very steep dip angles (70$^{\circ }$-90$^{\circ }$) are not new to the study area, such as the Zakros and West Kasos faults (i.e. Caputo and Pavlides 2013), nevertheless, their orientation is almost perpendicular to the strike of the steep dipping, N-S oriented nodal plane associated with the earthquake’s mechanism. Therefore, we computed kinematic slip models for both nodal planes based on the hypocentral solution obtained in Section 3.1 and the GCMT best-fitting double-couple solution (see also Section 2.2).

The fault plane was parameterised by 1 km $\times$ 1 km subfaults on a 30 km $\times$ 20 km planar surface and the nucleation point was set 15 km from each fault edge, along strike, and 7 km in up-dip direction. The input parameters for the inversion are summarised in Table 1. The slip model inversion requires prior knowledge of the slip rate duration. In order to obtain an estimation for the duration, we used a proxy of the slip rate duration being twice the GCMT half-duration (Duputel et al. 2013), and after some trial and error we found the value of 8 s as being optimal. Even though real world earthquakes may deviate from this theory, nevertheless, the validity of this proxy was verified against global, $M_W$ $\ge$ 7.5 earthquakes in Lentas et al. (2013), and also have been used in Lentas et al. (2021) with good results.

Fig. 8

Snapshots at 1 s time intervals showing the rupture evolution of the 12 October 2021, $M_W$=6.4, Zakros earthquake obtained from the kinematic inversion described in Section 2.2, with respect to the NE-SW oriented, shallow-dipping nodal plane. The white cross represents the rupture nucleation point

Fig. 9

(a) Map showing the slip model distribution for the 12 October 2021, $M_W$=6.4, Zakros earthquake (blue star) based on the NE-SW oriented, shallow-dipping nodal plane of the GCMT best-fitting double-couple solution. Aftershock locations are shown as time colour-scaled circles; (b) Moment rate function determined from the kinematic slip inversion in “a”; (c) Three-dimensional representation of the fault model where slip distribution is mapped along a fault dip projection. The surface trace of the planar fault in the slip model is plotted in blue for reference

Before we present results of slip model inversions based on real waveform data, we carried out a synthetic test in order to evaluate the performance of our inversion scheme based on the NE-SW orientation, shallow-dipping fault plane, using the same parametrisation as described above. A simple, single patch, slip model with maximum slip of 0.7 m was used as an input in order to compute synthetic data (Gallović and Zahradník 2011). Figure S5 in the supplementary material presents the input slip model and the obtained model after the inversion. The overall distribution of the obtained slip follows in good agreement the input slip distribution even though the station distribution leaves a large azimuthal gap. Only noticeable difference is the maximum slip being slightly overestimated by approximately 15$\%$. No other significant glitches or artifacts in the obtained slip model are shown, which is encouraging.

Figure 8 shows the real slip model inversion time evolution of the rupture for the mainshock in consecutive snapshots of 1 s intervals, based on the NE-SW oriented, shallow-dipping, nodal plane. Seismic station components showing bad data fit have been either removed or down-weighted in the inversions (Fig. S6 in the supplementary material). In general, the rupture model is rather simple, characterised by a single patch up-dip within the first second (pulse-like), and a second short duration patch (2 s) to the NE between 15 km and 20 km at depth. In essence, after the 4$^{th}$ second no significant slip is observed, and the rupture has terminated after 7 s.

The correlation between the aftershock seismicity and the slip distribution is presented in Fig. 9 where the composite slip model is shown along with the seismicity which followed the mainshock. The majority of aftershocks are distributed along the southern part of the rupture zone where slip is relatively low, whilst the area of maximum slip ($\sim$ 27 cm) is in excellent agreement with the absence of aftershock activity. The moment rate function determined from the kinematic slip model (Fig. 9b) also suggests the presence of a relatively short (3 s) and dominant episode of slip in the beginning of the rupture, which has faded away from the 4$^{th}$ second onwards.

Figure S7 in the supplementary material shows the time evolution of the rupture for the mainshock based on the N-S oriented, steep nodal plane. The rupture is characterised by a single patch between 15 km and 20 km in depth which fades out after the 4$^{th}$ second, in a similar manner as the case of the NE-SW oriented nodal plane.

Unlike the case of the NE-SW oriented, shallow-dipping, nodal plane, the maximum slip of the composite slip model for the N-S oriented nodal plane (Fig. S8 in the supplementary material) is correlated with the majority of the recorded aftershocks, which contradicts what one would expect. It is worth mentioning that the locations of the aftershocks could be characterised by large errors, as these seismic events have been located by using only direct P and S phase arrivals from seismic stations in Greece, associated with large azimuthal gaps. More accurate locations may have dramatically altered the observed correlation. Finally, the data fit of the obtained kinematic slip model is slightly worse in comparison with the data fit of the NE-SW oriented nodal plane by approximately 10$\%$ (Fig. S6 in the supplementary material), favouring the NE-SW oriented, shallow-dipping, nodal plane as being the fault plane associated with the mainshock.

3.4 Coulomb stress transfer

Our estimations of Coulomb stress changes due to the occurrence of the strong offshore Zakros earthquake were based on the kinematic slip model produced by the slip inversion analysis. Fault properties were adopted from the GCMT best-fitting double-couple solution and ($\Delta CFF$) was computed for both planes. The geometry of the rupture regards a rectangular plane with 30 km length and 20 km width along which variable slip is computed. Stress was computed at the depth of 18 km, which lays 1.9 km above the earthquake relocated hypocentre.

Fig. 10

Coseismic stress changes for the variable slip model of Fig. 9 at 18 km depth (black line). The white star denotes the hypocentral solution obtained in the current study. The nodal plane parametrisation is shown as a 1 km $\times$ 1 km grid. Aftershocks up to 30 days following the mainshock are also plotted for reference (see legend for details)

Fig. 11

Cross-section A1-A2 of Fig. 10, perpendicular to the strike of the rupture model of Fig. 9. Seismicity hypocentres within 5 km distance along side are also plotted as black dots

Coulomb stress change results for the north-dipping fault plane in Fig. 10 show a great resemblance to a uniform slip shallow-angle dipping fault since the slip model regards a single patch following the slip distribution pattern (see Fig. 9). A shadow zone in rectangular shape is developed along the estimated source fault, whereas stress enhanced areas are distributed around the zone with maximum values over the southern and the northern termination of the fault. Aftershock seismicity is sparse and is found both along the rupture zone and at the southern tips of the fault where stress changes are positively increased. Two earthquakes above magnitude 5.0, which have occured in the east of the $M_W$=6.4, Zakros earthquake, even though they appear on the positive lobe following the rupture, they are not triggered by the Zakros earthquake, and most likely are associated with the general seismicity of the area, as they are located $\sim$60 km away from the mainshock. A vertical cross section perpendicular to the fault strike is further constructed (horizontal projection demonstrated in Fig. 11) where the shadow zone is expanded from 16 km to 30 km at depth involving the majority of the subsequent earthquake hypocentres (within a 5 km distance along side). $\Delta CFF$ distribution has also been plotted for the south dipping fault plane source model and results for the depth of 18 km are depicted in the supplementary material (see Fig. S9). The poor association between the aftershock distribution and the stress enhanced areas does not provide robust evidence on which rupture model is best associated with the mainshock.

Fig. 12

(a) The periodograms of the unfiltered Kasos tide gauge time series 6-hr before and 6-hr after the earthquake. (b) The ratio of the two periodograms (before earthquake/after earthquake). Averaging of four overlapping segments corresponds to $\sim$ 8 degrees of freedom, and PSD 95$\%$ lower and upper confidence interval factors are 0.46 and 3.67, respectively

3.5 Kasos tide gauge record analysis and tsunami modelling

The $M_W$=6.4 Zakros earthquake on October 12$^{th}$, 2021, prompted the Tsunami Service Providers operating in the Eastern Mediterranean to issue local advisory messages (possibility of strong tsunami-induced currents in the nearshore for areas for up to 100 km from the earthquake epicentre). NOA’s tide gauge in Kasos (26.9217$^{\circ }$E, 35.4188$^{\circ }$N), which supports the operations of the Hellenic National Tsunami Warning Center (HL-NTWC, one of the three Tsunami Service Providers operating in the Eastern Mediterranean), picked up what appears to be a very small tsunami. No other tide gauge in the region showed any sea level excitation after the earthquake. Given the noise-level wave amplitudes of the Kasos tide gauge record, tsunami-ongoing messages were not issued by the Tsunami Service Providers, and the authors are not aware of sightings of tsunami waves or currents being reported. In this section, we analyse the Kasos tide gauge record and model the tsunami in an attempt to use the available data as further evidence for possibly favouring one of the two nodal planes of the slip model described in Section 3.3.

Following earthquake triggering, energy is generated in the 6.3–7.2 min period wave energy band (global wavelet spectrum shown in Fig. 2d). The wavelet figure does not reveal any other distinguishable frequency/period bands in which energy was generated after the earthquake during the time period of interest (i.e. the time period shown in Fig. 2c which includes the first 6 hr after the expected time of first-wave arrival).

Fig. 13

(a-b) Comparison between the Kasos high-pass filtered tide gauge record (black lines) and the mareograms extracted from the hydrodynamic model for the two initial conditions shown in Fig. S2 in the supplementary material; the blue lines to the MOST-extract time series of free surface elevation, and the red-dashed lines are the 1-min averaged MOST-extracted time series. (c) Comparison between the raw power spectra (two degrees of freedom) of the 2-hr high-pass filtered tide gauge record, and the 2-hr MOST-extracted numerical mareograms for the two nodal planes of the slip model described in Section 3.3

The non-time-dependent Welch (1967) averaged modified-periodogram is shown in Fig. 12. Two time series were used for the periodograms: a 6 hr segment of the tide gauge record before the earthquake, labeled “before earthquake”, and a 6 hr segment after the earthquake, labeled “after earthquake” (see Kalligeris et al. (2022) for methodology details). Figure 12a shows the distribution of energy for the two time series, with energy in both time series being concentrated mostly within narrow frequency/period bands, most probably corresponding to natural frequencies of the forced system in the study region (e.g. harbor basin). After the earthquake there is a clear energy gain across the whole frequency/period range shown in Fig. 12a. However, with the exception of the peaks at 6.6 and 9.5 min period, energy is gained in frequencies/periods already exhibiting peaks. Figure 12b shows the ratio of the two periodograms (“after earthquake” over “before earthquake”), which is used to identify functional characteristics of the source (Rabinovich 1997). Whilst the ratio values are evenly distributed across the frequency range of the plot, which is further evidence that if any tsunami signal exists it is close to background level, the peaks at 6.6 and 9.8 min period stand out in that the rise in energy is not narrow-peaked.

From the analysis of the Kasos tide gauge record, it cannot be concluded with certainty whether a (small) tsunami was recorded or not since the signal after the earthquake remains close to the background noise level. The oscillation energy marginally increased after the earthquake, but this alone does not prove the presence of tsunami waves, since storm waves could also have contributed. If tsunami waves were indeed recorded, the sign of first-wave arrival is the generation of spectral energy in the 6–10 min period range starting at $\sim$ 18 min after the earthquake, and peaking at the arrival of the first distinguishable drawdown of the water level at $\sim$ 39 min after the earthquake. The wavelet and periodogram analyses thus suggest that any tsunami spectral energy from the source would lie primarily in the 6–10 min period range.

Fig. 14

Intensity map product of USGS ShakeMap for the NE-SW oriented, shallow-dipping nodal plane of the GCMT best-fitting double-couple solution. The rupture area is represented by a black rectangle and the epicentre is shown as a black star. Strong motion stations are shown as triangles and circles represent EMSC testimonies. Colour shading follows the scale used as standard for USGS ShakeMap

The numerical mareograms for the two nodal planes (see Fig. S3c in the supplementary material for the location of the Kasos tide gauge) were compared to the high-pass filtered Kasos tide gauge record (Fig. 13a-b); since the Kasos tide gauge samples at 1 Hz and reports 1-min averaged values, we present both the model-extracted time series without averaging (blue lines in Fig. 13a-b), and also the 1-min averaged numerical mareograms (red lines in Fig. 13a-b) that are compatible with the tide gauge record. The numerical mareograms in Fig. 13a-b show that the first-wave arrival is in the form of a weak drawdown, followed by a weak elevation wave, which would be difficult to distinguish in the tide gauge record given the low signal/noise level. Therefore, there is no information available to evaluate neither the timing nor the amplitude of the first-wave arrival in the simulations. The overall amplitude of the numerical mareograms, whilst comparable to the tide gauge record, appears to be slightly over-predicted given that the tide gauge record contains the background noise. Moreover, the numerical mareograms appear to be out of phase with the tide gauge record. This is particularly evident at the sharpest drawdown recorded at $\sim$ 39 min after the earthquake, the timing of which is not matched by either simulation. The observed phase shift between the tide gauge record and the numerical mareograms, besides source characteristics, could also be attributed to inaccuracies in the regional bathymetry around the island of Kasos (see above numerical grids description).

In terms of the energy distribution across the period spectrum (see Fig. 13c), the numerical mareograms for both nodal planes mostly contain energy in the 12–15 min range, which is also prominent in the tide gauge record. However, since the tide gauge record contained energy in this period range prior to the earthquake, it is unlikely that it corresponds to the tsunami source, as explained in the previous section. In the 6–10 min period range, the numerical mareogram of neither nodal plane matches the two energy peaks of the tide gauge record. Only the power spectrum of the nodal plane with 226$^{\circ }$ strike features a peak at 8 s period, but its energy is deficient compared to the peak of the tide gauge spectrum. Last, the power spectrum of the nodal plane with 340$^{\circ }$ strike features a distinct energy peak at 5 s period, which is not observed in the power spectrum of the tide gauge record.

Overall, the comparison between the Kasos tide gauge record and the numerical mareograms for the two nodal planes of the slip model did not yield any conclusive evidence to favour any of the two nodal planes. Whilst the amplitudes of the numerical mareograms for the two nodal planes are reasonable when compared to the tide gauge record which contains the background noise, neither numerical mareogram matches the timing of the most distinctive drawdown recorded at $\sim$ 39 min after the earthquake. Since the low signal/noise ratio of the tide gauge record prevented a meaningful direct comparison between the (noisy) tide gauge record and the numerical mareograms, we also compared their respective power spectra. The spectrum of neither numerical mareogram matches the energy of the tide gauge record in the 6–10 min period range deduced earlier to possibly correspond to the tsunami source. However, the power spectrum of the nodal plane with 226$^{\circ }$ strike matches the spectral peak at 8 s period (albeit with deficient energy) and is overall closer to the spectrum of the tide gauge record.

3.6 Shakemaps

USGS ShakeMaps are produced by NOA-IG in a routine basis for all events recorded in Greece with magnitude above 4. In the present study we produced shakemaps offline with focus to the specific area and for the purpose to investigate the two proposed fault planes, in order to identify in the two corresponding resulted maps the preferred plane, as they can be compared with the reported shaking through the available EMSC testimonies.

In a straight comparison of the produced macroseismic intensity maps it can be identified a higher intensity shaking to the SE of Crete rather to the NE part. Thus, the area east of Ierapetra corresponds to the area where the high reported observations exist (Fig. 14), rather than in Siteia as it can be seen in the map of Fig. S10 in the supplementary material. This may show that shaking reported observations favours the shallow-dipping NE-SW oriented nodal plane. Analytical views of mapped Peak-Ground-Acceleration (PGA) are shown in Figs. S11-S12 in the supplementary material.

4 Discussion and conclusions

In this paper we studied the strong $M_W$=6.4, Zakros, Crete earthquake, using all the freely available parametric, seismic waveform, tide gauge and GNSS data up to date, associated with the mainshock. We started by relocating the mainshock using a wide range of phase arrival times on a global scale (Bondár and Storchak 2011). Using the improved hypocentral location we carried out kinematic slip inversions (Gallovič et al. 2015) for both nodal planes of the GCMT earthquake mechanism. Based on the rupture determined from our slip models we computed Coulomb stress changes (Deng and Sykes 1997) and we carried out tsunami modelling (Titov et al. 2016), attempting to reveal the activated seismic fault, since no significant aftershock sequence was recorded within the next 30 days after the mainshock. According to our analysis we believe that a NE-SW oriented, shallow-dipping to the NW fault plane is more plausible. The latter can be favoured by the shake maps produced in comparison for the same set of data but for the two different proposed fault planes.

The studied earthquake occurred offshore the east coast of Crete where the seismic station coverage from the Hellenic Unified Seismic Network (HUSN) is rather sparse, hence, the hypocentral solution provided by the Institute of Geodynamics of the National Observatory of Athens, which is the official seismological agency in Greece, showed a very wide azimuthal gap (228$^{\circ }$). Constraining earthquake hypocentres in areas where the station network coverage is poor can yield substantial epicentral and depth trade-offs (Gomberg et al. 1990), especially in areas asocciated with complicated geotectonic structures and heterogeneities in the crust and the upper mantle, such as subduction zones. Indeed, the velocity model used by NOA is a 1D, rather simplistic representation of the Earth’s crust. The ISC locator used in this study, also uses the 1D, ak135 velocity model (Kennett et al. 1995), nevertheless, the majority of the phase arrivals used in our relocated hypocentral solution are teleseismic phases which are associated with seismic rays that travel almost perpendicular to the Earth’s crust, hence, less prone to effects from unmodelled lateral heterogeneities. In addition, the ISC locator takes into account the structure-correlated errors, which yield more realistic locations and uncertainty estimates (Bondár and Storchak 2011) and allows conversions of phase characterisations according to travel times following the IASPEI Standard Seismic Phase List (Storchak et al. 2003).

Moreover, the mainshock is located in an area which lies beyond the strong detection capabilities of the HUSN seismological network. Specifically, the area south of Crete island is lacking station coverage and as a result the magnitude of completeness increases dramatically offshore the south and east coasts of Crete ($M_C$ $\ge$ 2), in comparison with the main island ($M_C$ $\le$ 1) where the sesmic station coverage is dense (see for example Figure 9 in Melis et al. (2023)). Another consequence of the limited station density is the large azimuthal gap, and hence the location uncertainty, that NOA hypocentre solutions in the epicentral area are characterised for. Apart from any issues regarding the reliability of the estimated earthquake parameters overall, there is no rich aftershock activity recorded as one would expect based on the mainshock’s magnitude and depth. For comparison, the shallow (9.5 km) 27 September 2021, $M_W$=5.9, Arkalochori earthquake on Crete island, was characterised by a rich aftershock sequence of over 1000 aftershocks within a 12-month time period, with $M_L$=0.5 being the smallest magnitude reported (Ganas et al. 2022), thanks to a dense temporary network deployment around the epicentre. Moreover, an offshore (east coast of Crete) $M_W$=6.0, thrust earthquake, at a depth of 22 km (based on the reviewed ISC location, http://www.isc.ac.uk/cgi-bin/web-db-run?event_id=610587689 &out_format=ISF2 &request=COMPREHENSIVE) was characterised by roughly 500 aftershocks within a 6-month period (Görgün et al. 2016). On the contrary, a search in the NOA database (https://bbnet.gein.noa.gr/HL/databases/database) shows that the studied earthquake is characterised by the presence of roughly 130 aftershocks within a 6-month period, with the majority being recorded within the first month after the mainshock. Even though the magnitude of completeness in each area in the above example may not be the same and would not allow for a direct comparison, nevertheless, it is obvious that the aftershock sequence of the studied earthquake seems to be poorer than expected. A more sophisticated examination of aftershock sequences based on normalising magnitude thresholds, and/or using general aftershock statistics could be an interesting, yet separate study, although this lies beyond the scope of the present paper. In conclusion, we believe that the lack of aftershocks is most likely attributed to the combination of the poor network detectability and the rheology of the epicentral area. For example, Yang and Ben-Zion (2009) studied the aftershocks productivity for different earthquakes in California and found it to be inversely correlated with the heat flow and existence of sedimentary rocks at seismogenic depths. Since the epicentral area in this study is very close to the Hellenic subduction front, with sediments that can easily subduct at seismogenic depth, and heat flow expected to be higher than the typical continental crust, this could potentially explain the somewhat depleted aftershock sequence. As a result, relocating the poor aftershock sequence using more advanced high accuracy techniques, such as those based in differential travel times (Waldhauser and Ellsworth 2000) did not allow for sharper seismic-tectonic images of the rupture area, as only half of the aftershocks met the selection criteria.

Using the improved location of the mainshock and the best-fitting double-couple solution from GCMT, we computed kinematic slip models for either of the two nodal planes using near-field seismic data. In general, kinematic slip inversions suffer from non-unique solutions (Monelli and Mai 2008; Mai et al. 2016), since a large number of model parameters is typically involved in these problems as a result of the parametrisation of even a simple planar fault. Thus, damping is necessary in order to stabilise the inversion, and in our case, this is achieved by applying non-linear constraints, such as positivity and spatiotemporal smoothing (Gallovič et al. 2015).

Due to the land distribution in the epicentral area, the azimuthal seismic station coverage is not uniform, and some bias from the nearest station (SIT2) can potentially affect the results, usually expressed as false unilateral propagation towards the nearest stations (Gallovič and Zahradník 2011; Gallovič et al. 2015). In our case, we did not observe this and the rupture is rather simple, characterised by short (pulse-like) patches in both cases. Maximum slip ($\sim$ 27 cm) in the slip model based on the NE-SW oriented, shallow-dipping nodal plane, is anticorrelated with respect to the spatial distribution of the aftershocks, whilst this is not the case for the N-S oriented, near vertical nodal plane. Nevertheless, the accuracy of the locations of the aftershocks is questionable as discussed above.

Further analysis of Coulomb stress transfer, and tsunami modelling using the mareograms of the Kasos tide gauge based on the obtained slip models, yielded similar patterns in either case, not favouring one nodal plane as the causative fault against the other. However, production of shakemaps for the two possible planes showed that shaking reported observations favours the shallow-dipping NE-SW oriented nodal plane. The latter comes into agreement with the seismotectonic and bathymentric evidence which support the existence of NNW-SSE grabens, east of Crete.

The occurrence of the $M_W$=6.4 earthquake which is analysed in this study needs to be interpreted under the framework of the complicated seismotectonic context of the convergence between the overriding Aegean plate and the down dipping African slab. The eastern part of the subduction zone is devoid of frequent or well-constrained strong earthquakes (Becker et al. 2009), hence its seismotectonic properties remain obscure compared to the western part (Shaw and Jackson 2010).

Fault mechanisms along the Hellenic arc vary from convergence (low-angle and steeply dipping reverse faults) related to the subducting plate, to arc-parallel extension along the dipping plane and strike slip faulting along the transtentional trenches to the south of Crete (Taymaz et al. 1990; Kiratzi 2003) where the majority of offshore microseismicity occurs (Becker et al. 2009). At the eastern termination of the subduction, in the vicinity of the 2021 epicentre, well-constrained fault mechanisms reveal not only thrust faulting, but also NE-SW left-lateral strike slip faults exhibiting SSW-WSW slip vectors, oblique to the arc strike (Shaw and Jackson 2010, and references therein). These fault properties agree with identified bathymetric lineaments, oblique to the Ptolemy trench, among others (Kreemer and Chamot-Rooke 2004). The relocated epicentre of the 2021 earthquake is located at the eastern frontal part forearc, northern than Ptolemy trench, which accommodates sinistral slip (Bohnhoff et al. 2005).

Our multidisciplinary analysis favours the activation of a shallow west dipping NE-SW normal fault with a significant strike slip component, different to the dominant high dipping angle seismotectonic features of eastern Crete and Kasos. NNE-SSW normal active faults like the east dipping Zakros fault which dominates in the area and sharply cuts the west coast of the Cretan land seems not to be the causative fault in our case, but rather a conjugate feature. Kiratzi (2003) and Shaw and Jackson (2010) showed earthquake mechanisms computed using waveform modelling in the same epicentral area, similar to the available earthquake mechanisms for the $M_W$=6.4, Zakros earthquake (see Table S1 in the supplementary material). Specifically, the 9 July 1990, $M_W$=5.2 earthquake ($\varphi$=217$^{\circ }$, $\delta$=56$^{\circ }$, $\lambda$=-21$^{\circ }$, see the electronic supplement in Shaw and Jackson (2010)) and the 30 April 1992, $M_W$=5.8 earthquake ($\varphi$=214$^{\circ }$, $\delta$=52$^{\circ }$, $\lambda$=-47$^{\circ }$, see the electronic supplement in Shaw and Jackson (2010)) which occurred at shallow depths (9 km and 7 km, respectively), compared to the deeper (19.9 km), 12 October 2021, $M_W$=6.4 event, which may reflect the deeper layer where overthrust seismicity occurs in the eastern part of the subduction (Bocchini et al. 2018). The aforementioned shallow earthquakes are associated with steeper fault planes, and combined with our findings, this could potentially indicate the existence of NE-SW oriented listric fault structures developed above the subduction interface. This agrees with the seismicity analysis from local deployments southeast of Crete, according to Brüstle (2012), who show that the epicentral distribution in this area develops along a NE-SW striking graben which intersects with the Ptolemy trench (morphologically identified by Kreemer and Chamot-Rooke (2004)).