1 Introduction

Elastic or seismic anisotropy and its effects on seismic wave propagation in the upper mantle (lower lithosphere and asthenosphere) are caused by aligned melt-bearing structures, so-called shape preferred orientation (SPO) (Kaminski 2006; Long and Silver 2009) or preferred orientation of anisotropic minerals, so-called lattice or crystallographic preferred orientation (LPO, CPO) (Mainprice and Silver 1993; Long and Becker 2010). Such preferred orientations can be explained by the frozen-in stress field or flow field of the last tectonic deformation or by recent mantle flow (Yuan and Romanowicz 2010; Fouch and Rondenay 2006). In the crust, in addition, aligned cracks or sedimentary layering and structures may cause seismic anisotropy (Crampin 1984). Thus, measuring and interpreting seismic anisotropy is an important tool to image geodynamic processes and to bridge seismology, geodynamics, and tectonics (Silver 1996; Savage 1999; Long and Silver 2009; Long and Becker 2010).

If a shear (S) wave propagates through an anisotropic medium, it is split into two quasi shear (qS) waves (analogue to optics birefringence). One qS wave is polarized in the direction of the elastically fast axis and the other one perpendicularly in the direction of the elastically slow axis. Since the two qS waves travel with different wave velocities, they accumulate a delay time δt which is preserved after leaving the anisotropic medium. At the surface, it is possible to measure the apparent fast polarization direction and the apparent time delay (splitting parameters, see below). Particularly for studying anisotropy in the (upper and lowermost) mantle, teleseismic S waves with the core-refracted phases SKS, SKKS, and PKS are analyzed. These waves propagate through the liquid outer core as compressional (P) wave and then convert (back) to an S wave at the core mantle boundary (CMB), in particular to a radially polarized SV wave. If this SV wave propagates through an anisotropic medium, it is split and an additional signal on the transverse component (SH wave) should be found (except for the special cases with an initial polarization direction along the fast or slow axis of the anisotropic medium). In a polarization diagram of the radial (R or Q) and transverse (T) components (Plesinger et al. 1986), shear wave splitting can be identified by an elliptical particle motion, whereas an unsplit S wave is linearly polarized along the Q component. Several methods are applied to extract the so-called splitting parameters the fast polarization direction ϕ (clockwise angle relative to north) and the delay time δt from the recordings (Vecsey et al. 2008).

A major problem is non-uniqueness concerning the structural interpretation of the measured apparent splitting measurements (Romanowicz and Yuan 2012). As SKS phases arrive steeply or near-vertically at the recording site, there is no good vertical resolution of anisotropic structures at depth. However, by analyzing recordings from neighboring sites, lateral variations may be resolved (e.g., Bastow et al. 2007; Walker et al. 2005). A major drawback in many regions is the limited azimuthal observation: since the backazimuthal coverage (BAZ, clockwise angle from north) depends on the (rare) occurrence of strong earthquakes (moment magnitude Mw higher than ca. 6) with epicentral distances of > 80°, an equal source coverage is often not fulfilled. E.g. in Central Europe, there are typical observational gaps towards north, southeast, and northwest due to the distribution of the main earthquake zones (Fig. 1, inset in the lower right corner). Another problem is the limitation in recording time, especially for temporary networks for high-resolution regional studies. During typical measurement durations of 1–3 years often less than ten SK(K)S phases are recorded for splitting measurements and these observations cover only a very limited backazimuthal range or only specific backazimuth directions. As result, structural anisotropy models are often completely underdetermined even for simple model assumptions such as laterally homogeneous one- and two-layer scenarios with transverse isotropy. Thus, the discrimination between one- or two-layer models with horizontal or dipping symmetry axis remains often open within the modeling uncertainties. Averaging of the splitting parameters across a wide or the whole backazimuthal range is sometimes done to obtain stable values. Thereby, resulting models can provide erroneous fast polarization directions which may cause misleading geodynamic interpretations. Another problem is the assumption of laterally uniform structural anisotropy around a recording station: backazimuthal variations of the splitting parameters may then be interpreted by affects due to anisotropy in one (possibly layered) laterally homogeneously anisotropic medium instead of lateral variations in anisotropy of the medium. This issue will be addressed here.

Fig. 1
figure 1

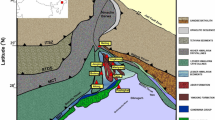
Location of the recording station Black Forest Observatory (BFO, blue triangle) in SW Germany and piercing points of SKS (red circles), SKKS (orange circles), and PKS (yellow circles) ray paths at 410 km depth calculated with the TauP Toolkit (Crotwell et al. 1999) based on the iasp91 Earth model (Kennett and Engdahl 1991). The Kaiserstuhl Volcanic Complex (VC) is highlighted in purple. The global map in the lower right corner displays the epicenter distribution (gray circles) for this study. Please note only those events are included for which at least one splitting measurement was obtained rated as good or fair (single- or multi-event analysis) including nulls. For the ray path from the lowermost mantle to the surface as well as SKS-SKKS pairs, see the Supplementary information (Fig. S4)

Full size image

In the following, we carefully analyze 25 years of recordings at a low-noise site in Southwest Germany, the Black Forest Observatory, and discuss the backazimuthal variation of SK(K)S splitting observations. After a discussion of the observations, we present a preliminary structural anisotropy model and conclude with recommendations for similar future anisotropy studies.

2 Station BFO and geological setting

The Black Forest Observatory (BFO) is located in the northern Alpine foreland in the Black Forest Mountains which are bounded by the Upper Rhine Graben (URG) in the west and the South German Block in the east (Fig. 1). The URG is a part of the European Cenozoic Rift System and an approximately 300 km long NNE striking continental passive rift (Kirschner et al. 2011), which extends from Basel in the south to Frankfurt am Main in the north. Its average width is 30–40 km and its total lithospheric extension is ca. 5–6 km. The graben structure is asymmetric, e.g., in the east, where there is the main boundary fault, the sedimentary infill is thicker compared to the west (Grimmer et al. 2017 and references therein). The only major volcanic complex within the URG, the Kaiserstuhl, was active in Miocene time and is situated about 50 km SW of BFO. The South German Block (Ring and Bolhar 2020) is characterized with smoothly SE dipping, mainly Mesozoic sedimentary rocks. In the central and southern Black Forest, these layers and the crystalline basement were strongly uplifted (up to 2.5 km) and eroded. The lithosphere around BFO consolidated mainly in late Paleozoic times (ca. 330–270 Myr) and it is about 60 km thick (Seiberlich et al. 2013; Meier et al. 2016). The former silver mine with the instruments of BFO is situated in the central gneiss complex of the Black Forest (Black Forest Observatory (BFO) 1971).

Due to its remote location, the stable environmental conditions inside the mine, and the excellent observers the recordings at BFO are of very high quality. Especially the noise level at BFO is among the lowest values worldwide in the Global Seismographic Network (Berger et al. 2004). Nowadays, more than 25 years of seismic broadband waveforms from BFO are available at data centers (e.g., IRIS Washington or BGR Hannover). This allows us to study weak and rarely occurring seismic signals such as SK(K)S phases. Furthermore, in average these long-term recordings from BFO represent the potentially expected teleseismic ray paths to Central Europe, hence, the expected backazimuthal coverage at seismological stations there (Fig. 1, inset in the lower right corner).

The analyzed teleseismic S waves propagate steeply through the upper mantle. The piercing points at the 410 km discontinuity for the SKS, SKKS, and PKS phases recorded at BFO are shown in Fig. 1. This distribution includes three major sampled regions in the upper mantle: below the South German block (NE of BFO), below the northern rim of the Swiss Alps (south of BFO) and below the French Vosges Mountains, the URG and the Kaiserstuhl Volcanic Complex (SW of BFO).

There is known seismic anisotropy at different depth levels underneath the region around BFO. Most studies find a prevailing fast wave propagation direction for P and S waves in roughly NE-SW direction. Lüschen et al. (1990) analyzed seismic near-vertical reflection data from the Black Forest and they used synthetic anisotropic modeling to explain their observations. As a result, they inferred a laminated lower crust with horizontal anisotropic layers due to alignment of hornblende crystals, with E-W fast P wave direction, NW–SE and NE-SW fast SV wave direction, and fast ESE-WNW SH wave directions. Eckhardt and Rabbel (2011) studied teleseismic P-to-S conversions from the Moho and found transversely polarized S waves with a split time of 0.2 s in the crust below BFO. Their observations could be best explained by a ca. 30° fast polarization direction. Underneath the Moho anisotropy was inferred from seismic wide-angle refraction studies by Fuchs (1983) and Enderle et al. (1996) in SW Germany. Their model has a fast Pn propagation direction of 31° and based on petrological modeling, they suggest a fast shear wave propagation direction of 76°. A similar result of ca. 35° for the fast P wave polarization direction in the lithospheric mantle was found by Song et al. (2004) by inverting travel times of Pn phases.

Vinnik et al. (1994) determined an effective ϕ of 40° and an effective δt of 1.0 s from SKS splitting measurements using BFO recordings that had been averaged over all backazimuths. Later a two-layer upper mantle model was proposed with fast polarization in 10–30° and 80–100° for the upper and lower layers, respectively, based on data from seismic stations around the URG (Granet et al. 1998). Walker et al. (2005) did a careful study of BFO recordings and observed a backazimuthal dependent SKS splitting. They suggest horizontal and dipping layer models for BFO and they also suggest a laterally varying anisotropy in comparison with two neighboring stations (STU Stuttgart to the NE and ECH Échery to the west of BFO). In their conclusions, they propose that there are different fast polarization directions on the eastern and western side of the southern URG with no splitting underneath the URG itself. However, they could not provide a more comprehensive model and propose two options for BFO: either one-layer with transverse isotropy with dipping symmetry axis (ϕ = 40–50°, dip ~ 30–50° or two different two-layer scenarios with transverse isotropy with horizontal symmetry axes (ϕ1 = 70° ± 5°, δt1 = (2.3 ± 0.7) s, ϕ2 = 0° ± 15°, δt2 = (1.1 ± 0.3) s or ϕ1 = 90° ± 5°, δt1 = (1.2 ± 0.4) s, ϕ2 = 40° ± 5°, δt2 = (1.4 ± 0.4) s). The results by Walker et al. (2005) demonstrate the problem of non-uniqueness of the anisotropy models derived from SKS splitting observations.

Using 15 splitting measurements, Walther et al. (2014) determined a two-layer model with ϕ1 = 170°, δt1 = 0.6 s, ϕ2 = 60°, δt2 = 1.4 s for BFO that is explained with URG tectonics (upper layer) and an underlying Variscan-like strike direction (lower layer). Recent large-scale studies to determine mantle flow related to Alpine geodynamic processes also indicate a ϕ with NW–SE direction at and around BFO (Petrescu et al. 2020; Hein et al. 2021).

More large-scale models from regional tomography using surface waves also find a possible NE-SW trend for ϕ. For example, the tomography model EU60 by Zhu et al. (2015) contains relatively low anisotropy below the BFO area compared to surrounding regions with ca. a NE-SW trend in 50–220 km depth.

3 Methods and data analysis

We analyzed 25 years of continuously recorded data (July 1991 – October 2016) from BFO. Due to the excellent signal-to-noise conditions at BFO, seismograms could be selected from a total 1166 teleseismic earthquakes with Mw ≥ 6 and epicentral distances between 90° and 130°. After a visual inspection of the waveforms, poor recordings were eliminated and unclear splitting measurements were rejected. This procedure left data from 318 events (Fig. 1, inset in the lower right corner) for the final analysis. Splitting parameters were determined using single-event and multiple-event techniques and actually represent apparent splitting parameters derived from measurements. In the following, they are just called splitting parameters.

All single-event shear wave splitting measurements were made with the MATLAB based software package SplitLab (Wüstefeld et al. 2008) using two different and independent approaches: the rotation-correlation method (hereinafter RC after Bowman and Ando 1987) and the energy minimization method (SC after Silver and Chan 1991). The multi-event analysis was done with the plugin StackSplit (Grund 2017) using the methods after Wolfe and Silver (1998) and Roy et al. (2017). We checked the relative temporal alignment of the single traces (N, E, Z components) regarding an error source in SplitLab. For some input options provided by SplitLab, the milliseconds or seconds of the starting times of the single traces are ignored. This can lead to a wrong temporal alignment of the different component traces of an earthquake and by this to wrong shear wave splitting measurements (Fröhlich et al. 2022). For the error estimation of all measurements, we applied the modified equations by Walsh et al. (2013) as implemented in StackSplit (Grund 2017) to correctly calculate the required degrees of freedom.

Prior to the actual splitting measurements, all waveforms were filtered with a third-order zero-phase Butterworth bandpass with corner frequencies of 0.01 Hz and 0.2 Hz (in some cases, slightly adjusted to 0.1 Hz) to improve the signal-to-noise ratio (SNR) and the waveform clarity. Although BFO is a relatively low-noise site, the noise level of some SK(K)S phases is quite high (Fig. 2, upper two rows). Non-null measurements of such noisy records (left panels) were only accepted, if a clear elliptical particle motion is observed in the data and a clear linear particle motion is present after the correction for the splitting (middle panels). In addition, consistent results with the SC and RC methods need to be achieved for records with increased noise including a narrow 95% confidence interval for both ϕ and δt (right panels). If possible, multi-event analysis techniques (Wolfe and Silver 1998; Roy et al. 2017) were applied to increase the SNR and to achieve stable splitting parameters. In this way, a reliable dataset could be determined (see Sect. 4). In the LQT coordinate system (Plesinger et al. 1986), we manually windowed the visible SK(K)S waveform (approx. 20 s) to measure ϕ and δt. The waveform examples in Fig. 2 represent typical observations with and without shear wave splitting. The analyzed time window is shaded in gray and phase arrival times for the Earth model iasp91 (Kennett and Engdahl 1991) are highlighted (Fig. 2). The horizontal particle motion is also displayed to visualize a possible shear wave splitting. The simultaneous application of the two different single-event methods (RC and SC) allowed us to cross-check the reliability of the measurements and to rate them using strict quality criteria (e.g., Wüstefeld and Bokelmann 2007). In Fig. 2, we display the results from the SC method as energy map for the transverse ground motion. As preferred values for ϕ and δt the minimum of the corrected T energy is selected and the 95% confidence region of the splitting parameters is used as uncertainty range (gray area in energy maps in Fig. 2).

Fig. 2
figure 2

Source regions and BAZ: Solomon Islands 45.3°, Papua New Guinea 50.6°, Papua New Guinea 55.8°, Minahassa Peninsula 72.6°. Left: waveforms with radial (Q) component (SV-polarization: blue dashed curve) and transverse (T) component (SH-polarization: red solid curve). Theoretical phase arrivals (vertical black dotted lines) are included and the time window in gray indicates the analyzed waveform segments. Center: particle motion diagrams of measured (blue dashed) and corrected (red solid) waveforms. Right: energy maps for the T component displaying the inversion result using the SC method (Silver and Chan 1991). The black area indicates the 95% confidence interval for the estimated ϕa and δta values

Waveform examples, particle motions, and apparent splitting results for SKS phases arriving from the NE backazimuthal quadrant. The backazimuth (BAZ) increases from 45° (top) to 73° (bottom).

Full size image

In the following, we report only results for which the SC and the RC methods agree within their error bounds (95% confidence area) and the SNR is ≥ 7, as recommended, e.g., by Restivo and Helffrich (1999). Additionally, we defined a quality categorization for the splitting measurements: good means that RC and SC results differ less than 5° for ϕ and 0.2 s for δt as well as that the 95% confidence region is < 40° for ϕ as well as the uncorrected particle motion is clearly elliptical. If the results are marked as fair the two methods RC and SC differ not more than 20° for ϕ and 1 s for δt. Measurements rated as poor do not fulfill the above-listed criteria, mainly due to too low SNRs.

Recordings which have a clear phase arrival on the Q component but no signal on the T component (except low amplitude noise) as well as a clear linear particle motion were classified as null. This classification means no splitting of the corresponding SK(K)S phase could be observed. In Fig. 3, we present four examples for null measurements. These observations cover four different BAZ directions (55.8°, 164.1°, 248.3°, 344.2°) and despite a very clear signal on the Q component (blue dashed), there is no signal on the T component (red solid). The horizontal hodograms in Fig. 3 do not indicate an elliptical ground motion that would be expected for a split SKS phase.

Fig. 3
figure 3

Source regions and BAZ: Hawaii 344.2°, Papua New Guinea 55.8°, Northern Chile 248.3°, Prince Edwards Islands 164.1°. The particle motion diagrams display a linear polarization along the R or Q component (i.e., the BAZ direction) with measured (blue dashed) and minimally corrected (red solid) waveforms

Examples for waveforms (dashed blue: Q component with SV-polarization; solid red: T component with SH-polarization) and particle motions (dashed blue: measured; solid red: corrected) of null split SKS or SKKS phases arriving from four different backazimuths (BAZ).

Full size image

To stabilize the results of measurements rated as poor, we applied the simultaneous inversion of multiple waveforms (SIMW) method (Roy et al. 2017) as implemented in StackSplit (Grund 2017). In this routine, phases of different earthquakes from the same source region (here within a narrow backazimuthal range of 3° and an epicentral distance range of 3°) are concatenated in the time domain. Then, these new traces are simultaneously inverted with the SC method to determine the splitting parameters. These SIMW measurements are included in the good/fair dataset, if they provide a stable result.

In Fig. 1, only events are displayed for which we retained a good/fair non-null or null measurement (single- or multi-event). To smooth the dataset for the modeling, we binned the single-event measurements in 5° backazimuthal intervals using the stacking method after Wolfe and Silver (1998). The individual error surfaces of the single-event measurements are summed to generate a set of splitting parameters that represents an average for each defined BAZ bin.

4 Observations

In total, we achieved 51 non-null (two good, 49 fair) and 227 null measurements from single SK(K)S phases which we rank as reliable. In addition, using SIMW, we receive two good and 24 fair non-null measurements from combining mostly poor single measurements. In addition, the application of SIMW adds another 14 null measurements.

The single splitting results are displayed in Fig. 4 as stereoplots for five year-long periods and the complete observational period of 25 years. The direction of the bars gives the direction ϕ of the fast polarization axis relative to north which is also color-coded for better visibility. The length of the bars scales with the delay time δt. Details on the good and fair measured values are listed in the Supplementary information for the single splitting results. The separate results of the different 5-year-long periods indicate that such an observational period is too short to achieve a representative result even for a low-noise recording site such as BFO. This is mainly due to the limitation to specific source regions and the rare concurrency of strong enough earthquakes. For example, from 1992 to 1996, only four reliable splitting measurements are possible. As two measurements have ϕ values of 59° and 67° and two have ϕ values of − 10° and 11°, these pairs are nearly perpendicular. Averaging these four values would result in a meaningless value, not representing the true polarization direction and this approach would lead to a wrong (one-layer) anisotropy model. Another clear observation from the 1992–1996 period is the tenfold occurrence of nulls compared to split waves, and the nulls also cover a wider backazimuthal range. This aspect also has a clear implication: leaving nulls out of modeling for anisotropic structure would be misleading, because the observational evidence for anisotropy is weak, although it is well known that nulls are predicted for many anisotropic models, see below.

Fig. 4
figure 4

Stereoplot representation of all SKS and SKKS splitting measurements at BFO rated with good and fair with the single-event analysis for different observational periods. Backazimuth is measured clockwise from north; incidence angle is along the radial axis in 5° intervals. The apparent delay time δta scales with the length of each bar and the apparent fast polarization direction ϕa relative to north is along the direction of the bars and also color-coded. Null measurements are marked as white circles with black outline

Full size image

The other four observational periods (1997–2001, 2002–2006, 2007–2011, and 2012–2016) also cover only a limited backazimuthal range each. Especially, measurements from backazimuth ranges of 90–180° (SE quadrant) and 270–30° (NW quadrant and NNE range) are rare and this wide range of more than half the complete backazimuthal range is only poorly covered during the 5-year periods.

The 25 years (1992–2016) observational period provides a reasonable basis of SK(K)S splitting measurements including two distinct points of interest (Fig. 4): firstly, nearly three-quarters of the BAZ range are dominated by nulls (Fig. S1) and secondly, in the NE range, there seems to be a short-scale flip of the fast polarization axis (Fig. S2). The SK(K)S phases from events beneath the southernmost Indian Ridge (BAZ 155–180°), southernmost Atlantic Ocean incl. the South Sandwich subduction (BAZ 180–220°), South and Central America, and one in the NE Pacific (BAZ ~ 340°) do not show a clear splitting. Six exceptions with particularly short δt do not seem to be representative due to the more than 20-fold occurrence of nulls. Possibly, these exceptions are due to unrecognized noise or wave scattering effects.

The NE quadrant of the 1992–2016 dataset includes a clear rotation of the fast axis direction from around ϕ = 70° (green bars) over ϕ = 110° (reddish bars) to ϕ = 15° (bluish bars) and ϕ = 30° (bluish-green bars). In between, we observe a sector (BAZ 60–75°) with more than 50 null measurements. Another sector (BAZ ~ 50°) also contains several nulls. The delay time of the split waves is mainly between 1 s and 2 s.

The reproducibility of the measured splitting parameters ϕ and δt is clear from Fig. 4. The fast axis directions and delay times (lengths of the bars) are clearly aligned for measurements from the same source region. This correlation is partly due to the rejection of measurements rated as poor which may blur the splitting parameter distribution with BAZ. Thus, only clear observations can be accepted to understand the anisotropic structure around a recording site. The determined values ϕ and δt do not differ between SKS and SKKS phases from the same source or source region (Fig. 4, time period 1992–2016; Fig. S4 left). This means that the splitting is probably caused by an anisotropic structure in the upper mantle and that variations of anisotropy in the lowermost mantle (e.g. Long 2009; Long and Lynner 2015; Deng et al. 2017; Creasy et al. 2017; Grund and Ritter 2019) do not seem to play a major role along the different ray paths of these two phases.

5 Modeling results and interpretation

To derive a structural anisotropy model for the region around BFO, we first restrict ourselves to the NE quadrant (here BAZ range 30–100°) and then continue with the incorporation of the nulls from the other quadrants.

The forward modeling or calculation is done based on the equations by Silver and Savage (1994) as implemented in the MATLAB Seismic Anisotropy Toolkit (MSAT) (Walker and Wookey 2012) in a ray theory reference frame. Our azimuthally limited dataset does not allow to constrain complicated models including multiple (> 2) or dipping layers.

The modeling is done with non-null measurements of the SC method. Long and van Hilst (2005) and Vecsey et al. (2008) showed that the SC method is the more stable technique compared to the RC method. This is consistent to the results of synthetic tests with high SNR data by Wüstefeld and Bokelmann (2007). They demonstrated that the splitting parameters are wrongly determined close to the null directions assuming one horizontal anisotropic layer. This effect is more severe for the RC method than for the SC method and causes a systematic pattern when the non-null results are plotted as function of backazimuth which can be used to determine null directions. A crucial point is that ϕ values have 45° slopes over backazimuth and a jump when the backazimuth coincides with the null direction. Eakin et al. (2019) proposed that for real data with a more realistic SNR of 5–10 also the SC method tends to show such a behavior. Silver and Savage (1994) showed that also for two-layer anisotropy, a jump in ϕ can appear for the SC method. Both this slope and a jump for ϕ can be found in our BFO shear wave splitting observations (Fig. S3).

We limit the tested models to one-layer and two-layer cases with transverse isotropy and with apparent splitting parameters for the two-layer case. A trial-and-error procedure is applied: a systematic sampling of the model space is done with 5° steps for the fast polarization direction and 0.25 s for the delay time of an S-wave with a period of 8 s. The predicted or synthetic ϕ and δt values are compared with the measured ones in the relevant backazimuth range. The goodness of fit is evaluated with the estimated root mean square error (RMSE) of the differences Δϕi and Δδti between the model curve and the individual measured data points i = 1,…,N. At first, the RMSE is calculated separately for ϕ and δt:

$${\mathrm{RMSE}}_{\phi }=\sqrt{\sum_{i}^{N}\frac{\Delta {\phi }_{i}^{2}}{N}}$$
(1)
$${\mathrm{RMSE}}_{\delta t}=\sqrt{\sum_{i}^{N}\frac{\Delta \delta {t}_{i}^{2}}{N}}$$
(2)

Then, these RMSE values are normalized (Liddell et al. 2017) and summed to get a joint total value

$${\mathrm{RMSE}}_{\mathrm{tot}}=\frac{{\mathrm{RMSE}}_{\phi }}{90^\circ }+\frac{{\mathrm{RMSE}}_{\delta t}}{4 \mathrm{s}}$$
(3)

in the following just called RMSE. The models with the smallest RMSEtot errors are assumed as the best-fit ones. Due to the limited resolution of our measurements and the sensitivity of the theoretical results on small changes of the input ϕ and δt values, we first examine the 20 best-fit models to estimate the stability of this approach. Only single splitting and SIMW results which have the quality good or fair, are used for the modeling. Besides fitting the good and fair splitting measurements (Fig. 5, Fig. 6), also a reduced dataset with average values in 5° BAZ intervals is used (Fig. 7, Fig. 8). This 5° smoothed dataset avoids the over-representation of data points within some BAZ ranges during the calculation of model parameters and RMSE.

Fig. 5
figure 5

The 20 best-fit one-layer models for all good and fair measurements in the NE quadrant (30–100° BAZ). a Apparent fast polarization direction ϕa, b apparent delay time δta. The color-coding of the symbols of the measured data corresponds to the colormap for ϕa used in Fig. 4. The 20 best-fit model parameter combinations are shown in c with their corresponding RMSE (gray colormap). The best-fit model is highlighted in orange (minimum RMSEtot). Note that several of the curves with the forward calculated splitting parameters in a and b lie atop each other even if the anisotropy models are partly different in c. Note that the nulls are not included in the modeling, but shown in a and b as white circles for the sake of completeness with δta manually set to zero

Full size image
Fig. 6
figure 6

The 20 best-fit two-layer models for all good and fair measurements in the NE quadrant (30–100° BAZ). a Apparent fast polarization direction ϕa, b apparent delay time δta, and c model parameter combinations. Symbols and colors as in Fig. 5

Full size image
Fig. 7
figure 7

The 20 best-fit one-layer models for the 5° BAZ binned dataset in the NE quadrant (30–100° BAZ). a Apparent fast polarization direction ϕa, b apparent delay time δta, and c model parameter combinations. Symbols and colors as in Fig. 5. Note that the nulls are not binned

Full size image
Fig. 8
figure 8

The 20 best-fit two-layer models for the 5° BAZ binned dataset in the NE quadrant (30–100° BAZ). a Apparent fast polarization direction ϕa, b apparent delay time δta, and c model parameter combinations. The light red and blue ranges outline the model parameter ranges covered by the 20 best-fit models for the lower and upper anisotropic layers respectively. Symbols and colors as in Fig. 5

Full size image

5.1 All measurements

For the NE quadrant (BAZ 30–100°) the one-layer modeling in Fig. 5 provides a stable result for a fast polarization axis of the medium in direction 35° and a time delay of 1.25 s. However, there are no observed nulls in the modeled fast polarization direction 35° as expected from theory, but nulls are observed in directions between 55° and 75°. The 20 best-fit models vary by ca. ± 20° in ϕ and ± 0.25 s in δt. The RMSE is about 0.5 with a minimum at 0.47. For the two-layer modeling with all good and fair splitting measurements (Fig. 6), we get similar RMSE values of ca. 0.46 for the 20 best-fit models. It is obvious that no theoretical curve for two-layer models fits very well the distributions of the measurements. The best model (orange curve with lowest RMSE) does reasonably well fit δt, but the fit to ϕ is poor. The upper layer (ϕ = 40° and δt = 1 s) has similar results as the one-layer model and the lower layer is not much different (ϕ = 45° and δt = 0.5 s). This is partly due to the uneven distribution of the measurements over backazimuth: modeling and RMSE determination are dominated by the data points between BAZ directions 60° and 90°.

5.2 5° bins

To avoid an over-representation of specific BAZ directions in the NE quadrant, we stacked the splitting parameters in 5° bins. This stacking results in a smooth representation of the ϕ and δt measurements (Figs. 7 and 8) that should allow a better model fitting procedure.

The one-layer models are not appropriate to fit the measurements (Fig. 7), because they do not properly fit the BAZ variation of ϕ and δt. The lowest RMSE reaches 0.51 for the one-layer case. The minimum RMSE is 0.36 for the two-layer modeling, so ca. 30% lower than for the one-layer case. The two-layer modeling results provide a much better fit for both, ϕ and δt (Fig. 8a,b). The main BAZ variation of ϕ is well matched (Fig. 8a) and the extrema of the predicted δt values are also recovered (Fig. 8b). The observed nulls at ca. 60–75° BAZ (Fig. 4) are close to the predicted minimum of δt Fig. 8a and the nulls at ca. 45° BAZ are at the predicted maximum of δt (Fig. 8a) which coincides with the theoretical ‘null’ direction for the two-layer case (Silver and Savage 1994). Our observed jump in ϕ (SC method) of around π/2 appears to be larger than the synthetic error or jump for a one-layer anisotropy model proposed by Eakin et al. (2019) (Fig. 7). It better coincides with the change in ϕ given in Silver and Savage (1994) (Fig. 8a).

Surprisingly, the model parameter distribution of the 20 best-fit models in Fig. 8c has a quite large scatter with regard to the small changes in RMSE (bluish and reddish areas). The upper (second) layer has a fast polarization direction of ca. 30° for δt2 > 0.5 s. The lower (first) layer has a fast polarization direction of ca. 50–60° for δt1 > 0.5 s, but reasonable fits can also be achieved for a wide range of ϕ1 around 90°. The synthetic effective splitting parameters for the best-fit model (upper layer: ϕ2 = 40° and δt2 = 1.75 s, lower layer: ϕ1 =  − 60° and δt1 = 1.0 s) are shown in Fig. 9. Compared to the measured data in Fig. 4, there is very good coincidence including the flip of the polarization direction and the position of the nulls in the NE quadrant.

Fig. 9
figure 9

Forward calculated theoretical splitting parameters for the best-fit two-layer anisotropy model in the NE quadrant (lower layer: ϕ1 =  − 60° and δt1 = 1.0 s, upper layer: ϕ2 = 40° and δt2 = 1.75 s; see Fig. 8). The dominant period is 8 s. The gray shaded area is not included in the model search (see text). The mainly null observations (see Fig. 4) do not fit to the prediction for the gray backazimuthal range, indicating a lateral variation of the anisotropy

Full size image

5.3 Null measurements

The very wide backazimuthal range of nulls at BFO (Fig. 4) is still puzzling because (i) it covers 155–335° BAZ, so half of the incoming directional range, and (ii) it is completely contrary to the observed splitting pattern within 30–100° BAZ. Since null measurements are not always unique (Wüstefeld and Bokelmann 2007), we carefully looked at the waveforms to confirm the missing signal on the T component for well-observed SK(K)S phases on the Q component. The following consideration may guide future studies to better understand this observation which we tentatively call the null anomaly:

(a) Compared to the NE quadrant the upper mantle structure underneath the other quadrants around BFO must be completely different, because the predicted splitting pattern in Fig. 9 would allow only three other distinct narrow backazimuthal ranges with nulls, so contrarily to our observations. An exception would be a model with two layers, which lie on top of each other and which have (nearly) identical delay times but orthogonal fast polarization directions. Such a constellation would cancel the splitting effects and nulls would be observed (Liu and Gao 2013). Few available regional studies do not support such a setting for the Upper Rhine Graben region (Granet et al. 1998; Walker et al. 2005; Walther et al. 2014).

(b) Other simple anisotropy models with transverse isotropy in a horizontal plane also seem to be unrealistic, because one-, two- and even three-layer scenarios would predict wide ranges without nulls. These ranges are not observed. This holds also for one-layer models with a dipping symmetry axis.

(c) Null measurements on nearly vertically propagating SKS phases can hint towards a fast axis direction in vertical direction, e.g., due to an upward mantle flow or a specific olivine CPO fabric type.

Such a flow pattern may be related to the Miocene uplift of the Black Forest, the Vosges Mountains, and possibly the local mantle upwelling underneath the Kaiserstuhl Volcanic Complex (Fig. 1). One may also speculate that previously existing anisotropic fabrics in the lower lithosphere and asthenosphere were overprinted by such vertically oriented processes.

Beside the commonly assumed A-type CPO fabric, other olivine CPO fabric types, like the C-type may be present. It has been shown in experimental studies that the quite complex CPO of olivine depends on stress, water content, temperature, and pressure conditions (Jung et al. 2006; Skemer and Hansen 2016). The assumption of A-type olivine CPO, i.e., a horizontally orientated olivine a-axis in the direction of maximum shear, is (only) valid for dry olivine aggregates (Long and Silver 2009; Long and Becker 2010). The C-type, i.e., a vertically orientated olivine a-axis, occurs at moderate to high water content and high temperature. Such conditions could be related to mantle magmatism of the Kaiserstuhl Volcanic Complex. Since the propagation velocity difference between the olivine b-axis ([010]) and c-axis ([001]) is small, nearly vertically propagating SKS phases experience only a weak anisotropy effect and by this show only weak to no shear wave splitting. This may result in the observation of reduced or small delay times or numerous nulls. However, such reasoning should be supported by further high-resolution regional studies.

(d) The medium related to the null anomaly may be very weakly anisotropic and the related wave effects may be close to the limit of detection. However, even SKS phase observations with a high SNR of the Q component do not show a split phase on the T component recording with a relatively low-noise level (Fig. 3).

(e) The medium may be isotropic (or nearly isotropic). This seismic isotropy could either be a pristine structural characteristic which is most possibly not reasonable, because the surrounding regions, mostly also of Variscan origin, have well-resolved anisotropy (Walker et al. 2005; Walther et al. 2014).

(f) Another option may be wave scattering effects due to strong heterogeneities that diffuses the, in general, already small wave amplitudes of the T component but leaving the R or Q component unaffected. The structure of the lithosphere and the asthenosphere underneath the southern Black Forest and the southern URG were possibly reworked during the rifting processes and the Kaiserstuhl magmatism (Ziegler et al. 2004) that may have imprinted structural heterogeneities. However, the question is open why the R or Q component recordings remain unscattered.

(g) At the seismological station DBIC (Côte D’Ivoire), a similar splitting pattern can be observed as at BFO with splits only in a limited backazimuth range and for the rest mainly nulls (Lynner and Long 2012). These authors explain this by lowermost mantle anisotropy for the observed splits and a nearly isotropic or apparently isotropic upper mantle for the nulls. An influence of anisotropy and splitting effects from the lowermost mantle cannot explain the null anomaly at BFO. Both phases, SKS and SKKS, are dominated by nulls within 155–355° BAZ and we do not observe clear discrepancies of the split or null signals between SKS and SKKS phases (Fig. S4 right) as in Long and Lynner (2015).

Based on the currently available observations at BFO, the mystery about the nulls is not yet solved and similar studies need to be done analyzing long-term recordings from surrounding seismological stations. This is work under way in our research group.

6 Discussion and conclusions

We observe 77 splits of SK(K)S phases and 241 null splits at the high-quality recording seismological station BFO, SW Germany. This plenty of measurements was only possible because continuous recordings from 25 years were carefully and manually checked and the splitting analysis was assigned to strict quality measures. Our 77 plus 241 observations are much more than reported in other studies. A comparison of different time periods (Fig. 4) indicates that five or even 10 years of continuous recording may be too short to obtain representative splitting observations in Central Europe, because SK(K)S phases from different backazimuths may not be available. Thus, very long observational records are required to gain a reasonable backazimuthal coverage which allows to resolve backazimuthal variations of SK(K)S splitting and by this both vertical and lateral variations in the anisotropy.

For three-fourths of the backazimuth range, we find that null measurements dominate at BFO. However, there is no structural anisotropy model which can explain this observation yet. It is necessary to conduct similar precise shear wave splitting measurements at surrounding seismological stations to better locate this null anomaly and possibly its depth extension. On the contrary, dense splitting observations in the NE quadrant of BFO contain a complete flip of the fast polarization axis at around 50° BAZ. This flip is currently explained best with a two-layer model with fast polarization directions of ϕ2 = 40° (upper layer) and ϕ1 =  − 60° (lower layer) (Fig. 8, Fig. 9). The RMSEs for the 20 best-fit two-layer models are very similar but the large scatter of their determined model parameters may point to a considerable uncertainty (± 10–20° for ϕ and ± 0.5 s for δt) even for the observationally well-covered NE backazimuthal range.

The observed backazimuthal variations of ϕ and δt at BFO do clearly not allow a backazimuthal averaging of the splitting parameters of all (good and fair) splitting measurements for the determination of a laterally homogeneous anisotropy model that was mainly done in the past. The averaging even across small backazimuthal gaps without observations may be misleading (Fig. 4), because short-scale changes of the splitting parameters (Fig. 9) can occur which might be due to both, vertical and lateral, variations of the anisotropy at depth. Such small-scale variations of the splitting parameters are also observed in other regions (e.g., Bastow et al. 2007). Thus, small-scale laterally varying anisotropy may play a more important role in the study region than previously thought.

For temporary measurements, at least in Europe with limited backazimuth observations, we propose to include long-term recordings from permanent stations in the study region (see, e.g., Grund and Ritter 2020). Then, subareas with similar splitting patterns should be outlined, e.g., based on ray paths or piercing points of the split phases. Only for those subareas with identical splitting pattern for crossing ray paths, a structural modeling should be conducted to resolve local lateral anisotropy instead of a station-wise modeling. Of course, a 3-D anisotropic wave propagation modeling (Tesoniero et al. 2020) may be preferred for the rare cases with enough azimuth-dependent observations.