1 Introduction

Hydrophones are sensors measuring pressure changes in the oceans with various applications in the scientific, industrial, and military fields. In seismological applications, they are widely used for seismic exploration of oil fields. In some cases, hydrophones can substitute ocean bottom seismometers (OBS) in the ocean as they are able to provide information about P-wave first arrivals and polarity (Fox et al. 2001; Bohnenstiehl et al. 2002). In facts, the hydrophone is sensitive to the pressure waves propagating in a fluid, while, as it is well-known by the elementary physics, it is irresponsive to shear changes. However, the information content of its recordings is poorer than those of a seismometer. Despite these limitations, the hydrophones contribute to the hypocentral location and computation of the focal mechanism. Furthermore, most of the studies on the T-waves are performed using data recorded by hydrophones. T-waves are seismic waves converted into acoustic waves at the seabed, propagating within a water layer called SOFAR. This is defined by an inversion of temperature (or sound velocity) of the water column which therefore acts as a wave guide. T-waves can propagate at a teleseismic distance while maintaining their amplitude almost unchanged; when they interact with the coast, they convert into seismic waves that can be recorded on land by seismometers. Since the propagation velocity of elastic waves in the ocean is much lower than that of seismic waves traveling in the solid Earth, the T-waves are recorded after the P- and S-waves and are designated as tertiary waves. The efficient propagation of T-waves over a great distance allowed the definition of a magnitude scale for this type of waves (Dziak et al. 1997).

In the case of hydrophone signals recorded nearby seismic sources or in areas of shallow sea water where T-waves cannot be generated, no reports on the possibility of estimating the event magnitude (or its energy) are available in literature. This possibility seems to be particularly useful when monitoring the seismicity around underwater volcanoes, where hydrophones are useful and much cheaper alternatives to seismometers, at least to identify and read the first P-pickings and the P-wave polarity. The availability of a methodology for estimating the magnitude would thus constitute an important add-on to this kind of observations.

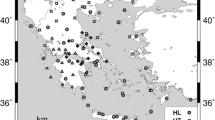
In this work, a simple method to estimate the earthquake magnitude from the hydrophone records of small earthquakes is developed. We present an application of this technique to earthquakes occurring in the Campi Flegrei caldera (CFC), close to the city of Naples. This is a high risk active volcanic zone where a modern network of seismometers, both on land and seafloor together with underwater hydrophones, is permanently installed with the aim of monitoring its peculiar volcano dynamics. The present activity of CFC is characterized by a high-rate ground deformation, accompanied by swarms of small volcano-tectonic and long-period earthquakes. This seismicity occurs exclusively within the caldera borders (Fig. 1) at a depth lower than 3 km and is concentrated in a high population density zone. A detailed analysis of Campi Flegrei seismicity and its relationship with the general volcanic activity of the area is reported in a wide and extensive literature, recently reviewed by Giudicepietro et al. (2021) and Tramelli et al. (2021).

Fig. 1
figure 1

a Map of Campi Flegrei with epicenter of earthquakes used in this study (green circles). Seismic stations are represented by triangles: yellow color for land stations, red for seafloor stations. b Example of the buoy layout. The seafloor monitoring module is linked by cable to the buoy. Hydrophone and seismometer are hosted in the module. The emerged part of the buoy is equipped with solar panels, meteorological sensors, GPS antenna, and Wi-Fi data communication system

Full size image

2 Data

The earthquake bulletins produced by INGV-OV (Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Vesuviano) show that the seismicity of Campi Flegrei is mainly located on shore in the central part of the caldera and is characterized by low-energy earthquakes with very shallow hypocenter (Fig. 1). More than 99% of the earthquakes occurred during the last 15 years had Md < 2.0 (duration-magnitude) and hypocenter depth H < 3 km, while the maximum magnitude was Md = 3.5.

The INGV-OV has developed in the last 15 years a complex system of geophysical and geochemical surveillance networks for monitoring the volcanic activity of the Campi Flegrei, greatly improving the already existing monitoring network which was operational since the volcanic unrest (1.5 m uplift in Pozzuoli town — see for an extensive review Zollo et al. 2006) occurred in 1982. In particular, the seismic network operating today has 22 three-component stations in the mainland and four stations in the marine sector of the volcanic area, the Gulf of Pozzuoli (Fig. 1a). The seafloor stations are components of MEDUSA, a marine multi-disciplinary permanent monitoring infrastructure, consisting of four buoys located in the Gulf of Pozzuoli at a distance between 1.1 and 2.5 km from the coast, at a sea depth ranging from 40 to 100 m. Each buoy is connected by cable to a multi-parametric sensors submarine module positioned on the seabed a few meters from the base of the buoy, and equipped with geophysical and oceanographic sensors (Fig. 1b). In particular, a 100 s–50 Hz seismic sensor and a low-frequency hydrophone with response in the 100 s–100 Hz frequency band. More details on MEDUSA marine infrastructure can be found in Iannaccone et al. (2018) and at http://portale.ov.ingv.it/medusa/. MEDUSA operates since April 2016 and contributes to the geodetic and seismic monitoring of the Campi Flegrei volcanic area.

In the present paper, the records from low-energy earthquakes acquired by the sensors of the buoys CFB1, CFB2, and CFB3 of MEDUSA infrastructure in the time interval between 01/06/2016 to 16/03/2022 were analyzed (Fig. 1). The start time coincides with the full operation of MEDUSA infrastructure. The CUMAS buoy module has been in maintenance for most of this time interval and therefore its data are not available. The seismic catalog of Campi Flegrei published by INGV-OV (http://terremoti.ov.ingv.it/gossip/) reports more than 2000 microearthquakes in the period here considered. Three events show a magnitude value greater than 3, Md = 3.1, 3.3 and 3.5 respectively, and 15 are in the 2.0 ÷ 3.0 Md range.

For the following analysis, we have selected all the earthquakes with Md > 2, comprising the most energetic ones, and 100 events with lower magnitude. A further selection was performed choosing the events showing hydrophone signals characterized by signal-to-noise (S/N) ratio greater than 5, computed using the most energetic part of the recording. Using both criteria we maintained 196 records of 123 earthquakes, as shown in Table 1.

Table 1 Number of records used for each station
Full size table

Figure 2 shows an example of seismic recording of the hydrophone compared to the seismometer.

Fig. 2
figure 2

Waveforms of a local earthquake, Md = 1.5, recorded by the hydrophone (lower trace) and the vertical component of the seismometer (upper trace). The two sensors are located on the seafloor module of the CFB1 buoy. Amplitudes are in physical units, µm/s and Pa

Full size image

The conversion from counts to Pascal was carried out using the transduction factor of the hydrophone provided by the manufacturer. Hydrophone calibration is known to be available and easy to perform at high frequencies, in the kHz band or higher (Dakin et al. 2014), while it is less reliable for frequencies of seismological interest, < 50 Hz. In the paper by Iannaccone et al. (2020), using the same hydrophones of the present paper, the perfect similarity between the earthquake compressional waves recorded by a hydrophone and a seismometer co-located on the seabed is demonstrated. This equivalence made it possible to verify the calibration of our hydrophones by comparing the waveforms with a reference calibrated instrument for a wide range of frequencies of seismological interest. In particular, the comparison of regional earthquakes recordings allowed to validate the used transduction factors at low frequencies, down to 0.5 ÷ 1 Hz.

3 Definition of a magnitude scale for hydrophones

The magnitude scale Md currently in use to quantify the Campi Flegrei seismicity and reported in the catalogs produced by INGV-OV was obtained empirically in the early 80's calibrating the earthquake duration recorded at local analogical (on land) stations respect the local magnitude, ML, calculated at the Mt. Vesuvius station (see, e.g., the review of this argument in Petrosino et al. 2008). Md is thus given as follows:

$${M}_{d}=-2.46+2.82\;lo{g}_{10}\,\tau$$
(1)

where τ is the earthquake duration in seconds measured on the seismogram.

The magnitude scale for Campi Flegrei area has been however revised by Petrosino et al. (2008) who introduced the moment magnitude Mw and the Wood-Anderson local magnitude ML, together with the mathematical relationships linking Mw and ML to Md. Md can be used only for comparing local events and is still routinely reported on the official reports to National Civil Protection, in order to avoid misinterpretations in the comparison of past event with recent seismic events. The present paper wants to add new information on the quantification of the Campi Flegrei events, adding a new magnitude relation based on the analysis of hydrophone sensors on the seafloor. We propose a numerical relation based on the estimation of the hydrophone signal amplitude Fourier spectrum. This quantity is then correlated with the moment magnitude estimated at seismic stations on land, yielding an empirical relation linking the hydrophone signal amplitudes to the moment magnitude. This relationship allows the determination of earthquake magnitude directly from the hydrophone records.

3.1 Using the duration of the recording

We first attempted to achieve an empirical relationship between the duration of the earthquakes recorded by hydrophones and Md values reported in the INGV-OV catalog. We used the following equation:

$${M}_{d}=a\;log_{10}\,\tau_h+b$$
(2)

where a and b are coefficients to be determined and τh is the time duration (in seconds) of the waveform measured on the hydrophone record. The distribution of the data in Fig. 3 clearly shows a low correlation when a least square fit of Eq. (2) to the data is performed. This evidence hinders the possibility of simply use the hydrophone signal duration to estimate an empirical duration-magnitude scale for the hydrophone records.

Fig. 3
figure 3

Plot of the logarithm of the time duration of the selected earthquakes recorded by the hydrophones vs their magnitude Md

Full size image

3.2 Using the hydrophone record spectra

Fourier spectra of the first 5 s of the selected earthquakes recorded by hydrophones were calculated and corrected for seismic attenuation and distance (geometrical spreading). Seismic attenuation was estimated assuming that most of the seismic energy is associated with shear waves propagating between source and receiver (set at the sea bottom, undersea). The hydrophone sensor is sensitive to the P-waves generated by the conversion between seismic shear waves to compressional waves and to the P-waves refracted at the sea bottom from land to sea. On the other hand, the seismic radiation travels from the source to the receivers, in a highly heterogeneous shallow crust (De Siena et al. 2010), approaching a diffusion regime. In such regimes, the highly heterogeneous media allow the rapid conversion of P-radiation to S-radiation in the points where the primary waves encounter the medium heterogeneities (Yamamoto and Sato 2010; De Siena et al. 2010). We can thus reasonably assume that in the first 5 s following the P-wave first pulse there is a predominance of S-waves on the seismogram recorded at the sea bottom. Consequently, in the first 5 s of the hydrophone signal, the S-radiation converted to P-radiation (traveling in the sea water from the sea bottom to the hydrophone) is predominant. This is the reason why we use the estimate of the seismic shear wave quality factor Q estimated by Petrosino et al. (2008) for the area of Campi Flegrei, given as follows:

$$Q\left(f\right)=21{\left(\frac{f}{{f}_{0}}\right)}^{0.6}$$

where f is the frequency of the wave motion (Hz) and f0 is a reference frequency (here set at 1 Hz), to correct the hydrophone radiation spectrum for the path effects. We used the value of Q estimated at 10 Hz, which corresponds to the maximum signal power in the spectra. The seismogram amplitude spectrum was estimated through fast Fourier transform (Mathematica™, “Fourier” routine) and successively averaged between 1 and 25 Hz. This average is proportional to the integral of the amplitude spectrum in the same frequency limits. We name it “integrated spectrum” in the following of this paper.

Moment magnitude Mw for the selected events was calculated from the duration of the seismic events using Eq. (13) of the paper by Petrosino et al. (2008):

$${M}_{w}=-1.4(\pm 0.1)+2.3(\pm 0.1)\;log\ \tau$$

Its uncertainty is estimated applying the ordinary error propagation laws. Uncertainty on τ is estimated applying the error propagation equation to Eq. (1), assuming that the uncertainty on Md is ±0.3 magnitude units, as reported on the official web page of INGV-OV (https://terremoti.ov.ingv.it/gossip/flegrei/index.html).

Using the amplitude spectrum average values, we fit the data couples {Mw, Intspectrum} with the following equation:

$${M}_{w}={a}_{w}+{b}_{w}{\mathit{\;log}}_{10}(In{t}_{spectrum})$$
(3)

For the sake of completeness, we fit the same data couples also with the follwing:

$${M}_{d}={a}_{d}+{b}_{d}{\mathit{\;log}}_{10}(In{t}_{spectrum})$$
(4)

where Md is the duration magnitude estimated routinely at INGV-OV.

The uncertainties on the integrated spectrum is estimated from the standard deviation of the mean of the spectral values.

All the fit procedures were carried out using the internal Mathematica™ “FindFit” routine disregarding the uncertainties on the integrated spectra as compared with those on magnitudes. A (positive) check of the correctness of this assumption was made using a Monte Carlo routine performing the linear fit considering both uncertainties (on Magnitude and integrated spectra) as described in Press et al. (1992).

The obtained values of the coefficients of Eqs. (3) and (4) are as follows:

$$\begin{array}{ccc}{a}_{w}=-0.2\pm 0.1& {b}_{w}=0.69\pm 0.04& \begin{array}{cc}{a}_{d}=-1.0\pm 0.1& {b}_{d}=0.84\pm 0.04\end{array}\end{array}$$

and the final formula for the computation of magnitude Mw and Md using record of local earthquakes obtained with hydrophones are as follows:

$${M}_{w}=-0.2\left(\pm 0.1\right)+0.69\left(\pm 0.04\right)\;lo{g}_{10}In{t}_{spectrum}$$
(5)
$${M}_{d}=-1.0\left(\pm 0.1\right)+0.84\left(\pm 0.04\right)\;lo{g}_{10}In{t}_{spectrum}$$
(6)

Relationships (5) and (6) are plotted together with the data in Fig. 4. Data show satisfactory correlation between the magnitude values and the (integrated) spectra. Using Eqs. (3) and (4), the (calibrated) magnitude of the seismic event can be estimated through the hydrophone record integrated (between 2 and 25 Hz) spectrum.

Fig. 4
figure 4

Upper panel: black, red and green circles (associated with their 1-sigma uncertainty bars) show the moment magnitude (Petrosino et al., 2008) calculated respectively at CFB1, CFB2, and CFB3 hydrophone sites, as a function of the log of the hydrophone record integrated spectrum. The semi-transparent blue strip represents the pattern of Eq. (5) (the dashed line in the middle) with its uncertainty. Lower panel: the same of the upper panel for the INGV-OV duration magnitude Md. The semi-transparent blue strip represents the pattern of Eq. (6) (the dashed line in the middle) with its uncertainty

Full size image

Finally, considering the high dispersion of the points around the fit lines (Fig. 4) for magnitudes lower than 2, we checked the results thus obtained for the moment magnitude using the weighted least square procedure described in Menke (2012). Results show that associating a weight equal to 0.5 to the data with magnitude less than 2.0 and a weight equal to 1 to all the other points, Eq. (5) becomes as follows:

$${M}_{w}=-0.4(\pm 0.1)+0.77(\pm 0.05)\;lo{g}_{10}In{t}_{spectrum}$$
(7)

As can be seen (Fig. 5), the coefficient of the regression lines given by Eqs. (4) and (6) is not significantly different from the statistical point of view, indicating a substantial stability of the regression coefficients estimates, at least in the interval of magnitudes considered.

Fig. 5
figure 5

The same data of Fig. 4 (upper panel). The semi-transparent blue strip represents the pattern of Eq. (7) (the dashed line in the middle) with its uncertainty

Full size image

4 Discussion and conclusions

The recording of an earthquake by a hydrophone in the ocean consists of pressure waves (acoustic waves) produced by the conversion of body waves at the seafloor interface and by T-waves. The seismic waves propagate inside of the Earth from the hypocenter to the hydrophone site where they are converted into acoustic waves that propagate in the water. When the hydrophone and a seismometer are co-located on the seabed, the arrival time of the seismic waves to the two sensors will be the same. The conversion of seismic waves into acoustic waves concerns the P-waves and part of the S-waves which are converted in P at the sea-bottom interface. Furthermore, acoustic waves propagating in the water can be reflected from the sea surface (water–air interface) and again from the seabed with a succession of multiple reflections that can make complex the seismic record. Anyway, in our case, multiple reflections have slight effect on the seismograms considering the shallow sea depth (< 70 m) and the dominant frequency content lower than 30 Hz of the record of local earthquakes. As a consequence of the above premises, the waveform of a local earthquake recorded by a hydrophone is simpler and shorter than that recorded by a seismometer, since most of the shear waves, surface, and coda waves, which are the main components of a seismometer record and define its signal duration, are missing. This is the main reason why determining a magnitude scale based on the duration of the recording is almost impossible, as demonstrated in Fig. 3.

On the other hand, the clear relationship between the earthquake spectral amplitude estimated by hydrophone records and the magnitude determined by a reference station come out clearly. Figure 4 shows an evident linear relationship between moment magnitude Mw and the logarithm of the hydrophone signal spectral amplitude integrated between 1 and 20 Hz. This observation allows to define an empirical formula for calculating the magnitude from the seismogram obtained from a hydrophone. The obtained relationship between Mw and the signal spectral amplitude, however, is strictly valid for the narrow range of magnitudes and the small range of distances (< 10 km) characteristic of the data set available. Despite this significant restriction, a magnitude scale from hydrophone records may have interesting applications in monitoring the seismicity of submarine volcanoes by hydrophones. Volcanic activity is frequently characterized by a low-energy background seismicity, increasing as number and energy during the pre-eruptive phase. The use of a seismic monitoring network consisting of hydrophones may be thus sufficient for providing the basic parameters of the seismic activity of a submerged volcano. With a network of underwater hydrophones, in fact, it is possible to determine hypocenter of earthquakes, focal mechanism using the polarities of the P-wave first arrivals and thanks to the relationships (6) and (7) also their magnitude, allowing a more complete seismological pre-analysis. Finally, the hydrophone is cheaper than a seismometer and easier to install as it does not require accurate coupling with the seabed and not even the need for precise leveling and positioning.