Fault shape effect on SH waves using finite element method

Abstract

In this paper, we analyse how the combination of fault zone shape and material properties affects the propagation of seismic waves in a two-dimensional domain. We focus on SH wave propagation through several faults with different thicknesses and bending radii, but the theory is easily generalized to the three-dimensional case. We show how the density of energy released is mostly a function of the radius and does not depend on the velocity inside a fault zone.

1 Introduction

According to the dictionary of Geology and Earth science, a fault zone (FZ) is defined as “a region, from meters to kilometres in width, which is bounded by major faults within which subordinate faults may be arranged variably or systematically. Single fault zones are marked by fault gouge, breccias, or mylonites” (Allaby 2013). It is well known that a FZ is able to trap and propagate low-velocity waves and/or guide head waves, modifying substantially the damage pattern and the seismic hazard of a strong earthquake. These effects have been observed in many different real situations, see, for example, Rovelli et al. (2002), Li et al. (2004), Li and Leary (1990), Li et al. (1994), and Lewis et al. (2005). More recently some evidence of this phenomena has been observed, for example during the earthquakes (the largest being a 6.1 Mw event) that hit the city of L’Aquila, in 2009 (Avallone et al. 2014; Calderoni et al. 2010). In particular, in Avallone et al. (2014) the authors hypothesize the existence of a low-velocity FZ able to trap the waves and amplify the signal. A comparison between recorded data and an analytical model is also presented.

Due to the well established impact of the fault zones on the damage distribution, the last decades have seen more effort spent modelling wave propagation through a FZ and, although analytical solutions are available in just a few simple cases such as in Ben-Zion and Aki (1990), numerical results are numerous and quite complete. The common methods that are used for the numerical solution of earthquake models in general, and the ones with faults in particular, are described in Igel (2017) and Hori (2011). They include spectral element method (SEM), finite difference method (FDM) (Erickson et al. 2017; Moczo et al. 2014), boundary element method (BEM) and finite volume method or a coupling of several methods (O’Reilly et al. 2015). Finite difference method provides simple ways of discretizing partial differential equations which correspond to the seismological problems, but it still has a number of drawbacks. First of all, FDM is incapable of treating complex geometries adequately. Besides, when using FDM, one should choose small grid sizes to avoid numerical dispersion (Moczo et al. 2000; Liu and Sen 2009b). Although different techniques help to partially eliminate many drawbacks of FDM, this method is not suitable for solving certain seismological problems.

The important aspect of the spectral element method (Komatitsch and Tromp 2002) is the fact that it can combine the approximations of different order in different subdomains, in particular outside and inside the fault. This is done by introducing the discontinuous Galerkin methods or mortar element methods. As a result, on the basis of the spectral element method various software has been created which help model earthquakes and fault zones for 2D and 3D models.

Unlike the SEM and FDM, BEM builds the approximate solution to seismological problems based on integral representation of the solution. The method consists in building the solution to certain boundary integral equations. The main advantage of this method is that it helps to decrease the dimension of the problem. Unfortunately, BEM is not efficient for solving nonlinear or non homogeneous problems. Moreover, the final matrix of the problem is in general full and non symmetric. There are techniques which reduce the number of drawbacks for non stationary problems, though the construction of efficient methods for simulating time-dependent realistic earthquake problems remains an open problem (Álvarez Rubio et al. 2004).

In this paper, we study how seismic waves, generated by a localized source, propagate through a FZ and what happens when the fault has a bend. We only consider the case of horizontally polarized shear waves (SH waves), the general case including pressure waves (P-waves) and vertically polarized shear waves (SV waves) will be discussed in a further paper, where a more general 3D case will also be analysed.

The propagation of SH waves in a homogeneous isotropic linear elastic medium is described by the following equation in a (x₁,x₂,x₃) Cartesian space.

$$ \frac{\partial^{2} u}{\partial t^{2}}-{V^{2}_{SH}}\left( {\frac{\partial^{2}}{\partial x^{2}_{1}}}+\frac{\partial^{2}}{\partial x^{2}_{2}}\right)u=S, $$

(1)

where u is the component of the displacement in the x₃ direction, $V_{SH}=\sqrt {\mu /\rho }$ is the shear wave velocity, and S is the body force, modelled as a delta-source

$$ S=\delta(\mathbf{x}-\mathbf{x_{s}})M(t), $$

(2)

where x = (x₁,x₂), x_s is the location of the source and

$$ M(t)=M_{0}\frac{t}{\tau^{2}}exp(-t/\tau), $$

(3)

is a moment-rate time variation and τ is a smoothness parameter related to the frequency which controls the amplitude of the oscillations (Igel 2017).

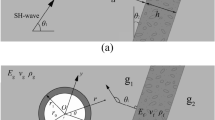
We consider a 2D model where the fault bends along the strike. Our computational domain is shown in Fig. 1. It can be read as a section of a possible 3D domain parallel to the surface. In this sense, the orientation of the fault is different from much of the literature (see Ben-Zion et al. 2003, Fig. 5). However, the main objective of this paper is to evaluate how the trapped energy is released by a FZ due to its bending. It is not important, at this stage, if it happens on the surface or at depth.

Fig. 1

A representation (not to scale) of the horizontal layer simulation domain in the case of a straight and curved fault. With the label S we identify the source location, with the labels LS_C, LS_R, LS_L we identify respectively the monitored points on the center, right and left side of the fault zone. For the curved fault the radius is labeled as r. The labels l_in and l_out refer to the cross-section of the fault

Moreover, this simple 2D model also allows a quantitative analysis (for example in the calculation of the parameter α introduced at the end of this section), that becomes much more complex in a 3D setting. The same problem will be addressed in a more realistic geological setting with 3D physically based simulations (preliminary results are available in Di Michele et al. 2021).

The energy lost as a consequence of the bend has been the subject of intensive study, especially in the field of optics, in order to avoid, or at least reduce the signal lost due to a bend in a waveguide.

The mechanism surrounding this phenomena is a simple application of Snell’s law, which says that at the interface between two different materials, having reflectionindex n₁ and n₂ respectively, the incident and refraction angle are such that

$$ \frac{\sin{\theta_{i}}}{\sin{\theta_{r}}}=\frac{n_{1}}{n_{2}}=\frac{V_{2}}{V_{1}}, $$

where V is the wave propagation velocity.

There exists a critical angle

$$ \theta_{c}=\arcsin(V_{2}/V_{1}), $$

(4)

for which the incoming waves are not transmitted but all the signal remains trapped inside the guide. For all $\theta _{i}<\arcsin (V_{2}/V_{1})$ the signal is partially transmitted in the medium labeled as 2. If the guide bends such that the incident angle exceeds the critical angle then all of the signal is reflected within the guide.

Obviously in geology it is not so easy to predict and/or evaluate the quantity of energy which will be released, due to the uncertainties in the geometric and mechanical parameters and the source structure. However it could be important to understand how the trapped energy is released as a consequence of the fault geometry and of the mechanical properties of the surrounding media.

During and after an earthquake, as a seismic wave propagates in a real media a certain amount of its carried energy is lost through being converted into heat. This effect is usually modelled introducing an attenuation coefficient named α:

$$ \alpha= \pi \frac{f}{V Q}, $$

(5)

where f is the frequency, V is the wave velocity inside the medium and Q is the so-called Q factor defined as

$$ Q=-\frac{E}{2\pi {\varDelta} E}, $$

(6)

where E is the peak strain energy and ΔE is the energy stored per cycle. The energy (density) E is the sum of the kinetic energy K and potential energy W, namely :

$$ E=K+W, $$

(7)

where

$$ K=\frac{1}{2}\rho \dot{u}^{2}, $$

(8)

and

$$ W=\frac{1}{2}\tau_{ij} e_{ij}, $$

(9)

In (9) τ_ij and e_ij represent the stress and the strain tensors, respectively (Shearer 2009). These quantities can be written as functions of the displacement and its derivative as follows

$$ \tau_{ij}= \lambda \delta_{ij} \partial_{k} u_{k}+\mu(\partial_{i} u_{j}+\partial_{j} u_{i}), e_{ij}=\frac{1}{2}(\partial_{i} u_{j}+\partial_{j} u_{i}). $$

(10)

According to our knowledge a specific theory of the bend loss for trapped seismic energy has not been yet developed. However, this phenomenon can also be described using Snell’s law and it looks reasonable to assume that a particular geometric configuration, such as the bending of a FZ, can be associated with an extra energy release as for an optical cable. For this reason we introduce a bending attenuation constantα_r, that is a complex function of the geometric and mechanical parameters of the problem. α_r can be modelled in many different ways, depending on the approximation adopted to solve the propagation of waves in guiding structure (see, for example, Gloge 1976; Marcuse 1971, 1976 and reference therein).

Here, due to the complexity of the FZ structure, we adopt the simplest approach by assuming

$$ \alpha_{r}=C_{1} e^{-C_{2} r}, $$

(11)

where r is the radius of curvature of the waveguide and C₁ and C₂ are constants. In the optical framework these constants depend on many parameters such as magnetic permeability of the free space, propagation constant, refractive indexes and many others. In this context due to the lack of a suitable theoretical model we calculate C₁ and C₂ experimentally at the end of Section 3. In Section 3 the values of these constants will be estimated using the numerical results in some simple configurations.

A third factor producing the seismic wave attenuation is the scattering, due to the presence of obstacles such as fractures and fluid filled pores that mostly constitute the fault zones. These irregularities and their distribution strongly contribute to the energy dissipation and to the seismic wave propagation. Many papers in the literature account for these effects, such as Jahnke et al. (2002) and Gulley et al. (2017b??, ??) and many others. However, in our model, we decide to neglect scattering attenuation, and focus on the geometric contribution to the FZ shape. The contribution of the anisotropies, both in the fault zone and in the bedrock, will be included in a forthcoming paper still in preparation.

2 Numerical method

Let us consider (1) supplemented with the absorbing boundary conditions

$$ \frac{\partial u}{\partial t}=-{V_{SH}}\frac{du}{d\mathbf{n}}, \quad \mathbf{x}\in\partial{\varOmega}, $$

(12)

where n is a unit outer normal vector to the domain Ω. As for the initial conditions, we assume that both the displacement and velocity at the starting time t = 0 are equal to 0, namely

$$ \frac{\partial u}{\partial t}=u=0 \quad \mathbf{x}\in{\varOmega}, t=0. $$

(13)

In order to obtain the weak formulation of problem (1) with boundary conditions (12) we first multiply equation (1) by the regular test function v, integrate over Ω, use Green’s formula and then boundary conditions (12), which results in

$$ a(u,v)=b(u,v)+l(v), \quad \forall v\in H^{1}({\varOmega}), $$

(14)

where

$$ a(u,v)={\int}_{{\varOmega}}\partial_{tt}uvd{\varOmega}, $$

(15)

$$ b(u,v)=-V^{2}_{SH}{\int}_{{\varOmega}}\nabla u\cdot\nabla vd{\varOmega}{-}V_{SH}{\int}_{\partial{\varOmega}}\partial_{t}uvd{\partial} {\varOmega}, $$

(16)

$$ l(v)={\int}_{{\varOmega}}Svd{\varOmega}. $$

(17)

Let us divide the domain Ω into triangles Ω_K, K = 1,...,n_e and choose the approximate solution u^h(t,x) in the form $u^{{h}}(t,\mathbf {x})=\sum u_{i}(t)\phi _{i}(\mathbf {x})$. Substituting the approximate solution into (14) and choosing v = ϕ_i(x) one arrives to the semi-discrete system

$$ M\ddot{U}+B\dot{U}=-AU+F, $$

(18)

where

$$ M=\{m_{ij}\}_{i,j=1}^{n},\quad m_{ij}={\int}_{{\varOmega}}\phi_{i}\phi_{j}d{\varOmega}, $$

(19)

$$ A=\{a_{ij}\}_{i,j=1}^{n},\quad a_{ij}=V_{SH}^{2}{\int}_{{\varOmega}}\nabla\phi_{i}\cdot\nabla\phi_{j}d{\varOmega}, $$

(20)

$$ B=\{b_{ij}\}_{i,j=1}^{n},\quad b_{ij}={\int}_{\partial{\varOmega}}\phi_{i}\phi_{j}d{\partial}{\varOmega}, $$

(21)

$$ F=\{f_{i}(t)\}_{i=1}^{n},\quad f_{i}={\int}_{{\varOmega}}S\phi_{i}d{\varOmega}, $$

(22)

$$ U=\{u_{i}(t)\}_{i=1}^{n}. $$

(23)

Let us denote U^k = U(t_k), F^k = F(t_k). For the time discretization we use the leapfrog method of the form

$$ \begin{array}{@{}rcl@{}} \left( M+\frac{{\varDelta} t}{2}B\right)U^{k+1}&=&(2M-({\varDelta} t)^{2}A)U^{k}\\ &&-\left( M-\frac{{\varDelta} t}{2}B\right)U^{k-1}+({\varDelta} t)^{2}F^{k}, \end{array} $$

(24)

with the first timestep

$$ MU^{1}=\left( M-\frac{({\varDelta} t)^{2}}{2}A\right)U^{0}+\frac{({\varDelta} t)^{2}}{2}F^{0}. $$

(25)

It should be noted that the choice of the leapfrog timestepping method is motivated by the fact that this method is explicit, and therefore, finding the solution on each timestep does not require solving a linear system (in the case of the mass lumping described below that leads to diagonal mass matrix) unlike in case of implicit methods. This is especially useful since the large number of finite elements in our problem would make it too time consuming to solve the linear system at each timestep (Igel 2017).

Besides, as we are dealing with a hyperbolic equation, the use of explicit over implicit methods is typical because of the CFL condition (Maggio and Quarteroni 1994; Wendroff 1968; Strikwerda 2004).

Let us now introduce the spectral element nodes and basis functions that lead to a diagonal mass matrix M as shown in Cohen et al. (2001). In the case of quadratic elements for the reference triangle the nodes are defined as S_i — the vertices of the triangle, M_i — the midpoints of the triangle sides, G — its centroid. The basis functions w^G, $w_{2i}^{S_{i}}$ and $w_{2i}^{M_{i}}$ in this case are described by

$$ w^{G}=27b, w_{2i}^{S_{i}}=p_{2i}^{S_{i}}+9b, w_{2i}^{M_{i}}=p_{2i}^{M_{i}}-12b, b=\lambda_{1}\lambda_{2}\lambda_{3}, $$

(26)

where λ_i are the barycentric coordinates and $p_{2i}^{S_{i}}$, $p_{2i}^{M_{i}}$ are the standard P₂ basis functions on triangular elements.

Finally, the corresponding weights in the quadrature formulae are given by w_s = 1/20,w_e = 2/15,w_G = 9/20. For the case of higher order elements, see Cohen et al. (2001), Giraldo and Taylor (2006), and Mulder (2001).

Unfortunately, in the case of triangular finite elements, the matrix $M+\frac {{\varDelta } t}{2}B$ is non-diagonal. In order to avoid inverting the matrix $M+\frac {{\varDelta } t}{2}B$ we proceed in the following way. Let us divide the finite element nodes in two sets: the ones lying inside the domain Ω and the ones lying on the boundary ∂Ω. On each timestep we find the approximate solution separately for these two sets. It can be seen that, for the points inside the domain, the corresponding matrix of the linear system is diagonal, so this part can be solved directly. As for the system that corresponds to the points lying on the boundary ∂Ω, the matrix of the related linear system is non-diagonal, but the dimension of this part is much smaller than of the original system. In other words, the space dimension of this part is reduced by one, since in this case we consider only the boundary nodes. As a result, if the original problem is two-dimensional, this part of the matrix $M+\frac {{\varDelta } t}{2}B$ can be inverted without major difficulties.

3 Results and discussion

We consider a two-dimensional (2D) domain Ω having sides of 10 × 20 km, containing a curved or a straight fault as in Fig. 1. The bottom left corner of the domain corresponds to the origin of the Cartesian coordinates, that is ((0,0) km). On all the boundaries absorbing conditions are prescribed as in (12).

The geometric parameters of the problem are the thickness of the fault h, the radius of the curvature r and the velocity ratio β, that is the velocity reduction inside the fault zone with respect to surrounding media. From the geological literature we know that h ranges between and hundreds of meters, whereas β is in the range 0.2–0.6 (Huang and Ampuero 2011; Li and Vidale 1996; Kuwahara and Ito 2002). Although β and h are, in general, variable within a real FZ structure, here we will assume that both are constant. From here we label all the physical and geometric parameters related to the fault zone with a subscript FZ and the parameters related with surrounding media with a subscript O.

Within this paper we consider a constant value for velocity in the surrounding media (V_O = 1000 m/s), and different values of the velocity inside the fault zone, namely V_FZ = 400,600,800 m/s. In other words we consider a velocity reduction of 60%, 40% and 20% with respect to the surrounding rock, that means β = 0.6,0.4,0.2 respectively. We also point out that in our framework the parameter choice refers to a superficial layer on the crustal model.

Three different values of the fault thickness are also considered, h = 0.25,0.5,1 km. We remark that a smaller thickness is theoretically possible but adds numerical difficulties as more finite elements and smaller timestep may be required to get favourable results.

Concerning the radius of curvature r, this parameter is more difficult to estimate because the fault zones are composed of a sequence of cracks and their structure is often very complicated and not well known. Here we consider r = 1 km and r = 4 km. The source, located at (5.0,3.5) km, is modelled as a delta-source using (2) and (3). Obviously it does not represent a real earthquake, but it is able to generate well trapped waves inside our structure, as we will show later. We remark that there are two parameters which characterize the source, namely M₀ and τ. The first controls the amplitude of the incoming waves, the second their frequencies, which we choose as τ = 0.05 s. The behaviour of the source together with its fast Fourier transform is given in Fig. 2a. Observing Fig. 2b it is clear that the source contains all frequencies, with most of the spectrum in the range [0–5] Hz. Low frequency f means a large wavelength λ (f = V/λ). The wavelengths corresponding to f = 5 Hz for the V_FZ considered within this paper are λ = 80 m for V_FZ = 400 m/s, λ = 120 m for V_FZ = 600 m/s, and λ = 160 m for V_FZ = 800 m/s. Therefore, all the wavelengths taken into account are small enough to see a fault zone having thickness in the range 0.25–1 km and we expect trapped waves to be observed.

Fig. 2

Source and its Fourier transform for τ = 0.05 s

Finally we remark that due to the linearity of the problem, M₀ plays the role of a scale factor. Here we set M₀ = 10¹⁶ Nm.

The signal, the displacement u in this case, is detected at three seismograph locations (LS). We name the LS point located inside the fault LS_C, whereas LS_R and LS_L are on the right and left side of the fault respectively, at distance (in the normal direction) of 500 m from the fault zone boundary. Some related test with distances equal to 50 m and 150 m will also be discussed at the end of this Section.

As we want to focus on the effects of the fault shape on the trapped waves, we locate the point source at the beginning of the fault far enough from the bend and boundary of the domain, in order to allow the wave to be well trapped and to avoid reflection from the domain boundaries.

The source point is located exactly in the middle of the fault although it is known that the maximum capability of the fault to trap waves can be observed for sources located at the fault boundaries. This is because in our model it is very important to have a symmetric source to observe the effect of the curvature. In other words, for a straight fault no differences can be observed for the displacement recorded by LS_L and LS_R due to the symmetry of the problem and all the differences recorded for the curved shape can be attributed mostly to the curvature itself.

However, for the sake of completeness we have also investigated the effect of the source position, the results of which are displayed in the ??.

First of all we verify that, as expected, the waves are well trapped before they reach the curve. We compare the displacement observed at LS_C for a straight fault with the signal detected at the same location in a plain domain. We analyse in detail the case corresponding to V_FZ = 600 m/s. The displacement has been recorded for all the three values of the thickness at LS_C and LS_R (see Fig. 3). For the straight fault, after the first peak arrives at LS_C, large oscillations in the displacement can be observed for many seconds, for all values of the FZ thickness. On the contrary, in the homogeneous case after the first waves arrive, the displacement decays quite quickly. A similar behaviour of the displacement can be observed at LS_R, the oscillations have a similar frequency but smaller amplitude compared to those inside the fault, this is due to the different mechanical properties between the FZ and the surrounding media as well as the transmission of the trapped signal at the interface between the two media. Similar behaviour can be observed for the other two velocities studied, V_FZ = 400 m/s and V_FZ = 800 m/s, see Fig. 14a and b in the ??. Finally, we observe that when decreasing the velocity inside the FZ the trapped waves become less compact as observed in Li and Vidale (1996).

Fig. 3

Displacement u for the velocity V_FZ = 600 m/s, detected at LS_C and LS_R, each curve refers to a different FZ thickness h = 1,0.5,0.25 km in red, blue, and green respectively. The black curve refers to the homogeneous case with V_O = V_FZ

As mentioned before, in our framework, the simulation parameters refer to the crustal layer. To analyse the wave behaviour at deeper regions we set V_O = 3000 m/s, V_FZ = 2000 m/s and compare the recorded signal at LS_L and LS_R for two different radii r = 1 km and r = 4 km. Three different values of fault thickness, h = 0.25,0.5,1 km, are considered in comparison with the homogeneous case (V_FZ = V_O = 2000). The results are displayed in Fig. 4, where we can observe a displacement behaviour qualitatively similar to the one already described above for lower wave speeds.

Fig. 4

Displacements at LS_L and LS_R for V_FZ = 2000 m/s and V_O = 3000 m/s. Two radii of curvature are considered r = 1 km and r = 4 km (first and second lines, respectively). (a) LS_L with r = 1 km. (b) LS_R with r = 1 km. (c) LS_L with r = 4 km. (d) LS_R with r = 4 km

Having verified that the fault zone, as we designed it, is able to trap waves, we start the parametric analysis of our model focusing on the effects of the curvature and on the trapped energy release. Also in this case we discuss in detail what happens for V_FZ = 600 m/s. We start by considering a width value h = 0.25 km, then we increase it until h = 1 km. A decrease in thickness leads to an increase in the frequency of the trapped waves, as expected. The displacement, recorded at the LS_R and LS_L, for each of the velocities are plotted in Fig. 5 for a radius of curvature r = 1 km and r = 4 km, and for the straight fault, namely $r_{\infty }$. The first peak has a similar amplitude of approximately 0.6 cm. However for $r_{\infty }$ the oscillation decays in amplitude quite fast, whereas for a bending fault the oscillation remains almost constant in amplitude for 10 s. On the opposite location, namely on the right side, for all three radii we observe similar behaviour.

Fig. 5

Displacement u for velocity V_FZ = 600 m/s detected at LS_L and LS_R, each line refers to a different FZ thickness h = 0.25,0.5,1 km, r = 1.0,4.0 km and $r=\infty$ in red, blue and green respectively

Similar effects can be observed for the other two velocities taken into account (see Fig. 15a and b in the ??), except the case V_FZ = 400 m/s and r = 4 km where the bending effect is smaller. Indeed according to the definition of the critical angle (4), 𝜃_c decreases as V_FZ decreases, and a larger amount of energy remains trapped, reducing the effect of the bending.

As noted in the previous section, the displacement in the direction of the LS_L is larger than that on the right side of the domain. Therefore, a strong release of energy from the curved faults in the left direction can be expected.

To quantify this effect we plot the integral kinetic energy normalized with respect to the density ρ, namely $I_{K}(t)={{\int \limits }^{t}_{0}} \dot {u}^{2}$.

We studied the amount of normalized kinetic energy I_K(t) transmitted by the fault to LS_L and LS_R for three different values of fault thickness h = 0.25 km, h = 0.5 km and h = 1 km. All the combinations of the fault zone velocity and radius of curvature are considered. We discuss, in detail, the case corresponding to the fault thickness of 0.5 km, plotted in Fig. 6 (plots related to the other two cases are reported in ?? Figs. 16 and 17).

Fig. 6

I_K for fault thickness h = 0.5 km at LS_L (red) and LS_R (blue), r = 1.0,4.0 km and V_FZ = 400,600,800 m/s

In the case r = 1 km we get $I_{K}|_{LS_{L}} >I_{K}|_{LS_{R}}$ for all the noted velocities. At the beginning of the curve, a transient time for which $I_{K}|_{LS_{R}} >I_{K}|_{LS_{L}}$ is observed. This effect is due to the first peak arrival time that is smaller for LS_R because this recorder is closest to the source. Similar observations can be done also for large curvature, that is r = 4 km, except for V_FZ = 400 m/s, where the behaviour is completely different and $I_{K}|_{LS_{R}} >I_{K}|_{LS_{L}}$ almost everywhere. As we have observed before in this case the effect of the bending is reduced and the effect of the distance between source point and LS point becomes dominant.

Similar behaviour can be observed in the ?? for the other fault thicknesses (h), as displayed in Fig. 16, for h = 0.25 km, and Fig. 17, for h = 1 km.

Let I_K(T_p) be the plateau value for the function I_K(t). We remark that the plateau is reached at a different time T_p for each FZ velocity we select. I_K(t) represents the kinetic total energy (normalized by the density) released in a certain point. In Fig. 7 the plateau value is plotted as a function of the radius of curvature, for all the velocities V_FZ and the FZ thickness.

Fig. 7

Dependence of the total energy I_K(T_p) on radius of curvature r for the fault thickness h = 0.5 km at LS_L, LS_C and LS_R, V_FZ = 400,600,800 m/s in red, blue and green respectively

The behaviour of the energy and of its cumulative function depends on many parameters, such as geometry and mechanical properties of the domain as well as source frequency spectrum. However some common threads can be observed in Fig. 7 (and Figs. 18 and 19 in the ??): a) $I_{K}(T_{p})_{LS_{R}}$ and $I_{K}(T_{p})_{LS_{C}}$ are almost constant except for the case V_FZ = 400m/s where some oscillations are visible, b) $I_{K}(T_{p})_{LS_{L}}$ looks almost radius independent anddecays as the radius of curvature increases, c) $I_{K}(T_{p})_{LS_{L}}>I_{K}(T_{p})_{LS_{R}}$. Concerning the last point, we remark that all the data presented within this paper refer to 0.5 km distance between the LS points and the fault boundaries, although we expect that the curvature effect will increase when that distance is reduced. Therefore, we compare the cumulative energy released by the fault at LS_R and LS_L for different LS-fault boundary distances (500, 150 and 50 m). In particular we consider V_FZ = 600 m/s and h = 0.5 km. Results are displayed in Fig. 9. We see that as the distance increases the energy released is increased and the fault bending effect becomes more pronounced. According to Fig. 7 (and Figs. 18 and 19 in the ??) the trigger parameter for the energy lost is the curvature radius of the fault, the ratio β between velocity inside and outside the FZ does not play any role. To verify this effect in Fig. 8 (and Figs. 20 and 21 in the ??) we plot I_K(T_p) as a function of the velocity inside the FZ. Also in this case some common threads can be observed: a) $I_{K}(T_{p})_{LS_{R}}$ and $I_{K}(T_{p})_{LS_{C}}$ decay quite fast, although some oscillation is noticeable for small velocities at LS_R, b)$I_{K}(T_{p})_{LS_{L}}$ looks velocity independent and remains almost constant in a wide range of velocities, c) $I_{K}(T_{p})_{LS_{L}}>I_{K}(T_{p})_{LS_{R}}$ for all velocities if r = 1 km (Fig. 9).

Fig. 8

Dependence of the total energy I_K(T_p) on FZ velocity V_FZ for the fault thickness h = 0.5 km at LS_L, LS_C and LS_R, r = 1.0,4.0 km in red and blue respectively

Fig. 9

I_K for velocity V_FZ = 600 m/s and FZ thickness h = 0.5 km, r = 1.0,4.0 km and $r=\infty$ with distance from the faults equal to 50, 150 and 500 m in red, blue and green respectively

Finally, to verify the formula (11) we compute numerically the parameter α_r, as

$$ \alpha_{r}=-\frac{1}{\pi r}\frac{I_{E_{out}}-I_{E_{in}}}{ I_{E_{in}}}, $$

(27)

where $I_{E_{in}}={{\int \limits }_{0}^{T}}{\int \limits }_{l_{in}}E_{in}dl_{in}dt$ and $I_{E_{in}}={{\int \limits }_{0}^{T}}$ ${\int \limits }_{l_{out}}E_{out}dl_{out}dt$ are the integrals of incoming energy E_in and outgoing energy E_out (given by (7)) that pass through the cross-sections l_in and l_out respectively (Fig. 1). In other words, $I_{E_{in}}$ and $I_{E_{out}}$ are calculated as the line integrals over time along the corresponding cross-section using numerical quadrature. The bending attenuation constant α_r is then obtained as the ratio between the integrals of total energy lost per unit fault length through the curved part of the fault and the integral of incoming total energy $I_{E_{in}}$. Since the length of the curved part of the fault is equal to $\frac {\pi r}{2}$, in order to obtain the energy lost per unit fault length of the curved part, we have to normalize it by the factor of $\frac {\pi r}{2}$. The exponential behaviour is well fitted by the numerical data at least for the higher velocities 600 m/s and 800 m/s (see Fig. 10). The constants C₁ and C₂ are estimated, for τ = 0.05 s, using a SCILAB function for a data fitting.

Fig. 10

Dependence of the parameter α_r on radius of curvature r for τ= 0.05 s

Test	C1, 1/km	C2, 1/km	e
τ = 0.05 s, VFZ = 400 m/s	0.20	1.02	4.56 ⋅ 10 − 4
τ = 0.05 s, VFZ = 600 m/s	0.43	0.95	2.79 ⋅ 10 − 4
τ = 0.05 s, VFZ = 800 m/s	0.51	0.65	3.37 ⋅ 10 − 4

4 Conclusions and further studies

In the paper we have investigated the effect of the fault geometry on the SH waves propagation. Contrary to the available literature (for example Ben-Zion 1989, 2003) where the 2-D vertical section is analysed, in this study the fault is located at a certain depth in the horizontal plane to better appreciate the effect of the bending. In other words we analyse a horizontal section of the fault zone instead of the usual vertical one. We have investigated bending effects while varying fault zone thickness and found (see Figs. 5 and 15 in the ??) that the fault zones are able to guide trapped waves through curved geometries according to the stated aim of this paper. In particular we have shown that a greater amount of energy is released in the direction of the negative curvature of the fault. According to our study, the velocity inside the fault does not affect the energy release in a strong way (see Figs. 7c and 18c and 19c in the ??). However it strongly depends on the radius of curvature (see Figs. 8c and 20c and 21c in the ??). We treated only simple 2D geometric cases, a deeper understanding of the phenomena could be obtained from an extension into 3D and the addition of realistic geological features inside the studied domain. This work was performed as a preliminary study into potential fault guide effects, which have been proven, before undertaking more complicated tests on a more realistic domain. A new set of tests will be performed by using SPEED (SPectral Elements in Elastodynamics with Discontinuous Galerkin- http://speed.mox.polimi.it/). SPEED is an open-source code able to simulate seismic events in a three-dimensional reconstructed domain (Mazzieri et al. 2013; Antonietti et al. 2012). Using this tool we will be able to include complex fault zones and we will evaluate in more detail the effects of the fault zone shape on wave propagation.

Appendix:

1.1 A.1 Derivation of the energy conservation law for seismic waves

The energy density carried by seismic waves can be expressed as a sum between the kinetic energy density (K) and the potential energy density (W ), as E = K + W while K, as usual, can be written as

$$K=\frac{1}{2} \rho\dot{u}^{2},$$

the derivation of W (strain energy functional), is classically based on mechanical and thermodynamic considerations (Aki and Richards 2002). Therefore, for convenience of the reader, in the following, we sketch the derivation of W (see Aki and Richards 2002 for more details). In our case we consider the system to be adiabatic, namely that there is no heat exchange with the exterior.

Fig. 11

A representation (not to scale) of the simulation domain in the case of a bent fault. With the labels S, S₁, S₂ and S₃ we identify the source locations, with the labels LS_R, LS_L we identify respectively the monitored points on the right and left side of the fault zone. The radius of the bent fault the is labeled as r

Fig. 12

Displacements at LS_L and LS_R for V_FZ = 800 m/s and V_O = 1000 m/s. Two radii of curvature (r = 1 km and r = 4 km) have been considered. The fault thickness is h = 1 km

Fig. 13

Dependence of the displacements u on the bending angle for the fault thickness h = 1 km and FZ velocity V_FZ = 800 m/s at LS_C, LS_R and LS_L, bending angles equal to 45, 60 and 90 degrees in red, blue and green respectively

Fig. 14

Displacement u for the velocity V_FZ = 400 m/s (a) V_FZ = 800 (b), detected at LS_C and LS_R, each curve refers to a different FZ thickness h = 1,0.5,0.25 km in red, blue, and green respectively. The black curve refers to the homogeneous case with V_O = V_FZ

Fig. 15

Displacement u for velocity V_FZ = 400 m/s (a), V_FZ = 800 m/s (b) detected at LS_L and LS_R, each row pair refers to a different FZ thickness h = 0.25,0.5,1 km, r = 1.0,4.0 km and $r=\infty$ in red, blue and green respectively

Fig. 16

I_K for fault thickness h = 0.25 km at LS_L (red) and LS_R (blue), r = 1.0,4.0 km and V_FZ = 400,600,800 m/s

Let B an elastic body having volume V and boundary surface S. The variation of the total energy (kinetic + potential) per “infinitesimal time” $\dot {E}$, coincides with the variation of the related mechanical energy.

In view of Gauss’s divergence theorem it is not difficult to show that

$$ \dot{E}=\frac{\partial}{\partial t}{\int}_{\textit{V}} \frac{\rho}{2} \dot{u}_{i}\dot{u}_{j} d\textit{V}+{\int}_{\textit{V}} \tau_{ij} \dot{e}_{ij} d\textit{V} $$

(28)

where u denotes the displacement vector and τ_ij and e_ij represent the stress and the strain tensors, respectively.

As mentioned previously the kinetic contribution to the energy increase follows the standard law of classical mechanics; therefore,

$$ \dot{K}= \frac{\partial}{\partial t}{\int}_{\textit{V}} \frac{\rho}{2} \dot{u}_{i}\dot{u}_{i} d\textit{V} $$

(29)

In view of the expressions (28)–(29) the internal energy U for adiabatic process, can be written in differential form as

$$ d\textit{U}=\tau_{ij} de_{ij}. $$

(30)

hence U = W. Then, for instance in the Hookean case, after some simple calculations it follows that

$$ \textit{W}=\frac{1}{2}\tau_{ij} e_{ij}. $$

(31)

1.2 A.2 Source position and bending angles effects

Within this work all of the tests use a source located at the center of the fault zone at the same distance with respect to the left and right fault boundary. In this way the system is symmetric except for the fault bending. To evaluate the effect of the source we consider four different sources at different positions as in Fig. 11. The results are displayed in Fig. 12, for two radii of curvature r = 1 km (Fig. 12a and b) and r = 4 km (Fig. 12c and d). The fault thickness is 1 km. For both LS_L and LS_R the behaviour of the recorded signal is quite close to each other, for S₃ this presents remarkable differences due to the fact that the source is located outside the fault in a material having different mechanical properties.

Fig. 17

I_K for fault thickness h = 1 km at LS_L (red) and LS_R (blue), r = 1.0,4.0 km and V_FZ = 400,600,800 m/s

Fig. 18

Dependence of the total energy I_K(T_p) on radius of curvature r for the fault thickness h = 0.25 km at LS_L, LS_C and LS_R, V_FZ = 400,600,800 m/s in red, blue and green respectively

Fig. 19

Dependence of the total energy I_K(T_p) on radius of curvature r for the fault thickness h = 1 km at LS_L, LS_C and LS_R, V_FZ = 400,600,800 m/s in red, blue and green respectively

Fig. 20

Dependence of the total energy I_K(T_p) on FZ velocity V_FZ from 400 to 1000 m/s for the fault thickness h = 0.25 km at LS_L, LS_C and LS_R, r = 1.0,4.0 km in red and blue respectively

Fig. 21

Dependence of the total energy I_K(T_p) on FZ velocity V_FZ for the fault thickness h = 1 km at LS_L, LS_C and LS_R, r = 1.0,4.0 km in red and blue respectively

Finally we discuss the effect of angle of bending that in Section 3 is assumed to be 90^∘. Here we consider and compare 3 different values of the bending angle, namely 90^∘, 60^∘ and 45^∘, to better approximate the real fault zone total bending angle (Fig. 13). According to this preliminary results for the selected frequency range, the effects of the bending values remain remarkable for angles greater then 60^∘, but different set of mechanical and physical parameters must be considered to better understand the phenomenon not only with respect to the main curvature of the FZ, but also with respect to the often more pronounced local curvatures.

1.3 A.3 Other tests

In this section we collect the figures mentioned in the main text and moved here for greater readability. All the pictures are cited in Section 3 and carefully described in the captions