Abstract
Site response is a critical consideration when assessing earthquake hazards. Site characterization is key to understanding site effects as influenced by seismic site conditions of the local geology. Thus, a number of geophysical site characterization methods were developed to meet the demand for accurate and cost-effective results. As a consequence, a number of studies have been administered periodically as blind trials to evaluate the state-of-practice on-site characterization. We present results from the Consortium of Organizations for Strong Motion Observation Systems (COSMOS) blind trials, which used data recorded from surface-based microtremor array methods (MAM) at four sites where geomorphic conditions vary from deep alluvial basins to an alpine valley. Thirty-four invited analysts participated. Data were incrementally released to 17 available analysts who participated in all four phases: (1) two-station arrays, (2) sparse triangular arrays, (3) complex nested triangular or circular arrays, and (4) all available geological control site information including drill hole data. Another set of 17 analysts provided results from two sites and two phases only. Although data from one site consisted of recordings from three-component sensors, the other three sites consisted of data recorded only by vertical-component sensors. The sites cover a range of noise source distributions, ranging from one site with a highly directional microtremor wave field to others with omni-directional (azimuthally distributed) wave fields. We review results from different processing techniques (e.g., beam-forming, spatial autocorrelation, cross-correlation, or seismic interferometry) applied by the analysts and compare the effectiveness between the differing wave field distributions. We define the M index as a quality index based on estimates of the time-averaged shear-wave velocity of the upper 10 (VS10), 30 (VS30), 100 (VS100), and 300 (VS300) meters and show its usefulness in quantitative comparisons of VS profiles from multiple analysts. Our findings are expected to aid in building an evidence-based consensus on preferred cost-effective arrays and processing methodology for future studies of seismic site effects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Microtremor observations are in frequent use for earthquake hazard studies, for building quasi-3D models of surficial geology, and for depth of cover studies in hydrology or mineral exploration surveys. Most modern earthquake building codes are based on a seismic site response parameters known as the time-averaged shear-wave velocity VS to the depth of 30 m (VS30) (BSSC 2003; EC8 2004). Although indirect proxy-based VS30 methods were applied (Yong, 2016), site seismic recordings are preferably the basis for modeling the one-dimensional (1D) VS profile and to derive VS30.
Since it was introduced by Borcherdt (1994), VS30 has been the most common ground motion model site index to account for seismic site conditions. Slowness (SS), the inverse of velocity, is a lesser known measure that has been known to be useful when highlighting detailed layers of the near surface (Brown et al. 2003; Boore and Asten 2008; Mital et al. 2021). Traditionally, invasive borehole (downhole, DH) methods were the standard practice for characterizing seismic site conditions and proved to be quite costly; some practitioners have ill-advisably considered DH methods to be the most accurate approach, and Socco and Strobbia (2004) and Thompson et al. (2009) (amongst others) have cautioned against the perceived superiority of DH methods (e.g., data contamination from reflected or downward wave propagation). In recent years, an impressive number of noninvasive geophysical site characterization methods were developed to meet the demand to accurately and cost-effectively provide these critical seismic parameters. Consequently, a number of studies have administered blind trials to evaluate different array and processing methodologies for extraction of VS profile information, or the equivalent inverse parameter shear-wave slowness SS. Examples of past notable blind trials that placed substantial emphases on interpretation and modeling of passive seismic (microtremor or ambient noise) site characterization data include the 2004 Coyote Creek (CA, USA) blind test (Boore and Asten 2008), the blind tests for the 2006 3rd International Symposium on the Effects of Surface Geology (Grenoble, France) (Cornou et al. 2007), and more recently, the 2015 Inter-comparison of methods for site PArameter and veloCIty proFIle charaCterization (InterPACIFIC) Workshop (Turin, Italy) (Garofalo et al. 2016). These trials commonly used a very large number of arrays and stations to provide information to produce the best-possible results for estimations of VS versus depth profiles from microtremor and other active-source methods. The participants of the aforementioned blind trial efforts were almost always exclusively comprised of globally recognized experts or practitioners with notable specialties in the limited methods tested. They, however, did not considered the issue of which basic arrays with a limited number of sensors might be practical and under what circumstances.
In this study, we address the important issue of how useful basic or sparse arrays can be in practical surveys for evaluation of site parameters. The study was conducted through the Consortium of Organizations for Strong Motion Observation Systems (COSMOS) using a set of blind trials which were conducted from June–November 2018. This COSMOS trial strategically employed a number of key ingredients (Asten et al. 2018a, b, 2019a, b). One such component was that the study used microtremor array data recorded from four sites in order to consider limitations imposed by differing geologies, sparse array geometries, and interpretation methodologies. Another important element was that these sites differ in the azimuthal coverage of microtremor ambient noise at each location. The COSMOS trial also deliberately used a four-phase approach in order to evaluate changes in blind interpretations as each phase introduced additional array data. Furthermore, this trial also incorporated results from a range of different geophysical methods, including processing techniques (algorithms) coded in software packages (or customized in-house computer programs) which were independently selected for analyses by the invited participants. The range of their experiences with microtremor array methods was broad as they were comprised of graduate-level students, commercial practitioners, and topical experts—some were also developers of the open-source and commercial software packages used in this trial. To encourage and sustain the voluntary contributions in as many of the phases as possible and to avoid the undesirable effects of competition, identities of the participants were anonymized (except to the COSMOS administrators). For each of the four sites, a data supplier and established user of the methods supplied not only the recorded microtremor data for each site, but a reference VS model constructed from all available geophysical, borehole, and geological data. The reference models were only disclosed to participants in phase 4 of the blind trial.
In this paper, we summarize the 2018 trial and results from blind interpretations by 17 analysts who analyzed all sites and phases (group 1 in Table 1). We also present limited results from a separate subset of 17 analysts (group 2) who participated in phase 3 only, by providing analyses for only two of the four sites (site 2 and site 4).
2 Methodology and data
2.1 Goals of the trials
The primary goal of the COSMOS trials was to evaluate the efficiency of microtremor methods to estimate VS profiles using surface-based arrays by progressively increasing site coverage through the densification of recording locations, from two-station arrays (N = 2) to sparse arrays (typically N = 3 or 4) and full arrays (N ≥ 6). An associated goal was to evaluate different techniques through multiple independent interpretations.
In order to achieve these goals, the trials were divided into four phases, with each of the four sites evaluated/re-evaluated in each of the phases:
-
Phase 1—two-station arrays (single pair of seismometers extracted from a larger array)
-
Phase 2—sparse arrays (four-station triangle)
-
Phase 3—full array data (nested triangles or circles of different diameters)
-
Phase 4—re-evaluation using geological and borehole data, as well as a reference model as provided by the data supplier for each site
2.2 Passive-source microtremor array methods tested
As a recognized approach to site characterization, microtremor array methods (MAM) share similar (if not identical) techniques to acquire field data; they, however, differ in their methods for post processing and analyses of the data. In the literature, the various types of MAM approaches were described in details by their respective developers and its top practitioners. Recently, a comprehensive review was performed by Asten and Hayashi (2018), as well as progress in an ongoing companion effort by COSMOS Site Characterization Project to develop guidelines when using noninvasive geophysical methods for characterizing seismic site conditions (https://www.strongmotion.org/Projects/CharacterizationGuidelines/2020SiteCharProject%20Update/; last accessed 27 February 2021). Thus, we defer detailed background information about MAM to the aforementioned efforts and provide only appropriate details herein. The MAM applied by all participating analysts mainly included the two approaches: the spatial autocorrelation (SPAC) (Aki 1957) and the frequency-wave number (FK) (Capon, 1969); a few analysts applied approach based on noise cross-correlation (CC) (Campillo and Paul 2003; Shapiro and Campillo 2004; Shapiro et al. 2005) or seismic noise interferometry techniques (SI) (Wapenaar 2004; Wapenaar et al. 2010a; 2010b) (Table 1). It should be noted that CC and SI are frequently used interchangeably because the approach is fundamentally defined as the cross-correlation of microtremors recorded at two stations (Bensen et al. 2007; Campillo and Roux 2015).
For accuracy, the SPAC approach relies on spatial azimuthal averaging of coherent plane waves propagating at a single scalar velocity at each frequency. The extended SPAC (ESAC) method was also applied by analysts of this study and as the name implies, ESAC is a variant of the SPAC method that fits estimates of phase velocity to multiple regular values of station spacings for a selected set of frequencies. FK array processing approaches (e.g., beam-forming and maximum likelihood methods) have four essential differences from SPAC; FK is capable of the following:
-
Performing at its optimum when unidirectional wave propagation is known to exist
-
Remaining effective when the array stations are irregularly spaced
-
Resolving (subject to limitations of the array response function) multiple velocities (or higher modes) of wave propagation
-
Providing robust estimates of wave velocity when incoherent noise is present in additional to the propagating wave signal
Advantages and disadvantages of either the SPAC and FK approaches were recently outlined in Foti et al. (2018) as well as in Asten and Hayashi (2018), and the two were demonstrated to have possible trade-offs in reliability between the them. For example, the SPAC approach fundamentally averages the propagation coherent waves; thus, it is not necessary to know a priori about the unidirectional nature of the propagating wave field as would when using the FK approach. To do so, the SPAC method requires regular (or multiple regular) station spacing, which limits its applicability at locations where space is limited due to either access related issues or complexity in terrain (or both combined). By comparison, FK remains effective when the array is irregularly spaced but its reliability is reduced when the number of optimally located recordings are limited.
The frequency- or time-domain CC (or SI) method is often considered a development from the original frequency-domain SPAC method of Aki (1957). Ekstrom et al. (2009) further developed CC in the frequency domain, which was applied recently by Pastén et al. (2016). Tsai and Moschetti (2010) notably investigated the exact equivalence between the CC approach and the SPAC approach. They found both approaches allow results from each to be used in the other. For example, noise tomography as derived from CC can be improved by inclusion of results from the fundamental process of azimuthal averaging used in the SPAC approach and SPAC can be improved from the time windowing of tomography as derived in the CC approach. Tsai and Moschetti (2010) suggested that the merger of the two methods are complementary thus will improve results. Asten and Hayashi (2018) corroborated the findings of Tsai and Moschetti (2010); Foti et al. (2018) provided similar observations; thus, we also limit our descriptions about the CC method herein and refer the reader to these publications for additional information about the CC (or SI) approach.
2.3 Sites investigated
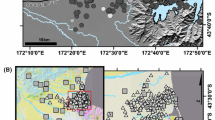
At the time of this study, the four sites chosen were associated with unpublished array data: along the Guadalupe River in San Jose, CA, USA; in Trois Rivieres, Quebec, Canada; in La Salle, Italy; and in Dolphin Park, Carson City, CA, USA (Supplementary Information, Figs. S1 to S4). Figure 1 shows the configuration of seismometer or geophone arrays used at each site. Site 1 was surveyed with three-component (3C) seismometers. The remaining sites recorded vertical components only (1C). Array geometries in Fig. 1 use different symbols to identify which seismometers were used for phases 1, 2, and 3 of the blind trials. In addition to the array data previously described, each site has a substantial history of multiple independent seismic noninvasive (both passive and active surface wave methods) and invasive investigations (DH methods: seismic cone penetrometer test (SCPT) or P-S suspension logging). Figure 2 shows layered earth VS reference models constructed by data suppliers familiar with the full range of available data at the respective sites. These reference models were not disclosed to analysts until phase 4 of the project and were used to judge the quality of interpretations produced by analysts in these blind trials. Figure 3 shows the corresponding Rayleigh wave phase velocity dispersion curves for the four sites, computed using forward modeling methods and codes from Herrmann (2013). Dispersion curves plotted include the fundamental mode (R0), two higher modes (R1 and R2), and the effective mode (Re), where the Re assumes a power partition between fundamental and higher modes based on theoretical response of a layered earth to a vertical impact (Ikeda et al. 2012). Vertical shifts in the modeled dispersion curves in Fig. 3 are a consequence of changes in power partition between modes as noted by Ikeda et al. (2012). Tabular versions of the reference models are included in the phase 4 section of accompanying data release (Asten et al. 2021). Detailed information of the four sites are as follows:
Layout of three-component seismometers (3C) or single-component (1C) geophones for four sites used in the blind trials. a Site 1, Guadalupe, CA, USA; the drill hole with PS log is located adjacent to point B2 on eastside of the array. b Site 2, Trois Rivieres, Quebec, Canada; the drill hole with SCPT log is located about 20 m northwest of the array center. c Site 3, La Salle, Italy; two drill holes located 300 m north and 500 m northwest of the array center are shown in Fig. S4. d Site 4, Dolphin Park, Carson, CA, USA. Drill hole Carson-1 used to acquire PS data is located 150 m east of the array center. All drill hole data remained blind to analysts in this project until the phase 4 review. Yellow symbols in plots a–c show stations used for two-station SPAC in phase 1. Blue lines show arrays (“sparse triangles” of 3 or 4 stations) used in phase 2. For site 4, phase 1 data consisted of three pairs of stations with separations at 15, 30, and 60 m, where pairs were independent and specified only by the separation distance. For site 4, phase 2 data from three independent four-station triangles were supplied without additional data (e.g., location) other than the triangle side lengths of 15, 30, and 60 m. The gray arrow in c shows approximate direction of dominant wave propagation at only this site
Reference VS models for the four sites in this study. Left column: VS versus depth. Right column: slowness (SS) versus depth. Black is reference model determined by data supplier for each site using all available data. See Asten et al. (2021) for tabular versions of reference models. a Site 1 (Guadalupe River, San Jose, CA, USA) has a VS borehole (downhole, DH) log (red curve) determined by Wentworth et al. (2015) and discretized into 5 m intervals by this study. b Site 2 (Trois Rivieres, Quebec, Canada) has an SCPT log (red curve) (Hayashi and Ito 2008). c Site 3 (La Salle, Italy) has logs determined from borehole (downhole, DH) seismic surveys in holes DH1 (red curve) and DH2 (yellow curve), located about 300 m north and 500 m northwest of the array (site E in Socco et al. 2008). d Site 4 (Dolphin Park, Carson, CA, USA) includes a borehole VS log (red curve) (Reichard et al. 2003)
2.3.1 Site 1: Guadalupe River, San Jose, CA, USA
Site 1 overlaps with the location of drill hole 006S001W26Q001 (longitude − 121.93505°, latitude 37.37770°) (Wentworth et al. 2015; Mankine and Wentworth 2016). Wentworth et al. (2015) and Mankine and Wentworth (2016) interpreted data from the drill hole and showed that a 407-m-thick strata of Quaternary sediments overlies a bedrock of late-Mesozoic Franciscan Group consisting of metamorphic sandstones. The upper 300 m of sediments shows eight cycles of coarse through fine sediments; a coarse unit of gravels at base of cycle 3 (depth range 103–116 m) serves as a marker separating slower VS above and faster VS below, as seen on the shear-wave borehole log of Fig. 2a. The base of the drill hole is at approximately 407 m, which corresponds to data from both geology and the shear-wave log.
The site was surveyed using broadband three-component (3C) intermediate sensors (flat response from 30 s to 50 Hz) deployed in three triangular arrays as shown in Fig. 1a. Inter-station spacings ranged from 17.3 to 300 m. Recording time ranged from 75 min for the small triangle to 30 min for the large triangle, with a sampling interval of 5 ms. Interpretations of microtremor and active surface wave data at this site and similar sites in Central California were published by Boore and Asten (2008).
2.3.2 Site 2: Trois Rivieres, Quebec, Canada
Site 2 has 30 m of soft clays over 30 m of firm overconsolidated clays. A nested triangular array consisting of ten receivers was used in the measurement (Fig. 1b). The maximum inter-station spacing was 50 m. The center of the array was located at longitude − 72.979202° and latitude 46.242401°. A cone penetrating test (CPT) and a seismic cone penetrating test (SCPT) to 29 m depth were performed inside of the array (Hayashi and Ito 2008). The site was surveyed using a 24-channel engineering seismograph and 2 Hz vertical-component geophones. Recording time was approximately 30 min.
2.3.3 Site 3: La Salle, Italy
Site 3 is located in a glacial valley in the foothills of the Alps, containing more than 200 m of firm sands and gravels (Socco et al., 2008). Location of the array center is latitude 45.743119° and longitude 7.077813°. It lies on a wide triangular alluvial fan lying on the west side of the Dora Baltea River. The fan is mainly composed of alluvial deposits (sand, gravel, and stones), slivers, pebbles, and blocks from multiple origins. The general geological evolution can be summarized as a succession of alluvial fan deposits of medium to coarse grain size, overlaid on deposits of a glacial environment. Two drill holes (DH1 and DH2) located respectively 600 m northwest and 400 m north–northwest of the array center provide geological data. The stratigraphic logs, conducted to a depth of about 50 m, show the typical chaotic sequences of gravely soils of alpine alluvial fans, with no marked layering.
Geophones were connected by cabling in two circular evenly-spaced arrays, each consisting of 24 geophones, at radii of 20 m and 37.5 m. The maximum inter-station spacing provided for this blind test is 64 m. Data were collected using a multichannel acquisition system and 48 vertical geophones with a natural frequency of 4.5 Hz. A sampling interval of 16 ms was adopted while recording files with lengths of 32,625 samples. Multiple files provided a total recording time of approximately 1 h.
2.3.4 Site 4: Dolphin Park, Carson, California
Site 4 (near Los Angeles) is situated on geology with a thickness of more than 400 m Holocene sediments. Drill hole Carson-1 (Well 4S/13 W-9H9; longitude − 118.2409°, latitude 33.8369°) and is also known as ROSRINE Site 26 (Reichard et al. 2003). The borehole was previously surveyed with a borehole P-S suspension logger to a depth of 340 m (Fig. 2d). Depth to basement is not known. Microtremor data were acquired using a nested triangular array, with maximum station spacing of 60 m. Sensors were 4.5 Hz vertical geophones that operated at a 4-ms sample rate with approximately 11 min of recording time. Note that although the drill hole and P-S log provided data to 340 m depth, the maximum depth of investigation provided by this microtremor survey is estimated from the lowest usable frequency (1.2 Hz in Fig. 12) and the corresponding Rayleigh wave phase velocity (450 m/s in Fig. 2) is approximated at the 190 m wavelength (using the half-wavelength approximation of Asten and Hayashi 2018). As a consequence of this limitation, analysis of site 4 data in these blind trials is constrained to ~ 100 m maximum resolvable depth (via the VS100 parameter) rather than the maximum geologically known depth of 340 m.
2.4 Defining accuracy relative to a reference model
We use the quality factor or “M index” (M) as estimates of the time-averaged shear-wave velocity of the upper 10, 30, 100, and 300 m. M is an empirical number (range 0 to 9, or 0 to 12), indicating the combined quality of the blind results for MVS10, MVS30, and MVS100 (and MVS300 where applicable) in terms of the fit against the site reference models, such as those representing VS10, VS30, and VS100 (and VS300 if available). To calculate the fit, we use the following equation:
-
If Misfit ≤ 10%, MVSN = 3.
-
If 10% < Misfit ≤ 20%, then MVSN = 2.
-
If 20% < Misfit ≤ 30%, then MVSN = 1.
-
If Misfit > 30% then MVSN = 0.
We define the M index to be:
A perfect score for an interpreted VS profile matching the reference model is given by
where terms in square brackets apply only for VS profiles extending to a depth of 300 m or greater.
Theoretically, an interpretation at sites 2 to 4 yielding scores of 3 each for MVS10, MVS30, and MVS100 will result in an overall perfect score of M = 9. For site 1 only, the greater depth of penetration allows estimation of VS300 and MVS300 and hence a perfect score is M = 12.
2.5 Choice of processing and techniques by analysts
Each of the 34 analysts who contributed to this study used their preferred MAM processing and analysis technique, as well as software (Table 1). The right-hand column of Table 1 indicates whether analysis was made assuming only the fundamental Rayleigh mode (R0) or the effective mode (Re). The majority heavily favored use of SPAC (equivalently, spatially averaged coherency methods) and their various extensions (ESAC-1 and ESAC-2 in Table 1). The terms ESAC-1 and ESAC-2 denote similar methods but implemented in independent software packages. See section Data and Resources for software availability. Only two analysts reported use of frequency wavenumber (FK) methods, an observation not surprising because FK methods are most applicable for arrays with larger numbers of sensors than were provided in phases 1 and 2 of this study. Of the two analysts who used the CC method, one used the time-domain approach while the other did not specify time- or frequency-domain implementation. Although Tsai and Moschetti (2010) suggested that the merger of the SPAC and CC methods will improve results, no analysts reported the application of their recommendation.
3 Lessons from phase 1 (two-station arrays)
Site 3 was the only one of the four sites to have a dominant direction of surface wave propagation, where the direction was approximately normal to the pair of array geophones. This wave propagation information was not provided to participants. The issue of using SPAC methods when the azimuthal spread of wave propagation is narrow was considered by Cho et al. (2008). The basic SPAC method uses only the real part of inter-station complex coherencies but in practice the imaginary part contains information which can assist in recognition of situations where the assumptions behind the SPAC method are not fulfilled. Asten (2006) noted the value of the imaginary part as a quality control tool. Cho (2020) developed a quantitative method for utilizing the imaginary part. However, a priori recognition of narrow-azimuth wave propagation remains difficult, and correction when observations are limited to a single pair of geophones is near-impossible.
Phase 1 site 3 data demonstrated the difficulty of this challenge. Only analyst 1 was close in the attempt to estimate a velocity profile similar to the reference model for phase 1 at this site. However, the analyst did not provide any indication in the form of a discussion item, during the phase 4 re-evaluation of results, as to how this was achieved. Seven of 17 analysts in group 1 submitted results for this phase/site, and Fig. 4 shows three representative interpretations using three different software packages. It is clear that all three were severely in error due to the directional nature of the source. However, the same three representative analysts obtained acceptable (M = 8 or 9) estimates of the VS profile when using data from two nested triangular arrays as supplied for phase 2 at site 3 (see Fig. 5).
Phase 1 site 3. Interpretation of layering from microtremor array method (MAM) models based on a two-station array. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black color denotes the reference model supplied to analysts after all phases of interpretation. Red, yellow, and blue colors denote independent interpretations from analysts #3, #4, and #11. Dashed lines are estimates of uncertainty provided by analyst #11. The VS estimates are severely in error, typically by a factor 2 to 3 for depths greater than 15 m; thus, M indices are not given
Phase 2 site 3. Interpretation of layering from microtremor array method (MAM) models based on a nested pair of three-station triangular arrays. Black color denotes the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from analysts #3, #4, and #11 with corresponding M indices 8, 9, and 8. Dashed lines are estimates of uncertainty provided by analysts #3 and #11
Figures 6, 7, and 8 show selected VS and SS profiles for phase 1 sites 1, 2, and 4. The results are useful, despite the limitations imposed by the use of simple two-station pairs of sensors. Improvements achieved with 2D arrays are discussed in the next section.
Phase 1 site 1. Interpretation of layering from microtremor array method (MAM) models based on a single pair of seismometers. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black color denotes the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from analysts #3, #7, and #8 with corresponding M indices 8, 7, and 5. Dashed lines are estimates of uncertainty provided by each analyst
Phase 1 site 2. Interpretation of layering from microtremor array method (MAM) models based on a single pair of seismometers. Black color denotes the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from analysts #11, #6, and #5 with corresponding M indices 8, 8, and 6. Dashed lines are estimates of uncertainty provided by each analyst
Phase 1 site 4. Interpretation of layering from microtremor array method (MAM) models based on a single pair of seismometers. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black color denotes the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from three analysts #3, #7, and #2 with corresponding M indices 9, 9, and 8. Dashed lines are estimates of uncertainty provided by each analyst
4 Phase 2 and 3 results for arrays on four blind test sites
Phases 2 and 3 of these trials evaluate microtremor methods as a tool for interpreting VS profiles using sparse and dense array data, respectively. Figures 9, 10, and 11 show three of the analysts’ results with the highest M indices (range 8 to 12) for phase 2, where data from a sparse triangular array is interpreted for each of sites 1, 2, and 4. Figure 5 (discussed previously) has the corresponding results for site 3 (M indices range 8 to 9). Within the limitations of the definition of the M index used here, we find that as with phase 1 results, there is no evidence for any one technique/software package being clearly superior.
Phase 2 site 1. Interpretation of layering from microtremor array method (MAM) models based on a sparse array (triangle) of seismometers. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black: the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from three analysts #17, #7 and #3 with corresponding M indices 12, 11, and 8. Dashed lines are estimates of uncertainty by each analyst
Phase 2 site 2. Interpretation of layering from microtremor array method (MAM) models based on sparse array (triangle) of geophones. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black color denotes the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from three analysts #6, #13 and #15 with corresponding M indices of 9, 9, and 9
Phase 2 site 4. Interpretation of layering from microtremor array method (MAM) models based on sparse array (nested triangles) of geophones. Left: the horizontal axis is shear-wave velocity VS. Right: the horizontal axis is slowness SS (inverse of VS). Black: the reference model supplied after all phases of blind interpretation. Red, yellow, and blue colors denote independent interpretations from three analysts #4, #12 and #16 with corresponding M indices 9, 9, and 8. Dashed lines are estimates of uncertainty by analyst #12. Discrepancies in depth estimates below 100 m do not affect values of the M index at this site
The site 2 reference model (Fig. 2b) shows a mild low-velocity layer (LVL) between the 25 and 35 m depth. It is significant that no analyst succeeded in resolving this LVL. This result is in accordance with experience elsewhere where inversion of surface wave data is found to be limited in its ability to resolve shear-wave LVLs. For example, Garofalo et al. (2016; Fig. 13) show similar results for a Grenoble site where a 10-m layer of soft clays underlie a surficial 25 m of harder glacial sediments. Asten and Hayashi (2018) and Hayashi et al. (2021) also provide detailed discussions on the difficulty of resolving LVLs. Farrugia et al. (2016) give examples where the thickness of the LVL (clays) is of similar or greater thickness than the higher-velocity overburden (hard limestones in their case); for such cases, surface wave data do prove to be effective in resolving the LVL.
Site 4 (Fig. 11) shows large discrepancies in VS estimates below the 100-m depth. As noted in the site description, the sensors used at this site were 4.5 Hz geophones and the most optimistic estimate for depth penetration in this blind study is on the order of 190 m deep. In order to make useful comparisons with the reference model, we restrict depth estimates to 100 m, while noting that the adjacent drill hole and P-S log provided independent VS data to the 340 m depth.
A clear outcome from the phase 1 and phase 2 results for site 3 was the demonstration of a major risk with the two-station method when energy is directional; it is difficult (or impossible) to recognize the problem of narrow-azimuth microtremor wave propagation oblique to the seismic line when data are limited to a single pair of seismometers. In such cases, interpretations are likely to be very misleading.
Interpreted VS- and SS-depth profiles for phase 3 interpretations at sites 1 to 4 are included as supplementary items (Figs. S5 to S12) in the electronic Supplementary Information of this article. Accuracy of interpretations relative to the reference models (combining experience from all analysts) is discussed in a later section.
5 Frequency bandwidth achieved with different processing techniques
Bandwidths achieved in Rayleigh wave dispersion analyses are an important factor in determining VS data over a wide range of depths. Figure 12 shows a summary of bandwidths achieved for phases 1, 2, and 3 at sites 1–4. As expected, the bandwidth generally increased as the number of seismometers/geophones in the array increased but equally important is the fact that bandwidth was affected by the choice of processing methodology. Orange bands in Fig. 12 highlight the analyst numbers which achieved optimum high and low frequencies. In principle, the low-frequency cut-off will be influenced by the geophone’s natural frequency but for sites 2–4 where geophones were used, and the useful low-frequency limit achieved was one or two octaves below the geophone resonant frequency. A wide range of public-domain, commercial, and in-house software packages were used by the 17 analysts of group 1, but if we apply a test of consistency over at least three of the four sites, two unrelated techniques proved most effective in terms of bandwidth achieved: the ESAC and the multimode SPAC (MMSPAC) techniques for direct fitting of coherency spectra (orange bands on Fig. 12). CC (SI) methods also proved very effective for obtaining high-frequency data, but less so for low-frequency data. This limitation at low frequencies is a consequence of the fact that the time-domain approach imposes a restriction whereby velocities of propagating waves cannot be determined for wavelengths greater than half (or in practice a third) of the maximum inter-station distance (Bensen et al. 2007; Luo et al. 2015, 2016). By contrast, frequency-domain methods such as SPAC and its variants are effective where wavelengths are as long as some multiple of the array aperture (Asten and Hayashi 2018).
Frequency ranges achieved by analysts in the blind trial using passive data. Note site 1 includes low frequencies not accessible by field instruments used at sites 2–4. Blue and red colors show useful lower and upper frequencies achieved by each analyst. Frequency limits where available in reference data are shown at analyst #0. Results for phases 1, 2, and 3 are identified by fractional shifts of the x-coordinate, thus Analyst#n (where n = 1, 2, …26) results for three phases are plotted at x-coordinates n.0, n.2, and n.4 respectively. Group 2 analysts (#18 to #34) provided interpretations for sites 2 and 4 but only two (analysts #24 and #26) provided dispersion curves with frequency ranges. The orange bands help identify software packages giving the best high or low frequencies or frequency bandwidth. Methods used as listed in Table 1: analyst #3 and #16 used ESAC-1; analyst #4 used ESAC-2; analyst #7 and #8 used CC; analyst#11 used MMSPAC (direct fitting); analyst#14 used Geopsy
6 Accuracy of interpretation in phases 1, 2, and 3
6.1 Accuracy of interpretation by phase and site
The M index provides a useful basis for comparison of a range of differing interpretations by a group of analysts. Figure 13 shows the quality of analyst results, averaged over all analysts, for each of the three phases and each of the four sites. A perfect score is M = 9 for sites 2–4 (depths of interest to approximately 100 m), or M = 12 for site 1 (depths of interest to 400 m). For sites 2–4, it is apparent that there is little improvement in the M indices when using arrays of greater complexity than the phase 2 sparse triangular arrays. Results for site 1 show improvement using the phase 3 arrays, illustrated by comparing Fig. 9 (phase 2 site 1) with Fig. S5 (phase 3 site 1) where it is obvious that the uncertainty ranges of slowness SS estimates decrease when using the phase 3 data. This improvement is probably because resolution of the range of depths of interest from 5 to 400 m requires the full range of array apertures (triangle side lengths are 30, 100, and 300 m).
While the M index is useful, it does not detect discrepancies between the reference and analysts’ models at depths below 100 m (sites 2–4) or below 300 m (site 1). Figure 11 shows where two curves describe departures from the reference curve below 100 m depth but still retain high M indices. Such discrepancies are especially evident where cross-correlation methods are used, which prove effective at high frequencies but are limited at low frequencies (long wavelengths) as discussed in the previous section. We note such limitations in VS and SS versus depth curves for results by analysts #8 and #7 shown in Figs. S6 and S12, respectively, in the electronic Supplementary Information of this article.
We have used the M index because it reflects soil properties over thicknesses from 10 to 100 m (or 300 m). However, as an example of comparison with the simpler compilation of VS30 and classification into site class (BSSC 2003), the Supplementary section contains Tables S1 to S4 which are compilations of phase 3 VS30 and site class for the four sites 1 to 4. These tables show results for all participating group 1 and group 2 analysts. For sites 2 and 3, the proportion of analysts estimating a VS30 within 10% of the reference model is about two thirds; for sites 1 and 4, the corresponding proportion is about one third of estimates within 10% of the reference model. There is no obvious reason in terms of site characteristics or analyst grouping for this systematic difference between site results.
6.2 Accuracy of interpretation by phase and analyst
Figure 14 shows the quality of analysts’ results averaged over all sites, for each of the most successful ten analysts; it also indicates the range of software packages used and does not indicate any packages performing superior than another. For site 1 only, the quality of fit also includes estimates of VS300; thus, analysts #3 (dark blue line) and #4 (orange line) were able to achieve indices > 9.
For the top six analysts, it is again apparent that there is little improvement in accuracy relative to the reference models from phase 2 (sparse triangular arrays on all sites) to phase 3 (denser arrays).
6.3 Accuracy of interpretation of depth to layer interfaces
The quality of results discussed previously (shown in Figs. 13 and 14) is determined by the M index which describes accuracy of estimates of VS averaged as VS10, VS30, VS100, and VS300. These parameters are of particular importance in earthquake hazard studies (BSSC 2003; EC8 2004). Also, a proposed new earthquake hazard code for Europe requires estimates of depth to basement as well as averaged VS (Pitilakis et al. 2019). Site 1 has a borehole P-S suspension log which provides clear evidence of two important interfaces (VS contrasts) in the depth range from 100 to 120 m and at the basement depth of 407 m. This site thus provides opportunity for an assessment of the utility of MAM for depth estimation of interfaces having moderate VS contrasts.
We consider an acceptance criterion on the of order 40% misfit for the upper interface and 15% for the deep interface (pre-Quaternary basement), shown with the VS reference model (Fig. 15 and Table 2). The VS borehole log for site 1 (Fig. 2a) and the geological log in Wentworth et al. (2015) show that the boundary is not a clear change in rock type but is probably spread over depths between 90 to 160 m. Detailed sensitivity studies by the supplier of the microtremor data using the reference model suggests the effective VS boundary to be 120 ± 40 m. The deep boundary of the geological contact in the drill hole is 407 m, but sensitivity analyses of the passive surface wave data suggest the effective boundary to be 390 ± 50 m. Note that because this deeper boundary lies below 300 m, success in achieving a high M index, as shown in Figs. 6 and 9 and in Supplementary Information Figs. S5–S6, is not necessarily reflected in the successful estimation of the boundary depth.
Black line denotes the reference shear-wave velocity (slowness) model for site 1, with vertical brown bars denoting acceptable depth estimate error ranges for an upper interface at 120 ± 40 m and lower interface at 390 ± 50 m. (The actual depth of metamorphic rock basement in a drill hole on the edge of the large triangular seismic array was 407 m.) The horizontal axis is slowness SS (inverse of VS)
We use these boundaries and uncertainties to tabulate the rate of success by analysts in picking one or both VS contrasts. Table 2 shows the results compiled from interpretations of phase 1, 2, and 3 data submitted by up to 16 analysts. The three analysts in phase 3 that show major layer boundaries within the acceptable ranges shown on Fig. 15, for both interfaces, used three different software packages. These were analyst #4 using ESAC-2 for phase 2 and analysts #5, #10, and #3 (in-house SPAC; SPAC Genetic Algorithm, GA; and ESAC-1) for phase 3. Thus, there is no obvious indication of a preferred software package. It is notable that the success rate in correctly interpreting these two known boundaries from passive microtremor data at site 1 is on the of order 20% with phase 3 data and a poor 10% for the phase 1 and 2 sparse array data. It is reasonable to draw the conclusion that where depths to VS boundaries are important, as distinct from average velocities, then the use of dense arrays such as multiple triangles is a necessary part of the survey design.
The role of microtremor horizontal-to-vertical spectral ratios (mHVSR) was not discussed by most analysts in these trials, presumably because only one site of the four provided 3C data (Molnar et al. 2018). Two analysts noted using mHVSR on site 1 to determine the fundamental site frequency which was then used to guide the inversion process. Others may have done so without comment. Figure 16 shows the modeled ellipticity of Rayleigh modes for the reference model of site 1 as used in Figs. 2 and 3. This modeled ellipticity is similar to the mHVSR for observed data except that mHVSR curves are in general shifted to higher values due to the inclusion of Love wave energy in observed microtremor signals. It is clear that the metamorphic basement at model depth 390 m (or based on drilled depth of 407 m) produces a strong mHVSR peak at 0.35 Hz in observed phase 1–3 data, which to some analysts represented a strong indicator of a layer boundary implying a high contrast in VS. (Analysts were not given the geological data until phase 4.) The frequency of the peak is clearly sensitive to basement depth on any modeling study of Rayleigh wave ellipticity. Multiple case histories have likewise used strong observed mHVSR peaks to guide the choice of a basement or other strong VS contrast (Asten et al. 2014; Macau et al. 2015). Inversion of mHVSR data combined with SPAC data was first described by Arai and Tokimatsu (2005) and Parolai et al. (2005); Piña-Flores et al. (2017) also provided examples. García-Jerez et al. (2016) described computer code for such a joint inversion, and the open-access surface wave interpretation Geopsy package also provides this capability (Wathelet et al. 2020).
Full 3C array processing of microtremor data using SPAC methods has been described by Kohler et al. (2007) and Puglia et al. (2011) and FK methods used by Fäh et al. (2008) and Poggi et al. (2017). In this study, two analysts reported experimenting with 3C processing with site 1 data. One used 3C processing in each phase of the site 1 study, with inclusion of both Love and Rayleigh wave dispersion data in the inversion for VS models. This analyst was one of the six in Table 2 who obtained a correct estimation of depth to the shallower interface of Fig. 15, but not for the deeper interface. The other analyst who used 3C processing noted some issues with orientation of seismometers to magnetic north versus position coordinates referenced to geographic north (magnetic declination at the site is 14° east). Additional processing by the analyst, described during phase 4 discussions, was successful in extracting both Love and Rayleigh wave dispersions curves through FK processing, but the recording time of 30 min for the 300-m array were apparently too short to allow definitive results.
We draw the conclusion (limited to site 1 only) in these blind trials that full 3C array processing did not demonstrate an obvious practical advantage over conventional SPAC processing with or without mHVSR information. Given the limitation that only one of the four sites had available 3C data, this cannot be presented as a general conclusion. However, it is consistent with a comment by Asten and Hayashi (2018) regarding the blind study described by Garofalo et al. (2016), which noted that four out of 14 analysts in that study made use of 3C array processing but no obvious improvement in the inversion to a VS model was noted for results from those four. It therefore appears that the merits of 3C array processing in such microtremor studies remain a question for further study.
7 Observations from phase 4 discussion by analysts
Site 4 and site 3 are regarded as the easiest and most difficult sites, respectively. This can be attributed to the fact that site 4 is near-ideal in array design and distribution of microtremor sources, while site 3 has a highly directional wave source. Two recurring majority themes in analyst feedback for all sites are (a) the advantages of the use of multiple arrays (i.e., dense arrays or multiple triangular or circular arrays) for higher confidence in microtremor-based interpretations and (b) highlights of the dangers of using two-station SPAC analysis where the character of azimuthal distribution of wave energy is not known. By contrast, there are opposite conclusions by some analysts to the effect that a sparse array can be reliable, and two-station SPAC is demonstrated to be useful (except for site 3). It should be noted that the view of a majority of analysts on the need for multiple arrays is not consistent with the observation in Fig. 13, which shows that at three out of four sites, the addition of multiple arrays (phase 3) produces a change in the all-analyst average M index of less than one unit. The exception (site 1) was a rare instance where the additional array was a small array which gives significantly improved resolution of layers in the upper 100 m. It is reasonable to conclude that where the basic requirement is for VS10, VS30, or VS100 information, the sparse arrays are sufficient for these time-averaged types of VS calculations. It follows that where earthquake hazard site class specification (without layer thickness detail) is required, sparse arrays are sufficient.
Three additional salient points from the phase 4 analyst comments are as follows:
-
A sparse array will typically deliver a narrower band of frequencies in the interpreted dispersion curve, which makes identification of the dominant Rayleigh wave mode more difficult. This can lead to errors in mode identification and subsequent errors in VS profile estimation.
-
3C data at sites 2, 3, and 4 would allow mHVSR analyses and improve VS estimates at depth. Use of FK methods tends to overestimate phase velocities at low frequencies, and mHVSR data can assist in obtaining correct estimates of VS at the greater depths.
-
Active-source surface wave data (e.g., MASW described by Park et al. 1999 and Xia et al. 2000), which is often richer in high-frequency information than passive data, should be included in order to improve resolution of near-surface data.
Regarding the second point (above), these blind trials did not produce any example where the use of 3C array processing (for both Rayleigh and Love waves) improved the interpretation, although advantages of 3C processing have been previously discussed by multiple authors (Poggi and Fäh 2010; Wathelet et al. 2018). The third point is not necessarily valid for all interpretation methodologies; when in consideration of Fig. 12 and associated discussions contributed by the analysts, the take-away point seems to indicate that the useful high-frequency limit of dispersion curve data may be algorithm dependent. It is therefore arguable that optimum processing of passive microtremor data may access high-frequency data and thus provide sufficient resolution so as to negate the need for supplementary active seismic surface wave surveys.
8 Use of the blind trial for graduate student training
This COSMOS blind trial exercise was also used as a graduate student training exercise at the University of Western Ontario (UWO) by Sheri Molnar. A team of four was assembled with each member designated a particular site. The team composition included Molnar as the expert-trainer (site 4), one PhD student (site 2), and two MSc students (Sites 1 and 3). All three students had been trained by their supervisor (S. Molnar) in field data acquisition and processing of ambient vibration and surface wave array data using the Geopsy software during a 2-week training course. Sites were assigned blindly to each team member by the supervisor based on their experience, using the assumption that site complexity may increase sequentially from site 1 to site 4.
The team began the blind trial at phase 2 which included the three-sensor array data and comprised the datasets of two team members. Each team member analyzed the blind trial phase 2 array data independently for their assigned site, including picking of fundamental-mode Rayleigh wave phase velocity estimates and inversion. The Geopsy software was used by all team members to calculate modified SPAC (MSPAC) dispersion estimates (SPAC curves are reviewed in selecting dispersion estimates but not used directly in the inversion) which were validated by comparisons with high-resolution FK dispersion estimates. Student team members then discussed their phase 2 dispersion picks, trials in model parameterization (not submitted to the trial), and inverted models with their supervisor prior to submission of an optimal VS profile. For site 1, the mHVSR was also calculated and inverted in phase 2 (no dispersion estimates were obtained). In phase 3, dispersion estimates were jointly inverted with the mHVSR data. Each team member repeated their independent dispersion assessments and inversions for their trial site with full array phase 3 data, in which results were reviewed by the supervisor prior to trial submission. The full array phase 3 data provided dispersion estimates at site 1, expanded the selected dispersion frequency bandwidth for site 3, and only provided confidence through consistency in the selected phase 2 dispersion estimates for sites 2 and 4.
Following the release of phase 4 site location and independent geophysical information, each team member evaluated their dispersion estimates and inverted VS model(s) in comparison with the phase 4 “ground truth” data. The four-member team discussed results in comparison to phase 4 information and shared lessons learned in regard to accuracy and frequency bandwidth of their dispersion estimates. Team members consistently obtain correct dispersion estimates in the mid-frequency dispersion curve range but tend to under- or overestimate dispersion estimates in the bottom (low frequencies) or top (high frequencies) of the curve. Overall, the blind trial provided empirical datasets with external expert-reviewed answers. This formed an important empirical benchmark exercise for the UWO team to test their skills in dispersion curve interpretation.
9 Discussion and conclusions
We conducted a blind trial to estimate VS profiles from data recorded by MAM and found that, subject to a sufficient azimuthal distribution of seismic noise sources, the use of sparse arrays is sufficient for accurate estimates of VS10, VS30, VS100, or VS300. Guidelines on the choice of array dimensions and desirable sensor bandwidth are given in reviews by Foti et al. (2018), Asten and Hayashi (2018), and Hayashi et al. (2021). We have introduced the M index (based on time-averaged shear-wave velocities over multiple depth ranges) as a tool for quantitatively comparing results from multiple analysts. No single processing or analytical technique is identified as optimal and no software packages were found to be superior. We found that the best six analyst results in Fig. 14 used five different techniques/software packages.
The two-station method does not directly address the critical factor relating to whether the energy source for microtremor wave propagation is directional. Thus, the two-station method should only be used when azimuthally distributed sources are known to exist. This cautionary point will also apply if linear or quasi-linear arrays are used. For the majority of sites in this study, azimuthal distribution of sources was in fact sufficient such that a two-station sparse array proved adequate for reliable estimation of averaged shear-wave velocities VS10, VS30, and VS100.
With respect to processing techniques, the widest usable bandwidths of Rayleigh wave dispersion curves of microtremor data, as determined in these blind trials, was obtained with the ESAC method and with the MMSPAC method based on direct fitting of coherency spectra.
Estimation of depth to known interfaces is a significantly greater challenge than estimation of VS10, VS30, and VS100. We find that the M index is not a useful measure of accuracy for estimates of depth to interfaces. A comparison of 16 analyst’s estimations of depth to known interfaces at site 1 showed that only about 50% of analysts were successful in estimating depth of one or both of the two known interfaces and only 10% of analysts in phases 1 and 2; only 20% in phase 3 succeeded in estimating both depths correctly. There were four successful estimations of depth for the pair of interfaces (Table 2, phase 2 plus phase 3) and these estimates used four different software packages. It is reasonable to conclude that analyst skill and experience may be a stronger factor than software choice in these comparisons. Where quantitative depth to interfaces is required, it is clear that arrays denser than the simple sparse arrays are to be recommended.
Analyses using mHVSR were found to assist in defining depth to the deep interface at one site (site 1). Where depth to interfaces (as distinct from averaged shear-wave velocities) is required, it is clear that acquisition of some 3C data for allowing HVSR processing, is to be recommended. The low success rate in defining depths to interfaces in this limited study suggests there is a need for development of clear guidelines for interpreters.
Only one of the sites included 3C data but only two analysts reported use of full 3C array processing, including Love wave dispersion analysis. We thus cannot draw any defensible conclusions from these blind trials regarding the usefulness of combined Rayleigh and Love wave dispersion analysis as applied to arrays of the types used in this study, and the subject remains an area for further research.
Availability of data, material, and codes
Microtremor array data used in this blind study, instrument specifications, relevant site geology, and drill hole logs, are available in Asten et al. (2021). The data are arranged in the four phases of data released in this project, thus facilitating its use as a teaching resource.
Software packages implementing methods listed in Table 1 are available as follows:
Geopsy: http://www.geopsy.org/, also see Wathelet et al. (2020)
Grilla: http://www.moho.world/download
SeisImager: http://www.geometrics.com/software/seisimager-sw/
Surface Plus: http://www.geogiga.com
Other software items noted in Table 1 are custom in-house codes. Test sites and results of selected Phase 3 interpretations of VS versus depth curves are in a Supplementary Information electronic file “Supplementary Figures and Tables S1 to S12.pdf”.
References
Aki K (1957) Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull Earthqu Res Inst Univ Tokyo 35(3):415–456
Arai H, Tokimatsu K (2005) S-wave velocity profiling by joint inversion of microtremor dispersion curve and horizontal-to-vertical (H/V) spectrum. Bull Seism Soc Am 95(5):1766–1778. https://doi.org/10.1785/0120040243
Asten MW (2006) On bias and noise in passive seismic data from finite circular array data processed using SPAC methods. Geophys 71:V153–V162. https://doi.org/10.1190/1.2345054
Asten MW, Hayashi K (2018) Application of the spatial auto-correlation method for shear-wave velocity studies using ambient noise. Surv Geophys 39:633–655. https://doi.org/10.1007/s10712-018-9474-2
Asten MW, Askan A, Ekincioglu EE, Sisman F, Ugurhan B (2014) Site characterization in northwestern Turkey based on SPAC and HVSR analysis of microtremor noise. Expl Geophys 45:74–85. https://doi.org/10.1071/EG12026
Asten MW, Yong A, Foti S, Hayashi K, Martin A, Stephenson WJ, Cassidy J, Coleman J (2018a) An assessment of array types and processing algorithms for microtremor observations through the COSMOS blind trials – phase 1 and phase 2 results. European Seismological Conference, Valetta, Malta, Sept 2018
Asten MW, Yong A, Foti S, Hayashi K, Martin A, Stephenson WJ, Cassidy J, Coleman J (2018b) An assessment of array types and processing algorithms for microtremor observations, via the COSMOS Blind Trials, Abstract #352019. American Geophysical Union Fall Meeting, Washington DC
Asten MW, Yong A, Foti S, Hayashi K, Martin A, Stephenson WJ, Cassidy J, Coleman J (2019a) An assessment of array types and processing algorithms for microtremor observations, via the COSMOS Blind Trials, Abstract #352019. Seismological Society of America Meeting – COSMOS Workshop, Seattle, April 2019
Asten MW, Yong A, Foti S, Hayashi K, Martin A, Stephenson WJ, Cassidy J, Coleman J (2019b) An assessment of array types and processing algorithms for microtremor observations, via the COSMOS Blind Trials. Expanded Abstract 184, Australian Exploration Geoscience Conference, Perth WA, Sept 2019
Asten MW, Stephenson WJ, Yong A, Foti S, Hayashi K, Martin A, Nigbor R (2021) Data release for: an assessment of uncertainties attributed by analysts, array types and processing algorithms for microtremor observations, using the phased 2018 COSMOS Blind Trials. U.S. Geological Survey data release, https://doi.org/10.5066/P9IA54PL
Bensen GD, Ritzwoller MH, Barmin MP, Levshin AL, Lin F, Moschetti MP, Shapiro NM, Yang Y (2007) Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys J Int 169:1239–1260
Boore DM, Asten MW (2008) Comparisons of shear-wave slowness in the Santa Clara Valley, California, using blind interpretations of data from invasive and non-invasive methods. Bull Seism Soc Am 98:1983–2003. https://doi.org/10.1785/0120070277
Borcherdt RD (1994) Estimates of site-dependent response spectra for design (methodology and justification). Earthq Spectra 10:417–453
Brown L, Boore DM, Stokoe KH (2002) Comparison of shear-wave slowness profiles at 10 strong-motion sites from noninvasive SASW measurements and measurements made in boreholes. Bull Seism Soc Am 92:3116–3133
BSSC (2003) NEHRP recommended provisions for seismic regulations for new buildings and other structures, part 1: provisions, FEMA 368. Federal Emergency Management Agency, Washington, D.C.
Campillo M, Paul A (2003) Long-range correlations in the diffuse seismic coda. Science 299:547–549
Campillo M, Roux P (2015) Crust and lithospheric structure: seismic imaging and monitoring with ambient noise correlations. Treatise Geophys . https://doi.org/10.1016/B978-0-444-53802-4.00024-5
Capon J (1969) High resolution frequency wavenumber spectrum analysis. Proc IEEE 57:1408–1418
Cho I (2020) Two-sensor microtremor SPAC method: potential utility of imaginary spectrum components. Geophys J Int 220:1735–1747. https://doi.org/10.1093/gji/ggz454
Cho I, Tada T, Shinozaki Y (2008) Assessing the applicability of the spatial autocorrelation method: a theoretical approach. J Geophys Res 113:B06307. https://doi.org/10.1029/2007JB005245
Cornou C, Ohrnberger M, Boore DM, Kudo K, Bard P-Y (2007) Derivation of structural models from ambient vibration array recordings: results from an international blind test. In: Bard P-Y, Chaljub E, Cornou C, Gueguen P (eds) Third international symposium on the effects of surface geology on seismic motion (ESG2006), Grenoble, France, 30 August–1 September 2006, vol 1. LCPC, Paris, pp 1127–1215
EC8 (2004) Eurocode 8: design of structures for earthquake resistance - part 1: general rules, 655 seismic actions and rules for buildings, EN 1998‐1, Draft 6, Doc CEN/TC250/SC8/N335. European Committee for Standardization (CEN), Brussels, Belgium. http://www.cen.eu/cenorm/homepage.htm
Ekstrom G, Abers GA, Webb SC (2009) Determination of surface-wave phase velocities across USArray from noise and Aki’s spectral formulation. Seismol Res Lett 36:L18301. https://doi.org/10.1029/2009GL039131
Fäh D, Stamm G, Havenith H-B (2008) Analysis of three-component ambient vibration array measurements. Geophys J Int 172:199–213. https://doi.org/10.1111/j.1365-46X.2007.03625.x
Farrugia D, Paolucci E, D’Amico S, Galea P (2016) Inversion of surface wave data for subsurface shear wave velocity profiles characterized by a thick buried low-velocity layer. Geophys J Int 206:1221–1231. https://doi.org/10.1093/gji/ggw204
Foti S, Hollender F, Garofalo F, Albarello D, Asten MW, Bard P-Y, Comina C, Cornou C, Cox B, Di Giulio G, Forbriger T, Hayashi K, Lunedei E, Martin A, Mercerat D, Ohrnberger M, Poggi V, Renalier F, Sicilia D, Socco V (2018) Guidelines for the good practice of surface wave analysis: a product of the InterPACIFIC project. Bull Earthq Eng 16:2367–2420. https://doi.org/10.1007/s10518-017-0206-7
García-Jerez A, Piña-Flores J, Sánchez-Sesma FJ, Luzón F, Perton M (2016) A computer code for forward calculation and inversion of the H/V spectral ratio under the diffuse field assumption. Comp Geosci 97:2016
Garofalo F, Foti S, Hollender F, Bard P-Y, Cornou C, Cox BR, Ohrnberger M, Sicilia D, Asten MW, DiGiulio G, Forbriger T, Guillier B, Hayashi K, Martin A, Matsushima S, Mercerat D, Poggi V, Yamanaka H (2016) InterPACIFIC project: comparison of invasive and non-invasive methods for seismic site characterization. Part I: intra-comparison of surface wave methods. Soil Dynam Earthq Eng 82:222–240
Hayashi K, Ito Y, Tanaka M (2008) Application of phase velocity analysis to determine S-wave velocity profile in seismic cone penetrating test. Zenchiren, Technical e-forum 2008, (in Japanese)
Hayashi K, Asten M, Stephenson W, Cornou C, Hobiger M, Pilz M, Yamanaka H (2021) Microtremor array method using SPAC analysis of Rayleigh-wave data. J Seismol. https://doi.org/10.1007/s10950-021-10051-y
Herrmann RB (2013) Computer programs in seismology: an evolving tool for instruction and research. Seismol Res Lett 84:1081–1088. https://doi.org/10.1785/0220110096
Ikeda T, Matsuoka T, Tsuji T, Hayashi K (2012) Multimode inversion with amplitude response of surface waves in the spatial autocorrelation method. Geophys J Int 190:541–552. https://doi.org/10.1111/j.1365-246X.2012.05496.x
Kohler A, Ohrnberger M, Scherbaum F, Wathelet M, Cornou C (2007) Assessing the reliability of the modified three-component spatial autocorrelation technique. Geophys J Int 168:779–796. https://doi.org/10.1111/j.1365-246X.2006.03253.x
Luo Y, Yang Y, Xu Y, Xu H, Zhao K, Wang K (2015) On the limitations of interstation distances in ambient noise tomography. Geophys J Int 201:652–661
Luo S, Luo Y, Zhu L, Xu Y (2016) On the reliability and limitations of the SPAC method with a directional wavefield. J Appl Geophys 126:172–182. https://doi.org/10.1016/j.jappgeo.2016.01.0230926-9851
Macau A, Benjumea B, Gabàs A, Figueras S, Vilà M (2015) The effect of shallow quaternary deposits on the shape of H/V spectral ratio. Surv Geophys 36:185–208. https://doi.org/10.1007/s10712-014-9305-z
Mankine EA, Wentworth CM (2016) Paleomagnetic record determined in cores from deep research wells in the Quaternary Santa Clara basin, California. Geosphere 12:35–57. https://doi.org/10.1130/GES01217.1
Mital U, Ahdi S, Herrick J, Iwahashi J, Savvaidis A, Yong A (2021) A probabilistic framework to model distributions of VS30. Bull Seism Soc Am. https://doi.org/10.1785/0120200281
Molnar S, Cassidy JF, Castellaro S, Cornou C, Crow H, Hunter JA, Matsushima S, Sánchez-Sesma FJ, Yong A (2018) Application of microtremor horizontal-to-vertical spectral ratio (MHVSR) analysis for site characterization: state of the art. Surv Geophys 39:613–631. https://doi.org/10.1007/s10712-018-9464-4
Park CB, Miller RD, Xia J (1999) Multichannel analysis of surface waves. Geophys 64:800–808
Parolai S, Picozzi M, Richwalski SM, Milkereit C (2005) Joint inversion of phase velocity dispersion and H/V ratio curves from seismic noise recordings using a genetic algorithm, considering higher modes. Geophys Res Lett 32:L01303. https://doi.org/10.1029/2004GL021115
Pastén C, Sáez M, Ruiz S, Leyton F, Salomón J, Poli P (2016) Deep characterization of the Santiago Basin using HVSR and cross-correlation of ambient seismic noise. Eng Geol 201:57–66
Piña-Flores J, Perton M, García-Jerez A, Carmona E, Luzón F, Molina-Villegas JC, Sánchez-Sesma FJ (2017) The inversion of spectral ratio H/V in a layered system using the diffuse field assumption (DFA). Geophys J Int 208:577–588. https://doi.org/10.1093/gji/ggw416
Pitilakis K, Riga E, Anastasiadis A, Fotopoulou S, Karafagka S (2019) Towards the revision of EC8: proposal for an alternative site classification scheme and associated intensity dependent spectral amplification factors. Soil Dynam Earthq Eng 126:105137. https://doi.org/10.1016/j.soildyn.2018.03.030
Poggi V, Fäh D (2010) Estimating Rayleigh wave particle motion from three-component array analysis of ambient vibrations. Geophys J Int 180:251–267. https://doi.org/10.1111/j.1365-246X.2009.04402.x
Poggi V, Burjanek J, Michel C, Fäh D (2017) Seismic site-response characterization of high-velocity sites using advanced geophysical techniques: application to the NAGRA-Net. Geophys J Int 210:645–659. https://doi.org/10.1093/gji/ggx192
Puglia R, Tokeshi K, Picozzi M, D’Alema E, Parolai S, Foti S (2011) Interpretation of microtremor 2D array data using Rayleigh and Love waves: the case study of Bevagna (central Italy). Near Surf Geophys 9:529–540. https://doi.org/10.3997/1873-0604.2011031
Reichard EG, Land M, Crawford SM, Johnson T, Everett RR, Kulshan TV, Ponti DJ, Halford KJ, Johnson TA, Paybins KS, Nishikawa T (2003) Geohydrology, geochemistry, and ground-water simulation-optimization of the Central and West Coast Basins, Los Angeles County, California. U.S. Geological Survey Water-Resources Investigations Report 03–4065
Shapiro NM, Campillo M (2004) Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys Res Lett 31:L07614. https://doi.org/10.1029/2004GL019491
Shapiro NM, Campillo M, Stehly L, Ritzwoller MH (2005) High-resolution surface-wave tomography from ambient seismic noise. Science 307:1615–1618
Socco LV, Strobbia C (2004) Surface wave method for near-surface characterization: a tutorial. Near Surf Geophys 2:165–185
Socco LV, Boiero D, Comina C, Foti S, Wisén R (2008) Seismic characterization of an Alpine site. Near Surf Geophys 6:255–267
Thompson EM, Baise LG, Kayen RE, Guzina BB (2009) Impediments to predicting site response: estimation and modeling implications. Bull Seism Soc Am 99:2927–2949
Tsai VC, Moschetti M (2010) An explicit relationship between time-domain noise correlation and spatial autocorrelation (SPAC) results. Geophys J Int 182:454–460. https://doi.org/10.1111/j.1365-246X.2010.04633.x
Wapenaar K (2004) Retrieving the elastodynamic Green’s function of an arbitrary inhomogeneous medium by cross correlation. Phys Rev Lett 93:1–4
Wapenaar K, Draganov D, Snieder R, Campman X, Verdel A (2010a) Tutorial on seismic interferometry: part 1—basic principles and applications. Geophys 75:75A195-75A209
Wapenaar K, Slob E, Snieder R, Curtis A (2010b) Tutorial on seismic interferometry: part 2—underlying theory and new advances. Geophys 75:75A211-75A227
Wathelet M, Guillier B, Roux P, Cornou C, Ohrnberger M (2018) Rayleigh wave three-component beamforming: signed ellipticity assessment from high-resolution frequency-wavenumber processing of ambient vibration arrays. Geophys J Int 215:507–523. https://doi.org/10.1093/gji/ggy286
Wathelet M, Chatelain JL, Cornou C, Giulio GD, Guillier B, Ohrnberger M, Savvaidis A (2020) Geopsy: a user-friendly open source tool set for ambient vibration processing. Seismol Res Lett 91:1878–1889. https://doi.org/10.1785/0220190360
Wentworth CM, Jachens RC, Williams RA, Tinsley JC, Hanson RT (2015) Physical subdivision and description of the water-bearing sediments of the Santa Clara Valley, California. U.S. Geological Survey Scientific Investigations Report 2015–5017, 73 pp. https://doi.org/10.3133/sir20155017
Xia J, Miller RD, Park CB, Hunter JA, Harris JB (2000) Comparing shear-wave velocity profiles from MASW with borehole measurements in unconsolidated sediments, Fraser River Delta, B.C., Canada. J Environ Eng Geophys 5:1–13. https://doi.org/10.4133/JEEG5.3.1
Yong A (2016) Comparison of measured and proxy-based VS30 values in California. Earthqu Spectra 32:171–192
Acknowledgements
The Consortium of Organizations for Strong Motion Observation Systems (COSMOS) consisting of the US Geological Survey, the Geological Survey of Canada, and a group of North American power companies, consisting of Southern California Edison and Pacific Gas and Electric, identified the need for these blind trials, for these guidelines for best-practices and provided funding and encouragement to facilitate the project. This material is also based upon work supported by the US Geological Survey under Cooperative Agreement No. G17AC00058. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the opinions or policies of the US Geological Survey. Mention of trade names or commercial products does not constitute their endorsement by the US Geological Survey. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the US Government, the Canadian Government, or COSMOS. This paper is Natural Resources of Canada contribution number 20200665.
Open Access publication fees for this paper were directly funded by COSMOS.
Array data for site 1 was supplied by the US Geological Survey. Data for site 2 was acquired and supplied by the Port and Airport Research Institute, Japan.
Data for site 3 was acquired for the Interreg III B—Alpinespace—Sismovalp project: “Seismic hazard and alpine valley response analysis” funded by the European Union.
The borehole survey at site 4 was conducted as part of the ROSRINE project funded by the US National Science Foundation, Pacific Earthquake Engineering Center, California Department of Transportation, and other organizations. The microtremor array data was acquired in 2003 as an internally funded research project by GEOVision, Inc.
The authors thank two anonymous reviewers for valuable comments and also thank the following US Geological Survey (USGS) colleagues for many remarks and recommendations: Annemarie Baltay and USGS reviewers Jack Odum and Sean Ahdi. Final USGS reviews by Shane Detweiler and Michael Diggles improved this article.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Asten, M.W., Yong, A., Foti, S. et al. An assessment of uncertainties in VS profiles obtained from microtremor observations in the phased 2018 COSMOS blind trials. J Seismol 26, 757–780 (2022). https://doi.org/10.1007/s10950-021-10059-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10950-021-10059-4