Reliable workflow for inversion of seismic receiver function and surface wave dispersion data: a “13 BB Star” case study

Abstract

Non-linear inverse problems arising in seismology are usually addressed either by linearization or by Monte Carlo methods. Neither approach is flawless. The former needs an accurate starting model; the latter is computationally intensive. Both require careful tuning of inversion parameters. An additional challenge is posed by joint inversion of data of different sensitivities and noise levels such as receiver functions and surface wave dispersion curves. We propose a generic workflow that combines advantages of both methods by endowing the linearized approach with an ensemble of homogeneous starting models. It successfully addresses several fundamental issues inherent in a wide range of inverse problems, such as trapping by local minima, exploitation of a priori knowledge, choice of a model depth, proper weighting of data sets characterized by different uncertainties, and credibility of final models. Some of them are tackled with the aid of novel 1D checkerboard tests—an intuitive and feasible addition to the resolution matrix. We applied our workflow to study the south-western margin of the East European Craton. Rayleigh wave phase velocity dispersion and P-wave receiver function data were gathered in the passive seismic experiment “13 BB Star” (2013–2016) in the area of the crust recognized by previous borehole and refraction surveys. Final models of S-wave velocity down to 300 km depth beneath the array are characterized by proximity in the parameter space and very good data fit. The maximum value in the mantle is higher by 0.1–0.2 km/s than reported for other cratons.

1 Introduction

Receiver function (RF) and surface wave dispersion (SWD) analyses both suffer from their inherent limitations when performed separately. In the former case, it is a non-uniqueness of the solution caused by a trade-off between the depth of the discontinuity and the velocity of the overburden (Ammon et al. 1990). The latter often fails to discriminate between fine structures due to a substantial width of surface waves sensitivity kernels (Tsuboi and Saito 1983; Romanowicz 2002).

The simultaneous inversion of RF and SWD, having been applied to study deep lithosphere for 20 years (Özalaybey et al. 1997; Du and Foulger 1999; Julià et al. 2000), mitigates these issues thanks to the complementary sensitivity of the data. Compared with inversion of each of these data types alone, it provides better vertical resolution than SWD, and, unlike RF, constrains absolute shear velocities (e.g. Shen et al. 2013). Even in this case however, there may remain a certain ambiguity that should be taken into careful consideration throughout the inversion. A single model obtained by minimization of the data misfit function cannot be regarded as a full solution of the inverse problem (Gubbins 2004), which is often the case in linearized inversion (Julià et al. 2003; Horspool et al. 2006; Wang et al. 2014; Sosa et al. 2014; Bao et al. 2015; Li et al. 2016). One needs to probe the whole space of physically plausible solutions, by drawing inferences from an ensemble (Sambridge and Mosegaard 2002). Bayesian Monte Carlo methods (Green and Hastie 2009; Bodin et al. 2012; Shen et al. 2013; Deng et al. 2015; Fontaine et al. 2015) appear to be a natural approach to achieve this goal, not only performing importance sampling (Sambridge 1999), but also properly exploiting a priori knowledge of the problem (Malinverno 2002). Nevertheless, Monte Carlo methods are not flawless and suffer from their own inherent nuisance, e.g. the lack of objective criterion of convergence (Roberts et al. 1996, 1997), not to mention the computational cost. They also require nontrivial tuning to prevent solutions from following the shape of prior velocity distributions other than homogeneous (Minato et al. 2008).

Here we propose a combination of the simplicity and transparency of a linearized method with a full solution to the inverse problem, by using an ensemble of starting models covering the entire space of acceptable solutions. We use this approach to invert teleseismic receiver functions and surface wave dispersion data for S-wave velocity structure at a cratonic margin. The data was collected in the “13 BB Star” experiment in the area of well-recognized crust – the a priori knowledge of which we incorporated into the inversion in two stages. The derived workflow seems to be robust and addresses problems common in a wide range of inverse problems of different data types.

The structure of this paper follows the subsequent steps of the case study. First we introduce the tools for tackling the research problem—the inversion scheme and the resolution tests. Then, we present the experimental data and the workflow that we derived to invert it successfully. After a brief discussion of the outcome, we conclude by generalizing the workflow.

2 Theoretical background

In this study we used a linearized damped least-squares inversion scheme implemented in the “Computer Programs in Seismology” (CPS) package (Julià et al. 2000; Herrmann 2013), capable of solving over-determined problems such as inversion of the receiver function. Both separate and joint inversion of SWD and RF were performed, the former serving as a tool for understanding the behavior of the latter. We inverted for S-wave velocity in each layer of a 1D model. P-wave velocity was updated based on a v_P/v_S ratio determined for each layer of the starting model, and the density was calculated from the Nafe-Drake relation (Nafe and Drake 1957). Below we summarize the theoretical background of this scheme.

The bottom line of every linearized inversion is to iteratively minimize some scalar-valued function (expressing the misfit between observed and synthetic data) starting from a certain initial model. The main step of this procedure consists in finding a general inverse of the forward operator matrix (a full, non-linear, forward function linearized in the current iteration), which is usually done through a singular value decomposition. The ultimate goal is to find all models explaining the data while remaining consistent with the prior knowledge of the problem.

A joint data vector is a concatenation of components corresponding to each data type, here RF and SWD:

$$ \boldsymbol{d}=\left( \boldsymbol{d}^{RF},\boldsymbol{d}^{SWD}\right)^{T}= \left( \begin{array}{c}\bar{r}_{1}\pm\sigma_{r_{1}}\\ \bar{r}_{2}\pm\sigma_{r_{2}}\\ \vdots\\ \bar{r}_{R}\pm\sigma_{r_{R}}\\ \bar{s}_{1}\pm\sigma_{s_{1}}\\ \bar{s}_{2}\pm\sigma_{s_{2}}\\ \vdots\\ \bar{s}_{S}\pm\sigma_{s_{S}} \end{array}\right) $$

(1)

where r_i stands for one of R samples of RF and s_j for one of S phase velocity values. In this respect, there is no fundamental difference between a joint inversion of two or more data sets and an inversion of a single data type.

For such a data vector, one can propose a simple misfit function (Julià et al. 2000):

$$ |\varDelta{d}|^{2}=\frac{1-p}{R}\sum\limits_{i=1}^{R}\left( \frac{\varDelta r_{i}}{\sigma_{r_{i}}}\right)^{2}+\frac{p}{S}\sum\limits_{i=1}^{S}\left( \frac{\varDelta s_{i}}{\sigma_{s_{i}}}\right)^{2}, $$

(2)

where Δr_i denotes the difference between the observed and the synthetic data for the i th RF sample, Δs_j for the j th point of the dispersion curve, and |Δd|² expresses a modified Mahalanobis distance (Mahalanobis 1936) between random vectors in the case of no correlation, i.e. for a diagonal covariance matrix (which is not true in general, especially for RF).

The parameter p is added to allow for weighting the relative influence of each data set. For p = 0 only RF is inverted, and for p = 1 only SWD. The thing worth noticing is that the uncertainties (denoted with σ) are squared, and thus contribute to the weighting of each datum more than p.

In order to stabilize the solution, it is desirable to add an extra term to the misfit function leading to a trade-off between final data fit and smoothness of the model. The extended objective function has a form:

$$ \varPhi(\boldsymbol{m})=|\varDelta\boldsymbol{d}|^{2}+\theta^{2}\cdot|\mathbf{T}(\varDelta\boldsymbol{m})|^{2}, $$

(3)

where 𝜃² is a positive parameter called damping, Δm is the difference between the model in the current and previous iteration, and T is a Toeplitz matrix such that:

$$ \begin{array}{c} \mathbf{T}(\varDelta\boldsymbol{m)}=\left( \begin{array}{ccccc}1 & -1 & 0 & {\cdots} & 0\\ 0 & 1 & -1 & {\cdots} & 0\\ 0 & 0 & 1 & {\cdots} & 0\\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & \vdots\\ 0 & 0 & 0 & {\cdots} & 1 \end{array}\right) \left( \begin{array}{c}\varDelta m_{1}\\ \varDelta m_{2}\\ \varDelta m_{3}\\ \vdots\\ \varDelta m_{M} \end{array}\right) \end{array} $$

(4)

As a consequence, the inversion penalizes both the data misfit and the sum of the differences Δm_i −Δm_i+ 1 between adjacent layers (the roughness of the model).

3 Resolution analysis

Since parameters such as 𝜃² and p introduced in the previous section determine stability and resolving power of the inversion, a choice of their values requires careful examination. Here we propose a 1D checkerboard-recovery test as a tool for tuning parameters of a general 1D inverse problem. We present it using SWD and RF data and compare it to the resolution matrix analysis.

3.1 Resolution matrix

Let us first recall the concept of the resolution matrix R. It is defined by a relation:

$$ \boldsymbol{m}=\mathbf{R}\boldsymbol{m_{true}}, $$

(5)

and in the case of damping can be expressed as:

$$ \mathbf{R}=(\mathbf{A}^{T}\mathbf{C}_{e}^{-1}\mathbf{A} + \theta^{2}\mathbf{T}\mathbf{A}^{T}\mathbf{C}_{e}^{-1}\mathbf{A}), $$

(6)

where 𝜃²T has the same meaning as in Eq. 3, A is a forward operator mapping the model vector into the data space, and C_e is the error covariance matrix (Gubbins 2004). In general, the presence of non-zero off-diagonal elements is caused by the smoothing and the correlation of the data.

The R matrix carries the maximum information one can get about the resolving power of a given inversion scheme and it is advisable to use it whenever possible (Gubbins 2004). A diagonal shape of R means perfect resolution limited only by model parametrization (in our case – thickness of model layers). Off-diagonal elements R_ij indicate that the data cannot resolve the i th and j th model parameter separately.

In Fig. 1 we show how the resolution depends on the data type used. We chose a relatively low value of damping (𝜃² = 0.1) to highlight the real resolving capability of the data. SWD data (periods 15–30 s) have maximum resolution of about 20 km in the shallowest part of the model, then it drops with depth very quickly (Fig. 1a). In contrast, the resolution of RF virtually does not depend on the depth, but some layers are not constrained independently due to interference of the multiple reflections and the direct phases. The time window of RF used in this test (up to 6.5 s) constrains the studied model down to about 70 − 75 km depth. The loss of resolution below this depth can be seen in the bottom-right corner of the matrix (Fig. 1b). Resolution of the joint inversion (p = 0.5) is a compromise between the single-data-type inversions. Some of the correlations are erased compared to the RF alone at the cost of slightly lower resolution inherited from SWD (Fig. 1c).

Fig. 1

Resolution matrix for the inversion of a SWD; b RF; and c both data types (SWD+RF) simultaneously. Parameters of the inversion: 𝜃² = 0.1, p = 0.5, 5 iterations. Model parametrization: 80 layers of 1-km thickness each. Inverted data: synthetics generated from a homogeneous model (v_S = 4.5 km/s) perturbed with a checkerboard anomaly pattern (size and amplitude of a single checker: 10 km, ± 5% of the background model, respectively). Data ranges: − 3–6.5 s time window of RF (time zero refers to the direct P-wave), 15–30 s period range of SWD. Starting model: homogeneous, v_S = 4.5 km/s

3.2 Checkerboard test for a general 1D problem

As mentioned above, the R matrix contains full information on the resolution, however reliability of the inversion depends also on adequacy of the starting model or stability of the scheme.

To be able to investigate those factors while retaining some insight into the resolution we adopted a checkerboard test known from the seismic tomography (e.g., Janutyte et al. 2015) to the 1D problem.

The algorithm consists of the following steps:

• 1. Add the pattern of alternating positive/negative anomalies of constant size (thickness) and amplitude (percentage of model velocity at given depth) to the inversion result (arithmetic mean of the ensemble of final models);

• 2. Compute synthetic data from the model perturbed as in step 1;

• 3. Invert the synthetics in the exactly same way as the unperturbed model;

• 4. Subtract the original model from the result of previous point to recover the anomaly;

• 5. Compare the recovered and original anomaly.

The test can provide valuable insight into the resolving power of the data as in Fig. 2 where information content is comparable to the resolution matrix. The same quantitative conclusions can be drawn regarding the resolvable length-scales and constraining the model by the RF data. The SWD data cannot discriminate between checkers below 20 km depth, the resolution of RF does not decrease with depth provided the model is constrained by the data (here down to 70 − 75 km depth), and the joint inversion is characterized by a slightly better match between the original and recovered pattern compared to the RF.

Fig. 2

Recovered checkerboard pattern for the inversion of a SWD; b RF; and c both data types (SWD+RF) simultaneously; Parameters of the inversion, model parametrization, inverted data, and the starting model are exactly the same as in Fig. 1

Unlike the R matrix, the checkerboard study proves useful in the case of trapping by local minima. In Fig. 3a the results of the inversion were obtained using a starting model close to the true one whereas in Fig. 3b an inadequate starting model caused the inversion to be trapped in a local minimum. The effect is clearly visible on the recovered patterns, but not on the resolution matrices. This behavior is more pronounced when both minima have similar values of the misfit and/or the error covariance matrix C_e (Eq. 6) is defined a priori, i.e., does not depend on the misfit.

Fig. 3

Comparison of the checkerboard and resolution matrix analyses for the joint inversion of SWD and RF in the case of an: a adequate; b inadequate starting model; Parameters of the inversion: 𝜃² = 1.0, p = 0.1; Model parametrization and the inverted data exactly the same as in Fig. 1. Starting model: homogeneous, av_S = 4.5 km/s (the same as the background model, see the caption of Fig. 1); and bv_S = 5.0 km/s

These properties of the checkerboard test can be utilized in combination with an ensemble inference (Section 5.3) to search for all possible solutions in the model space.

Despite the simplicity of the idea, checkerboard test may be misleading as has been shown for the tomographic problems (e.g., Leveque et al. 1993). Although the resolving power of joint inversion of RF and SWD depends on different factors, some care should be taken when analyzing the results also in this case.

For more complex background models and data dominated by the RF it is possible that only one of the two possible polarities of anomaly-pattern enables its correct recovery, different for a different size of the anomaly. This is most likely due to a correlation between samples of the RF time series leading to its unstable, non-linear behavior.

In general failure to recover the anomalies is indicative of no resolving power of the method regardless of the nature of the data.

4 Data

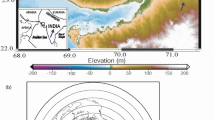
In order to study deep structure of the marginal zone of the East European Craton (EEC) we used data from the passive seismic experiment “13 BB Star” (Grad et al. 2015). It was conducted close to the Trans-European Suture Zone (TESZ) in northern Poland (Fig. 4). TESZ, a contact zone between the EEC and the Palaeozoic Platform (PP) located to the SW, is often referred to as the most fundamental lithospheric boundary in Europe (Pharaoh 1999). A large part is located in Poland, hidden beneath the cover of sedimentary rocks more than 10 km thick (Fig. 4). The TESZ is associated with a steep dip in Moho depth, from 30–35 km in the PP to 42–52 km in the EEC over a short lateral distance of less than 200 km (Grad et al. 2016).

Fig. 4

Location of the “13 BB Star” broadband seismic stations (red dots and white codes) superimposed on the main tectonic features of the region. Key: pink color—East European Craton; TESZ—Trans-European Suture Zone; isolines: thickness (km) of the sedimentary cover of the EEC; East European Craton margin in Poland corresponds to Teisseyre-Tornquist Zone (TTZ)

The study area is characterized by a relatively flat Moho topography (about 40–45 km variation beneath the stations), particularly favorable from the point of view of deep structure studies. The sedimentary and consolidated crust beneath the array has been relatively well-recognized in terms of P-wave velocity, mainly with refraction and borehole data (Grad et al. 2009; Polkowski and Grad 2015; Grad et al. 2016).

The “13 BB Star” array of ca. 120 km aperture consisted of 13 broadband stations, each equipped with an identical broadband seismometer REF TEK 151-120 “Observer” and a REF TEK 130 data logger. The “Observer” is a 3-component sensor characterized by a low level of noise and a flat velocity response in 0.0083–50 Hz frequency range (corresponding to periods 120–0.02 s). The data was sampled with 100 Hz frequency.

As all the instruments had exactly the same response and absolute amplitudes were not analyzed in this study, restitution filtering seemed to be counterproductive and was therefore not applied. More technical details of the experiment can be found in Grad et al. (2015).

The “13 BB Star” network operated from June 2013 to October 2016. The distance and azimuthal epicentral distribution of the subsets of the earthquakes used in the study are shown in Fig. 5.

Fig. 5

Epicentral distribution of the earthquakes used in the calculation of the receiver functions and surface wave dispersion curves plotted relative to the position of the central station (A0) of the network

4.1 P-wave receiver function

For each station of the array a record of P-to-S phases converted at crustal discontinuities directly beneath the station was extracted from seismograms using a receiver function technique (Langston 1977; Vinnik 1977).

The calculation was performed in a similar way to Wilde-Piórko (2015) and Wilde-Piórko et al. (2017), with some minor modifications described below. The full workflow was as follows:

• 1. Manual selection of the seismograms corresponding to events of magnitude 5.7 and higher.

• 2. Cutting the seismograms 300 s before and 300 s after the theoretical onset of the P-wave calculated for the iasp91 model (Kennett and Engdahl 1991) and rejection of the seismograms with no visible energy on the vertical component.

• 3. Two-pass low-pass filtering of the seismograms with a Butterworth filter of corner frequency 5 Hz before changing the sampling frequency to 20 Hz.

• 4. Cutting the seismograms 100 s before and 100 s after the theoretical onset of the P-wave calculated for the iasp91 model (Kennett and Engdahl 1991).

• 5. Filtering of the seismograms with a two-pass band-pass Butterworth filter with corner periods of 2 and 10 s corresponding to the frequency range of a teleseismic P-wave;

• 6. Rotation of N and E components of the seismograms with a backazimuth angle from 0 to 360^∘ every 1^∘; and computing for each angle a radial receiver function (RFR) using the time-domain Wiener deconvolution;

• 7. Choosing as a final result a radial receiver function with a maximal integral over a 0–1 s time range (equivalent to the rotation from a ZNE to ZRT coordinate system using a correct theoeretical value of the backazimuth angle); a comparison of the two methods of the ZNE-ZRT rotation is shown in Fig. 6.

• 8. Manual selection of the RFR with the highest signal-to-noise ratio; ultimately a total number of 99 events within a 30–100^∘ epicentral distance range was taken into consideration (Fig. 5).

• 9. Filtering with a Gaussian filter (parameter α = 4)

Fig. 6

Example of the rotation of teleseismic P-waves (columns 1–2) and RFs (column 3) for a C6 and b B6 seismic stations of the network calculated using the RF-rotation procedure (red line) and theoretical backazimuth angles (black line). Seismograms and RFs were filtered with a band-pass Butterworth filter of corner frequencies 0.01 and 0.8 Hz. Time zero refers to the direct P-wave

The RFRs of each station were move-out corrected for a mean slowness of the station and stacked. A standard deviation of the stacked RFR was used as a measure of its uncertainty in the interpretation of the inversion (Section 6). Since only the direct phases are properly aligned after the move-out correction, we limited our analysis to 0–6.5 s time window of the RFR using it only in the crustal inversion. The distribution of events in this data set did not allow for stacking over smaller slowness-ranges which would not need the move-out correction to be applied.

The RFR waveforms obtained (Fig. 7a) are quite complicated revealing complex geological structure of the region, especially within the sedimentary cover (first 2 seconds of the waveform). In this study we concentrate on the central station of the array (A0) even though the area covered by crustal piercing points is smaller than the inter-station distance (around 15 km for discontinuity at 50 km depth and epicentral distance 67^∘).

Fig. 7

Data acquired in the “13BB Star” experiment: a stacked RFR for all broadband seismic stations ordered by a thickness (km) of the sedimentary cover (in parentheses after the stations codes); b fundamental mode Rayleigh wave dispersion curve of the array: single phase velocity measurements corresponding to all analyzed events for all map cells (black dots), their arithmetic mean (green line) and a standard deviation of the mean (red lines)

4.2 Fundamental mode Rayleigh wave phase velocity dispersion

An average phase velocity dispersion relation of the fundamental mode of the Rayleigh wave beneath the array was obtained using the ASWMS (Automated Surface Wave Phase Velocity Measuring System) code (Jin and Gaherty 2015).

The package allows the extraction of phases and amplitudes of the surface waves from raw recordings of natural teleseismic events. It then uses these measurements to calculate phase velocity maps for different wave periods based on the Eikonal and Helmholtz equations.

Pre-processing of the data consisted of the following steps. Firstly, a list of all recorded events with magnitude higher than 4 was created and manually checked for quality. No prior constraints on hypocentral depth were involved. A total of 706 events recorded in the period from 2013-07-10 to 2016-09-23 were selected for further study. All the events were manually verified on a station basis. For each event a list of stations with good quality recording was prepared. The stations with no data, partial data or bad data quality were omitted. 135 events were selected as good quality on all 13 stations, 478 events were recorded with good quality on over 50% of the stations, and 103 events were rejected on all stations. From all 9178 station-event pairs, 5697 were selected as good quality (over 62%). On average, 8 stations were selected as good quality per event. Depths of the hypocenters were shallower than 100 km for most events, although strong surface waves were also recorded for some deep earthquakes. For each station-event pair raw seismic data was converted from daily mini-seed files to single SAC files with embedded event parameters (latitude, longitude, depth and magnitude). SAC data files were then imported by the ASWMS package and used for the phase velocity calculations.

Key features of the method implemented in ASWMS are as follows: (1) measurement of the phase delays through cross-correlation of the waveforms, (2) calculation of the phase velocity/slowness through a tomographic inversion of the phase delays based on the integral formulation of the Eikonal equation.

The cross-correlation is a highly precise tool for estimating a phase delay including circumstances when the delay is only a small fraction of the wave period. This is the case e.g. when the wavelength of the signal significantly exceeds the inter-station distance (and the assumption about the similarity of the cross-correlated waveforms is automatically respected).

In this study we analyze periods up to 30 s, 100 s, and 180 s for crustal and two mantle inversions respectively. In the last case the wavelength is several times larger than the aperture of the array (700 km versus 120 km). To make sure that the phase-delay measurements were reliable for these wavelengths, we show a manual analysis of a single earthquake (2015-04-25, M = 7.8, Nepal) for two-station pairs A0-C1 and C1-C4 (Fig. 8). The phase delay is clearly visible up to T = 220 s and 320 s period for A0-C1 and C1-C4 pair respectively.

Fig. 8

Manual estimation of phase delays for a single earthquake (2015-04-25, M = 7.8, Nepal): a seismograms for stations A0, C1 and C4 showing high-quality recordings of dispersed surface waves; b wave packages obtained through filtering of the seismograms around a central period (vertical axis) for the C1 (gray lines) and A0 (red lines) stations; blue frame in the left panel indicates the zoomed area shown in the right panel; Row c has the same meaning as b, but at station C4 instead of station A0

This example also confirms that the seismometers used in the study were capable of measuring coherent signal for periods as long as 180 s (used in the mantle inversion), even up to 300 s in special cases. As mentioned before, for relative-amplitude studies like this, the restitution filtering would be counterproductive and was not performed.

The second pivotal feature of the ASWMS is the tomographic inversion which means that a primary result of the study is a phase velocity map for a single event at a single period. The usage of all nearby station-pairs to construct such a map is a major advantage of this approach over, e.g., the two-station method which is limited to the station-pairs lying on the same great circle with the earthquake and which is likely to suffer from the multipathing effects.

For each cell of the map a dispersion curve may be calculated a posteriori as a secondary result derived from the map. Uncertainty of such a curve can be estimated as a standard deviation of the mean over all the events taken into account.

In this study the phase velocity maps consisted of cells 0.05^∘× 0.05^∘ big and were calculated for periods from 10 to 300 s every 1 s without smoothing. The lack of smoothing ensured that the values in different cells were not artificially correlated. Results were then prepared as dispersion curves, with values taken from corresponding grid cells of all the maps. The final dispersion curve was obtained by averaging all the dispersion curves and is shown in Fig. 7b, with an uncertainty expressed as a standard deviation of the mean. Additional averaging over the map, not only the events, might seem to affect the reliable estimation of the uncertainty, since a geological variability is not a random error. However, even for the shortest periods used in the inversion the lateral resolution of surface waves does not allow for any significant changes of the phase velocity between the stations of the array. This conclusion can be drawn from the analysis of the width of the first Fresnel zone adapted to a surface waves study (Yoshizawa and Kennett 2002), or from the phase velocity maps themselves. Low values of the standard deviation of the mean for the shortest periods confirm that the crustal variability does not contribute to the uncertainty. As the lateral resolution in the mantle is even worse, mantle variability should not affect the uncertainty estimation at all.

The observed curve (Fig. 7b) has uncertainty increasing with period, and is characterized by the anomalous dispersion for T > 100 s. The latter has not been observed in other studies in the region (Soomro et al. 2016; Meier et al. 2016) likely due to smoothness criteria applied there for the automated selection procedures. A local minimum between 60 and 85 s is probably a footprint of anisotropy since we also observe it on the group velocity curves, but cannot fit it with the synthetic data using the isotropic approximation.

5 Inversion workflow

We developed a workflow for a credible inversion of the data described in Section 4 in order to illuminate structure of the whole lithosphere. Below we summarize the key steps of this approach.

5.1 Exploitation of a priori information

The “13 BB Star” experiment was conducted in the area covered by a high-resolution 3D v_P model of the crust (Grad et al. 2016). As in the Bayesian inference (Sambridge and Mosegaard 2002), we wanted to include this prior knowledge in the starting models, which required a calculation of S-wave velocities. To this end we used v_P/v_S values of 1.8-1.9 in sediments and: 1.67, 1.73, 1.77 in upper, middle, lower crust respectively, roughly the same as reported by Środa et al. (1999). These assumptions along with the fact that the 3D model was derived from the measurements of different sensitivity (mainly P-wave ray-tracing) surely contributed to the large misfit between observed and synthetic RFs computed from this model. As we did not want this discrepancy to drive the inversion, we split the inversion into two steps. In the first we inverted for the crustal structure only, starting with the values from the 3D model (Section 6.1). In the second we incorporated the crust from the final models of the first step into full depth models (see Section 5.2 for details of choosing the right depth) and assigned lower weights to its layers (half the value of the mantle layers) to partly “freeze” it in the subsequent inversion (Section 6.2).

5.2 Choice of the model depth

The range of the inverted data determines the minimum depth of the model. The rationale for this is that the medium below the last layer of the starting model is usually assumed to be a homogeneous half-space. As a consequence, too shallow models may introduce some artifacts likely to appear e.g. while trying to fit the RF tail that represents structure below the bottom of the model. Such distortion can be observed in Fig. 9b where it is juxtaposed with the results for a correct model depth (Fig. 9a). In both cases a model of 50 km depth was inverted for, however a different model to generate synthetic data (RF) was used: 50 km and 500 km deep for Fig. 9a and 9b respectively. The corresponding time window of RF used in synthetic calculation and subsequent inversion was: 6.5 s (9a) and 30 s (9b).

Fig. 9

Checkerboard study showing the importance of choosing the correct model depth; synthetic data (RF) to invert was generated from a homogeneous background model (v_S = 3.5 km/s) with a checkerboard (size and amplitude of a single checker: 10 km, 5% of the background model, respectively) added across the full depth of the background model which was 50 km in a and 500 km in b. Depth and velocity of the starting models: 50 km and 3.5 km/s in each case; RF time window: − 3–6.5 s (a), and − 3–30 s (b) after the direct P-wave

For dispersion curves the reasoning behind the choice of the model depth with respect to the maximum period is slightly different due to the substantial widths of their sensitivity kernels for longer periods (e.g., Romanowicz 2002). However, it leads to similar conclusions – too shallow models may be affected by sampling the structure below the model depth. Using models considerably deeper than the part constrained by the data seems to avoid these problems.

For the crustal (first-step) inversion mentioned in Section 5.1 models 100 km deep were used to invert the SWD curve of 15–30 s period range, and the RF of time window from − 3 to 6.5 s after the direct P-wave.

In the second step we extended the model depth to 900 km when using 15–100 s and 15–180 s period ranges of the SWD data to invert for the deeper lithosphere.

5.3 Ensemble inference

Among the downsides of the linearized approach, trapping by local minima is listed as one of the most profound (Bodin et al. 2012), nonetheless Monte Carlo methods, are not completely free of it either (Minato et al. 2008; Wathelet 2008). Several solutions to this issue were suggested, e.g., for a full waveform inversion (FWI). Bharadwaj et al. (2016) proposed a functional that pulls the model out of the local minimum. As the RF and SWD inversion is not as computationally expensive as FWI (Warner et al. 2013), we take a different approach based on an ensemble of starting models, which densely covers the space of physically plausible solutions. In our case it consisted of 20 homogeneous mantle structures evenly distributed between 4 and 5 km/s, within which the great majority of S-wave velocities reported for cratonic mantle in other studies falls (Fischer et al. 2010; Vinnik et al. 2015). All mantle P-wave velocities were calculated assuming v_P/v_S = 1.73 after Vinnik et al. (2015).

The thickness of mantle layers was 5 km down to 300 km, and 10 km for 300–900 km depth for all models. Contrary to the prior distribution used in Bayesian analysis, the solution of linearized inversion can converge to the values beyond this range, which is a slightly weaker initial assumption. Homogeneity ensures that we do not make any guesses about the mantle which would drive the inversion towards the most “reasonable” structure. Rather, we let the data do it for us. Nonetheless, studies using inhomogeneous models can also be found, e.g., in Wilde-Piórko et al. (2005) and Graw et al. (2017). We emphasize the fact that a high density of the distribution of the starting models within a given interval (here every 0.05 km/s) enables coverage of the whole space of physically plausible solutions. At the same time, the computational cost of this approach is still much lower than of any Monte Carlo method. It usually takes 10–20 iterations for each model of the ensemble (which gives a total of 400 iterations for this study), whereas a typical Bayesian Markov Chain Monte Carlo (MCMC) requires at least 10⁵–10⁶ forward calculations (Bodin et al. 2012).

5.4 Tuning inversion parameters using resolution analysis

We incorporated the resolution analysis discussed in Section 3 as an integral step of the workflow to tune parameters such as 𝜃², p and number of iterations before the inversion of the observed data.

For these particular data types there are a few caveats to take into consideration. First, as the problem of calculating RF is highly non-linear (e.g., Bodin et al. 2012), synthetic tests of RF alone are generally not fully plausible. Even for quite similar structures there may exist a difference among the sets of inversion parameters illuminating them optimally. Second, it may seem that the influence parameter p is solely responsible for the relative weighting of different data sets with p = 0.5 implying their equal contribution to the solution. However, an even more important weighting factor is represented by a squared uncertainty of a given data point (Eq. 2). A stringent assessment of seismic data errors is in general highly challenging (Julià et al. 2000; Julià et al. 2003; Bodin et al. 2012), which makes the problem of finding the optimum value of p essential. Furthermore, in the CPS package only the SWD uncertainty is allowed to be predefined by the user (we used the values of 1σ presented in Fig. 7b). The uncertainty of each RF sample in turn is defined as a standard deviation of the misfit of the full time series, and thus, it changes from iteration to iteration. As a result, SWD data may be unintentionally favored at the beginning of the inversion. Overall, the proper weighting may require values of p other than 0.5, and this can be found only through synthetic tests.

Based on the resolution analysis (Fig. 10 and 11) we concluded that for the given starting model and data the optimal set of inversion parameters would be: 𝜃² = 1.0 and p = 0.1 ensuring a compromise between the stability and resolution. We expected the inversion to resolve the crustal structure on a 10–15 km length-scale (Fig. 10). The resolution of the mantle not constrained by the RF was predicted to be much worse, with a maximum of 100 km in the uppermost mantle (Fig. 11).

Fig. 10

Resolution analysis of the first-step inversion: the recovered checkerboard pattern (left) and the resolution matrix (right). Parameters of the inversion: 𝜃² = 1.0, p = 0.1, 20 iterations. Model parametrization: crustal layers of 0.5-km thickness each, mantle layers of 5-km thickness each; Inverted data: synthetics generated from the central (mantle velocity v_S = 4.53 km/s) model of the ensemble in the Fig. 12a, perturbed with a checkerboard anomaly pattern (size and amplitude of a single checker: 9 km and ± 5% of the background model, respectively); Data ranges: − 3–6.5 s time window of RF (time zero refers to the direct P-wave), 15–30 s period range of SWD. The ensemble of starting models the same as in Fig. 12a

Fig. 11

Checkerboard pattern recovery in the case of deeper mantle structure not constrained by the RF. Size and amplitude (percent of the background model) of a single checker: a 20 km, 1%; b 20 km, 5%; c 50 km, 20%; Parameters of the inversion in each case: 𝜃² = 1.0; p = 0.1; 20 iterations; the crust partly frozen (weight 0.5); Inverted data: synthetics generated from the average model of the ensemble from Fig. 16b. Data ranges: − 3–6.5 s time window of RF (time zero refers to the direct P-wave), 15–180 s period range of SWD

6 Results

As described in Section 5, the inversion was performed in two steps in order to take advantage of the a priori information in a proper way.

6.1 First step—the crust

Starting models for the first-step inversion (Fig. 12a) consisted of the crust from the 3D model (Grad et al. 2016) and 20 homogeneous mantle structures evenly distributed between 4 and 5 km/s down to about 100 km depth.

Fig. 12

First-step inversion: a starting and b final models. Depth of each model: 100 km. Parameters of the inversion: 𝜃² = 0.1, p = 0.1, 40 iterations. Inverted data: − 3–6.5 s time window (time zero refers to the direct P-wave) of the observed RF from Fig. 7a (A0 station), 15–30 s period range of the observed SWD from Fig. 7b. Each final model in b corresponds to the starting model in a of the same color

The resulting model (Fig. 12b) is characterized by a prominent low velocity zone (LVZ) at a depth of about 25 km, and an additional, thin layer within the sedimentary crust. Two major discontinuities: sedimentary/crystalline crust and Moho are much smoother compared to the starting models. Worth noticing is a small spread of the final models, especially for the initial diversity of the Moho contrasts. The data fit is satisfactory both for RF (Fig. 13a) and SWD (Fig. 13b), so the main goal of the first-stage inversion was met. Note that to improve the fit we used a slightly lower value of damping than evaluated in the synthetic tests, as it turned out that in this case it was possible without loss of stability.

Fig. 13

Data fit for the final models from Fig. 12b: a RF, b SWD; black solid lines: observed data; black dashed lines ± σ of observed data. Each synthetic data set was computed from the corresponding final model in Fig. 12b of the same color

6.2 Second step—the whole lithosphere

After the first step, we incorporated the crust of the final models into the full-size (900 km, i.e., reaching well below the resolving power of both data types) starting models of the second-stage inversion (Fig. 14a). The weight of 0.5 assigned to the crustal layers (half the value of the mantle layers) meant that they were partially frozen, allowing only for minor updates.

Fig. 14

Second-step inversion using SWD data with a maximum period of 100 s: a starting and b final models. Depth of each model: 900 km. Parameters of the inversion: 𝜃² = 1.0, p = 0.1, 20 iterations, weight of the crust in the inversion: 0.5 of the weight of mantle layers. Inverted data: − 3–6.5 s time window (time zero refers to the direct P-wave) of the observed RF from Fig. 7a (A0 station), 15–100 s period range of the observed SWD from Fig. 7b. Each final model in b corresponds to the starting model in a of the same color

The time window of RF remained the same as in the first stage. As mentioned in Section 4, the true amplitudes of reflected phases had been lost in the move-out correction and stacking. For this reason, most of the mantle was constrained only by SWD data.

We inverted separately the maximum period of 100 and 180 s, the former lying within the range of the flat frequency response of our seismometers and being the more reliable part of the curve. In both cases the resulting models of the ensemble are very close to each other (Figs. 14b and 16a) and the data fit is very good (Figs. 15 and 16b).

Fig. 15

Data fit for the final models from Fig. 14b: a RF, b SWD; black solid lines: observed data; black dashed lines ± σ of observed data. Each synthetic data set was computed from a corresponding final model in Fig. 14b of the same color

Fig. 16

Second-step inversion using SWD data with a maximum period of 180 s: a final models, b SWD fit for all the final models (black solid lines: observed data; black dashed lines ± σ of observed data). Depth of each model: 900 km. Parameters of the inversion: 𝜃² = 1.0, p = 0.1, 20 iterations, weight of the crust in the inversion: 0.5 of the weight of mantle layers. Inverted data: − 3–6.5 s time window (time zero refers to the direct P-wave) of the observed RF from Fig. 7a (A0 station), 15–180 s period range of the observed SWD from Fig. 7b. Each final model in a corresponds to the starting model in 14a of the same color. Each synthetic curve in b was computed from a corresponding final model in a of the same color. RF data fit was almost the same as in Fig. 15a and is not shown here

7 Discussion

To obtain the results presented in Figs. 14b and 16a we developed a multistep workflow for the linearized inversion, which aimed at obtaining credible models of S-wave velocity down to 300 km with RF (constraining only shallowest 60 km) and SWD data. Its key features include the following: synthetic analysis of the resolution which, e.g., allows for a correct tuning of damping and the parameter p weighting the influence of each data type; adaptation of the a priori knowledge on the crustal part of the model obtained with different methods; careful choice of the model depth relative to the range of observed data in order to prevent the synthetic data from sampling the bottom half-space instead of the real structure and thus distorting the inversion results; mitigating the inherent non-uniqueness of the inverse problem by using an ensemble of starting models permitting to find all of its physical solutions.

Following this workflow provided us with the models that exhibit very low spread (Figs. 14b and 16a) and that fit the observed data well, in most cases falling inside the range of one standard deviation of the mean (Figs. 15 and 16b). The blue models responsible for the RF misfit exceeding the accepted error do not differ from the others except for the part directly below the Moho. The inability of the synthetic curves to fit the notch present in the observed SWD curve between 60 and 90 s is likely related to the anisotropy which cannot be accounted for by an oversimplified, isotropic forward scheme used here.

One of the main targets of cratonic upper-mantle investigations is the lithosphere-asthenosphere boundary (LAB)/transition zone (Eaton et al. 2009). Numerous studies have shown that the LAB beneath Precambrian cratons is not easily detected by seismic methods, e.g., receiver function, because converted phases from smooth transition zones are not well pronounced (Kind et al. 2012). Geissler et al. (2010), using S receiver functions, show that beneath the stations located in the Precambrian platform of Eastern Europe LAB deepens to approximately 200 km. This value is consistent with LAB depths of other old cratons of the Earth (Eaton et al. 2009; Jones et al. 2010).

We used two period ranges of the SWD data of various reliability: 15–100 s and 15–180 s in separate inversions. The former led to the retrieval of a mantle structure with a maximum velocity of v_S = 4.78–4.80 km/s in a depth range of 100–120 km (for the various starting models) and a minimum velocity of v_S = 4.70–4.73 km/s in a depth range of 160–220 km (Fig. 14b). The latter resulted in a slightly smoother model with a maximum velocity of v_S = 4.85 km/s and a gentle decrease starting at about 160–180 km depth.

If the local drop of the v_S visible in both cases is associated with a top of the LAB, it is consistent with the previous studies of the deep lithosphere in this area. E.g. similar depth of the LAB has been obtained along the profile P4 located about 200 km south-east of “13 BB Star” array. It was derived from a study of relative P-wave residuals by Świeczak (2007), using the method of Babuška and Plomerová (1992). The average depth of the LAB for the EEC was estimated at 193 km, in a significant contrast to TESZ, where it lies at 119 km depth (Wilde-Piórko et al. 2010). However, cutting our RF just after the direct Moho conversions, caused the deeper structure to be constrained almost exclusively by the SWD data and the results must be treated carefully in this context due to their low resolution. As shown with the checkerboard tests (Fig. 11), the estimation based on SWD data only, like in this case, is not fully credible in terms of estimating the depth and character of the transition. Consequently, we do not draw any conclusions about them. Presumably the only parameter not affected by this limitation is the maximum velocity in the considered depth range. The values v_S = 4.80–4.85 found during the inversions are quite high even for mantle velocities beneath old Precambrian cratons (Fischer et al. 2010; Vinnik et al. 2015; Meier et al. 2016). This discrepancy results directly from the different shape of the dispersion curves between the studies. As mentioned in Section 4.2, e.g., Meier et al. (2016) applied an automated procedure of data selection (e.g., constraints on the smoothness), which might have rejected the data illuminating local structure on a finer scale. For a detailed discussion of the geophysical properties of the lithosphere in this area, see Grad et al. (2018).

8 Conclusions

We designed a versatile workflow that provides a full solution to a general inverse problem for any data type. It combines advantages of linearized and Bayesian Markov-chain Monte Carlo (MCMC) schemes. As opposed to standard linearized inversion, it finds all physical solutions, and makes an accurate starting model no longer necessary. Compared to typical MCMC inversion, it has a lower computational cost, fewer parameters to tune, and a clear convergence criterion. Its main steps can be summarized as:

• 1. Choice of a reliable data-range;

• 2. Setting a model depth so that it is distinctly larger than a maximum depth constrained by the data;

• 3. Preliminary tuning of inversion parameters through synthetic recovery tests using a simple, small-size model;

• 4. Tuning of inversion parameters through novel 1D checkerboard tests and resolution matrix analysis using a full-size model of the expected structure;

• 5. Preliminary inversion for a part of the model recognized by previous studies, treating minimization of the misfit as the only criterion of the result quality;

• 6. Inversion for the full-size model incorporating the result of the previous step in the starting models.

The key feature is the usage of the ensemble of homogeneous starting models covering the entire space of physically plausible solutions in order to mitigate non-uniqueness of the problem without driving the inversion towards any arbitrary minimum. Also worth emphasizing is the role of the resolution analysis as an integral part of the parameter-tuning process, and the proper way of exploiting a priori information.

Following this approach allowed us to obtain a credible S-wave velocity model of the subsurface beneath the “13 BB Star” network down to 300 km depth. Very good data fit and nearly identical structure of the final models suggests that the correct parameter-tuning successfully mitigated the ill-posedness of the problem. The mantle exhibits similar structure, but rather high (v_S ≈ 4.80 km/s) velocity values compared to those reported for other cratons. Further investigation should explain whether this reflects a local anomaly, or is due to an oversimplified assumptions behind the modelling.

9 Code availability

Python library and Bash scripts adapting the CPS package (Herrmann 2013) to the ensemble inference and checkerboard tests are available at https://github.com/kmch/CPyS or upon request from the corresponding author.