Percolation and the Phase Slip in Granular SmFeAsO_1-xF_x Thin Films

Abstract

A set of granular SmFeAsO_1-xF_x films were synthesized on LaAlO₃ substrates with different percentage of the coverage of the substrate surface, and then their electrical properties were studied. At high temperatures, as the substrate coverage is increased, the films go from an insulating to a metallic behavior; and then, at low temperatures, the films that present a resistance R_N of few kOhms in the normal state show a transition to the superconducting state with a width in the R(T) curves that changes with the coverage of the substrate surface. The line shape of these curves can be explained by the Ambegaokar-Halperin (AH) model of the resistance produced by the thermal activated phase slippage at the intergranular junctions if the dimensionality for the films is presumed appropriately. For the thicker films, that can be considered as a 3D network of the Josephson junctions, a temperature dependence of the AH parameter $\gamma$ given by $\sim$A(1 − t)^3/2, fits the R(T) curve satisfactorily. However, for the films that cover the surface of the substrates only partially, the AH model fits the R(T) curves only if $\gamma$ ~ A´(1 − t²)², which is suitable for a 2D network of the Josephson junctions.

1 Introduction

The percolating structures in superconducting materials usually give place to the superconducting–insulating-transition (SIT) phenomena, which results from the intergrain distance in a granular superconductor [1]. The SIT is more remarkable in thin granular superconducting films (quasi two dimensional superconductors), where the percolating structures can be created either by superconducting grains embedded in an insulating matrix or by changing the percentage of the area of the substrate that is covered by the superconducting film [2,3,4,5]. When a metallic film is fabricated, in the first stage usually it is formed by isolated grains or clusters which can be enlarged as more material is allowed to arrive at the surface of the substrate [6, 7]. As the grains are enlarged, they get irregular shapes and start to touch each other forming larger clusters that cover larger surface area and, finally, at some critical value of the covered area (percolation threshold) a set of elongated “clusters” starts to form a random network with large paths that extends through all the sample. Under this scheme, one can forecast different conductivity features that, in the normal state, will evolve from insulating to metallic behavior. If the material presents superconducting properties, in the superconducting regimen it will evolve from a local to a global superconducting state as the connectivity between the grains is improved. However, in this region the percolation process will be controlled not only by the metallic connectedness but by the tunneling of the Josephson junctions, too. The presence of the junctions gives place to the phase slip in the complex order parameter, which in turn results in the creation of Josephson vortices [8, 9]. The creation of these vortices and their thermal activated movement produces a dissipative process that causes a broad resistive transition previous to the emergence of the global superconductivity. Different models have been developed to describe this broad transition. Most of them are based on the work of Ambegaokar-Halperin (AH) which describes the resistance in Josephson junctions that comes from the phase slippage of the order parameter in the junction [10, 11]. The model indicates that this resistance as a function of the temperature is given by R = R_N[I₀($\gamma$/2)]⁻²; where R_N is the resistance in the normal state, I₀ is the modified Bessel function of the order zero, and $\gamma$ is a parameter that characterizes the ratio of the Josephson coupling energy E_J(T) to the thermal excitation energy k_BT (k_B, Boltzmann constant). The temperature dependence of $\gamma$ will determine the R(T) curve in the transition to the global superconductivity, which has an onset at some T_CJ. For a 3D network of Josephson junctions, Tinkham has proposed that the resistance generated by the thermal activated movement of the Josephson vortices is equivalent to the resistance created by the flux creep in bulk superconductors [12, 13]. So that in the AH model, he replaced E_J with the activation energy U₀(T,B) that the fluxons need to overcome to start a thermal activated movement across the junction. The phenomenological analysis of the flux creep indicates that the activation energy should be given by ${U}_{0}=p{(H}_{C}^{2}/8\pi )V$ where p is a numerical parameter (~ 1), H_C is the thermodynamic critical field, and V is a characteristic volume. By considering that in bulk superconductors the flux lines do not move individually but the movement is correlated, this volume use to be that of a bundle of fluxons. In the most general form of the flux creep theory, this volume use to be written as V = R_c²L_c, where R_c and L_c are the transversal and longitudinal pinning correlation lengths [14]. However, the simplest characteristic volume is the elemental volume of an Abrikosov unit cell: $V={a}_{0}^{2}\xi$, where a₀ is the Abrikosov lattice parameter ($\phi$₀/B)^1/2 and $\xi$(T) is the superconducting correlation length. Tinkham took this simplest volume and the appropriated approximation (near T_CJ) for the temperature dependence of both H_C(t) ~ H₀(1 − t²) and $\xi$(t) ~ $\xi$₀(1 − t)^1/.², (t = T/T_CJ, H₀ the critical field at T = 0 and $\xi$₀ the correlation length at T = 0), to obtain an expression for AH parameter $\gamma$$(=\frac{p{H}_{0}^{2}\left(0\right){\xi }_{0}{\phi }_{0}}{8\pi {k}_{B}} \frac{{\left(1-t\right)}^\frac{3}{2}}{B})$. From this, the following equation for the temperature dependence of the resistance produced by the intergrain Josephson junctions can be obtained [12].

$$\nicefrac{R}{{R}_{N}}={\left\{{I}_{0}(A{\left(1-t\right)}^{3/2}\right\}}^{-2}$$

(1)

Here A is a factor that absorbs all the numerical constants involved in $\gamma$. Although various authors claim that the Tinkham model fits quite well the resistive transition of granular superconductors [12, 13, 15], there are works where a different characteristic volume V is proposed to obtain an acceptable fitting of the R(T) curves. For example, it has been stated that for low applied fields, the characteristic volume V= $\xi$³(t) gives a temperature dependence for $\gamma =\frac{p{H}_{0}^{2}(0){\xi }_{0}^{3}}{8\pi {k}_{B}} {\left(1-t\right)}^{1/2}$ that fits the line shape of the resistive transition in a better way than the obtained from Eq. (1) [13, 16]. Nevertheless, although those models are good to describe the resistive transition of bulk superconductors, usually no one of those use to fit appropriately the resistive transition of granular thin films. This might indicate that a different characteristic volume V for the flux bundle must be chosen. In fact, it has been experimentally observed that for artificially grown superconductor/insulator superlattices, the characteristic volume is related to the superconducting layer thickness [17], which is temperature independent. In such a case, a different line shape in the R(T) curves should be observed.

In this work, we study the line shape of the resistive transition of a set SmFeAsO_1-xF_x polycrystalline thin films with a different surface coverage of the substrate, which creates different connectivity patterns between the crystallites. This gives the opportunity of studying percolation effects in granular SmFeAsO_1-xF_x superconducting films. In particular, it allows us to study a superconducting-insulating transition as well as the percolation controlled by the Josephson coupling. The results indicate that the line shape of the resistive transition can be explained by the phase slippage in the Josephson junctions if the appropriated characteristic volume for the flux bundle is chosen.

2 Experimental

SmFeAsO_1-xF_x polycrystalline thin films were grown on (100) LaAlO₃ substrates by metalorganic chemical vapor deposition (MOCVD) and an ex-situ diffusion process. The process is described elsewhere [18]. A precursor film of Sm and Fe oxide is deposited by MOCVD, afterwards arsenic and fluorine are integrated by diffusion process by annealing the precursor film along with a pellet that has a fixed SmFeAsO_1-xF_x stoichiometry. The deposition of precursor films with different thickness allows to produce SmFeAsO_1-xF_x granular films with different percentages of substrate surface coverage. After the diffusion process, the relative atomic composition of the metallic components (Sm:Fe:As) on the films, evaluated by energy dispersive X-rays spectroscopy (EDX), indicates an average ratio close to 1:1:1 for each film. For example, for S1, the atomic percentage is 32$\pm$1:37$\pm$3:31$\pm$3 an, for S2, it is 32$\pm$3:31$\pm$2:37$\pm$3. The same EDX indicates that the S1 and S2 films reported in this letter contain a relative atomic fluorine concentration of ~ 12 ± 2%; while for S3 and S4 [F] ~ 9%, which is close to the optimal doping in the SmFeAsO_1-xF_x superconducting phase. The X-ray diffraction characterization indicates the development of the quaternary SmFeAsO phase in all the samples, although in some cases, traces of an impure phase is observed. Because of the granular surface topography of the samples, the film thickness was difficult to measure by the profilometry technique. However, transversal scanning transmission electron microscopy (STEM) allows us to obtain a rough estimation of the thickness of the films reported in this letter. They are: ~ 130 (S1), 160 (S2), 220 (S3), and 300 nm (S4). Figure 1a shows a typical micrography obtained by the STEM technique. The temperature dependence of the surface resistance [$R_\square$] was measured in a Quantum Design PPMS system, using the standard low frequency ac four probe method, applying a 0.01 mA AC at 70 Hz. For the analysis of the resistance coming from the phase slippage, the electrical resistance immediately above the starting point to the global superconductivity in each sample was taken as the resistance R_N in the normal state. In the fitting procedure of the theoretical models to the experimental data, the transition temperature of the global superconductivity T_CJ was fixed as the experimental value defined by the intersection of the lines defined by the points at the normal and the initial transition to the global superconductivity, see Fig. 3.

Fig. 1

a Transversal scanning transmission electron microscopy (STEM) for sample S2. The thickness of the film is observed. b–c EDX analysis along a straight line in sample S2

Fig. 2

XRD pattern of the samples S1, S2, S3, and S4. Despite the presence of some small peaks associated with the impurity of the SmOF phase, most of the peaks are indexed to the SmFeAsO_1-xF_x phase

3 Results and Discussion

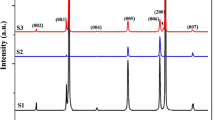
Figure 2 shows the X-ray diffraction pattern of the films studied in this report. The development of the 1111 crystalline structure is observed. By considering the presence of this structure and the appropriated fluorine content, as indicated by EDX, a superconducting transition should be expected [19]. Nevertheless, as it is observed in Fig. 3, the resistance as a function of the temperature shows an insulating behavior for the thinnest film, an incomplete superconducting transition for the films of intermedia thickness, and a transition to the zero resistance state is observed only in the thicker sample S4. An increase in the resistance as the temperature is decreased is contrary to the metallic character of the SmFeAsO quaternary compound [19]. So, the behavior perhaps is related to the thickness, and it seems that in these films, a SIT occurs as a function of the film’s surface coverage. This is the case that can be observed in the Fig. 4, which shows the surface morphology obtained by scanning electron microscopy. A different coverage of the substrate surface and a variety of connectedness are developed in each sample. The thinnest film consists of isolated grains and the connectivity is improved as the thickness is increased. A continuous analysis of chemical composition performed along a straight line in samples with poor coverage shows a drop of Sm, Fe, and As in the regions where no grains are observed, see Fig. 1b, c. Therefore, the films can be considered as a 2D granular system of SmFeAsO_1-xF_x phase, and their transport properties must be analyzed from the point of view of the percolation theory. In particular, the different behavior observed at low temperatures in the R(T) curve of each sample with different percentages of substrate coverage, clearly indicates the presence of a superconducting-insulating-transition driven by percolation.

Fig. 3

Resistance vs temperature curves for SmFeAsO_1-xF_x films with different surface coverage. Depending on the connectedness, the behavior is insulating (S1), quasi-reentrant (S2-S3), and superconducting (S4)

Fig. 4

SEM micrographs of SmFeAsO_1-xF_x films. It is observed that the surface morphology changes from insulated grains for the thinness film (S1) to well-connected grains for the thicker one (S4)

A feature of the SIT driven by percolation in 2D granular systems is the presence of a quasi-reentrant superconductivity [1, 2, 5, 20, 21]. That is the presence of a minimum in the R(T) curves before the emergence of the global superconductivity all over the sample. The presence of this minimum use to be associated with the intragrain superconducting transition at the bulk temperature, which in principle must be independent of the intergranular connectivity [20]. In the present case, a minimum is observed around 50 and 35 K for samples S2 and S3, respectively (see the insets in Fig. 3), which must be a manifestation of the local superconductivity inside the SmFeAsO_1-xF_x grains with a nearly optimal content of fluorine. After the minimum a slight increase in the resistance, as the temperature is further decreased, can be observed, and then the transition to the global superconductivity emerges at temperatures below 20 K. So that, the thinner films show the quasi-reentrant feature. It is interesting that even in the sample that shows an insulating behavior, a change in the slop of the R(T) is observed close to 50 K (see inset in the top panel of Fig. 3). However, the thicker film does not show such quasi-reentrant behavior, which might indicate that it does not have a 2D but a 3D character.

As commented in the introduction, although the metallic connectedness is necessary for the conductivity, it is not sufficient to observe the zero resistance state in the whole sample. The transition to the global superconducting state is controlled by the thermal activated phase slip at the intergranular junctions, which will produce a dissipative process that will not result in a sharp but in a broad resistive transition. We believe that it is what is observed in samples S2 and S3: an incomplete intergranular coherence that turns out in a very broad transition. Therefore, the resistance in these networks of Josephson junctions with percolative structure should be described by the Ambegaokar-Halperin theory. Figure 5 shows the fitting of the AH model under the approximation developed by Tinkham (Eq. 1) to our experimental data, where an expansion in series for the modified Bessel function to the fourth term was employed [22]. By considering the approximations made by Tinkham, the model should be particularly good close to the onset of the global superconductivity, that is to say, close to T_CJ. It can be observed that the model fits quite well the R(T) curve of our thicker sample not only close to T_CJ but in all the transition temperature range. Nevertheless, the model does not fit the line shape of the resistive transition of the films with a low surface coverage. A fitting of the experimental data to the Ambegaokar-Halperin model, with a temperature dependence for the AH parameter given by $\gamma \sim$A(1-t)^3/2, has been observed in various bulk superconducting materials [12, 15]. So, the good fitting observed in our thicker sample would indicate its 3D character of the Josephson junction, in agreement with the lack of reentrant effects in this sample, as discussed in the previous paragraph.

Fig. 5

Fitting to the Tinkham’s model of the R(T) curves during the transition to the global superconductivity for the samples S2-S4. A good fitting in the whole transition temperature range is observed only for the S4

As it was described at the introduction, in the Tinkham’s model the temperature dependence in $\gamma$ is determined by the temperature dependence of the critical field H_C(T) and the elemental volume of an Abrikosov unit cell V = a₀²ξ((T)), from which it follows $\gamma \sim$A(1-t)^3/2. However, in the case of a granular film with a percolating structure, the vortices jump from one junction to another. In such a case, the characteristic volume involved in the activation energy must be related to the volume of the clusters that form the percolating structure rather than to the volume of the Abrikosov unit cell. So, the activation energy that the vortex should overcome to move across the junctions should be written as: ${U}_{0}\approx p{(H}_{C}^{2}/8\pi$)Ad, where A should be the average surface area of the grains and d the film or grain thickness. Given that A and d are temperature independent, the dependence in the R(T) curves will be only limited by the temperature dependence on the critical field: H_C(T) ($\approx$H₀(1-t²)). So, by using similar approximations like those employed by Tinkham, it is straightforward to see that the AH parameter can be written as: $\gamma =A {(1-{t}^{2})}^{2}$, A´ would be a factor that absorbs all the numerical constants. Therefore, the line shape of the resistive transition of a granular superconducting film should be given by the following:

$$\frac{R}{{R}_{N}}= {\left\{{I}_{0}\left(A {(1-{t}^{2})}^{2}\right)\right\}}^{-2}$$

(2)

Figure 6 shows the fitting of our experimental data for the samples S2 and S3 to Eq. (2), where an expansion in series for the modified Bessel function to the fourth term has been used. One can see that the fitting is much better than the one given by the Eq. (1) (see Fig. 5). This indicates that indeed, in this case, the temperature dependence is limited by the temperature dependence of the critical field without contribution from the volume of the flux bundle. In the general landscape of the vortex dynamics, a characteristic volume for the activation energy that does not depend on the temperature has been observed in the 2D superconducting systems [14, 17]. So that, the present results indicate that our iron based superconducting films with a percolating structure can be considered as a 2D superconducting network of Josephson junctions. The argument of the Bessel function in Eq. (2), near T_CJ can still be approximated as (1-t²)² = [(1-t)(1 + t)]²$\approx$ (1-t)², a temperature dependence for the $\gamma$ parameter frequently observed in various granular superconductors [23, 24]. In the present case, a fitting to the AH model with $\gamma$ ~ (1-t)², gives good results, but the best is obtained if the t² is preserved, as indicated in Eq. (2).

Fig. 6

Fitting of the R(T) curves of the samples S2 and S3 to Eq. (2) during the transition to the global superconductivity

In summary, the transition to the global superconductivity state of a series of granular SmFeAsO_1-xF_x films with different grades of connectedness was studied by measuring the resistance as a function of the temperature. The results indicate that in these granular iron based superconducting samples, it is the phase slippage at the Josephson junctions the mechanism that controls the temperature dependence of the resistance during the transition to the global superconductivity. In a similar way as in other granular superconductors, the precise form of the line shape of the R(T) curve will depend on the dimensionality of the network of the Josephson junctions. In the thicker films, where a 3D network is formed, the curve is fitted by the Ambegaokar-Halperin model modified by Tinkham, which indicates a temperature dependence (1-t)^3/2 for the AH parameter $\gamma$. However in the thin granular films with a percolating structure, in which the presence of the quasi-reentrant superconductivity phenomena indicates that they can be considered as a 2D network of Josephson junctions, the line shape of the R(T) curve still can be described by the AH model if a (1-t²)² temperature dependence for $\gamma$ is presumed. Such temperature dependence would result from an activation energy ${U}_{0}=p{(H}_{C}^{2}(T)/8\pi )Ad$ for the Josephson vortices, where A and d are the surface area and thickness of the grains, respectively, which are temperature independent.