1 Introduction—Superconductivity (SC) in Nickel Perovskite Oxides

Transition metal oxides (TMO) possess a great variety of conduction properties. Recently two research teams have managed to make thin films of nickel oxides with valence Ni(III) [1] and Ni(I) [2, 3] superconducting (SC) in perovskite structures. The doped cuprate La2−xSrxCuO4 is SC for 0.06 < x < 0.25 [4, 5]. La2−xSrxNiO4 with similar structure is non-metallic for x < 0.8, but approaches a metallic, non-SC state for x > 0.8 [6, 7]. NiO and La2NiO4 do not become SC. Ni(II) ions prefer local Oh symmetry [6] in the bulk. The 3d-eg orbitals are degenerate and occupied with parallel spins according to Hund’s rule. High spin makes superconductivity (SC) impossible.

In refs. [1–3], superlattices with NiO2 planes are formed that emulate the CuO2 planes in perovskite structures. The local Ni site symmetry is D4h. The eg degeneracy is broken, resulting in singlet spin for Ni(II). Ni(I) and Ni(III) are now SC, but Ni(II) remains non-SC. Cuprates are SC for Cu(II) but not for Cu(I) and Cu(III). These predictions for perovskites and the problem of “collapse of U” [8] will be explained below.

2 Conductivity in the Normal Region is due to Marcus Electron Transfer

Hubbard U is defined for Ni(II) by the charge transfer reaction [9]:

$${\mathrm{Ni}}_{\mathrm A}\left(\mathrm I\mathrm I\right)+{\mathrm{Ni}}_{\mathrm B}\left(\mathrm I\mathrm I\right)+\hslash\omega\rightarrow \text{Ni}_{\text{A}}+{\mathrm{Ni}}_{\mathrm B}\left(\mathrm I\mathrm I\mathrm I\right)\qquad\left(\hslash\omega=U\right)$$
(1)

The left member of Eq. (1) corresponds to the case of equal charge and alternant spin (AS) and the right member to alternant charge (AC). Hubbard U ≈ 4 eV for Ni(II) and ≈2 eV for Cu(II). The Mott model works for “Mott insulators” but for doped TMOs the relative contribution to conductivity due to Eq. (1) is in fact negligible compared to the Marcus contribution.

Heikes and Johnston showed that conductivity in NiO increases by orders of magnitude in LixNi1−xO even at low doping [10]. Doping oxidizes a fraction (x) of Ni(II) to Ni(III). Electron transfer (ET) into the doped holes requires much less energy than with the Mott mechanism (U). Furthermore, in the Marcus model [11,12,13,14,15,16,17], a new hole is created on the site the electron was donated from. Sequential transfer along a chain of metal atoms is now possible.

Resistivity can be derived from ET probability in a hopping model [17]. By consecutive ET Ni(III) hole sites move in the direction of the field and act as electron acceptors according to:

$${\mathrm{Ni}}_{\mathrm A}\left(\mathrm I\mathrm I\mathrm I\right)+{\mathrm{Ni}}_{\mathrm B}\left(\mathrm I\mathrm I\right)\rightarrow{\mathrm{Ni}}_{\mathrm A}\left(\mathrm I\mathrm I\right)+{\mathrm{Ni}}_{\mathrm B}\left(\mathrm I\mathrm I\mathrm I\right)\quad\left({\Delta G}^0=0\right)$$
(2)

The activation energy for Eq. (2), Ea, is due to small changes in geometry when center A accepts an electron donated by B [11].

The necessary reorganization energy is λ but the activation energy Ea in the case of the Marcus model is:

$${\mathrm{E}}_{a} =\uplambda /4{\left(1 - \Delta /\lambda \right)}^{2} <\uplambda /4$$
(3)

which tends to zero when the coupling Δ (= 2H12) tends to λ.

From the probability for electron transfer in a hopping model, we obtain a resistivity in good agreement with the experiments [17–19]. The Marcus model explains the far IR absorption. It also tells us that the resistance in TMO is due to bond length fluctuations depending on the number of electrons at a site. Bond length differences disappear in the metallic state, implying λ = 0. Collapse of λ and U is an experimental fact [7, 8, 20]. Keeping U constant in the Mott model for increased doping is unphysical.

The bond lengths increase when antibonding orbitals are filled. The reorganization energy λ may be calculated if the force constants are known [12–14]. The radius of the copper ions decreases in the series Cu(I) → Cu(III). In slightly doped perovskite Cu(II) cuprates, Cu(III) sites appear as local sites with shorter CuO bond lengths compared to the bulk. For increased dopings, there is increased delocalization (Δ/λ → 0). The point of full delocalization is not reached in cuprates since the normal region resistivity curves suddenly tend to zero between x = 0.05 and x = 0.06. Pairing and SC sets in [8, 21] and completes the delocalization and λ = 0.

EA is on a free energy surface and can be thought of as the energy of a state. The activation energy U in the Mott model is incorrectly set equal to a constant in most papers. This is deeply unphysical since U and λ as defined above decrease by delocalization caused by doping. The activation energy for conductivity in the Mott model (U) is too large by at least a factor of four (Fig. 1) and decreases by further doping. The only reasonable interpretation of the far IR absorption tending to the Drude peak is that Ea → 0 [18, 19, 22] (Fig. 2). At strong coupling, Δ = λ is clearly possible in TMO and leads to “collapse of U” [Eq. (3)].

Fig. 1
figure 1

The Marcus model [11–17]. The activation energy Ea < λ/4. Δ = 2H12 where H12 is the coupling

Full size image
Fig. 2
figure 2

Delocalization in the Marcus model from non-adiabatic coupling (top curve) to large coupling with Ea = 0 [18, 19]

Full size image

Three other experimental facts are important: (1) repetitive systems are not always metals, (2) a system may be conducting even if it is not repetitive, (3) Marcus Ea = 0 is necessary and sufficient for metallic properties.

The BCS theory for SC in metals, based on k-space theories and Cooper pairs [23], was formulated in 1957. In those days, all known SCs were obtained by cooling ordinary metals below TC. Thirty years later Bednorz and Müller found SC in a system derived directly from a local system [4]. Unfortunately the BCS model cannot be derived in a local model.

In 1937, de Boer and Verwey had found that the simple repetitive system NiO is an insulator in spite of an unfilled valence band [24]. Since then the Mott–Hubbard model has been considered necessary to “prevent” metallic conductivity in NiO. The insulating properties are in reality due to the fact that there is no place for the electron to jump in the undoped, local system. For low doping, we have to accept the fact that r-space theories have to be used, not k-space band models. The resistivity of La2−xSrxCuO4 in the normal region agrees with experimental results [12, 13, 17, 25].

During doping in the strong coupling case, Ea → 0 and λ → 0, meaning that TMO after enough doping may become metals without bond length dependence on site occupations, i.e., λ = 0.

3 Optical Spectra of Nickelates and Cuprates

The larger x in La2−xSrxCuO4 the larger the mixing entropy ΔS and the more lowering of the free energy (ΔG) of the mixed-valence system:

$$\Delta G=\Delta H-T\Delta S\quad\left(T\mathrm{constant}\right)$$
(4)

From Eq. (4) follows that we may approach ΔG = λ = 0 by doping (collapse of U). The peak at 2 eV in La2CuO4 must be = U since there are no Cu(III) sites available at x = 0 (Eq. (1)). The larger the doping the larger the delocalization, and the smaller both λ and charge transfer energy U at a fixed structure. The collapse of U is approaching.

This way of reasoning does not include any “on-site repulsion.” In fact the latter concept is strange since there are always compensating attractions which are not accounted for. In a Mott model, there is no explanation of the collapse of U. U is simply assumed to remain constant during doping, which is preposterous.

Collapse of U was first described without name in the important paper by Uchida et al. [8]. Reflectivity spectra of doped cuprates are analyzed particularly with respect to optical conductivity. There is spectral density transfer from ≈2 eV to the mid- and far IR region [7, 8, 26, 27]. In the Marcus model (Eq. (3)), Ea is much smaller than λ. The density of states in the far IR region builds up with doping. The Marcus model thus explains not only the far IR states but also their convergence into the Drude state.

In the nickelate La2−xSrxNiO4, there are two mid-infrared peaks at x = 0.5 and 1.5 eV [7, 28]. The peaks merge to a single peak at x = 0.7 tending to a Drude peak at x = 0.9. For x > 1, there is mixing between Ni(III) and Ni(IV) which leads to a quite wide Drude peak, with disappearing temperature dependence [7]. The resistivity as a function of temperature has a typical Marcus behavior from x = 0.5 to x = 1.0 with doping dependence (Fig. 1 of ref. [7]) and a minimum tending to zero with doping. For x > 0.9, there is increasing metallic behavior with λ → 0. At x = 1.2, the bond distance difference is wiped out and we have a metal with only T or T3/2 metallic temperature dependence in the resistivity [7].

Although LaNiO3 is antiferromagnetic at very low temperatures [28–30], there is metallic conductivity of the form:

$$\rho \left(T\right) =A +{BT}^{3/2}$$
(5)

The 3/2 power of Eq. (5) and also a linear form originate in the Marcus equation, Eq. (2) [21, 22]. Most other RNiO3 crystals (R ≠ La) collapse to an insulating phase at low temperature with low symmetry. Above the transition temperature, the latter RNiO3 systems, for instance PrNiO3, have resistivities linear in T and are perfect metals [29, 30].

LaNiO3 has metallic absorption of light up to 7 eV [28]. In a metal, the reorganization energy is = 0 since all electrons are equally distributed band electrons. There is no localization due to electronic motion and thus λ = 0. No doping is necessary for metallic behavior in the bulk phase of LaNiO3 [1]. Ni(I) compounds are also SC in superlattices but doping is necessary in NdNiO2 [18, 19].

One role of superlattices of nickelates is to break the degeneracy between the 3d-eg orbitals x2 − y2 and z2 for Ni(II) to avoid the action of Hund’s high-spin rule. It seems that Ni(II) has a role to play even in Ni(III) and Ni(I) systems. This will be explained in the next section. In “Sect. 5,” we will show that the interactions for pair formation in Cu(II) compounds are absent for Ni(II) or Cu(III) with 3d8 occupation.

4 Pair Formation Consists of Two Coherent Marcus Steps

Very few TMO are metals in undoped form. It is therefore close to impossible to use k-space theory [23] of the BCS model to explain SC. Charge transfer excitations within the valence shell are hardly of any interest in BCS since U is always = 0. In Eq. (1) for cuprates La2CuO4, the excitation energy ħω ≈ 2 eV, only half of its value for La2NiO4. The on-site repulsion for the larger ion [Ni(II)] should be smaller than for a smaller ion copper Cu(II)!

Exchange of electrons and electron pairs between two metal ions requires that the oxidation states on adjacent sites are strongly coupled since the distance between the metal ions is large. CuA(II)/CuB(II) couples oxidation states CuA(I)CuB(III), resulting in electron pair transfer A → B [18]. In Ni(II), coupling is not possible in the same way; it is in fact forbidden.

A coherent transfer can be calculated by configuration interaction (CI). The overall symmetry is decisive for the overlap and similar to the case of the hydrogen molecule [31]. In the latter case, the so-called ionic wave functions play an unimportant role. Here we are talking about interaction between the alternant charge (AC) phase and the alternant spin (AS) phases. The AC phase corresponds to the ionic wave functions and the AS phase to the valence-bond wave function. The singlet spin function is written as (αβ − βα). α and β are orbital spins; a and b are wave functions centered on atoms A and B, respectively. From the AC “ionic” states, two functions arise:

$${\psi }_{2}\left(\mathrm{1,2}\right) = \left[a\left(1\right)a\left(2\right) + b\left(1\right)b\left(2\right)\right] \left(\alpha \beta - \beta \alpha \right)$$
(6)
$${\psi }_{3}\left(\mathrm{1,2}\right) = \left[a\left(1\right)a\left(2\right) - b\left(1\right)b\left(2\right)\right] \left(\alpha \beta - \beta \alpha \right)$$
(7)

The AS phase is represented by the valence bond wave function:

$${\psi }_{1}\left(\mathrm{1,2}\right) = \left[a\left(1\right)b\left(2\right) + b\left(1\right)a\left(2\right)\right] \left(\alpha \beta - \beta \alpha \right)$$
(8)

The interaction between Ψ1 and Ψ2 provides the “glue” for pairing.

The electronic picture is shown in Fig. 3a, b in terms of oxidation states. Electron pairs are formed and move forward. The first ET step in Fig. 3a is ET from the Cu(I) to Cu(III), forming the intermediate Cu(II)/Cu(II) state. The second step is ET from the left Cu(II) to the right Cu(II) forming Cu(III)Cu(I). Coherent transfer is equivalent to CI between Ψ1 and Ψ2.

Fig. 3
figure 3

Pair formation in r-space. a Two electrons move from A to B. b Pair flow in a chain from left to right involving three oxidation states

Full size image

The a and b orbitals have eg symmetry [3d(x2 − y2)] on the sites A and B. The energy of the non-interacting Bogoliubov state Ψ3 separates the SC gap from the pseudogap. The overlap integral:

$$\begin{aligned}&\int {\Psi }_{1}\left({1,2}\right)\;{\Psi }_{2}\left({1,2}\right)\;{{d}\mathbf{r}}_{1}{{d}\mathbf{r}}_{2}\\&\;\;= \int [{a}(1){b}(2) +{ b}(1){a}(2)]\; [{a}(1){a}(2) +{ b}(1){b}(2)]\; {{d}\mathbf{r}}_{1}{{d}\mathbf{r}}_{2} \\&\;\; =4\int {abd}{\mathbf{r}}_1\end{aligned}$$
(9)

The ground state of an electron pair contains components of all three oxidation states of copper: Cu(I), Cu(II), Cu(III) (with their coupled O2p components) in the description of the pair and its motion from A to B. Pair motion consists of two coherent ET steps. For T > TC, thermal motion prevents coherence.

Here we have ignored the orbital of the oxygen atom in between the metal atoms. a + b interacts with O2s and a − b with O2p. At the end, we will be interested in the most antibonding combinations within this set, meaning that the antibonding orbitals with respect to O2p particularly. For the Cu(II) and Ni(II) perovskite structures, this means that some of the so-called 3 deg orbitals will be the highest occupied ones. The pattern of interactions in Eqs. (6)–(8) will not be disturbed.

In spite of large inter-metal distances between the metal ions, the coupling is large between the AC configurations and the cuprate (II)/(II) configuration in Eq. (9). Hence, pair formation and pair transfer need three stable oxidation states to describe pair transfer. CI between Ψ1 and Ψ2 leads to the electron pair ground state, followed in energy by the Bogoliubov state and the antibonding CI state. This is consistent with experiments which show that the SC gap and the pseudogap have a common origin.

If the increase of doping leads to a metal, the system becomes visibly delocalized in the sense that all bond length differences disappear [32]. Next we will study the coupling and find that transfer of two electrons has to take place through the same orbitals to obtain coherent pair transfer and SC.

5 Why SC in Cu(II), Ni(I), and Ni(III) but not in Ni(II) and Cu(III)?

In Fig. 3, Ψ1 and Ψ2 must have a large coupling matrix element to create stable pairing and make electron pair transfer possible. For cuprates (Fig. 3):

$${\mathrm{Cu}}_{\mathrm{A}}(\mathrm{I}) + {\mathrm{Cu}}_{\mathrm{B}}(\mathrm{III}) \to {\mathrm{Cu}}_{\mathrm{A}}(\mathrm{II}) + {\mathrm{Cu}}_{\mathrm{B}}(\mathrm{II}) \to {\mathrm{Cu}}_{\mathrm{A}}(\mathrm{III}) + {\mathrm{Cu}}_{\mathrm{B}}(\mathrm{I})$$
(10)

The product of Slater determinants CuA(I) × CuB(III) integrated with CuA(II) × CuB(II) must be large and significant (Eq. (9)). In CuA(I) × CuB(III), both additional electrons in CuA(I) fill the eg(x2 − y2) orbital. Electron transfer to the empty eg spin orbital of CuB(II) is possible. Transfer from eg(x2 − y2) on CuA with different spin to CuB(II) is also possible (Fig. 3a).

We now compare Eq. (10) to the corresponding Eq. (11) for nickelates:

$${\mathrm{Ni}}_{\mathrm{A}}(\mathrm{I}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{III}) \to {\mathrm{Ni}}_{\mathrm{A}}(\mathrm{II}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{II}) \to {\mathrm{Ni}}_{\mathrm{A}}(\mathrm{III}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{I})$$
(11)

NiA(I) is a 3d9 system. Assuming that eg(x2 − y2) is the highest occupied orbital (HOMO), the electron in the eg(x2 − y2) can transfer to the empty eg(x2 − y2) of NiB. The eg(x2 − y2) on center NiA is now empty. Transfer of a second electron to eg(x2 − y2) of NiB cannot be carried out unless we take it from the eg(z2) orbital of NiA. The latter transfer needs energy which would lead to resistivity. Thus, an electron pair cannot be transferred from A to B in the Ni(II) case. Ni(II) cannot be SC.

Zhou et al. studied, however, an Ni(III) superlattice where Eq. (12) holds:

$${\mathrm{Ni}}_{\mathrm{A}}(\mathrm{II}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{IV}) \to {\mathrm{Ni}}_{\mathrm{A}}(\mathrm{III}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{III}) \to {\mathrm{Ni}}_{\mathrm{A}}(\mathrm{IV}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{II})$$
(12)

NiA(II) is a 3d8 system and NiB(IV) a 3d6 system. The singly occupied eg(x2 − y2) orbital (3dz2 is unoccupied [1]) plays the same role as the occupied eg(x2 − y2) in Cu(II). In the superlattice with NiO2-MnO2 planes in D4h geometry, Ni(II) has singlet spin due to loss of degeneracy. Ni(IV) always has a closed 3d(t2g)6 subshell. Equation (12) is thus useful for pairing in a superlattice. LaNiO3 becomes SC in a superlattice with TC ≈ 3.5 K. The other RNiO3 systems collapse to an insulator as mentioned above [29, 30].

Also in the case of ref. [2, 3], the strategy was to find a similar nickelate perovskite structure as in the II-cuprates. Li et al. reduced Nd1−xSrxNiO3 to Nd1−xSrxNiO2 and doped the latter to × ≈0.2. Equation (13) replaces Eq. (12).

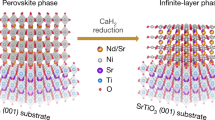
$${\mathrm{Ni}}_{\mathrm{A}}(\mathrm{II}) + {\mathrm{Ni}}_{\mathrm{B}}(0) \to {\mathrm{Ni}}_{\mathrm{A}}(\mathrm{I}) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{I}) \to {\mathrm{Ni}}_{\mathrm{A}}(0) + {\mathrm{Ni}}_{\mathrm{B}}(\mathrm{II})$$
(13)

The central oxidation state is Ni(I)-3d9 as in Cu(II) with AS ground state. Ni(0) with 3d10 configuration is a spin singlet state, and Ni(II) is a spin singlet state in the superlattice. Ni(0) and Ni(II) are both spin singlet states in ref. [2]. Ni(I) in LaNiO2 mimics Cu 3d9 well, as is the purpose. A problem is that the R ion La(III) is large and does not permit strong enough coupling. Li et al. [2] solved this problem by using Nd(III) instead of La(III) since Nd(III) is smaller than La(III). Nd1−xSrxNiO2 has as quite high critical temperature TC ≈ 15 K [2, 3].

We have thus explained the experimental results in both [1] and [2, 3]. The three important oxidation states are Ni(0)/Ni(I)/Ni(II) in [2, 3] and Ni(II)/Ni(III)/Ni(IV) in [1]. The spins are low spin on all nickel oxidation states from Ni(0) to Ni(IV) in the superlattice with D4h local symmetry.

We conclude that the requirements of pairing and spin reduce severely the possibilities for SC in TMO. The 3-oxidation states rule for pairing implies that since Cu(II) is SC, the previous element in the periodic table, also with perovskite structure, can be SC for Ni(I) and Ni(III), but not for Ni(II). This agrees with the experimental findings so far.

There is also a 1-oxidation state rule for insulators. If a metal ion in a conducting chain of a metal oxide only possesses a single oxidation state, the conductivity is severely depressed since donors and acceptors are missing. An example is zinc for which Zn(II) is the only possible positive oxidation state [33]. Replacing Cu(II) by Zn(II) leads to canceling of a channel for ET. The same is the case for the ions that are used as dopants.

Finally there is the 2-oxidation states rule for ordinary metals already mentioned above. With oxidation states different in one unit on adjacent ions, Marcus ET is possible as we see from Eq. (2) above. If Ea → 0 for T → 0 K, the system goes from a quite normal insulator → metal, i.e., from r-space to k-space. A single hole or single electron on adjacent atoms is sufficient to form a metal but three successive spin singlet oxidation states are necessary to form a superconductor.

The theory given here is consistent with the results of refs. [1–3] that SC exists for oxidation states I and III for nickel, compared to Cu(II) for copper. This also shows that the Marcus model is a very useful model for metal–insulator transitions at doping.

6 The Importance of Coupling

In the first submitted version of this paper, the referee gracefully pointed out that in LaNiAsO the oxidation state is obviously Ni(II), though three oxidation states are necessary for SC. LaNiAsO is itself a superconductor for T ∼ 2.75 K, in a compound where the oxidation state of Ni can only be Ni(II). However, the doped compound LaNiAsO0.9F0.1 shows sharp SC and specific heat jump at the critical temperature at TC ∼ 3.8. This hints that this pnictide is strongly coupled and is of the same type as the perovskite cuprates rather than a BCS superconductor [34]. The strong coupling is due to the much shorter distance between the directly coupled Ni(II) sites if bonded to the As(-III) ions as compared to the perovskites.

In a local system, bond lengths are different for different oxidation states in a mixed-valence system. In the limit of delocalization, after sufficient doping, the system is metallic without any bond length differences. This permits application of Bloch theory [35]. An experimental example is given in [32, 36] in the case of a doped Bi(III)-Bi(V) system.

The coupling between the Ni ions in the pnictides is sufficient to permit superconductivity and therefore no oxidation states with different bond distances can be detected.

7 Discussion and Conclusions

High TC superconductivity takes us from the r-space of oxidation states to the k-space of metals. In the cuprates, the difference in bond length between Cu(I), Cu(II), and Cu(III) sites disappears when the system becomes metallic. In LaONiAs, due to direct bonding between the Ni ions and short NiAs distance in the NiAs complex, the undoped system is already metallic.

Metallic properties and bonding properties are complimentary in a sense of Bohr [37]. In a metallic system, no oxidation state differences can exist. In local theory, the bond lengths depend on the oxidation state of the metal ion. In the TMOs, the HOMOs are antibonding, hence shorter bonds for higher oxidation state.

In the transport chain of Fig. 3, the average oxidation state is Cu(II). In this transport, Cu(III) also plays a role as we see. Cu(III) is the so-called Zhang-Rice singlet, since in its spin singlet state, it was considered to have a special role in superconductivity. Actually it plays exactly the same role as Ni(II) in superconducting Ni(I) and Ni(III) oxides, i.e., a secondary role according to Eqs. (12) and (13) of importance for pair motion.

A quite simple theory for superconductivity in TMO may now be formulated for perovskite doped “Mott insulators” La2CuO4, La2NiO4, LaNiO3, and NdNiO2. In the r-space description, the only way to get conductivity by electron pairs is by disproportionation, Eq. (1) (ħω = 0). As soon as Cu(III) ions appear by doping, conductivity increases by orders of magnitude. The Mott parameter U becomes zero in photoconductivity spectra after some doping [7, 8]. At the same time, the TMOs become metallic.

Is there any difference between λ and U? According to Mott, U is the excitation energy of a vertical optical transition where one electron jumps to the next metal site with the same charge, without change of nuclear coordinates. λ is the same except that there is one electron less. Hence, λ ≈ U. Both λ and U may collapse upon doping. The definition of U as on-site repulsion is not warranted. The curvature of the potential energy surfaces in the normal region is important in the Marcus model [12] and this leads to a low energy landscape in the far IR region.

Finally, the experimental data of [1–3] have been explained. We observe a connection between oxidation states and off-diagonal coupling matrix elements. Ni(I) and Ni(III) become SC in superlattices but not in the bulk. In the bulk, Ni(II) is high spin and therefore Ni(I) and Ni(III) cannot be SC. The coupling matrix elements to Ni(II) are equal to zero. Ni(II) cannot be SC even in a superlattice, due to the lack of coupling in Eq. (11).