Spin Switching Mechanism Stimulated by Linearly Polarized Femtosecond Optical Pump

Abstract

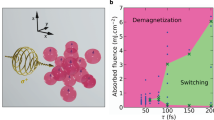
We propose the mechanism for the optical magnetization reversal of metallic ferrimagnets near the magnetic compensation temperature in a zero magnetic field using a femtosecond linearly polarized optical pumping. The mechanism is based on the spin sublattice model proposed by M. I. Kurkin and N. B. Orlova in 2019. This model assumes the formation of spin sublattices with the obligatory participation of magnetic anisotropy eliminating degeneracy in the spectrum of the exchange interaction operator. The discussed optical magnetization reversal was observed experimentally in the GdFeCo alloy near the magnetic compensation point.

Appendix. Peculiarities of the New Model of Spin Sublattices

The spins of electrons $\mathbf {s}_j$ (j is the spin number) are quantum objects; therefore, their states should be described by a wave function, which is a solution for the stationary Schrdinger equation [14]

$$\begin{aligned} \mathcal {H}\psi =E \psi . \end{aligned}$$

(19)

Here $\mathcal {H}$ is the Hamilton operator composed of interactions involving the spins $\mathbf {s}_j$. The strongest of these is the exchange interaction [13, 14]:

$$\begin{aligned} V_{ex} = \sum _{jk} J(\mathbf {r}_j -\mathbf {r}_k)(\mathbf {s}_j\cdot \mathbf {s}_k), \end{aligned}$$

(20)

$J(\mathbf {r}_j -\mathbf {r}_k)$ are the exchange parameters depending on the distance between the spins at the points with coordinates $\mathbf {r}_j$ and $\mathbf {r}_k$. The minimum $V_{ex}$ at $J(\mathbf {r}_j -\mathbf {r}_k)<0$ is attained for the ferromagnetic (F) orientation of the$\mathbf {s}_j$ and $\mathbf {s}_j$ spins. The corresponding wave function $\psi _F$ has these properties:

$$\begin{aligned} \left\langle \psi _F \left| s_j^z\right| \psi _F\right\rangle =\frac{1}{2}, \quad \left\langle \psi _F \left| S^z \right| \psi _F\right\rangle =\frac{N}{2}, \quad \mathbf {S} =\sum _{j=1}^N \mathbf {s}_j \end{aligned}$$

(21)

The equilibrium state of the spins $\mathbf {s}_j$ and $\mathbf {s}_k$ at $J(\mathbf {r}_j -\mathbf {r}_k)>0$ is achieved at their antiferromagnetic (AF) orientation. To describe the AF state of spins, the hypothesis of spin sublattices is usually used postulating the F-ordering of spins within each sublattice. The simplest AF ordering is described by two sublattices with spins [13]:

$$\begin{aligned} \mathbf {S}_1 =\sum _{j=1}^N \mathbf {s}_j, \quad \mathbf {S}_2 =\sum _{j=1}^N \mathbf {s}_k. \end{aligned}$$

(22)

According to the hypothesis of sublattices, the wave function $\psi _{AF}$ should provide the following values for the diagonal matrix elements of the operators $s_{j,k}^z$ and$S_{1,2}^z$

$$\begin{aligned} \left\langle \psi _{AF} \left| s_j^z\right| \psi _{AF}\right\rangle = -\left\langle \psi _{AF} \left| s_k^z\right| \psi _{AF}\right\rangle =\frac{1}{2}, \nonumber \\ \left\langle \psi _{AF} \left| S^z_1 \right| \psi _{AF}\right\rangle =- \left\langle \psi _{AF} \left| S^z_2 \right| \psi _{AF}\right\rangle =\frac{N}{2} \end{aligned}$$

(23)

However, quantum properties of the spins prevent the application of the sublattice hypothesis to the exchange interaction $V_{ex}$ (20) summing two parts:

$$\begin{aligned} V_{ex}= V^{zz}_{ex}+V_{ex}^{\pm }, \nonumber \\ V_{ex}^{zz} = \sum _{j,k} J(\mathbf {r}_j -\mathbf {r}_k) s_j^z s_k^z,\\ V_{ex}^{\pm } =\frac{1}{2} \sum _{j,k} J(\mathbf {r}_j -\mathbf {r}_k) \left( s^+_j s^-_k +s^-_js^+_k\right) \nonumber \\ s^{\pm }=s^x \pm i s ^y. \nonumber \end{aligned}$$

(24)

The $V_{ex}^{\pm }$ operator switches the antiparallel spins in the sublattices destroying the F-order in them. This effect of exchange mixing of spins doubts the possibility of using the sublattice hypothesis to describe antiferromagnets. Anderson [6] and Ziman [7] ] managed to overcome the exchange mixing problem by simplifying the equation

$$V_{ex}\psi _{AF}=E_{AF}\psi _{AF}$$

After simplification, the solution of this equation allows the existence of sublattices only for three-dimensional AF ordering with a slightly reduced sublattice length

$$\begin{aligned} \left\langle \psi _{AF} \left| S_1^z\right| \psi _{AF}\right\rangle = -\left\langle \psi _{AF} \left| S_2^z\right| \psi _{AF}\right\rangle = \frac{N}{2}(1-\Delta ). \end{aligned}$$

(25)

The value $\Delta \approx 0.1$ turned out to be independent of the number of spins N in the sublattice. This means that the quantum cancellation of the spins of the sublattices (22) is preserved even at the limit $N\rightarrow \infty$, when the spins $\mathbf {S}_{1,2}$ (22) can seem to be considered as classical vectors. Moreover, the Anderson-Ziman approximation cannot ensure the existence of spin sublattices for one- and two-dimensional AF orderings. The zero values of the diagonal matrix elements

$$\begin{aligned} \left\langle \psi _{AF} \left| S_{1,2}^z\right| \psi _{AF}\right\rangle =0 \end{aligned}$$

(26)

for such AF orderings correspond to the complete destruction of the sublattices.

Another approach to finding the sublattice solutions of Eq. (19) for AF states was used in [5]. Instead of simplifying the operator $\mathcal {H}$ in $\mathcal {H}$, we used solutions to auxiliary problems with Hamiltonians $\mathcal {H}$ of special artificial form allowing to obtain the exact solutions (19). Although these solutions have nothing to do with real-life antiferromagnets, they allowed us to reveal a number of properties of the sublattice wave functions $\psi _{\uparrow \downarrow }$, which are applicable to Eq. (19) with any $\mathcal {H}$. One of such artificial objects is a pair of antiparallel magnetic arrows. If we assume that the F-ordering in the arrows is caused only by the exchange interaction of spins inside the arrows $V_{ex}(1)$ and $V_{ex}(2)$, then in the absence of exchange interaction of different arrows, the spin wave function of such an object $\psi _{\uparrow \downarrow }$ should be a solution to the equation:

$$\begin{aligned} V_{ex} = \left( V_{ex}(1) + V_{ex}(2)\right) \psi _{\uparrow \downarrow }= E_{\uparrow \downarrow } \psi _{\uparrow \downarrow } \end{aligned}$$

(27)

Now it is necessary to take into account that the operator $V_{ex}$ has the following property:

$$\begin{aligned} \left[ V_{ex}, \mathbf {S}^2\right] = V_{ex}\mathbf {S}^2 - \mathbf {S}^2 V_{ex}=0, \quad \mathbf {S}= \mathbf {S}_1 -\mathbf {S}_2 \end{aligned}$$

(28)

is full spin of a pair of arrows.

The property (28) means that the wave function $\psi _{\uparrow \downarrow }$ must be an eigenfunction of the operator $\mathbf {S}^2$

$$\begin{aligned} \mathbf {S}^2 \psi _{\uparrow \downarrow }=S(S+1) \psi _{\uparrow \downarrow } =0 \end{aligned}$$

(29)

for the eigenvalue $S=0$. The exact solution (29) given in [4] has the following property:

$$\begin{aligned} \left\langle \psi _{\uparrow \downarrow } \left| S_{1,2}^z\right| \psi _{\uparrow \downarrow }\right\rangle =0 \end{aligned}$$

(30)

It means that the F-order in the arrows cannot be determined only by the exchange interaction $V_{ex}$ (27). Additional perturbations V(1) and V(2) are required with the following property

$$\begin{aligned} \left[ V(1), \mathbf {S}^2\right] \ne 0, \quad \left[ V(2), \mathbf {S}^2\right] \ne 0 \end{aligned}$$

(31)

Only under these conditions can the Eq. (29) and

$$\begin{aligned} (V_{ex}+V)\psi _{\uparrow \downarrow }= E_{\uparrow \downarrow }\psi _{\uparrow \downarrow }, \quad V=V(1)+V(2) \end{aligned}$$

(32)

have different solutions; therefore, the property (30) is not applicable to solutions (32) and cannot prevent the F-ordering in the discussed arrows.

The quantum mechanics (see, for example, [14]) admits the possibility of a strong influence of a weak perturbation V on the wave function $\psi _{\uparrow \downarrow }$, since the spectrum of the operator $V_{ex}$ is degenerate, and V eliminates this degeneracy. Magnetic anisotropy $V_{an}$ refers to this type of disturbance. However, this is not the only property of $V_{an}$, being necessary for the solution of the equation

$$\begin{aligned} (V_{ex}+V_{an})\varphi _{AF} = E_{AF}\varphi _{AF} \end{aligned}$$

(33)

to describe the spin sublattices. Such additional properties of $V_{an}$ were found with the help of one more auxiliary solution of Eq. (33) with $V_{ex}^{sp}$ and $V_{an}^{sp}$ of a special form, allowing to obtain its exact solution.

The exact solution of the equation obtained in [5]

$$(V_{ex}^{sp}+V_{an}^{sp})\varphi ^{sp}_{AF} = E_{AF}^{sp}\varphi _{AF}^{sp}$$

allowed to get the expressions for the matrix elements (23) in the form

$$\begin{aligned} \left\langle \varphi _{AF}^{sp} \left| s_j^z\right| \varphi _{AF}^{sp} \right\rangle = -\left\langle \varphi _{AF}^{sp} \left| s_k^z\right| \varphi _{AF}^{sp} \right\rangle = \frac{1}{2}\left( 1-\epsilon \pm \delta \right) \end{aligned}$$

(34)

under the condition

$$\begin{aligned} \epsilon = \frac{H_E}{H_A N} \ll 1 \end{aligned}$$

(35)

Here $H_E\approx 10^6-10^7$ Oe is an exchange field, which is usually used to estimate the value of $V_ex$, $H_A <10 ^ 3$ Oe is the corresponding value for $V_{an}$, N is the number of spins in the sublattice. The value $\delta \approx \epsilon ^2$ determines the calculation error of the matrix elements (34) in the linear approximation in $\epsilon$. The presence of a small parameter $\epsilon$ (35) makes it possible to find an approximate Eq. (33) for the interactions $V_{ex}$ and $V_{an}$, which are used to describe real antiferromagnets. Moreover, for the matrix elements (23) in the linear approximation in $\epsilon$ in [4], we obtained the formulas

$$\begin{aligned} \left\langle \varphi _{AF} \left| s_j^z\right| \varphi _{AF} \right\rangle = -\left\langle \varphi _{AF}\left| s_k^z\right| \varphi _{AF}\right\rangle = \frac{1}{2}\left( 1-\epsilon w \right) \end{aligned}$$

(36)

Formulas (34) and (36) differ by the coefficient w, for which the following estimate was obtained in [5]:

$$\begin{aligned} 0<w < 1. \end{aligned}$$

(37)

From (35) to (37), it follows that the quantum corrections to the spins of the sublattices can be neglected in the limit $N\rightarrow \infty$, and their dynamics can be described by the classical Landau and Lifshitz equations [8]. These equations have been used so long and successfully to describe the magnetic properties of antiferromagnets that the result obtained can be considered an argument in favor of the sublattice model proposed in [5]. However, we consider the most weighty argument in favor of this model the explanation proposed in this article for the destruction of sublattices with their subsequent reorientation under the condition $\tau _1<\tau _2$ (14) after linearly polarized femtosecond optical pumping.