1 Introduction

Rare earth perovskite manganites are known to exhibit interesting physical properties such as charge ordering, orbital ordering, and phase separation in addition to their well-known feature of colossal magnetoresistance (CMR) across the electrical and magnetic transition [1,2,3]. The magnetic field-induced first-order magnetic phase transition from charge-ordered antiferromagnetic phase (COAFM) to ferromagnetic metallic phase (FMM) is an interesting aspect of manganites that is vigorously pursued in the literature [4,5,6]. At lower temperatures, these systems exhibit phase coexistence which is highly sensitive to the external magnetic field, pressure, chemical substitution, and particle size reduction [7,8,9,10,11].

One of the popular ways of influencing the physical properties in manganites is by chemical substitution, which can be seen as inducing chemical pressure, substituting electrons for holes or vice versa, or simply creating a system where only electron count is altered to control the physical properties [12,13,14,15,16,17]. Hole doping in manganites is widely explored owing to the rich phase diagram, which is sensitive to the type of dopant and its concentration [13,14,15,16,17,18]. Apart from chemical substitution, external perturbation such as hydrostatic pressure [9, 11], magnetic field [7], and particle size reduction to nanoscale [19,20,21] can also be used to tune the physical properties of manganites. Recent studies on the influence of particle size reduction on the physical properties of manganite nanoparticles reveal the appearance of new features such as superparamagnetism, large coercivity, and low field magnetoresistance which are different from the bulk counterpart [22,23,24]. These unique characteristics enable their potential for application in magnetic hyperthermia, photocatalysis, magnetic sensors, etc. [25,26,27]. In addition to the above, the melting of the robust charge-ordered state in manganite nanoparticles results in large magnetization thus making them suitable for magnetic refrigeration application [19, 28].

Recent literatures on Bi3+ substituted perovskite system (i.e., LaSrMnO3 [29, 30], LaCaMnO3 [31, 32], PrSrMnO3 [33, 34], LaBaMnO3 [35], and LaAgMnO3 [36, 37]) reveal an overall reduction TC and net magnetization for partial Bi3+ content. However, as Bi3+ concentration increases, a change in magnetic ground state has been noticed for LaSrMnO3 [29, 38], LaCaMnO3 [31, 32], and PrSrMnO3 [34]. Whereas in case of Bi3+ substituted NdCaMnO3 [39] and NdSrMnO3 [40], an interplay between charge ordering and antiferromagnetism has been observed. The detailed analysis of our study describes that the systematic replacement of La3+ with Bi3+ in La0.7−xBixSr0.3MnO3 bulk polycrystals results in a cross-over from dominant FM interaction (x ≤ 0.25) to AFM interactions (x ≥ 0.4) with magnetic phase coexistence for x = 0.3 and 0.35 [10, 41,42,43,44,45]. Though x = 0.35 represents the half-doped regime of La3+ and Bi3+, where it is expected to have competitive phase coexistence of FM and AFM ground state [42, 44], we found that it is more AFM compared to x = 0.3. Thus, in the present work, we have chosen the phase-coexistence compound, La0.4Bi0.3Sr0.3MnO3 (x = 0.3) and subjected it to high-energy planetary ball mill for reducing the particle size. The results of structural and magnetic property studies are presented and discussed here in the context of understanding the influence of particle size reduction on the magnetic phase coexistence in La0.4Bi0.3Sr0.3MnO3 (henceforth referred to as LB3SMO).

2 Experimental Details

The polycrystalline bulk sample of LB3SMO was prepared by solid-state reaction of high-purity oxides of (all with stated purity ≥ 99.9%) La2O3 (Sigma Aldrich), Bi2O3 (Sigma Aldrich), SrCO3 (Sigma Aldrich), and MnO2 (Alfa Aesar) following the equation:

$$0.2\left({\mathrm{La}}_{2}{\mathrm{O}}_{3}\right)+0.15\left({\mathrm{Bi}}_{2}{\mathrm{O}}_{3}\right)+0.3\left({\mathrm{SrCO}}_{3}\right)+{\mathrm{MnO}}_{2}\to {\mathrm{La}}_{04}{\mathrm{Bi}}_{0.3}{\mathrm{Sr}}_{0.3}{\mathrm{MnO}}_{3}+x\;{\mathrm{CO}}_{2}\uparrow$$

The detailed methodology of the bulk synthesis is reported elsewhere [42, 43]. In the second step, the sintered pellets obtained at the end of the first step were crushed into a fine powder and then subjected to high-energy planetary ball milling to prepare nanoparticles. The detailed methodology of preparation of the nanoparticles has been reported in our earlier communications [45]. In the present case, the milling time was varied from t = 0 h (which is a bulk sample, finely ground) to 48 h. A small quantity of sample was removed after 0, 12, 24, 36, and 48 h of milling. The samples will be hence referred to as LB3SMO-0, LB3SMO-12, LB3SMO-24, LB3SMO-36, and LB3SMO-48, respectively.

Powder X-ray diffraction (XRD) measurements carried out on a Bruker D8 Advance powder X-ray diffractometer with a step-size of 0.02° (in 2θ) using Cu-Kα as the radiation source, establish the crystal structure and phase purity of the prepared samples. Neutron powder diffraction (NPD) measurements were carried out on LB3SMO-0 and LB3SMO-48 samples at room temperature using a position-sensitive detector-based focusing crystal diffractometer, PD-3 at Dhruva Reactor, Trombay [46]. Field emission scanning electron microscope (FESEM) was used to analyze the surface morphology using Oxford Zeiss Sigma Microscope. Transmission electron microscope (TEM) images were taken on LB3SMO-48 sample at room temperature on FEI Tecnai F30 Twin. Magnetic measurements were carried out using quantum design physical property measurement system (QD-PPMS)-based vibrating sample magnetometer (VSM) in magnetic fields up to ± 90 kOe and temperature down to 3 K.

3 Results and Discussions

3.1 Structural Studies

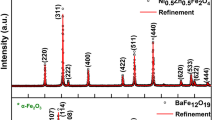
The XRD profiles of all samples of the LB3SMO series were analyzed by the Rietveld refinement method using the FullProf program [47]. It can be clearly seen from Fig. 1 that all samples crystallize in orthorhombic structure, space group Pnma. The LB3SMO-0 sample has a small fraction of the Mn3O4 phase (~ 5% of phase fraction) [48]. After ball milling, no additional peaks were observed in the XRD patterns, hence ruling out any contamination from the milling jars/balls. The refinement parameters are summarized in Table 1. With increasing milling time, Bragg peaks broaden (e.g., see the peaks (1 2 1), (2 0 2), and (3 2 1) in Fig. 2a), which is more than the instrumental line width, clearly indicating a reduction of particle size and increase in the microstrain. It can be seen in Fig. 2a that for LB3SMO-0 sample the peaks are sharp, which broadens with increasing milling and overlaps after a certain time of milling. Figure 2b shows the variation in full width at half maxima (FWHM) with milling time, of the peaks (1 2 1) at 2θ = 32.6° and (3 2 1) at 2θ = 58.2°, respectively. A significant increase in the FWHM is observed up to a milling time of 24 h, beyond which the FWHM attains saturation value. This observation indicates that ball milling can reduce the particle size down to a certain limit only.

Fig. 1
figure 1

X-ray diffraction patterns of LB3SMO-t samples refined using the Rietveld method are shown here. The vertical lines indicate the Bragg peak positions; first row indicates positions of the parent phase, LB3SMO, whereas the second row indicates positions for the secondary phase, Mn3O4

Full size image
Table 1 Unit cell parameters and Rietveld refinement parameters of X-ray diffraction patterns for bulk and ball-milled LB3SMO (orthorhombic structure, space group Pnma)
Full size table
Fig. 2
figure 2

(a) Broadening of (1 2 1), (2 0 2), and (3 2 1) Bragg peaks is shown for comparison between bulk and nanoparticles of LB3SMO samples. (b) Plot shows the variation in FWHM of (1 2 1) and (3 2 1) peaks as a function of milling time

Full size image

From the detailed analysis of the XRD data by the Rietveld refinement method using FullProf, an estimate of particle size and microstrain can be made. FullProf generates the microstructure file by an integral breadth method where the average size and strain for each reflection is computed [49]. Figure 3 illustrates the variation in particle size and microstrain with milling time. It can be noticed here that with the initial phase of ball milling (t = 0–24 h), there is a drastic reduction in particle size from 223 to 21 nm, similar to the trend observed in the variation of FWHM. Beyond 24 h of ball milling, particle size shows a small increment, i.e., 24 nm for 36 h and 23 nm for 48 h of ball milling. The increase is very small, i.e., 3 nm and cannot be considered significant change. Therefore, we conclude that the particle size tends to saturate beyond 24 h of ball milling, while the induced microstrain increases monotonously up to 36 h of ball milling and then decreases marginally. The observed slight increase in particle size beyond 24 h of ball milling may be assigned to the agglomeration resulting from the local heating effect during ball milling process due to constant collision between the ball and the sample mass with walls of the vials. Since the feed size at the beginning of the milling process is large, the enhanced rate of dislocation densities and defects induced in the starting step of ball milling results in a tremendous decrease in particle size. Further, Bi2O3 is a good ionic conductor and possesses a lower melting point, making it a suitable sintering aid [50]. It has been reported earlier that the addition of Bi results in agglomeration among the particles, thus ceasing the reduction of particle size below a certain limit [10, 41]. The agglomerated grain distribution in ball-milled powders has been validated from the FESEM and TEM images.

Fig. 3
figure 3

Variation of particle size and microstrain is shown as a function of milling time for LB3SMO sample

Full size image

In addition to XRD, room temperature neutron diffraction (ND) patterns were measured for LB3SMO-0 and LB3SMO-48 samples to understand the cationic distribution and other structural parameters. Figure 4 shows the ND patterns refined by the Rietveld method using the FullProf program [47]. ND patterns of both the samples were refined using the structural model that was used for XRD data analysis (i.e., orthorhombic structure, space group Pnma). The structural parameters and the reliability values of refinement are summarized in Table 2. The quantification of the secondary phase (i.e., Mn3O4 phase) in the bulk sample was done by carrying out two-phase Rietveld refinement using the FullProf program. The LB3SMO-0 sample shows the presence of ≈ 6% parasitic Mn3O4 phase which reduces to ~ 2% for LB3SMO-48, probably due to sintering caused by the heat generated during ball milling. Comparing the FWHM of the peaks of both LB3SMO-0 and LB3SMO-48 samples, it can be clearly seen that the peaks of LB3SMO-48 samples are broader than that of LB3SMO-0, indicating that ball milling does reduce the particle size, confirming the observations made from the XRD results. With the ball milling done up to 48 h, the average Mn–O bond length increases from 1.9561 Å for LB3SMO-0 to 1.9593 Å for LB3SMO-48 while the Mn–O–Mn bond angle decreases from 165.18° for LB3SMO-0 to 164.01° for LB3SMO-48. The tilting of MnO6 octahedra given by increases from 7.41° for LB3SMO-0 to 7.99° for LB3SMO-48, respectively. This shows that ball milling induces distortion in the system, which can alter the physical properties.

Fig. 4
figure 4

Neutron diffraction patterns of LB3SMO-0 and LB3SMO-48 samples refined using the Rietveld method are shown here. The first row of vertical lines indicates the Bragg positions for the parent phase (LB3SMO), whereas the second row indicates the Bragg peak positions for the secondary phase, Mn3O4

Full size image
Table 2 Summary of the unit cell parameters, Mn–O bond length, Mn–O–Mn bond angles, and Rietveld refinement parameters for neutron diffraction patterns of LB3SMO-0 and LB3SMO-48 samples (orthorhombic structure, space group Pnma)
Full size table

3.2 Microstructural Studies

3.2.1 Field Emission Scanning Electron Microscopy

FESEM images of the LB3SMO-0 (bulk pellet) and powders of LB3SMO samples ball-milled for different times are shown in Fig. 5a and b–e. The images were recorded after sonicating the powders in isopropyl alcohol for 10 min. The LB3SMO-0 sample exhibits a well-defined granular surface with clear grain boundaries (Fig. 5a), while the ball-milled LB3SMO powders are agglomerated with granular morphology (Fig. 5b–e). The elemental composition verified by energy dispersive X-ray analysis (EDAX) (Table 3) exhibits a good agreement between nominal and observed values.

Fig. 5
figure 5

(a) FESEM image of polycrystalline bulk pellet. (b–e) FESEM images of ball-milled powders at different milling times

Full size image
Table 3 Nominal and experimental compositions for LB3SMO bulk polycrystals
Full size table

3.2.2 Transmission Electron Microscopy

Room temperature TEM images of LB3SMO-48 sample are shown in Fig. 6a. Seen in Fig. 6a are the highly agglomerated particles with granular morphology, confirming the observations made from the FESEM studies. The electron diffraction pattern shown as the inset of Fig. 6a exhibits the crystalline nature of the nanoparticles. Figure 6b shows an enlarged image of the nanograin recorded. The image clearly distinguishes two regions, an ordered crystalline core where atomic planes are observed and the surface surrounding this core with no long-range crystalline order. The distorted non-crystalline surface represents the shell enclosing the core, thus confirming the core–shell structure in these nanoparticles.

Fig. 6
figure 6

(a) TEM image of 48-h ball-milled LB3SMO powder. Inset in (a) shows SAED pattern. (b) Core–shell structure of the nanoparticle

Full size image

3.3 Magnetization Studies

3.3.1 Magnetic Susceptibility (\({\varvec{\chi}}\) vs. T)

The magnetic susceptibility (\(\chi\) = M/H) as a function of temperature for LB3SMO-t (t = 0, 12, 24, and 48 h) samples was measured in an applied dc magnetic field of 100 Oe. \(\chi\) (T) was measured in zero field cooled (ZFC) and field cooled (FC) states of the sample. As Mn3O4 orders magnetically only below 50 K (TN ~ 42 K) [48], we have restricted all our studies down to 50 K only. Figure 7 shows the \(\chi\) (T) plots recorded in the temperature range 50–360 K. As the temperature is lowered from 360 K, a clear transition from paramagnetic (PM) to ferromagnetic (FM) state is observed at TC = 295 K (determined from the minima of dM/dT curve) for LB3SMO-0 sample [42, 43]. In the case of LB3SMO-12 and LB3SMO-24 samples, the PM to FM transition appears to be broadened and completely suppressed in the case of LB3SMO-48 sample. However, no changes in TC have been noticed with an increase in milling time. Similar observations were previously made for ball-milled nanoparticles [10, 41, 45, 51]. The unaffected value of TC demonstrates that the magnetic ordering in nanoparticles has major contribution from the core of the nanoparticles having same composition as that of the bulk, but the presence of surface disorder broadens the magnetic transition. In addition to the above observations, a broad hump in the \(\chi\) (T) curve is observed for LB3SMO-0 sample just below the completion of PM to FM transition. The hump in the \(\chi\) (T) becomes stronger and shifts towards the lower temperatures in the ball-milled samples. This disordered transition could be attributed to antiferromagnetic interactions in the system.

Fig. 7
figure 7

Plot of magnetic susceptibility as a function of temperature for LB3SMO-t (for t = 0, 12, 24, 48 h) samples

Full size image

The Curie–Weiss law [52],

$$\chi =\frac{C}{T-{\theta }_{p}};\mathrm{ where }\;C\;\mathrm{ represents\;Curie\;constant\;and}\;{\theta }_{p}\mathrm{\;is \;Curie}-\mathrm{Weiss\;temperature}$$

has been used to analyze the inverse magnetic susceptibility data (see Fig. 8) in the temperature region 340–360 K, which is well above the magnetic ordering temperature for all LB3SMO-t (t = 0–48 h) samples. From the linear part of the high-temperature region, θp values have been calculated and are shown as a function of the milling time, as inset, in Fig. 8. The positive values of θp confirm the predominant ferromagnetic interactions in the system. The values of effective paramagnetic moment estimated from the Curie constant are of the order of 4.6 µB. These values are tabulated in Table 4. By assuming the µeff values of Mn3+ and Mn4+ as 4.90 µB and 3.87 µB, respectively [52], the theoretical value of the effective paramagnetic moment for La0.43+Bi0.33+Sr0.32+Mn0.73+Mn0.34+O32− can be derived using the relation,

Fig. 8
figure 8

A plot of inverse magnetic susceptibility as a function of temperature for LB3SMO-t (t = 0, 12, 24, 48 h) samples. The solid line indicates the fit given to Curie–Weiss law. Inset shows the variation in Curie–Weiss temperature with milling time

Full size image
Table 4 Values of TC, θp, \({\mu }_{eff}\), M90 kOe, HC, M0, Msat, critical fields (HCR), and other calculated microstructural parameters for LB3SMO-t samples
Full size table
$${\mu }_{eff}^{2}=0.7\times {\mu }_{eff}^{2}\left({\mathrm{Mn}}^{3+}\right)+0.3\times {\mu }_{eff}^{2}{(\mathrm{Mn}}^{4+})$$
(1)

The theoretical value of µeff = 4.62 µB is in good agreement with the experimentally observed value of µeff. This also clearly rules out the role of the minor defective Mn3O4 phase in the magnetization of the main LB3SMO phase. Additionally, all samples show a deviation from linearity at temperature marked as T* suggesting the possible Griffith’s phase-like singularity [53, 54] or the presence of FM polarons above TC ≤ T ≤ T* [55].

3.3.2 Isothermal Magnetization Studies (M vs. H)

To get a better understanding of the magnetic ground state, field-dependent magnetization curves were recorded on LB3SMO-t (t = 0–48 h) samples up to ± 90 kOe at various temperatures (Figs. 9–11). At 300 K (Fig. 9), the M-H loops exhibit weak ferromagnetic features for LB3SMO-t (t = 0, 12, and 24 h) samples since the system is close to TC. However, the M(H) curves for LB3SMO-48 sample show almost like a linear variation of M with respect to H up to high fields and a slight deviation above 40 kOe, exhibiting weak magnetic interactions. It may be noted that, since the sample is weakly ferromagnetic at 300 K, room temperature neutron diffraction did not show any signs of magnetic ordering in LB3SMO-0 and LB3SMO-48 samples.

Fig. 9
figure 9

Magnetization (M) vs. ramping field (H) measured at 300 K for LB3SMO-t (t = 0, 12, 24, 48 h) samples

Full size image

From magnetic susceptibility measurements, it is understood that around 100 K, which is below the magnetic ordering, the system also exhibits a disordered antiferromagnetic phase. At 100 K (Fig. 10), the M-H curve for all samples displays metamagnetic transition, clearly seen by the step-like feature at a critical field. The initial magnetization curve (virgin curve) shows a small value of ferromagnetic spontaneous magnetization (M0) below an applied field ˂ 2.0 kOe. This could be due to the alignment of residual FM domains parallel to the applied magnetic field. The magnitude of M0 decreases from LB3SMO-0 to LB3SMO-12 sample, but for LB3SMO-24, the observed M0 value is higher than that of the bulk and then decreases for LB3SMO-48. A step in the magnetization has been observed in the virgin curve at a critical field, HCR1, above which magnetization increases abruptly and tends to saturate at fields ≥ 80 kOe. In the decreasing branch of M(H) loop, the system remains in the saturated magnetic state down to some field, HCR2, below which magnetization drops rapidly and approaches zero as the field, H, tends to zero. In the negative cycle of the magnetic field, the H increasing branch of the magnetization is different from the demagnetization curve of the positive H sweep. A step-like feature is observed for low fields and the magnetization increases moderately up to the critical value HCR3, beyond which an abrupt change in M is observed. However, the magnetization in H decreasing sweep of the negative field is similar to the demagnetization of the positive H cycle. These observed features suggest that the application of an external magnetic field induces the formation of FM phase in AFM matrix and the system transforms from AFM state to FM state [2]. When the field is removed, a fraction of aligned FM spins transforms to the initial AFM state, whereas some FM spins remain in the ordered state resulting in the coexistence of FM and AFM phases. It is interesting to note here that the virgin M-H curve for LB3SMO-24 exhibits a distinct response compared to other samples of the LB3SMO-t series. The virgin and the envelope M(H) curve along the H increasing branch appear to be overlapping. This observation suggests that the field-induced magnetic transition in LB3SMO-24 is reversible. Values of M0, HCR1, HCR2, HCR3, and Msat estimated from the extrapolation of the magnetization step and the saturation plateau (see inset of Fig. 10) are summarized in Table 4. It can be noticed that the value of Msat = 3.42 μB for LB3SMO-0 sample is close to its theoretically expected value of 3.6 μB. The Msat decreases as the milling time is increased. The critical field for the step-in virgin curve and envelope curve, HCR1 and HCR3, increases with the increase of milling time, suggesting that a higher magnetic field is required to transform the magnetic state of the material.

Fig. 10
figure 10

Magnetization (M) vs. ramping field (H) measured at 100 K for LB3SMO-t (t = 0, 12, 24, 48 h) samples. Inset shows the estimation of values of M0, HCR1, HCR2, HCR3, and Msat from the extrapolation of magnetization step and saturation plateau

Full size image

The M-H loops recorded at 50 K (Fig. 11) for LB3SMO-24 and LB3SMO-48 samples display a trend similar to that at 100 K. The presence of step-like metamagnetic features with a small value of spontaneous magnetization has been noticed in the virgin M-H curve. In the demagnetization cycle, the system remains in a high magnetic state down to 6 kOe and the magnetization rapidly decreases to 0 at zero fields. When the magnetic field is increased in the negative direction, the magnetization curve is similar to the demagnetization curve of the positive field and follows a similar pathway with further field sweep. This indicates that the field-induced transition from the AFM to FM state is irreversible and the induced FM phase is stable at this temperature. The values of M0, HCR1, and Msat are also summarized in Table 4. The Msat values for LB3SMO-24 and LB3SMO-48 samples at 50 K are higher compared to that at 100 K while M0 value for LB3SMO-24 at 50 K is lower compared to that at 100 K, which is inverse in the case of LB3SMO-48 sample. Also, the HCR1 value for LB3SMO-24 at 50 K is lower compared to that at 100 K whereas for LB3SMO-48 sample HCR1 is very large at 50 K compared to 100 K.

Fig. 11
figure 11

Magnetization (M) vs. ramping field (H) measured at 50 K for LB3SMO-t (t = 24, 48 h) samples

Full size image

From Table 4, it can be seen that there is an overall decrease in the magnitude of magnetization while the coercivity displays a monotonous rise as the milling time increases. The observed systematics can be understood by considering the core–shell model for the nanoparticles [56, 57]. According to this model, each magnetic nanoparticle has a magnetic (FM or AFM) core enclosed in a non-magnetic shell. The shell is made up of defects and dislocation densities thereby resulting in randomly oriented magnetic spins. The shell thickness can be estimated by assuming that the net magnetization of the shell is zero and by using the relation [58],

$${t}_{s}=\frac{D}{2}\left(1-{\left(\frac{{M}_{S \left(\mathrm{Nano}\right)}}{{M}_{S \left(\mathrm{Bulk}\right)}}\right)}^{1/3}\right)$$
(2)

where D represents the particle size, and MS (Bulk) and MS (Nano) correspond to the saturation magnetization in bulk and ball-milled nano-sized samples, respectively. In the present case, since the magnetization of the system tends to saturate at 100 K, an effort to estimate the shell thickness has been made by considering the MS values for bulk and ball-milled powders at 100 K. Figure 12 displays the variation in the shell thickness and the ratio of the shell thickness and particle size, as a function of the milling time. It is observed that the shell thickness increases as milling time increases, which affects the magnetization. Since ball milling induces more surface defects into the system, increased separation between the core results in the reduced magnetic interaction among the nanoparticle core, thereby resulting in the reduction of net magnetization, and increased coercivity. It is interesting to note that the theoretical value of the shell thickness estimated for LB3SMO-48 sample from the magnetization data (tS = 3.8 nm) is in good agreement with the experimental TEM results (tS = 4.0 nm) (see Fig. 6b), thus validating the core–shell structure for the nanoparticles of LB3SMO samples. The observed magnetic phase coexistence in bulk, as well as ball-milled nano-sized samples, suggests that this characteristic is a consequence of the magnetic interaction between cores, having properties similar to that of the bulk material. It is well established in the literature that La0.7Sr0.3MnO3 is a metallic ferromagnet [45] and Bi0.7Sr0.3MnO3 is a charge-ordered antiferromagnet [59]. Therefore, x = 0.3, i.e., La0.4Bi0.3Sr0.3MnO3, represents an intermediate system, as if it were a mixture of both the parent phases, showing signatures of magnetic phase coexistence. Similar characteristic of magnetic phase coexistence across intermediate concentration of Bi3+ has been previously observed in case of La0.67−xBixSr0.33MnO3, La0.7−xBixCa0.3MnO3, Pr0.6−xBixSr0.4MnO3 etc. [29,30,31,32,33,34]. Though substitution of La3+ by Bi3+ does not alter the Mn3+/Mn4+ ratio as there is no change in the valence state (no additional electron or hole added to the system), due to the presence of the 6 s lone pair electrons in the outermost orbital of Bi3+, there is a localization of charges across the Bi–O bonds. The spin direction of localized 2p electrons of oxygen is anti-parallel to Mn3+/Mn4+ thereby resulting in the antiferromagnetic super-exchange coupling between Mn–O–Mn around the Bi3+-rich region.

Fig. 12
figure 12

Plot shows the variation of shell thickness (tS) and the ratio of thickness and size (tS/D), as a function of milling time for LB3SMO

Full size image

Further, from the magnetization plots, the magnetic domain size can be estimated using the relation [60],

$${D}_{m}={\left[\frac{18{k}_{B}T}{\pi \rho {M}_{S}^{2}}{\left(\frac{dM}{dH}\right)}_{H\to 0}\right]}^{1/3}$$
(3)

where T = temperature, ρ = density of LB3SMO (≈10.028 g/cm3), dM/dH is the value of the slope of M-H curve at H = 0, kB = Boltzmann constant, and MS = saturation magnetization. The values of the domain size thus obtained are given in Table 4. The magnetic domain size decreases with an increase in milling time. Therefore, it can be concluded that the nanoparticles obtained from ball milling are multi-domain in nature.

4 Conclusions

Systematic analysis of the magnetization data for the bulk and nanoparticles of La0.4Bi0.3Sr0.3MnO3 (LB3SMO) has been carried out to understand the role of size reduction on the magnetic phase coexistence. The particle size could be reduced from 223 nm for LB3SMO-0 sample to 23 nm for LB3SMO-48 sample by high-energy planetary ball milling. Though there is no change in the structure of bulk and nano-powders, systematic analysis of the neutron diffraction data shows that there is a small variation in the Mn–O bond lengths and the Mn–O–Mn bond angle after ball milling. The dc magnetic susceptibility for nano-powders displays disordered broad magnetic transition. The PM to FM transition observed at 295 K for LB3SMO-0 gets completely suppressed in LB3SMO-48 sample. The presence of field-induced metamagnetic transition in bulk and ball-milled powders at 50 K and 100 K along with small spontaneous magnetization describes the magnetic phase coexistence in the system. The field-induced AFM to FM transition observed in the M(H) measurements at 50 K for LB3SMO-24 and LB3SMO-48 samples indicates that the transition is completely irreversible. The observation of core–shell structure in TEM images strengthens the use of core–shell model for the nanoparticles to explain the systematic decrease in the magnitude of magnetization in ball-milled samples.