1 Introduction

Transition metal nitride (TMNs) materials have recently attracted much attention due to their excellent structural, electronic, and magnetic properties [1, 2] that can be applied to many fields, including magnetic recording [3, 4], spin-injection contacts [5, 6], and microwave-absorbing materials [7]. Perpendicular magnetic anisotropy (PMA) is one of the most properties found in Mn4N thin film of TMNs [8]; this property makes it suitable for applications in spintronics device such as nonvolatile memory [5, 9,10,11].

The mechanical stability of Mn4N bulk was investigated in [12,13,14,15,16]; among the four different crystal stable phases, namely, η, ζ, 𝜃, and ε, ε-Mn4N is the most stable structure.

The Mn4N bulk is a ferrimagnetic metal with a high Curie temperature of TN = 738K and low magnetic moment [17]. The structure is cubic perovskite-type, crystallized with the face-centered cubic structure (space group \(Pm\bar {3}m\), No. 221). The unit cell contains five atoms, one nitrogen atom (N) at the body center positions (0.5, 0.5, 0.5), and four manganese atoms (Mn) distributed with two inequivalent magnetic sites. One at the corners labelled Mnc (cube corner position (0, 0, 0)) and the other at the face-centered labelled Mnf (cube face (0.5, 0.5, 0), (0.5, 0, 0.5), and (0, 0.5, 0.5) positions) (Fig. 1). The exchange coupling of both magnetic sites is antiferromagnetic [18].

Fig. 1
figure 1

The perovskite structure of Mn4N compound. The large balls depict manganese atoms, and the small blue ball represents the nitride atom

Full size image

In this paper, we study the structural, electronic, and magnetic properties of Mn4N. These properties have been investigated using density functional theory (DFT) implemented in Quantum ESPRESSO package. The obtained data from DFT calculations are used in Monte Carlo simulation with a mixed spin-5/2 and 1 Ising model to study the thermal magnetization and magnetic susceptibility and calculate the critical temperature (TC).

2 Computational Details

All the calculations are performed in the framework of the density functional theory (DFT), as implemented in the QUANTUM ESPRESSO package [19]. The exchange and correlation energies were calculated by the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) gradient corrected functional [20]. The Vanderbilt ultrasoft pseudopotentials [21] were used to treat the valence electrons for Mn (3d54s2) and N(2s22p3). Brillouin zone integration has been done using a Methfessel-Paxton [22] smearing of 0.01 Ry and a special k-points grid of 6 × 6 × 6 [23]. Khon-Sham states are expanded in plane waves with a kinetic energy cutoff of 520 eV, and the charge-density cutoff is kept at 8 times that of the kinetic energy cutoff.

3 Theory and Model

The Hamiltonian of the system with a ferrimagnetic spin-5/2 and 1 configuration including the nearest neighbors interactions and an external magnetic field is given by:

$$ H=-J_{\sigma S}\sum\limits_{<ij>}\sigma_{i}S_{j}-h_{ex}\left( \sum\limits_{i}\sigma_{i}+\sum\limits_{j}S_{j}\right) $$

where < ij > stands for the first nearest neighbor spins (i and j) and hex is the external magnetic field, and JσS is the exchange interactions between the first nearest neighbor magnetic atoms with the spins σ and S. The possible projections spin moment of atom Mnf are σ = − 1,0,1 and of Mnc are \(S=\pm \frac {5}{2},\pm \frac {3}{2},\pm \frac {1}{2}\).

4 Monte Carlo Study

The Mn4N is formed by two types of spins σ and S. The total number of spins N = Nσ + NS with Nσ = 375 and NS = 125. The Monte Carlo simulation reported in [24] is applied to simulate the Hamiltonian H. We have used the cyclic boundary conditions on the lattice which were imposed and were generated by sequentially traversing the lattice and making single-spin flip attempts. The Monte Carlo update was performed by choosing random spins and then flipped to opposite state with Boltzmann-based probability. In general, this can be done using the conventional Metropolis algorithm [25]. The flips are accepted or rejected according to a heat-bath algorithm under the Metropolis approximation. Our data were generated with 105 Monte Carlo steps per spin, discarding the first 104 Monte Carlo simulations. Our program calculates the following parameters:

The magnetizations of each atom of manganese Mnc and Mnf in Mn4N structure are given by:

$$ M_{\sigma}=\frac{1}{N_{\sigma}}\left<\sum\limits_{i}\sigma_{i}\right> $$
$$ M_{S}=\frac{1}{N_{S}}\left<\sum\limits_{i}S_{i}\right> $$

The total magnetization is given by:

$$ M_{tot}=\frac{N_{\sigma}M_{\sigma}+N_{S}M_{S}}{N_{\sigma}+N_{S}} $$

The internal energy E per site:

$$ E=\frac{1}{N_{S}+N_{\sigma}}\left<H\right> $$

The magnetic susceptibilities:

$$ \begin{array}{@{}rcl@{}} \chi_{\sigma}&=&\beta\left( <M_{\sigma}^{2}>-<M_{\sigma}>^{2}\right)\\ \chi_{S}&=&\beta\left( <{M_{S}^{2}}>-<M_{S}>^{2}\right)\\ \chi_{tot}&=&\frac{N_{\sigma}\chi_{\sigma}+N_{S}\chi_{S}}{N_{\sigma}+N_{S}}\\ \end{array} $$

where \(\beta =\frac {1}{k_{B}T}\) and T denotes the absolute temperature.

5 Results and Discussion

We have optimized the lattice parameter for two magnetic configurations: ferromagnetic (↑↑↑↑) all spins are up and parallels, antiferromagnetic (↑↓↓↓), one atom at the corner Mnc with the spin up, and three atoms at the face-centered Mnf with the spin down. The total energies variation as a function of lattice parameter obtained by using the local spin density approximation (LSDA) and (GGA) and fitting with Murnaghan’s equation of state [26] are presented in Fig. 2.

Fig. 2
figure 2

Total energy versus lattice parameter: a with AFM configuration and b with FM configuration

Full size image

The formation energy Ef per formula unit of manganese nitride can be expressed by [27]:

$$ E_{f}=E(Mn_{4}N)-(4E(Mn)+E(N_{2})/2) $$

where E(Mn4N) is the total energy of Mn4N bulk, E(Mn) the total energy of the Mn pure metal, and E(N2) is the total energy of the N2 dimer at equilibrium lattice constant. The values of the optimized lattice parameter, total energy, bulk modulus, and formation energy are listed in Table 1.

Table 1 Configuration, lattice constants, total energy, bulk modulus, and the formation energy per formula unit
Full size table

Table 1 shows that the FIM (↑↓↓↓) configuration is the most stable state in energy than FM configuration. The lattice constant obtained for FIM (↑↓↓↓) configuration is 3.7475Å. This value is in good agreement with other published theoretical works [28, 30], and less than the value (3.86Å) reported experimentally in ref. [29]. The results listed in Table 1 show that Mn4N is a hard material with 402.4 GPa and the hardness decreases from 490.0 GPa for ferromagnetic configuration to 402.4 GPa for ferrimagnetic configuration [28].

The calculated total and local magnetic moments in Bohr magnetons (μB) per formula unit of Mn4N for both FM and FIM configurations are listed in Table 2. Our obtained values in ferrimagnetic configuration (↑↓↓↓) are in good agreement with the experiment ones reported in ref. [31], with the moment of \(\mu _{Mn_{c}}=3.50\mu _{B}\) and the moment of \(\mu _{Mn_{f}}=-0.8686\mu _{B}\). The results listed in Table 2 show clearly that the Mn4N is ferrimagnetic material with low magnetic moment [17].

Table 2 Total and local moment, in Bohr magnetons (μB), per formula unit
Full size table

We have presented in Fig. 3 the variations of the magnetic moment of Mnf (Fig 3a) and Mnc (Fig 3b) versus lattice parameter. The magnetic moments increase when the lattice parameter increases, and in the vicinity of the optimal lattice parameter, both magnetic moments have large deviations.

Fig. 3
figure 3

Magnetic moment versus lattice parameter: a of Mnf and b of Mnc

Full size image

The total moment per formula unit for the Mn4N system with cubic structure can be expressed by the following expression:

$$ \mu_{tot}=\mu_{Mn_{c}}+3\mu_{Mn_{f}}. $$

The expected value of μtot is 0.5μB. Our obtained value in this work is 0.76μB. This value is greater than 0.5μB and less than that obtained experimentally (μexp = 0.9μB) [31].

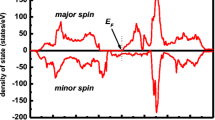
The total and partial density of state and band structure for Mn4N, deduced from the band structure calculations using GGA functional for the FIM configuration, at equilibrium lattice constant and along the high symmetry lines of the Brillouin zone for band structure are depicted in Figs. 4 and 5. Here, the zero energy corresponds to the Fermi level. The DOS characterized by an asymmetry of spin up and spin down contributions and dominated by the Mn atom originate essentially from contributions of 3D band which shows that ferrimagnetic behavior.

Fig. 4
figure 4

Total and partial dos of Mn4N

Full size image
Fig. 5
figure 5

Bands structure of Mn4N

Full size image

The projected density of state (PDOS) for Mnc and Mnf is depicted in Fig. 6 a and b, respectively. These PDOS provide more detailed picture on the Mn4N compound and show that the largest contribution close to the Fermi level comes from the dxy and \(d_{z^{2}}\) orbital and the N-p orbitals have only slight contributions.

Fig. 6
figure 6

projected dos of Mn-d orbital: a at the corner and b at the face

Full size image

The band structure and DOS of Mn4N show that the Fermi level is populated mainly by the Mn-d orbitals and demonstrates that Mn4N has a metallic behavior.

In order to investigate the magnetic properties of Mn4N system by mean field theory and Monte Carlo simulations. We have studied the magnetic interactions between ions of Mn by first principles calculations using the generalized gradient approximation (GGA). The energy difference between the ferrimagnetic and ferromagnetic orders can be expressed by [32, 33]:

$$ {\Delta} E=E_{FIM}-E_{FM} $$

where EFIM and EFM are the total energy of ferrimagnetic and ferromagnetic states, respectively.

Based on the mean field theory (MFT) and the method used by Holland and Brown in Ref. [34]. The Curie temperature of Mn4N system can be given approximately by:

$$ k_{B}T_{C}^{MFT}=\frac{1}{3}\sum\limits_{i\ne0}J_{0i} $$

Where the sum extends over all the first neighbor atoms and kB is the Boltzmanns constant (kB = 8,617330.10− 5eVK− 1).

$$ k_{B}T_{C}^{MFT} =\frac{1}{3}zJ_{\sigma S} S\sigma $$

z is the number of first nearest neighbors around Mn atom (z = 12).

Therefore, TC can be given as a function of ΔE by:

$$ T_{C}=\frac{\Delta E}{6K_{B} } =\frac{(E_{FiM}-E_{FM})}{6k_{B}} $$

where the energy difference is ΔE = 0.53eV

The exchange interaction can be expressed as a function of ΔE by the following expression:

$$ \frac{J_{\sigma S}}{k_{B}}=\frac{\Delta E}{2z\sigma S} $$

The obtained value of the exchange parameter with DFT calculation is used as input for Monte Carlo simulation to calculate the critical temperature.

Figures 7 and 8 show the total and partial magnetization of and magnetic susceptibility of each atom of manganese Mnc and Mnf with spins S = 5/2 and σ = 1, with zero external magnetic fields (hex = 0). The transition from ferrimagnetic phase to the paramagnetic one occurs at the Curie temperature TC = 705K, is deduced from the maximum of magnetic susceptibility in Fig. 8. The obtained value of TC is in good agreement with that obtained by Monte Carlo simulation in ref. [30]. This value is smaller than those obtained within MFT (\(T_{C}^{MFT}=1025K\)) and comparable with the experimental values obtained in previous works [17, 35].

Fig. 7
figure 7

The total and partial magnetization of Mn4N for hex = 0

Full size image
Fig. 8
figure 8

The total and partial magnetic susceptibility of Mn4N for hex = 0

Full size image

6 Conclusion

Structural, electronic, and magnetic properties of Mn4N with cubic perovskite structure have been investigated by first principles calculations of density functional theory. The results show that the Mn4N has a metallic behavior with a ferrimagnetic arrangement of spins and a low magnetic moment. The density of state study reveals that the DOS around the Fermi level originates mainly from the 3D band contributions of Mn. The critical temperature obtained by Monte Carlo simulation with mixed spin-5/2 and 1 Ising model is in good agreement with the experimental results.