Phase Diagrams and Electromagnetic Propertiesof s–wave Superconductivity of the Extended Hubbard Model with the Attractive Pair–Hopping Interaction

Abstract

The characteristics of the extended Hubbard model with the pair–hopping interaction J, i.e. the Penson–Kolb–Hubbard model, are analysed for the case of attractive J (J > 0). The effects of on–site U interaction on the properties of the s–wave superconducting state and mutual stability of the superconducting s–wave and magnetic orderings are examined. The electromagnetic and thermodynamic characteristics of the s–wave superconducting phase for arbitrary particle concentration n and interactions are analysed. The system is evaluated for the case of nearest–neighbours hopping on d–dimensional hypercubic d = 2 (SQ) and d = 3 (SC) nonfrustrated lattices. For SQ lattice the effects of phase fluctuations on the properties of the superconducting state are discussed within the Kosterlitz–Thouless (KT) scenario. The KT critical temperatures T_KT are calculated and compared to the T_c obtained within the BCS–HFA. The Uemura type plots, T_KT vs. λ²(0), are obtained and evaluated as a function of pairing strength and concentration. The results are compared with the case of repulsive J (J < 0) pair–hopping interaction.

1 Introduction

In this work we are interested in the pairing in the real space characterized by small coherence lengths. Superconductivity with short coherence length is appropriate to a description of the high–temperature superconductivity in materials such as the cuprates, doped bismuthates, iron–based systems, Chevrel phases, organic metals, fullerenes, etc. (for a review, see e.g. Refs. [1, 2, 4,5,6] and references therein).

One of the models often used for phenomenological description of dynamics of tightly–bound charged pairs is the attractive Hubbard (AH) model. In the AH model the effective on–site attractive interaction (U < 0) between charge carriers is responsible for pairs creation. Other models used to study the physics of pairing in the real space include the pair–hopping interaction J [8, 9, 11]. This interaction between the fermion pairs located at different sites (intersite charge exchange) can drive pairs forming and condensation.

In the present paper we analyse the Penson–Kolb–Hubbard (PKH) model which includes both the on–site term (U) as well as the pair hopping interaction J. This is conceptually a simple effective model for studying correlations, electron orderings and superconductivity in narrow band systems with almost unretarded short–range pairing [6, 9, 11,12,13,14, 16,17,18,19, 21, 23]. The model Hamiltonian is as follows:

$$\begin{array}{@{}rcl@{}} H&=&- \underset{ij\sigma}{\sum} t_{ij}\left( {{c}_{i\sigma}^{+}c_{j\sigma }+h.c.}\right) -\underset{i\sigma}{\sum} \mu n_{i\sigma } \\ &&+U \underset{i}{\sum} n_{i\uparrow}n_{i\downarrow } \\ &&-{{\frac 12 \underset{ij}{\sum} J_{ij} \left( {{c}_{i\uparrow}^{+}{c}_{i\downarrow }^{+}c_{j\downarrow}c_{j\uparrow}}+h.c.\right)}}, \end{array} $$

(1)

where t_ij are the single electron hopping integrals, U is the on–site density–density interaction, J_ij is the intersite charge exchange interaction between pairs, the chemical potential is represented by μ, $n_{i\sigma }={c}_{i\sigma }^{+}c_{i\sigma }$, and

$$ n=\frac{1}{N}\underset{i\sigma}{\sum} \langle n_{i\sigma}\rangle \ . $$

(2)

In the model J term competes with U interaction. When U = 0 Hamiltonian (1) transforms to the Penson–Kolb (PK) model [8, 12, 14, 17, 25,26,27,28,29], whereas for J = 0 and U < 0 one gets the Hamiltonian of the AH model [1, 30, 31, 33].

So far, the PK and PKH models have been investigated only in a few limits [2, 9, 11, 13, 35,36,37]. The main efforts concerned characteristics at the ground state (T = 0) at half–filling (n = 1) in one dimension (d = 1) [9, 11, 35]. At T = 0, for both signs of J and U, diagrams of the PKH model on d = 1 and $d=\infty$ hypercubic lattices have been evaluated within the broken symmetry Hartree–Fock approximation (HFA) and by the slave–boson mean field method in Ref. [11]. As demonstrated, the d = 1 diagrams at n = 1 are occupied by at least nine distinct orderings. Among them: charge–density–waves and superconducting states, site– and bond–located antiferromagnetic phases with their mixed states as well. With increasing lattice dimensionality, the bond–type orderings gradually disappear at $d=\infty$.

The d = 1 PK model T = 0 phase diagram obtained within the HFA at n = 1 [11] is consistent with the respective diagram derived within exact Lanczos diagonalizations [27, 39], density matrix renormalization group method [25, 26] and the continuum limit field theory calculations [9, 39]. For J > 0, these approaches yield the continuous 2nd–order transition to s–wave pairing phase at J = 0⁺ without any additional transition within the entire range of J > 0 interaction. This behaviour, at least for alternating lattices, is band–filling independent and it is retained for higher dimensions (including the exactly solvable case of $d=\infty$) [11].

We have already partially studied the superconducting characteristics of the PK and PKH models for the case of s–wave (Cooper–pair centre–of–mass momentum q = 0) [12, 13, 18, 40, 41] and eta–phase (q = Q [16,17,18] superconductivity. Preliminary investigation of the next–nearest neighbour hopping t₂ influence on both eta– and s–phase superconductivity in the 2–dimensional PK model has been also evaluated [18]. We have examined in that paper, the evolutions of the J vs. n phase diagrams and determined the T_c and T_KT transition temperatures with n and J. We have also derived, for t₂≠ 0, the Uemura–type plots for the s–phase.

We have analysed, for the PKH model on the nonfrustrated d = 2 SQ lattice, T = 0 phase diagrams involving homogeneous magnetic, charge–ordered and superconducting phases [23, 42, 43]. Moreover, within the variational approach (where the U term is treated exactly), the superconducting characteristics (for both s–wave and eta–phase) in the zero–bandwidth limit have been analysed [2, 6, 16, 19, 44].

In this work we extend our studies of the PKH model and analyse in details the evolution of the model’s properties for arbitrary concentration (0 < n < 2) for the attractive J (J > 0). Taking into account both the magnetic orderings and superconducting s–wave states, we investigate the impact of the on–site U interaction on the phase diagrams both at T = 0 and T > 0. The ground state diagrams involving only homogeneous phases are compared with those involving phase separated states. In both types of diagrams we mark a crossover to the Bose–Einstein Condensate (BEC) regime. Moreover, we present here an extensive analysis of the U interaction effect on the electromagnetic as well as thermodynamic characteristics of the s–phase. The evolutions of the properties with n and interaction parameters are determined. We compare the theoretical London penetration depth λ(n) plots with experimental measurements reported by Locquet [48] for La_2−xSr_xCuO₄ films.

For the PKH model on the 2–dimensional lattice, within the Kosterlitz–Thouless (KT) scenario, we investigate the phase fluctuation impact on the s–phase. The d = 2 KT transition temperature (T_KT) is calculated from the superfluid stiffness ρ_s evolution with temperature T, which is compared to the KT relation between ρ_s and T_KT. The KT scenario has already given reliable results for the models with attractive intersite density–density interactions [50, 52, 53] and the d = 2 AH model [31, 33]. In the former case a correct behaviour of T_KT vs. |U|/B in agreement with the available Quantum Monte Carlo (QMC) data was found [33]. The T_KT is compared with the critical temperature T_c obtained within BCS–HFA. The gap to critical temperature ratio is determined and the Uemura–type “universality plots” [55, 57]: T_KT vs. ρ_s(0) derived within the KT theory are examined. The theoretical Uemura–type plots are compared with the experimental data corresponding to Chevrel phases, doped BaBi0₃ (alternating cubic lattices) and cuprates (SQ lattice) [58, 59].

The superfluid properties of the PKH model were studied within a linear response theory [1, 30, 60, 62, 64], where the electromagnetic kernel was treated within the HFA–Random Phase Approximation (HFA–RPA) scheme. The HFA–RPA approach is known to be reliable in the case of Hubbard model and its various extensions in the area of the ordered states studied at T = 0, within the whole range of interaction interpolating between the weak and strong coupling limit [1, 11, 30]. Furthermore, for the electronic models with exclusively intersite interactions in the $d=\infty$ limit, the HFA leads to exact solutions for any For $d<\infty$ at T > 0, the HFA is much less reliable especially in the strong coupling limit and in low–dimensional systems as it neglects short–range correlations and phase fluctuation effects.

Hence the HFA neglects phase fluctuation effects and short–range correlations, it is much less reliable in $d<\infty$ at T > 0, especially for low–dimensional systems in the strong coupling limit.

In a separate work we will study the case of the PKH model with J < 0, which can stabilize eta–pairing.

Organization of the paper is as follows. In Section 2 there are the electromagnetic kernels and basic equations calculated to determine the basic properties of the studied system in the normal and s–wave superconducting phases. In Sections 3, 4, and 5 we present the numerical analysis of the system. The phase diagrams at T = 0 involving s–wave superconducting phase as well as nonordered, antiferromagnetic and ferromagnetic states are given in Section 3.1, and the T > 0 phase diagrams are analysed in Section 3.2. The ground state s–wave phase properties as a function of concentration and coupling strength for SQ and SC structures are shown in Section 4. In Section 5 we devote to superconducting properties analysis at the finite temperatures for the SQ lattice. Going beyond the HFA we calculate the KT critical temperatures T_KT and compare them with T_c obtained from BCS–HFA. In Section 5. we also demonstrate the Uemura–type “universality plots”. Finally, Section 6 contains concluding remarks. In addition, Appendix A is devoted to free energies and self–consistent equations for the phases competing with s–wave paring.

2 General Formulation

Taking into account the electrons coupling to magnetic field via the vector potential, the PKH model Hamiltonian takes the following form [9, 11,12,13, 29, 35]:

$$\begin{array}{@{}rcl@{}} H&=&-\underset{ij\sigma}{\sum} t_{ij}\left( e^{i{\varPhi}_{ij}}{c}_{i\sigma}^{+}c_{j\sigma }+h.c.\right) + \\ &&-\sum\limits_{i\sigma}\mu n_{i\sigma }+ U \underset{i}{\sum} n_{i\uparrow }n_{i\downarrow }+ \\ &&- \frac 12 J \underset{<ij>}{\sum} \left( e^{2i{\varPhi}_{ij}}{c}_{i\uparrow}^{+}{c}_{i\downarrow }^{+}c_{j\downarrow }c_{j\uparrow } +h.c.\right) , \end{array} $$

(3)

where the Peierls factors incorporate electrons coupling to magnetic field via its vector potential A(r) (diamagnetic effect):

$$ {\varPhi}_{ij}=-\frac{e}{\hbar c}{\int}_{\!\!\!\!R_{i}}^{R_{j}}d \mathbf{r}\mathbf{A}(\mathbf{r}) ,f $$

(4)

e is the electron charge, and < ij > limits the sum to nearest neighbours (nn). Other denotations are given after (1).

Following our earlier works on this matter we assume that the effective (phenomenological) model parameters t, U and J contain all possible renormalizations and contributions including those coming from the strong electron–phonon or from electrons and other electronic subsystems in chemical complexes or solid couplings [1] (e.g. coupling of electrons with intermolecular vibrations via modulation of the hopping integral [65] or the on–site hybridization in a generalized periodic Anderson model [67, 68]). In general, their values and signs could be arbitrary. Particularly interesting is the role of J interaction in a multiorbital model, because of its presence in the iron pnictides [70]. In the strong interaction limit, the J term may also be included in the effective models for Fermi gas on an optical lattice [69].

The self–consistent equations for electron thermal averages and free energy of the PKH model (1) can be determined (within the HFA approximation) by the standard equation of motion or Greens functions approaches [11].

The s–wave phase superconducting order parameter

$$ x_{s} =\frac{1}{N} \underset{i}{\sum} \left\langle c_{i\downarrow}c_{\iota \uparrow}\right\rangle = \frac{1}{N} \underset{k}{\sum} \left\langle c_{-k\downarrow}c_{k \uparrow }\right\rangle , $$

(5)

the Fock term

$$ p=-1/4N \underset{k\sigma}{\sum} \gamma_{k}\left\langle {c}_{k\sigma }^{+}{c}_{k\sigma }\right\rangle , $$

(6)

where $\gamma _{k}= 2\sum _{\alpha }\cos k_{\alpha }$, α = x, y, …, and μ are determined by the set of equations:

$$ {\frac{\partial F_{S}}{\partial x_{s}}= 0,\ \frac{\partial F_{S}}{\partial p}= 0,\ \frac{\partial F_{S}}{\partial \mu }= 0 .} $$

(7)

Free energy of the superconducting (S) phase is derived as:

$$\begin{array}{@{}rcl@{}} \frac{F^{S}}{N} &=&\bar{\mu}(n-1)+\frac{4}{z} {Jp}^{2}+\frac{Un^{2}}{4} \\ &&+(J_{0}-U){{x}_{s}^{2}} - \frac{2}{\beta N} \underset{\mathbf{k}}{\sum} \ln 2\cosh \frac{ \beta E_{\mathbf{k}}}2 . \end{array} $$

(8)

The explicit form of the self–consistent equations determining x_s, p and μ is the following:

$$ x_{s}=\frac{J_{0}-U}{N}\underset{k}{\sum}\frac{x_{s}}{2E_{k}}\tanh \left( \frac{\beta E_{k}}{2}\right) , $$

(9)

$$ p=\frac{-1}{N}\underset{k}{\sum} \overline{\epsilon}_{k}\gamma_{k}\frac{1}{2E_{k}} \tanh \left( \frac{\beta E_{k}}{2}\right) , $$

(10)

$$ n-1=-\frac{2}{N} \underset{k}{\sum}\frac{\overline{\epsilon}_{k}}{2E_{k}}\tanh \left( \frac{\beta E_{k}}{2}\right) , $$

(11)

where $E_{k}=\sqrt {{\overline {\epsilon }}_{k}^{2}+(-U+J_{0})^{2}{{x}_{s}^{2}}}$ is a quasiparticle energy, $\overline {\epsilon }_{k}=\epsilon _{k}-\bar {\mu }$, chemical potential: $\bar {\mu }=\mu -\frac {1}{2}Un$, N–number of sites in the system, $n=\frac {N_{e}}{N}$ (0 < n < 2) denotes number of electrons per site, J₀ = zJ, 𝜖_k = − $\widetilde {t }\gamma _{k} , \widetilde { t}=t + 2pJ/z$, z is the number of nearest neighbours (z = 6 and z = 4 for SC and SQ structures respectively), β = 1/k_BT.

Free energy of the normal (N) phase has the following form:

$$\begin{array}{@{}rcl@{}} \frac{F^{N}}{N} &=&\bar{\mu}_{N}(n-1)+\frac{4}{z} J{{p}_{N}^{2}}+\frac{U}{4} n^{2}+ \\ &&-\frac{2}{\beta N} \underset{\mathbf{k}}{\sum} \ln 2\cosh \frac{\beta \bar{\epsilon}_{\mathbf{ k}}}{2} , \end{array} $$

(12)

where $\bar {\mu }_{N}$ and p_N are determined as follows:

$$ n=\frac{1}{N}\underset{\mathbf{k}}{\sum}\left( 1-\tanh \frac{\beta \bar{\epsilon}_{\mathbf{k}}} {2}\right) , $$

(13)

and

$$p_{N}=\frac{1}{N} \underset{k}{\sum} \gamma_{k}\frac 12\tanh \left( \frac{\beta \bar{\epsilon}_{\mathbf{k}}}{2}\right) . $$

The equations of the other phases considered in this work are given in Appendix A. However, it should be underlined that all results presented in this work are obtained neglecting effects of the Fock term in all phases, i.e., assuming that p = 0 in each phase.

Based on the linear response theory calculations in the weak vector potential A(r) case, the expected value of the total current operator Fourier transform in the direction α (α = x, y, z) [12, 13, 60, 71] takes the given form:

$$\begin{array}{@{}rcl@{}} J_{\alpha}({\mathbf{q}},\omega)&=& N\frac{c}{4\pi}\underset{\beta}{\sum}\left[\delta_{\alpha\beta}K_{\alpha}^{dia}\right.\\ &&\left.+ {K}_{\alpha\beta}^{para}(\mathbf{{q}},\omega)\right]A_{\beta}(\mathbf{{q}},\omega) . \end{array} $$

(14)

The total reaction kernel K_αβ(q, ω) has been split up into the paramagnetic and diamagnetic parts, which were subsequently evaluated within the RPA–HFA scheme.

In particular, we get the diamagnetic part as follows:

$$\begin{array}{@{}rcl@{}} {K}_{\alpha}^{dia}&=&\frac{8\pi e^{2}|t|}{\hbar^{2}c^{2}a} \frac{1}{N} \underset{k}{\sum} \left[ 1-\frac{ \overline{\epsilon}_{k}}{E_{k}}\tanh \left( \frac{\beta E_{k}}{2}\right) \right] \cos (k_{\alpha}) \\ &&-\frac{32\pi e^{2}}{\hbar^{2}c^{2}a}\frac{{J_{0}}}z{{x}_{s}^{2}} , \end{array} $$

(15)

where x_s, p and μ are given by (9)–(11).

The expression for the paramagnetic part of the kernel is calculated to be

$$\begin{array}{@{}rcl@{}} {K}_{\alpha \beta}^{para}(\mathbf{q},\omega )&=& -\frac{1}{N} \frac{4\pi e^{2}t^{2}}{2\hbar^{2}c^{2}}\underset{\mathbf{k}}{\sum} 4\sin \mathbf{k}_{\alpha} \sin \mathbf{k}_{\beta} \\ &&\times \left[ \left( \frac 1{\omega -(E_{k-q}+E_{k})+i\varepsilon }-\frac 1{\omega +E_{k}+E_{k-q}+i\varepsilon}\right) \right. \\ &&\times \left( 1-\frac{\overline{\epsilon }_{k}\overline{\epsilon}_{k-q}+(-U+J_{0})^{2}{{x}_{s}^{2}}}{ E_{k}E_{k-q}}\right) \\ &&\times \left[ 1-n_{F}(E_{k})-n_{F}(E_{k-q})\right] \\ &&+\left( \frac 1{\omega -(E_{k-q}-E_{k})+i\varepsilon }-\frac 1{\omega +E_{k-q}-E_{k}+i\varepsilon }\right) \\ &&\left.\times \left( 1+\frac{\bar{\epsilon}_{k}\bar{\epsilon}_{k-q}+(-U+J_{0})^{2}{{x}_{s}^{2}}}{ E_{k}E_{k-q}}\right) \left[ n_{F}(E_{k})-n_{F}(E_{k-q})\right] \right] \end{array} $$

(16)

where n_F(E_k) is the Fermi–Dirac distribution function.

Within London limit the magnetic penetration depth λ is defined from the transverse part of the total kernel which in the static limit reads as follows:

$$ \lambda(T) =\underset{q_{y}\rightarrow 0}{\lim}[-{K}_{x}^{dia}-{K}_{xx}^{para}(q_{x}= 0,q_{y},q_{z}= 0,\omega = 0)]^{-1/2} , $$

(17)

where ${K}_{x}^{dia}$ is given by (15) and for the transverse part of the paramagnetic kernel in the static limit for $\mathbf {q}\rightarrow 0$ we obtain:

$$ {K}_{xx}^{para}(\omega = 0)=\frac{8\pi e^{2}t^{2}}{\hbar^{2}c^{2}}\frac{1}{N} \underset{\stackrel{\rightarrow}{k}}{\sum} \frac{\sin^{2}k_{x}}{k_{B}T\cosh^{2}\left( \frac{\beta E_{k}}2\right)} . $$

(18)

At T = 0 K the paramagnetic part is significant when calculating λ for non–local superconductors (Pippard superconductors), common among systems with low T_c. The materials with short coherence length, including superconductors with high T_c, represent the so-called London limit. For $\mathbf {q}\rightarrow 0$ and at T = 0 the magnetic penetration depth in the London limit is expressed with the diamagnetic component of the total kernel:

$$ \lambda =\frac 1{\sqrt{-K^{dia}}} . $$

(19)

We restrict our investigation to analyzing the system in the London limit in which we can apply the local approximation. Derived for this case λ is qualitatively well represented in the weak and strong interactions, moreover, for strong couplings, the results obtained in HFA coincide with those obtained from the perturbation theory.

Having the difference between the normal and superconducting phase free energys and the value of penetration depth we can derive formuls for the thermodynamic critical field H_c and the Ginzburg–Landau correlation length ξ_GL:

$$\begin{array}{@{}rcl@{}} \frac{{H_{c}^{2}}(T)}{8\pi} &=&\frac{F^{N}(T)-F^{S} (T)}{Na^{3}} , \\ \xi_{GL} &=&\frac{{\varPhi}_{0}}{2\pi \sqrt{2}\lambda H_{c}} , \end{array} $$

(20)

where a is the lattice constant, ${\varPhi }_{0}=\frac {hc}{2e}$, and we get the estimations for the critical fields:

$$ H_{c1}\simeq \frac{\ln \kappa }\kappa H_{c}; , $$

(21)

$$ H_{c2}={\varPhi}_{0}/(2\pi \xi_{GL}^{2}) , $$

(22)

where κ is the Ginzburg ratio: κ = λ/ξ_GL.

At T = 0, $\frac {F(0)}{N}=E_{0}=\frac {1}{N} \langle H\rangle _{(T = 0)}$. The HFA expressions determining normal and superconducting ground state energies, ${{E}_{0}^{N}}$ and ${{E}_{0}^{S}}$ are:

$$\begin{array}{@{}rcl@{}} {{E}_{0}^{N}} &=&\frac{F^{N}(0)}{N}={{E}_{N}^{K}}(0)+\frac{4}{z} J{p_{N}^{2}}+\frac{1}{4} Un^{2} , \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} {{E}_{0}^{S}} &=&\frac{F^{S}(0)}{N}= {{E}_{S}^{K}}(0) \\ &&+\frac{4}{z} {Jp}^{2}+\frac{(-U+J_{0})^{2}{{x}_{s}^{2}}}{U-J_{0} }+\frac{1}{4} {Un}^{2} , \end{array} $$

(24)

where

$$\begin{array}{@{}rcl@{}} {E}_{\text{N(S)}}^{K} &=&\frac{1}{N} \underset{\mathbf{k}\sigma}{\sum} \epsilon_{\mathbf{k}}\langle {c}_{\mathbf{k}\sigma}^{+}c_{\mathbf{k}\sigma}\rangle_{ \text{\tiny{N(S)}}} , \\ \langle {c}_{\mathbf{k}\sigma}^{+}c_{\mathbf{k}\sigma}\rangle_{S} &=&\frac{1}{N} \underset{\mathbf{k}}{\sum} \left( 1-\frac{\bar{\epsilon}_{\mathbf{k}}}{E_{\mathbf{k}\sigma}}\right) , \\ \langle {c}_{\mathbf{k}\sigma}^{+}c_{\mathbf{k}\sigma}\rangle_{N} &=&\frac{2}{N} \underset{\mathbf{k}}{\sum} \text{sign}(\epsilon_{\mathbf{k}}-\bar{\mu}) , \end{array} $$

(25)

${E}_{\text {S(N)}}^{K}$ is the mean kinetic energy of the superconducting (normal) phase.

From (9)–(11) and the condition ${\Delta } \rightarrow 0$, where gap amplitude parameter: Δ = (−U + J₀)x_s, one can calculate the HFA transition temperature T_c which is an estimation of the temperature of pair–formation [12, 33, 52].

Due to the phase fluctuation effects, for finite–dimensional lattice ($d < \infty$), transition to the superconducting phase occurs at temperature lower than T_c(HFA). We take into account the phase fluctuation effects by determining another characteristic temperature, the Kosterlitz–Thouless critical temperature (T_KT). For two–dimensional lattices (d = 2) the value of T_KT can be derived within the KT theory [12, 31, 33, 72, 73]. In terms of the theory the T_KT temperature is defined by vortex pair unbinding transition determined by universal jump of the superfluid stiffness (helicity modulus) ρ_s at T_KT:

$$ k_{B} T_{KT}=Q \rho_{s}(T_{KT}) , $$

(26)

where $Q\simeq 0.898$ (Monte–Carlo estimates for d = 2 XY model [33, 72]). The superfluid stiffness ρ_s, which is directly related to the London penetration depth λ and calculated within HFA–RPA scheme using (15), (18) and (17) has the following explicit form:

$$\begin{array}{@{}rcl@{}} \rho_{s}(T) &=&\frac{\hbar^{2}c^{2}}{16\pi e^{2}}\lambda^{-2}= \frac{-\hbar^{2}c^{2}}{16\pi e^{2}}\left[{K}_{x}^{dia}+{K}_{xx}^{para}(\omega = 0)\right] \\ &=&-{\frac{1}{2N}\underset{k}{\sum}| t| {\left[ 1-\frac{\overline{ \epsilon}_{k}}{E_{k}}\tanh \left( \frac{\beta E_{k}}{2}\right) \right] \cos (k_{\alpha })}} \\ &&+ 2\frac{{J_{0}}}{z}{{{x}_{s}^{2}}}-\frac{1}{2N}t^{2} \underset{k}{\sum} \frac{\sin^{2}k_{x}}{k_{B}T\cosh^{2}\left( \frac{\beta E_{k}}{2}\right)} . \end{array} $$

(27)

Thus, T_KT is determined by (9)–(11) and (26) with ρ_s given by (27). Since the formula (27) does not take into account the renormalization coming from the topological excitations (vortex–antivortex pairs) [31, 33], calculated this way T_KT is only an upper bound estimation of the actual KT transition temperature.

Using our approach one is able to analyse the crossover between BCS–like (extended Cooper pairs (“BCS”)) and local Cooper pairs superconductivity (composite bosons, Bose–Einstein Condensate (BEC)). The crossover takes place when increasing pairing interaction (J or |U| (U < 0)) one increases coupling from a weak to strong regime. At the ground state, one can approximate boundary between both regimes from the Leggett criterion [30, 74], which requires the chemical potential of the superconducting phase to be located at the bottom of the electronic band, i.e.:

$$ \bar{\mu}_{s}=-B/2 , $$

(28)

where B is the bandwidth of 𝜖_k (B = 2zt) and μ_s is determined from the self–consistent (9)–(11) solved at T = 0.

3 Phase Diagrams of the Model at T ≥ 0

We performed extensive analytical and numerical analysis of the electromagnetic and thermodynamic properties of the s–wave phase of the PKH model (3) for d–dimensional hypercubic lattices.

In this Section we discuss the phase diagrams for arbitrary n and interaction parameters, determined within the HFA in the ground state (Sec. A) and T > 0 (Sec. B), whereas the superfluid characteristics of s–wave phase are analysed in Sections 4 and 5.

For d = 2 we used the square lattice (SQ) density of states expressed with:

$$ D(\epsilon)_{2D}=\frac{1}{2t\pi^{2}}K\left( 1-\left( \frac{\epsilon}{4t}\right)^{2}\right) , $$

(29)

if |𝜖/4t| < 1 and zero otherwise, where K is the complete elliptic integral of the first kind. For d = 3 we use the analytical approximation to D(𝜖) as calculated numerically by Jelitto [75].

3.1 Ground State Phase Diagrams

Below we analyse phase diagrams at T = 0 for the SQ lattice involving the homogeneous: nonordered (N), s–wave pairing (S), ferromagnetic (F) and antiferromagnetic (AF) states and compare them with the phase diagram involving also phase–separated states. We only analyse the simple magnetic phases but consideration of more complex magnetic orderings would not modify significantly the results. In general, in the ground state, the S states are always stable with respect to the N–phase for J > U/z for arbitrary values of single electron hopping, U, J and n (0 < n < 2). In the figures we mark the crossover to the Bose–Einstein Condensate (BEC) which at T = 0 can be located from Leggett’s criterion [30, 74] (28). For selected interaction values we also plot the evolution of the order parameters of the respective phases as a function of n.

Figures 1 and 2 present the T = 0 phase diagrams U versus n (for J/4t = 1) and J versus n (for U/4t = 2 and U/4t = 3) respectively. The transition lines to N phase are of the 2nd–order, while those between the ordered states are of the 1st–order. As a result of competition between repulsive U and J, the s–wave pairing state is limited on the diagram, Fig. 1, for U < U_c (with U > 0), whereas the F and AF phases are stable for U above U_c (U > U_c). The F and AF phases occur in the diagram in the limited ranges of concentration n: for low and intermediate values of n and close to half–filling (n = 1), respectively. For U < U_c(n = 1) states S may occur within entire range of n. Because of the strong interactions the nonordered phase is not present on the phase diagram. For given concentration n, with increasing on–site U interaction, system exhibits several sequences of transitions: (i) a single 1st–order transition S $\rightarrow$ F, (ii) a sequence of 1st–order transitions S $\rightarrow$ AF $\rightarrow$ F (with increasing U, AF $\rightarrow$ F transition line asymptotically approaches half–filling) and (iii) at n = 1, a single 1st–order transition S $\rightarrow$ AF.

Fig. 1

The U vs. n phase diagram for fixed J/4t = 1 at T = 0. Denotations: s–wave superconducting state (S), ferromagnetism (F) and antiferromagnetism (AF). Dashed line denotes crossover to BEC regime. The phase transtion lines are of the 1st–order. Diagram is plotted for SQ lattice

Fig. 2

The J and n phase diagrams plotted for U/4t = 2 and U/4t = 3 at T = 0. All the transitions involving exclusively ordered states are of the 1st–order and those to nonordered (N) phase are of the 2nd–order. Diagrams are plotted for SQ lattice. Other denotations as in Fig. 1

The J vs. n phase diagrams, for fixed U at T = 0 is shown in Fig. 2. Analogously to the previous diagram (Fig. 1), the S–phase may occur in the diagram above a critical J_c(U, n). Increasing U reduces concentration ranges occupied by the AF and N phases and expands the range of F state stability in the diagram (comp. Fig. 2a and b). In both diagrams, with increasing J, the system can exhibit several different types of behaviour, depending on n: (i) a single 1st–order transition N $\rightarrow$ S, (ii) a single 1st–order transition F $\rightarrow$ S and (iii) a single 1st–order transition AF $\rightarrow$ S.

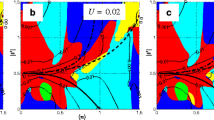
Figure 3b presents the phase diagram U versus n (for J/4t = 1.0) involving the phase–separated states (PS). This diagram is a preliminary result, a part of a broader analysis of phase diagrams involving PS states, which is soon to be published elsewhere.. In the figures presented here, for the sake of clarity, the μ–dependent plot (Fig. 3a) is given, which helps to determine boundaries between the PS states plotted in Fig. 3b. All homogeneous ordered states are separated by PS states (Fig. 3b). The transitions between homogeneous and the PS states are symbolically named “third order” transitions [6]. In the system that undergoes this type of transition, one of the domains in the PS phase gradually vanishes.

Fig. 3

The T = 0 phase diagrams as a function of repulsive U vs. a chemical potential μ, b carriers density n for fixed J/4t = 1. Denotations: phase separated states (PS), nonordered phase (N), s–pairing superconducting state (S), ferromagnetism (F) and antiferromagnetism (AF). Dashed line denotes the crossover to BEC regime. Diagrams are plotted for SQ lattice

In analogy to earlier presented diagrams involving homogeneous states only (cf. Fig. 1), also in this case (Fig. 3b) the states involving s–wave pairing are stable only below certain critical values U_c. For U > U_c(n = 1) superconducting S–states can be stable only within a limited range of n (n < 1) and appear in the diagram as a homogeneous or phase–separated states involving AF and F orderings. At half–filling, for U < U_c the S–phase may occur within the whole range of concentrations. The homogeneous AF phase occurs only for n = 1 when U > U_c. Away from n = 1, within a limited range of U, the AF phase may be stable in the diagram exclusively within the PS(S/AF) and PS(AF/F) states close to n = 1.

As the electron density increases towards half–filling, depending on U, the system exhibits a few distinct transition sequences: (i) a single 1st–order transition F $\rightarrow$ PS(AF/F) $\rightarrow$ AF, (ii) a sequence of four 1st–order transitions: S $\rightarrow$ PS(S/F) $\rightarrow$ F $\rightarrow$ PS(AF/F) $\rightarrow$ AF and (iii) a sequence of two 1st–order transitions: S $\rightarrow$ PS(S/AF) $\rightarrow$ AF.

In the plots (Figs. 1, 2 and 3) the crossover to BEC regime is denoted with dashed line. An obvious effect of the repulsive (attractive) U is the reduction (expansion) of the composite bosons (BEC) regime. As we see from the plots, with rising concentration n, the boundaries are moved towards greater values of interaction J for any U. Thus, within a definite range of U an J, the crossover from the weakly to the strongly coupled electron pairs can be achieved by lowering the electron density.

3.2 Finite Temperature Phase Diagrams

In this subsection we present a two examples of the finite temperature phase diagrams, as evolution with concentration (Fig. 4) and evolution with U (Fig. 5) for the repulsive on–site interaction U > 0.

Fig. 4

Finite temperature phase diagram for fixed values of interaction parameters U/4t = 3.0 and J/4t = 1.0. (SQ lattice)

For interaction parameters U/4t = 3.0 and J/4t = 1.0 (Fig. 4) with increasing temperature the system can exhibit the following phase transitions: (i) a single 2nd–order transition S $\rightarrow$ N (ii) a sequence of three transitions: 2nd–order S $\rightarrow$ N and reentrant 2nd–order N $\rightarrow$ F $\rightarrow$ N, (iii) a sequence of five transitions: 2nd–order S $\rightarrow$ N, reentrant 2nd–order N $\rightarrow$ F $\rightarrow$ N, reentrant 2nd–order N $\rightarrow$ AF $\rightarrow$ N, (iv) a sequence of 1st–order transition F $\rightarrow$ AF and 2nd–order AF $\rightarrow$ N and (v) a single 2nd–order transition AF $\rightarrow$ N.

The diagram T versus U for J/4t = 1.0 and n = 0.9 is given in Fig. 5. As one can notice from the plot, with increasing T the system can undergo either (i) a single 2nd–order transition S $\rightarrow$ N, (ii) a sequence of two transitions: 1st–order S $\rightarrow$ AF and 2nd–order AF $\rightarrow$ N , or (iii) a sequence of two transitions: 1st–order F $\rightarrow$ AF and 2nd–order AF $\rightarrow$ N.

Fig. 5

Finite temperature phase diagram for fixed values of interaction parameters J/4t = 1.0 and n = 0.9. (SQ lattice)

Fig. 6

The inverse square penetration depth $1/\lambda _{}^{2}$ and the gap parameter Δ = (J₀ + U)x_s at T = 0 as a function of U/B for n = 0.75 and fixed values of aJ₀/B = 0.0; 0.2; 0.4 plotted for SQ lattice and bJ₀/B = 0.0; 0.2; 0.6 plotted for SC lattice. $\lambda _{0}=\frac {\hbar c}e\sqrt {\frac {a^{d-2}}{4\pi B}},$B = 2zt is the bandwidth, a is the lattice constant

Fig. 7

Concentration dependence of 1/λ² and the gap parameter Δ at T = 0 for J₀/B = 0.5 and a few values of U/B: U/B = − 0.25; 0.0; 0.25 (SQ lattice)

Fig. 8

Concentration a and Ub dependencies of the reduced square value of thermodynamic critical field ${{H}_{c}^{2}}/{{H}_{0}^{2}}$ (${{H}_{0}^{2}}= 4\pi B/a^{d}$, B = 2zt = 8t) and the energy gap $E_{g}(0)=\min E_{k} - \max (-E_{k})$ at T = 0 for a) J₀/B = 0.5 and several values of U/B: U/B = − 0.25, U/B = 0.0, U/B = 0.25 b) n = 0.75 and J₀/B = 0.0, J₀/B = 0.2, J₀/B = 0.4 (SQ lattice)

Fig. 9

Concentration a and interaction Ub dependencies of the G–L coherence length ξ_GL/ξ₀ ($\xi _{0}=\frac {a}{\sqrt {2z}}$) and the Ginzburg ratio κ/κ₀ ($\kappa _{0}=\frac {\hbar c}{e}\sqrt {\frac {2}{\pi Ba^{4-d}}}$) at T = 0 plotted for a) J₀/B = 0.5 and U/B = 0.0, U/B = 0.25, U/B = − 0.25 and b) for n = 0.75 and J₀/B = 0.0, J₀/B = 0.2, J₀/B = 0.4. (SQ lattice)

4 Superfluid Characteristics of s–wave Phase at T = 0

Below we present the evolutions of the ground state superconducting properties of the s–wave phase with model parameters (Figs. 6, 7, 8 and 9). The plots were determined for the parameters’ ranges where superconducting S–phase is stable in the phase diagrams analysed earlier in the paper. Due to the electron–hole symmetry of the model all the plots are symmetric with respect to the transformation $n\rightarrow 2-n$. As one can see from the figures (cf. Figs. 1–3), where the superconducting characteristics are plotted as a function of U/B for J₀/B > 0, the S states can still be stable even for U > 0 (repulsibe U) when J₀ − U > 0. With increasing J₀/B the S–phase boundary shifts towards higher values of U/B.

In Fig. 6 we show plots of the inverse square value (1/λ²) of the London penetration depth and of the order parameter Δ as a function of U/B for fixed values of n and J₀/B at T = 0 for the SQ and SC lattices. These quantities plotted as a function of n for nonfrustrated 2D SQ lattice and selected values of J₀/B and U/B are presented in Fig. 7. As the pairing interactions J₀ or |U| (for U < 0) increase, the 1/λ², Δ and other superconducting characteristics evolve smoothly from the limit of weakly interacting single particle carriers (with λ^− 2 being proportional to the bandwidth B, ${\Delta } \sim \exp (\frac {-2B}{J_{0}-U}$) if n≠ 1) to the limit of tightly bound pairs (with ${\Delta } \sim J$, ${\Delta } \sim |U|$ and $\lambda ^{-2}\sim J$ if U = 0). For J₀/B = 0, the PKH model reduces to AH model. In this case λ^− 2 continuously decreases with increasing |U|/B for any |U| and $\lambda ^{-2}\sim t^{2}/|U|$ for |U|/B >> 1. For fixed J₀/B > 0 following the increase of -U/B, the λ^− 2 first grows, and subsequently it passes through a round maximum and drops at high -U/B proportionally to 2t²/|U| + J (cf. Fig. 6). With increasing J₀/B the maximum value of λ^− 2 increases. Notice that the increase in λ^− 2 as a function of J₀/B for any value of U/B (the increase is linear for large J) is significantly distinct form the behaviour observed for the AH model (J₀= 0, U < 0).

The following figures present the energy gap E_g(0) and the behaviour of the square value of thermodynamic critical field ${H_{c}^{2}}$ at T = 0 for SQ lattice. The quantities are plotted as a function of n for a fixed value of J₀/B and several values of U/B (Fig. 8a) as well as a function of U for a fixed n and several values of J₀/B (Fig. 8b). Both characteristics vanish at the empty–band limit (n = 0), reach a maximum at half–filling and increase linearly with increasing |U|/B for U/B >> 1, and in the weak coupling limit they are proportional to $\exp (\frac {-2B}{J_{0}-U}$).

The plots of G–L coherence length ξ_GL and the Ginzburg ratio κ versus U/B and n calculated for SQ lattice for selected values of respective interaction parameters are presented in Fig. 9. In the limit of weakly interacting single particle carriers the $\xi _{GL} \sim \exp \left [\frac {-2(J_{0}-U)}{B}\right ]$, $\kappa \sim \exp \left (\frac {B}{J_{0}-U}\right )$, and at tightly bound pairs regime, $\xi _{GL} \Rightarrow \frac {a}{\sqrt {2z}}$, $\kappa \sim \sqrt {\frac {1}{J}}$ for U = 0, and $\kappa \sim \sqrt {\frac {1}{2t^{2}/|U|+J}}$, if |U|/B >> 1, U < 0).

As concerns the concentration dependencies of various quantities (see Figs. 7, 8 and 9) one finds that in the low density limit for arbitrary coupling strengths $\lambda ^{-2}\sim n$ (as for the fermions in the continuum), ${\Delta } \sim \sqrt {n}$, ${H_{c}^{2}} \sim n$, $\kappa \sim \frac {1}{\sqrt {n}}$, whereas for (J₀ − U)/B >> 1 : Δ ⇒ (1/2) (J₀ − U) $\sqrt {n(2-n)}$, $\lambda ^{-2}\sim n(2-n)$, ${H_{c}^{2}} \sim n(2-n)$, $\kappa \sim \frac {1}{\sqrt {n(2-n)}}$, for any n. Beyond these limits the concentration dependencies are not universal. Their behaviour highly depend on the features of density of states. Notice, the resulting from the van Hove singularity in D(𝜖) for SQ lattice, substantial enhancement of Δ and ${H_{c}^{2}}$ close to n = 1 (Figs. 7 and 8) observed in the range of small and intermediate values of (J₀ − U)/B. Similar efect is observed for the local maximum of the Ginzburg ratio κ at n = 1 (Fig. 9a). In addition, in Fig. 9a one can see a significant variation of ξ_GL as a function of n in the weak and intermediate coupling strength.

5 Critical Temperatures for s–wave Phase and the Uemura–Type Plots

Apart form the weak coupling as well as from the case of $d=\infty$, the phase fluctuations exert a strong impact on the superconducting pairing, and the results display a clear energy scales separation for the pair formation ($\sim k_{B}T_{c}$) and phase coherence. The effects of the phase fluctuations are most clearly seen for d = 2 lattices, whose phase coherence temperature is determined by k_BT_KT (26), (27).

Between T_c and T_KT incoherent s–wave phase occurs, where the pseudogap opens up in the quasiparticle energy spectrum and the system exhibits non–Fermi liquid properties. Not at T_c, but only at T_KT the real transition to a superconducting state takes place, where the transition to a phase with bound vortex–antivortex pairs occurs. Certain pairing correlations are observed at all temperatures thus T_c does not represent a rigorous boundary line. It is rather a reliable estimate of the pair formation and the pseudogap emergence [12, 30, 36].

For SQ lattice the evolutions of T_KT and T_c with a change in n for fixed interaction parameters are shown in Fig. 10, whereas Fig. 11 present the plots of transition temperatures as a function of interactions. The T_KT temperature can be significantly reduced compared to T_c, where for U ≤ 0, J₀ > 0 the highest reduction occurs for low values of carriers density n (cf. eg. Fig. 10 and, for U = 0, Ref. [12]). Moreover, the difference between T_c and T_KT strongly increases with the increase of on–site attraction U < 0 (cf. Fig. 11). Analogously as found for PK [12] and AH [30] models, also for the PKH model one observes a monotonous increase in T_c with increasing interactions, (which is obviously a result of increasing pair binding energy) (cf. Fig. 11 [12]). On the other hand, apart from the weak paring strength regime T_KT evolution with interaction parameter is significantly distinct for these models. As we can see in Fig. 11, for the PKH model, similarly as we observe for the AH model, with interaction |U| increase the T_KT at first increases exponentially, and subsequently it passes a round maximum and then drops as t²/|U| at strong |U|. Analogous behaviour was found for the thermodynamic critical field H_c(0) [12, 30, 33]. On the other hand in the PK model, the model with intersite charge exchange, T_KT monotonously increases with J, and the growth of T_KT is linear at strong values of J (cf. Ref. [11, 12]). Due to the difference in the paring mechanisms, the dynamics of electron pairs is qualitatively different in both models. [11, 12, 30]. The PKH integrates both of the pairing mechanisms and the interplay between U and J interactions results in the differences in the thermodynamic and electrodynamic properties compared to those in the PK and AH models.

Fig. 10

Concentration dependencies of T_KT and T_c for SQ lattice plotted for several values of interaction parameters: J₀/B = 0.5 and U/B = 0.0, U/B = 0.25, U/B = − 0.25. B = 8t, J₀ = 4J, $T_{0}=\frac {B}{K_{B}}$

Fig. 11

Transition temperatures T_KT and T_c plotted as a function of U/B. For n = 0.75 and fixed values of J₀/B: J₀/B = 0.; 0.2; 0.4. T₀ = B/k_B (SQ lattice). B = 8t, J₀ = 4J, $T_{0}=\frac {8t}{K_{B}}$

In contrast to the BCS case, the phase fluctuations enhance the ratio of the ground state gap (E_g = minE_k − max(−E_k)) to the critical temperature. In Fig. 12a we present the ratios E_g(0)/2k_BT_KT/c vs concentration n for selected values of U/B and J₀/B.

Fig. 12

The gap to critical temperatures ratios E_g(0)/2k_BT_KT/c plotted (a) as a function of |n − 1| for J₀/B = 0.5 and U/B = 0.0, U/B = 0.25, U/B = − 0.25; (b) as a function of U for n = 0.75 and J₀/B = 0.0, J₀/B = 0.2, J₀/B = 0.4. (SQ lattice)

Fig. 13

The Uemura–type plots: T_c/pvs${\lambda _{0}^{2}}/\lambda ^{2}$, with the controlling variable n, for J₀/B = 0.5 and several fixed values of U (U/B = 0.0, U/B = 0.25, U/B = − 0.25). The straight dotted line marks an upper bound for the phase ordering temperature Qρ_s(0), ($Q\simeq 0.898$ see (26)). ${\lambda _{0}^{2}}/\lambda ^{2}= 4\rho _{s}/B$, $\lambda _{0}=\frac {\hbar c}e\sqrt {\frac {a^{d-2}}{4\pi B}}$. T₀ = B/k_B (SQ lattice).

Fig. 14

The Uemura–type plot: $\frac {T_{c}}{T_{c}^{m}}$ vs. $\frac {{\lambda }_{m}^{2}}{\lambda ^2}$ and $\frac {T_{KT}}{T_{KT}^{m}}$ vs. $\frac {{\lambda }_{m}^{2}}{\lambda ^2}$, where $\frac {{\lambda }_{m}^{2}}{\lambda ^2}$ is a ground state value. Plotted for controlling variable n, for J₀/B = 0.5 and several fixed values of U (U/B = 0.0, U/B = 0.25, U/B = − 0.25). λ_m corresponds to the relevant maximum transition temperature, ${T}_{c}^{m}$ or ${T}_{KT}^{m}$ respectively. (∘)-Tl₂Ba₂ Ca₂Cu₃ O₁₀, Tl_0.5 Pb_0.5Sr₂ Ca₂Cu₃ O₉, Bi_2−x Pb_xSr₂ Ca₂Cu₃ O₁₆; (◇)-Y_1−x Pr_xBa₂ Cu₃O_6.97; (△)-YBa₂ Cu₃O_x; (▽)-La_2−x Sr_xCuO₄; (⋆)-Bi₂Sr₂ Ca_1−x Y_xCu₂ O_{8 + δ}; (⊓)-LaMo₆ Se₂, PbMo₆ S₈, SnMo₆ S₄Se₄, SnMo₆S₇Se, SnMo₆S₁ Se₇, LaMo₈ S₈, PbMo₆ S₄Se₄; (⊕)-Tl₂ Ba₂ CuO_{6 + δ} (for overdoped range). Experimental data taken from [58, 59]

Notice that for T_KT this ratio can be much greater than for T_c. We have found, the enhancement of the ratio to be the highest at low concentrations, where it can be higher even by a factor 10 or more. Only for $\frac {J_{0}-U}{t}\rightarrow 0$ we recover the BCS ratio $E_{g}(0)/2k_{B}T_{c}\sim 1.76$. Let us stress that the gap ratio goes to infinity for the local pair (the strong coupling) regime if $n\rightarrow 0$, since E_g(0) remains finite in such a case (cf. Fig. 8a) and $T_{KT/c}\rightarrow 0$.

Within the KT scenario we also derived, for SQ lattice, the Uemura–type plots for the superconducting phase of the model, and examples of the T_KT/c vs. 1/λ² figures for controlling parameter n with fixed values of J₀/B and U are shown in Figs. 13 and 14. Apart from the weak coupling regime the curves plotted on the figures have shapes analogous to the Uemura’s plots experimentaly obtained [55, 57] for various classes of the “exotic” superconductors (the superconductors with short–coherence length) such as bismuthates, the organic materials and cuprates. For low concentration n the experimental points adhere to the universal Qλ²(0) line (the results presented in Figs. 13 and 14 were obtained for $Q\simeq 0.898$ (see (26)). It should be emphasized that T_c is not related to ρ_s and analogous plots with T_c cannot account for the scaling [12, 33, 52, 53]. Let us point out that for t₂≠ 0 [18] the densities of states for SQ and SC lattices are no longer symmetric and the function T_KT(1/λ²) does not represent the one–valued function, whereas it exhibits substantial hysteresis due to differences in positions of the maxima values of the T_KT(n) and 1/λ²(n).

In Fig. 14 we compared our results with experimental data corresponding mainly to SQ lattices (cuprates) and alternating cubic lattices (Chevrel phases, doped BaBi0₃) [58, 59, 76, 77]. In order to compare the results we have normalized T_c and T_KT to unity by scaling both temperatures over respective maximal values of the temperatures: ${T_{c}^{m}}$ and $T_{KT}^{m}$, and 1/λ² we scaled over a value $1/{{\lambda }_{m}^{2}}$ corresponding to the value of the respective maximal temperature. The experimental data were scaled analogously. Except for the overdoped cases the data compare best with the plots obtained for the values of coupling between strong and intermediate. The experimentally found deviations from the universal dependence in the strongly overdoped regime can be explained either by the asymmetry in ${\mathcal {D}}(\varepsilon )$ due to further neighbour hopping in the considered lattices or by the effects of intersite Coulomb interactions [79], which can be different for various families of materials.

In Fig. 15 we qualitatively compare the theoretical plots λ(n) obtained for the discussed simple effective model with penetration depth measurements reported by Locquet [48] for La_2−xSr_xCuO₄ films. The experimental data extend from the regime of heavily underdoped to heavily overdoped. The theoretical results fit well the experimental measurements.

Fig. 15

The λ(n)/λ(n = 1) at T = 0 K for J/B = 0.5 and several fixed values of U/B for SQ lattice, compared with experimental results [48] obtained for La_2−x Sr_xCuO₄ films (-39 nm) (full squares), λ₀ = λ(x = 0.159) = [6700 ± 500]Å

6 Conclusions and Remarks

We have explored in this work the ground state and final temperature phase diagrams as well as the superconducting properties of the Penson–Kolb–Hubbard model. The study have been performed for arbitrary electron density and J > 0. In this model, the intersite charge exchange interaction (a non-local interaction) is responsible for pairs formation and condensation.

The PKH model can be treated as an effective model of the s–wave superconductors with short coherence length, which can be of order of interparticle distance or even a lattice constant and can be applied to isotropic d = 3 structures (such as the barium–bismuthate compounds [80, 82], Chevrel phases [1] and fullerides [83,84,85,86,87]), as well as those with layered (d = 2) structures (such as heavy fermion systems and some organic superconductors). Moreover, the model may also lead to some qualitative understanding of the d = 2 high–T_c cuprates [76, 88, 91], iron pnictides and chalcogenides [5, 93].

For the SQ lattice we have determined the stability of s–wave pairing state with respect to F, AF and N phases. We have presented the ground state diagrams for homogeneous phases only (without considering PS states) and a preliminary phase diagram involving PS states (Figs. 1–3). In the diagrams the phase transitions to nonordered state are of the 2nd–order, and all the transition lines separating considered ordered states are of the 1st–order. Increasing U/4t broadened F phase concentrations n range and reduced the n ranges of AF and N phases occurrence. We have shown that at T = 0 for J > U/z, in the general case of arbitrary U/4t and J/4t the S–phase was always stable with respect to the N phase for any value of the concentration n and single electron hopping.

In the diagram involving PS states (Fig. 3) we have shown that the homogeneous ordered phases were separated by the respective PS states and homogeneous AF phase could occur only at half–filling. For n≠ 1 the AF ordering could appear only within the phase separated states: PS(S/AF) and PS(AF/F) in a limited extent of concentration n near to the half–filling.

At T = 0 the isotropic s–wave pairing, S–phase, stable for the attractiveJ (J > 0) and the attractiveU (U < 0) is found to exhibit a smooth crossover between the BCS–like regime and the tightly bound pairs limit with increasing pairing interactions. This behaviour is qualitatively different from the one observed for repulsive J (J < 0) when the transition into the eta–phase occurs only above a critical value |J_c| dependent on band filling (n) and lattice structure. In this case the system never manifests standard BCS–like features [16,17,18]. In the figures we have marked the crossover to the BEC which at T = 0 was located after Leggett’s criterion. Within homogeneous S–phase, for a given n, the system could undergo BCS–BEC crossover with decreasing U. The effect of the repulsive (attractive) U is the reduction (expansion) of the composite bosons (BEC) regime. We have demonstrated that in a specific range of U and J the crossover from the weakly to strongly coupled electron pairs could be achieved by lowering the n. With decreasing n the crossover regime is shifted towards lower values of pairing interaction. Notice that the crossover always occurs beyond the range of stability of the PS states involving s–wave domains (cf. Fig. 3). We have also presented examples of the finite temperature phase diagrams involving homogeneous states as a function of concentration and interaction U (Figs. 4 and 5).

The evolution of the thermodynamic and electromagnetic superconducting properties with electron concentration and pair interactions has been analysed for d–dimensional hypercubic lattices (primarily for SQ lattice) and the changes in the behaviour of these characteristics at the crossover between the BCS–like limit and the local pair regime superconductivity have been discussed. We have determined the evolution of the critical temperatures T_c (Hartree–Fock), T_KT (Kosterlitz–Thouless) as well as the critical fields, the penetration depth, the coherence length and Ginzburg ratio at T = 0 as a function of particle concentration n and interactions.

As the pairing interactions J₀ or − U increase the s–wave phase characteristics evolve smoothly between the regimes of the weakly interacting single particle carriers and of tightly bound pairs. The λ^− 2 increases with increasing J₀/B for any value of U/B, and the increase is linear for large J. This behaviour is qualitatively different from that found for the AH model (J₀ = 0, U < 0), where λ^− 2 continuously decreases with increasing |U|/B and $\lambda ^{-2}\sim t^{2}/|U|$ for |U|/B >> 1. In the strong interaction regime the electromagnetic and thermodynamic characteristics of the S–phase (for J > 0) become similar to the properties of the eta-phase (for J < 0). For the arbitrary coupling strengths in the low density regime $\lambda ^{-2}\sim n$ as for the fermions in the continuum.

The PKH model reduces to PK model for U = 0 and for J = 0 reduces to AH model. The evolution of superconducting characteristics with increasing pairing interaction is essentially different in both systems. For the PK model, in the limit of strong coupling, values of λ^− 2, H_c, T_KT, κ^− 1 increase with J while for the AH model the characteristics decrease with $\left | U\right |$.

Our results obtained for the case U = 0, J > 0 are consistent with those obtained for collective excitations performed using a generalized random–phase approximation [28, 36]. The collective mode velocity, in the PK model, rise with J [28] while in the AH model it drops with $\left | U\right |$ [36]. Moreover, for the studied models, the conclusions are in qualitatively good agreement with the results of perturbational expansions both in the weak and strong interaction regimes [30, 94, 95].

The S–phase can be stable for repulsive values of U (0 < U < U_c) as well. In the PKH model, repulsive U modifies the S–phase characteristics (cf. also [17]) and shrinks the extent of the superconducting phase stability. It also can induce 1st or 2nd order transitions to various nonsuperconducting phases.

Apart from the weak coupling regime one finds a substantial increase in the gap to critical temperature ratio resulting from the phase fluctuations and the energy scales separation for the pairs formation ($\sim k_{B}T_{c}$) and the phase coherence ($\sim k_{B}T_{KT}$). Between T_c and T_KT a disordered (incoherent) pair state is possible in which the single–electron excitation spectrum has a gap, but the pairs are phase disordered. The T_KT can be substantially lower than the T_c.

An important result of our work is the derivation of Uemura–type plots for the model considered. Beyond the regime of weak coupling and low concentrations the results show universal scaling: $T_{KT} \sim 1/\lambda ^{2}(0)$, similarly as it was found for the attractive Hubbard model [33], the PK model [12] and the extended Hubbard model with intersite attraction [52, 53]. Apart from the weak coupling regime, the resulting plots have a shape consistent with the experimental Uemura’s plots for various classes of superconductors with short–coherence length [17]. Our results support the conclusion [12, 30, 52, 53] that in materials with short coherence length, the ground for the Uemura scaling is a separation of the energy scales of the pairs formation and the phase coherence in the underdopped limit or in the strong interaction regime.

Appendix A: Free Energies and Self–Consistent Equations for the Magnetic Phases Competing with s–wave Paring

For arbitrary electron concentration n the stable solutions are determined as the minima of free energy of the system F_α (α = AF, F) with respect to the variational parameters x_α, μ and p, i.e. by the equations

$$ \frac{\partial F}{\partial x_{\alpha}}= 0 , \frac{\partial F}{\partial \mu}= 0 \text{ and } \frac{\partial F}{\partial p}= 0 , $$

(30)

from which we get sets of self–consistent equations for each considered ordering type. The order parameters for the phases considered: (i) antiferromagnetic (AF):

$$ x_{AF} =\frac{1}{2N} \underset{i,\sigma}{\sum} \sigma \exp (\mathbf{Q}_{i}\cdot \mathbf{R}_{i}) \left\langle {c}_{i\sigma}^{+} c_{\iota \sigma }\right\rangle , $$

(31)

(ii) ferromagnetic (F):

$$ x_{F} =\frac{1}{N} \underset{i,\sigma}{\sum} \sigma \left\langle {c}_{i\sigma }^{+}c_{\iota \sigma }\right\rangle , $$

(32)

The equations for the phases considered derived for the alternated lattice, (i.e. 𝜖_{k + Q} = −𝜖_k) in the (broken symmetry) HFA: the free energy of the ferromagnetic phase F_F:

$$\begin{array}{@{}rcl@{}} F_{F} &=& \bar{\mu}\left( n-1\right) +\frac{4}{z} Jp^{2} + \frac{1}{4} U {n}^{2} + U {{x}_{F}^{2}} + \\ &&-\frac{2T}{N} \underset{k,r}{\sum} \ln\left[2\cosh\left( \frac{{{E}_{F}^{r}}(k)}{2T}\right)\right] ,\end{array} $$

(33)

the thermodynamic potential of the ferromagnetic phase Ω_F:

$$\begin{array}{@{}rcl@{}} {\varOmega}_{F} &=& - \bar{\mu} +\frac{4}{z} Jp^{2} - \frac{1}{4} U n^{2} + U {{x}_{F}^{2}} + \\ &&-\frac{2T}{N} \underset{k,r}{\sum} \ln\left[2\cosh\left( \frac{{{E}_{F}^{r}}(k)}{2T}\right)\right] ,\end{array} $$

(34)

the set of self–consistent equations: (i) the equation for the number of particles of the ferromagnetic phase:

$$ n-1 = -\frac{1}{2}\underset{k,r}{\sum} \tanh\left( \frac{{{E}_{F}^{r}}(k)}{2T}\right) , $$

(35)

(ii) the equation for the order parameter of the ferromagnetic phase:

$$ x_{F} = -\frac{1}{2} \underset{k,r}{\sum} r \tanh\left( \frac{{E_{F}^{r}}(k)}{2T}\right) , $$

(36)

where ${E}_{F}^{\pm }(k) = \bar {\epsilon _{k}} \pm U x_{F}$, $\bar {\epsilon _{k}}=\epsilon _{k}-\bar {\mu }$, $\bar {\mu }=\mu -Un/2$.

The free energy of the antiferromagnetic phase F_AF:

$$\begin{array}{@{}rcl@{}} F_{AF} &=& \bar{\mu}\left( n-1\right) +\frac{4}{z} Jp^{2} + \frac{1}{4} U n^{2} + U {x}_{AF}^{2} + \\ &&-\frac{2T}{N} \underset{k,r}{\sum} \ln\left[2\cosh\left( \frac{{E}_{AF}^{r}(k)}{2T}\right)\right] ,\end{array} $$

(37)

the thermodynamic potential of the antiferromagnetic phase Ω_AF:

$$\begin{array}{@{}rcl@{}} {\varOmega}_{AF} &=& - \bar{\mu} + \frac{4}{z} Jp^{2} - \frac{1}{4} U n^{2} + U {x}_{AF}^{2} + \\ &&-\frac{2T}{N} \underset{k,r}{\sum} \ln\left[2\cosh\left( \frac{{E}_{AF}^{r}(k)}{2T}\right)\right] ,\end{array} $$

(38)

the set of self–consistent equations: (i) the equation for the number of particles of the antiferromagnetic phase:

$$ n-1 = -\frac{1}{2} \underset{k,r}{\sum} \tanh\left( \frac{E_{AF}^{r}(k)}{2T}\right) , $$

(39)

(ii) the equation for the order parameter of the antiferromagnetic phase:

$$ \frac{2}{U} = \underset{k}{\sum} \frac{\tanh\left( \frac{{E}_{AF}^{+}(k)}{2T}\right) - \tanh\left( \frac{{E}_{AF}^{-}(k)}{2T}\right) } {{E}_{AF}^{+}(k) - {}E_{AF}^{-}(k)} , $$

(40)

and the Fock term:

$$ p=\frac{-1}{4N} \underset{k}{\sum} \epsilon_{k}\gamma_{k}\frac{1}{{E}_{AF k}^{+}-{E}_{AF k}^{-}} \tanh \left( \frac{{E}_{AF k}^{+} + {E}_{AF k}^{-}}{2T}\right) , $$

(41)

where ${E}_{AF}^{\pm }(k) = \bar {\mu } \pm \sqrt {\epsilon ^{2}+U^{2} {x}_{AF}^{2}}$.