Topological Phases Emerging from Spin-Orbital Physics

Abstract

We study the evolution of spin-orbital correlations in an inhomogeneous quantum system with an impurity replacing a doublon by a holon orbital degree of freedom. Spin-orbital entanglement is large when spin correlations are antiferromagnetic, while for a ferromagnetic host we obtain a chain with only orbital interactions. In this regime, the orbital model can be mapped on spinless fermions and we uncover topological phases with zero energy modes at the edge or at the domain between magnetically inequivalent regions.

1 Introduction

Transition metal oxides are fascinating materials where several degrees of freedom (i.e., spin, orbital, charge, etc.) couple and, from a theoretical point of view, need to be treated on equal footing in order to provide reliable predictions. In undoped 3d Mott insulators large on-site Coulomb interactions localize electrons and the coupling between transition metal ions is controlled by a low-energy spin-orbital superexchange introduced first by Kugel and Khomskii [1]. As for spins, orbital degrees of freedom have a quantum character and can drive strong fluctuations which end in destroying long range order [2] or lead to exotic novel types of magnetic order [3]. However, such cases are rare in e _g systems and, typically, long range order in both spin and orbital sector develops in perovskite lattices [4], with the corresponding correlations following the Goodenough-Kanamori rules [5]. A well known example is the spin-orbital order in LaMnO₃[6], with different energy scales for spin and orbital order [7]. However, there are numerous deviations from these rules caused either by superexchange on non-linear bonds [8], or by lattice frustration such as for instance in LiNiO₂[9], or by spin-orbital entanglement [10], or, finally, by the presence of next nearest neighbor hopping [11]. In t _2g systems, orbital superexchange has leading contributions with SU(2) symmetry along a given cubic direction thus orbital fluctuations are much stronger [12] than in e _g and a spin-orbital liquid emerging from intrinsic frustration is more likely to occur [13,14,15]. On the other hand, ordered states may be even stabilized by orbital fluctuations [16] as for instance in LaVO₃ [17] and Ca₂RuO₄[18]—in this latter case spin-orbit coupling also plays a role [19]. Quantum fluctuations and spin-orbital entanglement [20] are of great importance in this class of materials and may lead to novel phenomena as superconductivity in the pnictides driven by competing symmetries at orbital degeneracy [21], or spectacular topological structure of the excited states in the one-dimensional (1D) SU(2)⊗XY model [22], or, finally, dimerised phases [23].

Doping of Mott insulators adds another charge degree of freedom in spin-orbital systems and leads to several remarkable phenomena. Recently, short-range charge-density wave called stripe phase was reported in doped cuprates [24]. It has been suggested that the critical charge, orbital, and spin fluctuations near the quantum critical point provide the pairing interaction [25]. As in doped cuprates, the holes doped in t _2g orbitals may be mobile due to three-site terms [26] or self-organization in stripe phases [27]. However, the formation of orbital molecules makes 1D insulating zigzag states kinetically more favorable than metallic stripes [28]. Insulating state is also found [29] when holes are confined near charge defects in Y_1−x Ca _x VO ₃ [30].

In contrast, neutral defects in spin-orbital systems lead to orbital dilution (with a local increase of spin to $S=\frac 32$) [31] or to charge dilution [32] (with invariant spin S = 1states), and to the changes in spin-orbital order [33]. These phenomena are distinct from the orbital dilution in cuprates where holes remove simultaneously spin and orbital degree of freedom [34]. The t _2g systems with charge dilution are unexplored yet—they will likely play a major role in future functional materials and, possibly, in novel electronic devices. The purpose of the paper is to investigate the consequences of charge dilution in a t _2g system due to the substitution of a d ⁴by a d ²transition metal ion. Such type of doping allows to uniquely design a spin-orbital correlated environment with an orbital degree of freedom having an inequivalent charge character. Indeed, for d ² and d ⁴ valence configurations, the empty orbital (i.e., holon) and the doubly occupied state (i.e., doublon) set the orbital degree of freedom, respectively. As an experimental motivation we mention, among the various emergent phenomena and the many possible hybrid oxides which could be designed, that (i) dilute Cr doping for Ru reduces the temperature of the orthorhombic distortion, induces ferromagnetic (FM) order and anomalous negative thermal expansion in Ca₂Ru_1−x Cr _x O ₄(with 0 < x < 0.13) [35], and (ii) Mn-substituted single crystals of Sr₃Ru_2−x Mn _x O ₇rapidly drive an unusual metal-insulator transition and E-type antiferromagnetic (AF) order at low doping [36]. The theoretical search for the consequences of holon-doublon substitution is performed for a 1D ring and we analyze both spin and orbital correlations around the charge defect. We give reasons why the FM regime is well designed to search for topological aspects of the present model.

2 Spin-Orbital Physics and Charge Dilution

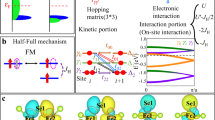
We consider a 1D ring made of d ⁴ transition metal ions in the insulating regime, with one d ²charge defect, see Fig. 1. The physics of the undoped system is governed by a spin-orbital superexchange model which is equivalent, through an electron-hole transformation, to that introduced for vanadates [37]. It depends on two Kanamori’s parameters: the intraorbital Coulomb element U ₂ and Hund’s exchange J ₂ for t _2g electrons [4], responsible for the high spin states with spin S = 1at the host d ⁴ions. In the regime of strong electron interactions, we obtain a spin-orbital model with spin S = 1at every site and an orbital degree of freedom described by a pseudospin $T=\frac 12$. Since we work in one dimension and with t _2g orbitals, we select the cubic axis c with the active orbitals [16]: |a〉 ≡ |y z〉 and |b〉 ≡ |x z〉.

Fig. 1

Artist’s view of a ring of length L = 8containing seven d ⁴host atoms $i = 2,\dots ,8$ with parameters {U ₂, J ₂}and one charge impurity d ²at site i = 1(filled circle), with parameters {Δ, J ₁}. The color convention for the bonds 〈i, i + 1〉is the same as in Figs. 2, 3, and 4

However, the situation becomes less familiar when some of the d ⁴ ions are substituted by the d ²ones. In the regime of low doping, all the bonds will be either between two d ⁴ ions, called host bonds, or between d ²and d ⁴ ions around an impurity site—these we call hybrid bonds. The superexchange Hamiltonian for both kinds of bonds has a generic form (all the bonds are along the cubic axis c in the 1D chain) [32],

$$ \mathcal{H}_{b}=J_{b}\sum\limits_{\langle i\rangle} \left\{K_{i,i + 1}^{(b)}\vec{S}_{i}\cdot\vec{S}_{i + 1}+Q_{i,i + 1}^{(b)}\right\}, $$

(1)

where the label b = {0,h} stands for the type of bond and the operators $\left \{K_{i,i + 1}^{(b)}\right \}$ and $\left \{Q_{i,i + 1}^{(b)}\right \}$ act in the orbital space at two sites, {i, i + 1}. These operators differ fundamentally for the hybrid and host bonds, i.e., for the host they take the U(1)symmetric form of,

$$\begin{array}{@{}rcl@{}} K_{i,i + 1}^{(0)}\!&=&A_{K}{\tau_{i}^{z}}\tau_{i + 1}^{z} +B_{K}\left( {\tau_{i}^{x}}\tau_{i + 1}^{x}+{\tau_{i}^{y}}\tau_{i + 1}^{y}\right)+C_{K}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} Q_{i,i + 1}^{(0)}\!&=&A_{Q}{\tau_{i}^{z}}\tau_{i + 1}^{z} +B_{Q}\left( {\tau_{i}^{x}}\tau_{i + 1}^{x}+{\tau_{i}^{y}}\tau_{i + 1}^{y}\right)+C_{Q}, \end{array} $$

(3)

whereas for the hybrid bonds the symmetry is lowered,

$$\begin{array}{@{}rcl@{}} K_{i,i + 1}^{\text{(h)}}\!&=&\!D_{K}{\tau_{i}^{z}}\tau_{i + 1}^{z} +E_{K}{\tau_{i}^{x}}\tau_{i + 1}^{x}+F_{K}{\tau_{i}^{y}}\tau_{i + 1}^{y}+G_{K}, \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} Q_{i,i + 1}^{\text{(h)}}\!&=&\!D_{Q}{\tau_{i}^{z}}\tau_{i + 1}^{z} +E_{Q}{\tau_{i}^{x}}\tau_{i + 1}^{x}+F_{Q}{\tau_{i}^{y}}\tau_{i + 1}^{y}+G_{Q}, \end{array} $$

(5)

Here, $\tau _{i}^{\alpha }$ are the Pauli operators describing doublon/holon fluctuating between |a〉 and |b〉 orbitals. They are defined by the Pauli matrices $\vec {\sigma }$ as

$$ \vec{\tau}_{i}=\left( \begin{array}[t]{cc} a_{i}^{\dagger} & b_{i}^{\dagger} \end{array}\right)\cdot\vec{\sigma}\cdot \left( \begin{array}[t]{cc}a_{i}^{} & b_{i}^{} \end{array}\right)^{T}, $$

(6)

where hardcore boson operators $a^{\dagger }_{i}$ and $b^{\dagger }_{i}$ create holon or doublon in the orbitals |a〉and |b〉, respectively.

Coefficient J _b in the spin-orbital model (1) is a superexchange constant and is given by $J_{0}= 4{t_{0}^{2}}/U_{2}$ and J _h = 2t h2/Δ (note that the excitations which provide the main contribution on the hybrid bond go in one direction only), where t _b (b = 0,h) is a hopping amplitude along host-host or impurity-host bond, and U ₂ is the Hubbard interaction for the host (d ⁴) atoms. Δ is a typical excitation energy scale in the virtual process ${d^{2}_{i}}{d^{4}_{j}}\Rightarrow {d^{3}_{i}}{d^{3}_{j}}$ (or charge transfer energy) given by,

$$ {\Delta}\equiv I_{e}+ 2U_{1}-3U_{2}-6(J_{1}+J_{2}). $$

(7)

Here, U ₁ and J ₁ are Hubbard and Hund’s interactions at the d ²impurity site. I _e is the energy mismatch of the electronic levels at two ions; since Δ must be positive and relatively large, this implies that I _e > U _i must be the largest energy scale in the system. The coefficients A _K(Q), …, C _K(Q)and D _K(Q), …, G _K(Q)in (2)–(5) are numerical constants depending on microscopic parameters of the ions: A _K(Q), …, C _K(Q) depend only on host’s parameter η ₀ and D _K(Q), …, G _K(Q) both on host’s and impurity’s Hund’s exchange η ₁and η ₂, where

$$ \eta\equiv\frac{J_{2}}{U_{2}}, \hskip .7cm \eta_{1}\equiv\frac{J_{1}}{\Delta}, \hskip .7cm \eta_{2}\equiv\frac{J_{2}}{\Delta}. $$

(8)

All these η’s measure the relative strength of Hund’s exchange with respect to typical excitation energy—in case of host bonds it is U ₂, whereas for hybrid bonds it is Δ(7). The exact functional forms of these coefficients are complicated and will be reported elsewhere.

The properties of the host and hybrid bonds are the following: a single host’s bond is always FM in spin and AF in orbital sector because of an orbital singlet which is formed on a bond [16]. This however is not stable when there are more than one bond—for a longer 1D system as for L = 8 chain considered here we find AF spin correlations for low η(8) turning FM in a high η limit. The case of a hybrid bond is much simpler: despite the complicated form of the Hamiltonian (1) it always gives AF spin correlations accompanied by FM ${\langle \tau ^{z}_{i}}\tau ^{z}_{i + 1}\rangle$ orbital correlations. Because of these intrinsic difference between host and hybrid bonds, it is essential to check the ground state properties of a finite system with single impurity, see Fig. 1.

In Fig. 2, we show the ground state spin and orbital correlations obtained for a closed chain of L = 8 sites with a single d ² impurity, see Fig. 1. The results are shown as functions of η for fixed values of J ₀, J _h, η ₁, and η ₂ which weakly influence the overall behavior. Due to translational invariance, one finds four inequivalent bonds, see Fig. 1. There are two regimes: (i) AF with total spin $\mathcal {S}= 2$ ($\left \langle {\sum }_{i} {S^{z}_{i}}\right \rangle = 2$) for η < 0.09, (ii) FM with $\mathcal {S}= 6$ ($\left \langle {\sum }_{i} {S^{z}_{i}}\right \rangle = 6$) for η > 0.09(however the hybrid impurity bonds are always AF). In the AF regime at η = 0, all the spin correlations are AF, but a level crossing occurs at η = 0.033where the magnetic moment delocalizes from the impurity to its two neighbors, remaining nearly constant within these three sites.

Fig. 2

Ground-state spin and orbital correlations on the bonds for a closed chain of length L = 8shown in Fig. 1. The computation is performed by means of exact diagonalization as a function of η. Left column—AF host with small η, right column—FM host with larger η. Rows: a spin $\langle \vec {S}_{i}\vec {S}_{i + 1}\rangle$ correlations, b orbital 〈τ i z τ i+ 1z〉correlations, and c orbital $\left \langle \tau _{i}^{+}\tau _{i + 1}^{-}\right \rangle$ ($\left \langle \tau _{i}^{+}\tau _{i + 1}^{+}\right \rangle$) correlations for the host/hybrid bond. Parameters: J ₀ = 1, J _h = 2, η ₁ = η ₂ = 1

Surprisingly, for increasing η < 0.09, the spin correlations between second and third neighbors of impurity become soon FM, due to spin-orbital entanglement, but the remaining spin correlations are AF. In the FM regime, all the host bonds have almost saturated FM spin correlations, ≃ + 1, while they tend to the classical value of − 1 for increasing η on hybrid bonds, see Fig. 2a. The orbital ${\langle \tau ^{z}_{i}}\tau ^{z}_{i + 1}\rangle$ correlations behave more regularly; they are AF for host bonds and FM for hybrid bonds in both regimes of η, see Fig. 2b. For the off-diagonal orbital correlations, we define the conventional $\tau ^{\pm }_{i}$ operators as $\tau ^{\pm }_{i}\equiv \frac 12({\tau ^{x}_{i}}{\pm \tau ^{y}_{i}})$ (here $\tau ^{x(y)}_{i}$ are normalized to ± 1). It turns out that 〈τ i + τ i+ 1−〉 correlations are significant only for the host bonds and $\langle \tau ^{+}_{i}\tau ^{+}_{i + 1}\rangle$ only for hybrid bonds and they are always AF, see Fig. 2c.

To investigate the spin-orbital entanglement, we introduce covariances for the various correlators,

$$\begin{array}{@{}rcl@{}} \mathcal{C}_{i,i + 1}^{zz}\!&=& \left\langle{\vec S}_{i}{\vec S}_{i + 1}{\tau^{z}_{i}}\tau^{z}_{i + 1}\right\rangle \,-\, \left\langle{\vec S}_{i}{\vec S}_{i + 1}\right\rangle \left\langle\tau^{z}_{i}\tau^{z}_{i + 1}\right\rangle, \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} \mathcal{C}_{i,i + 1}^{+\sigma}\!&=& \left\langle{\vec S}_{i}{\vec S}_{i + 1}\tau^{+}_{i}\tau^{\sigma}_{i + 1}\right\rangle \,-\, \left\langle{\vec S}_{i}{\vec S}_{i + 1}\right\rangle \left\langle\tau^{+}_{i}\tau^{\sigma}_{i + 1}\right\rangle +\text{H.c.}, \end{array} $$

(10)

with σ = ±. In Fig. 3, we show the spin-orbital covariances in the AF and FM regime. One finds that both longitudinal ($\mathcal {C}_{i,i + 1}^{zz}$) and transverse ($\mathcal {C}_{i,i + 1}^{+\sigma }$) covariances are large in the AF regime. Moreover, as one could expect, they are much lower at higher η > 0.1 when the host spin correlations are FM, while they tend to zero as η increases, see Fig. 3. Interestingly, the transverse covariance for the hybrid bond is positive ($\mathcal {C}_{i,i + 1}^{++}>0$) in the entire regime of parameters which suggests that double orbital excitations are strong on hybrid bonds. Thus, we conclude that the factorization into spin and orbital operators is a good approximation only in the FM regime and for this case we set the spin-spin correlations as equal to ± 1 for the host-impurity bonds.

Fig. 3

Ground state spin-orbital covariances $\mathcal {C}_{i,i + 1}^{\alpha \beta }$ on the bonds for a closed chain system of length L = 8(Fig. 1), obtained via exact diagonalization as functions of η for orbital correlations: a $\left \langle \tau ^{z}_{i}\tau ^{z}_{i + 1}\right \rangle$; b $\left \langle \tau _{i}^{+}\tau _{i + 1}^{-}\right \rangle$ ($\left \langle \tau _{i}^{+}\tau _{i + 1}^{+}\right \rangle$) for the host (hybrid) bonds. Left (right) column — AF (FM) host with small (large) η. Parameters: J ₀ = 1, J _h = 2, η ₁ = η ₂ = 1

3 Topological States in the Orbital Model

Factorization of spin and orbital degrees of freedom is allowed in the FM regime and leads to an effective orbital-only Hamiltonian,

$$\begin{array}{@{}rcl@{}} H_{i,j}^{\mathrm{0}}&=&\frac{1}{4}\,J_{\mathrm{0}}\, \frac{1}{1-3\eta}\,\vec{\tau}_{i}\vec{\tau}_{j}, \\ H_{i,j}^{\mathrm{h}}&=&J_{\mathrm{h}}\left( A_{xx}{\tau^{x}_{i}}{\tau^{x}_{j}}+A_{yy}{\tau^{y}_{i}}{\tau^{y}_{j}}+A_{zz}{\tau^{z}_{i}}{\tau^{z}_{j}}\right), \end{array} $$

(11)

for the host and hybrid bonds, respectively. This purely orbital Hamiltonian can be mapped on spinless fermions by the Jordan-Wigner transformations.

For symmetry reasons, we find an exact relation A _{z z} ≡−A _{x x} , and we also get that A _{x x} and A _{y y} almost compensate each other so their sum A _{x x} + A _{y y} = δ has a relatively small amplitude. It is however important to point out that δ≠ 0 because in the representation of Jordan-Wigner fermions δ is proportional to the hopping amplitude whereas A _{x x} − A _{y y} gives pairing amplitude — both are necessary to induce a topological non-trivial state. All the {A _{α, α} } coefficients are functions of η ₁ and η ₂, while we find that the dependence on η ₁ is very weak. Thus, we fix η ₁ = 4(η is already fixed as η = 0.2) and we show the behavior of the A _{α, α} coupling in Fig. 4c. We note that η ₂ = 0 is a high symmetry point where A _{α, α} ≡ 0.5for any η ₁.

Fig. 4

Orbital model results obtained in Hartree-Fock (11) in the regime of FM host as a function of η ₂ = J ₂/Δ: a bond correlations 〈τ i x τ i+ 1x〉and ±〈τ i y τ i+ 1y〉(solid and dashed lines), with color convention as in Fig. 1; b magnified view of (a) for η ₂ → 0; c orbital couplings A _{z z} and sum A _{x x} + A _{y y} (solid and dashed) for hybrid bonds, and d topologically relevant quantities, $\text {Im}\mathcal {D}_{\pi /2}$ and $\mathcal { D}_{0}\mathcal {D}_{\pi }$ (solid and dashed). Parameters: J ₀ = 1, J _h = 2, η ₁ = 4, η = 0.2

Hence, by means of the Hartree-Fock decoupling, we deal with fermion-interaction term ${\langle \tau ^{z}_{i}}\tau ^{z}_{i + 1}\rangle$ in a self-consistent manner and we obtain the bond $\left \langle \tau ^{\alpha }_{i}\tau ^{\alpha }_{i + 1}\right \rangle$ orbital correlations for a periodic (and infinite) system with one d ² impurity per every L = 8 sites. We find that in the present parameter regime the ${\langle \tau ^{z}_{i}}\tau ^{z}_{i + 1}\rangle$ vanish and one gets only the kinetic terms ${\langle \tau ^{x}_{i}}\tau ^{x}_{i + 1}\rangle$ and ${\langle \tau ^{y}_{i}}\tau ^{y}_{i + 1}\rangle$. For the host bonds, they are all AF while for the hybrid ones the xx correlations are AF and yy ones are FM, see Fig. 4a. Interestingly, we obtain a discontinuous transition at η ₂ = 0⁺ between anisotropic and isotropic phases—the difference between xx and yy correlations is triggered by any finite η ₂, see Fig. 4b. Finally, at finite η ₂, one always gets a regime with a non-trivial topological phase with respect to the Jordan-Wigner fermionic representation.

Indeed, the fermionic Hamiltonian in the momentum space is given by a matrix $\mathcal {H}_{k}$ that belongs to the BDI Altland-Zirnbauer class [38]. Thus, it can have a non-trivial Z topological number. The topological invariant can be determined by looking at $\mathcal {H}_{k}$ in the eigen-basis of the chiral symmetry where it consists of two anti-diagonal blocks u _k and $u_{k}^{\dagger }$. The determinant of u _k , $\mathcal {D}_{k}\equiv \det {u_{k}}$, is a complex number which yields a non-trivial topological number if it winds around the (0,0) point in the complex plane as k changes from 0 to 2π. In the present case, this happens if (i) the imaginary part of $\mathcal {D}_{\pi /2}$ is non-vanishing and (ii) the determinants $\mathcal {D}_{0}$ and $\mathcal {D}_{\pi }$ have opposite signs. In Fig. 4d, we observe that indeed these conditions hold as long as η ₂ > 0.

Recently, the topological phase diagram of a 1D tight-binding model of spinless electrons with an inhomogeneous distribution of pairing centers has been investigated [39]. The Hamiltonian includes inhomogeneities generated by diluted pairing centers with a given distribution profile in the unit cell of length L. For a periodic configuration with momentum k, we get,

$$\begin{array}{@{}rcl@{}} \mathcal{H}&=&\!\sum\limits_{p = 1\atop k}^{L}\! \left\{t_{p}^{} c_{kp}^{\dagger}c_{k,p + 1}^{} \,+\,{\Delta}_{p}^{} c_{kp}^{\dagger}c_{-k,p + 1}^{\dagger}\,+\,\textrm{H.c.} \,+\,\mu_{p}^{} c_{kp}^{\dagger}c_{kp}^{}\right\}\!, \\ \end{array} $$

(12)

with c _{L+ 1, k} ≡ e ^ik c _1,k and {t _p , Δ _p } being the nearest neighbor hopping and on-bond pairing amplitudes. There, we have found the topological invariant that can be generally expressed in terms of the physical parameters for any pairing center configuration [39].

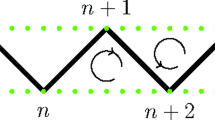
Here, we emphasize the occurrence of edge states and present the spectra around zero energy for a closed and open system, see Fig. 5a, b. We note that for an open system, there are two zero-energy states appearing in the gap. These are Majorana end modes that arise as a consequence of the bulk-boundary correspondence in a topologically non-trivial configuration. In Fig. 5c, d, the spatial occupation probabilities p _i for the two zero energy states are explicitly shown in order to confirm their degree of localization on the right/left edges of the 1D chain. We also point out that the modification of the kinetic term with the inclusion of long-range hopping is expected to lead to multiple Majorana end modes both in spinless [40] and spinfull p-wave superconducting chains [41].

Fig. 5

Energy spectra and edge states for a fully disordered 1D chain (12) of size L = 20000and N = 200random impurities for: a a closed chain, and b an open chain, exhibiting two zero energy states in the gap. The occupation probabilities {p _i }for the Majorana zero-energy states in the gap at: c the right chain edge, and d the left chain edge

4 Discussion and Summary

In conclusion, we have studied a one-dimensional hybrid d ²-d ⁴system with a single d ²impurity in a d ⁴spin-orbital correlated host. Remarkably, the exact diagonalization analysis allows to single out regimes for which the orbitals and spins can be factorized if the host configuration is FM. By this decoupling one finds interacting orbital pseudospins exhibiting fully isotropic exchange for the host bonds and fully anisotropic for the hybrid ones. A Jordan-Wigner transformation and Hartree-Fock decoupling allow, then, to map the system on non-interacting fermions and to find topological non-trivial states. Unexpectedly, a topological non-trivial state occurs for any finite value of J ₂, i.e., the amplitude of the Hund’s coupling at the host’s ions. For a long chain we explicitly demonstrate that Majorana-like modes occur at the edge of the system. We argue that inhomogeneous topological patterns [42] can be achieved in the present spin-orbital scenario with Majorana modes occurring, for instance, at the boundary of the FM region if the impurities drive a magnetic configuration that has alternating FM with AF domains.