1 Introduction

Interplay between impurities and superconductors is the focus of many studies [1]. Bound states near magnetic impurities in the conventional s-wave superconductor are an example of such interplay. This behavior was proposed by Yu [2], Shiba [3] and Rusinov [4] in the 1960s. In those pioneering papers, authors describe the possibility of pair breaking by a single magnetic impurity, that leads to emergence of in-gap quasi-particles states.

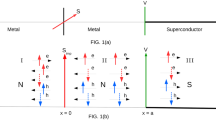
Recent experiments [5,6,7] show the possibility of realization of this bound state, called Yu–Shiba–Rusinov (YSR) bound state in NbSe2 with a quasi-two dimensional (2D) triangular lattice [8, 9]. A change in the coupling strength between the magnetic impurity and superconductor, can lead to the quantum phase transition (QPT) [10]. The main idea of this QPT is shown schematically in Fig. 1. When the coupling is weak, there are numerous bound Cooper pairs (left part). However, after QPT, when the coupling is strong enough, the local magnetic field, generated by the impurity, leads to pair breaking and formation of bound broken pairs (right panel).

Fig. 1
figure 1

Schematic representation of the main idea of the quantum phase transition in the presence of the magnetic impurity (big red arrow) in a conventional superconductor (shown by condensate of the singlet Cooper pairs). Quantum phase transition leads to a change of the ground state from bound states of non-broken (left) to bound states of broken (right) Cooper pairs

Full size image

In this paper, we discuss basic properties of the QPT in the case of triangular lattice by studying the evolution of YSR states using the Bogoliubov–de Gennes (BdG) equations. Our microscopic model and the BdG technique are shown in Section 2. Numerical results and discussion are presented in Section 3, and we summarize our work in Section 4.

2 Model and Methods

We study a 2D triangular lattice, described by attractive Hubbard model (U < 0). The Hamiltonian is given as:

$$\begin{array}{@{}rcl@{}} \mathcal{H} = H_{0} + H_{imp} + H_{sc}. \end{array} $$
(1)

Here

$$\begin{array}{@{}rcl@{}} H_{0} = - t \sum\limits_{\langle i,j \rangle \sigma } c_{i\sigma}^{\dagger} c_{j\sigma} - \mu \sum\limits_{i\sigma} c_{i\sigma}^{\dagger} c_{i\sigma} \end{array} $$
(2)

is the free-electron kinetic term. \(c_{i\sigma }^{\dagger }\) (c iσ ) denotes creation (annihilation) of electron with spin σ = {↑, ↓} at i-th lattice site, t is the hopping integral between nearest neighbors and μ is the chemical potential.

For simplicity, we neglect the local modification of chemical potential at impurity site. For a large spin number S, the magnetic impurity can be treated classically

$$\begin{array}{@{}rcl@{}} H_{imp} = J \sum\limits_{i \sigma } \sigma c_{i\sigma}^{\dagger} c_{i\sigma} \delta_{i0} . \end{array} $$
(3)

In this case, the potential J plays the role of local magnetic field at the impurity site.

On-site pairing is given by the Coulomb term

$$\begin{array}{@{}rcl@{}} H_{sc} = U \sum\limits_{i} n_{i\uparrow} n_{i\downarrow} . \end{array} $$
(4)

This part can be decoupled by means of the mean-field approximation, which gives:

$$\begin{array}{@{}rcl@{}} n_{i\uparrow} n_{i\downarrow} &=& {\Delta}_{i} c_{i\uparrow}^{\dagger} c_{i\downarrow}^{\dagger} + {\Delta}_{i}^{\ast} c_{i\downarrow} c_{i\uparrow} - | {\Delta}_{i} |^{2} \end{array} $$
(5)

where we define Δ i = 〈c i↓ c i↑ 〉 as the superconducting order parameter (SOP).

For the inhomogeneous system, the Hamitonian (1) can be diagonalized by Bogoliubov–Valatin transformation [11]

$$\begin{array}{@{}rcl@{}} c_{i\sigma} = \sum\limits_{n} \left( u_{in\sigma} \gamma_{n\sigma} - \sigma v_{in\sigma}^{\ast} \gamma_{n\bar{\sigma}}^{\dagger} \right) , \end{array} $$
(6)

where γ n and \(\gamma _{n}^{\dagger }\) are the fermionic quasi-particle operators, whereas u and v are the BdG eigenvectors. Then, the self-consistent BdG equations in real space take the form

$$\begin{array}{@{}rcl@{}} \mathcal{E}_{n\sigma} \left( \begin{array}{c} u_{in\sigma} \\ v_{in\bar{\sigma}} \end{array} \right) = \sum\limits_{j} \left( \begin{array}{cc} H_{ij\sigma} & U {\Delta}_{i} \delta_{ij} \\ U {\Delta}_{i}^{\ast} \delta_{ij} & -H_{ij\bar{\sigma}}^{\ast} \end{array} \right) \left( \begin{array}{c} u_{jn\sigma} \\ v_{jn\bar{\sigma}} \end{array} \right) , \end{array} $$
(7)

where H ijσ = −tδ 〈i, j〉−(μ − σJδ i0)δ ij is the single-particle Hamiltonian. The grand canonical potential \({\Omega } = -k_{B} T \ln \{ \text {Tr} [ \exp (- \mathcal {H} / k_{B} T ) ] \}\) can be expressed as

$$\begin{array}{@{}rcl@{}} {\Omega} &=& - \frac{k_{B} T}{2} \sum\limits_{n\sigma} \ln \left( 1 + \exp \left( \frac{-\mathcal{E}_{n\sigma}}{k_{B}T} \right) \right) \\ &&+ \mu N - U \sum\limits_{i} | {\Delta}_{i} |^{2} , \end{array} $$
(8)

where N is the total number of states.

The BdG (7) can be solved self-consistently, with respect to the SOP, which can be found as

$$\begin{array}{@{}rcl@{}} {\Delta}_{i} &=& \langle c_{i\downarrow} c_{i\uparrow} \rangle \\ &=& \sum\limits_{n} \left( u_{in\downarrow} v_{in\uparrow}^{\ast} f(\mathcal{E}_{n\uparrow} ) - u_{in\uparrow} v_{in\downarrow}^{\ast} f (- \mathcal{E}_{n\downarrow} ) \right) , \end{array} $$
(9)

where f(ω) = 1/ (1 + exp(ω/k B T)) is the Fermi-Dirac distribution. Similar, the local density of states (LDOS) for particles with given spin σ in i-th site [12] can be calculated from

$$\begin{array}{@{}rcl@{}} \rho_{i\sigma} (\omega ) \,=\, \sum\limits_{n} \left[ | u_{in\sigma} |^{2} \delta (\omega - \mathcal{E}_{n} ) + | v_{in\sigma} |^{2} \delta (\omega + \mathcal{E}_{n} ) \right] . \end{array} $$
(10)

whereas (total) density of states (DOS) \(\rho (\omega ) = {\sum }_{i\sigma } \rho _{i\sigma } (\omega )\).

The BdG equations method [13] can be useful in treating the general problem of superconducting state in a presence of the inhomogeneity like scalar non-magnetic impurity in a s-wave [14,15,16,17] or d-wave [17,18,19] superconductors, superconductivity in the presence of spin density wave [20] or vortices [21,22,23], ultracold Fermi gases in the external trap [24, 25] or unconventional FFLO superconducting phase [17, 18, 26, 27]. Moreover, this type of problems can be solved in different types of geometries, i.e., rings [28] or frames [29].

3 Numerical Results and Discussion

In this section, we turn our attention to numerical results for a 2D triangular lattice with N x × N y = 41 × 41 sites in real space. In our calculations we assume U/t = −3, μ/t = 0 and k B T/t = 0.

In the first step, we calculate the total DOS as a function of J (Fig. 2a). Constant value of U leads to superconducting gap (SG) of about 0.4 in the absence of impurity (J/t = 0). With increasing |J| we can observe the appearence of a bound state induced by magnetic impurity inside the SG (|ω|/t < 0.4). For any value of |J|, eigenvalues corresponding to those bound states are located symmetrically around ω/t = 0. Different spectral weight and opposite spin polarisation of positive and negative eigenvalues stems from the fact that YSR states are induced by magnetic impurity. In this sense, we can tell about spin polarized bound states [30], corresponding to nonzero value of ρ i↑ (ω) − ρ i↓ (ω).

Fig. 2
figure 2

DOS (a) and value of the SOP at the impurity site Δ imp (b and c) for different values of J. Results for U = −3t, μ = 0t and k B T = 0

Full size image

As we can see, in some critical value of J (show by yellow dashed line), the polarization of bound state are changed. This critical values J c correspond to QPT induced by magnetic impurity. One can observe that when J → J c eigenvalues corresponding to YSR states are approaching ω/t = 0. Moreover, during the QPT energy of bound states changes discontinuously.

Other signature of the QPT in this system is the sign change of the SOP at the impurity site Δ imp (Fig. 2b). On other hand, like in the case of a scalar impurity, increasing J leads to a decrease of |Δ imp |, i.e., when J/t →±∞ then |Δ imp |→ 0.

Fig. 3
figure 3

Compare of the grand canonical potential per state \(\bar {\Omega } = {\Omega } / N\) for different quantum phases, in which Δ imp are positive (red line) or negative (blue line). Results form parameter from Fig. 2

Full size image

When describing a QPT induced by magnetic impurity, it is important to look into the total energy of the system, by calculating the grand canonical potential Ω (8). For fixed parameter, the energy is only a function of the spatial decomposition of SOP in real space, i.e., Ω ≡ Ω(Δ). Here, Δ = (Δ1,Δ2,⋯) is a N x ×N y -component vector of the SOP at every site of real space. To compare the Ω of a system before and after QPT, we calculate the grand canonical potential in two cases: when the SOP at the impurity site is (i) positive and (ii) negative. We denote the grand canonical potential in these two cases \(\bar {\Omega }_{+}\) and \(\bar {\Omega }_{-}\), respectively. The comparison of those quantities is shown in Fig. 3, where the QPTs are marked by black arrows. As we can see the minimum energy of the system is given by \(\bar {\Omega }_{+}\) for |J| < |J c |, while in other cases by \(\bar {\Omega }_{-}\).

The QPTs induced by magnetic impurities are similar to the classical phase transitions e.g. from superconducting to normal state. On one hand, energy of the system is given by a global minimum of the energy of different states (bound Cooper pairs or broken pair bound states). When a change of ground state is more favorable energetically, we observe a phase transition. On the other hand, QPTs are discontinuous. This can be deduced from the fact that the eigenvalues of YSR states change discontinuously and from the sign change of the SOP at the impurity site.

4 Summary

The magnetic impurity in a conventional superconductor can lead to a quantum phase transition. In this paper, we described this possibility in the case of triangular lattice with on-site pairing. We described basic properties of the quantum phase transition induced by the the magnetic impurity, i.e., the change of polarization of the bound states, discontinuous change of energy of bound states induced by impurity and the sign change of the superconducting order parameter at the impurity site. We have shown that the quantum phase transition is connected to a change of ground state of the system, which chooses the more energetically favorable state.