1 Introduction

Over the past decade, significant advances have been made by the high-temperature superconducting (HTS) modelling community [1] to develop various numerical models to analyse the performance of HTS materials for a variety of practical engineering devices and applications. Numerical models are powerful tools for investigating the electromagnetic and thermal properties of HTS materials in various configurations: coils, cables, transformers and bulk HTS materials acting as powerful, trapped field magnets (TFMs) [2].

The Bulk Superconductivity Group at the University of Cambridge is currently investigating the use of HTS materials in wire and bulk form in order to increase the electrical and magnetic loadings of an axial gap, trapped flux-type superconducting electric machine [3]. As part of this research, accurate 2D axisymmetric and 3D finite element models of superconducting coils have been developed to investigate and simulate their electromagnetic behaviour [4–6]. In this paper, some of the recent advances on analysing the performance of HTS coils are highlighted, including the simulation of in-field performance, increasing the computational speed and accuracy of 3D models. Experimental results on the DC characterisation of a test circular, epoxy-impregnated HTS coil are compared with numerical simulation results using a 2D axisymmetric finite element model based on the H formulation, and then used to interpret the effects of degradation due to epoxy impregnation from the coil’s ideal performance.

2 Modelling Framework for HTS Coils

HTS coil geometries take a number of different forms, including circular, racetrack and triangular, and can operate under a combination of complex electromagnetic environments: with a DC or AC transport current and/or in a static or dynamic, time-varying background magnetic field. Numerical modelling tools—many of which use the finite element method (FEM)—have now been developed to an extent that many of these complex environments and geometries can be simulated effectively, including thermal considerations. FEM techniques have been applied to many superconducting material problems using a variety of formulations, and each of these formulations is equivalent in principle, but the solutions of the corresponding partial differential equations can be very different [7]. For more detailed information, including techniques not based on FEM, the reader may refer to recent review papers on numerical methods for calculating AC losses in HTS materials [8], and the modelling of bulk superconductor magnetisation [9] and HTS applications [2]. This paper focuses chiefly on the modelling of HTS coils using the H formulation.

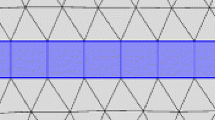
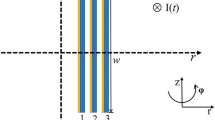
When modelling coils, the choice of coordinate system depends on the coil’s geometry: circular coils can be modelled using 2D axisymmetric models [4, 5, 10, 11] and racetrack and triangular coils can be modelled using a 3D model [6, 12]. The symmetry of the coil structure and the HTS tapes comprising the coil can be exploited to reduce the number of mesh elements required and improve computational speed [6, 12, 13]. Figure 1a shows a 2D axisymmetric model of a circular coil, and Fig. 1b shows an example of a 3D triangular coil model, where geometric symmetry is used to model only one sixth of the entire coil. Three-dimensional models can require 100,000s of elements and long computational times, particularly because of the large aspect ratio and the highly non-linear E–J power law relationship of the superconducting material. To overcome this issue, Hu et al. [6] used a novel combination of different mesh types (mapped, scaled and swept) to utilise the real superconducting layer without excessive computational requirements, and Zermeno and Grilli [12] and Zermeno et al. [14] introduced a homogenisation method to model a stack of tapes as an anisotropic bulk-like equivalent to simplify the geometric layout without undermining accuracy.

Fig. 1
figure 1

a Example of a 2D axisymmetric model of a circular coil. b Example of a 3D triangular coil model, where geometric symmetry is used to model only one sixth of the entire coil

Full size image

In the H formulation, the governing equations are derived from Maxwell’s equations, namely Ampere’s and Faraday’s laws

$$\nabla \times \mathbf{H}=\mathbf{J} $$
$$\nabla \times \mathbf{E}+\frac{d\mathbf{B}}{dt}=\nabla \times \mathbf{E}+\frac{d(\mu_{0} \mu_{r} \mathbf{H})}{dt}=0 $$

where H = [ H r, H z] represents the magnetic field components, J = [ J φ ] represents the current density and E = [ E φ ] represents the electric field in the 2D axisymmetric case. In 3D, H = [ H x, H y, H z], J = [ J x, J y, J z] and E = [ E x, E y, E z]. μ 0 is the permeability of free space, and for the superconducting and air sub-domains, the relative permeability can be assumed as simply μ r = 1. However, the formulation also allows the introduction of magnetic sub-domains into the model by introducing a relative permeability μ r ≠ 1, which may be not constant but varies with magnetic field, i.e. μ r(H) [15–20]. The electrical behaviour of the superconductor is modelled using the E–J power law, where E is proportional to J n, and when n > 20, it becomes a good approximation of Bean’s critical-state model (for which, n → ∞) [9]. In addition, E = ρ J, where ρ is the highly non-linear resistivity of the superconductor.

The most important characteristic of a superconductor for any practical application is its critical current density, J c, and therefore a crucial aspect of superconducting material modelling is its in-field performance, for which HTS tapes have an angular and temperature dependence, i.e. J c(B, 𝜃, T). It is also not difficult to implement position-dependent J c properties, such as non-uniformities along the length or width of the conductor [5]. This is usually input into the FEM model using a data fitting function, which can be quite complicated and can impact on the model’s computational speed. Recently, a two-variable direct interpolation, similar to a look-up table, was implemented in a 3D coil model [6] in COMSOL Multiphysics®; [21] that uses the experimentally measured J c(B, 𝜃) simply and directly as input data for the model. This type of direct interpolation can significantly improve the computational speed and convergence of the model, even when the real tape thickness is modelled, and avoids complicated data fitting while improving accuracy [22]. Another example of how to extract a J c(B, 𝜃) relationship from experimental data can be found in [23].

3 Assessing Coil Performance

The AC (AC loss) and DC (critical current) characteristics are two important performance criteria for HTS coils, and the DC characterisation allows the maximum allowable current to be determined, which can, for example, impact significantly on the size and weight of a superconducting electric machine. By applying integral constraints to each of the tapes in the coil, a ramped DC current can be applied, with appropriate boundary conditions set depending on whether the coil experiences a background field [4, 10]. There exist some more efficient techniques for estimating a coil’s critical current, such as [24]; however, the H formulation allows a high degree of flexibility for a variety of AC and DC electromagnetic conditions. The critical current can then be determined when the average electric field in the coil [4, 10] exceeds the characteristic electric field, E 0, which is normally assumed as 10−4 V/m for HTS materials, or when the electric field in one conductor exceeds E 0 in consideration of risks of coil quench/damage from excessive local current [24].

The combination of numerical simulations with experiments can help understand the observed experimental phenomena and the physical mechanisms underlying these and allows further refinement of the modelling framework to represent more realistic, practical situations. Figure 2 shows a test circular HTS coil used for DC characterisation. The coil was wound using a SuperPower’s SCS4050-AP-coated conductor [25] and then vacuum impregnated in epoxy, resulting in 47 turns from a total length of 19.3 m of tape. The same vacuum impregnation process was used as described in [6]. Ten voltage taps, spaced approximately every 2 m along the tape length, are used within the coil to provide more detailed information about the coil properties, with the first voltage tap wired 1 m from the coil’s inner copper current contact and the final voltage tap wired 0.3 m from the outer current contact to prevent an anomalous measurement due to localised heating of the tape near the coil terminals [6, 11]. A DC current was applied to the coil at a ramp rate of 0.5 A/s at 77 K in a liquid nitrogen bath.

Fig. 2
figure 2

A test circular, epoxy-impregnated HTS coil used for DC characterisation

Full size image

For the numerical simulation, the 2D axisymmetric model above is used, and the J c(B, 𝜃) dependence of a short sample taken from the same spool of tape provided in [22] (sample SP1 in this reference) is input using the direct interpolation described above. The inner radius of the coil is 60 mm, and the distance between each superconducting layer is 190 µm. The average electric field, E coil, can then be calculated by

$$E_{\text{coil}} =\sum\limits_{n\;=\;1}^{N} {\int {2\pi r_{n}} } E_{\varphi} \cdot ds_{n} \;/\;\sum\limits_{n\;=\;1}^{N} {2\pi r_{n} \cdot s_{n}} $$

where N is the total number of turns in the coil, r n is the radius of each turn, E φ is the local electric field and s n is the cross-sectional area of each turn. A similar method can be used to calculate the electric field in different voltage sections [6]. The applied current has a ramp rate of 7 A/s, and isothermal conditions are assumed; hence, no thermal model is included.

A comparison of the experimental and simulated current–voltage (I– V) curves is shown in Fig. 3a, where V 13 represents the total coil voltage. Figure 3b shows the I–V curves for each third of the coil, where V 10, V 11 and V 12 represent the inner, middle and outer thirds, respectively. There is a clear discrepancy between the critical currents: 19 A (experiment) and 56 A (simulation). The I c ranking of each third is also different between each third of the coil: I c(V 12) < I c(V 11) < I c(V 10) experimentally and I c(V 10) < I c(V 12) < I c(V 11) by simulation. Uniform J c(B, 𝜃), based on the short sample measurement, is assumed along the length of the tape in this simulation, and in this ideal case, it is expected that the inner turns, i.e. V 10, will see a relatively higher localised magnetic field, which would determine the overall critical current of the coil [4, 10, 11]. To provide more detailed information, the n values and critical currents in the non-uniform regions of the coil are analysed using all of the voltage taps. As described in [6], it is found that in some non-uniform regions, due to degradation from the epoxy impregnation, the n value cannot be considered as constant and varies when the magnitude of the current (I) is changed. The specific details are shown in Table 1, and this data is used to further refine the J c(B, 𝜃) assumptions in the model using the average magnetic field and orientation in each region [6]. For the other uniform regions (V 3, V 4, V 8 and V 9), the original J c(B, 𝜃) is assumed, along with an n value of 21. Almost no electric field appears in these regions when the input current is 32 A, so it can be assumed that the critical current in these regions is higher than 32 A. Figure 4 shows the results of the refined model, and Fig. 5 shows the I–V curves for each third of the coil. It is clear that by including this detailed characterisation, the model can reproduce the experimentally observed behaviour, which in this case is quite complex, with good accuracy.

Fig. 3
figure 3

a Experimental and simulated current–voltage (I– V) curves for the circular HTS coil, assuming uniform J c(B, 𝜃) characteristics across the entire length of tape comprising the coil. b I–V curves for each third of the coil, measured using voltage taps within the coil

Full size image
Table 1 Comparison of experimentally measured n values and critical currents in non-uniform regions of the test HTS coil and the refined critical current densities in the model
Full size table
Fig. 4
figure 4

Experimental and simulated I–V curves for the circular HTS coil after refining the model in different regions by considering the measured critical currents (Table 1) using all of the voltage taps

Full size image
Fig. 5
figure 5

Experimental and simulated I–V curves for each third of the coil, measured using voltage taps within the coil, after refining the model

Full size image

4 Conclusion

Numerical models are powerful tools for investigating the electromagnetic and thermal properties of HTS materials to assess the performance of coils, cables and other devices. In this paper, some of the recent advances, based on the H formulation, in analysing the performance of HTS coils are highlighted, including the simulation of in-field performance and increasing the computational speed and accuracy of 3D models. Experimental and simulation results for the DC characterisation of a test circular, epoxy-impregnated HTS coil are used to interpret the effects of degradation due to epoxy impregnation from the coil’s ideal performance. With this numerical modelling framework, it is possible to simulate a variety of complex devices in both 2D and 3D over a broad range of electromagnetic situations with good accuracy.