1 Introduction

In classical low-temperature superconductors, the resistive transition from the normal to the superconducting state is generally sharp and significant broadening of the transition is usually hardly observable. It is because in low-temperature superconductors, pinning is reasonably effective, while the fluctuating effects are relatively unimportant. So that there is a rather sharply defined resistive transition in which the resistance drops to zero in a very narrow temperature range. The applied magnetic field generally moves the resistive transition as well as the critical temperature to lower temperatures and increases the width of the resistive transition [1, 2]. The utterly different behaviors can be observed in high-temperature superconductors (HTSs) in which the width of the resistive transition is easy to observe and it can be anomalously broadened under the influence of the applied magnetic field. This effect was observed for almost all HTSs, particularly in the bulk [3, 4], single-crystalline [5], thin-film [6], and first-generation (1G) bismuth-based tape [7] forms. The width of the resistive transition of HTS can generally be described in the following form [6]:

$$ {\Delta} T=CH^{m}+{\Delta} T_{0} $$
(1)

where m = 2/3 and ΔT 0 denotes the width at the zero applied magnetic field. The exponent m is related to the exponent n that appears in the temperature dependence of the irreversibility field by the relation: m = 1/n. The coefficient (C) depends on the critical current at zero magnetic field as well as on the critical temperature. The high-temperature superconductors are an extreme second type with a large penetration depth (λ) of the order of 103–104 Å [8] and a very small coherence length (ξ) of the order of 10 Å [9]. This makes the Ginzburg–Landau parameter (κ = λ/ξ) of the order of 102 or more. Other important superconducting parameters are also extremely anisotropic (e.g., the ratio of c-axis to a–b plane direction of penetration depths (γ = λ c/λ ab) is of the order of 10–102 for YBCO and of the order of 104 for BSCCO) like the critical currents, the irreversibility fields, and others. This is due to the anisotropic layered structure of weakly coupled CuO 2 superconducting planes. Typical critical current densities of the 1G bismuth-based tapes are of the order of 15–35 kA cm−2 at 77 K in the own magnetic field [10] that gives the critical currents of the order of 120–170 A for typical tapes [11, 12]. These critical currents decrease to 20–60 A in the magnetic field of B = 1 T at 77 K. One of the highest critical current densities reported for 1G tapes was about 110 kA cm−2 at 77 K [13]. The critical current densities of YBCO c-axis-oriented film can reach 1.2 × 107 A cm−2 at 77 K in the self-magnetic field [14].

In this paper, the temperature dependencies of the magnetoresistance of commercial second-generation (2G) tape were measured and studied. The unique field dependencies of the transition width are reported and analyzed. The temperature dependencies of the irreversibility fields were obtained and interpreted within the vortex glass picture of HTS. The transport critical current at 77 K was measured. The absorption part of a.c. susceptibility was measured and used for calculations of the critical current densities using Bean’s critical-state model.

2 Experiment

The commercial 2G HTS tape was manufactured by SuperPower Inc. The width of the tape is 4 mm and its thickness is 50 μm. The average thickness of the superconducting material is about 0.001 mm.

The temperature dependencies of the magnetoresistance were measured using the standard four-point a.c. method option of the Quantum Design PPMS apparatus equipped with a 90 kOe superconducting magnet. The measurements were carried out for the two relative configurations of the tape plane and the applied magnetic field: perpendicular and parallel. The transport critical current density was measured at the liquid nitrogen temperature with the fourpoint method using a d.c. current power supply. For these measurements the H-shaped sample was prepared. The cross section of the superconducting film of the tape is 0.5 × 0.001 mm. The gap between the voltage contacts is 3 mm. The dispersion (χ ′) and absorption (χ ″) parts of the a.c. susceptibility as a function of temperature in the a.c. magnetic field amplitudes ranging from 0.098 Oe up to 11 Oe were measured by a standard mutual inductance bridge operating at the frequency of 188 Hz. A Stanford SR 830 lock-in nanovoltmeter served both as a source for the a.c. current for the coil which produced the a.c. magnetic field and as a voltage meter of the bridge. The temperature was monitored by a Lake Shore temperature controller employing a chromel–gold–0.07 % Fe thermocouple with the accuracy of ±0.05 K for this experimental setup. The magnetic field was parallel to the sample surface.

3 Results and Discussion

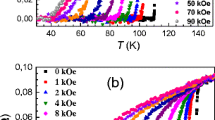
The temperature dependencies of the magnetoresistance for the parallel and perpendicular magnetic field orientations with respect to the tape plane are shown in Fig. 1a, b, respectively. At the zero magnetic field, the critical temperatures for this tape are of T c50 % = 91.5 K and T c0 = 90.0 K and the width of superconducting transition is ΔT 0 = 1.5 K. One can notice a significant shift of the superconducting transition to the lower temperatures if the applied magnetic field is increased and, at the same time, the transition from the normal to the superconducting state is not broadened. A bigger shift is observed if the applied magnetic field is perpendicular to the tape plane. The width of the resistive transition that is usually defined as ΔT = T 90 % − T 10 % is of the order of 1.5 K for the different applied magnetic fields for both orientations (see Table 1). A very important observation is that the transition from the normal to the superconducting state does not broaden if the applied magnetic field is increased up to 90 kOe and does not depend on the orientation of the magnetic field with respect to the tape plane.

Fig. 1
figure 1

Temperature dependencies of the magnetoresistance of the 2G tape for the parallel (a) and perpendicular (b) orientations of the applied magnetic field with respect to the tape plane

Full size image
Table 1 The width of the resistive transition for the different applied magnetic fields for both orientations of the field versus the tape plane
Full size table

The most important curve on the H–T phase diagram of HTS is the irreversibility line [15, 16] that separates the vortex glassy from the vortex liquid state. This line is determined by the temperature dependence of the irreversibility fields, and above it, the flowing current forces the vortices to move. It means that energy dissipation occurs and the supercurrent vanishes. From this point of view, the irreversibility field of HTS plays a similar role to that of the upper critical field in classical superconductors. The temperature dependence of the irreversibility field can be described by the following relation [15]:

$$ H_{\text{irr}} =H_{\text{irr0}} \left( {1-\frac{T}{T_{\text{c0}} }} \right)^{n} $$
(2)

where H irr0 is the irreversibility field at 0 K, T c0 is the zero critical temperature at zero magnetic field and the exponent n which is theoretically 3/2, can vary in wide range and depends on the vortex properties. One can assume [6] that the temperature at which the whole sample stays superconducting (resistance equal to zero) at the given magnetic field separates the reversibility from the irreversibility region. The data H irr(T) were derived from the magnetoresistance measurements and are shown in Fig. 2. The experimental data of H irr(T) were successfully fitted using (2) with the two fit parameters: n and H irr0. The zero field critical temperature T c0 = 90 K was taken from the experiment (solid lines in Fig. 2). The fit procedure delivers the following parameter values: n = 1.56 ± 0.02 and H irr0 = 9090 ± 420 kOe for the parallel direction and n = 1.08 ± 0.03 and H irr0 = 880 ± 60 kOe for the perpendicular direction. The exponent for the parallel direction is much higher than for the perpendicular one. The big difference of the values of the exponent n suggests that there is a high texture in the superconductor film of this tape and the a–b plane of HTS crystallites largely coincides with the tape surface. The irreversibility fields show an anisotropy, and at the liquid nitrogen temperature, they are as follows: H irr = 430 kOe and H irr = 106 kOe for the parallel and the perpendicular directions, respectively.

Fig. 2
figure 2

Irreversibility fields as a function of temperature for the perpendicular (open squares) and the parallel (open circles) orientations of the applied magnetic field with respect to the tape plane. Solid lines are the fits to (2)

Full size image

The anisotropy ratio can be expressed as [17]

$$ \gamma =\frac{\lambda_{c} }{\lambda_{ab} }=\frac{H_{c2 \|ab} }{H_{c2 \|c} }=\frac{H_{\text{irr}\|ab} }{H_{\text{irr}\|c}}, $$
(3)

where the upper critical fields parallel to the ab plane and to the c-axis, respectively, were replaced by the irreversibility fields corresponding to both directions. The anisotropy ratio amounts to γ = 4 at 77 K which is small in comparison with other HTS materials.

The transport critical current density for the 2G tape was measured at the liquid nitrogen temperature by the four-point technique using a d.c. current power supply. The voltage drop is shown as a function of the applied d.c. current in Fig. 3. According to this dependence, one can notice that at the current of I = 17.2 A, the voltage drop starts to increase following the E = 10−6 V cm−1 criterion. This value of the current was taken for evaluation of the critical current density. The H-shaped cross section of the superconducting film of the tape (0.5 × 0.001 mm) gives the cross-sectional area (S = 5 × 10−6 cm2), and the critical current density obtained amounts to J c = 3.44 × 106 A cm−2 at 77 K in the self-magnetic field.

Fig. 3
figure 3

Voltage drop as a function of the applied d.c. current. Inset shows that at the current I = 17.2 A, the voltage drop starts to rise

Full size image

The temperature dependences of the real (χ ′) and imaginary (χ ″) parts of the a.c. susceptibility measurements are shown in Fig. 4. On the transition from normal to the superconducting state, one can observe a sharp step in the χ ′(T) dependence and a very narrow peak of its imaginary component χ ″. The critical temperature determined from the χ ′(T) dependence is T c = 90.05 K (see the inset in Fig. 4), and the width of the transition determined from the χ ″(T) dependence is ΔT c = 0.5 K. These features give evidence of a good quality of the superconducting film used in this tape. The absorption part in the a.c. susceptibility is shown in Fig. 5 as a function of temperature for several values of the a.c. applied magnetic fields. It exhibits, in general, one peak related to the energy losses of the inter-granular region that moves to lower temperatures when the applied magnetic field amplitude is increased. These shifts are small, so it means that the critical current densities in the sample are very high.

Fig. 4
figure 4

Real (\(\chi ^{\prime }\)) and imaginary (\(\chi ^{\prime \prime }\)) parts of the a.c. susceptibility as a function of temperature for the 2G superconducting tape. Inset illustration of the way of the critical temperature determination

Full size image
Fig. 5
figure 5

Selected curves of the imaginary part of the a.c. susceptibility as a function of temperature

Full size image

The critical current densities were obtained from the peak positions in the absorption part of the a.c. susceptibility using Bean’s critical-state model which is expressed by the formula [18, 19]

$$ J_{\mathrm{c}} =\frac{2H_{\text{a.c.}} }{d} $$
(4)

where H a.c. is the a.c. magnetic field amplitude and d is the sample thickness in the direction perpendicular to the a.c. field. The critical current densities are shown in Fig. 6 as a function of temperature. They are related to the inter-grain properties of the superconducting material. According to the Ginzburg–Landau strong coupling limit approach, the critical current varies with temperature following the equation [20]

$$ J_{\mathrm{c}} =J_{\mathrm{c}0} \left( {1-\frac{T}{T_{\mathrm{c}} }} \right)^{n} $$
(5)

where T c is the critical temperature and J c0 is the critical current at 0 K. Originally, the exponent n was determined to be 1.5 [15, 21] but it may vary within a wide range [22]. If the exponent n is greater than unity, strong pinning occurs and a vortex glass structure can be observed. In this case, the function expressed by (5) has a slightly upward curvature which is typical for HTS. If the exponent n is less than unity, the pinning force is rather weak, which limits the critical current. Then, the function expressed by (5) has a downward curvature typical for low-temperature superconductors.

Fig. 6
figure 6

Critical current densities as a function of temperature (open circles). The solid line is the fit to (5)

Full size image

The temperature dependence of the critical current density of the tape was fitted using (5) in which the critical current at 0 K, J c0, and the exponent n are the fit parameters. The critical temperature value T c = 90.05 K was taken from the experiment. The fit to the temperature dependence of the critical current density is shown in Fig. 4 by a solid line. The fit parameters J c0 and n as well as the critical current density at the liquid nitrogen temperature (J c = 77 K), derived using (5), are the following: J c0 = 1.7 × 108 A cm−2, n = 1.8, and J c (77 K) = 5 MA cm−2. The transport critical current flows through the grains as well as through the inter-grain links which can be treated as Josephson junctions. The critical current is limited by the weakest junctions along the current percolative path. A comparison of the critical current densities at 77 K obtained from the transport and from the a.c. susceptibility measurements shows that these values are close to each other. So that one can realize that the a.c. susceptibility measurement is a convenient alternative method to get the critical currents to that from transport measurements and is much easier to carry out. The exponent n = 1.8 is much higher than unity that is typical for HTS, and it exhibits an upward curvature of J(T) dependence. It means that a vortex glass structure occurs with a strong pinning force, which plays an important role for the applied properties of this tape.

4 Conclusion

The superconducting second-generation tape studied exhibits good superconducting parameters: the high critical temperatures of T c50 % = 91.5 K and T c0 = 90.0 K and the width of superconducting transition of ΔT 0 = 1.5 K. A significant shift of the superconducting transition to lower temperatures with the increasing applied magnetic field is observed. A very important and unique feature of this tape is that the transition from the normal to the superconducting state does not meaningfully broaden in the applied magnetic field up to 90 kOe and does not depend on the orientation of the magnetic field with respect to the tape plane. The temperature dependencies of irreversibility fields were derived and successfully fitted using (2). The fit procedure delivers the following exponents: n = 1.56 ± 0.02 for the parallel direction and n = 1.08 ± 0.03 for the perpendicular direction with respect to the plane tape. The exponent for the parallel direction is much higher than that for the perpendicular one. A big difference of the values of the exponent n suggests that there is a high texture in the superconductor film of this tape, such that a–b plane largely coincides with the tape surface. The irreversibility fields show an anisotropy, and at the liquid nitrogen temperature, they are of H irr = 430 kOe and H irr = 106 kOe for the parallel and the perpendicular directions, respectively. The anisotropy ratio which amounts to γ = 4 at 77 K is quite small in comparison with other HTS materials. The critical current density measured by the transport method was found to be J c = 3.44 × 106 A cm−2 at 77 K in the self-magnetic field. The critical current densities were also obtained from the peak positions of the absorption part of susceptibility using Bean’s critical-state model. The temperature dependence of the critical current density of this tape was successfully fitted using (5). From the fit parameters, the critical current density in the liquid nitrogen temperature was derived according to (5) (J c (77 K) = 5 MA cm−2) in the self-magnetic field. The values of critical currents obtained with the transport method and the a.c. susceptibility measurements are in satisfactory agreement.