1 Introduction

Charge ordering is a phenomenon which is characterized by a spatial modulation of the electron density driven by strong Coulomb interactions. The investigations on this phenomena attract much attention due to the fact that charge-orderings can interplay with other types of electron orderings [1–20]. This interplay can lead to either mutual enhancement or reduction of mentioned phenomena, e.g. [10–15, 20]. Moreover, various types of charge-order exist in superconducting and multiferroic materials.

In this paper, we investigate one of the simplest models used for description of charge-order phenomena, i.e., the extended Hubbard model (EHM) [20–23]. In particular, we analyze the effects of longer-range intersite density–density interaction on various types of charge ordered states. For the simplicity, we consider the atomic limit of the EHM. The Hamiltonian considered has the following form:

$$ \hat{H} = U{\sum}_{i}{\hat{n}_{i\uparrow}\hat{n}_{i\downarrow}} + \frac{W_{1}}{2z_{1}}{\sum}_{\langle i,j\rangle_{1}}{\hat{n}_{i}\hat{n}_{j}} +\frac{W_{2}}{2z_{2}}{\sum}_{\langle i,j\rangle_{2}}{\hat{n}_{i}\hat{n}_{j}}, $$
(1)

where \(\phantom {\dot {i}\!}\hat {c}^{\dagger }_{i\sigma }\) (\(\phantom {\dot {i}\!}\hat {c}_{i\sigma }\)) denotes the creation (annihilation) operator of an electron with spin σ ( σ∈{↑,↓}) at site i, \(\phantom {\dot {i}\!}\hat {n}_{i}=\sum\limits_{\sigma }{\hat {n}_{i\sigma }}\), and \(\phantom {\dot {i}\!}\hat {n}_{i\sigma }=\hat {c}^{\dagger }_{i\sigma }\hat {c}_{i\sigma }\). U is the on-site Coulomb interaction, W 1 and W 2 are the intersite density-density interactions between the (first) nearest neighbors (NNs) and the next-nearest neighbors (NNNs, i.e., second-nearest neighbors), respectively. z 1 and z 2 are numbers of NNs and NNNs. The scaling ( ∝1/z m , m=1,2) ensures that thermodynamical potentials per site are finite in the limit of infinite dimensions ( z m ,d→ + ∞). \(\phantom {\dot {i}\!}\sum\limits_{\langle i,j\rangle _{m}}\) indicates summation over m-th nearest-neighbours independently. Finally, μ will be the chemical potential, which determines the total electron concentration \(\phantom {\dot {i}\!}n = \frac {1}{L}\sum\limits_{i}{\left \langle \hat {n}_{i} \right \rangle }\) in the system. L denotes the total number of lattice sites. \(\phantom {\dot {i}\!}\langle \hat {A} \rangle \) is the average value of operator \(\phantom {\dot {i}\!}\hat {A}\) in the grand canonical ensemble. The model exhibits particle-hole symmetry and thus all phase diagrams are symmetric towards half-filling (i.e., n=1 or \(\phantom {\dot {i}\!}\bar {\mu }=0\), equivalently; \(\phantom {\dot {i}\!}\bar {\mu }=\mu -U/2-W_{0}\), W 0=W 1+W 2).

Model (1) has been intensively studied by plethora of methods (for review, e.g., [16–19, 24–26] and references therein). The following analysis is based on a variational approach (VA) which treats the U-interaction exactly and the intersite interactions within the mean-field approximation (MFA) [10, 11, 17–19, 27, 28]. In this paper, we study four-sublattice orderings in contrary to the previous MFA works, where only two-sublattice orderings have been investigated. In the framework used, one gets a set of four nonlinear equations for concentrations \(\phantom {\dot {i}\!}n_{\alpha }=\tfrac {4}{L}\sum\limits_{i\in \alpha }\langle \hat {n}_{i} \rangle \) in each sublattice ( α = A,B,C,D), which is needed to be solved numerically at T ≥ 0 [17, 18].

In the following, we focus on model (1) with attractive effective on-site interaction ( U<0). In Section 2.1, we present the detailed discussion of the ground state ( T=0) for fixed μ and for fixed n. Section 2.2 is devoted to analysis of phase diagrams at finite temperatures ( T > 0) for both \(\phantom {\dot {i}\!}W_{1}\gtrless 0\). We conclude in Section 3, where supplementary discussion is also included.

2 Results and Discussion ( U<0)

In our system, only four inequivalent homogeneous phases which are determined by the relation between each n α ’s can be classified as follows: (i) non-ordered (NO) phase ( n A = n B = n C = n D ); (ii) checkerboard charge-ordered (CBO) phase ( n A =n C , n B =n D , n A ≠n B ); (iii) stripe charge-ordered (SCO) phase ( n A =n B , n C =n D , n A ≠n C ); and (iv) four-sublattice-type charge-ordered (FCO) phase ( n A = n C , n B ≠n D ). For each ordered phase, several equivalent solutions exist due to cyclic change of sublattice indexes α (2, 4, 4 solutions, respectively; depicted in Fig. 1). In Section 2.1, we use these denotations with modificators (e.g., with primes and asterisks) to distinguish different occurring phases at the ground state, which fulfill the same conditions mentioned in the definitions.

Fig. 1
figure 1

The schematic representation of all possible homogeneous solutions for 2D square lattice. Dashed squares encircle an elementary block in which the four-sublattice structure is presented. Different sizes of dots correspond to different concentrations n α ( α = A,B,C,D) in the sublattices. For each from inequivalent ordered phases (CBO, SCO, FCO) several equivalent solutions exist

Full size image

2.1 The Ground State ( T=0)

The grand canonical potential Ω per site in the ground state of model (1) can be calculated as \(\Omega = \langle \hat {H} - \mu \sum\limits_{i} \hat {n}_{i} \rangle / L = E_{U} + E_{W} + E_{\mu }\), where

$$\begin{array}{@{}rcl@{}} E_{U} = \tfrac{U}{8} \left( n_{A} + n_{B} + n_{C} + n_{D} \right), \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} E_{W} = \tfrac{W_{1}}{8}(n_{A} n_{B}+n_{A} n_{D} +n_{B} n_{C} + n_{C} n_{D}) +\tfrac{W_{2}}{4}(n_{A} n_{C}+n_{B} n_{D}), \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} E_{\mu} = - \tfrac{1}{4} \mu (n_{A} + n_{B} + n_{C} + n_{D}). \end{array} $$
(4)

The above form for contribution E U originating from U term is only valid for U<0, where all particles are locally paired. E W describes a contribution from intersite Coulomb interactions between NNs and NNNs. The ground state (free) energy E per site is determined by \(E=\langle \hat {H} \rangle /L=\Omega -E_{\mu } = E_{U}+E_{W}\).

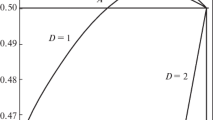
The T=0 phase diagrams as a function of shifted chemical potential \(\phantom {\dot {i}\!}\bar {\mu }\) are shown in Fig. 2. Each phase with minimal Ω is labeled by values of (n A ,n B ,n C ,n D ) on the diagrams. Naturally, for any U<0, the concentration in each sublattice can take only two values n α =0,2. Notice that none of the phases exhibits spin degeneracy. Therefore, the spin degrees of freedom are not relevant at T=0. Nevertheless, for T > 0, they affect the ordered phases stability. Moreover, the CBO phase is doubly degenerate, whereas the SCO, FCO, and FCO’ phases exhibit fourfold degeneracy. It is related to the symmetries of the considered lattices.

Fig. 2
figure 2

Ground state phase diagrams as a function of \(\bar {\mu }=\mu -U/2-W_{0}\) of the model with U<0 obtained in the four-sublattice assumption for a W 1 > 0 and b W 1<0 ( k = W 2/|W 1|). Each phase is also labeled by values of (n A ,n B ,n C ,n D ). All boundaries are discontinuous

Full size image

For U<0 and W 1 > 0, the phase diagram consists of six regions (Fig. 2a). The CBO phase can occur for k<1/2 ( k = W 2/|W 1|), whereas the SCO phase can appear for k > 1/2 (both phases with n=1). Moreover, for k > 0, the FCO (FCO’) phase is present with only one sublattice occupied (empty) for \(\phantom {\dot {i}\!}\bar {\mu }<0\) (\(\phantom {\dot {i}\!}\bar {\mu }>0\), respectively). For W 1<0, the diagram takes a simpler form (Fig. 2b). Apart from two non-ordered phases: NO with n=0 (fully empty) and NO’ with n=2 (fully filled) only the SCO phase can occur for k > 1/2. For both cases, all transitions are discontinuous.

We note that as the interfaces between the phases NO–CBO, CBO–NO’ and NO–NO’ possess non-zero energy, the degeneracy at the corresponding boundary lines at the diagram is finite. This implies that mentioned phases in thermodynamic limit can only be bound in a macroscopic clusters with clear domain walls. They cannot coexist on microscopic level. In contrary, the interfaces between domains of other neighboring phases in Fig. 2 do not change a total energy, thus the degeneracy is infinite at the boundary lines and so they can be mixed with each other microscopically.

In fact, it can be clearly seen that even at the mean-field level there is no long-range order in the regions of the occurrence of the FCO and FCO’ phases depicted in Fig. 2a. The proof for the square (SQ) lattice is given in [29] and for the base-centered cubic (BCC) lattice it is analogous. To reach the situation where in these regions a long-range charge-order is present an arbitrary weak interaction W 3 ≠ 0 between third-nearest neighbors is sufficient. An attractive interaction W 3<0 stabilizes the FCO and FCO’ phases on the SQ and BCC lattices, because its contribution in the case of these two lattices into Ω has a form: \(\phantom {\dot {i}\!}\tfrac {W_{3}}{8}({n_{A}^{2}}+{n_{B}^{2}}+{n_{C}^{2}}+{n_{D}^{2}})\). The statement is also true for 1D-chain, but in such a case the repulsive W 3 > 0 stabilizes the FCO and FCO’ phases, due to the fact that the contribution from W 3 interaction is \(\phantom {\dot {i}\!}\tfrac {W_{3}}{8}(n_{A} n_{D} + n_{A} n_{B} + n_{B} n_{C} + n_{C} n_{D})\).

Next, we determine the phase diagrams at T=0 as a function of n for U<0. Because the boundaries on the diagrams for fixed μ are associated with discontinuous change of n, it is necessary to consider also states with phase separation. The phase separated (PS) state is a state, in which two domains with different concentrations coexist [17, 18, 28, 30, 31].

In the region of the model parameters considered the following homogeneous phases can occur on the diagram: (i) the NO ∗ phase with (n,n,n,n) for 0<n<1; (ii) the FCO ∗ phase with (4n,0,0,0) for 0<n<1/2; (iii) the CBO ∗ phase with (2n,0,2n,0) for 0<n<1; (iv) the SCO ∗ phase with (2n,2n,0,0) for 0<n<1; (v) the FCO ∗∗ phase with (2,0,2(2n−1),0) for 1/2<n<1; (vi) the FCO ∗∗∗ phase with (2,2(2n−1),0,0) for 1/2<n<1. Moreover, the following phase separated (PS) states need to be considered: (vii) NO/CBO for 0<n<1; (viii) NO/FCO for 0<n<1/2; (ix) FCO/CBO for 1/2<n<1; (x) FCO/SCO for 1/2<n<1; (xi) NO/SCO for 0<n<1; (xii) NO/NO’ for 0<n<2. The phases in each of above PS states occur on both sides of corresponding discontinuous boundaries in Fig. 2. Their energy can be calculated by using the Maxwell’s construction [30, 31]. Notice that in this approach the energy of interfaces between domains is neglected (if it is not zero this assumption is justified in the thermodynamic limit if the size of the interface increases as L γ with γ<1).

The resulting T=0 diagrams for U<0 as a function of electron concentration n obtained are displayed in Fig. 3. One may distinguish several regions on the diagrams denoted as A, B, C, D for W 1 > 0 (Fig. 3a, presented only in range 0≤n≤1) and of three regions E, F and F ′ for W 1<0 (Fig. 3b). The regions are determined by model parameters k and n. We obtain that the following states (from (i)—(xii) mentioned above) have the lowest free energy in particular regions of the diagrams in Fig. 3: region (A) — (vii); region (B) — (ii) and (viii); region (C) — (v) and (ix); region (D) — (iv) and (x); region (E) — (xii); and region (F) — (xi). In the region F’ the state obtained by the particle-hole transformation exists, i.e. the PS: SCO/NO’ state. At the boundary for k=0, apart from the phases occurring in neighboring regions, also the phase (iii) has the same energy as (ii), (vii), (viii) (for n<1/2) or (v), (viii), (ix) for 1/2<n<1. At the boundary for k=1/2 and W 1 > 0 ( W 1<0), all phases occurring in the regions C and D (E and F/F’, respectively) are degenerated. For n=0, the NO phase exists, for n=1 and k > 1/2, the SCO phase is stable, whereas for n=2, the NO’ phase is present (any W 1≠0). Finally, for W 1 > 0, if n=1/2 and k > 0 the FCO phase occurs, whereas for n=1 and k<1/2 the CBO phase exists. Only the transitions with changing n for fixed k between homogeneous phases are associated with continuous change of all n α , whereas the PS states change continuously into homogeneous phases at \(\phantom {\dot {i}\!}n=0,\tfrac {1}{2},1,\tfrac {3}{2},2\) (if they can exist). Chemical potential changes discontinuously at the boundaries between regions.

Fig. 3
figure 3

Ground state phase diagrams as a function of n of the model with U<0 obtained in the four-sublattice assumption for a W 1 > 0 and b W 1<0 ( k=W 2/|W 1|). Capital letters A–F and F’ denote regions of the diagrams, where different states are degenerated. Each region is also labeled by the name of a state, which is stable at infinitesimally small T > 0

Full size image

As we will show in the next section any finite T > 0 removes the degeneracy of the states in regions A–D. Only at the C–D boundary, the degeneracy between the FCO ∗∗ phase and the PS:FCO/SCO state still remains. In Fig. 3, each region is also labeled by the name of a state, which is stable at infinitesimally small T > 0.

2.2 Finite Temperatures ( T > 0)

As we indicted in the previous section, on-site attraction does not effect the ground state diagrams. However, it determines the binding energy of on-site electron pairs and thus it determines critical temperatures above which phases with various long-range orders disappear.

For U<0 and half-filling, the phase diagram is very simple. For W 1 > 0 at sufficiently low temperature T for k<1/2, the CBO phase exists, whereas for k > 1/2 the SCO phase is stable. For U=0, the CBO–NO boundary is determined by k B T/|W 1|=(−k+1)/2, whereas the equation for the SCO–NO boundary is k B T/|W 1|=k/2. At k=1/2 and k B T<1/4 the first-order CBO–SCO transition occurs. On the diagram for W 1<0 and k=1/2, the CBO phase change into the PS:NO/NO state (for fixed n=1) or a first-order NO–NO boundary plane (for fixed \(\phantom {\dot {i}\!}\bar {\mu }=0\)). For U→−∞, the transition temperatures are two times larger that those for U=0. This is also applicable for any \(\phantom {\dot {i}\!}\bar {\mu }\) and k. Notice, however, that for intermediate values of −∞<U<0 the effect on various boundaries is different, but it is always monotonous. In particular, for W 1 > 0, k=0.25, and U/W 1=−1, the CBO–NO transition temperatures are more strongly reduced that those for the FCO–CBO boundary compared to the boundaries for U→−∞ (Fig. 4a, b).

Fig. 4
figure 4

Exemplary k B T/|W 1|-\(\bar {\mu }/|W_{1}|\) (upper row) and k B T/|W 1|-n (lower row) phase diagrams of the model obtained in four-sublattice assumption for different values of U/|W 1|=−10.0,−1.0,0.0 (as labeled) and: W 1 > 0, k=0.25 (left column); W 1 > 0, k=0.75 (middle column); and W 1<0, k=0.75 (right column). Details in text in Section 2.2

Full size image

For U<0 and W 1 > 0, one can distinguish a few ranges of k = W 2/|W 1| in which the structure of diagrams at T > 0 is qualitatively different. The case of k≤0 has been analyzed in details previously [17–19, 27]. Shortly reviewing those results, in that range of k only two-sublattice types of orderings occur. For k=0, the CBO–NO boundary is only second-order and any PS states do not occur for fixed n. For |k|<3/5, the CBO–NO line is first-order at low T and the first-order transition at T > 0 between two different CBO phases also occur. On the diagram, two critical points exist: bicritical-end point and critical-end point. For |k| > 3/5, only CBO–NO boundary occurs, which changes its order from first-order into second-order at the tricritical point. At |k|=3/5 the higher-order critical point occurs. The first-order CBO–CBO (only for |k|<3/5 and T > 0) and CBO–NO boundaries are associated with the occurrence of PS states: CBO/CBO and CBO/NO, respectively [17, 18].

For U<0, W 1 > 0 and W 2 > 0, the four-sublattice orderings occur on the diagrams. For small k, the CBO phase occurs and away half-filling at low enough T the FCO phase is also present (Fig. 4a,b). All transitions are second-order. The FCO phase is separated from the NO phase by the region of the CBO phase occurrence. For larger k > k 1 ( k 1≈0.35), the region of the FCO phase stability extends and a second-order FCO–NO transition occurs at high \(\phantom {\dot {i}\!}\bar {\mu }/W_{1}\) and low T (cf. Fig. 5). The FCO–NO, FCO–CBO, and CBO–NO boundaries merge in the D-point. Increasing k causes that the FCO–CBO line changes its curvature (shown in Fig. 5) and a multiple reentrant behavior emerges. With further increasing k the D-point goes to half-filling for k=1/2 and finally for k=1/2 the CBO and SCO phases are degenerate for T ≥ 0 (and fixed μ or n). Moreover, for k=1/2, the FCO–SCO (FCO–CBO) transition is first-order and its temperature decreases monotonously with increasing \(\phantom {\dot {i}\!}|\bar {\mu }|/W_{1}\). For fixed μ at k=1/2 in some region above these boundaries the first-order FCO–FCO transition also occurs. For larger k, the discontinuous FCO–SCO boundary for fixed μ changes its curvature (at low T initially), and for k > k 2 ( k 2≈0.66), it is an increasing function of \(\phantom {\dot {i}\!}|\bar {\mu }|/W_{1}\) (Fig. 4c). The FCO–NO, FCO–SCO, and SCO–NO boundaries merge in the bicritical B-point. On the diagram as a function of n for k > 1/2 the PS state: FCO/SCO is stable in definite ranges of n (Fig. 4d), whereas for 0<k<1/2 only homogeneous phases occur (Fig. 4b). For k=1/2 and fixed n the FCO phase is degenerated with the PS:FCO/SCO state in the PS state occurrence region for fixed n. In addition, on the phase diagram for fixed n<1 and k=1/2 a small region of the first-order FCO–FCO transition remains for T > 0 on the left from the region of that degeneracy occurrence.

Fig. 5
figure 5

k B T/|W 1|-\(\bar {\mu }/|W_{1}|\) phase diagrams of the model obtained in four-sublattice assumption for W 1 > 0, U=−1, and k=0.48. All boundaries are second-order

Full size image

In a case of U<0 and W 1<0, for k<1/2, only a first-order NO–NO transition occurs at sufficiently low temperatures for \(\phantom {\dot {i}\!}\bar {\mu }=0\). Thus, phase separation between two different NO phases occurs for define ranges of n (so-called state of electron droplets) [19, 28].

For k > 1/2 ( W 1<0), the SCO phase occurs at T ≥ 0 and SCO–NO transition is first-order at low temperatures, whereas at higher T it is second-order. The transition changes its order in tricritical M-point (Fig. 4e). The boundary line is a decreasing function of \(\phantom {\dot {i}\!}|\bar {\mu }|/|W_{1}|\). In such a case, the PS:NO/SCO state occurs in define range of n (Fig. 4f).

For larger \(\phantom {\dot {i}\!}k>k_{1}^{*}\) (e.g., for k=1.5, W 1<0), the SCO–NO boundary is no longer a monotonous function of \(\phantom {\dot {i}\!}|\bar {\mu }|/|W_{1}|\) and a SCO–NO–SCO–NO sequence of transitions can occur with increasing T. This behavior is present in very narrow ranges of \(\phantom {\dot {i}\!}\bar {\mu }/|W_{1}|\). For even larger \(\phantom {\dot {i}\!}k>k_{2}^{*}\) (e.g., for k=2.0), the tricritical T-point changes into critical-end point and a first-order SCO–SCO boundary line (ending at bicritical-end point) is present inside a region of the SCO phase occurrence at intermediate temperatures. It is a similar behavior to that of the CBO phase for W 1 > 0 and −3/5<k<0 [17–19]. In this regime for W 1<0 also a NO–SCO–NO sequence of transitions with increasing T is present on the diagram (in narrow ranges of \(\phantom {\dot {i}\!}\bar {\mu }/|W_{1}|\)). Notice that for W 1<0 and k=1/2 the PS:NO/NO state is degenerated with the SCO phase (only for n=1) and the PS:NO/SCO state in their ranges of occurrence for fixed n.

3 Conclusions and Final Remarks

In this paper, we analyzed the extended Hubbard model with intersite density–density interactions for the on-site attraction within the site-dependent mean-field approximation in the four-sublattice assumption. We have investigated the ground state of the model in details and obtained that it is highly degenerated (for W 1 > 0 and k ≥ 0). We have shown that finite temperature removes the degeneracy between homogeneous phases and phase separated states. It is associated with the fact that at T=0 all transitions are first-order for fixed μ, while at T > 0 some of them change their order. In fact, it occurs for FCO–NO and FCO–CBO boundaries, which are second-order for any T > 0. The FCO–SCO and NO–NO transitions are always first-order for fixed \(\phantom {\dot {i}\!}\bar {\mu }\) and thus corresponding PS states occurs at T > 0 for fixed n. The CBO–NO (for W 1 > 0) and SCO–NO (for W 1<0) are first-order for small T, whereas for sufficiently large T they change their order into second one. Notice also that first-order transitions between two CBO phases (for W 1 > 0 and 0 > k > −3/5) or two SCO phases (for W 1<0 and large \(\phantom {\dot {i}\!}k>k_{2}^{*}\)) also occur.

The attractive on-site U interaction does not change the diagrams of the model qualitatively. With decreasing |U| only the regions of ordered phases and states are reduced (for both repulsive W 1 > 0 as well as for attractive W 1<0). For U<0, the value of the ratio k=W 2/|W 1| between NN and NNN interactions determines a structure of k B T/|W 1|-\(\phantom {\dot {i}\!}\bar {\mu }/|W_{1}|\) and k B T/|W 1|-n phase diagrams.

Notice that model (1) in U→−∞ limit is equivalent with the S=1/2 Ising model with NN and NNN magnetic interactions (antiferromagnetic for W m > 0 and ferromagnetic for W m <0; m=1,2) in the magnetic uniform field \(\phantom {\dot {i}\!}\bar {\mu }\). Our results for model (1) are consistent with those for the Ising model with NN and NNN interactions obtained within the MFA [32–34], but we have found the behaviors not discussed previously (for W 1 > 0 and k 1<k<k 2 and for W 1<0 and \(\phantom {\dot {i}\!}k>k_{1}^{*}\)). Since the phase boundaries at T > 0 are calculated from the numerical solution of equations for n α ’s, a small jump of n α ’s and first derivatives of Ω’s at transition point can never be firmly excluded. The accuracy of our results is largely increased in comparison to the results for U→−∞ case considered in [34].

The VA results obtained in this paper are exact in d→+∞ limit [35–37]. Moreover, the VA results at T=0 for fixed μ are rigorous for any dimensionality d [19, 38, 39]. It is obvious that VA overestimates the transitions temperatures for order-nonorder transitions in systems with finite d. The limitations of the VA method for model (1) has been discussed in [17–19]. Notice also that for the SQ lattice the VA gives results in a reasonable qualitative agreement with Monte Carlo simulations (MCS) for W 1 > 0 and W 2=0 [25, 26], whereas for W 1 > 0 and k > 0 the VA does not predict properly the behavior of the system, even for U→−∞. In particular, the MCS predicts that FCO phase does not exist at any T > 0 [34]. Moreover, for \(\phantom {\dot {i}\!}\bar {\mu }=0\) and the SQ lattice the first-order CBO–SCO transition is not present at T > 0 and these two phases are separated by the NO phase region [34, 40, 41]. The situation changes in three dimensions for simple cubic lattice, where that transition occurs [42].