1 Introduction

Geometrically frustrated magnetic systems have received considerable attention in recent years due to the presence of extraordinary magnetic properties [1, 2]. Geometric frustration is a broad phenomenon that results from an intrinsic incompatibility between some fundamental interactions and the underlying lattice geometry usually based on triangles or tetrahedra. The delafossite CuFeO2 is of particular interest because of the discovery of multiferroic phenomena with either application of a magnetic field or the substitution of Fe3+ with nonmagnetic Al3+ ions [3, 4]. As a model material of triangular lattice antiferromagnet (TLA), CuFeO2 forms an Ising-like 4-sublattice antiferromagnetic order at low temperature, with spin moment pointing along the c-axis [5]. This TLA is one of typical models to test the resonating valence bond idea of a 2D spin liquid state which was first proposed by Anderson [6] and was applied to the theory of high- T c superconductivity [7, 8]. The so-called 120∘ spin structure is realized in the ATL Heisenberg model with the nearest neighbor bilinear coupling [9], while the actually realized phase is still controversial if the quantum fluctuation is enhanced by low dimensionality, quantum spin nature, and geometrical frustration [10, 11]. From experimental view points, no material has been confirmed to show a spin liquid state till now, but some ATL and related lattice compounds [12, 13] are proposed to demonstrate the quantum state.

In order to clarify the ground state and explore a novel phenomenon in such quasi-2D ATL compounds, it is useful to investigate impurity effects on the electronic and magnetic ground states, because, in strongly correlated electron or frustrated systems, exotic phenomena are often induced by changes of filling, bandwidth [14], and quenched random field [15, 16], with a substitution of impurities. In such a context, we have investigated various substitution effects on the electronic, magnetic, and thermal properties of delafossite oxide CuFeO2 [17].

CuFeO2 is one of the quasi-2D ATL compounds. It forms a rhombohedral lattice with the space group of R-3m, viewed as the alternating stacking of edge-shared FeO6 octahedral (FeO2) layers and Cu layers [17]. The Fe3+? ions (3 d 5, S = 5/2) form antiferromagnetic (AF) triangular sublattices and the compound shows a noncollinear 120° indicating they exist of the antiferromagnetic transitions in CuFeO2, from paramagnetic to collinear incommensurate T N1 = 14 K and then collinear commensurate below T N2 = 11 K [18, 19].

In this work, we report the preparation, structural characterizations and physical properties, and magnetic and electric polarization of several polycrystalline compounds belonging to the delafossite CuFe1−x Sc x O2 series. It is found that this introducing of the Sc into the Fe lattice sites in alternating ab layers has a significant effect on the structure. The occupied Fe 3d states interact covalently with the neighboring O atoms and hence indirectly modify the Cu 3d states, an effect which the 3 p 6 Sc atoms are unable to produce. This decreases the density of states at the top of the valence band, which are precisely those states expected to determine the mobility of p-type charge carriers formed on doping.

2 Experimental

Polycrystalline samples of CuFe1−x Sc x O20 ≤ x ≤ 0.25 were prepared by using the standard solid-state reaction. Stoichiometric mixtures (0.5 g) of Cu2O, Fe2O3, and Sc2O3 were ground and pressed in pellet, which were set in alumina crucible. The samples were fired several times at 1050 °C for 12 h. The X-ray powder diffraction patterns of the reacted pellets were collected with a PANalytical diffractometer equipped with a Cu K α source (K α1 and K α2) in the 2θ range from 10° to 90° at room temperature.

Strain and size components were extracted from line widths using the Williamson–Hall (WH) analysis [20]. This method uses the fact that the crystallite size contribution varies as tan θ. The equation used is

$$L\cos\theta=\lambda /D+k\varepsilon \sin\theta $$

where L is the integral width, λ is the wavelength used, D is the size of the coherent diffraction domain, k is a near-unity constant, and ε is the microstrain term. As a result, a plot of (L cos θ) as a function of (sinθ) yields D from the constant term and ε from the slope.

Magnetization dependence on temperature was measured in a superconducting quantum interference device (SQUID) magnetometer while heating from 4.0 to 300 K in 0.1 T.

The Raman spectra were recorded at room temperature with the 514.5 nm line of an Ar+ laser, excitation from a Spectra-Physics krypton ion laser. The compounds were studied with a low laser power (102 mW). One scanning of 60 s has been used for each spectral range. No damage of the material by the laser has been observed. The beam was focused onto the samples using the macroscopic configuration of the apparatus.

3 Results and Discussion

3.1 Structural Properties

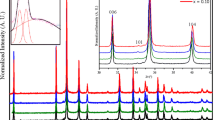
For studied x range (from 0.00 to 0.25) to series CuFe1−x Sc x O2, the powder X-ray diffraction patterns for all samples show the existence of the delafossite phase with the space group R-3m (Fig. 1). Both hkl h ≠ 0 or k ≠ 0 and 00l peaks are sharp, but other peaks are broadened, shifted and asymmetric due to stacking faults perpendicular to the c-axis (Fig. 1). Above 0.25 the peaks broadening is very important in a way that the phase identification is risky.

Fig. 1
figure 1

XRD patterns of CuFe1−x Sc x O2 (0 ≤ x ≤ 0.25) samples with a rhombohedral delafossite structure

Full size image

The obtained patterns were refined by Rietveld method using the FullProf software [21]. A typical example is given for CuFe0.9Sc0.1O2 (x = 0.1) in Fig. 2. The crystal structure consists of an alternative stacking along the c-axis (by using the hexagonal setting) of edge-shared (FeSc)O6 octahedra with the CdI2-type structure separated by copper atom layers. The trivalent cations form a planar triangular network in the (ab) plane (inset of Fig. 2).

Fig. 2
figure 2

Experimental powder X-ray diffraction data of CuFe0.9Sc0.1O2. Inset: Illustration of the deformation of the (Fe/Sc)O6 octahedra

Full size image

As shown in Fig. 3, the unit cell parameters present an important increases and monotonously with Sc substitution. They exhibit a larger variations compared with pure CuFeO2 [22], in agreement with ionic radii for sixfold coordination Fe3+ and Sc3+ (rFe3+ = 0.64 Å; rSc3+ = 0.72 Å) [23]. The variation of the cell parameter c (from 17.0902(4) Å for x = 0.00 to 17.0717(4) Å for x = 0.25) is twice greater than those reported in [24] for the CuFe1−x Rh x O2. This is again consistent with ionic radii, since the ionic radius of Fe3+ (0.64 Å) is much closer to r(Rh3+) than r(Cr3+).

Fig. 3
figure 3

Variation of refined unit cell parameters a and c as a function of x in CuFe1−x Sc x O2 (0 ≤ x ≤ 0.25)

Full size image

Strain generated by the Sc substitution was determined from the Williamson–Hall relationship. Plots of (L cos θ) as a function of (sin θ) are given in Fig. 4. They show a remarkable difference in angular dependence of the line width for different families of interreticular planes: the h 0 l planes yield an important contribution of microstrains (high slope), while this effect is almost negligible in 00l planes. This shows that this material behaves rather anisotropically, and that strains affect mostly bonding in the basal ab planes. Note that because of the high slope and the high inaccuracy of extrapolating to sinθ = 0, the grain size values for hkl h ≠ 0 or k ≠ 0 planes will be poorly defined.

Fig. 4
figure 4

Williamson–Hall plot of integral line width L

Full size image

Finally, we note that the oxygen stoichiometry cannot be reliably obtained by X-ray diffraction data, and the presence of three different mixed valences precludes a reliable use of chemical redox titration. However, all the samples being prepared in the same conditions (initial oxygen stoichiometry, amount of powder) and their oxygen content are assumed to close to 2 in all cases. This assumption is supported by a previous study of CuFeO2 showing that this compound does not accommodate large oxygen of stoichiometry [24]. This could be confirmed by neutron diffraction, which was not available to us during this study.

3.2 Raman Spectroscopy

The delafossite structure belongs to point group C 3v and space group \(R\overline 3 m\). The four atoms in the primitive cell of its rhombohedral (\(R\overline 3 m\)) structure give rise to 12 optical phonon modes in the zone center (k∼0), among them three are acoustic and nine are optical. Γopt.R3c = A 1g + E g + 3A 2u + 3E u, out of which two phonons with A 1g and E g symmetry are Raman active. Γopt.R−3m = A 1g + E g . A 1g modes represent the vibration of Cu–O bonds along the c-axis whereas the doubly degenerate E-modes describe the vibration along the a-axis. Since there is only one mode of each symmetry, the exact eigenvector is determined without any lattice dynamical model required. Pellicer-Porres et al. [25] had discussed the phonon dispersion at the zone center for CuGaO2 delafossite. They proposed that the inversion center is lost along the direction of Γ(T) direction and the symmetry is reduced from D 3d to C 3v . According to compatibility relations, A 1g and A 2u modes transform to A 1 modes and E g and E u modes become E modes.

Figure 5 shows the composition-dependent Raman spectra of single phase of CuFe1−x Sc x O2 (0 ≤ x ≤ 0.25) at room temperature. All the samples showed two Raman active modes in agreement with earlier results on CuFeO2 [26] and CuCrO2 [27], CuGaO2 [25]. These bands are identified as σ(A 1g ) at 692 cm−1 and σ(E g ) at 351 cm−1, respectively, and it has been suggested that these vibrations may be associated with the spectral features of edge-sharing FeIIIO6 octahedra and possibly the O–Cu−–O linear bond [28]. Raman spectra showed significant shift in both active modes towards lower frequency side and increase in intensity with increase of doping level. This increase in intensity is accompanied by a light shift of the peaks towards the left, i.e., variation of the Raman frequency. This proves well that the Raman spectra evolve move with the composition. These results confirm that the substitution of Fe by Sc in the investigated concentration range of the CuFe1−x Sc x O2 compound is possible without the change of delafossite structure. However, local changes do arise, and they are much more relevant in Raman spectroscopy, that is a local probe, more than X-ray diffraction, where the effects of cationic composition changes are averaged and show up mainly as peak broadening.

Fig. 5
figure 5

Raman spectroscopy of CuFe1−x Sc x O2(≤ x ≤ 0.25) bulk samples at room temperature

Full size image

3.3 Magnetic Properties

Zero-field cooled (ZFC) magnetic susceptibility data of CuFe1−x Sc x O20.0 ≤ x ≤ 0.25 were collected between 4 and 300 K under a 1000 Oe DC magnetic field and are presented in Fig. 6. We observe an antiferromagnetic cascade in the magnetic susceptibility of CuFeO2 working temperature between 4 and 15 K, in accordance with previous characterization [29]. This cascade is subdivided in two antiferromagnetic transitions in CuFeO2, from paramagnetic to collinear incommensurate (T N1 = 14 K) and then collinear commensurate below T N2 = 11 K [3] are known to be difficult to determine from the magnetic susceptibility χ(T) curves of polycrystalline samples. Our χ(T) curves, obtained from the magnetization ones for x = 0.25, a decreasing T from the paramagnetic region, the curve is characterized by a rather broad maximum followed by a more abrupt transition. The temperature of the χ maximum corresponds to T N1 = 14.5 K, and the second transition, corresponding to an abrupt decrease of the magnetic susceptibility, at 9.1 K for CuFeO2, can be associated to T N2. The latter has to be compared to the value found for the undoped compound [30] (=10.5 K), whereas T N1 is found to be rather independent on x. The Sc for Fe substitution in CuFe1−x Sc x O2 makes T N2 decreasing, but T N1 remains almost unchanged. The T N2 values, summarized in Table 1, reveal a rather monotonous T N2 decrease as x increases, from T N2 = 9.1 K down to T N2 = 5.9 K for x = 0.00 to 0.25, respectively. Such an evolution with x is much smoother than with Al3+ doping since as soon as x = 0.03 in CuFe1−x Al x O2, T N2 becomes lower than 2 K [31]. In fact, these phenomena of increasing T N2 in CuFe1−x Sc x O2 more closely resemble the H–T phase diagrams of the rare earth intermetallic compounds [32], rather than those of the ABX 3-type stacked triangular Ising antiferromagnets [33], such as CsCoBr3 and CsCoCl3. In particular, an incommensurate magnetic ordering occurring in rare earth intermetallic compounds at T N1 exhibits at some lower temperature a transition to a simpler structure with a shorter period. This happens because in the case of axially anisotropic systems, an incommensurate or long-period commensurate-modulated structure is unstable at 0 K [32]. At lower temperature, an applied magnetic field lowers the free energy of the incommensurate phases more rapidly than that of the simple commensurate phases; therefore, a reappearance of the incommensurability is often observed in these compounds in a magnetic field. Splitting of T N is also a common feature for ABX 3-type stacked triangular Heisenberg antiferromagnets with an easy axis type of anisotropy [34]; however, their behavior in an applied magnetic field are profoundly different to that of CuFeO2. Their magnetization curves demonstrate only one spin–flop transition at a critical field H c for a field applied along the hexagonal axis and the absence of any transitions for the field applied perpendicular to this axis. In addition, in ABX 3-type systems, the application of a magnetic field results in a decrease of the temperature difference between two phases transitions T N1 and T N2 [35], while for CuFeO2, the effect is the opposite; an applied magnetic field stabilizes an intermediate incommensurate structure.

Fig. 6
figure 6

The temperature dependence of zerofield-cooling susceptibility (χ–T curve) of CuFe1−x Sc x O2(≤ x ≤ 0.25) samples

Full size image
Table 1 Estimated Curie constant, Curie temperature, collinear commensurate T N2, and effective moments from the high-temperature paramagnetic region for CuFe1−x Sc x O2
Full size table

In antiferromagnetic oxide CuFe1−x Sc x O2, The plot of 1/ χ versus T (Fig. 7) shows an exactly linear relationship at high temperature, which is well fitted by the Curie–Weiss law (χ = χ 0 + C/(T − θ CW)) [36]. The magnetic characteristics of the solid solution, including Curie–Weiss effective moment (μ eff), Curie constant, theoretical magnetic ordering temperature θ CW, and T N2, are summarized and tabulated in Table 1. From the Curie–Weiss analysis, we find that, as expected for octahedral Fe3+, μ eff is nearly equal to the spin-only S = 5/2 value of 5.92 μ B throughout the mother solid solution CuFeO2. As evidenced by the negative θ CW, the dominant magnetic interactions are antiferromagnetic. The magnitude of θ CW is small for samples with low Sc/Fe content, but it quickly decreases with x as Sc–O–Fe superexchange interactions become more prevalent. At temperatures above the long-range ordering temperature, positive deviations from the ideal Curie–Weiss line reflect the presence of compensated antiferromagnetic short-range interactions, while negative deviations reflect uncompensated behavior (ferromagnetism or ferrimagnetism). Consistent with its magnetic frustration, CuFeO2 displays short-range antiferromagnetic interactions well above its Néel temperature [37]. While Curie–Weiss analysis shows that the dominant long-range interactions in CuFe1−x Sc x O2 are antiferromagnetic, the scaled Curie plot reveals the presence of short-range uncompensated behavior in all of the Sc-substituted samples which is likely a result of chemical disorder, which is in a good agreement with results reported by N. Terada et al. [31].

Fig. 7
figure 7

Temperature (T) dependence of the inverse susceptibility of CuFe1−x Sc x O2(0 ≤ is ≤ 0.25) samples Inset: Illustration of the incommensurate modulated structure taken from ref. [32] for the low ferromagnetic interactions J 1(1) and J 1 (2), and the unstable anti-ferromagnetic interactions (J 1(3), J 2, and J 3)

Full size image

The spin dynamics of the geometrically frustrated triangular antiferromagnet multiferroic CuFeO2 has been mapped out using inelastic neutron scattering [30]. They determined the relevant spin Hamiltonian parameters, showing that the sinusoidal model with a strong planar anisotropy correctly describes the spin dynamics. The weakly dispersive excitation along c reflects the 2D character of the magnetic interactions, but the spin dynamics in CuFeO2 clearly point out the relevance of the next-nearest-neighbor interaction to stabilize the magnetic order. As xincreases in CuFe1−x Sc x O2, in addition to strain effects, the number of magnetic nearest neighbor’s decreases and the magnetic ordering affect the coupling between in-plane next-nearest-neighbors interpreted as the signature of an important deformation of the perfect triangular lattice.

Correlating the increases in lattice parameters a in CuFe1−x Sc x O2 system to the nearest-neighbor magnetic exchange coupling J BB taken from magnetic structure (inset of Fig. 7) which is close to 5.0 meV for the mother CuFeO2 [30]. The Sc substitution (S = 0) at the Fe sites (S = 5/2) tend to suppress the low ferromagnetic interactions in the magnetic structure J 1(1) and J 1(2) [32]; however, the magnetic exchange coupling J BB decreases under 5.0 meV with increasing x. In the other hand, the increases in lattice parameters a which is due to the substitution at the Fe sites (r (Fe3+) = 0.64 Å) with larger atoms of Sc3+ (r (Sc3+) = 0.72 Å) tend to decrease the unstable AFM interactions through the incommensurate modulated structure (J 1(3), J 2, and J 3) [32] and will becomes increasingly stable. This decrease for the low FM and AFM interactions is a result of the mean field approximation breaking down as Fe composition decreases and next-nearest-neighbor interactions become less, and tend to suppress the magnetic order in CuFe1−x Sc x O2 system with increasing x content. The magnitude of J BB is similar to previous studies of Fe–O–Fe exchange in structurally similar spinels with edge-sharing octahedra of Fe [3, 37, 38]. A ZFC splitting occurs in the x = 0.25 sample below 4 K, which is consistent with splittings seen in low Al content samples studied by Okuda et al. [39]. Such behavior is attributed to chemical disorder that results in spin-glass behavior.

3.4 Electric Polarization

As shown previously in ACrO2 multiferroics [40], the larger variation of the electric polarization P is confirmed along the series CuFe1−x Sc x O2, as shown in Fig. 8a, by the P(T) curves collected in the absence of magnetic field. Starting from the low levels of Sc substitution characterized by P values close to 0, the P maximum value decreases with x up to 63 μC/m2 for 5 %-Sc to 22 μC/m2 for 25 %-Sc. As shown in Fig. 8a, P tends to be suppressed with increasing of the content x.

Fig. 8
figure 8

The P(T) curves evidencing the scandium effect on polarization in CuFe1−x Sc x O2: E = 135 kV m−1 is applied during cooling at different temperatures. The P values and the inflection point of the transition depend on the poling temperature, suggesting the existence of intrinsic magnetoelectric coupling and induce incommensurate magnetic structure

Full size image

The polarization of the CuFe1−x Sc x O2 samples (Fig. 8b) has been also measured using the same electric field cooling procedure as was applied for undoped CuFeO2. It also reveals a small electric polarization for pure all compounds, whose maximum at ∼ T N2 is correlated with anomalies in magnetic susceptibility. This provides new data for the physics of CuFeO2, since the electric polarization was reported in single crystal in the same temperature region but only under magnetic field application [3]. The existence of electric polarization in the polycrystalline pristine samples in zero external magnetic fields indicates that spontaneous electric polarization may exist along other crystallographic direction than those already tested in single crystals. Therefore this suggests that an electric polarization flop between different directions may be induced by magnetic field application in the single crystal of CuFeO2. The existence of electric polarization in all samples related to magnetic transition at T N2 implies the existence of intrinsic magnetoelectric coupling in the present polycrystalline samples. This is in accordance with a previous paper reporting on Al dopinginduced electric polarization in monocrystalline sample of CuFeO2 [4].

This effect can be compared with the induced change of the background magnetic state that has been reported for Al-doped crystals. Finally, the similarity of the effects induced by Al3+? or Sc3+? demonstrates that electronic configuration (S = 0) is highly favorable for doping-induced electric polarization effect. More importantly, the fact that polarization decreases in zero magnetic field indicates the possible advantage of the Sc3+ doping over the Fe3+ one which is reported to induce incommensurate magnetic structure [3], only in the doping range of 0.05 ≤ x ≤ 0.25.

4 Conclusion

In summary, we investigated an effect of spin dilution on the structural and magnetic properties of delafossite CuFeO2 having an S = 5/2 ATL by the substitution of Sc3+ for Fe3+. The spin dilution suppresses the long-range 120∘ Néel state and induces a dimensional crossover of low-energy magnetic excitation from that of the anisotropic 3D AF magnon to that of the 2D AF excitation which may be a mixture of contributions of a major short range 2D AF correlation manifested by the Warren-type magnetic peak profile and a minor conventional long-range 2D AF. Such a crossover is due to the increases of interlayer magnetic interaction (J BB) in the residual Fe ATL due to the disorder introduced by the Sc substitution, which is consistent with the gradual decrease of T N2 with increasing x content.

Electric polarization decreases with x up to 63 μC/m2 for 5 %-Sc to 22 μC/m2 for 25 %-Sc around T N2. This decrease reports the existence of intrinsic magnetoelectric coupling and induces incommensurate magnetic structure in the present polycrystalline samples.