1 Introduction

Enhancements or suppressions of the convection phenomena and improvement of heat and mass transfer continue to be an active research area, due to their significance for both fundamental interests and engineering applications, such as solar receivers, cooling of electronic devices, solidification of materials and so on. There are many methods of enhancements or suppressions of the convection phenomena, for example by placing fins on the heated wall, exerting electric and magnetic fields, etc. [1, 2].

Recently, magnetic force has received more attention in the field of metallic materials, and less in the field of non-metallic materials. With the development of a superconducting magnet providing strong magnetic induction of 10 Tesla or more in recent years, the suppression or enhancement of the natural convection of the paramagnetic fluids like oxygen gas and air by a magnetic field has become an interesting research topic investigated by many researchers. Many research works about magnetically induced natural convection have followed [3]. The effect of the magnetic buoyancy force on the convection of the paramagnetic fluids was first reported by Braithwaite et al. [4]. They used the magnetic field both to enhance and suppress the Rayleigh–Benard convection in a solution of gadolinium-nitrate in a shallow layer heated from below and cooled from above and showed that the effect depends on the relative orientation of the magnetic force and the temperature gradient. Carruthers and Wolfe [5] studied the thermomagnetic convection of oxygen gas in a rectangular container with thermal and magnetic field gradients theoretically and experimentally, and found that magnetic buoyancy force canceled out the influence of gravitational buoyancy force when the rectangular enclosure heated from one vertical wall and cooled from opposing wall was located in horizontal magnetic field with vertical magnetic field gradient, and horizontal magnetic field could enhance and suppress the Rayleigh–Benard convection when the rectangular enclosure heated from below and cooled from above was located with the same mode. Shigemitsu’s group [6] derived a model equation for magnetic convection using a method similar to the Boussinesq approximation and studied natural convection of paramagnetic, diamagnetic and electrically conducting fluids in a cubic enclosure with thermal and magnetic field gradients at different thermal boundaries numerically and experimentally. Tagawa and co-workers [7] studied natural convection of paramagnetic and diamagnetic fluids in a cylinder under gradient magnetic field at different thermal boundaries numerically and experimentally and found that the magnetic body due to gradient magnetic field could be used to control heat transfer rate of paramagnetic and diamagnetic fluids. Bednarz and co-workers [8] studied natural convection of paramagnetic fluids in a cubic enclosure under magnetic field by an electric coil numerically and experimentally and analyzed the effect of inclined angle of electric coil, location of electric coil, Ra number, γ number on heat transfer rate of paramagnetic fluids.

The above studies are concerned with the effect of magnetic force on natural convection of paramagnetic fluids. However, almost no attention has been paid to the combined effects of magnetic and gravitational forces on the natural convection of paramagnetic fluids in porous medium. Natural convection in an enclosure filled with a paramagnetic or diamagnetic fluid-saturated porous medium under strong magnetic field was numerically investigated by Wang et al. [9, 10]. Considering the effect of Darcy number, Rayleigh number and γ number, the results of numerical investigation showed that the magnetic force has a significant effect on the flow field and heat transfer in a paramagnetic or diamagnetic fluid-saturated porous medium. The application of strong magnetic field on porous medium may be found in the field of medical treatment, metallurgy, materials processing, combustion. There may be plenty of applications in the near future in the field of engineering operations. Thus, the study of the effect of magnetic force on natural convection in porous media is important for both scientific research and engineering application.

2 Physical Model

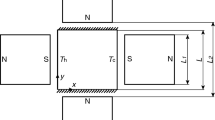
The schematic of the system under consideration is shown in Fig. 1. The system consists of a porous cubic enclosure which is kept in a horizontal position and four permanent magnets which generate a magnetic field. The porous cubic enclosure filled with air is heated isothermally from the left-hand side vertical wall and cooled isothermally from opposing wall while the other four walls are thermally insulated. The gravitational force acts in the minus Y direction. In the present study, the length of the enclosure L, the length of the permanent magnet L 1 and the distance of permanent magnets L 2 are 0.024, 0.02 and 0.03 m, respectively.

Fig. 1
figure 1

Physical model and coordinate system

Full size image

3 Mathematical Formulation

3.1 Governing Equations

The assumptions in the model are the following. The fluid is considered to be steady, incompressible, Newtonian. Both the viscous heat dissipation and magnetic dissipation are assumed to be negligible.

According to Braithwaite et al. [4], the magnetic force can be given as

$$ \mathbf{f}_{m} = \frac{\chi_{m}}{2\mu_{m}}\nabla \mathbf{b}^{2} = \frac{\rho \chi}{2\mu_{m}}\nabla \mathbf{b}^{2} $$
(1)

where f m is the magnetic force; χ m is the volumetric magnetic susceptibility; μ m is the magnetic permeability, H m−1; b is the magnetic flux density, T; ρ is the fluid density, kg m−3; χ is the mass magnetic susceptibility, m3 kg−1.

The Navier–Stokes equation which includes the magnetic force can be presented as

$$\begin{aligned} \frac{\rho}{\varepsilon^{2}}\mathbf{U} \cdot \nabla \mathbf{U} =& - \nabla p - \frac{\mu}{\kappa} \mathbf{U} + \frac{\mu}{\varepsilon} \nabla^{2}\mathbf{U} - \frac{\rho}{ \varepsilon^{3/2}}\frac{1.75}{\sqrt{150}} \frac{\vert \mathbf{U} \vert \mathbf{U}}{\sqrt{\kappa}} \\ &{} + \frac{\rho \chi}{2\mu_{m}}\nabla \mathbf{b}^{2} + \rho \mathbf{g} \end{aligned}$$
(2)

in which U is the velocity vector; p is the pressure, Pa; μ is the fluid kinematic viscosity, kg m−1 s−1;g is the gravitational acceleration, m s−2;ε is the porosity; κ is the permeability, m2.

At the reference state of the isothermal state, there will be no convection. Therefore Eq. (2) becomes

$$ 0 = - \nabla p_{0} + \frac{\rho_{0}\chi_{0}}{2\mu_{m}}\nabla \mathbf{b}^{2} + \rho_{0}\mathbf{g} $$
(3)

where p 0 is the pressure at reference temperature, Pa; ρ 0 is the fluid density at reference temperature, kg m−3;χ 0 is the mass magnetic susceptibility at reference temperature, m3 kg−1. Subtracting (3) from (2) gives

$$\begin{aligned} \frac{\rho}{\varepsilon^{2}}\mathbf{U} \cdot \nabla \mathbf{U} =& - \nabla p' - \frac{\mu}{\kappa} \mathbf{U} + \frac{\mu}{\varepsilon} \nabla^{2}\mathbf{U} - \frac{\rho}{ \varepsilon^{3/2}}\frac{1.75}{\sqrt{150}} \frac{\vert \mathbf{U} \vert \mathbf{U}}{\sqrt{\kappa}} \\ &{} + \frac{(\rho \chi - \rho_{0}\chi_{0})}{2\mu_{m}}\nabla \mathbf{b}^{2} + (\rho - \rho_{0})\mathbf{g} \end{aligned}$$
(4)

where p=p 0+p′, p′ is the pressure difference due to the perturbed state, Pa. Since ρ and χ are functions of temperature, according to Taylor expansion method, ρχ and ρ can be respectively indicated as

$$ \rho \chi = (\rho \chi )_{0} + \biggl(\frac{\partial (\rho \chi )}{\partial T} \biggr)_{0}(T - T_{0}) + \cdots $$
(5)
$$ \rho = \rho_{0} + \biggl(\frac{\partial \rho}{\partial T}\biggr)_{0}(T - T_{0}) + \cdots $$
(6)

For air as a paramagnetic fluid, mass magnetic susceptibility is in inverse proportion to absolute temperature; according to the Curie law:

$$ \chi = \frac{m}{T} $$
(7)

where m is the constant value; T is the fluid temperature, K; T 0=(T h +T c )/2, K; subscripts 0, h, c represent the reference value, hot and cold, respectively. So Eq. (5) can be written as

$$\begin{aligned} \rho \chi - (\rho \chi )_{0} =& \biggl( \frac{\partial \rho}{\partial T}\chi - \rho \frac{\chi}{T} \biggr)_{0}(T - T_{0}) + \cdots \\ =& \biggl( - \rho \beta \chi - \rho \frac{\chi}{T} \biggr)_{0}(T - T_{0}) + \cdots \\ = & - \rho_{0}\chi_{0}\beta \biggl(1 + \frac{1}{T_{0}\beta} \biggr) (T - T_{0}) + \cdots \end{aligned}$$
(8)

The higher order small amount in Eq. (8) is omitted and generated into Eq. (4), which becomes

$$\begin{aligned} \frac{1}{\varepsilon^{2}}\mathbf{U} \cdot \nabla \mathbf{U} =& - \frac{\nabla p'}{\rho_{0}} - \frac{\mu}{\rho_{0}\kappa} \mathbf{U} + \frac{\mu}{\rho_{0}\varepsilon} \nabla^{2}\mathbf{U} \\ &{} - \frac{1}{\varepsilon^{3/2}}\frac{1.75}{\sqrt{150}} \frac{\vert \mathbf{U} \vert \mathbf{U}}{\sqrt{\kappa}} \\ &{} - \frac{\chi_{0}\beta}{2\mu_{m}} \biggl(1 + \frac{1}{T_{0}\beta} \biggr) (T - T_{0})\nabla \mathbf{b}^{2} \\ &{} + \beta (T - T_{0})g \end{aligned}$$
(9)

where β is the thermal expansion coefficient, K−1.

For simplicity, subscripts of physical parameters and the superscript of pressure are omitted, so the governing equations can be written as:

Continuity equation:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(10)

Momentum equation:

$$\begin{aligned} &{\frac{\rho}{\varepsilon^{2}}\biggl(u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}\biggr) } \\ &{\quad {} = - \frac{\partial p}{\partial x} - \frac{\mu}{\kappa} u - \rho \frac{1.75}{\sqrt{150}} \frac{(u^{2} + v^{2})^{1/2}}{\sqrt{\kappa}} \frac{u}{\varepsilon^{3/2}} } \\ &{\qquad {} + \frac{\mu}{ \varepsilon} \biggl(\frac{\partial^{2}u}{\partial x^{2}} + \frac{\partial^{2}u}{\partial y^{2}}\biggr) \,{-}\, \biggl(1 + \frac{1}{T_{0}\beta} \biggr) \frac{\chi_{0}\beta (T - T_{0})}{2\mu_{m}}\frac{\partial (\mathbf{b}^{2})}{\partial x} } \\ \end{aligned}$$
(11)
$$\begin{aligned} &{\frac{\rho}{\varepsilon^{2}}\biggl(u\frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}\biggr) } \\ &{\quad {} = - \frac{\partial p}{\partial y} - \frac{\mu}{\kappa} v - \rho \frac{1.75}{\sqrt{150}} \frac{(u^{2} + v^{2})^{1/2}}{\sqrt{\kappa}} \frac{v}{\varepsilon^{3/2}} } \\ &{\qquad {} + \frac{\mu}{ \varepsilon} \biggl(\frac{\partial^{2}v}{\partial x^{2}} + \frac{\partial^{2}v}{\partial y^{2}}\biggr) \,{-}\, \biggl(1 + \frac{1}{T_{0}\beta} \biggr)\frac{\chi_{0}\beta (T - T_{0})}{2\mu_{m}}\frac{\partial (\mathbf{b}^{2})}{\partial y} } \\ &{\qquad {}+ \rho g\beta (T - T_{0}) } \end{aligned}$$
(12)

Energy equation:

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \biggl(\frac{\partial^{2}T}{\partial x^{2}} + \frac{\partial^{2}T}{\partial y^{2}}\biggr) $$
(13)

where: x, y are Cartesian coordinates; u, v are velocity components, m s−1;α is the fluid thermal diffusivity, m s−1;ν is the fluid dynamic viscosity, m2 s−1.

The above Eqs. (10)–(13) can be non-dimensionalized as follows:

Continuity equation:

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0 $$
(14)

Momentum equation:

$$\begin{aligned} &{\frac{1}{\varepsilon^{2}}\biggl(U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}\biggr) } \\ &{\quad {} = - \frac{\partial P}{\partial X} - \frac{\mathit{Pr}}{\mathit{Da}}U - \frac{1.75}{\sqrt{150}} \frac{(U^{2} + V^{2})^{1/2}}{\sqrt{\mathit{Da}}} \frac{U}{\varepsilon^{3/2}} }\\ &{\qquad {} + \frac{\mathit{Pr}}{\varepsilon} \biggl(\frac{\partial^{2}U}{\partial X^{2}} + \frac{\partial^{2}U}{\partial Y^{2}}\biggr) - \gamma\mathit{Ra}\mathit{Pr}\theta \frac{C}{2}\frac{\partial (\mathbf{B}^{2})}{\partial X} } \end{aligned}$$
(15)
$$\begin{aligned} &{\frac{1}{\varepsilon^{2}} \biggl(U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}\biggr) } \\ &{ \quad {}= - \frac{\partial P}{\partial Y} - \frac{\mathit{Pr}}{\mathit{Da}}V - \frac{1.75}{\sqrt{150}} \frac{(U^{2} + V^{2})^{1/2}}{\sqrt{\mathit{Da}}} \frac{V}{\varepsilon^{3/2}} } \\ &{\qquad {} + \frac{\mathit{Pr}}{\varepsilon} \biggl(\frac{\partial^{2}V}{\partial X^{2}} + \frac{\partial^{2}V}{\partial Y^{2}}\biggr) - \gamma\mathit{Ra}\mathit{Pr}\theta \frac{C}{2} \frac{\partial (\mathbf{B}^{2})}{\partial Y} + \mathit{Ra}\mathit{Pr}\theta } \end{aligned}$$
(16)

Energy equation:

$$ U\frac{\partial \theta}{\partial X} + V\frac{\partial \theta}{\partial Y} = \frac{\partial^{2}\theta}{\partial X^{2}} + \frac{\partial^{2}\theta}{ \partial Y^{2}} $$
(17)

The dimensionless variables and parameters in the above equations are defined as

$$\begin{array}{@{}l} \displaystyle X = \frac{x}{L}\qquad Y = \frac{y}{L}\qquad U =\frac{u}{\alpha /L}\qquad V = \frac{v}{\alpha /L} \\ \displaystyle \theta= \frac{T - T_{0}}{T_{h} - T_{c}}\qquad P = \frac{p}{\rho\alpha^{2}/L^{2}}\qquad \mathit{Ra} = \frac{g\beta (T_{h} - T_{c})L^{3}}{\nu \alpha} \\ \displaystyle \mathit{Pr}= \frac{\nu}{\alpha}\qquad \mathit{Da} =\frac{\kappa}{L^{2}}\qquad T_{0} = \frac{T_{h} + T_{c}}{2} \\ \displaystyle \mathbf{B} = \frac{\mathbf{b}}{b_{0}}\qquad b_{0} = Br\qquad C = 1 + \frac{1}{T_{0}\beta}\qquad \gamma = \frac{\chi_{0}b_{0}^{2}}{\mu_{m}\rho gL} \end{array} $$

where: X, Y are dimensionless Cartesian coordinates; U, V are dimensionless velocity components; P is the dimensionless pressure; θ is the dimensionless temperature; T h is the temperature of the hot wall, K; T c is the temperature of the cold wall, K; Pr is the Prandtl number; b 0 is the reference magnetic flux density, T; L is the length of the enclosure, m; L 1 is the length of the permanent magnet, m; L 2 is the distance of permanent magnets, m; Ra is the Rayleigh number; γ is the dimensionless magnetic strength parameter; B is the dimensionless magnetic flux density; and Da is the Darcy number.

3.2 Mathematical Formulation of Magnetic Field Calculation

Maxwell’s equations are applied to describe the magnetic quadrupole field:

$$ \nabla \cdot \mathbf{B} = 0 $$
(18)
$$ \nabla \times \mathbf{H} = 0 $$
(19)

where B is the magnetic flux density and H is the magnetic field intensity.

The constitutive relation that describes the behavior of the magnetic material is

$$ \mathbf{B} = \mu \mathbf{H} $$
(20)

The scalar magnetic potential φ m is commonly used to calculate the magnetic field and it satisfies

$$ \mathbf{H} = - \nabla \varphi_{m} $$
(21)

In homogeneous magnetic medium, the permeability is assumed to be constant. Combining Eqs. (20), (21) and (18), the scalar magnetic potential satisfies the Laplace’s equation

$$ \nabla \varphi_{m} = 0 $$
(22)

3.3 Boundary Conditions

Non-slip condition is imposed for the two velocity components on the solid walls. The temperature boundary conditions are: (1) Wall of the enclosure (U=V=0); (2) Left vertical wall (X=0):θ=0.5; (3) Right vertical wall (X=1):θ=−0.5; (4) Top and bottom horizontal adiabatic walls (Y=0,1):∂θ/∂Y=0.

3.4 Nusselt Number Calculation

In order to compare total heat transfer rate, Nusselt number is used. The average Nusselt number at the hot wall is defined as

$$ \mathit{Nu}_{m} = - \int_{0}^{1} \frac{\partial \theta}{\partial X}_{X = 0}\,dY $$
(23)

3.5 Numerical Procedure and Code Verification

The governing Eqs. (14)–(17) are discretized by the finite-volume method (FVM) based on a non-uniform grid system. The third-order Quick scheme and the second-order central difference scheme are implemented for the convection and diffusion terms. The set of discretized equations for each variable is solved by a line-by-line procedure, combining the tridiagonal matrix algorithm (TDMA) with the successive over-relaxation (SOR) iteration method. The coupling between velocity and pressure is solved by the SIMPLE algorithm. The convergence criterion is that the maximal residual of all the governing equations is less than 10−6.

The reliability and accuracy of the mathematical model and code must be checked before calculation. Three grid sizes 50×50, 60×60 and 70×70 are selected for analysis. The average Nusselt number for all three grid sizes is monitored at ε=0.5, Pr=0.71, Ra=1×105, Da=1×10−3, γ=10. The results showed insignificant differences for the 60×60 grids to the above. Therefore, for all computations in this article, a 60×60 uniform grid was employed.

In order to validate the numerical methods and codes of the present work, a recent, similar work by Lijun Yang et al. [11] was selected as the benchmark solution for comparison. Lijun Yang considered the thermomagnetic convection in an air-filled 2-D square enclosure confined to a magnetic quadrupole field under zero-gravity. Table 1 presents comparisons between the present results for Da=107, ε=0.9999, g=0 and those of Lijun Yang for the average Nusselt number, temperature field and velocity field [11]. It is seen that the present results are in very good agreement with those obtained by previous authors, which validates the present numerical code.

Table 1 Comparison of present results with Lijun Yang et al. [11]
Full size table

4 Results and Discussion

Ra becomes zero and γ becomes infinity when g=0, so that finite product γRa has to be used to describe non-gravity cases.

Figure 2 shows the streamlines and isotherms at various magnetic force numbers when Da=10−3 and ε=0.5. In each graphic shown, the porous enclosure was heated isothermally from left-hand side vertical wall and cooled isothermally from opposing wall. Obviously, the convection in the porous enclosure is strengthened with the increase of γRa. The distribution of streamlines suggests that the magnetic buoyancy force drives the air moving from the left hot wall to the right cold wall along the horizontal middle line of the porous enclosure; then the air is moving downwards and upwards to the top and bottom walls and returns to the middle of the hot wall, so that the flow in the enclosure is of two cellular structures with horizontal symmetry about the middle of the enclosure. The distribution of isotherms suggests that the isotherms in the porous enclosure are horizontally symmetric about the middle of the porous enclosure; isotherms are dense at the top and bottom of the hot wall and the middle of the cold wall. When γRa is relatively small, such as γRa=1×105, the convection of air in the porous enclosure is very weak so that the heat transfer is dominated by the conduction mechanism, when isotherms approximately exhibit a linear trend from the hot wall to the cold wall. With the increase of γRa, the convection in the porous enclosure is strengthened and the isotherms show severe deformation.

Fig. 2
figure 2

Effect of γRa on the streamlines (left) and isotherms (right) at Da=10−3 and ε=0.5

Full size image

Figure 3 illustrates the variations of the local Nusselt numbers along the left hot wall and the right cold wall at various γRa when Da=10−3, ε=0.5. It can be seen that the local Nusselt numbers are increased as the γRa increases; the local Nusselt numbers are symmetric about the horizontal centerline, which is consistent with the isotherms. For the hot wall, the minimum local Nusselt number appears in the middle position and the maximum appears in the top and bottom of the hot wall. For the cold wall, the local Nusselt number is maximal in the middle position and gradually presents monotonic decrease from the middle of the cold wall to its ends.

Fig. 3
figure 3

Effect of γRa on the local Nusselt numbers of the left (top) and right (bottom) side walls at Da=10−3 and ε=0.5

Full size image

5 Conclusion

The thermomagnetic convection of air in a two-dimensional porous square enclosure under a magnetic quadrupole field is numerically investigated under non-gravitational conditions. The results show that the flow of the air in the enclosure is of two cellular structures with horizontal symmetry about the middle of the enclosure. The local Nusselt numbers along the left hot wall and the right cold wall are increased as the magnetic force number increases and are symmetric about the horizontal centerline. The magnetic field intensity, the Darcy number and the Rayleigh number have a significant effect on the flow field and heat transfer in a porous square enclosure.