On the Theory of Kinetic Phenomena in 2D Doped Antiferromagnet with Strong Spin–Hole Interaction

Abstract

The problem of constructing the kinetic equation for a hole motion in systems with strong spin-hole interaction (such as HTSC) is treated in terms of the spin polaron concept for a regular 2d antiferromagnetic (AFM) s–d model. It is shown that kinetics is determined by the properties of the spin polaron bands (rather than “bar hole”) for which the hole residues Z _k can be far from 1. In both cases of low and optimal doping, the obtained electrical resistivity ρ(T) and Hall coefficient R(T) T-dependence demonstrates qualitative agreement with experimental data if we take into account the rearrangement of the lower polaron band spectrum and Z _k residues on doping, as well as a strong anisotropy of hole–spin scattering.

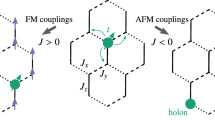
Anomalous properties of high-T _c cuprates include a complex behavior of the spectral properties and peculiar ρ(T) and R _H (T) T-dependence. Our study of kinetics is based on the microscopic description in terms of spin-fermion Hamiltonian. It consists of the motion of bare holes $\hat{H}_{0h}= \sum_{\mathbf{k}} \varepsilon _{\mathbf{k}} a_{{\mathbf{k}}{\sigma}}^{\dagger} a_{{\mathbf{k}}{\sigma}}$, AFM spin–spin interaction $\hat{I}= 1/2 \sum_{\mathbf{R},\mathbf{r}}I_{r} S_{\mathbf{R+ r}}^{\alpha } S_{\mathbf{r}}^{\alpha }$ and spin–hole interaction $\hat{J} =J\sum_{\mathbf{r}}a_{\mathbf{r},\gamma _{1}}^{\dagger }\hat{\sigma}_{\gamma _{1}\gamma _{2}}^{\alpha }a_{\mathbf{r}\gamma _{2}}S_{\mathbf{r}}^{\alpha }$.

To study the charge excitations we introduce a finite set of the basic operators: $\varphi _{\mathbf{r} \sigma}^{(1)}= a_{\mathbf{r} \sigma}$, $\varphi _{\mathbf{r} \sigma}^{(2)}= S^{\alpha}_{\mathbf{r}} \hat{\sigma}^{\alpha}_{\sigma \sigma_{1}} a_{\mathbf{r} \sigma_{1}}$, describing the in-site pairing of bare hole with the localized spin and the operators

corresponding to the spin polaron of the intermediate radius, which describe the pairing of local operators $\varphi _{\mathbf{r} \sigma}^{(1)}$ and $\varphi _{\mathbf{r} \sigma}^{(2)}$ with the spin wave operators $S^{\alpha}_{\bf q}$, ${\bf q}$ close to (π,π).

The standard Mori–Zwanzig projection procedure gives the Green’s functions of a bare hole in the mean-field approximation (see [1]), $G_{h}(\mathbf{k},\omega )= \langle a_{\mathbf{k}\sigma }; a_{\mathbf{k}\sigma}^{\dagger } \rangle = \sum_{s=1}^{4} Z_{\mathbf{k}}^{(s)}/\allowbreak(\omega -E_{\mathbf{k}}^{(s)})$, expressed in terms of the residue function $Z_{\bf k}^{(s)}$ and spin-polaron bands $E_{\bf k}^{(s)}$ (s=1–4 is the band number).

In the polaron representation, the Hamiltonian takes the form $\hat{H}=\sum_{\mathbf{k},s}E_{\mathbf{k}}^{(s)}\alpha _{\mathbf{k}\sigma }^{(s)\dagger }\alpha _{\mathbf{k}\sigma }^{(s)}+ \hat{\tilde{J}}+ \hat{I}$, $\hat{J}_{p}=\hat{P}\hat{J}\hat{P}$, $\hat{P}=\sum_{\mathbf{k,}s}|\alpha _{\mathbf{k,}\gamma }^{(s)}\rangle \langle\alpha _{\mathbf{k,}\gamma }^{\dagger (s)}|$. Here, $\hat{P}$ is the projection operator on the polaron space, $\varphi _{\mathbf{k},\sigma }^{(i)}= U_{ij}^{-1}(\mathbf{k}) \alpha _{\mathbf{k}\sigma }^{(j)}$. The matrix $U_{ij}^{-1}(\mathbf{k})$ is expressed in the explicit form in terms of the spin–spin correlation functions, which are in turn determined in terms of spin–spin susceptibility $\chi({\bf q}, \omega)$ for the frustrated AFM spin subsystem [4, 5].

In order to obtain an explicit form for ρ(T) and R _H (T), we take a multimoment variant of the linear-response theory where the deviation from equilibrium is characterized by a finite set of operators $\hat{F}_{l}^{s} =\sum_{\mathbf{k}}F_{l}^{s}(\mathbf{k)}\alpha _{\mathbf{k}\sigma }^{(s)\dagger }\alpha _{\mathbf{k}\sigma }^{(s)}$. The collision term is expressed in terms of moments $F^{s}_{l}$ (we introduce up to seven moments), residues $Z_{\bf k}^{(s)}$, polaron bands $E_{\bf k}^{(s)}$ and the imaginary part of spin–spin susceptibility χ′′(q,ω). For χ(q,ω) we adopt the spherical-symmetric form with damping γ: $\chi(\mathbf{q},\omega)= -A_{\mathbf{q}}/(\omega ^{2}-\omega _{\mathbf{q}}^{2}+i\omega \gamma)$; γ=γ(T). To obtain an explicit form for χ(q,ω) we use a full self-consistent approach with spin-constraint fulfilling. To test overdamped magnons approach, we also use the χ _ovd(q,ω) of the form $\chi_{\mathrm{ovd}} (\mathbf{q},\omega)= A_{\mathbf{q}}/(i\omega \gamma({\bf q}, \omega)- \omega _{\mathbf{q}}^{2})$. The details are in Refs. [2, 3].

Figure 1 presents the characteristic residue spectra function $Z_{\bf k}^{(1)}$ for lower polaron band in a case of a larger spin correlation length (ξ≃10g, g is the lattice constant) of underdoped cuprates. $Z_{\bf k}^{(1)}$ decrease from 0.24 to 0.04 when moving along the Fermi surface. This decrease qualitatively reflects the known opening of the pseudogap on the Fermi surface. For the number of holes n _h =0.08, calculations lead to ρ=230 μΩ cm, which is close to ρ(T=120 K)=220 μΩ cm for La_2−x Sr _x CuO₄ with x≈0.1 [6].

Fig. 1

Residue function $Z_{\bf k}^{(1)}$ (low doping) presented by contour curves in the first quarter of the Brillouin zone. The thick line is the Fermi surface

Our results for optimal doping, presented in Fig. 2, give, in accordance with the experiment [6], that ρ(T) curve exhibits T dependence close to a linear one starting from low T with the value ρ(400 K)/ρ(100 K)≈5. The overdamped $\chi_{\mathrm{ovd}}({\bf q}, \omega)$ strongly underestimates the scattering for large ω. The cotΘ _H exhibits nearly linear behavior on T ² in a wide T-range.

Fig. 2

ρ(T/I) and cotangent of the Hall angle cotΘ _H (T ²/I ²) at 10 T (upper inset). The solid lines correspond to $\chi({\bf q}, \omega)$. The dashed lines for $\chi_{\mathrm{ovd}}({\bf q}, \omega)$. Lower inset: the spectrum $\varepsilon_{\bf k}= const$; bold curve is the Fermi line for optimal doping

Given in Fig. 3 (optimal doping), R _H (T) decreases upon heating, which corresponds to the experimentally observed behavior. In the inset we show the dependence $\tau({\bf k})/\tau({\bf k}_{\mathrm{cold}})$ to demonstrate the presence of hot and cold spots.

Fig. 3

R _H (T) (optimal doping): curves a, b, c, correspond to $\chi({\bf q}, \omega)$ with γ values γ/I=0.5, 1.0 and 1.5, respectively; the dashed curve mf corresponds to mean-field spin spectrum. In inset, for T/I=0.3, 0.1, and 0.05, curves a----mf, b—mf, and c—mf demonstrate strong scattering anisotropy by showing the dependence $\tau({\bf k})/\tau({\bf k}_{\mathrm{cold}})$, $\tau({\bf k})$ to relaxation time. Angle ϑ is formed by the radius vector ${\bf k}$ lying on the circle arc k ₀=0.83π and the axis M(π,π)−X(0,π). The circle is centered at M and adjoins the Fermi surface

In summary, we show that the spin polaron concept (“good” quasi-particles are polarons, not bare holes) allows to reproduce T-anomalies for two kinetic coefficients simultaneously in a wide doping range. It gives a possibility to take into account strong dependence of polaron bands and bare hole residues Z _k on spin–spin correlation length from the very beginning. It is also important to treat the kinetic equation, namely for polarons, and to introduce a multimoment approach (seven $F^{s}_{l}$ operators give a possibility to take into account strong scattering anisotropy).