1 Introduction

The interplay and competition between superconductivity and charge orderings is currently under intense investigations (among others in high temperature superconductors such as cuprates, barium bismuthates, fullerenes, and several other nonconventional superconducting materials, e.g., the Chevrel phases) [1]. They belong to a unique group of extreme type II superconductors and generally exhibit low carrier density, a small value of Fermi energy (E F ≤0.1÷0.3 eV), and a short coherence length ξ 0 (ξ 0 k F ≈1÷10). These general features are consistent with short-range, almost unretarded effective interactions response for local pairing.

In this report, we will concentrate on the intriguing problem of phase separation and the competition between superconductivity and charge orderings. The model Hamiltonian considered has the following form:

(1)

where \(\hat{n}_{i}=\sum_{\sigma}{\hat{n}_{i\sigma}}\), \(\hat{n}_{i\sigma}=\hat{c}^{+}_{i\sigma}\hat{c}_{i\sigma}\), \(\hat{\rho}^{+}_{i}=(\hat{\rho}^{-}_{i})^{\dag}=\hat{c}^{+}_{i\uparrow}\hat{c}^{+}_{i\downarrow}\). \(\hat{c}^{+}_{i\sigma}\) (\(\hat{c}_{i\sigma}\)) denotes the creation (annihilation) operator of an electron with spin σ=↑,↓ at the site i, which satisfy canonical anticommutation relations:

$$ \bigl\{ \hat{c}_{i\sigma}, \hat{c}^+_{j\sigma'}\bigr\} = \delta_{ij}\delta_{\sigma\sigma'}, \{ \hat{c}_{i\sigma}, \hat{c}_{j\sigma'}\} = \bigl\{ \hat{c}^+_{i\sigma}, \hat{c}^+_{j\sigma'} \bigr\} = 0, $$
(2)

where δ ij is the Kronecker delta. ∑〈i,j〉 indicates the sum over nearest-neighbor sites i and j independently. z will denote the number of nearest-neighbors. U, I, and W are the interactions parameters, I 0=zI, W 0=zW. μ is the chemical potential, connected with the concentration of electrons by the formula: \(n = (1/N)\sum_{i}{ \langle \hat{n}_{i} \rangle}\), with 0≤n≤2 and N is the total number of lattice sites.

The interactions U, I, and W will be treated as the effective ones and will be assumed to include all the possible contributions and renormalizations like those coming from the strong electron-phonon coupling or from the coupling between electrons and other electronic subsystems in solid or chemical complexes [1]. In such a general case, arbitrary values and signs of U, I, and W are important to consider. In the absence of the external field conjugated with the SS order parameter (\(\varDelta =(1/N)\sum_{i}\langle \hat{\rho}^{-}_{i}\rangle\)), there is a symmetry between I>0 (s-pairing) and I<0 (η-pairing, ηS, \(\varDelta _{Q} = (1/N)\sum_{i}{\exp{(i\mathbf{Q}\cdot \mathbf{R}_{i})}\langle \hat{\rho}^{-}_{i}\rangle} \), Q is half of the smallest reciprocal lattice vector) cases for model (1), thus we restrict ourselves only to the I>0 case. The CO parameter is defined as \(n_{Q}=(1/N)\sum_{i}{\exp{(i\mathbf{Q}\cdot \mathbf{R}_{i})}\langle \hat{n}_{i}\rangle}\).

We have performed extensive study of the phase diagrams (PDs) of model (1) [2]. In this report, we investigate the properties of model (1) for the case of on-site attraction (U<0, local pair or Bose condensation limit [3–8]) and intersite repulsion (W>0). In the analysis of the model at T≥0, we have adopted a variational approach (VA), which treats the on-site interaction U exactly and the intersite interactions W and I within the mean-field approximation (MFA). The PDs of model (1) have been investigated until now for the special cases: W=0 [3–12] and I=0 [13–21] only. Some ground state results for W≠0 and I≠0 have been also obtained [5, 22, 23].

Within the VA the intersite interactions are decoupled within the MFA, which allows us to calculate the averages n, n Q , Δ, and Δ Q . It gives a set of four self-consistent equations (for homogeneous phases). The definitions of homogeneous phases with the values of order parameters are as follows: (i) SS—n Q =0, Δ≠0, Δ Q =0; (ii) CO—n Q ≠0, Δ=0, Δ Q =0; (iii) M—n Q ≠0, Δ≠0, Δ Q ≠0; (iv) NO—n Q =0, Δ=0, Δ Q =0. It is important to find a solution corresponding to the lowest energy.

Phase separation (PS) is a state in which two domains with different electron concentration: n + and n − exist in the system (coexistence of two homogeneous phases). The free energies of the PS states are calculated in a standard way, using Maxwell’s construction (e.g., [5, 18, 19, 24]). In model (1) for the range of parameters considered in this paper, only one PS state can occur, which is coexistence of the SS and CO phases.

In the report, we have used the following convention. A second- (first-)order transition is a transition between homogeneous phases with a (dis-)continuous change of the order parameter at the transition temperature. A transition between homogeneous phase and PS state is symbolically named as a “third-order” transition [5, 6, 17–21].

2 Results in the Local Pairing Limit

2.1 Phase Diagrams

One should noticed that PDs obtained are symmetric with respect to half-filling (n=1) because of the particle–hole symmetry of Hamiltonian (1), so the PDs will be presented only in the range \(\bar{\mu}=\mu-U/2-W_{0} \leq 0\) and 0≤n≤1.

For any U≤0 and fixed W>0, the PDs are qualitatively similar, all (first-order, second-order and “third- order”) transition temperatures decrease monotonically with increasing U and in the VA for U=0 the transition temperatures account for a half of those in the limit U→−∞, what can be symbolically written as

$$ k_B T_c(U\rightarrow-\infty) = 2 k_B T_c (U=0), $$
(3)

where T c denotes the transition temperature (which can be SS–NO, SS–CO, CO–NO, PS–CO, or PS–SS).

Notice that in the U→−∞ limit model (1) is equivalent with the hard-core boson model on a lattice [25–29]. Moreover, in that limit model (1) can be derived as effective Hamiltonian at the strong-coupling limit of the extended Hubbard model by the degenerate perturbation theory [22, 23, 30].

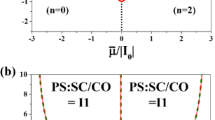
In the range of the attractive on-site interaction, the structure of PDs of model (1) depends on the ratio W/I only (cf. Fig. 1 for U/I 0=−1). One can distinguish two ranges of the ratio W/I in which the system exhibits substantially different behaviors:

Fig. 1
figure 1

k B T/I 0 vs. \(\bar{\mu}/I_{0}\) phase diagrams (upper row) and corresponding k B T/I 0 vs. n diagrams (lower row) for U/I 0=−1.0 and different values of W/I=0.5,1.1,2.0 (as labeled). Dotted, solid, and dashed lines indicate first-order, second-order, and “third-order” boundaries, respectively. B denotes bicritical points

Full size image

(i) 0≤W/I<1. In Figs. 1a,b, we present particular PDs for W/I=0.5. For 0<W/I<1 and U<0, only the second-order SS–NO transitions occur with increasing temperature. If we analyze the system for fixed n, for this range of model parameters, the PS states do not occur and the obtained PDs have the same structure as those derived in [3–5]. The transition between homogeneous SS and NO phases taking place with increasing temperature is second order for arbitrary \(\bar{\mu}\) and n, and it decreases monotonically with increasing \(|\bar{\mu}|/I_{0}\) and |1−n|.

(ii) 1<W/I. A few particular PDs in this regime are presented in Figs. 1c–f. For W/I=1 the SS, the CO and the M phases are degenerate at n=1. For W/I>1, three homogeneous phases (SS, CO, NO) appear. The SS–NO and CO–NO transitions are of the second order and these transition temperatures are decreasing function of \(|\bar{\mu}|\) and |1−n|. The SS–CO transition is discontinuous for fixed \(\bar{\mu}\), and thus the PS state SS–CO is stable in the definite range of n. All transitions lines meet at a bicritical point B. With increasing W, the B-point moves along the boundary between SS and NO phases toward larger \(|\bar{\mu}|\) (|1−n|). This is due to the fact that in the VA the SS–NO transition is independent of W (for fixed n). The region of the CO phase occurrence is extended, whereas the region of the SS phase stability is reduced by increasing the ratio W/I. The first-order SS–CO as well as the “third-order” SS–PS and PS–CO transition temperatures increase with \(|\bar{\mu}|\) and |1−n|, respectively.

One should notice that for W ij restricted to nearest neighbors (W 2=0) the PS state is strictly degenerated at T=0 with the M phase in the whole range of stability of both these states [22, 23]. This degeneration is removed at T>0, even for W 2=0 and the PS state occurs on PDs. Repulsive W 2>0 between next-nearest neighbors destabilizes the PS state with respect to the M phase, whereas attractive W 2<0 extends the stability region of PS state and eliminates the M phase.

In the case of attractive W<0 (precisely for W/I<−1), the model can exhibit phase separation NO–NO (electron droplets state) at low temperatures [20, 22, 23, 31] and for U<0 the PDs as a function of n have the similar structure as those derived in [31]. We leave deeper analysis of this problem to future publications.

2.2 Order Parameters and Thermodynamic Properties

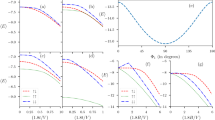
Let us focus now on the temperature dependencies of the order parameters and thermodynamic properties of the system at the sequence of transitions: SS → CO → NO for W/I=2.0, U/I 0=−1.0 and \(\bar{\mu}/I_{0}=-2.0\).

The temperature dependencies of the order parameters: Δ and n Q are presented in Fig. 2. It is clearly seen that at the SS–CO transition (at k B T c1/I 0=0.40) the both order parameters change discontinuously. The CO–NO transition at k B T c2/I 0=0.83 is of the second order.

Fig. 2
figure 2

Temperature dependencies of (a) superconducting order parameter |Δ| and (b) charge order parameter n Q for W/I=2.0, U/I 0=−1.0 and \(\bar{\mu}/I_{0}=-2.0\)

Full size image

Calculating the grand potential per site \(\omega=-{1}{/(N\beta)}\*\ln{(\mathrm{Tr}[\exp(-\beta\hat{H})])}\) within the VA one can obtain thermodynamic characteristics of the system for arbitrary temperature. The entropy s and the specific heat c can be derived as s=−(∂ω/∂T) and c=−T(∂ 2 ω/∂T 2). ω, s, and c as a function of temperature are shown in Fig. 3. s increases monotonically with increasing T. It is discontinuous at T c1 whereas it is continuous at T c2. One can notice that in the high-temperature limit s/k B →ln(4)≈1.386 (there are four possible configurations at each site). The peak in c(T) is associated with the first-order transition (at T c1), while the λ-point behavior is typical for the second-order transition (at T c2).

Fig. 3
figure 3

Temperature dependencies of thermodynamics parameters: (a) the grand potential ω, (b) the entropy s, and (c) the specific heat c for W/I=2.0, U/I 0=−1.0 and \(\bar{\mu}/I_{0}=-2.0\)

Full size image

3 Conclusions and Final Remarks

In this report, we have presented some particular PDs of the extended Hubbard model with pair hopping and intersite density-density interactions in the zero-bandwidth limit for the case of local attraction U<0. One finds that the system considered can exhibit very interesting multicritical behaviors. Our investigations show that, depending on the values of interaction parameters (the ratio W/I), the system can exhibit three homogeneous phases: superconducting, charge-ordered and nonordered. The SS–NO and CO–NO transitions are of the second order. The SS–CO transition is discontinuous (for fixed μ), what leads to phase separation on the phase diagrams as a function of n for W/I>1. The homogeneous mixed phase (with nonzero both charge-ordered and superconducting order parameters) never occurs on PDs at T>0, at least in the absence of the next-nearest neighbors interactions. On the contrary, the PS state: SS–CO is found to be stable in definite ranges of model parameters and temperatures.

Our results are exact in the limit of infinite dimensions, where the MFA treatment of intersite terms is rigorous one [3–6, 11]. In finite dimensions due to quantum fluctuations connected with the I term, the regions of the ordered homogeneous phases occurrence are extended in comparison with the VA results [5, 6].