Radiation Heat Transfer and Its Impact on Stability Against Quench of a Superconductor

Abstract

Stability functions are an important analytical/numerical tool for appropriate design of conductor geometry and dimensions to prevent conductor losses under a transport current. While standard stability calculations following the Stekly, adiabatic, or dynamic stability models apply purely solid thermal conduction mechanism and derive results under (quasi) stationary conditions, the present paper investigates if, and to which extent, also radiation heat transfer, in addition to solid conduction, can exert impacts on conductor stability. Further, the full transient conductor temperature evolution after a disturbance is calculated. The analysis applies an interplay between Monte Carlo radiative transfer calculations, to describe absorption of heat pulses and their distribution in the conductor, and a rigorous finite element method to calculate the resulting temperature field and stability functions. The results show that radiative heat transfer cannot be neglected in particular if periodic disturbances have to be considered that can arise, e.g., in a flux flow fault current limiter.

Appendix

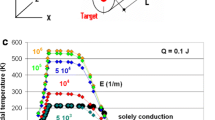
If not available from transmission measurements, extinction coefficients for the superconducting and normal conducting states can be estimated from literature values of spectroscopic measurements of reflectivity and corresponding Kramers–Kronig analysis. From the large variety of reflectivity measurements with high temperature superconductors reported in the literature, we in the following apply results from Kamarás et al. [13] and Chen for YBaCuO [14]. First, Kamarás et al. [13] showed that the mid-infrared absorption is a direct electronic absorption, with an onset at 140 cm⁻¹ in YBa₂Cu₃O_7−δ . The authors find that absorption across the gap is weak because the investigated high-T _c materials was in the clean limit, and this weak absorption is masked by the mid-infrared absorption. Chen [14] then applied a two component mode for the dielectric function. Figures 3.13 and 3.17 in this reference exactly cover the region of wave numbers to be considered in the present paper. From the complex optical conductivity for optimally doped YBaCuO, σ=σ ₁+iσ ₂, a mean value of the extinction coefficient, E=4πk/Λ, in the order of 10⁷ m⁻¹ in the superconducting state at a mean Λ=50 μm has been estimated on basis of the usual relations n ²−k ²=ε ₁ and 2nk=ε ₂=2σ/ω, with k the imaginary part of the index of refraction, ε _1,2 the real and imaginary part of the dielectric constant, and ω the frequency. In the normal conducting state, the spectral response of the optical conductivity, in particular at small wave numbers, is clearly different. Both real and imaginary parts of the optical conductivity are definitely smaller than in the superconducting state (the imaginary part by at least an order of magnitude). This means also the extinction coefficient is reduced, to a mean value of about E=5×10⁶ m⁻¹ taken over the same interval of wave numbers. Also, note that the analysis in [14] was applied to thin film samples prepared by pulsed laser ablation from a stoichiometric YBaCuO-target onto SrTiO₃ substrates. For the wire modeled in the present paper, we instead expect a polycrystalline material with smaller extinction coefficient than the values obtained from the optical conductivity reported in [14] (the absorption coefficient, A, is definitely smaller, but there will be some scattering contributions, S=ΩE, to the total extinction coefficient).

Accordingly, Monte Carlo calculations were performed for the series 5×10³≤E≤10⁶ m⁻¹. If the series would be continued up to E=10⁷ m⁻¹, the mean free path, l _m , of the bundles between two interactions becomes very small, l _m =0.1 μm, and the optical thickness, τ, of the sample in y-direction accordingly very large, τ=4×10⁴. Such a large number of absorption/remission and scattering events would very strongly increase computation time in the Monte Carlo analysis to unacceptably long periods of time (this extends to the order of days on a PC under Windows XP using a 3.8 GHz processor and 4GB work space).