Abstract
Objectives
Parole is an important mechanism for alleviating the extraordinary social and financial costs of mass incarceration. Yet parole boards can also present a major obstacle, denying parole to low-risk inmates who could safely be released from prison. We evaluate a major parole institution, the New York State Parole Board, quantifying the costs of non-risk-based decision-making.
Methods
Using ensemble machine Learning, we predict any arrest and any violent felony arrest within three years to generate criminal risk predictions for individuals released on parole in New York from 2012–2015. We quantify the social welfare loss of the Board’s non-risked-base decisions by rank ordering inmates by their predicted risk and estimating the crime rates that could have been achieved with counterfactual, risk-based release decisions. We also estimate the release rates that could have been achieved holding arrest rates constant. We attend to the “selective labels” problem in several ways, including by testing the validity of the algorithm for individuals who were denied parole but later released after the expiration of their sentence.
Results
We conservatively estimate that the Board could have more than doubled the release rate without increasing the total or violent felony arrest rate, and that they could have achieved these gains while simultaneously eliminating racial disparities in release rates.
Conclusions
This study demonstrates the utility of algorithms for evaluating criminal justice decision-making. Our analyses suggest that many individuals are being denied parole and incarcerated past their minimum sentence despite being a low risk to public safety.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Over the last decade, after more than thirty years of dramatic prison growth in the U.S., there has been a growing recognition of the enormous economic and social costs of mass incarceration and its rapidly diminishing marginal crime savings (Johnson and Raphael 2012; Raphael and Stoll 2013; Mauer 2018). Parole boards, vested with almost unlimited discretionary power to determine how long individuals serving indeterminate sentences (i.e. sentences with a minimum and maximum range such as “15 years to life”) spend in prison, represent an important release valve. While some form of risk assessment has been used to inform parole decisions since the 1920s (Burgess 1928), there has been a recent resurgence of risk assessment instruments in the criminal justice system to reduce prison populations without compromising public safety (Monahan and Skeem 2013), and a number of states have adopted data-driven instruments to guide parole board decisions (Schwartzapfel 2015).
New York is one such state: in 2011, the legislature amended the Executive Law governing parole to require the New York State Board of Parole to center decisions on individual’s rehabilitation in prison and risk of recidivism. The amendment was intended to counter the Board’s tendency to focus on the inmate’s commitment offense rather than their risk of offending if released. The Board adopted COMPAS Risk and Needs assessment, an actuarial tool that predicts inmates’ risk of violence and re-offending based on both static and non-static factors, such as an inmate’s education level, age at conviction, and re-entry plans (Walker 2013).
Despite the legal mandate, in the years following, critics have argued that the Board continues to incarcerate individuals well beyond their minimum sentence, not out of concern for public safety, but because of the nature and severity of the original commitment offense (New York Times Editorial Board 2014). A 2021 Vera Institute of Justice report examining 168 transcripts of hearings for individuals denied parole reported that most individuals had ‘low risk’ COMPAS scores, in addition to comprehensive release plans and positive records of in-prison education and vocational programming, yet they were still denied parole based simply on their original commitment offense (Heller 2021). Media reports have also alleged that the system is racially biased. A 2016 New York Times analysis reported that stark racial disparities—fewer than one in six Black and Hispanic men were released after their first parole hearing, as compared to one in four White men—was one of many manifestations of “a broken system” that also included heavy caseloads and cursory hearings (Winerip et al. 2016). A New York Bar Association Task Force echoed concerns that the Board was understaffed, with insufficient time to give careful and complete consideration to each case (Task Force on the Parole System 2019). The 2021 Vera report also noted staffing shortages, with commissioner case loads at times exceeding 1,000 per commissioner, and interview panels of only two commissioners rather than three, resulting in deadlocked cases (Heller 2021).
While there has been a great deal of criticism of the Board and calls for reform, the magnitude of its shortcomings has not been quantified. In this paper, we use a risk-prediction algorithm to evaluate the Board’s decision making. We generate machine learning predictions of criminal risk for individuals released on parole in New York State between 2012 and 2015. Specifically, using Super Learner, an ensemble machine learning algorithm (Van der Laan et al. 2007), we predict any arrest and any violent felony arrests within three years post release. We quantify lost social welfare of their decisions by rank ordering inmates by their predicted risk and estimating the crime rates that would have been observed with counterfactual, risk-based release decisions. We also estimate the release rate that could be achieved holding arrest rates constant.
Our focus is on the extent to which the Board’s decisions deviate from risk-based decisions. However, we acknowledge that the Board is permitted to make a holistic determination of parole “dessert” by considering objectives beyond risk. Because algorithms cannot generally incorporate these other factors, a comparison of algorithms to humans can be hindered by an omitted payoff bias (Kleinberg and Ludwig 2018; Ludwig and Mullainathan 2021). While these other objectives such as rehabilitation and retribution are not accounted for in our evaluation, we argue that comparing their decisions to counterfactual risk-based decisions is nonetheless valuable. First, the normative assumption that risk is or should be the central element of criminal justice decisions, particularly in the bail and parole context, is a common one (Slobogin 2021). Second, even normative perspectives that view factors such as retribution to be important still consider risk a legitimate consideration, and as such, purely risk-based evaluations such as ours remain relevant. We note that, insofar as the law permits or encourages non-risk considerations, our assessment and quantification of welfare loss is an evaluation of not just the Board’s decision-making, but also of the law that allows them to consider other factors.
Our aim in this paper is to evaluate the Board’s decision making so as to estimate the room for improvement. Importantly, we are not advocating for the use of our risk-prediction algorithm to guide parole decisions. While risk algorithms could be an important tool in reform efforts, it is not our intent here to take a position in that debate. The use of algorithms in the criminal justice system continues to be fiercely debated around questions of algorithmic fairness and racial bias (Kleinberg and Ludwig 2018; Berk and Heidari 2021; Hellman 2020), the relative benefit of algorithms over human decision-making, (Jung et al. 2020; Dressel and Farid 2018), and the extent to which decision-makers actually follow algorithmic guides such that risk tools might help achieve efficiency gains (Stevenson and Doleac 2021). Irrespective of these debates, we argue that algorithms can at least excel at diagnosing the extent of problems in our decision-making systems. This is critical as the extent of these problems is undoubtedly relevant to the seriousness with which we should pursue reform, including reform via algorithmic risk assessment.
Even for the limited purpose of evaluating institutions, a major empirical challenge in constructing accurate algorithms is the so-called selective labels problem (Kleinberg and Lakkaraju 2018; Lakkaraju et al. 2017; De-Arteaga et al. 2018; Slobogin 2021). The selective labels problem refers to the concern that risk prediction tools are necessarily constructed and validated on arrest outcomes only for individuals released by a decision-maker, but may not be accurate for those ‘unlabeled’ individuals who were denied parole and for whom we do not get to see arrest outcomes. If there is some unobserved variable, Z, that is not in the administrative data but is observed by the parole board and results in a reduced probability of release and is associated with increased risk, then the risk predictions for the non-paroled will tend to understate the true risk (Lakkaraju et al. 2017; Kleinberg and Ludwig 2018). Of course, it is also possible that there are unobservables that decrease the probability of release and also decrease risk. This would cause risk predictions to overstate the true risk, such that our estimates of crime savings and potential release rates would be even higher than those presented. Because our concern is to assure that we do not overstate the potential for improvement, we focus on addressing unobservables that are associated with increased risk.
The selective labels problem is a special case of sample selection bias: training and test data are drawn from different distributions such that the algorithm has less opportunity to detect patterns on cases that had little or no probability of appearing in the training data (Huang 2006; Zadrozny 2004). If there are no unobservables and all cases have a non-negligible probability of appearing in the training data, sample selection bias can be addressed with methods such as inverse probability weighting. The presence of unobservables presents a more challenging problem. Our focus is thus on sample selection bias due to unobservables, though testing for that bias simultaneously addresses any bias due to selection on observables.
Some prior work showing machine learning risk assessments can improve parole release decisions implemented a randomized experiment (Richard 2017), and therefore the selective labels problem was not a concern. In other work evaluating criminal justice decision-making with observational data, researchers have exploited inter-judge differences in decision making (Kleinberg and Lakkaraju 2018; Lakkaraju et al. 2017). Kleinberg et al. 2018 describe a contraction method in which they fit a model on individuals released by harsh judges—who release relatively few inmates—and test the accuracy of the model on the larger set of individuals who are released by lenient judges. Such a process allows them to evaluate how the model would perform on individuals who were not released by a harsh judges. The contraction approach is unavailable to us, as we do not have data on the identity of the assigned parole board commissioners. Even if we did have such data, the contraction approach is also limited. It leverages information from the most lenient judges to reach deeper into the full population of individuals. But, depending on the leniency of the most lenient judge, this reach can be very short. In the parole context, where the rates of release are generally low, the most lenient parole board member will likely still not be releasing many of the eligible inmates who are up for parole. For example, if the most lenient parole board member grants parole at a rate of 40%, the contraction approach does not directly address algorithmic accuracy with respect to the remaining 60% of the population.
In this paper, we attend to the problem of selective labeling with three different approaches. First, we show that the predicted probabilities of release for denied individuals’ do not overstate their release rates in subsequent hearings only two years later, suggesting that unobserved features do not substantially reduce individuals’ chances of release. Second, we test the validity of the algorithm for individuals who had hearings 2012–2015, were denied parole by the Board, but were later released after the expiration of their sentence. We find that the algorithm is accurate at predicting overall arrests but slightly underestimates the risk of violent arrest. Finally, we examine one-year arrest rates for individuals who had hearings in 2017, leveraging a plausibly exogenous increase in the rates of release in 2017 (from an average 20% in 2012–2015 to 31% in 2017). We find the model accurately predicts rearrest for violent crimes for the larger percentage of individuals who were released in 2017, though it slightly underestimates the arrest rate for non-violent crimes. Note that the latter two tests also estimate bias due to any sample selection on observables.
In sum, our tests suggest that sample selection bias is manageable. To account for for any bias, we conduct sensitivity analyses that assume the counterfactual arrest rate for those denied parole is as much as twice as high as our risk predictions. Our results suggest the parole board is detaining many low-risk individuals and releasing a substantial number of high-risk individuals. Even if we assume that risk is 100% higher than predicted, we estimate that the Board could have granted parole more than twice as often without increasing either the overall or violent arrest rate, or it could have released the same number of people while approximately halving both overall and violent arrest rates. Further, we find that they could have achieved these gains while simultaneously eliminating racial disparities in release rates.
Methods
Data
We identified individuals released by the New York State Parole Board using the Parole Hearing Data Project repository (New York State Parole Board Data 2014) and web-scrapping code available on the Project Github page (https://github.com/rcackerman/parole-hearing-data). This dataset is generated from records scraped from the New York State Parole Board’s online interview calendar, which is updated monthly and includes newly scheduled hearings and determinations. The dataset contains hearings from 2012–2018. The hearing data includes individual sex, race/ethnicity, commitment crime, housing facility, parole board interview type, and the interview decision.
We obtained criminal history records for all individuals who had a recorded parole hearing from 2012 through 2018 from the New York State Department of Criminal Justice Services (DCJS). DCJS maintains data on every finger-printable unsealed arrest and all associated criminal court outcomes in the state of New York. We linked these data to the parole hearing data using the unique New York State Identification Number (NYSID). We have arrest records through February 2019. Secondary dissemination of these individual criminal history data is prohibited, but these records may be obtained through the New York State Department of Criminal Justice Services.
Study Sample
We restrict our analyses to Black, Hispanic, and White male inmates. Our risk prediction algorithm is trained on the 4,168 individuals who were released on parole between 2012 and 2015 (a total of 19,713 individuals had parole hearings during this period). There were 393 inmates granted parole during this period who were not released, perhaps because parole was revoked for disciplinary reasons or failure to develop a satisfactory plan for housing; these individuals are not included.
Analyses of the selective labels problem test the accuracy of the algorithm on different populations than the population on which it was built. These include (a) 6784 individuals who were denied parole between 2012–2015 but were ultimately released after the expiration of their sentence and before February 2016 (such that we have three years of post-release follow up) and (b) 1998 individuals who were released in 2017, some fraction of whom we hypothesize would not have been released in previous years given the plausibly exogenous increase in the release rate.
Outcomes
Our primary outcomes are any recorded arrest within three years post-release and any violent felony arrest, as defined by New York Penal Law 70.02 (New York Consolidated Laws, Penal Law - PEN §70.02 n.d.), within three years post-release. We note that our estimates of criminal risk are necessarily based on administrative data records of arrests, which may be subject to data entry errors (McElhattan 2021). Our specific attention to arrest for felony violent crime is motivated by two factors. First, violent crime, which is by far the most costly, is of particular importance in the context of risk-based parole decision-making (Richard and Justin 2014) where incapacitation rather than deterrence is the primary aim. Second, focusing on felony violence should minimize the concern that our outcome may be subject to downstream criminal justice system biases (Skeem and Lowenkamp 2020; Blumstein 1993). Differential policing has been documented for discretionary crimes, particularly drug possession (Geller and Fagan 2010), but studies comparing crime victimization surveys with violent crime arrests suggest that the racial gap in the violent crime arrest is explained by greater minority involvement rather than differential detection (Skeem and Lowenkamp 2016; D’Alessio and Stolzenberg 2003).
Predictors
We use a large set of predictors to predict criminal risk: a total of 91 variables, including age, minimum and maximum sentence, prison and prison type, race, whether it is an individual’s first hearing, and time in prison. We also use information regarding arrest history, including the offenses that lead to the period of incarceration for which individuals are being considered for parole. Appendix 6 shows the full list of predictors.
We note that the inclusion of race and other strongly race-correlated variables in decision-guiding algorithms is currently the subject of ongoing empirical, political, and legal debate (Berk and Heidari 2021; Huq 2018; Gillis 2020; Nyarko et al. 2021). However, the same legal and political issues surrounding the inclusion of race (a protected characteristic under the Equal Protection Clause) and race-correlated variables are less relevant here, where the sole intent is to evaluate the Board. Further, to the extent that there may be bias in measurement of criminal history, the inclusion of race in the model may actually help account for such biases, whereas excluding it could generate a more problematic algorithm with respect to race (Mayson 2018; Nyarko et al. 2021). For example, if biased policing generates inflated prior arrest records of Black individuals, such records will be less informative regarding criminal risk than those for a white individual; an algorithm that excludes race will tend to overstate the risk of Black individuals relative to white individuals. Nonetheless, because the Board is not legally permitted to consider race in their determinations, we also generate the estimated risk predictions excluding race from the algorithm to ensure our estimates are not sensitive to this information.
Analyses
Predicting Criminal Risk
We use machine learning, specifically the R SuperLearner package, to predict the probability of any arrest as well as any violent felony arrest within three years. Super Learner is a loss-based stacking ensemble approach that uses v-fold cross-validation to find the optimal combination of a collection of learning algorithms that are then combined into a single prediction function (Van der Laan et al. 2007).
Note that all risk predictions for paroled individuals are generated and evaluated using validation set (hold-out set) data. That is, the predictions for each paroled individual are generated from a Super Learner model that excluded that individual as a data point when being trained. For individuals denied parole, the risk predictions are generated from a Super Learner model fit on the full population of paroled individuals.
The Super Learner stacking ensemble involves the following steps:
-
1.
Select a v-fold split of the training data, randomly splitting the data into v groups (10 is a common choice). One fold is used as the validation set and the remaining (v − 1) are used as the training set. The process is repeated until each unique set has been used as the validation set (“Appendix1”, Fig. 13).
-
2.
For each fold in \(v = {1,\ldots , 10}\)
-
(a)
Select m base models or algorithms and fit each on observations in the training set. The algorithms can be any number of parametric models or non-parametric algorithms (e.g. OLS, Logistic Regression, Random Forest, LASSO, etc).
-
(b)
For each algorithm, use its estimated fit to predict the outcome for each observation in the validation set and assess model performance (e.g. minimizing mean squared error (\(L_2\) loss) between the observed outcomes in the validation set and the predicted outcomes based on the algorithms’ fit on the training set.)
-
(a)
-
3.
Average the loss (e.g. mean squared error) across the folds to obtain a single estimate of performance for each algorithm.
-
4.
Use non-negative least squares to regress the actual outcome on the algorithm predictions (suppressing the intercept and constraining the coefficients to be non-negative and sum to 1) to obtain normalized coefficients or weights for each base model.
-
5.
Use the estimated coefficients to generate the Super Learner, i.e. a weighted (convex) combination of each base algorithm’s predictions. This involves re-fitting the algorithms on the full data and combining the predictions using the weights. e.g.
$$\begin{aligned} \hat{Y}_{SL} = \alpha _{1}\hat{Y}_{RF} + \alpha _{2}\hat{Y}_{LASSO} + \alpha _{3}\hat{Y}_{glm} \end{aligned}$$
Figure 1 from the original paper (Van der Laan et al. 2007) summarizes this process.
Finally, an addition layer of cross-validation is often applied so as to evaluate the performance of Super Learner itself and ensure against over-fitting. This “CV Super Learner” involves first partitioning the data into v folds and then running the whole Super Learner algorithm process (outlined above) to generate hold-out predictions from the Super Learner for each fold.
We implement CV Super Learner with 10-fold cross-validation. Thus, the data is first separated into 10 outermost folds, so as to fit a separate Super Learner that will be used to generate predictions for each fold when that fold was not used to fit the Super Learner. Second, when fitting a Super Learner on 9/10th of the data, we again separate the data into 10 folds so that the performance of the base algorithms may be evaluated using hold-out set predictions.
Our final Super Learner ensemble includes four algorithms: a simple prediction of the mean, Random Forest classification (Breiman 2001) implemented via ranger (Wright et al. 2020), a LASSO (Tibshirani 1996) via GLM-Net (Hastie and Qian 2014), and a BART (Chipman et al. 2010). Random Forest has been shown to be among the strongest performing classifiers (Fernández 2018), particularly with respect to forecasting criminal justice behavior (Richard and Justin 2014). In brief, Random Forest works by aggregating many hundreds of classification trees, each of which represents a recursive partitioning of the training data. Each classification tree creates binary splits of the data based on a sample of predictor variables, drawn randomly at each partition, and selecting the best split, measured as the split that creates the two most homogeneous or “pure” groups possible with respect to the outcome. The tree is grown, without pruning, until either purity (homogeneity) or node size 1 is reached. Finally, the classification trees are aggregated to create the random forest algorithm, and each observation receives a score based on the proportion of trees that assign it to the positive class. We use the default tuning parameters, growing 1,000 trees and randomly selecting one-third of the predictor variables at each partition.
BART, like Random Forest, is tree-based approach. The BART model consists of two parts: a sum-of-trees model (the sum of a series of sequential non-overlapping small trees fit via a back-fitting algorithm), and a set of priors on the parameters of that model. The aim of the priors is to provide regularization, constraining the size and fit of each tree such that no single tree from dominates the total fit (Chipman et al. 2010; Kapelner and Bleich 2013). We use the default parameters for the number of trees (\(\hbox {n} = 50\)), alpha (\(\alpha =0.95\)), beta (\(\beta =2\)), the prior probability interval (\(k= 3\)), and the error variance (\(q=.90\)).
The GLM-Net algorithm fits a generalized linear model via penalized maximum likelihood. In our case, this is a binomial GLM with a LASSO (L1) penalty term, which constrains the sum of the absolute values of coefficients, shrinking some parameters towards or to zero. This effectively provides feature selection and can improve predictive performance by avoiding over-fitting. We again use the default tuning parameter for alpha (\(\alpha =1\)) and select the regularization parameter through LASSO’s internal 10-fold cross-validation procedure.
We implement model calibration to improve correspondence between the predicted probability and the observed arrest rates for paroled individuals. To do so, we use an ensemble of logistic regression models that fit the observed outcomes on the original, uncalibrated predictions. We use four total candidate logistic regressions, ranging from a simple model of arrest on uncalibrated predictions to a flexible model with a quadratic term. We again use Super Learner to select an optimal level of flexibility and generate hold-out set predictions for paroled individuals. We then use the same model to generate predicted probabilities for the individuals who were not paroled. As the original predictions were fairly well calibrated, the changes in predictions are minor: for the general three-year arrest predictions, the mean of the absolute change is .033, and for the three-year violent arrest predictions, the mean of the absolute change is .012.
Addressing the Selective Labels Problem
Selective labeling complicates the evaluation of an algorithm relative to human decisions because those very decisions are what determined the instances that were ‘labeled’ to begin with, and these cases may not represent a random sample of the full population. If there are unobserved variable(s) (observed by the parole board) that result both in a reduced probability of release and are associated with increased risk, then our risk predictions for the non-paroled will tend to be understated. We address the magnitude of this potential bias in three ways.
First, we use the repeat hearings to conduct a preliminary test for unobservables that dramatically decrease the true probability of release. There are 3642 individuals who had a hearing between 2012 and 2015, were denied parole, and then had a second hearing before the end of 2015. When an individual is denied release, they may be held for up to two years until the next appearance; the default is the full two years. Using the same Super Learner algorithm (and constituent base learners) and variables that we used to train predictive models of arrest, we train predictive models of the parole decision to assess whether predicted probabilities of release correspond with observed rates of release. Details of the Super Learner model predicting release are provided in the “Appendix2”. Intuitively, if unobservables (e.g., aggravating details regarding the commitment offense) are substantially decreasing the probability of parole for inmates that were denied parole, then we should expect the observed parole rate in the second hearing to be lower than the predicted probabilities of release in the first hearing. For example, if we predict that individuals denied parole in their first hearing had an average probability of release of 20%, and in their second hearings only 5% of these individuals are released, that would be strong evidence that unobservables are in fact decreasing the probability of parole.
More formally, let \({P_{ih}}(Parole)\) be the true probability of parole for inmate i in observed hearing h. If there is a selective labels issue, then \({P_{i1}}(Parole)< \hat{P_{i1}}(Parole|X)\): the true probability of release would be lower than the estimated probability of release because the board denies parole on the basis of factors that are unobserved by us. While we cannot observe the true probability of release in the first hearing, we can observe the mean probability of release in the second hearings: \(Parole Rate{_2}\) \(\approx\) \(\dfrac{1}{n}\sum _{i=1}^{n}{P_{i2}}(Parole)\).
In an ideal experiment, we would observe parole outcomes from i.i.d draws: denied inmates would immediately receive a new hearing in front of a new panel, ignorant of the previous panel’s decision. Under those hypothetical conditions, the difference between the mean of the predicted probabilities in the first hearing and the release rate in the second hearing would reveal the degree to which unobservables cause the true probability of release to be lower than estimated. More formally, it would be the case that \({P_{i1}}(Parole) = {P_{i2}}(Parole)\), such that \(\dfrac{1}{n}\sum _{i=1}^{n}{P_{i1}}(Parole) \approx Parole Rate{_2}\). Thus, \(\dfrac{1}{n}\sum _{i=1}^{n}\hat{{P_{i1}}}(Parole)- Parole Rate{_2}\) would approximate the average by which estimates of probability of parole for those denied parole are higher than the true probability of parole.
Of course, we do not have access to the ideal experiment—the second hearings are usually two years later, and thus \({P_{i1}}(Parole)\) is probably not exactly equivalent to \({P_{i2}}(Parole)\). A number of factors could cause the inequality: the Board’s second decision might be influenced by the first decision, the Board itself might change, and an inmate might change between the two hearings.
The first two are unlikely to be significant factors. First, there is little indication that the Board changed. The parole rate increased from only 18–20% from 2012 to 2015, so there does not appear to have been large changes in the Board’s leniency. Second, the treatment effect from a previous denial could plausibly go in either direction: it is possible that the Board in the second hearing defers to the decision in the first hearing, but it is also possible that previous denial fulfills some retributive function that increases an inmate’s chances of being paroled in the second hearing. Regardless, were this to be a significant factor, it supports the general argument that the Board is failing to make risk-based decisions and would suggest the selective labels problem is minimal, as selective labeling is only a problem if there are both unobservables impacting the probability of release among those denied parole and those unobservables are positively associated with risk.
The third concern is more significant. Given the standard two-year lag between hearings, it is possible that inmates became less risky and that the Board was thus more likely to release them. Consider, for example, the worst-case scenario: despite our predictions that the denied inmates had an average probability of release of 20% in the first hearings, they had true probabilities of release of 0%. Then, by the time of their subsequent hearings, approximately 20% of inmates had become—in the eyes of the Board—ready for parole. Thus, the fact that the release rate in period two is roughly equivalent to the mean predicted probability of release in period one would not show that the selective labels problem is minimal.
While we cannot rule out the possibility of substantial changes to inmates, testing of conditional release rates can provide support for the hypothesis that predicted probabilities of parole for the denied are not seriously inflated. If, as we hypothesize, \(\hat{{P_{i1}}}(Parole)\) \(\approx\) \({P_{i1}}(Parole)\) \(\approx\) \({P_{i2}}(Parole)\), then \(\hat{{P_{i1}}}(Parole)\) should approximate the observed parole rate in period two, both on average and across the distribution of estimated parole probabilities. That is, parole rates in period two, when conditioned on estimated probabilities of parole in period one, should approximate the conditioned on estimated probabilities of parole. If, instead, there had been significant changes in the true probability of parole between hearings, there would be little reason to expect such conditional approximations.
This first approach to the selective labels problem assesses only whether there are unobservables impacting the probability of release among those denied parole; for selective labels to bias our risk predictions, these unobservables must also be positively associated with risk. Our second and third approach assess this possibility. The second approach tests the accuracy of the algorithm for individuals who were denied parole by the Board, but were eventually released from prison after serving their maximum sentence (and for whom we have three years follow-up). The third approach, with one year follow-up, assesses the accuracy of the algorithm for individuals who were granted parole in 2017. The rate of release had increased in 2017 from an average of 20% (2012-2015) to 31%, suggesting a significant number of individuals released in this period would likely have been denied parole in the earlier period. Based on observable characteristics, this large shift in release rates does not appear to be due to changes in the eligible prison population. It has been hypothesized that the increase in the release rate beginning in 2017 was potentially related to political pressures following negative media attention in 2016, and Governor Cuomo’s appointment of six new, more racially and professionally diverse, parole commissioners in June 2017 (“New York State Parole Board: Failures in Staffing and Performance” 2018). Additionally, in that year, Cuomo decided not to reappoint three commissioners whose terms were expiring.
Estimating Welfare Losses
To estimate the welfare losses of the Board’s decision-making, we rank-order all inmates by the algorithm’s risk predictions and estimate the crime savings that could be had with the same rate of release, and the increased rate of release that could be achieved keeping arrest rates constant. We estimate arrest rates using the observed outcomes for those who were released on parole, and the mean of the risk probabilities among the hypothetically released. To calculate the release rate holding arrest rates constant, we search over a series of weighted combinations of the total and violent arrest predictions and possible release rates, calculating the estimated total and violent felony arrest rate, until we find the combination of weights and release rates that yield the highest release rates without going over historical total and violent arrest rates.
Because we find some evidence of downward biased risk predictions due to selective labels, we present a range of conservative estimates assuming that our risk predictions are artificially low for the selectively unlabeled population. We estimate the welfare gains that could be achieved if counterfactual arrest rates were up to 100% higher than predicted.
Evaluating Racial Disparities
Finally, we evaluate the Board’s decision-making with respect to race. Racial disparities in rates of prison release are not, in and of themselves, an indication of racial discrimination, as there may be factors that can appropriately influence the release decision that also correlate with race. Estimating racial discrimination is empirically challenging. A simple regression approach is susceptible to the criticism that any estimated “effect” of race might actually be explained by unobserved variables that are omitted from the regression and that correlate with race. The outcome test (Gary 1957), an alternative that is not subject to omitted variable bias, looks at the success or failure rates of a decision across groups (e.g. Black vs White rearrest rates among parolees, or Black vs White contraband recovery rates among individuals searched by police), and assumes that if the rates differ across groups, the decision-makers were applying a different standard. Recent work has noted that even if differences in outcomes are noted across races, the test cannot identify whether this was caused by racial bias or instead judges basing their decisions on other race-correlated factors (Hull 2021). The outcome test is also known to suffer from the problem of infra-marginality: even absent racial bias, the rearrest rates might differ if the two groups have different underlying risk distributions (Ayres 2002). The threshold test (Simoiu et al. 2017; Emma 2020) has been proposed as a solution: the test jointly estimates race-specific decision thresholds and risk distributions to identify whether decision-makers are applying different standards to different racial groups. However, insofar as the Board is not making risk-based determinations, it makes little sense to conceptualize the Board as applying a risk-based threshold for any racial group. Thus, we focus our analyses on the effect of the Board’s sub-par decision-making on different races, irrespective of their intentions. We assess existing disparities in parole rates in comparison to the parole rates that would exist if the Board were making more risk-optimal decisions.
Results
Descriptive Statistics
From 2012–2015, 4561 individuals were granted parole; 16,068 individuals were denied one or more times (there were 18,794 denials during this period). Table 1 presents the average number of prior arrests and select commitment offenses among those granted versus those denied parole. Those granted as compared to those denied parole were fairly similar with respect to age and prior criminal history. The racial composition differed more significantly. More White individuals were granted parole (among those released, 37.4% were White; among denials, 31.5% were White) and more Black individuals were denied parole (among those released, 42.8% were Black; among denials, 48.1% were Black).
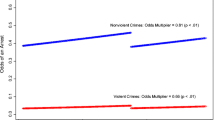
Figure 2 presents the grant rate for White, Black and Hispanic individuals from 2012 to 2018. From 2012–2015, the overall parole release rate was just under 20%. By 2017, the overall release rate had increased to 31%; in 2018, it was up to 44%. In all years, the rate of parole release was higher for White individuals as compared to Black or Hispanic individuals.
Evaluation of the Risk Prediction Algorithm
We begin the evaluation of the risk prediction algorithm with standard model performance metrics. The area under the receiver operating characteristic curve (AUC), a common metric for measuring risk assessment prediction accuracy, is in line or above conventional risk assessment tools. AUC gives the probability that a randomly chosen observations with \(Y = 1\) is ranked higher (i.e. has a higher predicted probability) than a randomly chosen observations with \(Y = 0\). The AUC for the model predicting any arrest is .79; the model predicting violent felony arrest is .72. According to Northpointe, the developers of COMPAS, the consensus in the field of recidivism research is that 0.65–0.69 is fair, 0.70–0.75 are good, and 0.76 and above are excellent (Northpoint 2019).
In addition to discrimination (the ability of a model to rank individuals according to risk), which is measured by AUC, calibration (the agreement between the estimated and the “true” risk of an outcome) is also of importance. That is, we want a group with X% probability of arrest to have an observed arrest rate of X%. Figure 3 shows the distributions of predictions for paroled inmates on the bottom panels; the top panels show the predicted probabilities of arrest against observed arrests with the calibration curve fitted as a generalized additive model (GAM). For ease of visualization, we exclude the highest 2% of predicted probabilities, as these outliers generate patterns with extremely wide confidence intervals. The predictions are well calibrated for both any and violent arrests, largely tracking the 45 degree line.
Figure 4 presents the the distribution of risk predictions for any arrest and violent felony arrest for individuals who were both released and denied parole (2012–2015). The risk predictions of those denied parole and those released on parole are quite similar, which suggests, if our risk predictions are even reasonably accurate, that the parole board is far from making risk-optimal decisions. There are many low risk inmates being denied parole. Conversely, high risk inmates are being granted parole.
Figure 5 shows the relationship between predicted risk and the predicted probability of parole (also generated via Super Learner). This conveys the same story: there is only a weak relationship between arrest predictions and the predicted probability of parole. While the predicted probability of parole decreases as the predicted probability of arrest goes up, the weakness of the relationship suggests that the Board is still denying parole to many low-risk people and granting parole to many high-risk people.
The key question is the extent to which the risk predictions are in fact accurate with respect to the full population (i.e. not just those who were granted parole). We now turn to estimating the magnitude of the selective labels problem.
Evidence that the Selective Labels Problem is not Severe
As noted above, we address the extent of the selective labels problem in three ways. First, we present evidence from repeat hearings on the magnitude of any unobserved variable(s) that might impact the probability of release. This does not, however, speak to the question of whether there is an unobserved Z that reduces the probability of release and is associated with increased risk. The second and third approach provide evidence on this later question, using , respectively, (a) outcomes for individuals denied parole but released at the expiration of their maximum sentence and (b) outcomes for individuals released in 2017, when there was a plausibly exogenous increase in the release rate such that individuals who might have previously been denied parole were released.
Preliminary Evidence from Repeat Hearings
The average release rate in second hearings (24%) is slightly higher than the average of the lagged predicted probabilities of parole (20%). This provides initial evidence that there are not unobservables reducing the probability of release for denied individuals. In expectation, denied individuals cannot have a true probability of release that exceeds their predicted probabilities, thus, this suggests that there has been some increase in true probabilities between hearings. Part of the increase is likely explained by the Board’s increasing leniency over time, as the overall parole rate increased from 18 to 20% from 2012 to 2015. The Board might also be treating the previous denial as a punishment that partially satisfies retributive goals, thus leading to higher parole rates in the second hearing.
While the fact that parole rates in second hearings are not lower than the mean predicted probability of parole in the first hearing is evidence against substantial, time-invariant unobservables that reduce the true probability of release, it may be true that changes to inmates between their hearings are keeping \(ParoleRate_2\) from being lower than \(\dfrac{1}{n}\sum _{i=1}^{n}{P_{i1}}(Parole)\). If true probabilities significantly increased between hearings, then unobservables could be depressing the probability of release in the first hearing, despite the fact that release rates in the second hearings are not lower than the average of predicted probabilities in the first.
Figure 6 suggests this story is unlikely. Probabilities of parole in the first hearing efficiently predict parole rates in the second hearing. If changes in inmates were responsible for the predictive power, those parole-increasing changes would have to have occurred in rough proportion to the predicted probabilities of parole in the first hearing. At the very least, the results rule out severe selective labeling. Were true probabilities of parole in the first hearing zero or close to zero, there would be absolutely no reason to expect that predicted probabilities of parole in the first hearings—which would contain little to no information regarding the true probabilities of parole—would so powerfully predict release rates in the second hearings.
In summary, the evidence from repeat hearings largely supports the inference that there are not unobservables that are dramatically reducing the true probability or release. Moreover, as noted above, for selective labels to bias our risk predictions downward, there must not only be unobservables that decrease the probability of release for denied individuals, but those unobservables must also be positively associated with risk. Next, we use arrest outcomes of those who were denied parole but released upon sentence expiration to test the composite role of unobservables (as well as any bias due to sample selection on observables).
Evidence from Arrest Rates of Individuals Denied Parole and Released Upon Sentence Expiration
We evaluate whether predictions generated from the model built on paroled individuals are accurate with respect to individuals who were never granted parole but for whom we get to observe outcomes because they were eventually released after the expiration of their maximum sentence. We restrict our attention to unique individuals for whom we have at least three years of post-release follow up (n = 6784).
Figure 7 presents the distribution of risk predictions, model calibration (predicted probabilities of any and violent arrest against observed arrests), and validation-set AUC. We find the model performs almost as well at ordering risk (discrimination) as it did on the paroled population: the AUC is slightly lower, but still in the range of what is considered “good” in recidivism research. The model is also well-calibrated for any arrest within three years. For violent felony arrests within three years, observed rates of violent arrest are systematically, though not dramatically, higher than predicted, particularly among the higher risk.
In sum, the validation suggests the predictive model does not underestimate the risk of any arrest but that it slightly underestimates risk of violent arrest. The difference between the average predicted probabilities of violent arrest and the observed rate of violent arrest is 2.7 percentage points. Overall, we predicted a violent arrest rate of 9% but observed a violent arrest rate of 11.7%, indicating that true risk is 30% higher than predicted.
It is possible that this understates the selective labels problem. Specifically, it is possible that an inmate’s risk level is higher when their parole is denied, with risk declining as they serve the remainder of their sentence (e.g. because they age) such that they would be lower risk when released. If so, we might unfairly criticize the Board for denying release to individuals who only later became lower risk. However, this does not appear to be the case. The typical interval between an inmate’s last hearing and their release upon expiration of their sentence is fairly short (both the mean and median are approximately nine months), mitigating concerns that risk on the date of the hearing is substantially different from risk at the time of release. In our evaluation of the Board, we assume that the true counterfactual arrest rates are up to 100% higher than predicted. Larger divergences between truth and predictions would require what we think are implausibly large changes in risk over short periods of time. If true risk were 100% higher, then the inmates analyzed here would have had a true counterfactual violent arrest rate of 18% at the time of denial. It is doubtful that an additional nine months in prison could reduce that risk from 18% to 11.7%, particularly given the average age of those individuals being denied and then released upon the expiration of their sentence is 38, well beyond the peak and steep decline of the “age-crime curve.” Further, the broader literature is uncertain as to whether additional prison time has any effect on re-offending, especially among those sentenced for serious offenses (who are thus older and on the flatter part of the general age-crime curve when released). Indeed, there is some evidence that time in prison increases risk (Berger and Scheidegger 2021).
Furthermore, we test for, and fail to find, a negative relationship between arrest and waiting interval. If anything, the evidence suggests that the probability of an arrest actually increases with the time between an inmate’s last hearing and release upon completion of their sentence: an extra year of time in prison is associated with a 5% increase in overall arrest rate, though we see no association for violent arrest. In summary, the analysis of individuals released upon sentence expiration indicates that is conservative to assume that the true counterfactual arrest rate is up to 100% higher than our predictions.
Evidence from a Plausibly Exogenous Increase in the Parole Rate
Finally, we evaluate the accuracy of our risk predictions for individuals who were released in 2017, when the rate of release increased by approximately 50% compared to the period in which our model was built, from 20 to 31%. This increase does not appear to have been related to changes in inmates characteristics. Among individuals with hearings in 2016 and 2017, the standardized mean difference (SDM), a common metric used to test for covariate balance in matching studies, does not exceed a threshold of 0.10 for any of the coviarates included in the model. SDMs close to zero indicate good balance and current practice suggests .1 is an appropriate conservative upper limit (Stuart et al. 2013; Zhang 2019). Additional details are provided in the “Appendix3”.
Our model performs fairly well with respect to discrimination: we have an AUC of .74. With respect to calibration, we find the observed arrest rate for 2017 parolees largely matches the predictions, indicating that predictions based on paroled individuals are generally well calibrated for the wider population of inmates. As shown in Fig. 8, we do underestimate risk of any arrest. We predicted an arrest rate of 15% and observed an arrest rate of 17.6%, approximately 17.3% higher than predicted. But that figure likely understates the severity of the selective labels problem. If we assume that the discrepancy is due solely to the additional parolees in 2017, then the discrepancy is driven by about 35% of the total paroled population in 2017. For that subgroup to have generated the discrepancy among the total paroled population, the observed rate for that subgroup would have to have been approximately 50% higher than predicted.
We do not have sufficient data to assess observed versus predicted probabilities across the distribution for violent felony arrest within one year. But we can compare the predicted mean to the observed rate. The average predictions of 3% matches the observed violent felony arrest rate, suggesting that there is no selective labels problem with respect to violent arrests.
Estimating Welfare Losses
We estimate the potential welfare losses due to the Board’s sub-optimal decision-making. We do this in two ways. First, we estimate how low the arrest rates could be if the Board released the same number of individuals, but only the lowest risk individuals. Second, we estimate how many more people could be released, holding the arrest rate constant. We present results using observed parole release and arrest rates for 2015. We also present results for 2018. For 2018, we use the observed release rates, but compare counterfactual release decisions to predicted arrest rates based on the model because we do not have complete follow-up.
The evidence presented above suggests that the selective labels problem is not severe, but there is some evidence that the non-paroled are riskier than their observables would suggest. Our first test revealed no evidence of selective labeling. Our second test did not reveal selective labeling with respect to arrest generally, but it indicated that the true violent risk for the non-paroled is 30% higher than predicted. And while our third test did not reveal selective labeling with respect to violent risk, it indicated that the true risk of any arrest is 50% higher than predicted. We thus generate a wide range of estimates of crime and prison savings assuming that our risk predictions are artificially low for the selectively unlabeled population. We present estimates under a range of assumptions: from the assumption that counterfactual arrest rates are accurately estimated by risk predictions to the assumption that counterfactual arrest rates are 100% higher than predicted.
Figure 9 presents the estimated arrest rates holding the 2015 parole release rate constant. The left hand side shows results minimizing any arrest; the right hand side shows results minimizing violent arrest. In both cases, we find that with the same rate of release, the Board could obtain a substantially lower violent felony arrest rate and total arrest rate. For example, minimizing the violent arrest rate and assuming the risk predictions are accurate, we estimate the three year total rearrest rate could have been as low as 10% (vs 33% observed) and the three year violent felony arrest rate could have been as low as 2% (vs 6% observed). If we assume the predictions are 100% higher than estimated, we estimate that the total arrest rate could have been 17% (vs 33%) and that the violent felony arrest rate could have been reduced to 3% (vs 6%).
In the “Appendix4” we also present the above data on violent arrest in terms of the parole board “error rate.” Assuming the goal is to minimize violent arrests and that predictions for the selectively unlabeled are 100% higher than estimated, our estimates suggest that 62% of the individuals paroled by the board could have been replaced by lower risk individuals.
Figure 10 presents the possible prison release rates ensuring neither the total arrest rate or the violent felony arrest rate are higher than observed. If the risk predictions are accurate, we estimate the release rate could have been three times higher than observed (80% vs 20%). Assuming the risk predictions are 100% higher than estimated, we estimate that the parole release rate could have more than doubled (from 20% to 49%).
By 2018, the Board had increased the rate of prison release rate from 20% to 43%; however, we still find risk-based decisions could have reduced arrest rates (holding constant release rates) or increased the number of individuals released from prison (holding crime rates constant). This is shown in Figs. 11 and 12. If the risk predictions are accurate, we estimate that the release rate could have almost doubled without increasing either the total or violent felony arrest rate; if the true risk is twice as high as the estimated risk, the release rate could still have been almost 50% higher than it was in 2018 (estimates for both 2015 and 2018 are comparable when we exclude race from the predictive model).
While we have shown that different decisions could have reduced the overall and violent arrest rate (or allow for the release of more people while holding the arrest rate constant), there remains the possibility that perhaps the Board was justifiably focused on minimizing especially high cost crimes, such as murder, and we have not sufficiently distinguished between the degree of harm associated with different arrest types. While it appears they are not attending to individual criminal risk, perhaps they are succeeding in the effort to release people that are at low risk of arrest for murder?
While murder is sufficiently rare to permit a detailed analysis, the evidence suggests that they are failing to efficiently reduce murder arrests. There were 21 arrests for murder among the 4,168 paroled individuals in our data set. Holding the number of people released constant, and drawing only from individuals with the lowest predicted probabilities of violent arrest whose arrest records are observed (those paroled and released on sentence expiration), there would have been only 14 arrests for murder, a 33% reduction. We expect that number would fall much further if we also drew from the large population of low-risk individuals who remained in prison.
Racial Equity
As noted above, current statistical tests of racial discrimination (i.e. the outcome test and threshold test) assume that decision-makers are making risk-based determinations. The threshold test, designed to overcome the infra-marginality problem of the outcome test, estimates the threshold or standard above which the decision-maker will release inmates (or stop and search an individual, in the police context). But, as our results have shown, the New York State Board of Parole is making determinations that are largely divorced from risk. Thus, using the threshold test makes little sense in our setting. We therefore assess existing disparities in parole rates in comparison to the parole rates that would exist if the Board were making more risk-optimal decisions.
For both 2015 and 2018, holding the total and violent arrest rates constant, we find that the Board could have completely eliminated racial disparities in release rates while still increasing release rates by essentially the same fraction (within 1%) of the unconstrained optimal release rates presented in the section above.
In sum, our findings indicate that, were the Board to make risk optimal decisions, it could simultaneously eliminate racial disparities, increase the number of individuals released from prison, and maintain existing arrest rates.
Discussion
Discretionary prison release can serve as a critical tool for achieving “decarceration” after decades of prison expansion (Rhine et al. 2017), yet modern parole boards have been criticized for unnecessarily detaining low risk inmates, making purely punitive determinations that individuals have not served sufficient time. We find the New York Parole Board has been largely failing to release individuals on the basis of risk, resulting in the incarceration of many low-risk individuals and the release of high-risk individuals.
Importantly, we find that they could have achieved dramatic prison reductions while simultaneously eliminating racial disparities in release rates. This is similar to other recent work that has found there are no efficiency costs associated with eliminating racial disparities in motor vehicle searches (Feigenberg and Miller 2022).
We cannot determine whether the Board is simply not as good at determining risk as our risk prediction algorithm or is simply prioritizing factors other than risk, such as retribution for the commitment offense. However, our findings are consistent with the Vera Institute of Justice report finding that the Board denies parole to many individuals with low-risk COMPAS scores (Heller 2021), and the common complaint that the Board is driven by retributive impulses, risk aversion, and fear of the political repercussions that they might face were they to release an individual convicted of murder, for example, who went on to be arrested for murder again (Reitz and Rhine 2020).
While exploring the nature of the Board’s failure to make risk-optimal decisions is necessarily speculative, some very basic statistics examining the relationship between observed predictor variables and subsequent arrests are highly suggestive. We use the outcome test on all of the predictor variables, results of which are presented in Appendix 6. The exercise can be insightful despite the well-known infra-marginality limitation of the outcome test: large differences in arrest rates are unlikely to be explained by differences in underlying risk distributions, and it is useful to know which groups are subject to differential decision-making even if we cannot be sure of the cause. Looking at the two most common commitment offenses, second-degree murder and third-degree burglary, we find a commitment for second degree murder is associated with a violent arrest rate that is six percentage points lower than the broader paroled population, while a commitment for third-degree burglary is associated with a violent arrest rate that is four percentage points higher. The differential treatment between these two groups is substantial: only about 1% of those committed for second degree murder are rearrested for a violent offense after release, as compared to almost 12% of those committed for third-degree burglary. This suggests that the Board is either pursuing retribution or protecting themselves against political backlash. The results on other variables largely support that interpretation: the highly “offensive” crimes (e.g., first-degree robbery, any murder offense, manslaughter, sexual offenses, offenses with no maximum sentence) are associated with low rearrest rates, and the less “offensive” crimes (third-degree robbery, criminal possession of stolen property, offenses with low maximum sentences) are associated with higher arrest rates.
Overall, these results suggest that the Board is at least partially pursuing retribution and/or insulating themselves from political fallout; however, it might also be the case that the Board is simply not capable of accurately assessing risk with its current tools. Insofar as that is true, our results suggest that an algorithmic or actuarial risk assessment approach is a promising one, particularly with respect to identifying the many low risk individuals who could be safely released (Reitz 2020). At a minimum, consistent with a recent burgeoning interest in using algorithms to evaluate the law (Doyle 2021), our analyses point to the utility of algorithms in evaluating decision-making in the criminal justice system. Even if political or ethical considerations prevent the adoption of algorithmic decision aids, the gap between the status quo and the possibilities identified by our algorithm show that the Board is far from making risk-optimal decisions. If the goal is to release individuals on the basis of risk, there is substantial room for improvement, and there are likely alternative reforms that could promote the identification and release of the many low-risk individuals who remain in prison.
More radically, given the costs of maintaining a parole system and the ineffectiveness of current decisions with regard to inmate risk, our results raise the question as to whether the parole system is worth maintaining. A number of states have moved away from indeterminate sentencing and discretionary parole release. If the prison sentence were set at the minimum sentence length of current indeterminate sentences, this would clearly reduce incarceration rates. If our predictions are unbiased, the cost in terms of increased arrest rates would be minimal. Between 2012 and 2015, the average three-year rearrest rate for inmates released in a year was 31%, with an average three-year violent arrest rate of 6.9%. If the Board had simply released everyone, we predict a 35% overall arrest rate and an 8% violent arrest rate.
In addition to contributing to the literature on algorithms as a tool for evaluating decisions, our findings also have implications for the literature on racial bias. The threshold test (Simoiu et al. 2017) promises to mitigate the infra-marginality problem by combining information on both decision rates and outcome rates to infer group-specific risk distributions and decision thresholds. If decision thresholds differ by race, it is evidence of discrimination. However, the assumption that criminal risk is the sole or even primary decision factor may not be plausible, and it therefore makes little sense to estimate a decision threshold. At least in the parole context, our findings suggest that criminal risk plays a relatively minor role in decision-making. Recent research on racial disparities in NYPD stop and frisk practices similarly indicates that officers are only marginally responsive to, or not good at assessing, risk (Goel et al. 2016). The authors find that in 43% of criminal possession of a weapon stops, the probability of recovery of a weapon was less than 1%; were officers to make only the highest ex ante hit rate stops, they could conduct only 6% of stops and recover 50% of weapons.
While standard statistical tests of racial bias may not apply in contexts where risk does not appear to be the central consideration, we can still demonstrate that the absence of risk-based decision-making has important racial equity implications. Our analyses shows that the Board could eliminate racial disparities in release rates and achieve significant prison reductions without impacting total or violent felony arrest rates.
Finally, our study also contributes an alternative approach to the assessing selective labeling. The contraction approach that has been used to date requires the identity of the decision-maker. It is also limited in that it only validates the algorithm on the population released by the most lenient decision-maker, but not the full population or the highest risk population. In testing the validity of the algorithm for individuals who had hearings and were denied parole but were later released after the expiration of their sentence, we are able to assess its accuracy on a low-probability-of-release population where you would expect the selective labels problem to be most severe.
There continue to be efforts to encourage the New York State Parole Board to focus on inmate risk. In 2016, regulations were passed that required written explanation when a parole denial departed from the COMPAS risk scores (Benjamin 2016; New York Codes, rules and regulations 2020), and, more recently, proposed legislation would shift the default position such that the Board would release “any incarcerated person appearing before the board who is eligible for release on parole, unless the parole case record demonstrates there is a current and unreasonable risk the person will violate the law if released and such risk cannot be mitigated by parole supervision” (NY state Senate Bill S1415A 2021). The proposed legislation would also remove portions of existing statute including the criteria that release is warranted so long as it is not “incompatible with the welfare of society and will not so deprecate the seriousness of his crime as to undermine respect for law.” Our analysis lends support for the urgency of such reforms, at least insofar as risk is the central concern.
Change history
01 February 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10940-023-09568-x
References
Ayres I (2002) Outcome tests of racial disparities in police practices. Justice Res Policy 4.1–2:131–142
Benjamin J (2016) Newly proposed parole regulations. In: Communities. https://www.nysba.org. Accessed 5 Dec 2022
Berger E, Scheidegger K (2021) Sentence length and recidivism: a review of the research. SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3848025. Accessed 5 Dec 2022
Berk R, Heidari H et al (2021) Fairness in criminal justice risk assessments: the state of the art. Sociol Methods Res 50.1:3–44
Blumstein A (1993) Racial disproportionality of US prison populations revisited. Univ Colo Law Rev 64:743
Breiman L (2001) Random forests. Mach Learn 45.1:5–32
Burgess EW (1928) Factors determining success or failure on parole. In: Bruce A, Burgess E, Harno A (eds) The workings of the indeterminate sentence law and the parole system in Illinois. Springfield, IL.: Illinois State Board of Parole, pp 221–234
Chipman HA, George EI, McCulloch RE (2010) BART: Bayesian additive regression trees. Ann Appl Stat 4.1:266–298
D’Alessio SJ, Stolzenberg L (2003) Race and the probability of arrest. Soc Forces 81.4:1381–1397
De-Arteaga M, Dubrawski A, Chouldechova A (2018) Learning under selective labels in the presence of expert consistency. arXiv preprint arXiv:1807.00905
Doyle C (2021) How algorithms expose the law. SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3894617. Accessed 5 Dec 2022
Dressel J, Farid H (2018) The accuracy, fairness, and limits of predicting recidivism. Sci Adv 4.1:eaao5580
Emma P et al (2020) A large-scale analysis of racial disparities in police stops across the United States. Nat Hum Behav 4.7:736–745
Feigenberg B, Miller C (2022) Would eliminating racial disparities in motor vehicle searches have efficiency costs? Q J Econ 137.1:49–113
Fernández A et al (2018) Learning from imbalanced data sets, vol 10. Springer, New York
Gary SB (1957) The economics of discrimination. Am Cathol Sociol Rev 18:276
Geller A, Fagan J (2010) Pot as pretext: marijuana, race, and the new disorder in New York City street policing. J Empir Leg Stud 7.4:591–633
Gillis TB (2020) False dreams of algorithmic fairness: the case of credit pricing. SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3571266. Accessed Jan 2021
Goel S, Rao JM, Shroff R (2016) Precinct or prejudice? Understanding racial disparities in New York City’s stop-and-frisk policy. Ann Appl Stat 10.1:365–394
Hastie T, Qian J (2014) Glmnet vignette, pp 1–30. https://hastie.su.domains/glmnet/glmnet_beta.html. Accessed 9 June 2016
Heller B et al (2021) Toward a fairer parole process. https://www.vera.org/publications/toward-a-fairer-parole-process. Accessed 5 Dec 2022
Hellman D (2020) Measuring algorithmic fairness. Va Law Rev 106.4:811–866
Huang J et al (2006) Correcting sample selection bias Byun labeled data. Adv Neural Inf Process Syst 19:601–608
Hull P (2021) What marginal outcome tests can tell us about racially biased decision-making. Technical report, National Bureau of Economic Research
Huq AZ (2018) Racial equity in algorithmic criminal justice. Duke LJ 68:1043
Johnson R, Raphael S (2012) How much crime reduction does the marginal prisoner buy? J Law Econ 55.2:275–310
Jung J, Goel S, Skeem J et al (2020) The limits of human predictions of recidivism. Sci Adv 6.7:1
Kapelner A, Bleich J (2013) Machine: machine learning with Bayesian additive regression trees. arXiv:1312.2171
Kleinberg J, Lakkaraju H et al (2018) Human decisions and machine predictions. Q J Econ 133.1:237–293
Kleinberg J, Ludwig J et al (2018) Algorithmic fairness. AEA Pap Proc 108:22–27
Lakkaraju H et al (2017) The selective labels problem: evaluating algorithmic pre-dictions in the presence of unobservables. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pp 275–284
Ludwig J, Mullainathan S (2021) Fragile algorithms and fallible decision-makers: lessons from the justice system. Technical report, National Bureau of Economic Research
Mauer M (2018) Long-term sentences: time to reconsider the scale of punishment. UMKC Law Rev 87:113
Mayson SG (2018) Bias in, bias out. Yale Law J 128:2218
McElhattan D (2022) Punitive ambiguity: state-level criminal record data quality in the era of widespread background screening. Punishm Soc 24(3):367–386
Monahan J, Skeem J (2013) Risk redux: the resurgence of risk assessment in criminal sanctioning. Fed Sentenc Rep 26:158
New York Codes, Rules and Regulations (2020) 8002.2 Parole release decision-making. https://casetext.com/regulation/new-york-codes-rules-and-regulations/title-9-executive-department/subtitle-cc-division-of-parole/part-8002-parole-release/section-80022-parole-release-decision-making
New York consolidated laws, executive law—exc x 259-i: Findlaw (n.d.). https://perma.cc/87RA-2BQY
New York Consolidated Laws, Penal Law - PEN § 70.02 https://codes.findlaw.com/ny/penal-law/pen-sect-70-02.html
New York State Parole Board Data (2014). https://datahub.io/dataset/nys-parole-board-data
New York State Parole Board: Failures in Staffing and Performance (2018) In: Parole preparation project 8. https://ir.lawnet.fordham.edu/pp/9
New York Times Editorial Board (2014). New York’s broken parole system. https://www.nytimes.com/2014/02/17/opinion/new-yorks-broken-parole-system.html
Northpoint (2019) Practitioner’s guide to COMPAS Core. http://www.equivant.com/wp-content/uploads/Practitioners-Guide-to-COMPAS-Core-040419.pdf
NY state Senate Bill S1415A (2021) https://www.nysenate.gov/legislation/bills/2021/S1415
Nyarko J, Goel S, Sommers R (2021) Breaking taboos in fair machine learning: an experimental study. In: Equity and access in algorithms, mechanisms, and optimization, pp 1–11
Raphael S, Stoll MA (2013) Why are so many Americans in prison? Russell Sage Foundation, New York
Reitz KR (2020) The compelling case for low-violence-risk preclusion in American prison policy. Behav Sci Law 38.3:207–217
Reitz KR, Rhine EE (2020) Parole release and supervision: critical drivers of American prison policy. Ann Rev Criminol 3:281–298
Rhine EE, Petersilia J, Reitz KR (2017) The future of parole release. Crime Justice 46.1:279–338
Richard B (2017) An impact assessment of machine learning risk forecasts on parole board decisions and recidivism. J Exp Criminol 13.2:193–216
Richard B, Justin B (2014) Forecasts of violence to inform sentencing decisions. J Quant Criminol 30.1:79–96
Schwartzapfel B (2015) How parole boards keep prisoners in the dark and behind bars. The Washington Post. https://www.washingtonpost.com/national/the-power-and-politics-of-parole-boards/2015/07/10/49c1844e-1f71-11e5-84d5-eb37ee8eaa61_story.html
Simoiu C, Corbett-Davies S, Goel S (2017) The problem of infra-marginality in outcome tests for discrimination. Ann Appl Stat 11.3:1193–1216
Skeem JL, Lowenkamp CT (2016) Risk, race, and recidivism: predictive bias and disparate impact. Criminology 54.4:680–712
Skeem J, Lowenkamp C (2020) Using algorithms to address trade-offs inherent in predicting recidivism. Behav Sci Law 38.3:259–278
Slobogin C (2021) Just algorithms: using science to reduce incarceration and inform a jurisprudence of risk. Cambridge University Press, Cambridge
Stevenson MT, Doleac JL (2021) Algorithmic risk assessment in the hands of humans. SSRN 3489440
Stuart EA, Lee BK, Leacy FP (2013) Prognostic score-based balance measures can be a useful diagnostic for propensity score methods in comparative effectiveness research. J Clin Epidemiol 66.8:S84–S90
Task Force on the Parole System (2019) Report of the New York state bar association task force on the parole system. https://nysba.org/app/uploads/2019/12/NYSBA-Task-Force-on-the-Parole-System-Final-Report.pdf
Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Ser B (Methodol) 58.1:267–288
Van der Laan MJ, Polley EC, Hubbard AE (2007) Super learner. In: Statistical applications in genetics and molecular biology, vol 6, p 1
Walker J (2013) State parole boards use software to decide which inmates to release. Wall Street Journal, 11
Winerip M, Schwirtz M, Gebeloff R (2016) For blacks facing parole in New York state, signs of a broken system. The New York Times, 4
Wright MN, Wager S, Probst P (2020) Ranger: a fast implementation of random forests. In: R package version 0.12 1
Zadrozny B (2004) Learning and evaluating classifiers under sample selection bias. In: Proceedings of the twenty-first international conference on machine learning, p 114
Zhang Z et al (2019) Balance diagnostics after propensity score matching. Annals of translational medicine, 7(1).
Acknowledgment
These data are provided by the New York State Division of Criminal Justice Services (DCJS). The opinions, findings, and conclusions expressed in this publication are those of the authors and not those of DCJS. Neither New York State nor DCJS assumes liability for its contents or use thereof.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Acknowledgment has been included in the article.
Appendices
Appendix 1: Super Learner
Super Learner relies on v-fold cross-validation. This is a sample splitting technique to assess model performance using data drawn from the same distribution. The process of v-fold cross validation involves partitioning the data in v sets of size n/v. For a given fold, one set us used as the validation and the remaining \(v - 1\) are used to construct the candidate estimators. As shown in Fig. 13, the validate set rorates v times such that each set is used as the validation set once.
The Tables 2 and 3 present the cross-validated mean squared error of the Super Learner model and the underlying base learners. The Super Learner ensemble included a simple prediction of the mean, Random Forest, implemented via Ranger, the LASSO Regularized Generlaized Linear Models (GLM-Net), and BART.
For the algorithm predicting any arrest within three years, Random Forest (Ranger) received the most weight (.46). GLM-net had an average of .34 and BART had an average of .2. For the algorithm predicting any violent felony arrest within three years, GLM-Net received the most weight, an average of .55; Random Forest received an average weight of .3, and BART an average weight of .15. In neither model did the mean receive weight.
Appendix 2: Predicting the Probability of Parole Release
Using the same Super Learner algorithm (with Random Forest, GLM-Net and the mean) and the same variables that we used to train predictive models of arrest, we train predictive models of the parole decision to assess whether predicted probabilities of release correspond with observed rates of release.
Figure 14 below shows the basic evaluation of the machine learning model predicting the probability of release and the distribution of predicted probabilities (bottom panel). The AUC is .78; the GAM smoothed curve indicates the model is well calibrated. Figure 15 shows the predicted probabilities among the paroled. As we would expect, these individuals have higher probabilities of release than the full population.
Figure 16 shows that an inmate’s predicted probability of release in their first hearing predicts the rate at which they are scheduled for an early hearing providing further evidence that predicted probabilities are good approximations of true probabilities.
Appendix 3: Comparison of Individuals Released in 2017 Versus 2016
Our third test for a selective labels problem relies on the significant increase in the parole release rate in 2017. While we cannot assess whether there were shifts in the unobservable characteristics of those who went before the Board, we can compare them on observable characteristics. The Table 4 presents the standardized mean difference, a common metric used to generate balanced tables in studies employing matching techniques, for a number of variables related to the individuals time in prison, prison type, criminal history, and demographic characteristics. The standardized mean difference (SDM) is calculated as the difference in means of a covariates across the two groups of interest, divided by the standard deviation in the “treated” group. SDMs close to zero indicate good balance. Current practice suggests .1 is an appropriate threshold for assessing imbalance (Zhang 2019). We find none of the measured covariates exceed a threshold of 0.10. Using a more conservative mean difference of .05, we find that only 4 of 136 factor and continuous variables exceed this threshold: the SDM in the number prior murder convictions (− 0.059), prior convictions for A Crimes (− 0.058), prior convictions for kidnapping (.052), and age (− 0.059).
Appendix 4: Board Error Rates
As an alternative means of quantifying the Board’s sub-optimal decision-making, we estimate the error rate of their decisions. To calculate the error rate, we first subset to the X% of individuals with the lowest predicted risk of rearrest for violent crime within three years, where X is the Board’s actual parole rate in a year. We then calculate the percentage of the individuals who were released by the board but should not have been (Fig. 17).
Appendix 5: Background on New York State Parole
New York penal law 70.00 allows the court to sentence individuals convicted of certain crimes to indeterminate sentences, with a minimum and maximum term of imprisonment. Inmates serving indeterminate sentences are entitled to a parole release hearing at least one month before the minimum period of incarceration, or potentially earlier with a merit time reduction of the minimum sentence. If an individual is denied release, they may be held for up to two years until the next Parole Board appearance. Inmates serving indeterminate sentences have a conditional release date equal to one-third off their maximum sentence. During our study period, approximately half of New York State inmates were serving indeterminate sentences.
The New York State Board of Parole consists of up to 19 members appointed by the Governor and confirmed by the Senate for a six-year term. For a given parole release hearing, the typical panel consists of two to three Board members.
Parole commissioners are instructed by Executive Law 259-i to consider a range of factors when determining the release decisions. These include an individual’s institutional record, participation in prison programming, their COMPAS risk score, letters of support, release plans, behavioral record while incarcerated, and victim impact statements. The law stipulates: “Discretionary release on parole shall not be granted merely as a reward for good conduct or efficient performance of duties while confined but after considering if there is a reasonable probability that, if such [person] is released, he will live and remain at liberty without violating the law, and that his release is not incompatible with the welfare of society and will not so deprecate the seriousness of his crime as to undermine respect for law.” (New York Consolidated Laws, executive law - exc §259-i: Findlaw n.d.)
Appendix 6
See Table 5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Laqueur, H.S., Copus, R.W. An Algorithmic Assessment of Parole Decisions. J Quant Criminol 40, 151–188 (2024). https://doi.org/10.1007/s10940-022-09563-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10940-022-09563-8