Prying Open the Black Box of Causality: A Causal Mediation Analysis Test of Procedural Justice Policing

Abstract

Objectives

Review causal mediation analysis as a method for estimating and assessing direct and indirect effects. Re-examine a field experiment with an apparent implementation failure. Test procedural justice theory by examining to which extent procedural justice mediates the impact of contact with the police on police legitimacy and social identity.

Methods

Data from a block-randomised controlled trial of procedural justice policing (the Scottish Community Engagement Trial) were analysed. All constructs were measured using surveys distributed during roadside police checks. Treatment implementation was assessed by analysing the treatment effect’s consistency and heterogeneity. Causal mediation analysis, which can derive the indirect effect even in the presence of a treatment–mediator interaction, was used as a versatile technique of effect decomposition. Sensitivity analysis was carried out to assess the robustness of the mediating role of procedural justice.

Results

First, the treatment effect was fairly consistent and homogeneous, indicating that the treatment’s effect is attributable to the design. Second, there is evidence that procedural justice channels the treatment’s effect towards normative alignment (NIE = − 0.207), duty to obey (NIE = − 0.153), and social identity (NIE = − 0.052), all of which are moderately robust to unmeasured confounding (ρ = 0.3–0.6, LOVE = 0.5–0.7).

Conclusions

The effect’s consistency and homogeneity should be examined in future block-randomised designs. Causal mediation analysis is a versatile tool that can salvage experiments with systematic yet ambiguous treatment effects by allowing researchers to “pry open” the black box of causality. The theoretical propositions of procedural justice policing were supported. Future studies are needed with more discernible causal mediation effects.

Introduction

The majority of tests of cause-and-effect relations in the social sciences address the first order question of whether a treatment affects an outcome, and leave unexplored the underlying processes that transmit the putative effect. The failure to focus on mechanisms limits the power and purchase of explanatory frameworks (Bullock et al. 2010; Imai et al. 2011). Impact evaluations in criminology tend to focus on whether a desired outcome was achieved, not on how that outcome was produced (Famega et al. 2017). For example, a number of randomised controlled trials (RCTs) have tested the efficacy of hot-spots policing (X) (Sherman and Weisburd 1995; Weisburd and Green 1995), but the lack of assessment of how it transmits its effect (at least partially) through an intervening (mediator) variable (M) to the outcome (Y) means that we do not know how and why hot-spots policing works.

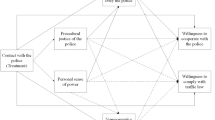
This paper discusses causal mediation analysis as a tool to address this “black-box” view of implementation and causality (Fagan 2017). The contribution of this article is twofold. First, the study uses causal mediation analysis to test a fundamental assumption of the theory of procedural justice policing: namely, that the perceived procedural justice of the police channels the impact of previous contact with the police towards police legitimacy and social identity (for an outline of the models, see Fig. 1). It is particularly important to understand the influence of police–citizen encounters in countries such as the United States and the United Kingdom, which have seen a marked shift in the last couple of decades from reactive to proactive policing tactics (Loader 2014; Tyler et al. 2015; Weisburd and Majmundar 2018). The key tenet of procedural justice policing is that contact with the police is a teachable moment (Tyler et al. 2014) in which fair and respectful treatment by the police can create a reservoir of trust (Weisburd and Majmundar 2018, p. 69). This, in turn, can strengthen identification with the police (Bradford et al. 2014b; Murphy and Cherney 2012) and bolster the perceived legitimacy of the police as an institution (Hough et al. 2013; Huq et al. 2017) ultimately leading to increased cooperation and compliance with the law (Trinkner et al. 2018). Thus, the expectation is that by adopting procedurally just practices police behaviour can meaningfully improve confidence in the police and the law, and lead to prosocial and law-abiding behaviours in communities. Using causal mediation analysis, this paper examines to what extent the perception of procedural justice transmits the impact of previous contact with the police during roadside checks on social identification and police legitimacy.

Fig. 1

Outline of the tested models

As a preliminary to that, this paper also shows how to assess the usefulness of—and extract value from—an RCT that experienced a particular form of implementation failure. The Scottish Community Engagement Trial (ScotCET) (MacQueen and Bradford 2015) was designed to estimate the effect of procedurally just policing on people’s experience of procedural justice. Yet, the RCT produced findings contrary to expectations, in that those who received the designed procedurally just treatment reported experiencing lower average levels of procedural justice compared to the control group. Qualitative process evaluations can address what went wrong during implementation (Haberman 2016; MacQueen and Bradford 2017) but such endeavours are retroactive, only focus on startling cases, and can suffer from verification bias. Problematic datasets with unusual results are also often discarded without proper statistical tests having been carried out on the treatment’s effects. This paper shows how to test whether value can be extracted by focussing on selection bias, treatment effect inconsistency, and treatment effect heterogeneity—that is, by assessing whether the systematic variation in the dataset is attributable to the research design. To foreshadow the results, an assessment of selection bias, treatment effect consistency, and effect homogeneity supports the idea that the unintended negative treatment effect in ScotCET was produced by the treatment assignment, i.e., that value can be extracted from ScotCET.

Second, the paper considers the strong assumptions and limitations of the traditional approach to mediation analysis (the product method, see Baron and Kenny 1986) which has been widely used in observational research, especially in the literature of structural equation modelling, where direct and indirect effects are routinely estimated (Mackinnon 2008; Mackinnon et al. 2013). Some users of this method may be unaware of the strong and often unattainable underlying assumptions for estimating indirect effects, which if not met can lead to unreliable and unsound estimates. The current paper demonstrates how to test causal mediation effects using a technique developed by Imai and colleagues to overcome the limitations of traditional approaches to produce potentially causally interpretable results (Imai et al. 2010a, b, 2011). Notably, causal mediation analysis assumes “no unmeasured confounding”,¹but nonetheless still improves upon the traditional approach to mediation analysis. This approach also includes sensitivity analysis techniques to assess the robustness of results to such unmeasured confounding.

Causal mediation analysis shifts the focus from the total effect of the treatment to the indirect (mediated) effects, hence, experiments with systematic but ambiguous treatments can become interpretable, rendering the initial model of ScotCET testable. Findings from causal mediation analyses seem to support a central prediction of procedural justice theory, i.e., that perceived procedural justice mediates the impact of contact with the police on police legitimacy (with moderate levels of robustness to unmeasured confounding) and social identity (with relatively limited robustness to unmeasured confounding).

Procedural Justice Theory and the Scottish Community Engagement Trial (ScotCET)

Procedural justice theory posits that, when thinking about how the police wield their power and authority, citizens place a good deal of importance on whether officers act—and make decisions—in fair, neutral and respectful ways, and that this process matters more than outcome (Sunshine and Tyler 2003). General perceptions of procedural justice are thought to be influenced by legal socialisation (e.g., Trinkner and Tyler 2016) and direct/vicarious contact with the police (e.g., Bradford 2017; Tyler et al. 2014). Finally, both the experience and perception of procedural justice are thought to influence people’s judgements on the legitimacy of the police as an institution.

Thus far, the evidence base points to the idea that, even in countries as diverse as the US, Australia, Israel, Finland, France, Germany, the UK and China, public concerns about process are more important predictors of police legitimacy than public concerns about effectiveness and fair allocation of outcomes across social groups (Jackson 2018). But as Nagin and Telep (2017) noted, the evidence base is dominated by survey-based studies, limiting our ability to estimate causal effects. There have been a few field and laboratory experiments (Murphy and Tyler 2017), and of particular relevance to the current paper is the Queensland Community Engagement Trial (QCET). QCET found that when officers followed a “procedurally fair” script, citizens tended to view their experience with the police as more procedurally just, and that this experience of procedural justice in turn predicted police legitimacy (Mazerolle et al. 2013).

The current focus is ScotCET, which was designed as a partial replication of QCET. As with QCET, ScotCET tested procedural justice theory in the context of roadside checks, where drivers were stopped by the police for vehicle safety checks and alcohol testing. ScotCET was fielded during the Festive Road Safety Campaign in the December of 2013 and January of 2014 in Scotland, with the design block-randomising ten matched pairs of police units to minimise bias across delivery units. Officers in the treatment group were given a series of talking points, with the aim of communicating procedurally just messages, while officers in the control group carried on with their usual behaviour during these police encounters. After the roadside checks, more than 12,000 questionnaires were handed out to drivers, of which 305 were returned before (122 from the pre-treatment and 183 from the pre-control group), and 510 after the start of the treatment period (176 from the treatment and 334 from the control group). Altogether approximately 6.6% of questionnaires were returned.

I link (a) police behaviour in a police-citizen encounter to (b) the subjective experience of procedural justice in that encounter to (c) broader attitudes towards the legitimacy of the police as an institution (Nagin and Telep 2017). Following Hough et al. (2013) and Huq et al. (2017), legitimacy is defined and measured along two connected dimensions. First, normative alignment with the police reflects the degree to which the police respect the societal norms that determine how authority should be rightfully exercised—the inference here is that normative appropriateness justifies the possession of power. Second, duty to obey encapsulates people’s willing consent to follow police orders—the inference here is that duty to obey reflects the belief that the police are entitled to make decisions, enforce the law, and dictate appropriate behaviour. A key goal of the current study is to assess the extent to which the putative causal effects of police behaviour on normative alignment and duty to obey are transmitted through the experience of procedural justice. Procedural justice is also posited to mediate the causal effect of police behaviour on citizen social identity. According to procedural justice theory, police officers are representatives not only of the state, but of the communities they serve (Bradford 2014), and if the police treat someone fairly, with respect, and provide citizens with a voice, those citizens will strengthen people’s social bonds with that particular community (Murphy and Cherney 2012). Thus, another key goal is to assess to what extent the putative causal effects of police behaviour on social identity are transmitted through the experience of procedural justice.

Before turning to the apparent failure of implementation, I will briefly discuss the measurements used in this paper. There are seven pre-treatment covariates included in all subsequent analyses (unless otherwise noted): age, gender, marital status, educational attainment, employment status, housing, and whether a breath test was conducted by the police during the encounter. Treatment is a binary variable where 0 refers to the control and 1 to the treatment group. Being in the treatment group means that the respondent had a roadside check with members of the police who were instructed to relay procedurally just messages, whilst in the control group the officers were allowed to carry on with their usual behaviour. All subsequent analyses included this treatment variable, only the data from the treatment period are examined (n = 510). Procedural justice, normative alignment, duty to obey, and social identity, were measured using multiple items. They were entered in a confirmatory factor analysis and factors scores were derived for subsequent analysis. For further details regarding the question wording, the confirmatory factor analysis, and the correlation between the different constructs, please refer to “Appendix A”. For further information regarding the survey design please consult the appendices of MacQueen and Bradford (2015).

ScotCET’s Implementation Failure

ScotCET produced the opposite effect to that intended: namely, those who received the treatment reported lower levels of experienced procedural justice compared to the control group (MacQueen and Bradford 2015). In a retroactive qualitative process evaluation, MacQueen and Bradford (2017) conducted nine group interviews with police officers who had taken part in the experiment, revealing a number of issues that may have impacted negatively on the treatment implementation. ScotCET coincided with a period of heightened anxiety among officers due to a substantial and unpopular organisational reform in the Scottish police force. Moreover, the participating officers had not been properly briefed regarding the purpose of the study. They had received opaque instructions, assumed that the experiment would have a negative impact on their interactions with members of the public, and felt that the prompts and questionnaire had been assembled by out-of-touch researchers. The focus groups revealed unanimous signs of discontent and negativity towards the experiment. It is conceivable this had a diffuse negative effect on the officers’ attitudes and behaviour during encounters in the treatment groups, which may explain (at least partially) the contradictory findings (MacQueen and Bradford 2017).

Despite the apparent failure of implementation mentioned earlier, MacQueen and Bradford (2017) insisted that the treatment effect was still interpretable due to the robustness of the study design. In other words, they argued that the treatment and its effects were real, even if both were different in nature from the intentions and expectations of the researchers. MacQueen and Bradford’s (2017) claim was mainly based on three considerations. First, there was no selection bias in the original study, where they showed that there was no difference between the control and treatment groups in pre-treatment covariates, either before or during the treatment period (i.e., the randomisation appeared to be successful). Second, the implementation of the treatment did not have an impact on the share of responses in the treatment group (i.e., there was no change in the number of responses received compared to the pre-treatment period, or compared to the control group in the post-treatment period). This would suggest that the overall low response rate of 6.6% does not have an impact on the internal validity of the results, as long as the same kind and proportion of people decide to self-select in the study for both the treatment and control group. Finally, the views regarding the police were on average the same in the control and treatment groups before the treatment period, and they only started to diverge after the treatment implementation (i.e., controlling for all else, the changes can be only attributed to the treatment) (MacQueen and Bradford 2015). Crucially, the second and third considerations constitute direct assessments of the potential nonresponse biases that could emerge in post-intervention surveys due to the treatment potentially affecting the propensity and the kind of participants opting in to the study (Antrobus et al. 2013), and find no signs of either selection bias or the changes in the share of responses in the treatment group.

Although the 6.6% response rate might, on the face of it, be concerning, careful analysis of survey studies (Groves and Peytcheva 2008) and, more recently, of RCTs (Hendra and Hill 2018), find that response rates are largely unrelated to nonresponse bias. Moreover, the estimation of the total effects and their generalisability to the full population, are influenced by other factors that can be more significant: either the impact of the experiment on the proportion and kind of people that self-select to participate in the survey (discussed above) or treatment effect heterogeneity (discussed below) (Kohler et al. 2018). Therefore, even if the sample is not fully representative of the population of stopped motorists in Scotland, given that these other influential factors are not present, the emerging causal effects can be considered close (unbiased) approximations of population average effects.

Nonetheless, further research is needed. Police officers reportedly differed in how they had carried out the treatment. Based on their own admissions, some recited the provided messages verbatim, some completely disregarded the prompts, and some only handed out the questionnaires (MacQueen and Bradford 2017). It follows that there are other sources beyond the self-selection bias that might have adversely affected the results. In particular, it is possible that (1) the treatment effect varied across the different matched pairs because the officers interpreted and implemented the instructions in different ways (i.e., treatment effect inconsistency) and (2) the treatment had a different impact on certain subgroups, thus leading to biased estimates (i.e., treatment effect heterogeneity). The inherent features of block-randomisation can be harnessed to test both of these potential limitations. The pairs created during block-randomisation can be considered a series of “mini-experiments” that can be compared to each other (Weisburd and Gill 2014), thus permitting the assessment of treatment inconsistency and heterogeneity.

Causal Mediation Analysis

Classical Definitions of Direct and Indirect Effects

In this article I hypothesise that the quality of contact with the police (X) shapes respondents’ attitudes (regarding procedural justice) (M), which in turn influences—among other things—their views on the legitimacy of the police (Y). Because traditionally X refers to any kind of (even unobserved) variable, this paper will denote the antecedent variable as T, which indicates the randomised treatment. In addition, it is conventional to control for a vector of pre-treatment covariates C (see Fig. 2). Using the traditional decomposition of the product method, and as depicted by Fig. 2, ‘c’ is a regression coefficient that stands for the direct effect of T on Y, while the product of ‘a’ and ‘b’ (i.e., the estimates of T’s effect on M, and M’s effect on Y) stands for the indirect effect of T that goes through M towards Y. Following Baron and Kenny’s (1986) seminal article, product method mediation analysis with a single mediator can be expressed as:

Fig. 2

Outline of a mediation model with a single mediator

$$\begin{aligned} {\text{M}} & =\upbeta_{0} +\upbeta_{1} {\text{t}} +\upbeta_{2} {\text{c}} +\upvarepsilon_{1} \\ {\text{Y}} & =\uptheta_{0} +\uptheta_{1} t +\uptheta_{2} {\text{m}} +\uptheta_{3} {\text{c}} +\upvarepsilon_{2} \\ \end{aligned}$$

(1)

In the first equation, β₁ denotes the effect of the treatment on the mediator (‘a’ in Fig. 2) after taking into account the covariates (β₂) with the intercept (β₀) and error term (ε₁). In the second equation, θ₁ is the direct effect of T on Y (‘c’ in Fig. 2) after controlling for M (θ₂) (‘b’ in Fig. 2) and C (θ₃) with the constant (θ₀) and error terms (ε₂). The mediated (indirect) effect is the product of the coefficient of the treatment in the regression for the mediator (β₁) and the coefficient of the mediator in the regression for the outcome (θ₂).

However, several criticisms have emerged regarding the applicability of the product method. First, the product method is only capable of identifying² direct and indirect effects if the linearity assumption holds (Imai et al. 2010b; Jo 2008). This means that for non-linear (e.g., multinomial) models the indirect effect cannot be computed relying on the product method. The second caveat, prescribes that there cannot be an interaction between the treatment and the mediator which affects the outcome (i.e., referred to as the no-interaction assumption). The absence of interaction is important, because it permits the effect decomposition and also provides a good indication for effect homogeneity, which is a further requirement (i.e., the causal effects are constant across cases). In the presence of an interaction (e.g., between the treatment and procedural justice in this paper), the method of identification of the direct and indirect effects breaks down as it becomes unclear how to calculate the total effect. Yet, the lack of interaction is not sufficient, because effect homogeneity needs to apply to each individual case, which is an untestable (and highly unlikely) assumption.

A further limitation concerns the applied literature rather than the method itself. Causal mediation analysis relies on “no unmeasured confounder” assumptions which are usually addressed by the random assignment of participants, ensuring that people will not differ across influential measured and unmeasured characteristics (e.g., age, education, previous experience with the police), and hence the exogeneity assumption is met. However, even if the treatment T is randomly assigned, the mediator–outcome relationship is not randomised, which might result in people self-selecting for their mediators independent of the treatment and due to an unmeasured confounder U (depicted in Fig. 2). This issue has been mostly overlooked, partly because it was not discussed in the classic article by Baron and Kenny (1986); although it was mentioned in an earlier paper of one of the authors (Judd and Kenny 1981).

To further complicate matters, randomisation of the mediator, as proposed by some (Bullock et al. 2010; Spencer et al. 2005; Walters and Mandracchia 2017), is not sufficient either for assessing the indirect effect. When both the mediator and treatment are randomly assigned, the exogeneity assumption is satisfied for each, however, it does not apply to the combination of the two. In such cases, the treatment can causally affect the mediator, and the mediator can causally affect the outcome, however, the mediator does not transmit the effect of the treatment anymore due to its random assignment (Imai et al. 2010a; Keele 2015). Thus, special design-based strategies need to be applied for a better chance of identifying causally mediated effects (Imai et al. 2011, 2013). A careful selection of pre-treatment covariates might mitigate the possibility of an unmeasured influential U, but it can rarely solve the issue altogether (VanderWeele 2015). To better understand the assumptions and estimation needed for causal mediation, it is crucial to introduce a more general definition of direct and indirect effects.

Counterfactual Definitions of the Direct and Indirect Effects

In the following paragraphs the controlled direct effect, natural direct effect, and natural indirect effect are discussed as more general definitions of the direct and indirect effects from the product method. These new, general definitions rely on the potential outcome framework and counterfactual way of thinking (Pearl 2001; Robins and Greenland 1992) and are given assuming a binary treatment variable T, mirroring the one used in ScotCET. For all effects, we compare two hypothetical worlds where T is set to 0 (i.e., control) or set to 1 (i.e., treatment) within the same individual at the same moment in time. Using ScotCET as an example, this would mean that the same person would have been exposed to both the treatment and the usual police practice during the roadside check at the very same moment in time from the very same officer(s). Although in real life we can never know what would have happened to that individual had that person been assigned to the other group³ instead of the observed one, hypothetically we can conceive these two separate counterfactual outcomes. It follows that counterfactual inference can only be derived for a population, thus, population average effects are expressed as conditional expectations of the individual-level effects. All the expected values E(.) of random variables below denote expectations over distributions in the population of respondents.

There are different ways of defining direct and indirect effects in this framework. The controlled direct effect (CDE) considers a specified value of M = m and defines the direct effects as:

$${\text{CDE}}\left( {\text{m}} \right) = {\text{E}}\left[ {{\text{Y}}\left( {1,{\text{m}}} \right) - {\text{Y}}\left( {0,{\text{m}}} \right)} \right]$$

(2)

This captures the expected increase in Y when T changes from T = 0 to T = 1 while M is held at the value m for everyone (i.e., within the individual M is kept constant, while she receives both the control and treatment at the same time). This is a direct effect since the effect of T is not transmitted through M. The value of CDE might change depending on the chosen value of m, which also means that relying on CDE does not allow the decomposition of the total effect.

The natural direct effect (NDE) is defined as

$${\text{NDE}} = {\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 0 \right)} \right) - {\text{Y}}\left( {0,{\text{M}}\left( 0 \right)} \right)} \right]$$

(3)

This is similar to the controlled direct effect, in that it estimates the expected increase in Y when T changes from T = 0 to T = 1. However, the NDE does not hold the value of M constant, instead it permits it to take its value in the “natural” way for each individual if that individual had been assigned to the control condition, hence allowing the decomposition of the total effect.

The natural indirect effect (NIE) is defined as:

$${\text{NIE}} = {\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 1 \right)} \right) - {\text{Y}}\left( {1,{\text{M}}\left( 0 \right)} \right)} \right]$$

(4)

It contrasts with NDE as it approximates the expected increase in Y when the treatment is kept at T = 1, while M is freed to take its natural value for the treatment and the control group respectively. This is an indirect effect that captures the effect of T on Y which is transmitted through M.

Importantly, both the direct and indirect effect can be defined through holding M at its potential outcome given T = 1 for the direct effect, while holding Y at its potential outcome T = 0 for the indirect effect:

$${\text{NDE}}_{\text{alt}} = {\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 1 \right)} \right) - {\text{Y}}\left( {0,{\text{M}}\left( 1 \right)} \right)} \right]$$

(5)

$${\text{NIE}}_{\text{alt}} = {\text{E}}\left[ {{\text{Y}}\left( {0,{\text{M}}\left( 1 \right)} \right) - {\text{Y}}\left( {0,{\text{M}}\left( 0 \right)} \right)} \right]$$

(6)

These will produce identical results in respect of the total effect, as shown in (7) below. However, these alternative definitions differ in where the effect of the potential T–M interaction term is assigned (Daniel et al. 2015). In (3)–(4), the interaction term is assigned to the indirect effect, while in (5)–(6) it is assigned to the direct effect. To avoid confusion, sometimes the words “total” and “pure” are added to the direct and indirect effects, therefore, (4) is the total indirect effect (TNIE), while (3) is the pure direct effect (PNDE). Conversely, (5) and (6) refer to the total direct effects (TNDE) and pure indirect (PNIE) respectively.

Using either of these definitions of natural effects, the total effect (TE) of T on Y can be decomposed as the sum of direct and indirect effects, i.e.:

$$\begin{aligned} {\text{TE}} & = {\text{E}}\left[ {{\text{Y}}\left( 1 \right) - {\text{Y}}\left( 0 \right)} \right] \\ & = {\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 1 \right)} \right) - {\text{Y}}\left( {0,{\text{M}}\left( 0 \right)} \right)} \right] \\ & = \left\{ {{\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 1 \right)} \right) - {\text{Y}}\left( {1,{\text{M}}\left( 0 \right)} \right)} \right]} \right\} \\ & \quad + \,\left\{ {{\text{E}}\left[ {{\text{Y}}\left( {1,{\text{M}}\left( 0 \right)} \right) - {\text{Y}}\left( {0,{\text{M}}\left( 0 \right)} \right)} \right]} \right\} \\ & = {\text{NIE}} + {\text{NDE}} = {\text{NIE}}_{\text{alt}} + {\text{NDE}}_{\text{alt}} \\ & = {\text{TNIE}} + {\text{PNDE}} = {\text{PNIE}} + {\text{TNDE}} \\ \end{aligned}$$

(7)

These natural effects do not posit the no-interaction assumption and they are nonparametrically identifiable, thus do not require the linearity assumption either (Pearl 2001).

Estimation of the Natural Direct and Indirect Effects

To estimate the kinds of effects defined above, first specify models for Y given T, M, and C, and for M given T and C, estimate these models using the observed data, and apply formulas which are analogous to (2)–(6) to these fitted models. Consider the models given in Eq. (1), but now with the added interaction between T and M, θ₄, assuming the linearity of the effects. Notice that unlike in (1), the error terms are no longer present as they are expected to be E(ε) = 0. Provided certain assumptions hold for the respective effects (these are discussed in the next section), on average for the population, the following can be derived:

$${\text{CDE}} = \left( {\uptheta_{1} +\uptheta_{4} {\text{m}}} \right)$$

(8)

$${\text{NDE}} = \left( {\uptheta_{1} +\uptheta_{4} \left( {\upbeta_{0} +\upbeta_{1} {\text{t}} +\upbeta_{2} {\text{c}}} \right)} \right)$$

(9)

$${\text{NIE}} = \left( {\uptheta_{2}\upbeta_{1} +\uptheta_{4}\upbeta_{1} {\text{t}}} \right)$$

(10)

From these formulas it can be easily discerned that when θ₄ = 0, (8) and (9) coincide (CDE = NDE = θ₁), and (10) is simplified to the traditional product method (NIE = θ₂β₁). It follows that the product method is a special case of causal mediation analysis which is obtained under assumed linear models with no interaction (Imai et al. 2011). To see a more general version of these equations for non-binary treatments, please refer to VanderWeele and Vansteelandt (2009, p. 461).

Imai et al. (2011) have proposed a semiparametric estimation approach as an alternative to these parametric models: firstly, two regression models are fitted for the mediator and the outcome of interest, similarly to the parametric approach. Likewise, two sets of mediator (conditional on T and C) and outcome (conditional on M, T, and C) values are generated for every observation for each level of treatment T = t₀ and T = t₁, and the effects are computed through averaging the differences between the predicted potential values. The semiparametric approach is superior in that it is applicable for any kind of link function, while the parametric one is only suitable to a couple of link functions (i.e., linear and binary logistic with rare outcome variables) (VanderWeele 2015). Although Marginal Structural Models can also be used to derive natural effects (Coffman and Zhong 2012), this technique would not be appropriate for the current models, because the weighting method produces unstable estimates in the case of continuous mediators (Moerkerke et al. 2015). Hence, the semiparametric approach was used here because of its flexibility. Notably, for linear outcome variables, the parametric and semiparametric approaches generate almost identical results.

Finally, all approaches recommend using resampling techniques, such as the nonparametric bootstrap or Monte Carlo approximation to correctly represent the prediction uncertainty of the estimates. For all models in this paper, the treatment was binary, and the mediator and outcome variables were continuous, with all covariates included in the models. The “mediation” R package (Tingley et al. 2014)⁴ was used with interaction allowed between the treatment and the mediator, and 1000 bootstrap replicates were specified for estimation of standard errors.

Assumptions of Causal Mediation Analysis

To make causal claims using the estimators outlined above, the sequential ignorability assumption needs to be satisfied (Imai et al. 2010a). This “no unmeasured confounder” assumption lists the different sources of unmeasured confounders U that can produce biased results and requires that, after controlling for all pre-treatment covariates C, there is no unmeasured confounder for:

• (a) The relationship between the treatment (T) and outcome (Y)

• (b) The relationship between the mediator (M) and outcome (Y), also controlling for the treatment (T)

• (c) The relationship between the treatment (T) and mediator (M)

  and,

• (d) There is no post-treatment mediator–outcome confounder (L) that was affected by the treatment

From these, (a) and (c) constitute exogeneity assumptions usually applied to determine the total effect and are automatically satisfied in the case of random assignment of T (as it was done with ScotCET). For (b) to be fulfilled, M either needs to be as-if-randomly assigned (using data from special research designs which are not considered here (Imai et al. 2013)) or assumed that it is as-if randomly assigned after controlling for T and C. Markedly, assumptions (a)–(c) are similar to the “no unmeasured confounder” assumptions that need to be made for matching, making causal mediation analysis a (part) observational method. Therefore, an exhaustive set of relevant pre-treatment covariates are required to reduce the likelihood of an unmeasured influential U (i.e., third common cause, Nagin and Telep 2017) affecting the results.

To accomplish the final point (d), one needs to rely on a parsimonious model similar to Fig. 2, as it posits that there cannot be other post-treatment confounders (essentially other mediators) that are not included in the model. From the four assumption, (a) and (b) are sufficient to derive the CDE(m),⁵ while (a)–(d) are needed for the NDE and NIE. Finally, as with randomised experiments in general, the stable treatment unit value assumption also needs to be met.

Sensitivity Analysis

Similarly to other techniques in the causal inference literature, causal mediation analysis relies on untestable and non-refutable assumptions (Manski 2007). Nevertheless, sensitivity analyses can be utilised to quantify the robustness of the results and assess the potential influence of unmeasured confounder U (see assumption (b)). As there are no established benchmarks upon which one could decide on the absolute robustness of results, inferences must be informed by previous findings from the field and should be compared with the impact of other measured confounders. There are several different sensitivity analysis techniques (Ding and Vanderweele 2016), of which two will be discussed here, that work especially well with continuous mediators and are capable of gauging the robustness of the NDE and NIE.

The first technique (Imai et al. 2010a, 2011; Imai and Yamamoto 2013) fits two regressions, one for M and the other for Y with a T–M interaction, and takes the error terms (ε) specifying a correlation between them denoted by ρ. These error terms incorporate the impact of U, thus the value of ρ will relatively increase if there is an influential U that affects both M and Y. Thus, the sensitivity of the results can be tested by systematically increasing the correlation between the two εs and evaluating the extent to which the estimates are altered, with higher values implying relatively more robust results. A mathematically equivalent but perhaps more intuitive way of reporting the results is to consider the R-squared statistics and interpret the results in terms of U’s explanatory power. The R² for the residual variance shows the proportion of previously unexplained variance that is explained by U. Alternatively, the R² for the total variance represents the same, but for the proportion of the original variance. In the case of the R²s, higher values will indicate relatively lower sensitivity to the violation of the sequential ignorability assumption compared to results from similar studies.

The other sensitivity analysis technique is called the left out variable error method (LOVE) (Cox et al. 2013), which assesses the extent to which an unmeasured variable U would have to affect the association between M and Y in order for the observed association to be attributable to this confounding alone. LOVE relies on the correlation between T–M, T–Y, and M–Y to approximate the correlation between U–Y and U–M. The average of the U–Y and U–M correlation corresponds to a correlation coefficient that would make the observed mediated effect zero, hence, higher coefficients entail less sensitive results. The LOVE technique enables a less convoluted assessment of the effect of U on the M–Y relationship, however, it does not include pre-treatment covariate Cs, which considerably limits its authenticity for the model under scrutiny.

Results

Assessment of Treatment Effect Heterogeneity and Treatment Effect Inconsistency

To evaluate treatment effect consistency, methods commonly used in meta-analysis can be employed, as each matched pair in ScotCET can be considered an individual study (Weisburd and Gill 2014). STATA’s metaan package was used to perform a random-effect meta-analysis with the treatment as the explanatory variable and all covariates included in each regression. Weights are attributed to the specified regressions for each matched pair, based on the effect sizes and standard errors, and the weights are considered when estimating the total effect (the formula for calculating these weights is available on Kontopantelis and Reeves 2010, p. 400). This method also assumes that despite the differences of the underlying effect sizes, all are related through some distribution (i.e., the treatment is specified as a random slope in the model) (Kontopantelis and Reeves 2010). Random-effect meta-analysis also permits the computation of two measures of effect consistency: Cochran’s Q and I². Cochran’s Q is a statistical test for inconsistency, with the null-hypothesis that all studies in the meta-analysis have the same underlying magnitude of effect and non-significant results indicating consistency. I² estimates the proportion of variation in the point estimates due to between-study variation. Usually values below 50% are considered as a sign of low inconsistency, while values over 75% are considered high (Rhodes et al. 2016). Due to the lack of control units in one pair, only nine matched pairs were included in the analysis (n = 485).

Figure 3 shows a ‘forest plot’ with the treatment’s effect on procedural justice across the different matched pairs, and the estimated total effect (also denoted β below) at the bottom (for the forest plots of the other outcomes please refer to “Appendix B”). The first three columns of Table 1 summarise the results from the analysis. The treatment has a significant negative effect on procedural justice (β = − 0.435, p < 0.05) and duty to obey (β = − 0.579, p < 0.05), however the rest of the effects are not significant. These are in line with the findings of the original study (Macqueen and Bradford 2015), and suggest that the contact with the officers in the treatment group diminished people’s views about the police compared to the encounters in the control group. Importantly, Cochran’s Qs are not significant, and the I²s show either low (duty to obey: I² = 43.06%; social identity: I² = 42.42%) or minimal (procedural justice: I² = 2.1%, normative alignment: I² = 8.8%) inconsistency. This lack of inconsistency across delivery units implies that even if the police officers acted in a different manner, the impact of their interactions during the police stops was fairly similar across the pairs.

Fig. 3

Treatment effect consistency for procedural justice

Table 1 Total effects from the random-effects meta-regression, Cochran’s Q, I², design and covariate heterogeneity, and treatment–covariate interactions

A second potential complication in this study is the treatment’s systematic variation across subgroups within the population. In case of such heterogeneity, the assumption that the total effect is the same for each individual might not be tenable, and thus the various estimators of the treatment effect might be altered even in the absence of selection or confounding bias (Kohler et al. 2018). The block-randomised design permits two different analyses of effect heterogeneity: (1) treatment effect heterogeneity, which scrutinises the total effect’s dependency on pre-treatment covariates and (2) design heterogeneity, where in addition to the pre-treatment covariates, the treatment’s dependence on the different blocks is also testable. Because there was no initial expectation with regards to treatment–covariate and treatment–matched pair interactions, an automated solution, the “FindIt” R package and Squared Loss Support Vector Machine (L2-SVM) (Imai and Ratkovic 2013) was applied. This L2-SVM model first rescales the covariates (using a LASSO-regularisation), then fits the model (again, with a series of iterated LASSO fits) by also relying on generalised cross-validation statistics. This approach automatically tests the potential interactions between the various covariates in the model, as well as the interaction between the covariates and the treatment, only flagging the influential ones. Two L2-SVM models were fitted for each outcome and were subsequently compared to each other and to the total effect. The first model only considered the covariates, the second one both the covariates and the blocking design. As indicated by the fourth column in Table 1, accounting for the treatment effect heterogeneity only led to limited changes in the total effect, with alterations in the point estimates ranging from 0.016 to 0.038. The fifth column shows that after adding the matched pairs to the analysis, these differences dropped even further, with miniscule changes ranging from 0.006 to 0.015. This drop is anticipated, since the blocking was designed to account for the sampling variability. Finally, no treatment–covariate interaction emerged in either of the models. The lack of interactions and the small changes in the total effects indicate that the treatment effect can be considered by and large homogeneous. Therefore, the treatment’s effect from ScotCET had very similar impact in the population and there were no subgroups which were more or less receptive to its influence, or delivery units that had disparate impact on the results.

To summarise, the examination of selection bias, treatment effect inconsistency and treatment effect heterogeneity provided strong evidence regarding the internal validity of the treatment’s effect. These demonstrated that the same kind of people answered the surveys in the treatment and control group, that they were affected in a very similar way by the treatment across the matched pairs, and that the treatment’s effect did not vary across the subgroups either. Thus, these tests all substantiate MacQueen and Bradford’s (2017) assertion about the robustness of the research design, and that the effect of police encounters during the roadside checks was significantly different in the two experimental conditions: for the treatment group, the experience during the encounter with the police was on average more negative compared to the control group.

There are two complementary explanations for these negative treatment effects (MacQueen and Bradford 2017). First, as noted earlier, some of the officers who were chosen to carry out the procedurally just messages felt that the researchers trespassed upon their working lives, telling them how to do their jobs. The ongoing and unpopular organisational changes taking place during the fielding of the study (i.e., the centralisation of regional forces to Police Scotland) had already made many of the officers disgruntled, and randomly enlisting them into this trial could have increased their exasperation further. Second, the example scripts given to the officers could have made the otherwise free-flowing, natural encounters more structured and formal, even bureaucratic, perhaps even among the officers who might have felt positively towards the trial. Additionally, the script could also have lengthened the otherwise brief encounters, and longer encounters are generally perceived as less procedurally fair (Mazerolle et al. 2015). Therefore, it is conceivable that the combination of these factors is responsible for the arising negative effects. With all these considered, this paper proceeds to examine the mediating effects and tests a fundamental question found in the procedural justice literature: whether the impact of a person’s previous positive/negative contact with the police is channelled through procedural justice to affect certain outcome variables (e.g., legitimacy).

Causal Mediation Analysis

The causal mediation analysis results are displayed in Table 2. For each model, the treatment (T) is a binary variable representing the encounter with the officer(s) from the treatment or control group, the mediator (M) is procedural justice, and the outcome (Y) is either normative alignment with the police, duty to obey the police, or social identity. Both the natural direct effect (NDE) and natural indirect effect (NIE) in Table 2 take the average of the direct and indirect effects estimated in (3) and (5) and (4) and (6) respectively.

Table 2 Causal mediation analysis results with averaged NDE and NIE effects and sensitivity analyses

I use the model fitted for normative alignment (first row) to exemplify the interpretation of the results. The total effect is the sum of the NIE and NDE, or − 0.214. The decomposition of this total effect indicates that 84.2% of the effect of contact with the police on normative alignment is mediated by the perception of procedural justice, which corresponds to an NIE point estimate of − 0.207, which is significant on the 5% level. Conversely, the direct effect is very close to zero (NDE = − 0.007) and non-significant, implying that the perception of procedural justice fully mediates the impact of the treatment on the outcome.

Sensitivity analyses techniques can help to evaluate the NIE’s and NDE’s robustness to unmeasured confounding. To make the NIE of procedural justice on normative alignment zero (i.e., non-significant), the mean correlational coefficient between the error terms from the model for the mediator and outcome would need to be 0.6. Expressed with R-squared transformations, ρ = 0.6 suggests that the unmeasured pre-treatment confounder U would need to be able to account for at least 36% of the residual and 20% of the total variance in the model to nullify the results. Thus, this relationship seems to be less sensitive or, in other words, fairly robust to unmeasured confounding. By contrast, for the NDE’s effect to reach zero, this correlation coefficient would only need to approach 0.1, with the power to explain 1% of the residual variation and less than 1% of the total variation. Therefore, this result is highly sensitive to unmeasured confounding, which stands to reason as the NDE value is already very close to zero and non-significant. Finally, the left-out-variable error value (LOVE) implies that, on average, an unmeasured confounder would need to have a 0.7 correlation with the mediator and the outcome to make the NIE non-significant. Overall, the results from the causal mediation and sensitivity analyses suggest that contact with the police during roadside encounters boosts the perception of shared values with the police through the citizens’ attitudes towards fairness of the police. This mediated effect appears to be relatively robust to unmeasured confounding.

Accordingly, procedural justice seems to fully channel the effect of the treatment to normative alignment (as discussed in the previous paragraph). In comparison, procedural justice only partially mediates the impact of contact with the police on duty to obey (NIE_mean = − 0.153, p < 0.05, Mediate % = 34.9%, ρ = 0.5, ${\text{R}}_{\text{residual}}^{2}$ = 0.25, ${\text{R}}_{\text{total}}^{2}$ = 0.17, LOVE = 0.7) and social identity (NIE_mean = − 0.052, p < 0.05, Mediate % = 16.9%, ρ = 0.3, ${\text{R}}_{\text{residual}}^{2}$ = 0.09, ${\text{R}}_{\text{total}}^{2}$ = 0.12, LOVE = 0.5). In case of normative alignment, the treatment does not have a significant direct effect, whilst for both duty to obey (NDE_mean = − 0.279, p < 0.05, ρ = 0.7, ${\text{R}}_{\text{residual}}^{2}$ = 0.49, ${\text{R}}_{\text{total}}^{2}$ = 0.32) and social identity (NDE_mean = − 0.243, p < 0.05, ρ = 0.8, ${\text{R}}_{\text{residual}}^{2}$ = 0.64, ${\text{R}}_{\text{total}}^{2}$ = 0.466) the direct effect is not only significant, but stronger than the indirect effect. The partial mediation of the treatment effect on duty to obey and social identity hints that procedural justice might not be the only mechanism that could expound how and why roadside encounters change citizens’ attitudes about consent towards police actions and connection to their communities. Notably, and despite the difference in the magnitude of the effect size of the NIE, normative alignment and duty to obey both have the same LOVE-score and very close ρ scores for their NIEs, indicating similar levels of robustness to unmeasured confounding. In comparison, social identity’s NIE appears to be more sensitive, suggesting that less credence should be given to this mediated effect compared to the others.

Another improvement of causal mediation analysis is that it manages to resolve the inclusion of the interaction effect while still guaranteeing a meaningful decomposition. In Table 2 the average NIE and NDE were included. By contrast, Table 3 has the NIEs and NDEs discussed in the methodological overview: NIE corresponds to (4), NDE to (3), while NIE_alt corresponds to (6), and NDE_alt to (5).⁶ Taking normative alignment as an example, when the whole interaction is attributed to the indirect effect (NIE), it has an effect size of − 0.244, mediating almost perfectly the effect of the treatment (Mediate % = 98.9%), with a ρ = 0.7 needed to make the indirect effect non-significant, with 49% of the residual, and 25% of the total variation explained. Conversely, if none of the interaction is attributed to the mediated effect (NIE_alt), it has an effect size of − 0.171 and procedural justice only mediates a little more than two-thirds of the treatment’s effect (Mediate % = 69.5%), with a mean ρ = 0.5, which coincides with the residual variance of 25%, and the total variance of 13%. These results suggest, that if the mediated effect is dependent on the treatment–mediator interaction, then virtually the full impact of the treatment on normative alignment is channelled by procedural justice. On the other hand, if this is an additive interaction between contact with the police and procedural justice, only a little over two-thirds of the effect of the treatment on normative alignment is mediated by procedural justice. Because most theories in the social sciences do not have strong rationales regarding where to assign the treatment–mediator interaction, in practice the NIE_mean and NDE_mean (Table 2) are used.

Table 3 Causal mediation analysis results with the interaction’s effect attributed either to the NIE or NDE, and sensitivity analyses

Even if it is difficult to determine where to assign the effect of the interaction, Table 3 can help to inform the researcher about the presence/absence of an influential T–M interaction. Based on the magnitude of change in the effect size, normative alignment is the most affected by the allocation of the interaction. However, in case of duty to obey a smaller change influences the significance of the NDE. Similarly, in case of social identity the significance of the NIE is dependent on the assignment of the interaction effect. Therefore, examining the interactions could be considered another robustness test: the significance of the direct effect in the model for duty to obey and the indirect effect in the model for social identity appear to be affected by the assignment of the interaction. In other words, police contact during the roadside check might not have a separate impact on duty to obey the police beyond the effect going through procedural justice. By contrast, it is conceivable that procedural justice might not transmit the effect of the treatment towards social identity. These examples underline the importance of including the interaction in the analysis, and the limitations of the product method which would not have accounted for the impact of the T–M interaction.

Discussion

Causal mediation analysis allows a change in the focus of the analysis, partitioning the causal effect of police contact that goes through subjective procedural justice from the part that does not. The rich set of pre-treatment covariates from the ScotCET dataset allowed a robust test of the theory of procedural justice policing, indicating that police–citizen encounters during roadside checks affect the perceived value congruence with the police (normative alignment) entirely through procedural justice, whilst fair treatment by the police only partially transmits the effect on consent to police actions (duty to obey) and identification with the police (social identity). It is notable that in the case of duty to obey and social identity, the direct effect of police contact remained significant, indicating that not all aspects of the treatment’s impact are mediated by procedural justice. This implies that there are potentially other causal mechanisms, such as police effectiveness or respect for boundaries, which might be able to complement the indirect effect of procedural justice (Hamm et al. 2017).

These findings make some headway toward examining the ‘causal linkage’ (Nagin and Telep 2017) between police contact, procedural justice, social identity, and legitimacy. Provided that the identifying assumptions are satisfied (i.e., there are no influential unmeasured confounders), this paper finds indicative causal evidence that police-stops shape the social identification and perceived legitimacy of citizens through procedural justice. Thus, a basic message of this analysis is that citizens’ perceptions of procedural justice are important. When people perceive that the police decisions are fair, that the police listen to them, and treat them with dignity and respect, citizens are more inclined to find police behaviour appropriate, recognise police authority to dictate appropriate behaviour, and are more likely to identify with their community at large. Future studies should replicate the findings of this paper and extend the analysis in at least two ways: (1) by including societally desirable outcomes in the model, such as cooperation with the police and legal compliance (Pósch 2019) and (2) by studying the effects of procedural justice in more varied policing contexts that go beyond routine roadside checks, and which might be even more conducive of legitimacy (Epp et al. 2014).

Much empirical research in the social sciences is focussed on identifying causal relationships, yet, most of these efforts only scrutinise the average causal effects and are not concerned with underlying causal processes and mechanisms. This article has discussed causal mediation analysis as a promising statistical method to “pry open” this black box of causality by assessing natural direct and indirect effects. The results from this approach can hint at the success of interventions in the presence of certain causal mechanisms. This approach goes beyond the traditional product method and can be applied to models with non-linear link functions and interactions, without positing the effect homogeneity assumption, while quantifying the potential influence of unmeasured confounders for the mediator–outcome relationship through sensitivity analyses (Imai et al. 2010a, b, 2011). Unlike in previous criminological work, where causal mediation analysis has been used in a longitudinal research context (Walters 2015, 2017), here it is employed in an experimental setting. Moreover, this paper went beyond a recent review of applied literature on causal mediation in criminology (Walters and Mandracchia 2017) by (a) presenting a versatile statistical technique and (b) utilising the potential outcome framework to outline fundamental causal assumptions and describe new definitions of direct and indirect effects. Furthermore, it recommends two sensitivity analysis methods that can be easily used in most applied settings.

To exemplify the utility of causal mediation analysis, this paper chose to reanalyse the ScotCET dataset. The assessment of the selection bias, treatment effect consistency, and effect homogeneity showed that the treatment effect does not affect people’s self-selection in the study, that it is very similar across the matched pairs, and that there is small covariate and minimal design heterogeneity—suggesting that the emerging causal effects were unbiased. Conducting similar evaluations for other experiments with block-randomised designs should be common practice and imperative in examining the identifiability of the total effects.

The potential outcome framework used in this article is a rigorous tool, making modelling assumptions explicit and offering new definitions of direct and indirect effects, which can be identified based on whether particular assumptions are satisfied. Future research would benefit from considering each step of the sequential ignorability assumption, and gauging whether the proposed causal mediation models are identifiable. Sensitivity analysis techniques would provide further insight into the robustness of emerging results, and could make tenuous relationships easily affected by third common causes (Nagin and Telep 2017) more discernible. At times, when parts of the experimental community are preoccupied with the “replication crisis” and “p-hacking”, these sensitivity analysis techniques could be readily applied as further tests regarding the viability of results.

As with every method, causal mediation analysis faces certain challenges that need to be addressed. Even with a randomised treatment, the sequential ignorability assumptions are very demanding. For instance, in case of ScotCET, there might be influential covariates that were not measured and thus not included in the models (e.g., earlier contact with the police, victimisation). Moreover, the results of the sensitivity analyses cannot be assessed on their own, but only with regard to the list of pre-treatment covariates that are accounted for. Noticeably, some of the results become more robust to unmeasured confounding when the covariates are not included in the models (see: “Appendix C” Table 6). This means that the robustness of the results can only be determined in comparison to other variables in the models, unless sensitivity benchmarks have been established.

Furthermore, most traditional experiments and RCTs, such as ScotCET, are cross-sectional in nature, thus making it difficult to establish temporal order, and opening the door to the possibility of reverse causation (i.e., that the effect of the treatment might be transmitted by the outcome on the mediator, instead of the other way around) (Nagin and Telep 2017; Weisburd and Majmundar 2018, pp. 157–158). Unfortunately, there is no statistical test that could rule out this possibility (VanderWeele 2015). Nevertheless, the existing evidence in case of procedural justice makes this an unlikely proposition. Several cognitive psychological studies have shown that the perception of procedural justice is a fundamental psychological process (‘fairness heuristic’, see Barclay et al. 2017; Lind 2001; Proudfoot and Lind 2015), whilst relational identification (i.e., social identity) and constructs that require deliberation (i.e., legitimacy) are more complex (Barclay et al. 2017; van Lier et al. 2013; Tabibnia et al. 2008). Although this line of reasoning might be alien to criminological audiences, in the psychological literature it is widely accepted that more basic psychological processes are affecting (and informing) more complex ones down the line (Von Hippel et al. 2005; Kahneman 2012). Despite the qualified support provided by the psychological literature, future studies with a longitudinal component should provide a direct assessment of the model outlined above.

Another potential criticism of causal mediation analysis is that it requires the assumption that only a single mediator will channel a treatment’s effects towards the outcome. Yet, in the social sciences, theories often posit multiple pathways. In non-Western countries, for example, police effectiveness is usually considered alongside procedural justice (Bradford et al. 2014a). However, this would violate assumption (d) of the sequential ignorability assumption, which does not allow the presence of further mediators. Hence the method presented here can only be applied to relatively simple models, and other more complex solutions need to be pursued when multiple mediators are present (Daniel et al. 2015; Pósch 2019; VanderWeele and Vansteelandt 2014).

Finally, this study’s treatment merits some discussion. Even though the diagnostics indicate that the treatment’s effect is only attributable to the design, still without knowing exactly what transpired during the roadside encounters, only speculative interpretation can be provided, which renders any explanation of the direct effects ambiguous. I argued that the combination of two factors contributed to the emerging negative treatment effects: (1) officers made even more disgruntled by being enlisted into the trial during a period of low organisational legitimacy at the time of the RCT, and (2) potential issues surrounding the treatment delivery. Future studies should strive to gain proper buy-in from police organisations,⁷ and spend more time and resources on the training of officers. As with other experimental results, multiple trials are needed to revisit the findings presented here. Yet, by relegating the treatment’s effects and elevating the mediated effects, causal mediation analysis permitted a clarification regarding to what extent these experiences were mediated by procedural justice, thus producing theoretically valuable findings.

Appendices

Appendix A: Measurement

In this paper, several different constructs were measured with multiple items: procedural justice (4 items), normative alignment (3 items), free duty to obey (3 items), and social identity (2 items). The question wording and response alternatives are all detailed in Table 4.

Table 4 List of constructs, measures, and response alternatives

All constructs with multiple items were entered in a confirmatory factor analysis, the results are depicted by Fig. 4. According to the model fit indices (CFI = 0.977, TLI = 0.968, RMSEA = 0.056, SRMR = 0.033) the model fit the data well. The factor loadings were relatively high (λ = 0.629–0.916) for all latent variables which implies that the measurement models performed well. After the confirmatory factor analysis, factor scores were derived and used in all subsequent analysis.

Fig. 4

Confirmatory factor analysis of the constructs used in the article (all relationships are significant on the p < 0.001)

Correlational Results

The correlational results (Table 5) show that the treatment had a weak negative association with the other variables. The correlation between treatment and social identity emerged with the biggest magnitude (r = − 0.150, p < 0.05), followed by duty to obey (r = − 0.144, p < 0.01), normative alignment (r = − 0.114, p < 0.05), and procedural justice (r = − 0.103, p < 0.05).

Table 5 Correlational results

The mediator of interest, procedural justice, followed the expected pattern: it had a strong positive correlation with normative alignment (r = 0.698, p < 0.01) and duty to obey (r = 0.463, p < 0.01), and a moderately strong one with social identity (r = 0.298, p < 0.01).

Finally, the remaining variables had the anticipated significant positive bivariate relationships with one another with varying magnitudes (normative alignment: r = 0.352–0.632, p < 0.01; duty to obey: r = 0.356–0.632, p < 0.01; social identity: r = 0.352–0.356, p < 0.01).

Appendix B: Forest Plots

See Figs. 5, 6 and 7.

Fig. 5

Treatment effect consistency for normative alignment

Fig. 6

Treatment effect consistency for duty to obey

Fig. 7

Treatment effect consistency for social identity

Appendix C: Causal Mediation Analysis Results Without Covariates

See Table 6.

Table 6 Causal mediation analysis results without accounting for the pre-treatment covariates