Skip to main content

Advertisement

SpringerLink
Log in

Can Cohort Replacement Explain Changes in the Relationship Between Age and Homicide Offending?

  • Original Paper
  • Published:
Journal of Quantitative Criminology Aims and scope Submit manuscript

Abstract

This paper focuses on shifts in the age distribution of homicide offending in the United States. This distribution remained remarkably stable with small but significant changes over a long period of time. Then between 1985 and 1990 the rates of homicide offending doubled for 15-to-19 year olds and increased nearly 40% for 20-to-24 year olds, while the homicide offending rates decreased for those over 30. In addition to this “epidemic of youth homicide,” which lasted through the mid-1990s, there have been systematic changes in the age distribution of homicide in the United States associated with cohort replacement over the past 40 years. We introduce an estimable function approach for estimating the effects of age, period, and cohort. The method allows us to assess simultaneously the impacts of periods and cohorts on the age distribution of homicide offending. We find that although the age curve remains relatively stable, there are shifts in it associated systematically with cohort replacement. Cohort replacement accounts for nearly half of the upturn in youth homicides during the epidemic of youth homicides, but a significant fraction of that upturn is not associated with cohort replacement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. In the mid-1980s Cook and Laub (1986) pointed to a surprising stability of youth crime rates given major changes in the family structure.

  2. There were many other papers published that discussed the invariance of crime rates and what invariance would look like; see, for example, Britt (1992); Greenberg (1994); Steffensmeier et al. (1989). From these papers and others we would conclude that the age distribution of crime is not strictly invariant.

  3. Hirschi and Gottfredson (1983) view the age distribution of homicide as universal and not socially determined. That is, it is likely to be biological/genetic (see Gove 1994, for a similar view on age and violence). In contrast, David Greenberg (1977, 1985) portrays this distribution as socially created by the social position of youth in economically advanced societies. Our data will not be able to adjudicate between these sorts of explanations.

  4. The UCRs provide the number of those arrested for homicide in the United States in various age categories for those agencies reporting 12 months of data during the year. We used these age-specific arrest counts to calculate these and other rates as described in the methods section of this paper.

  5. Our data come from the Uniform Crime Reports and that source reports the number of arrests for those (for example) who are 25–29 in 1970. These reports do not tell us the year in which these people were born. It turns out that someone who is 29 in 1970 could be born in 1940 or 1941, and those who are 25 in 1970 could be born in 1944 or 1945. So to say that they are from the cohort born between 1940 and 1944 is “shorthand” and no better than saying they were born between 1941 and 1945 or that they were born between 1940 and 1945. This final classification would create overlapping birth cohorts when we classified each of the age groups to their birth cohort. This problem is well illustrated using Lexis diagrams (Vandeschrick 2001).

  6. “Crack cocaine is a smokeable, solid form of cocaine that is obtained by evaporating a solution of cocaine, sodium bicarbonate (baking soda), and water … crack was a technological innovation in that it was much easier and less hazardous to produce than other forms of ‘freebase,’ which typically necessitated the use of flammable ether” (Cork 1999, p. 381).

  7. This means that these dummy variables are fixed effects so the estimated coefficient for a period is the same across all age groups in that period; the estimated coefficient for an age group is the same across all periods in that age group, the estimated coefficient for a cohort is the same across all combinations of age and period within that cohort.

  8. Smith (2004, p. 113) states, “regardless of the identifying constraint, the estimated model has the same degrees of freedom and the same goodness-of-fit. This means that the test for whether an APC decomposition of variance is better than one based on, say, age and period alone is independent of the constraint chosen.”

  9. “[T]he estimates from the full APC models are sensitive to the choice of equality constraints on the parameters of the model. Specifically, different restrictions that equate coefficients of different subsets of adjacent categories can lead to widely different trend estimates of age, period, and cohort effects, all of which fit the data equally well” (Yang et al. 2004, p. 96).

  10. See Searle (1971) for a comprehensive discussion of generalized inverses and estimable functions. A briefer, but adequate, discussion for the presentation in this paper is found in Rawlings (1988).

  11. Yang et al. (2004) argues that a particular generalized inverse is the best one to use, and this provides a rationale for a particular b 0 vector being superior to other such vectors. If they are correct, that justifies the use of the individual regression coefficients in an APC model as the best estimates. For a discussion of the strengths and weaknesses of this approach see (Smith 2004). The procedure we use does not suggest that one b0 is superior to another.

  12. A generalized inverse is a default in PROC GLM in SAS (2004) for situations in which the X′X matrix is singular.

  13. In SAS we used the program below to provide the estimates of the age-period-specific homicide offense rates based on age, period, and cohort dummy variables and age by period interactions:

    • PROC GLM; CLASS cohort agegroup period;

    • MODEL lnhom1564 = period agegroup cohort age1*period90 age1*period95 age2*period90 age2*period95/SOLUTION PREDICTED;

    • RUN;

  14. Savolainen (2000) analyzed Public Use Micro Samples (PUMS) census data to estimate the percentage of those in 5-year birth cohorts who lived in single parent families when they were ages 5-to-9. These data were not available for all years or for all 10 year census periods, so he used interpolation for several of his estimates. Still, the percentage of non-marital births and the percentage of cohort members in single parent families at ages 5-to-9 are highly correlated. Using data based on cohorts born from the 1915–1919 to 1975–1979, the correlation between these two measures is 0.98. For the first differences of the measures, the correlation is 0.90. The data on single parent families were supplied by Jukka Savolainen.

  15. The shape of the age curve is proportionately the same—invariant—at each period.

  16. We tested this by entering age by period interactions for the largest discrepancies for each age in each period and assessing whether the interaction significantly improved the fit of the model that contained the age, period, and cohort dummy variables and the four interactions associated with the epidemic of youth homicide. We report the results of this procedure for each of the discrepancies—keeping the interactions that are statistically significant (p < 0.05) in the equation and searching for others to add. We began in the earliest period and proceeded to the most recent. If an interaction became insignificant (p > 0.05) in our model, we eliminated it. This is an informal way of testing for the most important discrepancies. We note that this procedure probably is too generous in including interaction terms. Since there are 86 such significant tests for the interactions (excluding the four associated with the epidemic of youth homicide), the Bonferroni corrections suggests that we use an alpha value of 0.0006.

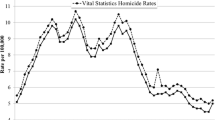
  17. This estimate for the log of the homicide rate for those 15-to-19 in 1985 is the log of the sum of the intercept—which is the same across all of the periods—plus the age effect for those from 15-to-19—which is the same across all of the periods, and the period effect. It is only the period effect that varies from period to period which increases or decreases the absolute value of the predicted age-period-specific homicide rate for that age group for that period. The same can be said for each of the age groups in any period. If we convert this logged age-period-specific rate predicted from the age-period model to the “raw” age-period-specific rate for say the youngest age group in the third period (1975) (see Fig. 1) by exponentiating it, we have e(u + a1 + p3), which we can also write as eu × ea1 × ep3. Clearly this shift is proportional since ep3 is constant for all the age-period-specific rates in period 3 and its effect is multiplicative.

  18. These sums of squares differ from those in Tables 1 and 2, because we do not have data on the percentage of nonmarital births for the cohorts born from 1910 to 1914 and before. Thus, this data is missing for those age 50–54 and above in 1965; 55–59 and above in 1970; and 60–64 in 1975. The sums of squares reported in this paragraph are based on analyses in which these six cases are not included in any of the analyses.

References

  • Baumer E, Lauritsen JL, Rosenfeld R, Wright R (1998) The influence of crack cocaine on robbery, burglary, and homicide rates: a cross-city, longitudinal analysis. J Res Crim Delinq 35:316–340

    Article  Google Scholar 

  • Blau JR, Blau PM (1982) The cost of inequality: metropolitan structure and violent crime. Am Sociol Rev 47:114–129

    Article  Google Scholar 

  • Blumstein A (1995) Youth violence, guns, and the illicit drug industry. J Crim Law Criminol 86:10–36

    Article  Google Scholar 

  • Blumstein A, Cork D (1996) Linking gun availability to youth gun violence. Law Contemp Probl 59:5–24

    Article  Google Scholar 

  • Blumstein A, Rosenfeld R (1998) Explaining recent trends in U.S. homicide rates. J Crim Law Criminol 88:1175–1216

    Article  Google Scholar 

  • Britt CL (1992) Constancy and change in the US age distribution of crime: a test of the ‘invariance hypothesis’. J Quant Criminol 8:175–187

    Article  Google Scholar 

  • Cook PJ, Laub JH (1986) The (surprising) stability of youth crime rates. J Quant Criminol 2:265–276

    Article  Google Scholar 

  • Cook PJ, Laub JH (1998) The unprecedented epidemic in youth violence. In: Tonry M (ed) Crime and justice: a review of research, vol 24. University of Chicago Press, Chicago, pp 27–64

    Google Scholar 

  • Cook PJ, Laub JH (2002) After the epidemic: recent trends in youth violence in the United States. In: Tonry M (ed) Crime and justice: a review of research, vol 28. University of Chicago Press, Chicago

    Google Scholar 

  • Cork D (1999) Examining space–time interaction in city-level homicide data: crack markets and the diffusion of guns among youth. J Quant Criminol 15:379–406

    Article  Google Scholar 

  • Easterlin RA (1978) What will 1984 be like? Socioeconomic implications of recent twists in the age structure. Demography 15:397–421

    Article  Google Scholar 

  • Easterlin RA (1987) Birth and fortune: the impact of numbers on personal welfare. University of Chicago Press, Chicago

    Google Scholar 

  • FBI (1961, 1966,...,2006). Crime in the United States (1960, 1965,...,2005). US Government Printing Office, Washington DC

  • Fryer RG, Heaton PS, Levitt SD, Murphy KM (2005) Measuring the impact of crack cocaine. NBER Work Pap Ser 11218:1–65

    Google Scholar 

  • Gove WR (1994) Why we do what we do: a biopsychosocial theory of human motivation. Social Forces 73:363–394

    Article  Google Scholar 

  • Greenberg DF (1977) Delinquency and the age structure of society. Contemp Crises 1:189–223

    Article  Google Scholar 

  • Greenberg DF (1985) Age, crime, and social explanation. Am J Sociol 91:1–27

    Article  Google Scholar 

  • Greenberg DF (1994) The historical variability of the age-crime relationship. J Quant Criminol 10:361–373

    Article  Google Scholar 

  • Hirschi T, Gottfredson M (1983) Age and the explanation of crime. Am J Sociol 89:552–584

    Article  Google Scholar 

  • Hirschi T, Gottfredson M (1985) Age and crime, logic and scholarship: comment on Greenberg. Am J Sociol 91:22–27

    Article  Google Scholar 

  • Huff-Corzine L, Corzine J, Moore DC (1986) Southern exposure: deciphering the South’s influence on homicide rates. Social Forces 64:906–924

    Article  Google Scholar 

  • Jacobs D, Helms R (1996) Toward a political model of incarceration: a time-series examination of multiple explanations for prison admission rates. Am J Sociol 102:323–357

    Article  Google Scholar 

  • Mason KO, Mason WH, Winsborough HH, Poole WK (1973) Some methodological issues in cohort analysis of archival data. Am Sociol Rev 38:242–258

    Article  Google Scholar 

  • McLanahan S, Sandefur G (1994) Growing up with a single parent, what hurts, what helps. Harvard University Press, Boston

    Google Scholar 

  • Messner SF (1983) Regional and racial effects on the urban homicide rate: the subculture of violence revisited. Am J Sociol 88:997–1007

    Article  Google Scholar 

  • Messner SF, Sampson RJ (1991) The sex ratio, family disruption, and rates of violent crime: the paradox of demographic structure. Social Forces 69:693–713

    Article  Google Scholar 

  • National Center for Health Statistics (2003) Vital statistics of the United States: natality. US Government Printing Office. Available at: http://www.cdc.gov/nchs/data/statab/natfinal2003.annvol1_17

  • O’Brien RM (2000) Age period cohort characteristic models. Soc Sci Res 29:123–139

    Article  Google Scholar 

  • O’Brien RM, Stockard J, Isaacson L (1999) The enduring effects of cohort characteristics on age-specific homicide rates, 1960–1995. Am J Sociol 104:1061–1095

    Article  Google Scholar 

  • O’Hare WP (1996) A new look at poverty in america. Popul Bull 51(2):48. Population Reference Bureau, Washington DC

    Google Scholar 

  • Rawlings JO (1988) Applied regression analysis: a research tool. Wadsworth & Brooks/Cole, Pacific Groove, CA

    Google Scholar 

  • Robertson C, Gandini S, Boyle P (1999) Age-period-cohort models: a comparative study of available methodologies. J Clin Epidemiol 52:569–583

    Article  Google Scholar 

  • Sampson RJ (1985) Race and criminal violence: a demographically disaggregated analysis of urban homicide. Crime and Delinq 31:47–82

    Article  Google Scholar 

  • Sampson RJ (1986) Effects of socioeconomic context on official reaction to juvenile delinquency. Am Sociol Rev 51:876–886

    Article  Google Scholar 

  • Sampson RJ (1987) Urban black violence: the effects of male joblessness and family disruption. Am J Sociol 93:348–382

    Article  Google Scholar 

  • Sampson RJ, Wilson WJ (1995) Toward a theory of race, crime, and urban inequality. In: Hagan J, Peterson RD (eds) Crime and inequality. Stanford University Press, Stanford California, pp 37–54

    Google Scholar 

  • SAS (2004) SAS/GLM: Version 8. SAS institute incorporated, Cary NC

  • Savolainen J (2000) Relative cohort size and age-specific arrest rates: a conditional interpretation of the Easterlin effect. Criminology 38:117–136

    Article  Google Scholar 

  • Scheffé H (1959) The analysis of variance. Wiley & Sons, New York

    Google Scholar 

  • Searle SR (1971) Linear models. Wiley & Sons, New York

    Google Scholar 

  • Smith HL (2004) Response: cohort analysis redux. In: Stolzenberg RM (ed) Sociological methodology 2004. American Sociological Association, New York, pp 111–119

    Google Scholar 

  • Steffensmeier DJ, Allan EM, Harer MD, Streifel C (1989) Age and the distribution of crime. Am J Sociol 94:803–831

    Article  Google Scholar 

  • Steffensmeier D, Harer MD (1999) Making sense of recent U.S. crime trends, 1980 to 1996/1998: age composition and other explanations. J Res Crime Delinq 36:235–274

    Article  Google Scholar 

  • US Bureau of the Census (1995, 2000, 2005 a) Current population surveys: series P-25. US Government Printing Office, Washington DC (Numbers 98, 114, 170, 519, 870, 1000, 1022, 1058, 1127, for 1995, 2000, 2005 data). http://www.census.gov/popest/states/tables/NST2007-01.xls and www.census.gov/popest/archives/EST90INTERCENSAL/US-EST90INT-dataset.html

  • US Bureau of the Census (1946, 1990, b) Vital statistics of the United States: natality. US Government Printing Office, Washington DC

  • Vandeschrick C (2001) The Lexis diagram, a misnomer. Demogr Res 4:97–124

    Article  Google Scholar 

  • Williams KR (1984) Economic sources of homicide: re-estimating the effects of poverty and inequality. Am Sociol Rev 49:283–289

    Article  Google Scholar 

  • Williams KR, Flewelling RL (1988) The social production of criminal homicide: a comparative study of disaggregated rates in American cities. Am Sociol Rev 53:421–431

    Article  Google Scholar 

  • Yang Y, Fu WJ, Land KC (2004) A methodological comparison of age-period-cohort models: the intrinsic estimator and conventional generalized linear models. In: Stolzenberg RM (ed) Sociological methodology 2004. American Sociological Association, New York, pp 75–110

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Sociology, University of Oregon, Eugene, OR, 97403, USA

    Robert M. O’Brien

  2. Planning, Public Policy and Management, University of Oregon, Eugene, OR, USA

    Jean Stockard

Authors
  1. Robert M. O’Brien
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean Stockard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robert M. O’Brien.

Rights and permissions

Reprints and permissions

About this article

Cite this article

O’Brien, R.M., Stockard, J. Can Cohort Replacement Explain Changes in the Relationship Between Age and Homicide Offending?. J Quant Criminol 25, 79–101 (2009). https://doi.org/10.1007/s10940-008-9059-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10940-008-9059-1

Keywords

Search

Navigation