Constant infusion case of one compartment pharmacokinetic model with simultaneous first-order and Michaelis–Menten elimination: analytical solution and drug exposure formula

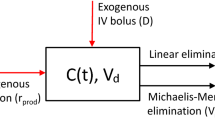
Abstract

The main objective of this article is to propose the closed-form solution of one-compartment pharmacokinetic model with simultaneous first-order and Michaelis–Menten elimination for the case of constant infusion. For the case of bolus administration, we have previously established a closed-form solution of the model through introducing a transcendent X function. In the same vein, we found here a closed-form solution of constant infusion could be realized through introducing another transcendent Y function. For the general case of constant infusion of limited duration, the closed-form solution is then fully expressed using both X and Y functions. As direct results, several important pharmacokinetic surrogates, such as peak concentration $C_{max}$ and total drug exposure AUC$_{0-\infty }$, are found the closed-form expressions and ready to be analyzed. The new pharmacokinetic knowledge we have gained on these parameters, which largely exhibits in a nonlinear feature, is in clear contrast to that of the linear case. Finally, with a pharmacokinetic model adapted from that formerly reported on phenytoin, we numerically analyzed and illustrated the roles of different model parameters and discussed their influence on drug exposure. To conclude, the present findings elucidate the intrinsic quantitative structural properties of such pharmacokinetic model and provide a new avenue for future modelling and rational drug designs.

Appendices

Appendix 1: Proof of Lemma 1

Proof

(i) It is clear that $C^{\infty }$ is the unique positive equilibrium of Model (8) since $\frac{dC(t)}{dt}\bigg |_{C(t)=C^{\infty }}=0$. Moreover, we have $C'(t)>0$ as long as $0\le C(t)< C^{\infty }$, resulting in C(t) is monotonically increasing as t increases. Hence, $C^{\infty }$ is an upper bound for C(t) for $t>0$. As well, when $0\le C(t)<C^{\infty }$, the second order derivative

$$\begin{aligned} \frac{d^2C(t)}{dt^2}=-\left( k_{el}+\frac{V_mK_m}{(K_m+C(t))^2}\right) \cdot \frac{dC(t)}{dt}<0, \end{aligned}$$

implying $C'(t)$ decreases to zero as $t\rightarrow \infty$. By the monotone bounded convergence theorem, we can deduce that $C^{\infty }$ is the upper limit for C(t).

(ii) Denote a function by $f(x)=\sqrt{x^2+a}+x\,(a>0)$ for a real variable x. It follows $f'(x)=x/\sqrt{x^2+a}+1>0$ that f(x) is strictly increasing with respect to x. Let $a= 4\frac{r}{k_{el}}K_m>0$, then we obtain

$$\begin{aligned} \displaystyle C^{\infty }_{\beta }=\frac{1}{2}f\left( C_\beta -\frac{r}{k_{el}}\right) >\frac{1}{2}f\left( K_m-\frac{r}{k_{el}}\right) =K_m \end{aligned}$$

since $C_{\beta }>K_m$□.

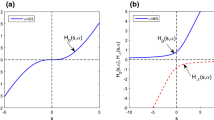
Appendix 2: Illustration of $X_0$ and $Y_0$ for different values of $p_1$, $p_2$, $q_1$ and $q_2$

In Fig. 5, we plot how parameters $p_1$, $p_2$, $q_1$ and $q_2$ change the appearance of X and Y functions in the first quadrant, where $p_1+p_2=1$ and $q_1+q_2=1$ are considered. As shown in Fig. 5a, when $p_1$ varies from a small value of 1/500 to a large value of 1/2, we observe that $X_0(s,p_1,p_2)$ tends to increase faster for a larger value of $p_1$, and when $p_1$ is close to unity, $X_0(s,p_1,p_2)$ is close to the identity line as $X_0(s,p_1,p_2)=s$. In Fig. 5b, $Y_0(s,q_1,q_2)$ shows a similar property as a faster increase of $Y_0(s,q_1,q_2)$ can be observed for a larger $q_1$. Meanwhile, the $Y(s,q_1,q_2)$ is also close to the identity line as $Y_0(s,q_1,q_2)=s$ when $q_1$ is close to unity. The range of $Y_0(s,q_1,q_2)$ is $(0,q_1/(q_1+q_2))$ that depends on the choice of $q_1$ and $q_2$.

Fig. 5

Illustration of how parameters $p_1$, $p_2$, $q_1$ and $q_2$ affect the graphs of principal real branches $X_0$ and $Y_0$ transcendent functions in the first quadrant, where $p_1+p_2=q_1+q_2=1$, $X_0\in (0,\infty )$ for all $s>0$ and $Y_0\in (0,q_1)\subset (0,1)$ for all $s\in (0,q_1^{q_1}q_2^{q_2})\subset (0,1)$

Appendix 3: Proof of Proposition 1

Proof

(i) By checking the explicit expressions of $C^{\infty }$ and $C^{\infty }_{\beta }$, it is easy to see $C^{\infty }=0$ and $C^{\infty }_{\beta }=C_{\beta }$ when $r=0$.

(ii) If $\displaystyle C_{\beta }=\frac{r}{k_{el}}$, namely $r=k_{el}C_{\beta }=k_{e,tot}K_m$, then we have $\displaystyle C^{\infty }=C^{\infty }_{\beta }=\sqrt{\frac{k_{e,tot}}{k_{el}}}K_m$. If $\displaystyle C_{\beta }>\frac{r}{k_{el}}$, namely $r<k_{el}C_{\beta }$, then we obtain $C^{\infty }_{\beta }>C^{\infty }$. If $\displaystyle C_{\beta }<\frac{r}{k_{el}}$, we have $r<k_{el}C_{\beta }$ and $C^{\infty }_{\beta }<C^{\infty }$.

(iii) Consider the derivatives of $C^{\infty }$ and $C^{\infty }_{\beta }$ with respect to variable r. With straightforward calculations and denote $\displaystyle x=\frac{r}{k_{el}}$, we obtain

$$\begin{aligned} \frac{d C^{\infty }(r)}{dr}=\frac{K_m+C^{\infty }}{\sqrt{(C_{\beta }-x)^2+4K_mx}}\frac{1}{k_{el}}>0 \end{aligned}$$

and

$$\begin{aligned} \frac{d C^{\infty }_{\beta }(r)}{dr}=\frac{K_m-C^{\infty }_{\beta }}{\sqrt{(C_{\beta }-x)^2+4K_mx}}\frac{1}{k_{el}}<0 \end{aligned}$$

due to $K_m<C^{\infty }_{\beta }$ by Lemma 1. Therefore with respect to r, $C^{\infty }$ is an increasing function and $C^{\infty }_{\beta }$ is a decreasing function.

Now we consider the limit of $C^{\infty }_{\beta }$ as r tends to infinity. Multiplying by

$$\begin{aligned} \sqrt{(C_{\beta }-\frac{r}{k_{el}})^2+4\frac{r}{k_{el}}K_m}-(C_{\beta }-\frac{r}{k_{el}}) \end{aligned}$$

at both the numerator and denominator for expression of $C^{\infty }_{\beta }$ if we write $C^{\infty }_{\beta }$ as $C^{\infty }_{\beta }/1$, we obtain

$$\begin{aligned} \begin{aligned} \lim _{r\rightarrow +\infty }C^{\infty }_{\beta }= \lim _{r\rightarrow +\infty } \frac{\frac{2}{k_{el}}K_m}{\sqrt{(\frac{C_{\beta }}{r}-\frac{1}{k_{el}})^2+4\frac{K_m}{k_{el}r}}-(\frac{C_{\beta }}{r}-\frac{1}{k_{el}})}=K_m. \end{aligned} \end{aligned}$$

$\displaystyle \lim _{r\rightarrow +\infty }C^{\infty }=+\infty$ is obvious.□

Appendix 4: Explicit solutions of one-compartment models with a single elimination pathway, linear or Michaelis–Menten, in the case of constant infusion

One-compartment pharmacokinetic model with a single linear elimination pathway for a constant infusion:

$$\begin{aligned} \left\{ \begin{array}{ll} C'(t)=f(t)-k_{el}C(t), t>0\\ C(0)=0, \end{array} \right. \end{aligned}$$

(25)

where f(t) is given by Eq. (18). Its explicit solution is

$$\begin{aligned} C(t)=\left\{ \begin{array}{ll} \frac{D}{TV_dk_{el}}\left( 1-e^{-k_{el}t}\right) ,\quad 0\le t\le T,\\ C(T)e^{-k_{el}(t-T)},\quad t\ge T. \end{array} \right. \end{aligned}$$

(26)

One-compartment pharmacokinetic model with a single Michaelis–Menten elimination pathway for a constant infusion:

$$\begin{aligned} \left\{ \begin{array}{ll} C'(t)=f(t)-\frac{V_{m}\cdot C(t)}{K_m+C(t)}, t>0\\ C(0)=0, \end{array} \right. \end{aligned}$$

(27)

where f(t) is given by Eq. (18). Its explicit solution is

(i) If $0\le t\le T$, we have

$$\begin{aligned} C(t)=\left\{ \begin{array}{ll} \displaystyle -K_m+\sqrt{K_m^2+2V_mK_mt},\quad R=V_{m}V_d,\\ \displaystyle -\frac{DK_m}{D-TV_{m}V_d}-\frac{K_m T V_{m}V_d}{D- T V_{m}V_d}W\left( -1,-\frac{D}{TV_{m}V_d}\exp \left( -\frac{DK_m T V_d+(D-TV_{m}V_d)^2t}{K_mV_{m}(TV_d)^2}\right) \right) ,\quad R>V_{m}V_d,\\ \displaystyle -\frac{DK_m}{D-TV_{m}V_d}-\frac{K_m T V_{m}V_d}{D- T V_{m}V_d}W\left( 0,-\frac{D}{TV_{m}V_d}\exp \left( -\frac{DK_m T V_d+(D-TV_{m}V_d)^2t}{K_mV_{m}(TV_d)^2}\right) \right) ,\quad R<V_{m}V_d. \end{array} \right. \end{aligned}$$

(28)

(ii) If $t\ge T$, we have

$$\begin{aligned} C(t)=K_m\cdot W\left( 0,\frac{C(T)}{K_m}\exp \left( \frac{C(T)-V_{m}\cdot (t-T)}{K_m}\right) \right) . \end{aligned}$$

(29)