Introduction

Vascular adhesion protein-1 (VAP-1) is a 180 kDa transmembrane homodimeric glycoprotein [1, 2]. As an amine oxidase, it catalyzes the oxidation of amines to form aldehydes, hydrogen peroxide and ammonia. VAP-1 has both enzymatic and non-enzymatic activities, and plays an important role in leukocyte trafficking and adhesion [3,4,5]. Membrane bound VAP-1 (mVAP-1) can be cleaved by metalloproteinases and shed as soluble VAP-1 (sVAP-1). sVAP-1 concentrations increase at sites of inflammation and its upregulation and subsequent increased oxidase activity plays a role in many inflammatory diseases [6, 7]. sVAP-1 is upregulated in diabetic patients [8, 9] and subjects with early stages of chronic kidney disease [10], where VAP-1 activity is thought to play an important pathogenic role.

ASP8232 is a small molecule VAP-1 inhibitor that was evaluated for the treatment of diabetic kidney disease (DKD) as an add-on to first-line antihypertensive therapy in a Phase 2 study (ALBUM study). In this trial, ASP8232 was found effective in reducing albuminuria following a 12-week treatment with daily oral doses of 40 mg ASP8232 in DKD patients receiving standard of care, i.e. angiotensin converting enzyme inhibitor (ACEi) or angiotensin receptor blocker (ARB) therapy [11]. A 98.6% inhibition of VAP-1 activity was observed after 2 weeks of ASP8232 treatment, and this suppression remained throughout the treatment duration [11]. However, a quantitative understanding of the pharmacokinetic-pharmacodynamic (PK-PD) relationship following ASP8232 administration is currently lacking. Characterizing this relationship would provide the ability to predict the time to steady-state ASP8232 concentration and the VAP-1 inhibition response to different ASP8232 concentrations, to identify individual covariate effects which influence this relationship, and to simulate the expected dose – PD response curve for DKD patients.

Population PK-PD models describe the absorption and disposition of a drug and characterize the relationship between compound and its target. Occasionally, the target can influence the disposition, i.e. distribution and elimination processes, of the drug. These processes can be described using target mediated drug disposition (TMDD) models, which incorporate target binding and turnover concepts and allow for a semi-mechanistic interpretation of drug disposition [12, 13]. Estimating the parameters for a full TMDD model requires a rich dataset and information during each phase of the PK profile [13]. Therefore, approximations to the full TMDD model were introduced, such as the quasi-equilibrium, quasi-steady state and Michaelis–Menten TMDD approximations [14,15,16]. These approximations rely on certain assumptions, e.g. rapid binding of drug to its target, which need to be checked for their validity given the data.

In this study, a population TMDD model was developed which characterizes the PK-PD relationship of ASP8232 and quantifies the relationship between VAP-1 concentrations and activity. The model simultaneously describes PK, sVAP-1 and VAP-1 plasma activity data from four clinical trials over a range of oral APS8232 doses in healthy volunteers, DKD patients and patients with diabetic macular edema (DME). The model was applied to predict the time to steady-state ASP8232 concentration and expected VAP-1 inhibition following a one year treatment with different ASP8232 doses.

Methods

Clinical studies

ASP8232 and sVAP-1 plasma concentrations, and VAP-1 plasma activity measurements from four clinical studies were included in the PK-PD analysis:

  1. 1.

    A Phase 1, first-in-human study in healthy male and female subjects (study 8232-CL-0001),

  2. 2.

    a Phase 1 study in patients with renal impairment and patients having Type 2 diabetes mellitus (T2DM) with chronic kidney disease (CKD) (study 8232-CL-0002),

  3. 3.

    a Phase 2 study in patients with DME (VIDI study),

  4. 4.

    a Phase 2 study in patients with DKD (ALBUM study; [11]).

sVAP-1 concentrations were not measured in studies 8232-CL-0001 and 8232-CL-0002. In total, 3498 ASP8232 plasma concentration records, 5893 VAP-1 plasma activity records and 1714 VAP-1 plasma concentration records from these four clinical studies were included in the PK-PD analysis. A study overview and the distributions of continuous covariates and baseline PD measurements and categorical covariates can be found in Table 1, 2 and 3, respectively.

Table 1 Study overview and number of records used for PK-PD modeling
Full size table
Table 2 Baseline and continuous covariate distributions
Full size table
Table 3 Categorical covariate distribution
Full size table

Study 8232-CL-0001 was a Phase 1, double-blind, randomized, placebo-controlled, single and multiple ascending oral dose study of ASP8232 in healthy subjects (unpublished data). In the single dose cohort, 10 doses were evaluated (0.1, 1, 3, 10, 30, 100, 300, 1000, 3000 or 6000 mg) with 8 subjects per group (6 active; 2 placebo). The multiple dose cohort of the study consisted of 3 groups, each with 16 subjects (12 active; 4 placebo). In the low dose group, a single dose of 0.2 mg ASP8232 or placebo was administered on day 1, followed by a loading dose of 1 mg on day 8, and thereafter 13 daily doses of 0.2 mg until day 21. In the mid dose group, subjects received 200 mg ASP8232 on day 1, 600 mg (loading dose) on day 2, and 200 mg daily from day 3 to 14, or placebo from day 1–14. In the high dose group, subjects received 800 mg ASP8232 on day 1, 1100 mg (loading dose) on day 2, and 800 mg daily from day 3 to 14, or placebo from day 1–14.

Study 8232-CL-0002 was a Phase 1 study to evaluate the effect of renal impairment on the PK, PD and safety of ASP8232 (part 1) and a multiple dose, placebo-controlled study in subjects with Type 2 diabetes mellitus and CKD, i.e. DKD (part 2) (ClinicalTrials.gov NCT02218099). In part 1, 8 subjects with either mild, moderate or severe renal impairment and 16 matching healthy subjects received a single 200 mg oral ASP8232 dose. In part 2, 15 DKD subjects (10 active; 5 placebo) received a loading dose of 250 mg ASP8232 on day 1 followed by daily dosing of 150 mg ASP8232 for 27 days.

Study 8232-CL-3001 (VIDI study) was a Phase 2, double-blind, randomized study in subjects with DME (ClinicalTrials.gov NCT02302079). Data from a 4-week screening, 12-week treatment and 12-week follow-up period were available for 31 subjects receiving placebo and 0.3 mg intravitreal ranibizumab injections, 32 subjects receiving 40 mg daily oral ASP8232 and 33 subjects receiving 40 mg daily oral ASP8232 and 0.3 mg intravitreal ranibizumab injections.

Study 8232-CL-0004 (ALBUM study; [11]) was a Phase 2 double-blind, randomized, placebo-controlled study in DKD patients (ClinicalTrials.gov NCT02358096). Data from a 1-week screening, 5-week pre-treatment, 12-week treatment and 24-week follow-up period were available for 60 subjects receiving 40 mg daily oral ASP8232 and 60 subjects receiving placebo.

Analytical methods

Plasma samples for the PK of ASP8232 were analyzed using a liquid chromatography-mass spectrometry assay measuring total ASP8232 concentrations, i.e. ASP8232 unbound and bound to sVAP-1 in plasma. sVAP-1 plasma concentrations were analyzed using an enzyme linked immunosorbent assay based on a commercial kit (Human sVAP-1 ELISA, BE59091, IBL International, Hamburg, Germany; with assay performance according to the packaging insert of the manufacturer) measuring total sVAP-1 concentrations, i.e. sVAP-1 unbound and bound to ASP8232 in plasma. Plasma samples for enzymatic activity of VAP-1 were analyzed using an enzymatic assay with a radioactive substrate (14C-benzylamine hydrochloride) via liquid–liquid extraction followed by liquid scintillation counting. These assays were formally validated and the lower limit of quantification was 0.1 ng/mL and 0.625 ng/mL for the plasma PK and sVAP-1 assay, respectively. For plasma VAP-1 activity, no measurements were reported below the quantification limit.

Main modeling assumptions

The following assumptions, relevant for the modeling analysis, were made:

  1. 1.

    The PK of ASP8232 was not influenced by binding to any other target than VAP-1. ASP8232 could potentially bind to sVAP-1 in the central compartment and to mVAP-1 in the central and peripheral compartments.

  2. 2.

    The measured VAP-1 plasma activity was driven by the unbound sVAP-1 plasma concentrations and this relationship was assumed to be constant over time.

  3. 3.

    Compared with other processes, binding of ASP8232 to VAP-1 was assumed to be rapid while VAP-1 turnover and elimination of the VAP-1-ASP8232 complex were assumed to be negligible.

  4. 4.

    The dissociation constant (KD) was assumed to be the same for binding of ASP8232 to sVAP-1 and mVAP-1 across all model compartments.

  5. 5.

    The VAP-1 concentration may differ for each model compartment.

  6. 6.

    The molecular weight, used to convert dose or concentrations to molar units, was 444 g/mol for ASP8232 (free base) and 84,622 g/mol for the VAP-1 monomer (UniProt nr. Q16853) with difference between mVAP-1 and sVAP-1 assumed to be negligible as the cleavage site for mVAP-1 is close to the membrane [7].

Population analysis methodology and computation

The PK-PD data were analyzed using a population approach, also called mixed-effects modeling. A population model is composed of a structural model parameterized with structural (fixed effects) parameters, and a stochastic model quantifying the inter-individual (IIV) and residual variability [17]. Parameter estimation and model simulations were performed using NONMEM version 7.3 in combination with PsN version 4.6.0 [18, 19]. Processing of NONMEM output was performed using R version 3.3.2 and RStudio version 1.0.44.

ASP8232 PK-PD TMDD model development

The starting PK-PD TMDD model was a first-order absorption three compartmental model with binding of ASP8232 to VAP-1 according to the main modeling assumptions. In short, target binding was assumed to be at equilibrium and consequently the dissociation constant (KD) was given by Eq. 1.

$$ K_{D} = \frac{{\left[ {ASP8232_{unbound} } \right] \cdot \left[ {VAP1_{unbound} } \right]}}{{\left[ {ASP8232 - VAP1complex} \right]}} $$
(1)

From this equation the free fraction was derived for (i) ASP8232 in the central compartment (ϕdrug,c), (ii) ASP8232 in each peripheral compartment ( ϕdrug,p1 and ϕdrug,p2) and (iii) total VAP1 (tVAP1c = sVAP1c + mVAP1c) in the central compartment (ϕtVAP1,c) (Eq. 2–5).

$$ \phi_{drug,c} = \frac{{\left[ {ASP8232_{c} } \right] - \left[ {tVAP1_{c} } \right] - K_{D} + \sqrt {(\left[ {ASP8232_{c} } \right] - \left[ {tVAP1_{c} } \right] - K_{D} )^{2} + 4 \cdot K_{D} \cdot \left[ {ASP8232_{c} } \right]} }}{{2 \cdot [ASP8232_{c} ]}} $$
(2)
$$ \phi_{drug,p1} = \frac{{\left[ {ASP8232_{p1} } \right] - \left[ {mVAP1_{p1} } \right] - K_{D} + \sqrt {(\left[ {ASP8232_{p1} } \right] - \left[ {mVAP1_{p1} } \right] - K_{D} )^{2} + 4 \cdot K_{D} \cdot \left[ {ASP8232_{p1} } \right]} }}{{2 \cdot [ASP8232_{p1} ]}} $$
(3)
$$ \phi_{drug,p2} = \frac{{\left[ {ASP8232_{p2} } \right] - \left[ {mVAP1_{p2} } \right] - K_{D} + \sqrt {(\left[ {ASP8232_{p2} } \right] - \left[ {mVAP1_{p2} } \right] - K_{D} )^{2} + 4 \cdot K_{D} \cdot \left[ {ASP8232_{p2} } \right]} }}{{2 \cdot [ASP8232_{p2} ]}} $$
(4)
$$ \phi_{tVAP1,c} = \frac{{\left[ {tVAP1_{c} } \right] - \left[ {ASP8232_{c} } \right] - K_{D} + \sqrt {(\left[ {tVAP1_{c} } \right] - \left[ {ASP8232_{c} } \right] - K_{D} )^{2} + 4 \cdot K_{D} \cdot \left[ {tVAP1_{c} } \right]} }}{{2 \cdot \left[ {tVAP1_{c} } \right]}} $$
(5)

With the derived free fractions, the starting TMDD PK-PD model was described by the following differential equations (Eq. 6–9) with A1, A2, A3 and A4 defined as the drug amount in the depot, central, first peripheral and second peripheral compartment, respectively.

$$ \frac{{dA_{1} }}{dt} = - k_{a} \cdot A_{1} $$
(6)
$$ \frac{{dA_{2} }}{dt} = k_{a} \cdot A_{1} - \phi_{drug,c} \cdot k_{20} \cdot A_{2} - \phi_{drug,c} \cdot k_{23} \cdot A_{2} + \phi_{drug,p1} \cdot k_{32} \cdot A_{3} - \phi_{drug,c} \cdot k_{24} \cdot A_{2} + \phi_{drug,p2} \cdot k_{42} \cdot A_{4} $$
(7)
$$ \frac{{dA_{3} }}{dt} = \phi_{drug,c} \cdot k_{23} \cdot A_{2} - \phi_{drug,p1} \cdot k_{32} \cdot A_{3} $$
(8)
$$ \frac{{dA_{4} }}{dt} = \phi_{drug,c} \cdot k_{24} \cdot A_{2} - \phi_{drug,p2} \cdot k_{42} \cdot A_{4} $$
(9)

The dependent variables for the PK-PD analysis were the log-transformed total ASP8232 and sVAP-1 plasma concentrations, as well as VAP-1 plasma activity, which were predicted by the model according to the following individual prediction (IPRED) Eqs. (10–12).

$$ IPRED_{drug} = \log \left( {\phi_{drug,c} \cdot \frac{{A_{2} }}{V2} + \left( {1 - \phi_{drug,c} } \right) \cdot \frac{{A_{2} }}{V2} \cdot \frac{{sVAP1_{c} }}{{tVAP1_{c} }}} \right) $$
(10)
$$ IPRED_{sVAP1} = \log \left( {sVAP1_{c} } \right) $$
(11)
$$ IPRED_{{VAP1_{act} }} = \log \left( {SL \cdot \left( {\phi_{tVAP1,c} .sVAP1_{c} } \right)^{POW} } \right) $$
(12)

Log-transformed data were modeled with additive residual error. Initially, improvements or simplifications of the structural model were considered, which included the estimation of one shared volume parameter for the two peripheral compartments. Absorption transit compartments were evaluated as a mechanism to account for a delay in oral absorption. Alternative relationships between sVAP-1 plasma concentrations and VAP-1 plasma activity, such as a linear relationship, were evaluated.

Hereafter, an appropriate individual random effect structure was implemented following standard model selection and acceptance criteria (see section Model Evaluation). Inter-individual variability (IIV) was included by using an exponential relationship assuming log-normal distributions. Subsequently, a limited covariate analysis was performed to allow integration of data from the different studies. Since an exhaustive covariate analysis was not a specific objective of this analysis, only key covariates that were expected to explain differences between studies were selected, e.g. because of different inclusion criteria. The possible effect of sex, body weight and baseline estimated glomerular filtration rate (eGFR) using the CKD-EPI equation [20] were evaluated on the model parameters with IIV included. In addition, these possible covariate effects were also evaluated on the volume of distribution as it is expected that body weight and sex may have an effect on this parameter based on physiological grounds. A power or sigmoid emax relationship was evaluated for continuous covariates, while a sex effect was tested using a separate estimate for females. The possible effect of each covariate was tested in a univariate manner and ranked according to the extent of the drop in objective function value. Subsequently, each covariate that had a significant effect at p < 0.01 (drop of at least 6.63 points; χ2, 1 degree of freedom) was added to the model one-by-one according to their initial rank order until no more covariates could be added, i.e. p > 0.01. Each relationship was retained if upon backward deletion, it was significant at a stricter criterion of p < 0.001 (drop of at least 10.8 points; χ2, 1 degree of freedom).

Model evaluation

Standard model acceptance criteria were applied during model development and a range of goodness-of-fit plots were inspected visually to evaluate the model fit [21,22,23,24]. Visual predictive checks (VPC [25, 26]) were performed based on 100 replications of the original dataset, using scheduled time as independent variable and stratified per variable, treatment group and study.

For evaluation purposes, VAP-1 activity values were transformed to VAP-1 inhibition percentages via the individual baseline VAP-1 activity as follows (Eq. 13):

$$ VAP1_{inhibition,\% } = 100 \cdot \frac{{VAP1_{act,bsl,i} - VAP1_{act,j,i} }}{{VAP1_{act,bsl,i} }} $$
(13)

where VAP1act,bsl,i is the median of pre-dose VAP-1 activity observations for an individual i, and VAP1act,j,i the jth VAP-1 activity observation of individual i.

Model simulation

Individual parameters were obtained using empirical Bayes estimation (EBE) in NONMEM. Based on these parameters and the final model, simulations were performed for a virtual DKD population predicting the AUC24h,52w and VAP-1inhibition,52w for a dose range of 0.1 to 40 mg daily dosing, which have potential to be used in a dose-finding study. These simulations were based on individual predictions (IIV included; parameter uncertainty and residual variability excluded) based on 10,000 virtual DKD patients, with sex distribution as observed in the ALBUM study and individual eGFR values sampled from a normal distribution with mean and standard deviation as observed in the ALBUM study. In addition, simulations were performed to predict the ASP8232 concentration—time profile after 52 weeks of daily ASP8232 dosing for a typical male subject with eGFR of 44 mL/min/1.73m2, i.e. the median value observed in the ALBUM study. The 52 week dosing period was selected to ensure steady state was reached at all dose levels. From these simulations, the following key secondary ASP8232 PK parameters were derived: steady-state exposure (AUC24h,52w), maximum plasma concentration at steady state (Cmax52w) and the corresponding time at which Cmax is reached (Tmax52w), the time to reach steady state (Tss) and the apparent half-life (t1/2). Tss was defined as the time to reach 97% of the trough concentration predicted after 52 weeks of daily ASP8232 dosing. The apparent half-life (t1/2) was derived from the simulated Tss by dividing the simulated Tss by 5.

Results

ASP8232 PK-PD TMDD model

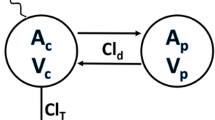
The PK-PD of ASP8232 was best described by a three compartmental model with ASP8232 distribution from the central compartment (parameterized with volume V2) into two peripheral compartments (with volume V3 = V2 to reduce parameter correlations, and inter-compartmental clearance Q, and volume V4 and intercompartmental clearance Q2, respectively) (Fig. 1). Elimination of unbound ASP8232 plasma concentration from the central compartment was characterized by estimating clearance (CL), and thus the elimination rate constant (kel) via CL/V2. Drug absorption was modeled via a first order absorption rate constant (ka) and the addition of a transit compartment with estimated lag time (LAG). The addition of the transit compartment resulted in a more stable model with similar objective function value (difference of 0.0640 points). The concentration of sVAP-1 in the central compartment (sVAP-1c) was estimated. The concentrations (amount accessible from the central or peripheral compartment volumes) of mVAP-1 in the central and two peripheral compartments (mVAP1c, mVAP1p1 and mVAP1p2) were estimated relative to sVAP-1c. Binding of ASP8232 to sVAP-1c and to mVAP-1 in all compartments was parameterized with KD. VAP-1 plasma activity was a function of unbound sVAP-1 plasma concentration according to a power model with estimated slope parameter (SL) and power coefficient (POW). IIV was implemented on CL, SL and sVAP-1c. Data were log-transformed and modeled with additive residual error, with separate estimates for data from the Phase 2 studies (ALBUM and VIDI study) implemented by estimating a factor for ASP8232 plasma concentrations and VAP-1 plasma activities. In addition to estimation of the variances for IIV on CL, sVAP-1c and SL, all covariances were estimated (full omega block). IIV was not included on V2, due to instability of the resulting models.

Fig. 1
figure 1

Schematic representation of the ASP8232 PK-PD model. Drug absorption is characterized via estimated lag time and ka including one transit compartment (Transit). Unbound ASP8232 is eliminated from the central compartment via kel, and can distribute to the peripheral compartments. In the central compartment ASP8232 can bind to sVAP-1c or mVAP-1c, while in the peripheral compartments ASP8232 can bind to mVAP-1p1 = mVAP-1p2. ASP8232 in complex with target cannot distribute or be eliminated, and binding is assumed to occur at equilibrium with estimated KD. Rate constants kel, k23, k32, k24 and k42 are secondary parameters, based on estimated parameters CL, V2, V3 = V2, V4, Q and Q2. VAP-1 plasma activity is a function of free soluble VAP-1 plasma concentration according to a power model with estimated slope and power parameters, SL and POW, respectively

Full size image

The final model contained an effect of eGFR on CL, which was implemented via a sigmoid Emax relationship with power estimate fixed to a large value (10) indicating an on or off effect relative to the estimated EC50 of this relationship. In addition, a sex effect on the VAP-1 concentrations, and an effect of eGFR on the relative bioavailability via a power relationship, were included in the model. The VAP-1 concentrations were found to be 12.5% higher for females. The combined effect of all covariates on ASP8232 steady-state exposure, AUC24h,52w, and maximum steady-state concentration, Cmax52w, is presented in Fig. 2. AUC24h,52w and Cmax52w are expected to increase with decreasing eGFR, i.e. with impaired renal function. The EBE-based individual derived AUC24h,52w and Cmax52w are scattered around the population prediction for this relationship (Fig. 2; dots). The influence of sex on both parameters is predicted to be minimal, as seen by the overlapping lines for a typical male and female subject (Fig. 2; lines). During model development, it was found that differences in exposure between healthy volunteers and patients were covered entirely by their difference in eGFR.

Fig. 2
figure 2

Influence of sex and eGFR on ASP8232 AUC24h,52w (a) and Cmax52w (b) based on empirical bayes estimates from the model for subjects receiving 40 mg daily dosing (ALBUM and VIDI study). Individual (dots) and population predictions (lines) for females (blue) and males (red). The line for females is barely visible due to overlap with males (Color figure online)

Full size image

The ASP8232 exposure appeared to increase less than proportional for doses ≥ 300 mg. These dose levels were excluded during model development, as they were outside the considered clinically relevant exposure range. During development, outliers were identified (defined as CWRES > 3 or < -3) and excluded from further analysis to stabilize the model. As such, 1.8% of the ASP8232 plasma concentrations, 2.3% of the VAP-1 plasma activities and 1.4% of the VAP-1 plasma concentrations were identified as outliers. Re-estimation of the model including all data did not noticeably impact the estimates or any conclusions drawn.

Model evaluation

All fixed and stochastic parameters were estimated with good precision (RSE < 35%, Table 4). The eta shrinkages were 8, 9 and 18% for IIV on CL, sVAP-1c and SL, respectively, while the epsilon shrinkages were 3, 6 and 3% for ASP8232 concentration, sVAP-1 concentration and VAP-1 activity, respectively. Correlations between structural parameter estimates were between − 0.95 and 0.95, with the strongest correlation, 0.91, observed between the KD and power of the VAP-1 concentration—activity relationship. The NONMEM model code is available in the Supplementary Material: in this code, sVAP-1c, mVAP-1c, mVAP-1p1 and mVAP-1p2 are referred to as Bmax, Bmax2, Bmax3 and Bmax4, respectively. Overall, the ASP8232 PK-PD model is able to describe the observed ASP8232 and sVAP-1 plasma concentrations and VAP-1 plasma activities well across studies. For the ALBUM study, the VPCs show that the model is able to adequately describe the central tendency and variability in the data for the ASP8232 and sVAP-1 plasma concentrations and the plasma VAP-1 activity (Figs. 3–5). For the three other clinical studies, the VPCs for ASP8232 and sVAP-1 plasma concentrations and VAP-1 plasma activities are presented in the Supplementary Material.

Table 4 Parameter estimates of the ASP8232 PK-PD TMDD model
Full size table
Fig. 3
figure 3

Visual predictive check of ASP8232 plasma concentration in the ALBUM study. ASP8232 was dosed once daily during 12 weeks (2016 h). ASP8232 plasma concentration were measured at week 2 (336 h), 4 (672 h), 8 (1344 h), 12 (2016 h), 16 (2688 h), 24 (4032 h) and 36 (6048 h). Observed data (black dots), observed median (blue line), observed 5th and 95th percentiles (dashed red lines), predicted median (black line) and 90% prediction interval (shaded area) covering the predicted 5th and 95th percentiles (Color figure online)

Full size image
Fig. 4
figure 4

Visual predictive check of VAP-1 plasma concentration in the ALBUM study. ASP8232 or placebo was dosed once daily during 12 weeks (2016 h). VAP-1 plasma concentration was measured at baseline (0 h) and at week 2 (336 h), 4 (672 h), 6 (1008 h), 8 (1344 h), 12 (2016 h), 16 (2688 h), 24 (4032 h) and 36 (6048 h). Observed data (black dots), observed median (blue line), observed 5th and 95th percentiles (dashed red lines), predicted median (black line) and 90% prediction interval (shaded area) covering the predicted 5th and 95th percentiles (Color figure online)

Full size image
Fig. 5
figure 5

Visual predictive check of VAP-1 plasma activity in the ALBUM study. ASP8232 or placebo was dosed once daily during 12 weeks (2016 h). VAP-1 plasma activity was measured at baseline (0 h) and at week 2 (336 h), 4 (672 h), 6 (1008 h), 8 (1344 h), 12 (2016 h), 16 (2688 h), 24 (4032 h) and 36 (6048 h). Observed data (black dots), observed median (blue line), observed 5th and 95th percentiles (dashed red lines), predicted median (black line) and 90% prediction interval (shaded area) covering the predicted 5th and 95th percentiles (Color figure online)

Full size image

The concentration-effect relationship (ASP8232 plasma concentration-VAP-1 percent inhibition) shows that, as observed in the data, the model predicts a near-complete VAP-1 inhibition for ASP8232 concentrations > 50 ng/mL, while below 0.2 ng/mL the inhibition is expected to be minimal (Fig. 6). 50% VAP-1 inhibition is expected at an ASP8232 concentration of approximately 2 ng/mL, irrespective of sex. Below 0.5 ng/mL, there appears to be a bias toward a lower population prediction for VAP-1 inhibition compared with the observed data, as the model predicts that the VAP-1 inhibition should tend to zero with decreasing ASP8232 concentration, while from the observed data, VAP-1 inhibition remains at approximately 20%, even at the lowest measured concentrations.

Fig. 6
figure 6

ASP8232 plasma concentration—VAP-1 inhibition effect relationship. Observations (grey dots) and population prediction of the model for males (red line) or females (blue line). The observed VAP-1 inhibition values were obtained as described in Eq. 13. Negative VAP-1 inhibition observations result from measurement error (Color figure online)

Full size image

Model simulation

Simulations were conducted for DKD patients given between 0.1 and 40 mg of ASP8232 daily for 52 weeks. The median, 5th and 95th percentiles of the simulations are shown in Fig. 7. On average, the inhibition of VAP-1 is expected to be above 90% for ≥ 3 mg daily doses, while inhibition is expected to drop below 50% for < 0.3 mg daily doses. The larger between subject variability in response for doses < 1 mg as compared to higher doses, is expected, as VAP-1 inhibition cannot exceed the maximum of 100%. Similar simulations were conducted to describe the relationship between dose and dose normalized AUC24h,52w. Due to VAP-1 binding, ASP8232 is subjected to target mediated drug elimination, and thus the ASP8232 pharmacokinetics are non-linear. The impact of this non-linearity was visualized by dose-normalizing with 40 mg as reference, whereby the exposure increases less than proportional with dose, and whereby doses ≥ 30 mg result in similar dose normalized exposure as 40 mg (Fig. 8). Compared with 40 mg daily dosing, the dose-normalized exposure is expected to be approximately fourfold higher than daily dosing with 0.1 mg for 52 weeks. In addition, this non-linearity is apparent from the typical individual simulations predicting the ASP8232 concentration – time profile, and the corresponding key secondary PK parameters, for a range of daily ASP8232 doses (Fig. 9, Table 5 and Supplementary Figure S16). From these simulations, the time to reach steady state for ASP8232 concentrations is predicted to be one week for daily doses ≥ 10 mg, and higher for lower doses, e.g. > 40 weeks for 0.1 mg daily dosing (Fig. 10 and Table 5).

Fig. 7
figure 7

Model-predicted average 24 h inhibition of VAP-1 activity (%) versus ASP8232 dose after 52 weeks of daily oral dosing for DKD patients. Simulation based on individual predictions; Median (blue), 5th and 95th percentile (dashed red) of 10,000 replicates (Color figure online)

Full size image
Fig. 8
figure 8

Model-predicted dose-normalized ASP8232 AUC24h,52w, normalized to a dose of 40 mg, versus ASP8232 dose after 52 weeks of daily oral dosing for DKD patients. Simulation based on individual predictions; Median (blue), 5th and 95th percentile (dashed red) of 10,000 replicates. Dose-normalized AUC’s, with 40 mg qd dosing as reference, were obtained via 40*AUC/Dose (Color figure online)

Full size image
Fig. 9
figure 9

Simulation of ASP8232 plasma trough concentration (nM) over time for a typical subject receiving 1, 10 or 40 mg daily ASP8232 doses. Typical subject was defined as a male subject with eGFR of 44 mL/min/1.73m2, i.e. the median value observed in the ALBUM study. Simulated trough concentrations were plotted

Full size image
Table 5 Secondary ASP8232 PK parameters for a typical subject
Full size table
Fig. 10
figure 10

Simulation of the time to reach steady state for ASP8232 plasma concentration or a typical subject receiving a range of daily ASP8232 doses between 0.1 and 40 mg. Time to steady state was defined as the time to reach 97% of the concentration predicted after 52 weeks of daily ASP8232 dosing. Typical subject was defined as a male subject with eGFR of 44 mL/min/1.73m2, i.e. the median value observed in the ALBUM study. Dashed line at 1 week for clarity

Full size image

Discussion

The PK and PD of ASP8232 were successfully characterized using a TMDD model based on data from healthy volunteers, subjects with renal impairment, patients with DKD, and patients with DME. Differences between these populations could be fully explained by an eGFR effect on CL and F1, and no additional descriptive population effects had to be included. Renal excretion of ASP8232 is a minor part of the total elimination of ASP8232. An effect of eGFR exposure (CL and F1) might be explained by the presence of uremic toxins that inhibit pre-systemic metabolizing enzymes in subjects with decreased renal function [27, 28]. Subsequently, the resulting relationship between exposure and eGFR was visualized (Fig. 2), showing that on average, the AUC24h,52w is expected to be 3.3 fold higher for a typical subject with baseline eGFR of 20 versus 110 mL/min/1.73m2. Females were found to have 12.5% higher VAP-1 concentrations. However, the impact of this effect appeared to be minimal in terms of AUC24h,52w and VAP-1 inhibition (Figs. 2 and 6, respectively).

The developed TMDD model relies on several assumptions. A critical assumption was that of binding equilibrium, i.e. compared with other processes, binding of ASP8232 to VAP-1 was assumed to be rapid, while VAP-1 turnover and elimination of the VAP-1-ASP8232 complex were assumed to be negligible. As such, although mechanistically expected, there was no target turnover or elimination of the complex implemented in the model. This model limitation was deemed acceptable, given that the TMDD model was able to successfully describe the observed ASP8232 and sVAP-1 plasma concentrations, as well as the VAP-1 plasma activities across all studies. Thus, the need for a more complex model was not pursued in favor of the more parsimonious alternative. However, caution is advised when interpreting simulations beyond the available dose range in the clinical studies, as VAP-1 turnover might be relevant, and thus its exclusion could lead to some bias in the estimated parameters. Another assumption was that the measured VAP-1 plasma activity was driven by the unbound sVAP-1 plasma concentrations and this relationship was assumed to be constant over time. The placebo data support the assumption that the VAP-1 plasma concentration-activity relationship was constant over time as both the VAP-1 plasma concentration and activity did not change over time.

The model was able to adequately describe the data for all studies. However, below ASP8232 concentrations of 0.5 ng/mL, a discrepancy between model predictions and observations was seen for VAP-1 activity expressed as percent inhibition of activity (Fig. 6). It was a conscious decision to stick with a model without inhibition of VAP-1 activity in the absence of ASP8232 exposure, despite the discrepancies with the observed data. This model was considered more mechanistically plausible, and the observed higher VAP-1 activity was thought to be non-drug related. One possible explanation could be that the baseline VAP-1 observation was lower than the actual endogenous level, which influences the observed, and to a lesser extent, the model-predicted VAP-1 inhibition. This hypothesis is supported by higher measurements on day 1 as compared to the baseline observation. Another explanation could be a variation in VAP-1 activity over time, which was seen in the placebo groups of study 8232-CL-0001.

Nonetheless, at higher concentrations, the model adequately predicts the increase in VAP-1 inhibition with ASP8232 concentration. The model was therefore used to predict the VAP-1 inhibition for dose levels not currently evaluated in the clinic to aid drug development, for example for selecting the doses to be included in a Phase 2 dose-finding study. Population simulations were performed predicting the expected PD response in DKD patients upon 1-year treatment with 0.1 to 40 mg daily ASP8232 (Fig. 6). The results indicate that a low effect response (defined as below 50% VAP-1 inhibition) would be obtained on average in DKD patients by ASP8232 dosing below 0.3 mg, while a high response (above 90% VAP-1 inhibition) would be achieved by doses above 3 mg.

In conclusion, the PK-PD of ASP8232 was successfully characterized using a TMDD model. This model provides a robust tool to simulate plasma VAP-1 activity in relation to drug exposure and may be used to guide dose selection in future clinical trials with ASP8232.