1 Introduction

Thermal Energy Storage (TES) serves as a crucial bridge between periods of energy harvesting and times of energy demand and therefore facilitates the utilization of renewable energy sources [1, 2]. Different TES technologies have been used for heating and cooling applications and power generation [3, 4]. There are three forms in which domestic heat storage can be implemented: sensible, latent, and thermochemical heat storage (TCHS) [2, 3, 5, 6]. Moreover, the categorization of each heat storage method can be refined based on the materials employed for heat storage and the underlying operational principles [7]. Thermochemical heat storage (TCHS) system relies on a reversible gas–solid reaction [2]:

$$C+Heat\leftrightarrow A+B$$

In this reaction, the solid material (\(C\)) referred to as the thermochemical material (TCM) [8] absorbs energy to chemically transform into two components (\(A\) and \(B\)). The reverse reaction combining \(A\) and \(B\) to form \(C\), releases energy/heat/enthalpy, which constitutes the thermal energy in the TES system. The storage capacity is determined by the heat of reaction when the material \(C\) is formed. Hence, it involves the physisorption or chemisorption of a sorbent gas within a thermochemical material (TCM) [9]. The reaction typically involves water, ammonia, or methanol vapor as the sorbent gas. However, for safety and environmental considerations, reactions involving water (H2O) are most commonly employed in domestic applications [8, 10]. A significant advantage of TCHS over other heat storage systems lies in its capability for long-term, nearly loss-free energy storage. This is because energy is released in TCHS only when both reactants are in contact with each other. In contrast, sensible and latent heat storage systems rely solely on the temperature change of the storage material, making them susceptible to self-discharge due to heat dissipation [6]. Salt hydrates are regarded as a highly promising group of substances that can be used as Thermochemical Materials (TCMs), for domestic applications. Their suitability stems from the ability to safely combine with water vapor as a sorbate, offering a high energy density and charge–discharge temperatures compatible with the built environment [11, 12].

Among various TCMs investigated for low-temperature thermal energy storage, K2CO3 shows great promise [8]. It can be stored indefinitely by storing the anhydrous salt and water separately. The investigation outlined in reference [13] highlights the benefits of a potassium carbonate-water vapor system. This system exhibits a reaction enthalpy (ΔHr) of 64.01 kJ/mol of water, yielding a maximum energy density of 1.30 GJ/m3 [14]. The equilibrium reaction between the gas and solid phases for K2CO3 is given by:

$${K}_{2}C{O}_{3} \left(s\right)+1.5{H}_{2}O \left(g\right)\leftrightarrow {K}_{2}C{O}_{3}1.5{H}_{2}O \left(s\right)+\Delta H$$

The forward hydration process is exothermic, resulting in the release of energy due to the intake of water vapor. Conversely, the backward dehydration reaction is endothermic, requiring the addition of heat to facilitate the desorption of water.

For usage of material in a heat storage device, the material is frequently treated in a packed bed that contains millimeter-sized particles. The material is loaded into the reactor, forming several porous layers with channels through which incoming water vapor traverses [12, 15]. These channels facilitate fluid flow within the reactor, ensuring that the pressure drop, and consequently flow resistance, remains within acceptable limits. Pressure drop signifies the energy dissipation resulting from fluid flow through the reactor bed. Controlling the temperature and vapor pressure of the incoming airflow enables the controlled hydration or dehydration of the packed bed [12]. The usage of salt hydrate generally comes with certain constraints. The upper limit for the water vapor pressure employed is determined by the deliquescence conditions. The phase diagram of potassium carbonate [15] indicates that above the deliquescence line, the salt goes into deliquescence and forms a saturated solution. Hence, the operational parameters of the packed bed can be determined according to the phase diagram.

However, the formation of salt agglomerates in the bed occurs due to two main reasons. First, when a solid experiences stress, specific areas become more soluble than those unaffected—a phenomenon referred to as 'pressure solution.' Under stress, grain contacts dissolve, and grain boundaries in contact with the pore solution expand, reducing porosity and strengthening the formation. Essentially, chemical changes occur in stressed areas, causing dissolution and growth at grain boundaries [16]. When the material swells and shrinks during cycling, it creates stress in the bed hence resulting in the agglomeration of grains. The second reason is local variations in temperature and relative humidity throughout the operation. Individual hydrated grains often crack during dehydration, hindering TCM application and leading to pulverization and poor mechanical stability over repeated cycles [8]. Agglomeration or filling of the void space in the bed by powdered material reduces permeability and void space, affecting the fluid flow. Permeability is a measure of how easily fluids can flow through a porous medium, and closed porosity may reduce overall permeability. Granular materials with smaller particle sizes and lower porosity exhibit reduced fluid permeability. Further, the internal structure of pores in granular materials is determined by the configuration of the particles, their sizes, and shapes. This means that the properties of the particles and how they are packed together both contribute to determining the material's overall mechanical properties, porosity levels, and fluid flow characteristics [17]. For instance, the ability of a granular material to allow fluid to flow through it decreases as the particle size becomes smaller and the porosity becomes lower. This phenomenon forms the foundation of the Kozeny-Carman equation, which links the particle size, porosity, and permeability of the material [18].

Open porosity is essential in a packed bed as it provides a path for the fluid to flow efficiently. Furthermore, assessing open and closed porosity is crucial when examining the mechanical characteristics and structural soundness of porous materials. Understanding the pore morphology involves determining key factors such as the quantity and proportion of both open and closed pores, along with the overall percentage of pore volume. Figure 1 illustrates the diverse types of pores. Open pores constitute expansive interlinked networks that extend from the material's surface to its core in any Cartesian direction. In contrast, closed pores are isolated and do not connect to the surface in any direction. Open pores provide pathways for the fluid to flow through the packed bed. The interconnected void spaces between solid particles create channels or conduits for the fluid to move, allowing for effective permeation of the bed.

Fig. 1
figure 1

A schematic of open, closed, and blind pores [19]

Full size image

Literature underscores the promising potential of utilizing K2CO3-packed beds as a heat battery [11]; however, further research is imperative before contemplating commercial implementation. An in-depth exploration of the internal structure of the bed resulting from hydration and dehydration processes is crucial, particularly to understand the impact of volume variation and agglomeration on bed properties. These properties, in turn, will define the thermal and chemical characteristics of the salt hydrate-packed beds in question. Additionally, gaining insights into the flow characteristics of packed beds will enable the optimization of future reactor designs, paving the way for more efficient thermal energy storage systems. To explore the impact of various transport processes in a packed bed before and after cycling, the use of an imaging tool is required. It enables the visualization and three-dimensional reconstruction of the internal structure of porous materials.

Incorporating X-ray computed tomography (XCT) scans into the study of packed bed reactors with salt hydrates introduces an innovative and virtually nondestructive technology that transcends the limitations of traditional experimental analyses [20, 21]. XCT scan’s non-invasive nature preserves the integrity of the reactor and the salt hydrate material, allowing for repetitive scans without compromising the system. X-ray computed tomography allows for a three-dimensional exploration of the microstructure of samples in a nearly natural state, providing unparalleled resolution in the process [22]. This advantage positions Micro X-Ray Computed Tomography as an indispensable tool for gaining a deeper understanding of the complex interplay between the reactor's design, salt hydrate behavior, and overall system performance. By analyzing the 3D volume, the porosity of the structure can be calculated. This information is crucial for understanding the available void spaces and how they contribute to fluid flow, heat, and mass transfer. It can be used for detailed examination of pore structures within the packed beds. It provides information on pore size distribution, connectivity, and geometry, contributing to a comprehensive understanding of the internal architecture and flow characteristics of the medium. This information also aids in understanding the impact on effective thermal conductivity. For instance, regions with higher particle density may exhibit different thermal conductivity than the presence of more void spaces. Imaging helps identify preferential flow paths, bottlenecks, or areas of potential channeling within the packed bed. This is vital for understanding how fluid permeates through the material and whether there are regions with reduced permeability due to agglomeration. To clarify the intricacies of heat and mass transfer and consequently enhance the design and selection of optimal operating conditions in packed bed systems, it is essential to thoroughly evaluate the fluid flow. Micro-X-ray computed tomography offers a solution to this challenge via computational fluid dynamics simulations. The primary benefit of employing XCT data for characterizing the packed bed and performing CFD simulations lies in the fact that the simulation geometry derived from XCT measurements precisely matches the experimentally studied geometry [23].

In this study, a comparison of pore size distribution, and its evolution in uncycled and cycled reactors is done using the XCT data at a granular level. Additionally, the grain size estimation has been performed. At a system scale, the effect of cycling and agglomeration on heat transfer is analyzed by calculating the effective thermal conductivity of the bed. Ultimately, A comparison of flow profiles has been reported.

2 Materials and Experimental Methods

2.1 Materials

The incorporated composite material, supplied by Cellcius [24], includes pure potassium carbonate combined with 3% graphite (CAS NUMBER: 584-08-7), utilizing graphitherm 23/99.9 graphite from Caldic [25]. Caldic B.V. (Caldic Ingredients Deutschland GmbH, Düsseldorf) manufactures the granules by directly mixing the base material with graphite, resulting in an ash-grey powder. After mixing, the material undergoes compaction into flat pellets with a binder, which are then broken into irregularly shaped grains. The compaction process involves roll-pressing the base material with a force of 50–60 kN, producing flat pellets measuring 40 mm × 12 mm (area 48·10 − 5 m2) with a maximum thickness of 4 mm. Grains ranging from 3 to 5 mm are sieved and utilized for characterization, considering the impact of particle radius on permeability within the 1–5 mm range [11, 25].

2.2 Experimental Methods

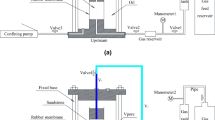
The tested packed bed reactor, developed at the University of Twente, has an outside vacuum-insulated glass unit to prevent heat loss during the hydration and dehydration of the material. The experimental setup and the schematic are shown Fig. 2. A plate is attached to the bottom of the reactor to prevent further heat loss for incoming air. The reactor is connected to a controlled evaporator mixing unit (CEM). The CEM unit provides dry and humid air at given temperature and humidity conditions. The operating conditions used for the experiment are presented in Table 1. At the top of the reactor, a thermocouple is connected to measure the temperature change at the outlet. An optical Keyance digital microscope(VHX-970FN) [26] has been connected at the side of the reactor to continuously monitor the swelling and shrinkage of the material.

Fig. 2
figure 2

Experimental set-up (left) and schematic of the set-up (right) consisting of a glass reactor and a thermocouple to monitor temperature evolution

Full size image
Table 1 Experimental conditions for dehydration and hydration of salt samples
Full size table

Before the experiment is started the sample preparation is done by placement of 17.5 g uncycled potassium carbonate grains inside the reactor. It is detached from the set-up and mounted securely on a sample holder equipped with a wide plate. The reactor is scanned at the University of Twente, using the Zeiss Xradia Context Micro CT device. This configuration was chosen to ensure stability and minimize any potential disturbance to the position of particles during subsequent scanning processes. The sample underwent an initial scanning session lasting 14 h within the Xradia Context micro CT machine. A total of 4501 projections were acquired during this period, and notably, no filtering was applied during the scanning process. The objective was to capture a comprehensive set of structural details without compromising the fidelity of the imaging. All the scanning parameters are listed in Table 2.

Table 2 Scanning parameters
Full size table

Post-initial scan, the reactor-encased sample is connected back to the CEM unit, and it undergoes a series of 10 hydration and dehydration steps. The microscope is set to take pictures of the reactor every 2.5 s. Following the hydration and dehydration treatment, the sample was rescanned using the same scanning parameters employed in the initial session. This step allowed for the investigation of any changes in the bed’s internal structure induced by the hydration and dehydration cycles.

The raw reconstructed data generated by the Xradia Context's scan program, including Scout and scan, was utilized to create a TIFF stack [27]. This three-dimensional representation of the sample's structure served as the basis for further post-processing and analysis. The TIFF stack obtained from the reconstructed data was cropped to remove the glass reactor wall and perforated base and then subjected to post-processing in GeoDict software [28] to extract relevant microstructural information.

2.3 Image Segmentation Methodology

Image segmentation is a crucial step in data analysis, enabling the identification and extraction of meaningful objects and features from the images. In this study, the GeoDict software (Math2Market GmbH, Kaiserslautern, Germany) is employed to conduct image segmentation, which involves the use of a combination of AI segmentation modules. The AI module features a technique that involves the automatic partitioning of an image into multiple segments or regions. Boosted tree, Unet2D, and Unet3D are the three options available for segmentation. Unet3D is a type of AI segmentation that is used to segment 3D images, such as magnetic resonance imaging (MRI) scans and XCT data. It is based on the UNet architecture, which is a convolutional neural network (CNN) that is widely used for image segmentation tasks. The UNet3D architecture is an extension of the UNet architecture that is specifically designed for 3D medical image segmentation tasks. It is capable of segmenting 3D medical images with high accuracy and has been used in various medical applications, such as brain tumor segmentation [29]. The UNet3D architecture outperforms the Boosted tree approach due to its superior accuracy and efficiency. While the Boosted tree approach relies on a decision tree for image segmentation, it struggles with complex images featuring multiple regions and overlapping boundaries. Conversely, UNet3D excels in handling such complexities [30]. Upon removing the material from the reactor, it was observed that the material was agglomerated. To achieve a more precise representation of each grain, the segmentation in this study employed the use of UNet3D.

The first step in the segmentation methodology involves training a deep-learning model, on a dataset of labeled images [31]. The number of materials is defined as two, potassium carbonate as solid and the pore as air. During training, the model is presented with numerous labeled image slice examples, allowing it to learn the underlying patterns and relationships that differentiate the solid and void space. The model is designed to extract and learn high-level features from the image data, enabling it to effectively distinguish between different objects and features [32, 33]. The resulting data after segmentation is termed as structure which can be used in various modules for the calculation of bed characteristics.

3 Results

A visual comparison has been presented in Fig. 3 related to the increase in height of the bed due to swelling of the TCM grains Qualitatively, it can be observed in the figure that following 10 cycles, there is an increase in the average height of the bed. Just by general observation, it can be seen that there is slight pulverization of the material and the glass wall of the reactor is covered with powdered potassium carbonate. This is important to note because it gives a small insight into the mechanical stability of the material. The generation of powder can clog the void space present in the bed, restricting the fluid flow and further aiding the agglomeration. In Fig. 4, grayscale representations of both uncycled and cycled beds are displayed, depicting cross-sections obtained from micro CT raw data in top-down and frontal perspectives, illustrating different views of the bed structure. The first scan is performed before starting the experiment and the second after the end of the 10 cycles.

Fig. 3
figure 3

Images of (left) the uncycled and (right)cycled bed showing the height change after 10th hydration cycle

Full size image
Fig. 4
figure 4

Cross-sectional (grey scale) views of micro-CT raw data showcasing the top-down (right) and frontal (left) perspectives of uncycled bed (a) and cycled bed (b)

Full size image

After scanning the material, the sample taken out of the reactor is shown in Fig. 5. It should be noted that free-flowing grains were filled in the reactor but the resultant grains were agglomerated after the completion of 10 cycles. To study the influence of cycling on the bed performance, various parameters are computed and a comparison between the uncycled and cycled bed is made for better insight.

Fig. 5
figure 5

Agglomerated grains after 10 cycles (Video 1 presented as supplementary material is a good visualization for the swelling and shrinkage phenomena in bed as it is cycled.)

Full size image

3.1 Pore Size Distribution

The PoreDict module helps in characterizing the pores in the three-dimensional structure generated after segmentation. While calculating Pore Size Distribution (Granulometry), the algorithm employed for pore size does not distinguish between through pores, closed pores, and blind pores, thus operating solely on geometric principles. The process involves establishing a pore's radius by fitting spheres into its volume. To elaborate further, a point is deemed part of a pore with a radius exceeding 'r' if it lies within any sphere of radius 'r' that can snugly fit within the pore space. As an input, a bin size of 2 voxels was provided with a symmetric boundary condition.

In Fig. 6, the comparison between pore size distribution in the uncycled and cycled bed is presented, a separate distinction between the type of pores is stated in Table 3. The pores in the packed bed allow fluid to flow through and react with the solid particles. The pore size distribution (PSD) is an important characteristic of the packed bed, as it affects the mass transfer, heat transfer, and pressure drop in the reactor. The figure indicates that the uncycled packed bed has a large volume fraction of small pores and an even number of large pores ranging from 3 to 6 mm. The volume fraction of pores in a packed bed refers to the ratio of the volume of void spaces or pores within the bed to the total volume of the bed. It can also be observed that pores in the range 7 mm and 8 mm constitute between 1.2 and 1.8% volume fraction respectively. The figure shows that the majority of the pores have a diameter between 0 and 2 mm, with a sharp decrease in volume as the pore diameter increases. This suggests that the packed bed has a high surface area and a low void fraction. A high surface area means that the solid particles have more contact with the fluid, which can enhance the reaction rate. As the grains swell and agglomerate after cycling, the packing density decreases, and the PSD shifts to the left, indicating that the pores become smaller and more uniform in size. The maximum pore size in the bed contradictory to the uncycled bed is in the range of 3.5–4 mm.

Fig. 6
figure 6

Pore Diameter Distribution with Corresponding Volume Fractions in the uncycled bed (blue) and cycled bed (red) after 10 cycles

Full size image
Table 3 Porosity parameters in uncycled and cycled bed
Full size table

The packing has even smaller and less diverse pore sizes, ranging from 0 to 1.5 mm but they constitute a large volume fraction. Agglomeration and swelling of grains after cycling resulted in low void fraction meaning that the packed bed is now densely packed, which can increase the pressure drop in the reactor. However, a high number of small pores can also cause diffusion limitations and mass transfer resistance, which can lower the reaction efficiency.

4 Open and Closed Porosity in the Bed

A comparison of open and closed porosity has been performed for the uncycled and cycled reactor and is tabulated in Table 3. Open and close pore submodule present in the PoreDict module of GeoDict has been used for the calculation. To calculate open and closed porosity, periodicity in the structure has not been imposed in any direction for the calculation. During the configuration of calculations, the Neighborhood Mode plays a crucial role in defining the extent to which voxels from the porous material within the structure are considered part of a connected group. Opting for the "Checking Face" mode is more restrictive compared to selecting "Face" or "Edge" individually. The most lenient condition for Neighborhood Mode is "Face, Edge, or Vertex." In this specific instance, the "Face, Edge, or Vertex" option was selected.

Open pores can be further classified into two subcategories: dead-end pores, which have sole contact with one of the inflow planes, and through pores, which establish contact with multiple inflow planes. In Table 3, it can be observed that the number of dead-end pores is significantly higher in the cycled bed. With only one contact point with an inflow plane, dead-end pores hinder effective mass transport, impeding the efficient utilization of the material and potentially compromising the overall reaction kinetics.

After 10 cycles, the overall porosity of the bed decreased from 41.34 to 19.91%. The decrease in porosity can be attributed to the agglomeration of grains as well as swelling during hydration. After successive hydration and dehydration resulting in swelling and shrinkage of the grains, the grains increase in volume and do not return to their original size, thus filling up the void space in the bed. The number of pores and open porosity decreases significantly after cycling the material. A decrease in porosity can lead to less interaction of humid/dry air with the potassium carbonate grains thus resulting in incomplete hydration and dehydration of the material. This can be a disadvantage as it will decrease the overall output temperature and render the material useless in the long run. The open porosity directly influences the pressure drop across the packed bed. According to Ergun's equation [34], the pressure drop is inversely proportional to the porosity of the bed. Lower porosity results in increased pressure drop, reflecting greater hindrance to fluid flow through the more densely packed bed. Higher open porosity generally leads to lower resistance to fluid flow, resulting in a lower pressure drop. This is particularly important in thermochemical storage systems where minimizing pressure drop is critical. Closed porosity, by contrast, does not contribute directly to fluid flow pathways. Instead, closed pores within solid particles can influence the permeability of the bed. Closed pores contribute to increased tortuosity, meaning the fluid has to flow through a more convoluted path through the bed. This increased tortuosity can lead to a higher pressure drop in the packed bed.

4.1 Grain Size Distribution

In the GrainFind module of GeoDict, “Estimate Grain Diameter” helps in estimating the diameter of the grain by fitting the spheres into the structure obtained after segmentation and calculating their diameter. The grain diameter estimation algorithm starts by assigning a Grain Diameter of 0 to each voxel and then inserts the largest possible sphere into the geometry. If the sphere fits within the geometry, it assigns the sphere's radius to any voxel that lacks a grain diameter assignment. Otherwise, the algorithm reduces the sphere's radius and repeats the process until the sphere can fit within the geometry. This iterative process effectively identifies the dominant grain size at each voxel location.

A grain fragment refers to a continuous area with an identical assigned grain diameter. The presence of grain fragments at the boundary can introduce uncertainty in grain diameter estimation, as it is unclear whether these fragments extend beyond the domain or are truncated by the boundary. Although it should be noted that, removing boundary grains can reduce uncertainty in grain diameter estimation, it also introduces a bias towards smaller grains, as larger grains are more likely to be touching the boundary and they get removed thus underrepresenting larger grains. Remove grain boundary fragment was chosen for the calculation. A minimal grain diameter of 0.0005 m is chosen to remove the powdered substance and also the pulverized material during cycling. Grain fragments with an assigned grain diameter lower than the Minimal Grain Diameter are discarded. If they are connected to larger grain fragments, they are merged into the larger fragments, and the larger diameter value is retained. Otherwise, they are removed from the structure.

Grain size distribution for both uncycled and cycled beds is shown in Fig. 7. The grain diameter is the average size of grains in the bed, measured in millimeters. On the y-axis is the volume fraction of grains of a given size, which is the percentage of the total volume of the bed that is occupied by grains of that size. Both the figures show that the grain size distribution in an uncycled packed bed is typically unimodal, meaning that there is a single most common grain size. The general trend is grain diameter ranges from 0.5 to 4 mm in the uncycled bed but in the cycled it is from 0.5 to 5 mm, indicating the occurrence of agglomeration after cycling. The shape of the grain size distribution curve is influenced by several factors, including the packing process, the shape of the grains, and the presence of any fines (very small grains) in the bed.

Fig. 7
figure 7

Grain Size Distribution in the uncycled bed

Full size image

A general trend of increase in size can be attributed to the water vapor uptake by potassium carbonate grains and thus swelling in the process. The repeated cycling leads to a permanent increase in size and it cannot return to its original size. Moreover, adherence of grains due to agglomeration results in bigger size grains. This phenomena of agglomeration resulting in big-sized particles leads to a reduced surface area available for interaction between the fluid (water vapor) and solid phase. This diminished surface area hinders the efficiency of the reaction as it limits the contact between the reactants. Likewise, larger particles contribute to increased local void spaces within the packed bed, leading to decreased bed density. The lower density results in inadequate contact and mixing between the fluid and solid phases, negatively impacting the reaction kinetics. It can increase the pressure drop across the reactor, which can affect the flow rate and the mass transfer of the reactants and products. The diffusion of reactants in and out of large particles becomes slower, impeding the overall reaction rate. This is because diffusion distance increases with larger particle sizes, making it more challenging for the reactants to reach the active sites within the particles.

Using GeoDict's GrainFind module, it is possible to identify individual grains within structures, even in cases where the grain boundaries were previously unidentified. For each identified grain, the module calculates a best-fit shape and determines its orientation within the structure. Identify grain function present in the module identifies, individual grains within a given structure and helps in further analysis. The analysis encompasses assessing grain volume, and sphericity, and determining the orientation of the grains. The primary foundation for the grain identification process within GrainFind relies predominantly on the Watershed algorithm. A representation of all the individual identified grains colored and coded according to equivalent diameter in an uncycled bed is presented in Fig. 8.

Fig. 8
figure 8

Size-Color Mapping- Visualizing Grain Distribution in the uncycled bed (left) and the cycled bed

Full size image

Each grain is depicted with a distinct color corresponding to its size, facilitating easy identification and interpretation of the size distribution across the bed. Through this color-coded visualization, smaller grains may appear as darker shades, while larger grains are represented by lighter tones, providing a comprehensive overview of the packing arrangement and highlighting any clustering or segregation tendencies based on grain size.

4.2 Effective Thermal Conductivity

The ConductoDict module calculates the effective conductivity of porous and composite materials by assuming the heat transfer occurs through conduction. Thermal conductivity is the rate at which heat is transferred through a specific material per unit area, considering a temperature difference or gradient across the material's cross-sectional area. It is governed by Fourier’s Law of Conduction given by Eq. 1:

$$\dot{q}=-K\Delta T$$
(1)

where \(\dot{q}\) is heat flux [W/m2], \(K\) is the effective thermal conductivity in [W/m K] and \(T\) is the temperature [K]. Usually, \(K\) is a second-order tensor presented in Eq. 2. For isotropic material, a scaler can be used because of similar properties in all directions.

$$K=\left(\begin{array}{ccc}{k}_{xx}& {k}_{xy}& {k}_{xz}\\ {k}_{yx}& {k}_{yy}& {k}_{yz}\\ {k}_{zx}& {k}_{zy}& {k}_{zz}\end{array}\right)$$
(2)

The Poisson Equation is given by \(\nabla \cdot \left(\kappa \nabla T\right)=0\) (where, \(\kappa\) is the local thermal conductivity tensor in [W/m K]) is solved on the whole domain to compute thermal conductivity and Fourier’s Law is used to obtain the effective thermal conductivity; The complete approach is described in [35]. The set of partial differential equations are solved by an EJ (explicit jump) solver. In this iterative method, an initial guessed value is improved in the iterative steps and the process is repeated until the specified tolerance is reached (stopping criteria). As an input, the thermal conductivity of the potassium carbonate as 1 W/mK [36] was used. All X, Y, and Z computation directions and a periodic boundary condition in heat flux direction were selected. Similarly for tangential direction, a periodic boundary condition was chosen. The inlet and outlet temperature was defined as 35 °C and 60 °C, respectively, to define the temperature difference across the material structure. A total of 21, 22, and 26 iterations were performed for each computational direction X, Y, and Z, respectively.

Table 4 presents a comparison of effective thermal conductivity tensor’s diagonals elements between uncycled and cycled packed beds. An increase in value is noticed in all the directions. It is attributed to the agglomeration of grains and a decrease in void space in the bed. It can be seen that the thermal conductivity in the Z-direction is comparatively lower compared to X and Y. Thus further analysis has been conducted for the cycled bed to compute the effective thermal conductivity in three different layers by dividing the bed into three equal sections as shown in Fig. 9.

Table 4 Effective thermal conductivity tensor's diagonal components for uncycled and cycled packed bed
Full size table
Fig. 9
figure 9

Three layers of cycled bed

Full size image

To prevent ambiguity due to the presence of a few particles at the top and their contribution to thermal conductivity, a set of voxels was not selected in the topmost layer. Every layer is shown in Fig. 9 has a length of 11.6 mm. For each layer effective thermal conductivity is calculated separately using the same boundary conditions. The temperature distribution in each layer is comparatively similar, except for a slight variation observed in the top layer, which can be attributed to changes in the effective thermal conductivity value. In Table 5, it can be seen that the effective thermal conductivity in the Z-direction is less compared to other directions. This is due to the presence of more void space in the Z-direction. Additionally, the swelling and shrinkage of grains during hydration and dehydration are limited in horizontal directions due to the presence of the wall of the reactor thus, resulting in more vertical size variation.

Table 5 Effective thermal conductivity tensor's diagonal elements among three layers for a cycled packed bed
Full size table

Due to the inherently low thermal conductivity of potassium carbonate, an increased thermal conductivity after cycling can help in improving the heat transfer during the reaction. However, the heightened thermal conductivity may not be favorable for several reasons. Increased thermal conductivity can lead to enhanced heat transfer, which might seem beneficial at first. However, in certain scenarios, it can result in challenges. For instance, during the exothermic reaction (hydration), higher thermal conductivity may intensify the heat transfer, potentially leading to temperature spikes or uneven heat distribution within the reactor. This could result in hotspots and affect the overall efficiency of the reactor. Similarly, during endothermic reactions (dehydration), increased thermal conductivity may make it challenging to maintain the desired temperature levels within the reactor. Insufficient heat retention could impede the progress of the reaction and compromise the reactor's performance. It can also cause local variation in relative humidity and temperature which will result in the formation of liquid bridges between adjacent grains and further lead to the formation of solid bridges resulting in further agglomeration of material.

4.3 Percolation Path Inside the Bed

The Percolation Path function is available through MatDict and PoroDict modules. It can identify percolation paths within the pore space or through a specified material.

Percolation paths in Fig. 10 show that the path in the cycled bed is more convoluted and unevenly distributed compared to those in the uncycled bed. The percolation path plays a crucial role in determining how fluids move through the packed bed. Identifying these paths helps optimize the design for efficient vapor flow, ensuring the entire TCM bed is effectively utilized. Understanding percolation paths enables the enhancement of mass transfer, facilitating more effective contact between the salt hydrate and water vapor, hence promoting reaction efficiency. As cycling of TCM involves heat exchange, percolation paths influence the distribution of thermal energy within the packed bed. Identifying these paths aids in optimizing heat transfer, ensuring uniform temperature profiles, and preventing localized hotspots or cold zones.

Fig. 10
figure 10

Percolation Path in the uncycled bed (left) and the cycled bed (right)

Full size image

4.4 Fluid Flow in the Bed

FlowDict calculates permeability, and average flow velocity (or pressure drop) across porous media. Permeability, an intrinsic property of the structure, is significantly influenced by its geometric characteristics. Hence, the selection of physics equations to address is contingent not just on delineating the fluid flow but also on the specific nature of the material. In the case where the material comprises solely empty and solid voxels, such as in a porous material, the suitable equations encompass the Stokes equations or the Navier–Stokes equation. In instances where particles are considerably smaller than the structural scale, the requisite equations are the Brinkman equations, which may include the Stokes–Brinkman or Navier–Stokes–Brinkman formulations. In this case, the Stokes–Brinkman conservation of momentum equation given by (3) has been used.

$$- \mu \Delta {\vec{\text{u}}} + \mu K^{ - 1} {\vec{\text{u}}} + \nabla p = 0$$
(3)

where \({\vec{\text{u}}}\) is the fluid flow velocity, K is the permeability tensor, μ is the fluid viscosity, and p is the pressure.

It should be noted that the flow equations utilized in the computations of the FlowDict solvers are applicable exclusively under stationary flow conditions, excluding transient (time-dependent flow). To maintain stationary flow at the media boundary, it is essential to incorporate both an inlet (inflow region) and an outlet (outflow region). For both the case of uncycled and cycled beds, an implicit inflow and outflow region was provided by including 20 voxels. The boundary conditions used for the computation are as follows: The computation direction -Z was selected with a periodic boundary condition in the flow direction. A flow rate of 0.3 l/min was provided which is the same as the flow rate used for experiments. A periodic boundary condition was provided in the tangential direction. LIR solver was used by providing an error bound of 0.01 as the stopping criteria.

Figure 11 shows a clear 3D visualization of the volumetric flow velocity distribution, where streamlines are color-coded based on their velocity magnitude. The streamlines depict a wave-like flow pattern in both the cycled and uncycled packed bed structures, with occasional channeling events characterized by high flow velocity, attributed to the presence of void spaces. Moreover, the streamlines appear denser in the uncycled bed, reflecting the abundance of void spaces, whereas in the cycled bed, this density diminishes due to agglomeration and swelling of grains.

Fig. 11
figure 11

A volumetric flow velocity field in the uncycled bed (left) and the cycled bed (right)

Full size image

Table 6 provides the computed permeability comparison for uncycled and cycled beds. The decrease in permeability from uncycled to cycled bed could result from various factors such as agglomeration of the bed material, leading to blockage of pores or channels within the bed, or changes in the arrangement of particles due to swelling and shrinkage leading to a reduction in the interconnected void spaces.

Table 6 Z- component of the permeability tensor for uncycled and cycled bed
Full size table

The pressure drop for fluid flow in both uncycled and cycled beds was examined at a mean flow velocity of 0.0041 m/s, revealing an increase from 0.31 to 4.88 Pa. The primary contributors to pressure drop within a reactor include factors like wall friction, acceleration of the gas phase, and pressure drop induced by the fluid distribution. The observed increase in pressure drop for fluid flow from uncycled to cycled bed could be attributed to several factors. One possible reason is the altered flow dynamics due to the agglomeration of grains within the packed bed, leading to increased resistance to fluid motion. This change also resulted from variations in the bed structure, particle packing due to swelling of grains after 10 cycles, and pulverization resulting in the filling of void space in the bed restricting the fluid flow. Pressure drop plays a crucial role in assessing energy dissipation, determining the appropriate sizing of compression equipment, evaluating liquid retention, understanding the gas–liquid interfacial area, and establishing the mass transfer coefficient [37]. A substantial pressure drop across the cycled system not only demands significant energy input but also restricts the operation of the unit at elevated fluid velocities, consequently imposing limitations on throughput.

Similarly, the flow resistivity increased from 2120.56 kg/m3s for the uncycled bed to 35,058.4 kg/m3s for the cycled bed. Flow resistivity is a property that characterizes the resistance of a porous material to the flow of fluids (such as air or water) through its structure and is the ratio of fluid viscosity and permeability. This resistance is influenced by factors such as the size, shape, and arrangement of particles, as well as the properties of the fluid itself. In the cycled bed it has been noted in Sect. 3.3, that the increase in the size of the particle complies with the flow resistivity result.

As flow resistivity rises, the pressure drop across the packed bed is likely to increase. This means that it would require more force or pressure for the fluid to flow through the bed, impacting the overall energy requirements of the system. Higher flow resistivity may lead to changes in fluid flow patterns within the packed bed. It could result in more localized flow paths, uneven distribution of fluid, or changes in mixing behavior which is not desirable for TCM systems. Further, the resistance to flow influences mass transfer and heat transfer within the packed bed. An increase in flow resistivity may affect the rates at which vapor is transported through the bed thus, potentially affecting reaction kinetics. This, in turn, can alter the system's heat storage and release capabilities. and the efficiency of heat exchange processes as it can lead to reduced convective heat transfer rates within the bed. Additionally, it can lead to uneven temperature distribution, potentially causing thermal stresses in the materials constituting the packed bed. Over time, this could contribute to material degradation, affecting the longevity and reliability of the system. Thus, balancing the need for efficient heat transfer and reaction kinetics with the practicalities of fluid flow through the bed is crucial for optimizing the thermochemical energy storage system.

5 Conclusion

In this research, a comprehensive analysis of a salt hydrate-packed bed before and after undergoing hydration and dehydration reactions was conducted through Micro-Computed Tomography Scans and further analysis of the volumetric data with GeoDict22. The findings reveal noteworthy changes in the packed bed characteristics such as packing density, bed porosity, and effective thermal conductivity. The observed decrease in porosity suggests a densification of the salt hydrate bed, indicating a more compact and closely packed structure after the reaction cycles. This reduction in porosity from 41.34 to 19.91% could be attributed to the rearrangement of salt hydrate grains during the hydration and dehydration processes, volume change, and agglomeration. Additionally, the increase in grain size post-reaction is a significant observation. This enlargement in grain size may be indicative of agglomeration or growth of individual grains, potentially influencing the overall thermal and transport properties of the packed bed. An increase in effective thermal conductivity after 10 cycles is noticed. This enhancement in thermal conductivity can be associated with the changes in void space in the bed and grain size, influencing the overall heat transfer efficiency within the material. The densification and growth of grains might lead to improved thermal pathways and enhanced thermal conduction but lead to an overall decrease in reaction rate due to the absence of a path for water vapor to interact with the material. This heightened pressure drop and flow resistivity in cycled beds may adversely impact thermochemical energy storage systems by requiring more force for fluid flow, potentially causing non-uniform flow patterns, and influencing mass and heat transfer. Optimizing the balance between efficient heat transfer and practical fluid dynamics is crucial for enhancing the overall performance and reliability of thermochemical energy storage systems.

Overall, the micro-CT analysis provides valuable insights into the evolving microstructure of the salt hydrate-packed bed during thermochemical reactions. These findings not only contribute to a deeper understanding of the material behavior but also have implications for optimizing the design and performance of thermochemical systems utilizing salt hydrates. Further research can delve into the specific mechanisms behind these observed changes and explore ways to leverage them for enhanced thermal energy storage and release applications.