NDE of Concrete Strength and Elasticity Modulus Based on Jerk Measurement

Abstract

The quality assessment of concrete material for new or existing buildings is critical to civil and structural engineers. In this scope, the development of nondestructive testing methods (NDT) has received significant attention and becomes essential for enhancing the on-site assessment of concrete performance. The Schmidt hammer (SH) test is one of the most widely used NDT for quantifying concrete strength. However, the reliability of this test and its accuracy are questioned by many researchers. In this study, the measurement quality of SH has been improved by attaching a developed cantilever-based jerk sensor to the SH mass. The theoretical model of the proposed measurement technique has been formulated and discussed. The experimental approach, jerk sensor design, SH body modification, electronic reading unit, testing, and construction of the calibration curves have been presented. Experimental results revealed that the accuracy of the developed SH has increased by 13% for concrete strength measurement, and the correlation coefficient of the strength calibration curve is 0.94. At the same time, the calibration curve of the concrete elasticity modulus showed a 0.93 correlation coefficient with 92% measurement accuracy. Analytical and experimental results have confirmed the applicability of the modified Schmidt hammer since it is reliable and more accurate compared to the traditional Schmidt Hammer.

1 Introduction

Concrete is one of the most widely used construction materials worldwide. Concrete structures are susceptible to damage from many sources; externally, such as overloading due to soil settlements, earthquakes, and blasts, or internally within the material, such as loss of strength due to cracks formation, chlorides penetration, alkalis attacks, fire exposure and freeze–thaw cycles [1]. Therefore, assessing concrete quality is very important for civil engineers to quantify the damage. There are several nondestructive test (NDT) methods used for this purpose such as ultrasonic surface wave and impact echo [2]. Although these methods can determine concrete elasticity, they are expensive and require extensive training. A technical challenge that still faces the assessment of concrete quality is the need to develop a practical, robust, reliable, and cost-effective NDT method.

Schmidt hammer (SH)—invented by Ernst Schmidt [3]—is a quick, cost-effective, NDT method used to assess the compressive strength of concrete through a surface hardness indicator [4]. However, SH results are less reliable than the destructive test (DT) methods, such as the core test [5]. It is worth mentioning that there are DT methods other than the cores. However, they do not directly measure the concrete strength, but rather estimate it by measuring a specific response that is well correlated to the strength, such as the pullout and loading tests which indicate concrete strength through the pullout force and deflection response, respectively [6, 7]. Abdelaziz et al. [8] investigated the reliability of SH readings in assessing the strength and variability of concrete; their results showed that many factors, including the relative location of the measurement within the structural element, influenced the readings. Moreover, they concluded that direct conversion of rebound number using the supplied calibration curves failed to predict the concrete cube strength accurately. Similar conclusions were reported by Sanchez et al. [9] and Mir et al. [10]. Atoyebi et al. [11] investigated SH reliability by comparing the compression test conducted on normal and high-strength concrete mixes with the SH test results. The comparison showed that the coefficient of variation decreases as the strength increases. They concluded that a slight change in concrete mix composition might lead to significant errors in the strength estimation based on correlation curves of similar concretes. Kocáb et al. [12] investigated the use of characteristic curves (a characteristic curve is a specific model of the relationship between the rebound number and compressive strength for only one concrete) in determining concrete strength by the SH test. They stated that the determination of the relationship between the rebound number and compressive strength based on linear regression models could be misleading since other parameters (e.g., cement type, aggregate, and w/c ratio) should be taken into consideration in addition to the rebound number. However, they tackled this issue using a characteristic curve from a linear regression model to indicate the strength with 95% reliability.

Despite the importance of SH reliability, very little research has been done to develop the measuring technique of the Schmidt hammer. Recently, a rebound-hammer model named SilverSchmidt (SS) was introduced [12]. SS is based on measuring the hammer mass velocity just before and after impact utilizing optical sensors returning the Q-value instead of the rebound distance. The previous technique enables SS to measure high and low strength concretes of 5 MPa. SS is also used to assure concrete strength consistency and pinpoint weak zones. Kovler et al. [13] tested concrete using the Leeb rebound hammer (LH) [14], which is used in the geological and metallographic fields. They concluded that LH rebound numbers are more consistent than SH. In addition, due to its low impact energy, LH can test concretes of strength lower than 7 MPa; hence, it can be used to test early age concretes. However, the LH rebound test requires careful surface preparation because of its sensitivity to surface conditions. Chingălată et al. [15] tried to overcome the SH reliability problem by combining the ultrasonic pulse velocity (UPV) and SH tests and correlating the results using empirical linear regression models. The authors concluded that—following a specific empirical relation—the combined method results are more accurate when compared to the single methods.

On the other hand, SH reliability can be enhanced if the measurement technique is developed to indicate the elasticity modulus. Young's modulus is one of the essential parameters of concrete material because it represents the material deformation under loading and directly controls the displacement of structures. Moreover, Young's modulus is correlated to compressive strength. Consequently, the evaluation of this parameter is important for the assessment of concrete quality. Many national standards have postulated direct relationships between the static modulus of elasticity and compressive strength, including EN 1992-1-1, ACI 318-08, and BS 8110: part 2. Other standards include concrete density as a second parameter. The fact that several relations exist indicates the difficulty of estimating the compressive strength based on the static modulus of elasticity and vice versa. Several researchers reported issues when trying to develop a direct relationship. Ispir et al. [16] investigated the modulus of elasticity of low-strength concrete. They concluded that the relations suggested by codes are not valid for low-strength concrete. Krizova et al. [17] evaluated static elasticity modulus based on concrete compressive strength. They discussed that many factors are introduced during the production process, which affects the modulus of elasticity, including raw materials, admixtures, and type of cement. In addition, they stated that the experimentally measured elasticity modulus values might significantly differ from the guide values. From previous studies, static modulus might not accurately indicate compressive strength. However, a more accurate relationship can be obtained using the dynamic modulus of elasticity. Jurowski et al. [18, 19] studied the influence of different factors, including the type and amount of aggregate and binder type, on the relationship between the dynamic elastic modulus and compressive strength. They concluded that their proposed relation could allow the use of the impulse excitation method as an NDT method for concrete strength.

Nowadays, NDE is transitioning to the fourth revolution (NDE 4.0) focusing on digitalizing measurements using innovative sensors, collecting digital data to enable the construction of data models, developing software algorithms for machine learning, and ultimately enhancing the robustness and reliability of current measurement techniques to overcome the uncertainties challenge in inspection methods [20]. To tackle the previous challenge, smart-materials-based sensors in the field of analytical dynamics can be applied to develop force-based measurement techniques. In this scope, jerk sensors are emerging and promising research area since they can measure the rate of change of force in dynamic systems subjected to impulses and impact (e.g., Schmidt hammer). This paper focuses on developing the standard Schmidt Hammer (SSH) through a proposed cantilever-based jerk sensor attached to the hammer mass for measuring concrete strength and elasticity modulus. The jerk sensor is connected to a programmed reading unit to enable digital measurement and avoid the uncertainty of the mechanical analog indicator of SSH. The jerk sensor's primary function is to directly estimate concrete strength and elasticity modulus based on the measured jerk value during impact. The paper first presents the measurement technique concept and the design and manufacturing of the jerk sensor. Next, the jerk sensor sensitivity and its response to impact were studied. Then, the modified Schmidt Hammer (MSH) calibration curves for concrete compressive strength and elasticity modulus were established through testing concrete mixes of different grades in the range 20~55 MPa. Finally, the results were compared, discussed, and concluded.

2 Materials and Methods

2.1 Overview of the Proposed Measurement Approach

Figure 1 shows an overview of the proposed concrete strength and elasticity measurement approach, which depends on the jerk generated during impact. The measurement approach can be briefly explained in four stages. In stage one, a cantilever-based jerk sensor was designed and fabricated. Then, the sensor was calibrated using a high-frequency electrodynamic shaker, and the sensitivities to input jerk and acceleration were obtained. In stage two, the SH body was modified to accommodate the sensor. Then, a reading unit was manufactured and mounted on the SH. In stage three, cubic and cylindrical specimens of eight different concrete grades in the range 20~55 MPa were cast. Next, compression and elasticity modulus tests were conducted by using a universal testing machine (UTM). Then, the SSH and MSH devices were used to test the specimens. In stage four, correlations among the SSH and MSH readings, concrete compressive strength, and elasticity modulus were established. A detailed explanation of each step is presented in the following sections.

Fig. 1

Overview of the proposed concrete strength and elasticity measurement approach

2.2 Concept of the Modified Measurement Technique

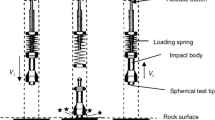
The measurement technique of SH is entirely mechanical. The hammer performs an impact of specific energy on the surface of a concrete element using a mass-spring system and then reports the rebound distance of the mass on a graduated scale. The most common type of SH is the N-type which generates an impact energy of 2.207 J. In this paper, the measurement technique was modified by attaching a cantilever-based jerk sensor to the hammer mass. In this manner, the jerk sensor directly measures the rate of change of the input acceleration (jerk ($j$) with unit m/s³). The measured jerk can be utilized to calculate the rate of change of force during the impact period which is related to the concrete strength and elasticity modulus. For instance, under constant impact energy, the higher the concrete elasticity modulus, the smaller the energy absorbed by the material during impact. Also, the greater the impulse and force rate of change during impact, the greater the momentum change and rebound distance of the hammer mass after impact. Therefore, through the attached jerk sensor, the rate of change of force versus concrete strength and elasticity modulus can be directly determined in terms of the jerk ($j$) signal.

An illustration of the modified measurement technique is shown in Fig. 2. The jerk sensor consists of a metal cantilever, and a gyroscope (angular velocity meter) mounted at the cantilever free tip, as shown in Fig. 2a. When the cantilever is subjected to base excitation due to impact, the cantilever tip is excited with a range of frequencies. The driving excitation is a function of the impulse. However, based on the authors’ previous work [21, 22], it has been proved that the cantilever tip oscillates predominantly at the first mode natural frequency (${\omega }_{\text{nc}}$) as an underdamped single degree of freedom (SDOF) system, as illustrated in Fig. 2b. Depending on the impact force generated by the mass-spring system, the generated impact acceleration (${a}_{p}$) causes the mass to reverse its velocity and the cantilever deflects simultaneously (${u}_{(y,t)}$) relative to the mass position (${x}_{(t)}$). The amplitude of the output angular velocity at the cantilever tip (${\Omega }_{tip}$) is directly proportional to the input jerk (${j}_{i}$) due to impact. The proportionality constant which is the jerk sensor sensitivity (${S}_{j}$) must be evaluated at the cantilever's natural frequency (${\omega }_{\text{nc}}$). The concept of the modified measurement technique has been achieved through theoretical (analytical model) and experimental approaches, as explained in the following subsections.

Fig. 2

Illustration of the modified measurement technique (a) jerk sensor model and (b) vibrations of the mass and the cantilever tip due to impact

2.2.1 Theoretical Approach

The equation of motion of the cantilever tip relative to the base (hammer mass) can be represented by the equation of an underdamped SDOF system undergoing base-excitation as given in Eq. 1. During the SH test, the cantilever is subjected to an input force defined as follows; when ($t>0$), the cantilever is subjected to forced vibration (Eq. 2) governed by the SH mass-spring system where (${\omega }_{i}$) is the natural frequency of the mass-spring system, and when ($t\ge {t}_{0}$), the cantilever is subjected to a triangular pulse force (Eq. 3) as shown in Fig. 2b. The pulse force acts for a very short period ($\Delta t$) where (${t}_{0}=\pi /2{\omega }_{i}$) is the impact instant, (${t}_{1}={t}_{0}+0.5\Delta t$) and (${t}_{2}={t}_{0}+\Delta t$).

$$m\ddot{u}+c\dot{u}+ku=-\left({f}_{1}+{f}_{2}\right)$$

(1)

$$\begin{aligned}{f}_{1(t)}&={F}_{i}{e}^{-{\zeta }_{i}{\omega }_{i}t}\left[\frac{{\zeta }_{i}}{\sqrt{1-{{\zeta }_{i}}^{2}}}{\rm{sin}}\sqrt{1-{{\zeta }_{i}}^{2}}{\omega }_{i}t-{\rm{cos}}\sqrt{1-{{\zeta }_{i}}^{2}}{\omega }_{i}t\right],\\ &\qquad \left(0 \leq t\right) \end{aligned}$$

(2)

$${f}_{2(t)}=\left\{\begin{array}{c}0, \left(0\leq t<{t}_{0}\right)\\ \frac{{F}_{p}}{0.5\Delta t}\left(t-{t}_{0}\right), \left({t}_{0}\leq t<{t}_{1}\right)\\ -\frac{{F}_{p}}{0.5\Delta t}\left(t-t_2\right), \left({t}_{1}\leq t<{t}_{2}\right)\\ 0, \left({t}_{2}\leq t\right)\end{array}\right.$$

(3)

The cantilever deflection response due to the SH mass-spring force (${f}_{1(t)}$) is the sum of the homogeneous and particular solutions given in Eq. 4.

$$\begin{aligned} {u}_{1(L,t)} & ={e}^{-\zeta {\omega }_{\text{nc}}t}\left[\frac{\left({\dot{u}}_{0}-v\right)+{\omega }_{\text{nc}}\zeta \left({u}_{0}-d\right)}{{\omega }_{\text{nc}}\sqrt{1-{\zeta }^{2}}}\right.\\ &\qquad\left.\text{sin}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}t+\left({u}_{0}-d\right)\text{cos}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}t\right]\\ &\qquad+\frac{{F}_{i}}{k}{e}^{-{\zeta }_{i}{\omega }_{i}t}\\&\qquad\times\left[\left(\frac{{\zeta }_{i}}{\sqrt{1-{{\zeta }_{i}}^{2}}}B+A \right) \text{sin}\sqrt{1-{{\zeta }_{i}}^{2}}{\omega }_{i}t\right.\\&\qquad\left.+\left(\frac{{\zeta }_{i}}{\sqrt{1-{{\zeta }_{i}}^{2}}} A-B\right) {\rm{cos}}\sqrt{1-{{\zeta }_{i}}^{2}}{\omega }_{i}t\right]\end{aligned}$$

(4)

where, ${u}_{0}=0, {\dot{u}}_{0}=0, \beta ={\omega }_{i}/{\omega }_{\text{nc}}$, and:

$$d=\frac{{F}_{i}}{k}\left(\frac{{\zeta }_{i}}{\sqrt{1-{{\zeta }_{i}}^{2}}} A-B\right), v=\frac{{F}_{i}}{k}{\omega }_{i}\left(\frac{1-2{{\zeta }_{i}}^{2}}{\sqrt{1-{{\zeta }_{i}}^{2}}} A+2{\zeta }_{i}B\right), \frac{{F}_{i}}{k}=-\left(\frac{{L}^{3}}{EI}\left(\frac{{m}_{1}}{3}+\frac{{\overline{m} }_{2}L}{8}\right)\left({x}_{0}{{\omega }_{i}}^{2}\right)\right)$$

$$A=\frac{2\beta \left(\zeta -{\zeta }_{i}\beta \right)\sqrt{1-{{\zeta }_{i}}^{2}}}{{\left(2\beta \right)}^{2}{\left(\zeta -{\zeta }_{i}\beta \right)}^{2}\left(1-{{\zeta }_{i}}^{2}\right)+{\left(1-2\zeta {\zeta }_{i}\beta +\left(2{{\zeta }_{i}}^{2}-1\right){\beta }^{2}\right)}^{2}}$$

$$B=\frac{1-2\zeta {\zeta }_{i}\beta +\left(2{{\zeta }_{i}}^{2}-1\right){\beta }^{2}}{{\left(2\beta \right)}^{2}{\left(\zeta -{\zeta }_{i}\beta \right)}^{2}\left(1-{{\zeta }_{i}}^{2}\right)+{\left(1-2\zeta {\zeta }_{i}\beta +\left(2{{\zeta }_{i}}^{2}-1\right){\beta }^{2}\right)}^{2}}$$

The cantilever deflection response due to the triangular pulse force (${f}_{2(t)}$) is based on the convolution integration of the delta-Dirac equation (Eq. 5) [23].

$$\begin{aligned} {u_{2(L,t)}} & = \frac{{{\omega _{\text{nc}}}}}{{k\sqrt {1 - {\zeta ^2}} }}\int_{{\rm{T}} = {t_0}}^{{\rm{T}} = t} {{f_{2\left( {t = {\rm{T}}} \right)}}\left( {{e^{ - \zeta {\omega _{\text{nc}}}\left( {t - {\rm{T}}} \right)}}} \right)}\\&\quad{\left( {\sin \sqrt {1 - {\zeta ^2}} {\omega _{\text{nc}}}\left( {t - {\rm{T}}} \right)} \right)d{\rm{T}}}.\end{aligned}$$

(5)

Therefore, the overall solution for the deflection response of the cantilever tip can be theoretically obtained by superposition, as given in Eq. 6.

$${u}_{\left(y=L,t\right)}=\left\{\begin{array}{l}{u}_{1\left(L,t\right)}, \left(0\leq t<{t}_{0}\right) \\ {u}_{1\left(L,t\right)}+{\left.{u}_{2\left(L,t>{t}_{0}\right)}\right|}_{{t}_{0}}^{t}, \left({t}_{0}\leq t<{t}_{1}\right)\\ {u}_{1\left(L,t\right)}+{\left.{u}_{2\left(L,t>{t}_{0}\right)}\right|}_{{t}_{0}}^{t}-{\left.{u}_{2\left(L,t>{t}_{0}\right)}\right|}_{{t}_{1}}^{t}\\ \quad+{\left.{u}_{2\left(L,t>{t}_{1}\right)}\right|}_{{t}_{1}}^{t}, \left({t}_{1}\leq t<{t}_{2}\right)\\ {u}_{1\left(L,t\right)}+{\left.{u}_{2\left(L,t>{t}_{0}\right)}\right|}_{{t}_{0}}^{t}\\ \quad-{\left.{u}_{2\left(L,t>{t}_{0}\right)}\right|}_{{t}_{1}}^{t}+{\left.{u}_{2\left(L,t>{t}_{1}\right)}\right|}_{{t}_{1}}^{t}\\ \quad-{\left.{u}_{2\left(L,t>{t}_{1}\right)}\right|}_{{t}_{2}}^{t}, \left({t}_{2}\leq t\right)\end{array}\right.$$

(6)

The deflection response due to the conditions before impact (${u}_{1(L,t)}$) can be neglected as the ratio between the mass-spring natural frequency to the cantilever's natural frequency is approaching zero, and the ratio between the mass-spring acceleration to the impact acceleration is insignificant. Therefore, the deflection response at the cantilever tip can be obtained only due to the triangular pulse input while neglecting the response due to the mass-spring input. The final solution after the impact duration time (i.e., at $t\ge {t}_{2}$) is given by Eq. 7.

$$\begin{aligned} & {u}_{(L,t\ge {t}_{2})}\\ &\quad=\frac{1}{0.5\Delta t}\frac{{F}_{p}}{k{\omega }_{\text{nc}}}\Bigg\{-\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{0}\right)}\right)\Bigg[\frac{1-2{\zeta }^{2}}{\sqrt{1-{\zeta }^{2}}}{\rm{sin}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{0}\right)\\ &\qquad-2\zeta {\rm{cos}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{0}\right)\Bigg]\\ &\qquad+2\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{1}\right)}\right)\Bigg[\frac{1-2{\zeta }^{2}}{\sqrt{1-{\zeta }^{2}}}{\rm{sin}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{1}\right)\\ &\qquad-2\zeta {\rm{cos}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{1}\right)\Bigg]\\ &\qquad-\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{2}\right)}\right)\Bigg[\frac{1-2{\zeta }^{2}}{\sqrt{1-{\zeta }^{2}}}{\rm{sin}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{2}\right)\\ &\qquad-2\zeta {\rm{cos}}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{2}\right)\Bigg]\Bigg\} \end{aligned}$$

(7)

where

$$\frac{{F}_{p}}{k}=-\left(\frac{{L}^{3}}{EI}\left(\frac{{m}_{1}}{3}+\frac{{\overline{m} }_{2}L}{8}\right){a}_{p}\right)$$

Based on the impulse-momentum relation (Eq. 8), the peak acceleration (${a}_{p}$) generated during the impact can be estimated from Eq. 9, where (${\dot{x}}_{0}^{-}$) and (${\dot{x}}_{0}$) are the velocities of the SH mass before and after impact. (${\dot{x}}_{0}^{-}$) is constant since the SH stroke and spring are already specified, while (${\dot{x}}_{0}$) depends on the strain energy absorbed by the concrete material (i.e., the loss in the kinetic energy of the hammer mass).

$$impulse=\int\limits_{{t}_{0}}^{{t}_{2}}{f}_{2(t)}dt=\frac{1}{2}{\mathrm{m}}_{3}{a}_{p}\Delta t={\mathrm{m}}_{3}({\dot{x}}_{0}-{\dot{x}}_{0}^{-})$$

(8)

$${a}_{p}=\frac{2({\dot{x}}_{0}-{\dot{x}}_{0}^{-})}{\Delta t}$$

(9)

We should emphasize that the angular velocity response (${\Omega }_{(y,t)}$) must be obtained to calculate the sensitivities to input acceleration and jerk. Since the impact duration is too small and less than a quarter of the periodic time of the cantilever's natural oscillation ($\Delta t<0.25T$), the max angular velocity response (${\Omega }_{tip}$) will always occur after the impact duration time ($\Delta t$) or when ($t\ge {t}_{2}$). Consequently, (${\Omega }_{tip}$) is calculated by differentiating the final solution (Eq. 7) once w.r.t. to the cantilever's axial direction ($y$), and again w.r.t. time ($t$) as given in Eq. 10.

$$\begin{aligned}{\Omega }_{(L,t\ge {t}_{2})}&=\frac{d}{dt}\left(\frac{d{u}_{(L,t\ge {t}_{2})}}{dy}\right)\\ &=\frac{{\overline{\theta }}_{tip}{a}_{p}}{0.5\Delta t}\Bigg\{-\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{0}\right)}\right)\Bigg[\mathrm{cos}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{0}\right)\\ &\quad+\frac{\zeta }{\sqrt{1-{\zeta }^{2}}}\mathrm{sin}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{0}\right)\Bigg]\\ &\quad+2\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{1}\right)}\right)\Bigg[\mathrm{cos}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{1}\right)\\ &\quad+\frac{\zeta }{\sqrt{1-{\zeta }^{2}}}\mathrm{sin}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{1}\right)\Bigg]\\ &\quad-\left({e}^{-\zeta {\omega }_{\text{nc}}\left(t-{t}_{2}\right)}\right)\Bigg[\mathrm{cos}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{2}\right)\\ &\quad+\frac{\zeta }{\sqrt{1-{\zeta }^{2}}}\mathrm{sin}\sqrt{1-{\zeta }^{2}}{\omega }_{\text{nc}}\left(t-{t}_{2}\right)\Bigg]\Bigg\}\end{aligned}$$

(10)

Figure 3 shows graphical representations of the hammer mass displacement and the cantilever’s deflection and angular velocity responses at different kinetic energy losses depicting the effect of input triangular pulse. The representations are constructed considering an arbitrary cantilever’s natural frequency of 100 Hz and an impact duration time of 10^–3 s. It is shown in Fig. 3a3, b3 that the effect of the hammer mass displacement on the cantilever response is insignificant compared to the triangular pulse effect. In addition, the max angular velocity response occurred after the pulse duration time, hence using Eq. 10 to obtain sensitivities. We should emphasize that when ($\Delta t$) approaches zero, the shape of the input pulse (shown in Fig. 2) does not affect the deflection and angular velocity responses since the input, in this case, will be treated as an impulse.

Fig. 3

Graphical representations of the hammer mass displacement and the cantilever’s deflection and angular velocity responses at different kinetic energy losses depicting the effect of input triangular pulse

Assuming undamped oscillation ($\zeta =0$), the sensitivities to input acceleration and jerk at maximum responses are given by Eqs. 11 and 12, respectively. The residual cosine terms of Eq. 10 are mere terms of data periodicity. However, they have a scaling effect that is automatically compensated through calibration.

$${S}_{a}=\frac{{|{\Omega }_{(y=L,t\ge {t}_{2})}|}_{max}}{{|{a}_{(t)}|}_{max}}=\frac{\frac{{L}^{2}}{EI}\left(\frac{{m}_{1}}{2}+\frac{{\overline{m} }_{2}L}{6}\right)\left(\frac{{a}_{p}}{0.5\Delta t}\right)}{{a}_{p}}=\frac{{L}^{2}}{EI}\left(\frac{{m}_{1}}{2}+\frac{{\overline{m} }_{2}L}{6}\right)\frac{1}{0.5\Delta t}$$

(11)

$${S}_{j}=\frac{{|{\Omega }_{(y=L,t\ge {t}_{2})}|}_{max}}{{|{j}_{(t)}|}_{max}}=\frac{\frac{{L}^{2}}{EI}\left(\frac{{m}_{1}}{2}+\frac{{\overline{m} }_{2}L}{6}\right)\left(\frac{{a}_{p}}{0.5\Delta t}\right)}{\frac{{a}_{p}}{0.5\Delta t}}=\frac{{L}^{2}}{EI}\left(\frac{{m}_{1}}{2}+\frac{{\overline{m} }_{2}L}{6}\right)$$

(12)

$${S}_{j}={S}_{a}.\left(0.5\Delta t\right)$$

(12a)

$${|{j}_{(t)}|}_{max}=\frac{{|{\Omega }_{(y=L,t\ge {t}_{2})}|}_{max}}{\frac{{L}^{2}}{EI}\left(\frac{{m}_{1}}{2}+\frac{{\overline{m} }_{2}L}{6}\right)}$$

(12b)

Equation 12b gives the analytical model of the measurement technique concept in which an angular velocity signal is directly transformed into a jerk signal through the cantilever length, mass, area moment of inertia, and its material elasticity modulus. From the experimental point of view, Eq. 12b implies that to measure jerk, we just need a gyroscope mounted on a cantilever tip. Also, Eq. 12 ensures constant sensitivity to input jerk. Therefore, the proposed measurement technique leads to a direct measurement of concrete strength in terms of the jerk signal and overcomes the high uncertainty due to mechanical errors in the traditional SH.

Regarding the effect of gravity on jerk sensor readings according to different SH orientations, it should be noted that, since the angular velocity is calculated by taking the derivative of the deflection angle with respect to time, the effect of any constant (static) deflection angle will be zeroed. Thus, the change in angle of deflection (i.e., angular velocity) will be only related to the change in input acceleration (i.e., jerk). Therefore, in general, jerk sensor readings are not affected by gravity. This can be considered as an additional strength point for using jerk sensors. However, since gravity affects the hammer mass motion, SH orientation affects the impact energy and, consequently, the measured jerk value. Upward orientation will cause less impact and, therefore, lower jerk readings. Downward orientation will cause more impact and, therefore, higher jerk readings.

2.2.2 Experimental Approach

The jerk sensor sensitivity (${S}_{j}$) at the cantilever's natural frequency (${\omega }_{\text{nc}}$) was determined through calibration by subjecting the jerk sensor to various transient accelerations (${a}_{p}$) while measuring the angular velocity response at the cantilever tip (${\Omega }_{tip}$). For calibration purposes, the jerk value was calculated by using an accelerometer mounted at the cantilever base and differentiating its recorded signal w.r.t. time. Next, the calibration curve was constructed by plotting the angular velocity response versus the jerk. Then, the jerk sensitivity (${S}_{j}$) was obtained. Once the sensitivity is verified to be constant, the calibration curve is confidently used to measure jerk from the gyroscope signal directly.

For more emphasis, during the MSH test, the jerk value ($j$) can be directly obtained by Eq. 13 from the gyroscope signal (${\Omega }_{tip}$) and the calibrated jerk sensor sensitivity (${S}_{j}$). In addition, from Newton's second law, the rate of change of force ($\dot{F}$) during the impact period can be obtained according to Eq. 14, where (${m}_{3}$) is the SH mass.

$$j=\left|\frac{{\Omega }_{tip}}{{S}_{j}}\right|$$

(13)

$$\dot{F}={m}_{3}.j$$

(14)

2.3 Selection of Cantilever Dimensions for the Jerk Sensor

The cantilever dimensions were selected considering four criteria. First, the dimensions of the SH casing provide limited space to accommodate the jerk sensor size. Second, the dimensions of the gyroscope mounted on the cantilever tip. Third, the cantilever should remain within the elastic region. Fourth, the appropriate cantilever's natural frequency. It is known that the cantilever's natural frequency depends mainly on its material and dimensions. And jerk sensitivity depends on the ratio between the gyroscope reading (${\Omega }_{tip}$) to the input jerk ($j$). Therefore, there should be an appropriate compromise among these four factors. Eight cantilever models of 5 mm width with different lengths and thicknesses have been theoretically examined by Eq. 15 to determine the proper cantilever natural frequency for SH application. Table 1 shows the dimensions of the eight cantilever models and their corresponding first-mode natural frequency (${f}_{n}$).

Table 1 First mode natural frequencies of eight cantilever models as estimated from Eq. 15

$$2\pi {f}_{n}\cong \sqrt{\frac{{k}_{1}}{{m}_{1}+\frac{33}{140}{\overline{m} }_{2}L}}$$

(15)

where (${k}_{1}=3EI/{L}^{3}$) is the cantilever stiffness due to the gyroscope point mass (${m}_{1}$) and the mass equivalent to the cantilever’s distributed self-mass (${\overline{m} }_{2}$) placed at the free end.

It was found that the L-408 jerk sensor has a deflection response within the elastic limit, and an angular velocity response within the gyroscope measuring range, enabling a proper sensitivity to the impact force during the SH test. Hence, the experimental work has been carried out using the L-408 model.

2.4 Manufacturing and Characterization of the L-408 Jerk Sensor

The L-408 jerk sensor cantilever of dimensions 40 × 5 × 0.8 mm³ was cut from 0.8 mm austenitic spring stainless-steel sheet in the rolling direction using a laser cutting machine with precision 10 μm. The cantilever surface was polished and relieved of stress using a Struers polishing device. The chemical composition of the stainless-steel cantilever material was measured by a spark optical emission spectrometer and listed in Table 2. The density was measured using an electronic densimeter. The tensile properties were obtained according to ASTM-E8 by testing three specimens using a 100 kN AG-X plus Shimadzu universal testing machine under a strain rate of 1 × 10^–3 s⁻¹ at room temperature. The strain was measured using a mechanical extensometer in the elastic zone. Hardness was measured using the HMV Shimadzu Vickers microhardness machine by taking the average value of 5 indentations. The tested properties of the stainless-steel cantilever material are shown in Table 3.

Table 2 Chemical composition of the stainless-steel cantilever material

Table 3 Mechanical properties of the stainless-steel cantilever material

2.5 Calibration of the L-408 Jerk Sensor

The L-408 jerk sensor was calibrated using the high-excitation computer-controlled electrodynamic shaker shown in Fig. 4. The shaker specifications are shown in Table 4. The shaker was programmed to generate three transient excitations at 19 individual accelerations in the range of 0.8~8 G, which means a total of 57 excitations. Every three excitations were monotonic (generated at the same torque) and successive at 2 s intervals. The input acceleration and output angular velocity were measured for each, and the average of the three peaks was taken.

Fig. 4

High-excitation computer-controlled electrodynamic shaker for calibrating the L-408 jerk sensor

Table 4 Specifications of the electrodynamic shaker

Two 9-axis MEMS sensors (MPU9250) were used to measure acceleration and angular velocity. MPU9250 has three 16-bit ADCs for digitizing the analog signal output and operates at a reference voltage of 2.5 V. Arduino IDE software was utilized to program the MPU9250 gyroscope to measure the angular velocity at the cantilever tip in the range of ± 2000 dps with a digital sensitivity of 16.4 LSB/dps, which corresponds to an analog sensitivity of 0.63 mV/dps. Similarly, the MPU9250 accelerometer was programmed to measure the input acceleration at the shaker stage in the range ± 16 G. Signals from the two MPU9250 sensors were recorded simultaneously using an Arduino Uno Rev3.0 DAQ at a sampling rate of 256 Hz.

MATLAB software was utilized for three tasks; first, differentiate the recorded accelerometer signal by the gradient function to obtain the input jerk. Second, analyze the recorded gyroscope signal by the Morse discrete wavelet analysis function [24] to get the cantilever's natural frequency and angular velocity amplitude. Third, obtain the experimental sensitivity of the L-408 jerk sensor by linear data fitting.

2.6 Modification of SH Body

Two Schmidt hammers of N-type were used; the first one was equipped with the L-408 jerk sensor, while the second remained intact and was used as a reference for comparing the results obtained from the modified one. The modified hammer is illustrated in Fig. 5. The jerk sensor was attached to the back of the hammer mass (no. 1) through a metal part (no. 7) by two small bolts. The metal part was made of aluminum, and its weight is minimal compared to the hammer mass, so its effect on the impact energy is negligible. A longitudinal open slot (no. 12) was milled through the SH casing (no. 11) to allow axial movement of the cantilever (no. 8) attached to the hammer mass (no. 1). The open slot also works as a guide for the sensor base to prevent it from rotating during and after impact.

Fig. 5

3D solid work drawing showing the modified Schmidt Hammer equipped with the L-408 jerk sensor

2.7 Reading Unit for SH

A standalone electronic reading unit was manufactured to display the concrete strength and elasticity modulus. As shown in Fig. 6, the reading unit consists of Arduino Uno Rev 3.0 (i.e., DAQ) and a Liquid Crystal I2C display equipped with a keypad shield (i.e., interactive screen). The reading unit also includes a sound buzzer (i.e., notifier) and a Raspberry Pi Power Pack Board (i.e., power source). These electronic components were installed inside a special acrylic box fabricated by a Laser Printing Machine. The microcontroller of the Arduino board was programmed to show a graphical interface that allows users to check the status of the MPU9250 gyroscope sensor, initiate testing mode, navigate through the readings, overwrite a specific reading, and finally display the average of the readings.

Fig. 6

3D solid work drawing showing the electronic reading unit and its components

2.8 Preparation of Concrete Specimens

2.8.1 Materials

The concrete elasticity modulus depends on the moduli of elasticity of its composition [25]. Therefore, the composition materials should be specified before casting the concrete specimens. The binder was Ordinary Portland Cement (OPC) type I, grade 42.5 N, with a specific surface area of 3280 cm²/gm. The fine aggregate (FA) was natural siliceous sand of 2.67 specific gravity and 2.82 fineness modulus. The coarse aggregate (CA) was crushed dolomitic limestone of 2.62 specific gravity and average abrasion resistance of 22.15%. The maximum nominal size of CA1 is 10 mm, and CA2 is 20 mm. The sieve analysis test results for aggregate are illustrated in Table 5. The workability admixture was a polycarboxylate-based high-range-water-reducing (HRWR) super-plasticizer of type G. The mixing water was drinkable tap water.

Table 5 Passing percentage per sieve size for CA2, CA1, and FA as obtained from sieve analysis

2.8.2 Mix Design

Eight mixes were designed to obtain compressive strengths in the range of 20~55 MPa. The mix design proportions were obtained by the absolute volume method. Table 6 shows the proportions required to produce one cubic meter of concrete for all mix designs. Figure 7 shows concrete mix compositions as volume percentages of one cubic meter. In three steps, the mixing process was carried out using a tilting mixer drum with a maximum volume of 50 L. First, cement and aggregate were mixed in the dry state for 2 min until the dry mixture became homogeneous. Second, the super-plasticizer was mixed with water and added to the dry mixture during the mixing process. Third, the mixing process continued for another 2 min in the wet state until the final mixture became completely homogeneous. Slump and air content tests were conducted on the fresh concrete before casting in the molds.

Table 6 Proportions required to produce one cubic meter of concrete and fresh-concrete properties (Slump and air content values) for all mix designs

Fig. 7

Concrete mix compositions as volume percentages of one cubic meter

2.8.3 Specimens and Curing Conditions

For each concrete mix, six cubes of dimensions 150 × 150 × 150 mm³ and three cylinders of diameter 150 mm and height 300 mm were cast. The cubic specimens were used to obtain the cube compressive strength (${F}_{cu}$) and the SSH and MSH values. Whereas the cylindrical specimens were used to obtain the static elasticity modulus (${E}_{c}$) and cylinder compressive strength (${F}_{cu,cy}$). Molds were filled and rodded according to ASTM-C31 and then disassembled after 24 h. The specimens were cured in the air at ambient conditions of temperature and humidity till the day of testing. Figure 8 shows a photo of typical cubic and cylindrical test specimens from different concrete mixes.

Fig. 8

Typical cubic 15 × 15 × 15 cm³ and cylindrical ϕ15xL30 cm test specimens from different concrete mixes

2.9 Testing Procedures

Slump and air content tests were conducted on fresh concrete to assess the quality of each mix according to ASTM-C143 and ASTM-C231, respectively. Compressive strength, static elasticity modulus, standard Schmidt hammer (SSH), and modified Schmidt hammer (MSH) tests were conducted for each mix at the age of 28 days. The compression test was conducted on three cubic specimens using a universal testing machine (UTM) of load capacity 3000 kN, and the average compressive strength was calculated. The static elasticity modulus test was conducted on three cylindrical specimens according to ASTM-C469, and the average tangent elasticity modulus was calculated.

Three cubic specimens were taken from each mix for the SSH and MSH tests. Their side surfaces were carefully polished (Fig. 9a) and marked into a 5 × 5 grid (Fig. 9b, c), then they were held firmly by Shimadzu UTM upper and lower plates at a load of 50 kN as shown in Fig. 9d. The SSH and MSH tests were conducted at zero-degree orientation. For each specimen, 15 readings were taken by the SSH according to ASTM C805. Whereas, from the statistical point of view, five readings were taken by the MSH since the measurement technique is newly proposed.

Fig. 9

Photo showing 5 × 5 marked cubic specimens and the method of holding them by UTM

2.10 Data Analysis

For the SSH test, the 15 readings were filtered by removing the extreme readings due to surface anomalies, and the average was calculated. Then, the strength results were obtained based on the calibration curve supplied by the manufacturer. For the MSH test, the Arduino DAQ inside the reading unit scans the gyroscope signal for 0.128 s during impact at a 10³ Hz sampling rate. The scanned data points were analyzed by the FFT algorithm programmed into the DAQ to obtain the angular velocity peaks and their corresponding frequencies. The average of the highest three peaks was taken as the nominal gyroscope amplitude for each reading and automatically interpreted to jerk value using the preprogrammed sensor calibration curve. In other words, the jerk value was calculated based on the nominal gyroscope reading and the L-408 jerk sensor sensitivity (${S}_{j}$). An example of the interpretation of the MSH reading is explained in detail in the results section.

2.11 Calibration of the Modified Schmidt Hammer

Compressive strength and elasticity modulus UTM-results of all concrete mixes were correlated to SSH and MSH results. Exponential data models were used to fit the MSH jerk results to the UTM results to get the experimental calibration curves. These calibration curves were used to estimate the concrete strength and elasticity modulus according to the signal-processing diagram shown in Fig. 10. Data correlation, the goodness of fit, and error percentage for both SSH and MSH tests were measured by Pearson's coefficient (${r}^{2}$), determination coefficient (${R}^{2}$), and root-mean-squared percentage error (RMSPE), respectively.

Fig. 10

A diagram showing the signal processing by the MSH reading unit

3 Experimental Results and Discussion

3.1 Jerk Sensor Sensitivity

Figure 11a–c shows a sample of accelerometer, jerk, and gyroscope signals. These signals were recorded during the three successive monotonic excitations generated at 300% torque. Figure 12 shows the Morse wavelet analysis of the three consecutive excitations of the gyroscope signal. From Fig. 12, it is observed that the experimental natural frequency of the L-408 jerk sensor is around 79 Hz, which disagrees with the theoretically predicted value (106 Hz) in Table 1. The change in the cantilever's natural frequency can be attributed to the stiffness of the four wires connecting the gyroscope to the DAQ that were ignored in the theoretical model.

Fig. 11

A sample of accelerometer, jerk, and gyroscope signals recorded at 300% torque

Fig. 12

Morse wavelet analysis of the three consecutive excitations of the gyroscope signal

Figure 13a, b shows the correlation of the wavelet analysis amplitudes of all the gyroscope signals versus input acceleration and jerk, respectively. The slopes of the curves in Fig. 13 give sensitivity values of 18.47 mV/G to input acceleration and 0.17 mV/(G/s) to input jerk. The data correlation coefficient was 0.98, indicating high confidence in the L-408 jerk sensor sensitivity at 79 Hz.

Fig. 13

Correlation of the wavelet analysis amplitudes of all the gyroscope signals versus input a acceleration and b jerk; slopes represent the L-408 jerk sensor sensitivity to input acceleration and jerk

3.2 Slump and Air Content Test Results

The slump test results are within the range of 8~22 cm, indicating a suitable concrete workability that prevents the formation of undesired air pockets inside the test specimen. The air content test results are between 2 and 4%, indicating a low air-entrained concrete and confirming the goodness of the mixing process in favor of strength. Consequently, the concrete specimens are good representatives of standard structural concrete.

3.3 Compressive Strength and Elasticity Modulus Test Results by UTM

Figure 14 shows the cube compressive strength, cylinder compressive strength, and elasticity modulus of all concrete mixes tested by UTM. Results show that the designed concrete grades lie between 20 and 55 MPa, covering the testing range of SH. Figure 15 shows the typical strength-elasticity curves for cubic and cylindrical specimens. Correlation factors between the concrete compressive strength and the elasticity modulus for cubic and cylindrical specimens are 0.93 and 0.89, respectively. The result of Fig. 15 suggests that the cube compressive strength can be relied on to estimate the static elasticity modulus of concrete instead of cylinder compressive strength since the correlation factor of cube compressive strength results is 0.93.

Fig. 14

Cube and cylinder compressive strength and elasticity modulus of all concrete mixes tested by UTM at the age of 28 days

Fig. 15

Correlation between the concrete compressive strength and the elasticity modulus for cubic and cylindrical specimens

3.4 Interpretation of MSH Readings

A signal sample was taken as an example to explain how the MSH test obtained the jerk values. For instance, Fig. 16a illustrates a gyroscope signal recorded during testing M1-C20. FFT analysis was performed to obtain the frequency spectrum of this sample as shown in Fig. 16b. It is found that the highest peak value occurred at frequency 81 Hz, which is close to the jerk sensor's natural frequency (79 Hz). The other lower peaks in the spectrum are due to the local natural frequencies of the SH components, such as the springs, rods, masses, and wires connecting the gyroscope. This may mean that the variations in MSH readings are attributed to the combination of local and global vibration modes that appeared in the FFT amplitude spectrum (Fig. 16b) after impact.

Fig. 16

A signal sample recorded during testing M1-C20 a gyroscope signal and b FFT amplitude spectrum

3.5 MSH Calibration Curves

Figure 17 shows the strength calibration curve of the MSH based on testing eight concrete grades. It is observed that there is a high correlation between the cube strength and the jerk value with an r-squared (${r}^{2}$) value of 0.94. The proper data model representing the relation was an exponential function with a determination coefficient (${R}^{2}$) of 0.90.

Fig. 17

The strength calibration curve of the MSH based on testing eight concrete grades

Figure 18 shows the correlations between the concrete elasticity modulus and the rebound number of SSH and jerk values of MSH. The results show that the correlation coefficient (${r}^{2}$) and determination coefficient (${R}^{2}$) for MSH are 0.93 and 0.87, respectively, whereas, for SSH, they are 0.92 and 0.88. It is found that MSH has almost similar correlations to concrete elasticity as SSH.

Fig. 18

Correlations between the concrete elasticity modulus and the rebound number of SSH and jerk values of MSH

3.6 Comparison between Standard and Modified Schmidt Hammers

Table 7 shows the average concrete strength and elasticity modulus values obtained by UTM, SSH, and MSH for all mixes. It is noted that the estimated concrete strength by SSH (column 5) is exaggerated compared to the experimental values obtained by UTM (column 2). In comparison, the concrete strength estimated by MSH (column 8) is relatively near the actual measured values of UTM. However, the SSH and MSH estimated the elasticity modulus (column 6 and column 9) relatively near the UTM values (column 3).

Table 7 The average concrete strength and elasticity modulus values as obtained by UTM, SSH, and MSH

Figure 19a shows the error between the estimated and actual strength for SSH and MSH. From the results, the SSH estimated the concrete strength with an RMSPE of 25%. However, the MSH test estimated the concrete strength relatively more accurately with an RMSPE of 12%. Therefore, MSH has improved the measuring accuracy by 13%. On the other hand, Fig. 19b shows the error between the estimated and actual elasticity modulus. Both tests estimated the elasticity modulus with 8% RMSPE and were more accurate in determining the concrete elasticity modulus than the strength.

Fig. 19

The error between the estimated and actual a strength and b elasticity modulus for SSH and MSH

The relative error in SSH results is due to the significant difference between SSH and MSH measurement techniques. SSH depends on the mechanical response of the mass-spring system in terms of mass displacement after impact. However, MSH relies on the degree of responsiveness of the free end of the cantilever to the rate of change of impact force in terms of jerk value during impact, which is a more realistic direct measurement than mass displacement. In addition, there might be some uncertainty about the calibration curve supplied by the manufacturer, as previously stated by [6, 9, 10]. This explains why the civil engineering society does not rely much on SSH estimation since its readings are considered approximate values and are insensitive to impact force fluctuations.

On the other hand, the modified measurement technique focuses on eliminating post-impact errors (e.g., analog scale indicator, spring inefficiency, internal friction, labor unsteady hands), which is the same aim of modern rebound hammers such as SilverSchmidt [12]. However, the variation between the SSH and MSH does not mean that MSH estimation is necessarily better. We need more investigation considering a larger sample size of concretes to establish more accurate calibration curves. In addition, the MSH uses a prototype jerk sensor which concept is still new. A parametric study is needed to understand the relation of jerk signal parameters to other concrete properties. For instance, the MSH might correlate better with concrete dynamic properties (e.g., dynamic elasticity modulus).

4 Summary and Conclusions

In this paper, Schmidt Hammer was modified by introducing a cantilever-based jerk sensor attached to the hammer mass to estimate the concrete compressive strength and static elasticity modulus. A theoretical approach was introduced to design and select the jerk sensor sensitivity for the modified Schmidt Hammer. A high-excitation electrodynamic shaker was used to obtain the calibration curve of the jerk sensor. Fresh and hardened concrete tests were conducted on eight concrete mixes, and the tested mixes were good representatives of the concrete grades in the range of 20~55 MPa. The experimental calibration curves of the modified Schmidt hammer were constructed in this range. For comparison purposes, the SSH manufacturer calibration curve was used as it is, while the elasticity modulus calibration curve was experimentally established. Correlations between the modified Schmidt hammer and concrete strength and static elasticity modulus were investigated and compared to the standard Schmidt hammer test. The following conclusions were drawn:

• The L-408 jerk sensor was designed and manufactured based on the analytical model, and its natural frequency was experimentally determined and found to be 79 Hz.

• The experimental sensitivity of the jerk sensor for impact NDT was obtained using a high-excitation electrodynamic shaker and found to be 0.17 mv/(G/s) or 0.27 dps/(G/s).

• MSH calibration curves were established by correlating the jerk readings to concrete strength and modulus of elasticity and were found to have a correlation coefficient of 0.94 and 0.93, respectively.

• The RMSPE of the SSH and MSH in estimating the concrete cube strength were compared and found to be 25% and 12%, respectively. The jerk sensor successfully estimated the cubic strength of concrete with better accuracy than the SSH rebound number by 13%.

• The RMSPE of the SSH and MSH in estimating the concrete elasticity modulus were compared and found to be of a similar value of 8%. The jerk sensor estimated the static elasticity modulus of concrete with the same accuracy as the SSH.

• The errors in MSH results can be attributed to the wires, which affect the global natural frequency of the jerk sensor and induce higher damping to the angular velocity signal. The jerk sensor is recommended to be re-designed in the MEMS scale to eliminate the undesired effects caused by the wires connecting the gyroscope to the DAQ.

• More investigations with a larger sample size are needed to establish good calibration curves since we used a prototype jerk sensor.