1 Introduction

Thermographic nondestructive evaluation (NDE) methods cover a large variety of modalities, including different excitation sources (optical, mechanical and electromagnetic), temporal schemes, and spatial distributions of the excitation. These methods are all based on making use of an infrared (IR) camera to monitor the surface temperature of a sample subjected to an excitation, aimed at producing a thermal unbalance. The presence of surface breaking or sub-surface defects results in anomalies in the surface temperature, which are the indications of flaws. A throughout revision of the application of thermographic methods to detect defects can be found in [1].

Different mechanisms make buried defects visible in thermographic methods. In optically excited thermography, the input energy is typically absorbed at the surface, diffuses in the material as thermal energy, and defects such as cracks or delaminations (filled with air) act as thermal resistances that hinder the propagation of heat [2,3,4,5]. In the case of horizontal defects (delaminations, inclusions, etc.) that intercept the in-depth propagation of thermal energy, the surface temperature features indications after a surface/defect/surface round-trip of heat. Because of the diffusive nature of heat propagation, the effects of flaws on the surface temperature diminish with the defect depth, and only a limited material layer is testable. Another characteristic of optical excitation is that the defect signature is superimposed to the background temperature generated by the excitation.

On the contrary, in ultrasound excited thermography performed in metals, the heat is generated basically at the defects, due mainly to friction between the asperities of both sides of the discontinuity [6,7,8] (in polymers and composites there is an additional bulk heating due to thermoelastic effect [9, 10]). Similarly, metallic inclusions in electrical insulators, excited inductively [11, 12] act as heat sources. In both cases, the defects generate heat in a cold environment and the indication is a hot spot at the surface, on top of the buried defect. In the case of horizontal defects, as the heat generated at the flaw travels just one way to the surface, deeper defects are detectable if compared with optically excited thermography. Furthermore, inductive thermography is advantageous in terms of being a non-contact technique [13]. However, it should be noted that the main application of inductive thermography is on metallic parts, in which Eddy currents produce heat regardless of the presence of flaws. In a cracked material, the cracks intercept either the Eddy currents or the heat flux, giving rise to anomalies in the surface temperature distribution, which is typically calculated making use of finite elements modelling [14].

The characterization of heat sources generated at flaws in vibrothermography or inductive thermography has attracted a great deal of attention in the last decade. The challenge in determining the shape, size and depth of heat sources in these experiments is to deal with heat diffusion, which degrades the information available at the surface (temperature) coming from a deep defect, making the characterization an ill-posed inverse problem. Different strategies have been proposed in the literature to deal with this difficulty. By assuming a particular geometry of the heat source [12, 15, 16] the ill-posedness of the problem diminishes, as the characterization of the flaw is reduced to a parameter estimation problem with a small number of unknowns (defining the assumed geometry). A more ambitious approach consists in tackling the inverse problem in a general form, ignoring the geometry of the heat source. This blind search of heat sources beneath the surface can be addressed as a least squares minimization problem, which is severely ill-posed and requires regularization. Regularization is typically performed by adding to the objective function a penalty term that drives the search among solutions that fulfill a certain pattern (sparcity, sharpness, etc.), which is known beforehand. The relevance of the penalty functional is controlled by a factor, the regularization parameter, which tunes the relative weight of the regularization term with respect to the original objective function. A successful reconstruction requires a wise adjustment of the regularization parameter to balance stability of the inversion and adequacy of the solution to the original problem. This strategy has been successfully applied to characterize vertical cracks from vibrothermography data, both in lock-in [17,18,19] and burst regimes [20]. Another blind approach to identify buried heat sources is the virtual wave concept [11], in which a “virtual wave” (true wave counterpart of the diffusion thermal field) is calculated from the diffusion field and can be used to trace back the original temperature pattern. This approach also involves solving an ill-posed inverse problem that needs regularization: the calculation of the virtual wave from the thermal data. This methodology has been applied successfully to detect defects in composites [21], as well as in additively manufactured parts [22].

Even if the regularization procedures mentioned above have been successful in finding and characterizing inner defects, they require mathematical and computing skills, and need to address specific issues, such as selecting the value of the regularization parameter. This is probably the reason why such general approaches have not become widespread in the literature. On the other hand, when searching for a specific type of defect, such as delaminations, despite the intrinsic academic interest of determining the particular geometry of the flaw, in practice such information is usually not relevant to evaluate the eventual impact of the defect on the mechanical properties of the structure, just an estimation of the area and depth of the delamination is required. In this regard, image processing methods such as Principal Component Analysis, (PCA) [23], Pulsed Phase Thermography (PPT) [24, 25], or Thermal Signal Reconstruction [26] have been introduced in thermographic inspection to identify delaminations. The delamination area is often evaluated using segmentation techniques such as the Otsi algorithm [27], which are purely phenomenological approaches based on thresholding the thermal images. Moreover, these approaches are not useful to estimate the delamination depth.

With the aim of proposing a simple, yet quantitative methodology to characterize buried defects, in this work we address the estimation of the area and depth of horizontal heat sources (parallel to the sample surface) using inductive thermography. Other than being parallel to the surface, we do not assume any specific geometry of the heat source. In particular, we heat metallic inclusions in a 3D printed resin sample by means of a brief Eddy current burst and we measure the evolution of the surface temperature distribution using an IR camera. In order to estimate the area and depth of the heat source, we propose to fit the surface temperature data to a model that considers a heat source of circular shape. We fit data consisting of a combination of temporal and spatial information. As temporal information, we select the temperature evolution at the central point of the heated surface region. As spatial information, we select the thermogram obtained at the end of the burst (or a later instant with good enough SNR). In order to smooth out the features of the specific (unknown) geometry of the heat source on the surface temperature distribution, this thermogram is averaged in circumferences concentric with the centre of the heated area. This results is an averaged radial temperature profile that shapes the spatial information used for the fitting to the circular heat source model. By fitting synthetic data corresponding to rectangular heat sources with added random noise, we analyse the effect of the true heat source aspect ratio on the fitted parameters and we determine the maximum aspect ratio for which the method is reliable. We also analyse the maximum depth for which the method provides accurate enough results and we establish the range of optimum excitation durations as a function of the depth. Finally, in order to test the method experimentally, we present fittings of experimental data obtained with inductive thermography by exciting thin Cu films embedded in 3D printed resin samples.

2 Theoretical Approach

As mentioned in the introduction, the approach to estimate the area and depth of buried heat sources from temperature data measured at the surface involves the fitting of the data to a circular heat source model.

Let us consider a sample of thermal conductivity K and diffusivity D, that is infinite in the x and y directions. The material surface is located at z = 0 and the sample is thick enough to neglect the effect of the back surface. Upon excitation with a burst of duration τ, a heat source of area A parallel to the surface and located at a depth d is activated. We will consider two different geometries of the heat source: a circle of radius R and a rectangle with dimensions a (along the x axis) and b (along the y axis). The geometry of the problem is shown in Fig. 1.

Fig. 1
figure 1

a Diagram of a thick sample, infinite in x and y directions, containing a heat source of area A, parallel to the sample surface (z = 0), and buried at a depth d. b Circular heat source of radius R. c Rectangular heat source of base a and height b

Full size image

In order to calculate the evolution of the temperature distribution at the sample surface, we start considering a point-like heat source in an infinite medium. The heat source is located at position \(\vec {r}^{\prime}\) and emits with constant power P in a time interval [0,τ] [12]:

$$T(\vec {r},t)=\frac{P}{{4\pi K\left| {\vec {r} - \vec {r}^{\prime}} \right|}}Erfc\left[ {\frac{{\left| {\vec {r} - \vec {r}^{\prime}} \right|}}{{\sqrt {4Dt} }}} \right]\quad 0 \leqslant t \leqslant \tau$$
(1a)
$$T(\vec{r},\,t) = \frac{P}{{4\pi K\left| {\vec{r} - \vec{r}^{\prime}} \right|}}\left\{ {Erfc\left[ {\frac{{\left| {\vec{r} - \vec{r}^{\prime}} \right|}}{{\sqrt {4Dt} }}} \right] - Erfc\left[ {\frac{{\left| {\vec{r} - \vec{r}^{\prime}} \right|}}{{\sqrt {4D(t - \tau )} }}} \right]} \right\}\quad \tau < t$$
(1b)

Next, we take into account that the sample is semi-infinite (thick and infinite in both x and y directions), with an adiabatic surface located at z = 0. The presence of the surface can be accounted for by considering the effect of a reflected image of heat source at z = 0. Given the symmetry of the problem, the resulting surface temperature is just twice the values in Eqs. (1a) and (1b).

Finally, the evolution of the surface temperature distribution corresponding to an area A, emitting a heat flux \(\Phi \,(\vec {r}^{\prime})\) can be calculated by integrating the contribution of point-like heat sources of infinitesimal area ds’, over the emitting surface A.

$$T(\vec{r}_{{z = 0}} {\text{,}}\,t) = \iint\limits_{A} {\frac{{\Phi \,(\vec{r}^{\prime})}}{{2\pi K\left| {\vec{r}_{{z = 0}} - \vec{r}^{\prime}} \right|}}}Erfc\left[ {\frac{{\left| {\vec{r}_{{z = 0}} - \vec{r}^{\prime}} \right|}}{{\sqrt {4Dt} }}} \right]ds^{\prime}\quad 0 \le t \le \tau$$
(2a)
$$T(\vec{r}_{{z = 0}} ,\,t) = \iint\limits_{A} {\frac{{\Phi \,(\vec{r}^{\prime})}}{{2\pi K\left| {\vec{r}_{{z = 0}} - \vec{r}^{\prime}} \right|}}}\times\left\{ {Erfc\left[ {\frac{{\left| {\vec{r}_{{z = 0}} - \vec{r}^{\prime}} \right|}}{{\sqrt {4Dt} }}} \right] - Erfc\left[ {\frac{{\left| {\vec{r}_{{z = 0}} - \vec{r}^{\prime}} \right|}}{{\sqrt {4D(t - \tau )} }}} \right]} \right\}ds^{\prime} \tau < t$$
(2b)

In the particular case of a horizontal circular heat source of radius R buried at a depth d and emitting a homogeneous flux Φ (Fig. 1b), the temperature can be expressed as:

$$ T{\mkern 1mu} (x,{\mkern 1mu} y,{\mkern 1mu} 0,{\mkern 1mu} t) = \frac{\Phi }{{2\pi K}}\int\limits_{0}^{{2\pi }} {} \int\limits_{0}^{R} {\frac{{Erfc\left[ {\frac{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }}{{\sqrt {4Dt} }}} \right]}}{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }}r^{\prime}dr^{\prime}d\varphi ^{\prime}} \quad 0 \le t \le \tau $$
(3a)
$$ \begin{aligned} & T(x,\,y,\,0,\,t) \\ & \quad = \frac{\Phi }{{2\pi K}}\int\limits_{0}^{{2\pi }} {} \int\limits_{0}^{R} {\left[ \begin{gathered} \frac{{Erfc\left[ {\frac{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }}{{\sqrt {4Dt} }}} \right]}}{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }} - \hfill \\ - \frac{{Erfc\left[ {\frac{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }}{{\sqrt {4D(t - \tau )} }}} \right]}}{{\sqrt {(x - r^{\prime}\cos \varphi ^{\prime})^{2} + (y - r^{\prime}\sin \varphi ^{\prime})^{2} + d^{2} } }} \hfill \\ \end{gathered} \right]r^{\prime}dr^{\prime}d\varphi ^{\prime}} \\ & \quad \tau < t\end{aligned} $$
(3b)

For a homogeneous rectangular heat source of sides a and b in the x and y directions respectively (Fig. 1c),

$$\begin{aligned} & T(x,y,0,t) = \frac{\Phi }{{2\pi K}}\\ & \quad \times \int\limits_{{ - b/2}}^{{b/2}} {} \int\limits_{{ - a/2}}^{{a/2}} {} \frac{{Erfc\left[ {\frac{{\sqrt {(x - x^{\prime})^{2} + (y - y^{\prime})^{2} + d^{2} } }}{{\sqrt {4Dt} }}} \right]}}{{\sqrt {(x - x^{\prime})^{2} + (y - y^{\prime})^{2} + d^{2} } }}dx^{\prime}dy^{\prime}\\ & \quad 0 \le t \le \tau\end{aligned}$$
(4a)
$$\begin{aligned} & T(x,y,0,t) = \frac{\Phi }{{2\pi K}}\\ & \quad\times \int\limits_{{ - b/2}}^{{b/2}} {} \int\limits_{{ - a/2}}^{{a/2}} {\frac{{Erfc\left[ {\frac{{\sqrt {(x - x^{\prime})^{2} + (y - y^{\prime})^{2} + d^{2} } }}{{\sqrt {4Dt} }}} \right] \!-\! Erfc\left[ {\frac{{\sqrt {(x \!-\! x^{\prime})^{2} \!+\! (y \!-\! y^{\prime})^{2} + d^{2} } }}{{\sqrt {4D(t - \tau )} }}} \right]}}{{\sqrt {(x - x^{\prime})^{2} + (y - y^{\prime})^{2} + d^{2} } }}} dx^{\prime}dy^{\prime}\\ & \quad \tau < t\end{aligned}$$
(4b)

In a previous work, we addressed the characterization of vertical heat sources from time domain experiments and we concluded that the optimum information to characterize the heat source was a combination of spatial and temporal information: the thermogram obtained at the end of the excitation and the evolution of the temperature at the center of the heated region [16, 20]. We will follow this general idea for the characterization of horizontal heat sources. As an illustration, in Fig. 2 we show 3D plots of the surface temperature distribution calculated at the end of a τ = 1 s excitation, corresponding to horizontal heat sources of area A = 4 mm2, buried at a shallow depth of d = 0.1 mm and emitting a flux of Φ = 104 W/m2 in a thermal insulator (thermal diffusivity D = 0.1 mm2/s, and conductivity K = 0.5 W/m2). Three geometries of the heat source are represented: a square (a = b = 2 mm, aspect ratio AR = 1/1), a rectangle (a = 1.4142 mm, b = 2.8284 mm, aspect ratio AR = 1/2), both calculated using Eq. 4 and a circle (R = 1.1283 mm), calculated using Eq. 3. Figure 2d represents the temporal evolution of the temperature at the center of the heated region (x = y = z = 0) for the three cases.

Fig. 2
figure 2

Surface temperature calculated for horizontal heat sources of the same area A = 4 mm2, buried a depth d = 0.1 mm and emitting the same homogeneous flux Φ = 104 W/m2 during a time interval τ = 1 s in a material of thermal diffusivity D = 0.1 mm2/s and conductivity K = 0.5 W/mK. Thermograms calculated at t = τ = 1 s for: a a square heat source, a = b = 2 mm. b a rectangular heat source a = 1.4142 mm, and b = 2.8284 mm. c a circular heat source R = 1.1283 mm. d Temporal evolution of the temperature at (0,0,0) for the same heat sources

Full size image

As can be observed, for the selected parameters (area, depth, τ, and material properties), the surface temperature distribution brings to light the disparity between the three geometries. However, the temperature evolution at (0,0,0) is quite similar for the three cases, the rectangular heat source, with AR = 1/2, featuring a slightly larger difference.

Of course, the geometry of the heat source impacts more clearly on the surface temperature distribution for shallow heat sources and short excitations. In Fig. 3a, b we show surface temperature data calculated the same square heat source as in Fig. 2a (a = b = 2 mm, Φ = 104 W/m2), excited with a τ = 1 s burst but buried at depths d = 0.7 mm and d = 0.1 mm. Figure 3c, corresponds to the same depth d = 0.1 mm but has been calculated after a τ = 0.1 s excitation.

Fig. 3
figure 3

Surface temperature distributions calculated for horizontal square heat sources (a = b = 2 mm), emitting the same homogeneous flux Φ = 104 W/m2 in the same material as in Fig. 2. a Thermogram calculated at t = τ = 1 s for d = 0.7 mm. b Thermogram calculated at t = τ = 1 s for d = 0.1 mm. c Thermogram calculated at t = τ = 0.1 s for d = 0.1 mm

Full size image

Figure 3a, b show that for the same duration of the excitation (τ = 1 s) the geometry of the heat source is washed out by diffusion for the deepest heat sources and the maximum surface temperature is strongly reduced with the depth. The same occurs with the duration of the burst (Fig. 3b, c): a heat source excited with a shorter burst results in a better defined thermogram at the end of the excitation. However, the price to be paid is a reduction of the temperature elevation. This fact limits the possibility of identifying the geometry of deep heat sources. In Fig. 4a we show the temperature evolution at the center of the heated region for the three heat sources depicted in Fig. 2a–c (square a = b = 2 mm, rectangle a = 1.4142 mm, and b = 2.8284 mm, and circle R = 1.1283 mm, respectively) but now buried at a depth of d = 0.7 mm. The duration of the excitation is τ = 1 s. There are several conclusions that we can draw from the graph. First, from Figs. 2d and 4a we see that, up to AR = 1/2, the time evolution of the temperature at (0,0,0) is not very sensitive to the particular geometry of the heat source and seems to be basically dependent on the depth. We have checked that this is the case for depths ranging from d = 0.1 mm up to d = 8 mm and any (sensible) τ, i.e. from \(d<<\sqrt A\) down to \(d=4\sqrt A\). Second, the maximum temperature elevation (about 1.1 K) occurs after the end of the excitation (shortly after t = 2 s, in this case). Actually, at the end of the excitation (t = τ = 1 s) the temperature elevation is only 0.4 K (see also Fig. 3a). In a real experiment with a temperature noise of 0.1 K, this temperature elevation would be too low to provide a good enough signal to noise ratio. The temperature elevation can be increased by: (a) increasing the emitted flux, (b) taking the thermogram not at the end of the burst but at the time when the maximum elevation is reached, or (c) increasing the duration of the excitation. The first solution results in a thermogram scalable to the one depicted in Fig. 3a with a higher temperature elevation. It can be applied whenever more excitation power is available without damaging the material. Otherwise, the remaining solutions need to be applied. In Fig. 4b and c we show surface temperature thermograms corresponding to the same heat source as in Fig. 3a (a = b = 2 mm, d = 0.7 mm, Φ = 104 W/m2), excited with τ = 1 and 2 s, respectively. In Fig. 4b, we depict the thermogram calculated at t = 2 s (close to the maximum temperature elevation for τ = 1 s, see Fig. 4a), and in Fig. 4c we show the thermogram calculated at t = τ = 2 s.

Fig. 4
figure 4

a Temporal evolution of the temperature at (0,0,0) for an excitation of τ = 1 s and of flux Φ = 104 W/m2, corresponding to the three geometries depicted in Fig. 2, but buried d = 0.7 mm. Thermograms corresponding to a square heat source (a = b = 2 mm), buried d = 0.7 mm and emitting the same flux calculated at t = 2 s with excitations of: b τ = 1 s and c τ = 2 s

Full size image

As can be seen, the temperature elevation in the thermograms is higher than in Fig. 3a at the expense of more diffusion. Moreover, for the same observation time, the maximum temperature elevation is higher in the case of the longer burst.

The previous analysis indicates that, in order to detect deep defects, long excitation periods are needed, which results into blurred surface temperature images due to diffusion, i.e., in general, it is not possible to identify the geometry of the heat source from surface temperature data (and fit the data to the actual geometry). Moreover, in experiments with real delaminations or inclusions, the geometry if the heat source is unlike to be regular. The difficulty in identifying the geometry of the heat source from the surface temperature distribution and the fact that the evolution of the temperature at (0,0,0) for a given area Α depends basically on the depth and not significantly on the aspect ratio, encourages considering the possibility of fitting the surface temperature data to a circular heat source model. In order to facilitate this fitting and reduce the effect of the particular heat source geometry, we propose to perform an averaging of the values of pixels in circumferences concentric with the center of the heated region. The selected thermogram to do the circular averaging should feature a good enough signal to noise ratio: we propose to work with the thermogram obtained at the end of the excitation (t = τ) or with a later thermogram (t > τ) in case the temperature elevation at t = τ is week (poor SNR). This could be the case when the depth of the heat source is larger than the thermal diffusion length (\({\mu _\tau }=\sqrt {4D\tau }\)) associated to the longest available excitation τ.

The proposed procedure consists in fitting the resulting averaged radial profile (in the following, \(T_{r}\)) together with the temperature evolution at (0,0,0) (in the following Tt) to a circular heat source model (Eq. 3a and 3b), with three fitting parameters: the intensity of the heat flux Φ, the depth d, and the radius R, from which the area A (quantity of interest) can be calculated. The methodology is addressed at evaluating deep heat sources, featuring diffuse thermal signatures.

3 Analysis of the Method: Synthetic data

Following the previous ideas, in this section we analyze the accuracy of the methodology in the estimation of the area and depth of horizontal heat sources depending on the AR, depth, and excitation duration. We generate surface temperature data corresponding to rectangular heat sources of different AR using Eq. 4a and 4b, and we apply the procedure presented at the end of Sect. 2.

First of all, in order to illustrate the effect of the circular averaging, in Fig. 5 we consider two heat sources of area A = 4 mm2 and different aspect ratios, AR = 1/1 (a = b = 2 mm) and AR = 1/2 (2a = b = 2.8284 mm), emitting a homogeneous and constant flux of Φ = 104 W/m2 during a time interval τ = 1 s. We plot three noise free profiles: the profile along the x direction (angle with the x axis ϕ = 0°, red curves), the diagonal profile passing through the rectangle corners (angles ϕ = 45° for AR = 1/1 and ϕ = 63.4° for AR = 1/2, blue curves) and Tr, the profile obtained by averaging the calculated temperature in circles concentric with position (0,0,0) (black curves). Figure 5a, b correspond to AR = 1/1 and 1/2, respectively, calculated for t = τ = 1 s, and the heat source depth is d = 0.1 mm in both cases. As can be seen, for these shallow heat sources, the averaged profile is rather smooth and runs between the profiles corresponding to the x axis and the diagonal. The faint features that appear for the heat source with AR = 1/2 at d = 0.1 mm are washed out by diffusion when the depth increases (Fig. 5c).

Fig. 5
figure 5

Temperature profiles along the x axis (red), diagonal (blue) and radial profile resulting from the circular averaging of the surface temperature (black) calculated at t = τ = 1 s for heat sources of area A = 4 mm2 emitting a flux of Φ = 104 W/m2. a AR = 1/1, d = 0.1 mm, b AR = 1/2, d = 0.1 mm, c AR = 1/2, d = 0.7 mm (Color figure online)

Full size image

Although the main purpose of the circular averaging is to generate radial profiles that can be fitted to a circular heat source model, the procedure has an additional beneficial by-product. The circular averaging provides an efficient way to reduce the noise in the radial profiles: at short distances to the center of the heated region [position (0,0,0)], the signal is the highest and is averaged in a small number of pixels corresponding to circumferences of small radii. On the contrary, the week and noisy signal at long distances is averaged in larger radii circumferences, i.e., more pixels are used to average noisy signals, resulting in an efficient and simple noise reduction procedure. As an example, in Fig. 6 we show Tr and Tt data corresponding to a square heat source, AR = 1/1, a = b = 2 mm), buried d = 1 mm, and emitting a flux of Φ = 104 W/m2 during a time interval τ = 1 s, with added noise of 0.1 K. In Fig. 6a we have the evolution of the temperature at (0,0,0), Tt, and Fig. 6b, c display in symbols a single radial profile (along the x axis) and in continuous line the circularly averaged radial profiles, Tr, for t = τ = 1 s, and for t = 3 s (time for maximum temperature elevation).

Fig. 6
figure 6

Calculated Tr and Tt with 0.1 K added random noise for a square heat source of area A = 4 mm2 emitting a flux of Φ = 104 W/m2 during τ = 1s, and buried d = 1 mm. a Evolution of the temperature at (0,0,0). b Radial profile along the x axis (symbols) and circularly averaged radial profile for t = τ = 1 s. c Radial profile along the x axis (symbols) and circularly averaged radial profile for t = 3s

Full size image

The data show that for such a depth, not only the maximum temperature elevation is small, but also individual radial profiles obtained at the end of the excitation (symbols in Fig. 6b) are useless due to the poor signal to noise ratio. Even in such unfavorable situation, the noise reduction in the averaged profile (continuous line) makes it suitable for the fitting. The averaging also improves significantly the quality of the profiles obtained at t = 3 s.

In order to analyze the accuracy of the estimated heat source area and depth with the proposed procedure, we have generated synthetic surface temperature data for rectangular heat sources of area A = 4 mm2 and different AR, located at different depths d and excited with different durations τ. In order to work in rather conservative (not too optimistic) conditions, we have added random noise of 0.1 K and we have averaged the noisy data in circles concentric with (0,0,0). The resulting averaged profile Tr and the temperature evolution at (0,0,0) Tt are then fitted to Eq. 3a and 3b.

As an example, in Fig. 7 we plot calculated noisy data together with the fittings for two rectangular heat sources of area A = 4 mm2 and AR 1/1 and 1/2, buried d = 0.1 mm below the surface. The heat flux is Φ = 104 W/m2 and the radial profiles correspond to t = τ = 1 s (Fig. 7a, b), and to t = τ = 5 s (Fig. 7c). The values of the fitted parameters and their uncertainties are shown in the insets.

Fig. 7
figure 7

Calculated Tr and Tt (dots) for two rectangular heat sources of area A = 4 mm2 emitting fluxes of Φ = 104 W/m2, and buried d = 0.1 mm. The continuous lines are the fits to a circular heat source model (Eq. 3a and 3b). a Square heat source (AR = 1/1), t = τ = 1 s. ,b Rectangular heat source (AR = 1/2), t = τ = 1 s. c Rectangular heat source (AR = 1/2), t = τ = 5 s

Full size image

As can be seen, for the heat source of AR = 1/2, d = 0.1 mm and t = τ = 1 s the circular averaging results in a radial profile that can hardly be fitted by a circular heat source model, but the fitting of the temperature evolution is much more accurate. On the contrary, the quality of the fitting for the square heat source (AR = 1/1) for the same depth and time is very good, indicating that the circular model can be adequate to describe the averaged radial profiles. If, instead of having a τ = 1 s excitation we take τ = 5 s, the fitting of Tr for the AR = 1/2 rectangle looks better due to diffusion. Regarding the values of the fitted parameters, the accuracy for AR = 1/1 is excellent and, despite the poor appearance of the fitted Tr curve for AR = 1/2, the fitted area features an accuracy of 6.25% and uncertainty of 5%. The estimation of the area is even better (accuracy better than 1%) for t = τ = 5 s. The accuracy of the estimated depth is better than 5% in all cases. It should be noted that, being the procedure especially addressed at characterizing deep heat sources, these results indicate that the estimated area and depth feature good accuracy and precision, even for a heat source as shallow as d = 0.1 mm.

In Fig. 8 we summarize the values of the fitted area A and depth d, as a function of the actual depth, for three durations of the excitation (τ = 0.1 s, τ = 1 s, and τ = 5 s, corresponding to thermal diffusion lengths (for D = 0.1 mm2/s) \({\mu _\tau }=\sqrt {4D\,\tau }\) of 0.2, 0.6, and 1.4 mm, respectively) and three AR, namely, 1/1, 1/2, and 1/3. The black symbols correspond to fittings taking Tr at t = τ and symbols in color to t > τ (t, specified in the inset), when the signal is higher. The hollow symbols correspond to a flux of Φ = 104 W/m2 and the solid symbols to Φ = 5.104 W/m2. The results show that, for AR = 1/1 and \(d\, \leqslant \,1.5\,{\mu _\tau }\), the area of the heat source is retrieved with high accuracy (better than 5%) and uncertainties below 5%, regardless of the duration of the excitation. The estimation of the area when \(d>1.5\,{\mu _\tau }\) becomes less accurate with an uncertainty that increases with the depth. As can be seen in all the figures, when \(d>1.5\,{\mu _\tau }\) the accuracy and precision can be improved by taking Tr at longer times, t > τ, (colored symbols) corresponding to \({\mu _t} \,\geqslant \,1.5\,d\). This improves the accuracy in the estimated area to 2.5% and the uncertainty to 10%. This improvement might be limited by a poor signal to noise ratio: we have checked that, in order to have an estimation of the area with uncertainty and accuracy better than 10%, the noise should not exceed 35% of the maximum signal.

Fig. 8
figure 8

Fitted values of the area and depth of rectangular heat sources of area A = 4 mm2 and AR: a 1/1, b 1/2 and c 1/3, as a function of the depth, obtained by fitting Tr and Tt to a circular model. Three durations of the excitation have been considered: τ = 0.1 s (top), τ = 1 s (center), τ = 5 s (bottom). The fitted Tr and Tt data correspond to a flux of Φ = 104 W/m2 (hollow symbols) and Φ = 5 × 104 W/m2, (solid symbols). The colors in the symbols correspond to different time instants for the calculated radial profiles (see legends in the insets). The continuous lines correspond to the actual area and depth of the heat sources (Color figure online)

Full size image

For AR = 1/2 at the shortest excitation, the area is slightly underestimated (5%) down to depths d = µτ. For longer excitations the estimated area tends to increase with the depth of the heat source with an accuracy that stays within 10% for \(d \,\leqslant \,{\mu _\tau }\), and an uncertainty in the fitted area similar to AR = 1/1. For \(d>{\mu _\tau }\) the accuracy and precision diminish, staying within 25%.

Finally, for AR = 1/3, the fitted areas feature deviations of more than 30% in almost all cases and cannot be trusted.

As a summary, for AR up to 1/2, the area is estimated within 25% accuracy up to d = 1.5 µτ, from data affected by random noise smaller than 35% of the maximum signal, with significantly better accuracy and precision for AR = 1/1.

Regarding the estimation of the depth, the inversions of synthetic data are remarkably robust featuring very high accuracy and precision (better than 2%) for all cases, including AR = 1/3. Only for the deepest (d = 2, 3 mm) AR = 1/3 heat sources and the longest excitation the uncertainty in the depth reaches 25% although the accuracy stays excellent (better than 3%). This is very likely due to the poor effect of the shape of the heat source on Tt, as illustrated in Figs. 2d and 4a.

The previous analysis has been conducted basically for small depths (\(d<\sqrt A\)). In order to test how the procedure performs for deeper heat sources and following the conclusions derived from the analysis of Fig. 8, we have inverted synthetic data corresponding to \(d>\sqrt A\), using for each depth a value of τ such that d < 1.5 µτ, and a value of the emitted power Φ that guarantees that the noise stays below 35% of the maximum signal. Given that the results for rectangular heat sources with AR = 1/3 at \(d<\sqrt A\) were not satisfactory, we have restricted the analysis to AR = 1/1 and 1/2. Figure 9 displays the fitted area and depth for actual depths ranging from d = 3 mm to 7 mm.

Fig. 9
figure 9

Fitted values of the area and depth of rectangular heat sources of area A = 4 mm2 and AR: a 1/1, b 1/2 and as a function of the depth, obtained by fitting Tr and Tt to a circular model. The fitted Tr and Tt data were calculated with a flux of Φ = 5 × 104 W/m2 and added noise of 0.1 K. The continuous lines correspond to the actual area and depth of the rectangular heat sources used to calculate the data

Full size image

For the most favorable case, AR = 1/1, the area is estimated with an accuracy of about 4% but the precision is reduced progressively, until it reaches 50% for \(d=3\,\sqrt A\). For AR = 1/2, the area is systematically overestimated in about 25% down to about \(d=3\,\sqrt A\), and even more for deeper heat sources. The accuracy in the estimation of the depth stays as in Fig. 8 for all the cases analyzed. The analysis above indicates that the accuracy and precision in the estimation of the area of heat sources with AR = 1/1 is reliable down to \(d=2.5\,\sqrt A\). For heat sources with AR = 1/2, the overestimation of 25% in the area starts at \(d=\,\sqrt A\), and stays in the same percentage till \(d=2.5\,\sqrt A\). The estimated depth is very accurate and precise (about 3%) for all the cases analyzed.

4 Experiments and Experimental Results

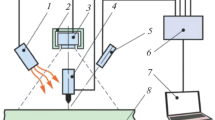
In order to check the ability of the method to estimate the area and depth of horizontal buried heat sources, we have performed induction thermography experiments on samples where we excite calibrated heat sources. We have fabricated 3D printed resin samples consisting of parallelepipeds of dimensions 3 × 3 × 1.5 cm, where we have embedded thin (25 μm thick) Cu films of known dimensions, parallel to the surface and buried at known depths. The samples are excited inductively, with a Trumpf TruHeat HF 5005 generator that feeds a water cooled TruHeat external circuit with a dedicated inductor. The excitation current is selected between 4 and 8 A, depending on the depth of the heat source and the duration of the excitation ranges between τ = 1 and 8 s. The samples are opaque in the IR range of sensitivity of the camera detector. The IR camera is a FLIR X6800sc model (In Sb detector, sensitive in 3–5 μm, 640 × 512 pixels, 25 μm pitch, NETD < 20 mK, 502 images/s at full-frame) equipped with a 50 mm focal length lens, with which we achieve a spatial resolution of 212 μm/pixel. The optical axis of the camera is perpendicular to the sample surface, so that the spatial resolution is homogeneous across the detector. The samples are oriented with the surface where data are taken and the Cu slab perpendicular to the coil axis, so that Eddy currents are generated in closed paths within the Cu film. We cover the sample surface with a thin graphite layer to improve IR emissivity. The dimensions of the Cu films and the corresponding depths are summarized in Table 1: samples 1 to 3 contain Cu slabs with AR ranging from 1/1.3 to 1/1.45 and samples 4 and 5 correspond to AR closer to 1/1. The depths rage between 0.18 and 0.7 mm.

Table 1 Lateral dimensions (a and b) and depth (d) of the Cu slabs in the samples analyzed
Full size table

A picture of one the samples and the inductor can be seen in Fig. 10.

Fig. 10
figure 10

Picture of the dedicated inductor with one of the samples in place

Full size image

After recording the evolution of the temperature distribution of the sample surface, we take the thermogram obtained t = τ, and we extract the time evolution of the temperature at the center of the heated region. As an illustration, in Fig. 11 we show experimental data corresponding to Sample 2 excited with τ = 4 s and Sample 3 excited with τ = 2 s. Figure 11a shows the thermograms obtained at the end the excitation, where we have marked with a red dot the center of the heated region. This position is chosen as the center for the circumferences of increasing radii where the temperature is averaged (symbols in Fig. 11b). Moreover, this is also the position where the temporal evolution of the temperature is extracted (symbols in Fig. 11c). The solid lines correspond to the fittings to Eq. 3a and 3b, and the values of the fitted area and depth are displayed in the inset.

Fig. 11
figure 11

a Thermograms recorded at the end of an excitation of duration τ = 4 s in Sample 2 and τ = 2 s in Sample 3. The red point indicates the center of the heated region. b Temperature averaged in circumferences concentric with the red point in Fig. 10a as a function of the radial distance (symbols), together with the fitting (solid line). c Temperature evolution at the red point in Fig. 10a (symbols), together with the fitting (solid line). Values of the fitted area and depth in the inset

Full size image

In Table 2 we summarize the results obtained in all the rectangular samples for different durations of the excitation: from τ = 0.5 s to τ = 8 s (the latter, for the deepest heat sources).

Table 2 True and fitted values of the area and depth of the Cu slabs for several excitation durations
Full size table

As can be seen, in almost all the data sets, the accuracy in the estimated area is better than 10%, with scattered cases of disagreement above 20%. The estimated depth accuracy is better than 10% in most of the cases, and the fitted depths are consistent for different values of τ, as expected from the analysis of synthetic data.

These results show that for heat sources of AR below 1/2, the methodology is able to estimate the area and depth of horizontal heat sources with accuracy of 10%. The conditions for such achievement include a noise level below 35% of the maximum signal and the use of spatial information obtained at a time t = τ, corresponding to a thermal diffusion length \({\mu _t} \,\geqslant \,d\) It is worth mentioning that the data processing and fitting is fast. The whole process is completed in less than 1 min in a tabletop PC: the circular averaging takes about 5 s and the fitting is completed in around 35 iterations, in less than 45 s.

Finally, with the idea of detecting and characterizing deep heat sources (d > 1 mm), we prepared samples with embedded circular Cu slabs of and we excited them during τ = 8 s. In Fig. 12 we show the experimental averaged radial profiles Tr and Tt together with the fittings, for d = 0.9, 1.5, and 4 mm. The thermograms to perform the radial averaging and obtain Tr were selected at t = τ = 8 s, for d = 0.9 and 1.5, and at t = 24 s for d = 4 mm. The fitted values of A and d are shown in the insets.

Fig. 12
figure 12

Experimental (symbols) Tr (top) and Tt (bottom) after a τ = 8 s excitation together with the fittings to Eq. 3a and 3b (solid lines) for circular Cu slabs of area A = 11 mm2 buried at depths: (a) d = 0.9 mm, Tr obtained at t = τ = 8 s, (b) d = 1.5 mm, Tr obtained at t = τ = 8 s, (c) d = 4 mm, Tr obtained at t = 24 s

Full size image

As can be seen, although the areas are overestimated between 10 and 20%, the heat source is clearly detected and the depths are obtained with accuracy of about 2%, which is a remarkable result for such a thermal insulator.

5 Summary and Conclusions

We have developed a simple and reliable methodology that allows estimating the area and depth of horizontal heat sources with aspect ratio below 1/2 with accuracies of 10% and 2%, respectively, without previous knowledge of the geometry of the heat source. The method involves averaging the thermogram obtained at the end of the excitation in circles concentric with the center of the heated area, to obtain a radial profile averaged in all directions of the sample surface. This radial profile, together with the temporal evolution of the temperature at the center of the heated region, is fitted to a circular heat source model. By fitting synthetic data it has been shown that, down to depths equal to twice the square root of the area, the area of rectangular heat sources of aspect ratios below 1/2 can be estimated with 2% (for AR = 1/1) and 10% for (AR = 1/2), provided that the thermal diffusion length associated to the time at which the thermogram is analyzed is at least equal to the depth of the heat source. For heat sources deeper than the area, the accuracy in the area is about 4% for AR = 1/1 and is overestimated about 25% for AR = 1/2, but the uncertainties increase up to 50% when \(d>3\sqrt A\). The estimation of the depth of the heat source is very robust with accuracy and uncertainty better than 3% when the noise is below 35% of the maximum signal.

The method has been checked with inductive thermography experiments on 3D printed resin samples containing thin Cu slabs, parallel to the sample surface, that behave as heat sources under inductive excitation. The results are consistent at different excitation durations and show that the area and depth of rectangular Cu slabs of aspect ratio below 1/1.5 can be obtained with accuracy of about 10%. Moreover, it has been shown that circular heat sources as deep as 4 mm can be characterized from experimental data in this poor conducting resin. It has to be noted that the methodology can be also applied to the characterization of delaminations in vibrothermography experiments.

The access to both the area and the depth of the heat source/defect makes the method suitable for fast, simple and quantitative estimation of deep horizontal defects that produce heat in thermographic nondestructive methods.