1 Introduction

Conventional structural material development is time consuming and very costly because of the time intensive and complex investigation chain, which includes material synthesis, specimen production, heat treatment, testing, and data analysis. As an alternative development method, the high throughput analysis ongoing at the University of Bremen, Germany in the Collaborative Research Center “CRC 1232 Farbige Zustände” can be used for material properties qualification and prediction. For its realization short time material characterisation methods are developed [1]. Eddy current testing is already a widely used method for the detection of local defects and cracks [2, 3]. On the other hand, eddy current testing methods are well suited for material characterization due to the sensitivity of these methods to the microstructure-dependent properties, such as conductivity and permeability of investigated material [4,5,6]. Due to thermal or mechanical treatment, changes in the microstructure take place at different length scales, which then have an impact on these properties [7, 8]. Consequently, the eddy current method can be used to qualify the material state. As it is shown in [9], the changes in the obtained eddy current values can correlate with material properties, such as hardness, making the eddy current analysis suitable for the prediction of mechanical properties. Other advantages of this method are non-destructivity and high measurement speed, which make eddy current analysis suitable for high throughput material screening. For this, automatized screening systems are required. The so-called Barkhausen noise and Eddy current Microscope (BEMI) developed and produced by Fraunhofer IZFP in Saarbrücken, Germany, complies with the requirements and offers the additional advantage of local investigations with high spatial resolution of up to 20 μm [10]. These features can be used to investigate small-scaled samples or analyze 2D mappings of property distributions in samples with local gradient in properties.

In the present study, investigations were performed on semi-spheres of ferromagnetic steels produced by different manufacturing chains. The semi-spheres were obtained by grinding of embedded spherical samples, which were produced by droplet generation [11] or by application of conventional steel balls production for bearings [12]. The high throughput method principles described in [13] note that there are material state qualification methods requiring specific sample geometry. Based on the sample geometry, boundary effects can occur in varying extents depending on the eddy current frequency leading to different penetration depths [14]. Eddy current signal modelling based on the theory of electromagnetic fields shows that this eddy current distribution for non-planar samples depends on the shape of the sample and the tilt angle [15]. Moreover, other factors like lift-off, surface defects, temperature fluctuations and other can have an influence on the obtained values [4].

1.1 Barkhausen Noise - Eddy Current Microscope

The employed Barkhausen-eddy current microscope (BEMI) is a special application of 3MA (Micromagnetic Multiparameter Microstructure and Stress Analysis) measurement technique [16], developed by Fraunhofer IZFP, Saarbrücken, Germany. Its measurement principles are described in [17, 18]. The multichannel signal processing allows the parallel use of up to four different measurement techniques: Barkhausen noise analysis, multi-frequency eddy current analysis, incremental permeability analysis and harmonic analysis. The analysis of the obtained signal in 3MA-technique is performed by low-noise pre-amplification of 60 dB, followed by band-pass filtering (cut-off frequencies to be adjusted), rectifying, low-pass-filtering in order to receive the envelope of the high-frequency content of the noise, and final amplification [19].

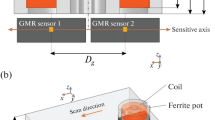
The (multi-frequency) eddy current analysis is a widely used method based on electromagnetic induction. The eddy current testing device uses a current-carrying coil, i.e. a primary coil, placed in proximity to the test sample, which is electrically conductive. By alternating the current in the coil at high frequency, a changing magnetic field is created. This changing magnetic field interacts with the sample and generates eddy currents, which can be measured by using a secondary sensing coil or by detecting the impedance changes in the primary coil [20]. BEMI makes it possible to perform simultaneous analysis with four different frequencies in the range of 10 kHz − 10 MHz in one measurement cycle. The BEMI-setup is shown in Fig. 1.

Fig. 1
figure 1

BEMI – Setup: (A) BEMI with control system, (B) sensor holder placed on the sample carrier, (C) sensor and its iron core and (D) close-up view of the sensor head [10]

Full size image

Miniaturized sensors for BEMI-setup (Fig. 1 C and 1D) were developed by Fraunhofer IZFP with an industrial partner, the EXABYTE Magnetics GmbH. The sensors or probes are inductive ferrite heads similar to the heads that are used in magnetic data storage [21]. The XYZ-manipulator allows the positioning of the sensor with high precision of up to 10 μm. The manipulator allows performing automated investigations of different samples ordered on a sample holder (Fig. 1B) or in high spatially resolved 2D-scan mode over the surface of one sample. In this case, the distribution of several micromagnetic parameters can be obtained over an area. The movement of the manipulator also makes it possible to realize high-throughput screening of a large number of the samples positioned in sample patches with defined arrangement. The sensor height position is not fixed in the Z-Plane but is held by a lever arm attached to a cushioning system for a slight Z-movement up and down. This ensures that, the samples with slight height variation or changing topography can be investigated without the risk of sensor damaging. For the present paper, the sample geometry was not suitable for the harmonic analysis as well as for Barkhausen noise and incremental permeability analysis, since external magnetization of the micro-samples embedded in isolating polymer had not been possible. Therefore, only eddy current analysis was employed.

1.2 Eddy Current Analysis

The measured eddy current signal depends on the total opposition to the current flow of a pick-up coil. This is a complex number that can be decomposed into two parts: the real part (resistance) and the imaginary part (reactance). The full resistance is called impedance [22] and is given by Eq. 1.

$$Z=Re+jIm$$
(1)

where Re is the real part of the eddy current signal, Im is the imaginary part and j is a factor equal to \(\sqrt{-1}\). This point in the complex plane can also be described by the magnitude of a vector from zero to the given impedance value and the phase angle (Ph). The relation between the magnitude of this vector (Mag) and its real and imaginary components is given by Eq. 2

$$Mag=\sqrt{{Re}^{2}+{Im}^{2}}$$
(2)

The data output of BEMI eddy current analysis includes the calculated imaginary part, the real part, magnitude and phase angle for each of the four possible exciting frequencies. Each of these values can be considered as a separate material-state-sensitive descriptor in the context of high-throughput material screening. Direct correlation of these parameters was already investigated and demonstrated, for example, in [23] where the martensite content correlated to normalized impedance, or in [24], where the normalized impedance decrease was in good correlation with the Vickers hardness increase for Fe-based dual-phase steel of different heat-treated conditions. In [25] it was demonstrated that the phase angle decrease of the eddy current signal depends on the increase in martensite caused by cold forming of these steels, and that this value was practically not affected by other microstructural changes occurring during the deformation. In these studies the single signal parameters, such as magnitude or phase, are generally considered as representable parameters and are investigated separately. This consideration can also be applied for high-throughput material screening by BEMI due to the non-linear and frequency-dependent correlation of real and imaginary parts.

The aim of the present study is to analyze the data obtained by multifrequency eddy current testing with high spatial resolution performed by BEMI to optimize measurement conditions and data analysis. The second aim is to analyze the correlations of the obtained data and microstructural features of the samples to evaluate the suitability of BEMI for material characterization for high throughput material screening. For this the data was collected using microscaled steel samples heat treated to different material conditions.

2 Samples and Measurement Parameters

The samples investigated in this study are microscaled spherical steel samples from 100Cr6 steel (material number 1.3505, EN 100027-2:1999) with a diameter of around 0.8 mm. These were obtained through a conventional process of steel balls production for small bearings using wire with a chain of mechanical treatments in ferritic-pearlitic condition. The samples were additionally heat-treated to achieve different microstructural conditions and various mechanical properties. Achieved conditions are shown in Table 1. The states demonstrate large differences in hardness, phase composition, grain size and other properties, as for example residual stress state.

Table 1 Material conditions achieved and studied
Full size table

The microscaled spheres were embedded in non-conducting polymer (Varidur 3003). Following that, they were ground up to equatorial plane with the final polishing using diamond suspension (3 μm) at the end. The investigations were carried out directly on these prepared surfaces.

From each state around 30 samples were prepared and measured in the high-throughput screening mode with 30 measurements per sample with the sensor positioning in the center of the prepared surface. Four exciting frequencies of 10 kHz, 100 kHz, 1 MHz and 10 MHz were selected. The measurements were performed in the mid-point of the samples with manual positioning of the sensor and 30 measurements cycles per sample. The complete screening procedure of the sample career containing 30 samples took slightly less than 1 h. The measurement data extracting and analysis was easily performed using implemented software. The total time for the preparation/measurement/evaluation of one material state in the high-throughput screening mode with 30 samples was about 1.5-2 h. Additional improvement of sample career tolerances would further reduce the sample screening time due to the possibility of automatizing of sensor scanning.

Additional complementary analysis methods were used in order to achieve microstructural and mechanical characterization of different states: X-ray diffraction for phase contents and dislocation density analysis, metallographic investigations for present phases and local microstructure as well as hardness tests. It should be noted that the hardness measurements were performed using 3 to 5 points with HV0.3 method for Q850 and Q850T180 states while HV1 method was applied for S and B conditions. These complementary measurements were carried out on only one sample for S, Q850 and Q850T180 conditions. The dislocation density was determined based on the X-ray diffraction patterns recorded with Cr-kα radiation using Williamson-Smallman Eq. (3), where ε is the microstrains value, D0 is domain size, K = 14.4 is a material based constant parameter, n = 1 is the interaction factor and b = 2.458·10-8 cm is Burgers vector [26]. The correction of the instrumental broadening contribution was performed by measurement of LaB6 standard powder.

$$\rho =\sqrt{3nK}\left(\frac{?{\epsilon }^{2}?}{b{D}_{0}}\right)$$
(3)

The magnetic permeability of the investigated samples has not been measured experimentally. There are however few sources available, providing data for comparable conditions. According to [27] the hardened 100Cr6 has a relative permeability of 700 and the soft states 200. In [28] a value of 300 is provided for the relative permeability without giving the detailed condition of the “as received” material, which is normally an annealed state.

3 Results and Discussion

3.1 Material Conditions and Properties

The microstructure of the investigated material conditions performed by the metallographic investigations are shown in the Fig. 2.

Fig. 2
figure 2

Microstructure of (a) speroidized carbides, (b) quenched, (c) quenched and subsequently tempered, d)  bainitic material conditions performed by optical microscope investigations

Full size image

As Fig. 2 shows, the microstructure of the samples is varying significantly. For example, the carbides of the spheroidized states are larger as for the tempered state as well as for quenched state. The quenching and as well as subsequently tempering produce martensitic microstructure with very finely dispersed retained austenite (Fig. 2b and c). As expected the bainitic state is consisting of fine non-lamellar structure of cementite and ferrite. Vickers hardness, retained austenite content and determined dislocation density for the given material conditions are shown in Fig. 3. Because of the different heat treatments, the microstructure varies, and, therefore, the hardness. The bainitic (B) sample contains bainitic ferrite and carbides (undissolved secondary Fe3C + finely dispersed Fe3C forming during the bainitic treatment), while the spheroidized carbides (S) material condition has a ferritic matrix with about 16 wt.-% of spheroidizied cementite. Both conditions are softer than the quenched Q850 and quenched and tempered Q850T180 conditions with their microstructure consisting in (as quenched or tempered) martensite with retained austenite and few percent of undissolved secondary Fe3C. As expected, the retained austenite content for the S condition is 0, while the quenched samples exhibit about 10 to 12 Mass-% of retained austenite, undependently of the subsequent tempering treatment. The bainitic state shows an almost negligible low amount of retained austenite of around 2 Mass-%. The hardness of the presented material conditions is increasing in the following order: S, B, Q850T180 and Q850 and in the same order for the dislocation density (Fig. 3b), which is ranging over almost two order of magnitude between the different conditions. It should be noted that the evaluation of the dislocation density could not be performed reliably at the spheroidized condition due to large crystallites and, hence, low effects on broadening. However, based on the literature on comparable states, it should have the lowest dislocation density of about 108 cm-2 [29].

Fig. 3
figure 3

Experimentally determined average values of (a) Vickers hardness (black circles) and retained austenite content (red squares) and (b) dislocation density for the investigated material conditions: S - spheroidized carbides condition, Q850 – quenched material condition, Q850T180 – quenched and subsequently tempered material condition, B – bainitic condition

Full size image

3.2 Eddy Current Analysis

The experimental results obtained for patches of four different material states are presented in Fig. 4. The results are plotted in the complex impedance plane, where the determined real part values are plotted versus the imaginary part. Each data point represents one of the investigated samples and its value is averaged from 30 measurements performed on each sample. The measurements were performed by manual positioning of the sensor at the center of the prepared sample surface, without moving the sensor during the measurement sequence.

Fig. 4
figure 4

Average impedances for four different heat treatment states of steel 100Cr6, measured at: (a) 10 kHz, (b) 100 kHz, (c) 1 MHz and (d) 10 MHz. Red ovals are representing outliers of the corresponding data point groups

Full size image

A group of points of the same material condition builds a pile-up of points in the complex plane. The position of these point pile-ups or their superposition can be used to differentiate the states from each other, in particular for the high eddy current frequencies. With decrease of exciting frequency, an overlapping of these pile-ups for the given material conditions can be observed. For the lowest frequency of 10 kHz the data points build a line, without clear separation of the values belonging to different material states. On the other hand, the data points obtained at 10 MHz frequency are separated in four regions without strong overlapping. However, at 10 MHz the pile-ups of conditions S and B show larger scattering of the single samples within the groups, compared to Q850 and Q850T180 states. The higher dispersion of these conditions could be explained by their higher sensitivity to sample orientation and segregations present in the material as well as increased impact of the sample preparation (polishing). Indeed, softer material states could be more affected due to local plastification by grinding and final polishing. On the other hand, this effect was not studied in detail and requires additional experiments to confirm this hypothesis. As a consequence, the average values obtained for the different conditions have varying dispersion and confidence intervals. For the frequencies of 100 kHz and 1 MHz the point clouds can be separated with small overlapping. It should be mentioned that the position of the outlier data points seemingly tends to the same regions in the complex plane.

The average results calculated from the 30 investigated samples for each condition are represented in the Fig. 5 in order to evaluate their potential for a robust assessment and differentiation of the various states.

Fig. 5
figure 5

Average values of the analysed signal for the different heat treatment conditions of steel 100Cr6: (a) real and imaginary part at 10 kHz, (b) magnitude and phase at 10 kHz, (c) real and imaginary part at 100 kHz, (d) magnitude and phase at 100 kHz, (e) real and imaginary part at 1 MHz, (f) magnitude and phase at 1 MHz, (g) real and imaginary part at 10 MHz, (h) magnitude and phase at 10 MHz

Full size image

The mean value calculation results (Fig. 5) show that not all of the parameters have significant differences between the different states. For several measurement conditions, the difference of the mean values is observed to be smaller than the standard deviation resulting from the analysis of several samples for lower frequencies. Due to the small size of the investigated samples and of the probed volume, variations of the material state or of the measured signal could lead to scattering of the measured signal. Through analysis of a high number of samples, statistical deviations can be considered. With the frequency increase, the differences between the average values increase and become larger than the deviations. This would enable assessing one material state and comparing it with other material states in order to determine relevant correlations to conventional material properties. The largest differences between the four material conditions can be observed at the highest frequency of 10 MHz. In particular, the imaginary part and the magnitude allow a robust differentiation of the heat treatment conditions. The plot of the mentioned parameters and Vickers hardness is shown in Fig. 6. As expected, the decrease of both descriptor values is related to the increase of the hardness, but it should be noted that the Q850 and Q850T180 cannot be directly correlated to hardness. Other microstructural features mentioned above, such as retained austenite content or dislocation density, can cause this deviation from the linear trend, because as it is known from the literature, these microstructural features cause opposite changes of the measured values. However, further detailed investigation should be carried out to analyze this hypothesis.

Fig. 6
figure 6

Magnitude and imaginary part values plotted versus hardness for the four material conditions

Full size image

3.3 Impact of Sample Positioning on Measured Signal

In order to evaluate the robustness of the method, possible sources of signal variations, which are not induced by the material state, but by the disturbing effects, should be addressed. The sample positioning has been determined to be one of major aspects for reproducible and reliable high-throughput investigations of micro-samples. Indeed, the local signal variations could be observed over the surface of small micro-samples, which have been determined to be depending on the geometry (size) of the samples. In order to evaluate the impact of the sensor location on the resulting signal, samples were investigated in 2D-scan mode over the entire surface of a sample in Q850 state. This scan was obtained by the sensor scanning over a region of 1.5 × 1.5 mm² with 0.02 mm step in x- and y-directions. Each pixel represents an average value from 10 measurement cycles in one position. The results are presented in Fig. 7 for two frequencies: 10 kHz and 10 MHz.

Fig. 7
figure 7

Distribution of real part value of eddy current measured for (a) 10 kHz and (b) 10 MHz. Obtained in 2D-scan mode (step size 20 μm) over a sample in Q850-condition (quenched). The top and left distributions are determined along the drawn red dot lines along X and Y axes from the 2D-distribution

Full size image

As shown, the distribution is symmetrical and is in accordance with semi-spherical sample shape. The visible diameter of the equatorial plane is measured from 36 (x-direction) to 38 (y-direction) pixels. This corresponds to a diameter of 720–760 μm. The averaged diameter of the spherical samples after heat treatment is 794 μm. The maximum value for the real part of the eddy current signal (10 kHz) is obtained in the center of the sample, while the values decrease towards the outer diameter. In this position, there is a pole of the semi-sphere below the surface. The decrease depends on the exciting frequency. For example, real part values at 10 kHz change by up to 72%, at 100 kHz the value change is up to 68%, at 1 MHz – up to 15%, and it is only 6% at 10 MHz. The sample microstructure is considered homogeneous and without pronounced microstructural gradients, which is supported by metallographic investigations of several samples. The values close to the boundary of the sample are changing more rapidly than in the center of the sample. At the boundary, the volume of the investigated material decreases, and it affects strongly the measured signal. This effect depends on the exciting frequency due to the variation of the penetration depth and apparent current density effect produced by its variation. Due to this, there is no jump in the values, but a continuous change resulting in a transient region where obtained values are strongly affected and cannot be considered as robust and reliable. All the obtained values (real part, imaginary part, phase angle and magnitude) exhibit similar behavior for whole frequency spectrum used in this study. They reached their maximum (or minimum) stabilized value in the center region of the sample and there is a continuous change of the values from the center to the outer diameter in radial direction. It is to notice that in the X-direction the background values are different between left and right areas close to the sample surface. This occurs due to anisotropy of the signal and of the interacting sample region related to the sensor geometry (Fig. 1). This effect increases with the frequency. As shown in Fig. 7, there is a typical form built by the data points obtained over the whole measurement area (1.5 × 1.5 mm2). Similar figures were obtained for all the investigated material conditions. The most important factor for these shapes is the exciting frequency.

For a closer data analysis, the data was divided into groups. The first group contains all the values obtained in 2D-scan mode. The other group contains values obtained from the measured sample surface within concentric circles with different radii: a full sample surface radius and a sample radius divided by 2, 4 and 8. The visualization of the group definition is presented in Fig. 8 and the mean values of the values contained in respective circles are plotted and shown in Fig. 9.

Fig. 8
figure 8

The data region definition for closer data analysis shown on real part values distribution of a Q850-sample measured with a frequency of 10 MHz

Full size image
Fig. 9
figure 9

Average values obtained from respectively circles inside the sample surface for: (a) quenched sample at 100 kH, (b) quenched sample at 10 MHz, (c) spheroidized carbides sample at 100 kHz, (d) spheroidized carbides sample at 10 MHz.

Full size image

The data points in circles of different radii represent the mean values obtained from the corresponding areas (Fig. 8). It is seen that the values included in the largest circle are showing high deviations, since the outer values are strongly influenced by the sample outer boundaries, and it is difficult to identify precisely the contour of the samples. The values are already much more stable within the circle with a half radius, while a shift in the average values can be observed with a circle radius decreasing. A further slight shift and a reduction of scattering are observed for the decreasing circle radius.

If during high-throughput analyses, when only one position of the sample is measured, the positioning of the sample is not exactly in the centre of the samples, and the sensor is located in an area closer to the outer diameter, a disturbance of the signal may occur. To evaluate the impact of the position error on the signal, the deviation of the signal caused by manual sensor positioning and the mean value (MVD) obtained for the “radius/8” data region, which is seen as the real value within the samples, can be considered. For this consideration, the value can be normalized by the Eq. 4.

$$MVD\left(x, y\right)=\frac{\left(\left(SV(x, y)\right)-\left(MR8\right)\right)}{\left(MR8\right)}*100$$
(4)

where MVD(x, y) is the considered deviation for the signal obtained from the position with the coordinates (x, y), SV(x, y) is the value of the descriptor obtained for these coordinates, and MR8 is the mean value for the “radius/8” region. Figure 10 shows MVD values change from the visible centre of the obtained signal in radial direction to the boundary of the sample region.

Fig. 10
figure 10

Position dependent mean value deviations (MVD (x, y)) obtained for radius/8-region: (a) real part, (b) imaginary part, (c) magnitude and (d) phase, measured at 10 kHz and 10 MHz respectively

Full size image

As the Fig. 10 shows, the signal deviation of up to 70% can occur if the position is reaching the outer diameter. The sensitivity to the positioning error is generally higher for lower exciting frequencies, while at 10 MHz, only up to 6% of the signal variation can occur. The tendencies of the curves are similar for different material states, however, the deviations from the mean value obtained from the centre vary. It is to mention that the penetration depth cannot be evaluated with good accuracy by using the well-known formula 5 for the calculation of the skin depth due to complexity of the sensor geometry causing anisotropic signal measurement.

$$\delta =\sqrt{\frac{1}{\pi f\mu \sigma }}$$
(5)

where δ is the skin depth, µ is relative magnetic permeability, σ is electric conductivity and f is the frequency. The standard depth of penetration widely used as a guide for eddy current inspection purposes is calculated for a plane electromagnetic wave incident perpendicularly on a conducting half-space and is thus a material/test parameter rather than a true measure of penetration [30]. Due to the core geometry of the present sensor and the dimension of the sensor the true penetration depth calculations are complicated.

However, there is a proportion between the exciting frequency and the penetration depth of the excited eddy current. The penetration depth at 10 MHz should be around 30 times less than at 10 kHz for each of the material conditions.

In the present paper, the semi-spherical sample geometry was investigated. This technique can be applied for samples of other geometries, such as small wires, plates or tubes. Any effects caused by the boundary condition effects, including the apparent current density, will be investigated in the consequent research by varying the sample radii.

4 Conclusion

The BEMI is suitable for the material state qualification due to the sensitivity of micromagnetic methods to the microstructural changes, occurring from the heat treatment of ferritic steel. For the high-throughput material screening method, the multi-frequency analysis can be used to qualify material states achieved in micro-samples in short time. The qualification can be performed by analyzing single parts of the measured signal. On the other hand, the sensor positioning can influence the signal in the case of micro-samples. In order to ensure the robust analysis, the highest magnetization frequency of 10 MHz has been identified to give the best results, since it allows a clear differentiation of different material conditions while the sensitivity to the position variation is very low.