Abstract
This work investigates the influence of acceleration on the leakage signal in magnetic flux leakage type of non-destructive testing. The research is addressed through both designed experiments and simulations. The results showed that the leakage signal, represented by using peak to peak value, decreases between 15.1% and 26.6% under acceleration. The simulation results indicated that the main reason for the decrease is due to the difference in the distortion of the magnetic field for cases with and without acceleration, which is the result of the different eddy current distributions in the specimen. The findings will help to allow the optimisation of a magnetic flux leakage system to ensure that main defect features can be measured more accurately during the machine acceleration phase of scanning. It also shows the importance of conducting measurements at constant velocity, wherever possible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Non-destructive testing (NDT) covers a whole range of techniques that can help prevent disasters similar to the Buncefield incident [1]. Many NDT methods have been developed. Here, we only focus on the magnetic flux leakage (MFL) method [2], as applied to the inspection of bulk liquid storage tank floors. For such inspection, MFL systems are employed to detect and record locations of material losses normally due to corrosion. MFL systems are suitable for the detection of material losses which are as small as a few millimetres in diameter in areas which typically exceed 100 m\(^2\) [3].
MFL systems have many advantages including their speed of operation [4]. However, it is worth pointing out that sometimes the magnet and sensors are sensitive to lift off variations from the settlement and construction of the tank floor which is a consequence of the environment. The principle of the MFL method is based on the following: when a magnetic field is applied to a ferromagnetic material, the discontinuity of the geometry (ferromagnetic material) causes the leakage of the magnetic field and this leakage can be captured by magnetic sensors [5], such as Hall probe etc.. The main reason for the leakage is due to the difference of the magnetic permeability of the mediums at the interface. This leakage signal is usually used to predict the defect features: the defect characteristics, such as shapes, dimensions and locations, can be determined by the leakage signals. It should be noted that the MFL inspection process is a transient process and the leakage signal is influenced by the scanning velocity. This is due to the generated eddy currents in the conducting permeable specimens due to a moving magnet. The magnetic Reynolds number for this type of problem is of the order of hundreds (\(>>\) 1), which indicates that the effect of eddy currents cannot be neglected [6].
Snarskii et al. [7] developed an integral equation model, for a given defect, to calculate the leakage signal. Compared to the previous finite element method (FEM) model, this method is more efficient with a shorter simulation time. Altschuler E. and Pignotti A. [8] investigated the optimisation of the applied field to detect the defect and to determine the difficulty of examining an internal flaw. Huang et al. [9] discussed the relationships between the 3D defect parameters and the MFL signals: e.g. the lift-off value influence. The results also indicated that 3D simulations give more accurate geometry description of defects, compared to 2D simulations. The main research on the influence of the scanning velocity on the leakage signal is summarised in Table 1.
It shows that the different excitation sources and scanning velocity of the investigated MFL systems [10,11,12,13,14,15,16,17,18,19,20,21,22, 26, 29]. The research work also showed a trend of study methods in terms of the MFL phenomenon, through combinations of modelling and experimentation. In each publication, the results showed that the leakage signal decreases as the scanning velocity is increased. However, Wang et al. [23] determined that the magnitude of the leakage signal increases as the scanning velocity is increased for near side defects, which is contradictory to the previous results. Pullen et al. [28] further investigated the results obtained by Wang et al. and explained that the main reason for their finding was the saturation issue: if the plate is not saturated, the near side defect responses are amplified and this results in the increased leakage amplitude when the velocity is increased. Pullen et al. also found that as velocity is increased, the distribution of the induced flux becomes more focussed on the near side, which agrees with the findings of Feng et al. [30]. This result further indicates that the far-side defect is difficult to measure for a thick plate at higher scanning velocity. For a high scanning velocity, the sensor location is critical in order to measure the leakage accurately [31, 32]. The distortion of the magnetic field can cause the displacement of the maximum peak to peak location, towards the rear pole of the system, as discussed by Zhang et al. [24]. This result was also demonstrated by Antipov [27]: the sensor is better located nearer to the rear pole, especially for higher scanning velocity. To compensate for the leakage signal reduction due to the velocity effect, Park et al. [17] developed a scheme to eliminate the velocity induced signal distortion. Lei et al. [33] also investigated the compensation scheme based on the Radial Basis Function (RBF) method. The above short review shows that the scanning system’s acceleration was not considered in any of the previous research.
In practice, there are at least three stages, in terms of machine velocity, whilst the machine is measuring a specimen: the acceleration stage, the constant velocity scanning stage and the decelerating stage. Figure 1a is an exaggerated illustration of the 3 stages of a scan where region (I) illustrates the acceleration, (II) represents the region of constant velocity, (III) the deceleration phase. Each sinusoidal response at each stage comes from a defect of the same geometry.
(a) A diagram of the whole inspection (scanning) process and: (I) MFL system accelerating stage, (II) constant scanning stage and (III) decelerating stage. The blue curve represents the leakage signal. (b) Leakage signal (blue curve) responses for different depth of the defect: 80% represents the defect depth is 80% of the inspection plate thickness
From the short literature review above, all previous research has focused on the steady scanning stage (stage II in the Figure 1). This opens the important questions:
-
Does an accelerating MFL scanner influence the leakage signal?
-
If yes, does the peak to peak measurement of the corresponding MFL defect signature vary with respect to acceleration magnitudes [34]?
The main novelty of this work is to provide an answer to these two questions through both modelling and experimental methods by following the trend indicated in Table 1. This paper focuses on contrasting MFL signals from the same defects when in stages (I) and (II) in an attempt to ascertain whether the response differs with acceleration of the magnetic system. Figure 1b presents a recorded MFL signal from a set of four semi-spherical defects ranging in depths of 80%, 60%, 40% and 20% from left to right. Notice the acceleration and deceleration phases toward the end and start of the MFL signal. In this paper the deceleration stage is not considered. Answering these two questions will help to optimize the system to ensure that defect features that are scanned whilst the machine is accelerating can be measured accurately. A possible explanation as to why no previous work has been published on this subject is that the time of the acceleration and deceleration stages is short: approximately within 1 second, depending on the final velocity. In bulk storage tank inspection, many scans are conducted with many starts and stops. This is due to the relatively small plate geometries, in the region of tens of meters as compared to the kilometres of scanning in piggable pipeline applications.
The present paper is organised as follows. The experimental set-up and the procedures are introduced in Sect. 2.1. The numerical set-up is discussed in Sect. 2.2. The results are presented in Sect. 3, including the background magnetic field for different scanning speed, the overview of leakage signal for both with and without system acceleration and the acceleration effect. Finally, the discussion and the conclusions are given in Sect. 4.
2 Methodology and Experiment Set-Up
2.1 Experimental Facilities, Set-Up and Procedures
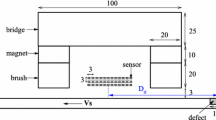
The adopted experimental facilities are identical to the work of Pullen et.al. [28], however the experimental procedures are different: the MFL scanning acceleration is considered. The facilities set-up is shown in Figure 2.
A commercial magnetic flux leakage system was adapted to conduct the experiments [35, 36]. The magnetic yoke in this design is asymmetric so that an additional set of magnetic sensors are used to measure changes in the magnetic field in the air gap between the pole and the test surface. These sensors primarily measure near-side only flaws. When combined with MFL, which detects both near and far-side defects, then the originating surface of the flaw can be determined. The machine has a scanning velocity magnitude range between 0.5 m/s and 1 m/s. A high-resolution magnetic sensor array comprising of 64 channels is placed between the poles with fixed lift-off values relative to the specimen and the signal is transferred to the data acquisition system. A 1010 grade mild steel plate (0.5 m \(\times \) 1.15 m \(\times \) 6 mm) was chosen as the specimen. The reason for this selection is that 1010 grade steel is a typical parent material for storage tank floors and this thickness ensures the plate can be saturated under the current MFL assembly [3]. Four artificial cone shape defects were manufactured with the maximum defect depths: 1.2 mm (20% of plate thickness 6 mm), 2.4 mm (40%), 3.6 mm (60%) and 4.8 mm (80%), respectively. The artificial defect shapes are in accordance with width to depth ratios described in API Standard 653 [37]. The defects are uniformly distributed at intervals of 0.1 m. The MFL system’s velocity and acceleration were determined from data captured using a position encoder.
Three sets of experimental trials (Trial A, B & C) were conducted and they are summarised as follows:
-
1.
Trial A: the machine was used to measure the magnetic flux leakage from a defect free specimen at three scanning velocities magnitudes (0.5 m/s, 0.75 m/s and 1 m/s). The aim for Trial A was to determine the background magnetic field for typical measurement velocities. The constant speed can be pre-set by MFL system.
-
2.
Trial B: the machine was used to measure the magnetic flux leakage from a specimen with defects at three scanning velocities magnitudes (0.5 m/s, 0.75 m/s and 1 m/s). The aim for Trial B was to determine the magnetic flux leakage for defects at different constant velocities.
-
3.
Trial C: the machine was used to measure a specimen with defects. The experiments were performed such that the system was accelerating when the sensor was passing over the defects. The aim for Trial C was to determine the magnetic flux leakage using an accelerating MFL system. The velocity and acceleration were calculated using the results from the position encoder. The position encoder records the position at a given frequency. This allowed the distance moved for a given time to be calculated, and the resulting velocity to be calculated. To determine the acceleration the change in velocity was calculated for a given time.
For Trials B and C, the leakage was obtained from all four defect depths (1.2 mm, 2.4 mm, 3.6 mm and 4.8 mm) located as both top (near side) and bottom (far side) surface defects.
2.2 Numerical Set-Up
Figure 3 shows the diagram of experiment.
For the eddy current problem involving a conductor, the Maxwell equations simplify to:
where E, B, t, H, \(\sigma \), V are electric field, magnetic flux density, time, magnetic field, the electric conductivity and the moving system velocity, respectively. The transmission conditions which apply at the material interfaces are:
where n is the unit vector outward normal and ‘[ ]’ denotes the jump (e.g. between the plate and free space). The decay condition, applied on the interface between conducting and non-conducting regions, is:
where x is the coordinate vector. NdFe52 is selected as the magnet material and steel 1010 is selected as the bridge, poles and the plate’s material. Figure 4 shows the B-H curve for steel 1010.
It shows the non-linear constitutive behaviour, B =B(H) in \(\varOmega _s\). In \(\varOmega _m\), we have the linear constitutive relationship B= \(\mu _r \mu _0\)H with \(\mu _r\) =1.43 and in \(\mathrm{I\!R}^3\) \(\setminus \) (\(\varOmega _s \cup \varOmega _m)\) then we have simple relationship B= \(\mu _0 \textbf{H}\) where \(\mu _0\) is the permeability of free space.
The governing equations for the modelled problem are as follows:
The transmission and decay conditions are as in Eq.4, 5 and 6. For the current case, we have \(\sigma _s\) = 2\(\times \)10\(^6\) S/m and \(|{\textbf {H}}_c|\)= 7.96\(\times \)10\(^5\) A/m.
2.2.1 Two-Dimensional Simulation
In 2D a vector potential formulation of Eq. 7, 8 and 9 are adopted such that B = \(\nabla \times \) A where A is vector potential in the form A= \(A_z\)(x,y) e\(_z\), where \({\textbf {e}}_z\) is the unit vector along z direction. Figure 5 shows the diagram of simulation.
The decay condition (Eq. 6) is approximated by the balloon boundary condition [38], applied on the region edges, in the simulation: the z component of the magnetic vector potential, \(A_z\), goes to zero at infinity. Note that in the simulations the bridge is fixed in position and the plate is moving, which is the opposite to the real situation. However, the overall effect is the same.
We employ ANSYS Maxwell finite element package for the approximate solution of the system described above. This includes a Newton-Raphson algorithm for dealing with the non-linear constitutive relationship in \(\varOmega _s\). We set the required tolerance for this iterative scheme to be such that the relative residual is smaller than 0.0001. Time integration of the transient system is achieved by Runge-Kutta scheme (third order accurate in time). In the work of Zhang etc. [24] a mesh size sensitivity for a similar problem has already been conducted. It was established that a minimum mesh (mesh type: triangle) density of 0.5 mm (element maximum length between two poles) and a time step size of 0.0005 s is sufficient to achieve reliable results for this problem and is employed also here.
2.2.2 Three-Dimensional Simulation
The simulation of the 3D problem is also performed using the ANSYS Maxwell solver using a similar setup to the 2D problems described in Sect. 2.2.1 apart from the use of physical fields rather than a vector potential formulation. Compared to the 2D balloon conditions, zero tangential H field is applied at the region surfaces and the domain is chosen to be sufficient large. Since the problem has a symmetry to \(x-y\) plane, only half the problem is modelled to reduce computational expense. Therefore, a symmetry boundary condition (magnetic flux tangential) is applied at the middle surface of the whole domain. For this 3D complicated geometry problem, it is hard to conduct the mesh sensitivity test. A minimum mesh (mesh type: tetrahedron) density of 1 mm (element maximum length between two poles). The simulation time step is 0.001 s. Newton-Raphson algorithm for dealing with the non-linear constitutive relationship in \(\varOmega _s\) and the nonlinear residual is 0.005.
3 Results
To answer the questions raised in Sec.1, the influence of the MFL system scanning acceleration on the leakage signal was studied both through experiments and numerical simulations.
3.1 Background Magnetic Field
We first conducted the experiment Trial A, as mentioned in Sec.2.1. The commercial machine Floormap 3Di was used to scan a plate without defect at different scanning velocities: 0.5 m/s, 0.75 m/s and 1 m/s, respectively. Figure 6 showed the leakage signals variations with scanning location.
Experimentally, as showed in Figure 6a, the results indicated that leakage signals (axis component: B\(_y\)), represented by the voltage, were approximately constant when the system was moving with a given velocity: e.g. the scan position (x) was after 1100 mm. Small fluctuations appeared due to the specimen surface condition. Constant signals indicated that B\(_y\) retained a constant magnitude whilst scanning the defect free plate. Further, voltage magnitude increased as the scanning velocity was increased.
Furthermore, 2D simulations were conducted with the aim to gain an understanding into the mechanisms causing the results. In order to compare with the experiment results, scanning velocity magnitudes of 0.5 m/s, 0.75 m/s and 1 m/s were simulated. Also, a static case was simulated as a baseline. Figure 6b shows simulation results of B\(_y\) at different constant scanning velocities for a defect free specimen. It depicted that B\(_y\) increased as the scanning velocity was increased, which was in an agreement with the experimental results. Figure 7 shows the magnetic flux line distributions for the static and transient (velocity magnitude is 5 m/s) cases, respectively. Figure 8 shows the \(B_y\) and eddy current distributions for the static and transient (velocity magnitude is 5 m/s) cases, respectively.
The results showed that the magnetic flux lines and B\(_y\) were distorted by the existence of a scanning velocity. Figure 8a and b shows the induced current in the plate. It showed the existence of the velocity induced current in the plate whilst the MFL system is moving.
3.2 Overview of Leakage Signals: Without and With Acceleration
Experiment Trials B & C were conducted, as mentioned in Sec.2.1. The MFL scanning system scanned the plate with artificial defects at a constant velocity (Trial B) and with an acceleration (Trial C). Each scan was repeated several times. Figure 9 showed the overview of the leakage signal for the cases both with and without scanning system accelerations.
The results showed that the scanning acceleration of the system did not change the general signatures of the leakage signal: peaks appeared when the sensor met the defect edges. There is however an influence on the amplitude of the defect signature. It is also noticed that the positions of the peaks are different between the cases with and without acceleration. The main reason for that is that we need to reach a ‘constant’ velocity to measure amplitude without acceleration. The FM3Di still requires an acceleration phase until a constant velocity is reached. This means that the position of the defect must be offset to a distance so that when the FM3Di is at a constant velocity, the defect travels under the sensor, hence the position offset with reference to the x-axis, i.e. distance in mm.
3.3 Acceleration Effect
3.3.1 Peak to Peak Value Comparison at Similar Scanning Velocity
Figure 10 showed the peak to peak (p-p) value variations of B\(_y\) for trials both without acceleration (Trial B) and with acceleration (Trial C) at similar velocities for different defect depths.
The results indicated that the leakage signal drops for the acceleration scanning trials, compared to constant velocity scanning trials. Tab.2. summarized the percentages of the signal drop for different experiment trials.
3.3.2 Acceleration Magnitude Influence
Figure 11 shows the p-p value variations with different acceleration values.
The results showed the leakage signal had a obvious drop if the MFL system passed the defect with an acceleration. For different magnitudes of acceleration, the signal drop was not so sensitive. The system currently has a small window of acceleration based on the design of the control system. To measure a range of accelerations to find this threshold would require a new test apparatus to be designed to accelerate the FM3Di beyond its current limit. It must also be noted that increasing the acceleration will reduce the area which flaws may be affected, in combination with the relatively slow speed of 100’s mm/s that the FM3Di travels, then this threshold may never be reached.
The 3D simulations were also conducted. In simulation, the scanning velocity magnitude was 0.75 m/s for the constant velocity scanning process and the acceleration magnitude was 2 m/s\(^2\), which had the same direction as the scanning velocity. Figure 12 shows the B\(_y\) distribution with scanning time (left) and the peak to peak (p-p) value for different system accelerations (right). The 3D numerical results showed that the presence of the acceleration does not change the trend of B\(_y\) signal, as shown in Figure 12 (left).
In terms of the leakage value, Figure 12 (right), a clear reduction in magnitude is seen for an accelerating system. The simulation results also show that the magnitude of leakage reduction does not change when the system acceleration is further increased. These results are in agreement with the experimental results.
Figure 13 showed B\(_y\) distribution for the case with and without acceleration at the moment when the sensor met the defect front edge, the defect middle and the defect rear edge, respectively.
Simulation results: B\(_y\) contours in the vicinity of sensor. Contours plotted when the sensor meets the front defect edge (Left), the defect middle (Middle) and the rear defect edge (Right). Different magnetic field distortions are presented for the cases with and without system scanning acceleration. The acceleration, a, is in the same direction as velocity. For the a = 0 m/s case, the magnitude of scanning velocity is 0.75 m/s. For the a = 2 m/s case, the magnitude of scanning velocity is 0.75 m/s at the moment when the sensor meets the defect
The results indicated that higher magnitude of B\(_y\) is obtained for the case without acceleration for all three positions, especially for the position when the sensor met the front edge of the defect. This is in agreement with the results shown in Figure 12 (left).
4 Discussion and Conclusions
We address the two questions raised in Sect. 1 as follows. Firstly, we have shown in that the acceleration of the MFL system does not influence the trend and features of the leakage signal and this can be observed in our experimental results shown in Fig. 9. This is due to the nature of the dynamic inspection remaining the same, irrespective of whether there is an acceleration or not. However, it does influence the magnitude of the signal and this can be seen in our experimental results in Figs. 10, 11 and simulation results in Fig. 12, respectively. Both the experimental and the numerical findings show that the leakage signal under acceleration evaluated by using peak to peak value, will reduce in a range of 15.1% to 26.6%. Preliminary simulation results showed that the largest difference is present when the sensor meets the front edge of the defect for cases with and without acceleration.
Secondly, addressing whether the peak to peak (p-p) measurement of the corresponding defect signature varies with respect to acceleration magnitudes, our experimental (Fig. 10) and simulation (Fig. 12) results show the p-p values are not sensitive to the acceleration magnitude varying. The results from all the experimental trials also show that the magnitude of the reduction of the leakage signal is not sensitive to the magnitude of the acceleration, up to 6 m/s\(^2\). Still further we have observed that the magnitude of background magnetic field (y-axis component: direction perpendicular to scanning velocity) increases with increased scanning velocity. We conjecture this is due to the eddy current effect, which is generated in the specimen.
In conclusion, our answers to these questions indicate that a magnetic flux leakage system should ideally account for signal measurements during the acceleration stage, and where possible measurements should be obtained when the system is moving with constant velocity. These findings could help to optimise the MFL system to capture the defect feature more precisely if defects are scanned during a phase of machine acceleration. It also shows the importance of conducting measurements at constant velocity, wherever possible.
The acceleration phase can be 5 times longer than the deceleration phase meaning that more area is covered during this action. The mass of the machine and the induced eddy currents need to be overcome meaning that the desired speed takes is not reached quickly. The deceleration phase is much quicker as the momentum and eddy current effect acts as a break on the system. It is also customary for the user to turn off the motor and suddenly stop the machine at the end of a plate, further reducing the active area of deceleration. In this paper, acceleration, and in particular the covered distance, is considered the key criteria that can influence the severity of the flaws measured and so only acceleration is examined. Deceleration will be considered in future work.
Further work could also include making improvements to the experimental setup to enable measurements to be performed more precisely. The numerical simulations could also benefit from an improved algorithm designed for the problem, which is currently not available in commercial solvers.
References
Buncefield Major Incident Investigation Board. The Buncefield incident 11 December 2005. The final report of the Major Incident Investigation Board (2008)
Dobmann, G., Cioclov, D.D., J.H.Kurz, N.: DT and fracture mechanics. How can we improve failure assessemnt by NDT? Where we are-where do we go? Insight-Non-Destructive Testing and Condition Monitoring, 53(12), 1–5 (2011)
Pearson, N.: Band-limitations and non-linearities of magnetic flux leakage in context of non-destructive testing, Ph.D. dissertation, College of Engineering, Swansea University, Swansea, U.K., (2014)
Markov, A.A.: Problems of the high-speed flaw dection of railway rails laid into the tract. Radioelektronika i Svyaz 1(5), 23–28 (1999)
Dobmann, E., Walle, G., Holler, P.: Magnetic leakage flux testing with probes: physical principles and restrictions for application. NDT Int. 20(2), 101–104 (1987)
Goedbloed, J.P.H.: Principles of Magnetohydrodynamics. Cambridge University Press, Cambridge, UK (2010)
Snarskii, A.A., Zhenirovskyy, M., Meinert, D., Schulte, M.: An integral equation model for the magnetic flux leakage method. NDT & E Int. 43, 343–347 (2010)
Altschuler, Eduardo, Pignotti, Alberto: Nonlinear model of flaw dection in steel pipes by magnetic flux leakage. NDT & E Int. 28(1), 35–40 (1995)
Huang, Z., Que, P., Chen, L.: 3D FEM analysis in magnetic flux leakage method. NDT & E Int. 39, 61–66 (2006)
Niikura, S., Kameari, A.: Analysis of eddy current and force in conductors with motion. IEEE Trans. Magn. 28(2), 1450–1453 (1992)
Shin, Y.K., Lord, W.: Numerical modeling of moving probe effects for electromagnet nondestructive evaluation. IEEE Trans. Magn. 29(2), 1865–1868 (1993)
Sun, Y.S., Lord, W., Katragadda, G., Shin, Y.K.: Motion induced remote field eddy current effect in a magnetostatic non-destructive testing tool: a finite element prediction. IEEE Trans. Magn. 30(5), 3304–3307 (1993)
Katragadda, G., Sun, Y.S., Lord, W., Udpa, S.S., Udpa, L.: Velocity effects and their minimization in MFL inspection of pipelines–a numerical study. Rev. Prog. Quant. Nondestr. Eval. 14A, 499–505 (1995)
Katragadda, G., Lord, W., Sun, Y.S., Upda, S., Upda, L.: Alternative magnetic flux leakage modalities for pipeline inspection. IEEE Trans. Magn. 32(3), 1581–1584 (1996)
Mandayam, S., Upda, L., Upda, S.S., Lord, W.: Invariance transformations for magnetic flux leakage signals. IEEE Trans. Magn. 32(3), 1577–1580 (1996)
Shin, Y.: Numerical prediction of operating conditions for magnetic flux leakage inspection of moving steel sheets. IEEE Trans. Magn. 33(2), 2127–2130 (1997)
Park, G.S., Park, S.H.: Analysis of the velocity-induced eddy current in MFL type NDT. IEEE Trans. Magn. 40(2), 663–666 (2004)
Li, Y., Tian, G.Y., Ward, S.: Numerical simulation on magnetic flux leakage evaluation at high speed. NDT & E Int. 39, 367–73 (2006)
Du, Z., Ruan, J., Peng, Y., Yu, S., Zhang, Y., Gan, Y., Li, T.: 3-D FEM simulation of velocity effects on magnetic flux leakage testing signals. IEEE Trans. Magn. 44(6), 1642–1645 (2008)
Chen, Z., Xuan, J., Wang, P., Wang, H., Tian, G.: Simulation on high speed rail magnetic flux leakage inspection. In: IEEE International Instrumentation and Measurement Technology Conference, p. 2011. Hangzhou, China (2011)
Gan, Z., Chai, X.: Numerical simulation on magnetic flux leakage testing of the steel cable at different speed title. In: International Coriference on Electronics and Optoelectronics (ICEOE 2011), pp. 316–319. Dalian, Liaoning, China (2011)
Antipov, A.G., Markov, A.A.: Evaluation of transverse cracks detection depth in MFL rail NDT. Russ. J. Nondestr. Test. 80(8), 481–490 (2014)
Wang, P., Gao, Y., Tian, G., Wang, H.: Velocity effect analysis of dynamic magnetization in high speed magnetic flux leakage inspection. NDT & E Int. 64, 7–12 (2014)
Zhang, L., Bellblidia, F., Cameron, I.M., Sienz, J., Boat, M.A., Pearson, N.R.: Influence of specimen velocity on the leakage signal in magnetic flux leakage type nondestructive testing. J. Nondestr. Eval. 34, 6 (2015)
Liu, B., Cao, Y., Zhang, H., Lin, Y.R., Sun, W.R., Xu, B.: Weak magnetic flux leakage: a possible method for studying pipeline defects located either inside or outside the structures. NDT & E Int. 74, 81–86 (2015)
Lu, S., Feng, J., Li, F., Liu, J.: Precise Inversion for the Reconstruction of Arbitrary Defect Profiles Considering Velocity Effect in Magnetic Flux Leakage Testing. IEEE Trans. Magn. 53(4), 6201012 (2017)
Antipov, A.G., Markov, A.A.: 3D simulation and experiment on high speed rail MFL inspection. NDT & E Int. 98, 177–185 (2018)
Pullen, A.L., Charlton, P.C., Pearson, N.R., Whitehead, N.J.: Magnetic flux leakage scanning velocities for tank floor inspection. IEEE Trans. Magn. 54(9), 7402608 (2018)
Yang, S., Sun, Y., Upda, L., Upda, S.S., Lord, W.: 3D simulation of velocity induced fields for nondestructive evaluation application. IEEE Trans. Magn. 35(3), 1754–1756 (1999)
Feng, B., Kang, Y., Sun, Y., Yang, Y., Yan, X.: Influence of motion induced eddy current on the magnetization of steel pipe and MFL signal. Int. J. Appl. Electromagn. Mech. 52(1–2), 357–362 (2016)
Sziekasjim, K., Kloster, A., Dobmann, G., Scheel, H., Hillemeier, B.: High-speed, high-resolution magnetic flux leakage inspection of large flat surfaces. ECNDT 1-8 (2006)
Li, Y., Tian, G.Y., Ward, S.: Numerical simulation on electormagnetic NDT at high speed. Insight-Non-Destr. Test. Condition Monit. 48(2), 103–108 (2006)
Lei, L., C.Wang, F.J., Wang, Q.: RBF-based compensation of velocity effects on MFL signals. Insight-Non-Destr. Test. Condition Monit. 51(9), 508–511 (2009)
Lord, W., Bridges, J.M., Palanisamy, R.: Residual and active leakage fields around defect in ferromagnetic materials. Materials Evaluation July, 47–54 (1978)
Pearson, N.R., Boat, M.A.: A novel approach to discriminate top and bottom discontinuities with the Floormap3D. 6MENDT (2012)
Neil Randal Pearson, Simon Andrew Horsfall Packer, Robin Harald Priewald. Methods And Apparatus For The Inspection Of Plates And Pipe Walls. Patent: EP2506003B1
American Petroleum Institute - API standard 653. Tank inspection, repair, alteration and reconstruction (2014)
ANSOFT Corporation. Maxwell V14.0 Manual 2010
Acknowledgements
The authors would like to acknowledge the ASTUTE 2020 (Advanced Sustainable Manufacturing Technologies) operation supporting manufacturing companies across Wales, which has been part-funded by the European Regional Development Fund through the Welsh Government and the participating Higher Education Institutions. The authors would also like to acknowledge the contribution of Eddyfi Technologies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, L., Cameron, I.M., Ledger, P.D. et al. Effect of Scanning Acceleration on the Leakage Signal in Magnetic Flux Leakage Type of Non-destructive Testing. J Nondestruct Eval 42, 14 (2023). https://doi.org/10.1007/s10921-023-00925-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10921-023-00925-1