Ultrasonic Echo Localization Using Seismic Migration Techniques in Engineered Barriers for Nuclear Waste Storage

Abstract

In the framework of non-destructive-testing advanced seismic imaging techniques have been applied to ultrasonic echo data in order to examine the integrity of an engineered test-barrier designed to be used for sealing an underground nuclear waste disposal site. Synthetic data as well as real multi-receiver ultrasonic data acquired at the test site were processed and imaged using Kirchhoff prestack depth migration reverse time migration (RTM). In general, both methods provide a good image quality as demonstrated by various case studies, however deeper parts within the test barrier containing inclined reflectors were reconstructed more accurately by RTM. In particular, the image quality of a specific target reflector at a depth of 8 m in the test-barrier has been significantly improved compared to previous investigations using synthetic aperture focusing technique, which justifies the considerable computing time of this method.

1 Introduction

The safe storage of nuclear waste in an underground repository is of utmost importance. Especially the different sealing elements of the repository, e.g. engineered barriers, must meet high demands with respect to their integrity, stability and watertightness. In order to investigate and evaluate these conditions, sophisticated non-destructive testing (NDT) methods are needed which can image the interior of the elements at the best possible resolution and with sufficient penetration depth.

In this paper, an engineered test-barrier with dimensions of approximately 5 m × 5 m × 25 m within an underground mine for nuclear waste storage is investigated (Fig. 1). It consists mainly of a 25 m long salt-concrete block separated into three sections by two metal plates. Salt concrete uses crushed rock salt instead of sand and gravel as aggregate to provide a similar chemical and rheological behavior as the surrounding material. The barrier is surrounded by halite (rock salt), except for the front side which is accessible for measurements. The back side contains a pressurized chamber for the injection of fluid into the salt concrete structure. In case of connected cracks or fissures parallel to the barrier axis, the associated permeability allows the injected fluid to migrate from the back to the front side of the barrier. Under such conditions the barrier would be considered as unsafe because leakages are possible. However, no significant drop in fluid pressure has been observed for years which implies that no significant number of cracks is present and/or the cracks are not interconnected. In addition, the very low fluid flow out of the pressurized chamber proves the tightness of the test-barrier. However, one of the major aims of this study is to detect and image existing cracks within the barrier in order to assess the potential for leakage at any given time, which is important for the assessment of the long-term sealing capabilities of such engineered barriers.

Fig. 1

Schematic side view of the engineered barrier (black: air/fluid—halite transition; blue: salt concrete—halite transition; green: salt concrete—fluid transition; dark red: position of the aperture) (Color figure online)

The imaging methods employed in this study are Kirchhoff prestack depth migration (KPSDM) and reverse time migration (RTM). The theory behind these techniques is described in detail in the subsequent section.

In order to better assess the possibility of imaging the cracks within the barrier for the specific acquisition geometry, a synthetic model representing the barrier has been generated in a first step. The corresponding forward-modelled ultrasonic data have been processed and the imaging results have been analyzed and compared for both applied imaging techniques, KPSDM and RTM, respectively.

Furthermore, ultrasonic measurements have been conducted at the front face of the barrier within the underground test site. The survey was designed to image the interior of the engineered barrier up to a distance of approximately z = 8 m from the front face, where the first separating metal plate is located. Acquisition, processing and analysis of the real dataset is described in detail in the section on real data.

The obtained imaging results for the synthetic and the real data are evaluated in terms of the capability of both methods to image the cracks within the barrier and conclusions are drawn from the results with respect to the overall frame of the study in the last section.

2 Material and Methods

KPSDM and RTM are well known and widely used in seismic investigations of the Earth’s interior. More recently, these methods have also been employed in NDT [1,2,3,4] while being compared to the SAFT (Synthetic Aperture Focusing Technique) which up to now represents the standard output of most ultrasound data processing routines. SAFT is frequently used for the evaluation of single sided measurements, the detection of defects and thickness measurements [5]. The 2D SAFT algorithm is used to focus reflection signals in a B-scan to their spatial origin [6]. The summation within the B-scan along the hyperbolic function associated with a point diffractor in the actual medium is characteristic of the SAFT algorithm [7]. It is therefore closely related to Kirchhoff Migration using a constant velocity field. SAFT reconstructions are commonly represented using the envelope of the raw output of the algorithm [5, 6].

In the following, the theory behind KPSDM and RTM as well as their implementation used in this study are described in more detail. Both methods use the wavefield $u({x}^{\prime},z=0,{t}^{\prime})$ recorded along a line (in the 2D case) or an area (in the 3D case) at the Earth’s surface or at the accessible surface of the specimen ($z=0$) as input data. In a land-seismic context wavefields proportional to the particle velocity are recorded using geophones whereas ultrasonic transducers used in NDT commonly record particle acceleration.

2.1 Kirchhoff Prestack Depth Migration (KPSDM)

In KPSDM [8], each point in the model is assumed to be a potential point diffractor. For a medium with constant velocity, the travel times from such a point diffractor to the receivers at the surface plotted as a function of offset describes a diffraction hyperbola. For KPSDM, the wavefield $u({x}^{\prime},z=0,{t}^{\prime})$ is summed/integrated along the diffraction hyperbola which corresponds to the considered subsurface point. The receivers are located at the coordinates $\left({x}^{\prime}, 0\right)$ and $t{^{\prime}}$ refers to the seismogram time, i.e. the time in the recorded traces. The output is the migration image $M(x,z)$:

$$M\left(x,z\right)=\frac{1}{\pi }{\iint }_{-\infty }^{+\infty }\frac{\partial u\left({x}^{\prime},0,{t}^{\prime}\right)}{\partial {t}^{\prime}}W\left(x,z,{x}^{\prime},t^{\prime}\right)dt^{\prime}dx^{\prime}$$

(1)

where W is a weighting function given by

$$W\left(x,z,{x}^{\prime},t^{\prime}\right)= \frac{-\tau zH\left(\tau -\frac{r}{c}\right)}{{r}^{2}\sqrt{{\tau }^{2}-{\left(\frac{r}{c}\right)}^{2}}}$$

(2)

The integral in Eq. (1) is evaluated for each subsurface point $\left(x,z\right)$. During the integration, the weighting function W (Eq. (2), Fig. 2) is applied which depends on the distance $r=\sqrt{{\xi }^{2}+{z}^{2}}$ between the receiver and the image point (with their lateral distance $\xi = x-x^{\prime}$) and the travel time $\tau =t^{\prime}-{t}_{I}$ from the image point to the receiver. ${t}_{I}$ is the so-called imaging time and corresponds to the travel time from the source to the image point. For a constant velocity medium, ${t}_{I}$ can be calculated trigonometrically using the coordinates of the source and the image point and the wave velocity inside the medium. $H\left(\tau -\frac{r}{c}\right)$ is the Heaviside step function which turns from 0 to 1 for times larger than the travel time from the image point to the receiver.

Fig. 2

Weighting function for an image point at ξ = 0

The highest values of the weighting function occur along the diffraction hyperbola of the respective image point. For travel times earlier than the diffraction hyperbola the weighting function vanishes due to the Heaviside step function, while for later travel times the weighting function decreases rapidly according to Kirchhoff theory [9]. Due to the small values of the weighting function for travel times later than the diffraction hyperbola, these samples are commonly neglected, and the integral is only evaluated along the diffraction hyperbola. This approach results in an almost identical migration image while gaining performance of the algorithm. However, this simplification is not implemented in our algorithm for demonstration purposes. The time derivative is applied to the input data before migration to account for the application of the time integral during the algorithm (Eq. (1)).

For a fixed source position, the recorded data set is a so-called shot gather with the number of traces equivalent to the number of receivers used. It might be expressed as a B scan of the receiver with the source fixed. The input for the migration procedure is the time derivative of the traces within the shot gather according to Eq. (1). In practice, the following steps must be performed for each image point in the model space to compute the migrated shot gather:

• 1. Compute the corresponding weighting function.

• 2. Multiply the data samples with the weighting function.

• 3. Sum/integrate along the weighted wavefield

• 4. Save the value of the integration procedure to the position of the current image point.

As a final step, all migrated shot gathers are summed up and yield the final migrated image. In that approach, the migration process is performed in the depth domain according to Kirchhoff theory before the summation (stacking) of various offsets (source-receiver distances) and is therefore referred to as prestack Kirchhoff Depth Migration. In an NDT context, a different terminology is commonly used, e.g. a similar version of pre-stack summation is known as total focusing method (TFM). In the TFM approach an unweighted summation along the diffraction hyperbola is performed [10]. The weighting function (Eq. (2)) in KPSDM originates from Kirchhoff theory [9]. Using a weighting functions in Kirchhoff migration schemes produces sharper reflectors by reducing their lateral extent and the formation of migration smiles. Migration smiles appear as remnants of the wavefield which is smeared along isochrones throughout the subsurface and appear at the boundaries of the illuminated part of the reflector due to insufficient constructive interference of these wavefield isochrones.

2.2 Reverse Time Migration (RTM)

The RTM technique [11, 12] uses a different approach compared to Kirchhoff migration. In RTM, wavefield simulations are conducted using a previously defined velocity model and a representative source wavelet extracted from the data. For the example presented in this article, the wavelet is taken from the direct wave which is travelling directly from the source to the receivers without being reflected or scattered. However, more advanced methods of wavelet guessing are applicable here as well [13]. In our implementation, the following RTM steps are performed for each source location:

• 1. Compute the wavefield with a finite difference (FD) scheme for the source location of the data record that must be migrated and using the previously extracted source wavelet as well as a predefined velocity model. The result of this simulation is the so-called source wave field S(t_i,x,z) calculated at each time step t_i.

• 2. Time-reverse the traces of all receivers and compute the wavefield in the same way as in step 1 but with the time-reversed traces as source functions and the receiver locations as source positions. The source functions (time reversed traces) are excited simultaneously into the same model. The result of this simulation is the so-called receiver wave field R(t_i,x,z).

• 3. Cross-correlate the source and receiver wave field according to Eq. (3). Starting with the last time slice of the source wave field and the first time slice of the receiver wave field, all wave fields are multiplied by means of an element wise matrix–matrix multiplication. The products are then summed up. The order of multiplication is important, i.e. the time slices of the source wave field are input to the correlation in negative time direction (i.e. starting from the last time slice ${t}_{n}$ that was computed last, where n is the number of time steps computed), whereas the receiver wave field is used in the order as it was computed.

As indicated above, this process is repeated for each shot gather (and thus for each source position). The migrated shot gathers are stacked to obtain the final migration image just like with the KPSDM algorithm. This migration procedure is therefore also referred to as prestack RTM.

The cross-correlation process results in the migrated section M(x,z) and can be expressed as

$$ M\left( {x,z} \right) = \sum\nolimits_{{t_{i} = 0}}^{{t_{n} }} S \left( {t_{i} ,x,z} \right)R\left( {t_{i} ,x,z} \right) .$$

(3)

Note that in the calculation of the receiver wavefield, time is running backwards from ${t}_{\text{n}}$ until time zero since the input source functions are reversed in time. This has the consequence that the last time slice of the source wavefield corresponds to the same time as the first computed time slice of the receiver wavefield, namely ${t}_{n}$. The penultimate time slice of the source wavefield then corresponds to ${t}_{n-1}$ as well as the second time slice of the receiver wavefield. The result is the value of the cross-correlation function between $S\left({t}_{i},x,z\right)$ and $R\left({t}_{i},x,z\right)$ for a time shift of zero.

Equation (3) is the most common and robust imaging condition for RTM implementations. However, it may produce strong source/receiver artefacts, which can be significantly reduced by a division through the intensity of the source wave field or the receiver wave field [14]. This results in the source illumination imaging condition in Eq. (4) and the receiver illumination imaging condition in Eq. (5), respectively.

$$M\left(x,z\right)=\frac{{\sum }_{{t}_{i}}^{{t}_{n}}S\left({t}_{i},x,z\right)R\left({t}_{i},x,z\right)}{{\sum }_{{t}_{i}}^{{t}_{n}}{S}^{2}({t}_{i},x,z)}$$

(4)

$$M\left(x,z\right)=\frac{{\sum }_{{t}_{i}=0}^{{t}_{n}}S\left({t}_{i},x,z\right)R\left({t}_{i},x,z\right)}{{\sum }_{{t}_{i}=0}^{{t}_{n}}{R}^{2}({t}_{i},x,z)}$$

(5)

After testing both imaging conditions it was found that the source illumination imaging condition yields the best images with least migration artefacts. For that reason, this imaging condition was chosen for all RTM results presented in the following.

3 Simulation of the Elastodynamic Wave Field

Simulating the wave field in the context of this article is necessary:

• 1. to generate synthetic ultrasound data and

• 2. to compute the source and receiver wave fields for RTM.

All simulations were performed using a finite-difference seismic modeling suite developed at the Institute of Geophysics and Geoinformatics at TU Bergakademie Freiberg based on an implementation by Bohlen [15]. The program solves the wave equation for a given medium, source position and source signal on a 2D staggered grid [16]. PMLs (Perfectly Matched Layers) at the edges of the model absorb the incident wave energy and thus simulate an infinite continuous half space around the model. Only at the top boundary of the model a free surface simulates the front face of the engineered barrier, i.e. incident wave energy is reflected back into the model.

The grid spacing and the maximum time step of the simulation are limited by the Courant–Friedrichs–Lewy criterion [17] and depend on the minimum propagation velocity within the medium and the maximum frequency of the source wavelet. Using a Ricker wavelet with a center frequency of f_c = 25 kHz results in a maximum frequency of approximately 75 kHz [18]. Together with a minimum velocity of 2250 m/s this leads to a required grid spacing from 3 to 1.5 mm and a time step of $3.3\cdot {10}^{-7}$ s to avoid numeric instabilities and grid dispersion.

The acquisition aperture and the size of the engineered barrier result in a relatively large model and a notable computational effort for the simulation. Therefore, only a 2D simulation was performed to limit the computational effort to a reasonable time frame.

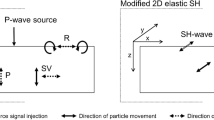
Consistently with the wave type generated by the acquisition system only the propagation of horizontally polarized shear waves (SH waves) has been simulated. In a 2D medium (Fig. 3) no conversion to other wave types (e.g. P or SV) occurs at internal or external interfaces if the shear wave is polarized perpendicular to the drawing plane. Under this assumption, no velocity model is needed for compressional waves. In reality, 3D effects cannot be entirely excluded. However, the amplitudes of converted wave types are small in our case and the directional characteristic of the acquisition tool reduces type conversions to a minimum.

Fig. 3

Sketch of the synthetic model (all units are in cm). The blue line indicates the front face. For the acquisition of the synthetic dataset, the total width of the front face was used. Velocity is considered invariant within the halite and salt concrete regions, respectively

4 Synthetic Data

A synthetic model with velocity and density values representative for the real data set acquired at the test site has been constructed (Fig. 3). It comprises a block of salt concrete bounded by halite on both sides, a rectangular steel block representing a built-in monitoring device, a sinusoidal air-filled crack at z ≈ 6 m as well as a separating steel plate at z ≈ 8 m. The physical properties of the various elements used for wavefield simulation are listed in Table 1. While attenuation of the wavefield by geometrical spreading is accounted for by the simulation program, intrinsic attenuation (i.e. absorption losses) has been neglected at this point. However, a depth-dependent gain adjustment of the reconstruction images described in the subsequent sections accounts for these kinds of attenuation as well.

Table 1 Medium parameters used for the synthetic model

The finite difference simulations of the wave field were performed as described in the previous section and yielded the particle acceleration at receivers with a spacing of 10 cm along the front face of the salt concrete block. The full synthetic data set consists of 44 single shot gathers each having a different source location at one of the previously defined receivers. Figure 4 shows a single shot gather for a source located at x = 2.8 m along the front face. The reflections from the monitoring device, from the crack as well as from the steel plate are clearly visible.

Fig. 4

Representative shot gather for the synthetic model (source location at x = 2.8 m). D: direct wave; 1: reflection from the sine-shaped crack; 2: reflection from the monitoring device; 3: reflection from the separating plate

The processing of the simulated data before migration was kept to a minimum and only involved a top mute of the direct wave: since this wave type does not travel through the model, it does not add any additional information to the migration images. Therefore, it was discarded, and the traces were set to zero for times earlier than the arrival of the direct wave. This is a fundamental step during seismic data processing. KPSDM was performed using a constant velocity of 2250 m/s which corresponds to the shear wave velocity of salt concrete (Table 1).

As mentioned above, the velocity model shown in Fig. 3 was used to compute the synthetic data set by FD modeling. For the FD wave field simulations involved in RTM, the monitoring device, the crack and the separating plate were removed from the velocity model since the aim of the migration procedures is to find these features. The FD simulations were therefore conducted in a velocity model containing the salt concrete block surrounded by halite as only a priori information which is the initial situation known before the reconstruction. It can be seen as an advantage of RTM that other a priori information can be easily added to the migration scheme by altering the velocity model accordingly.

Both migration approaches yield comparable results (Fig. 5). The top edge of the monitoring device (feature 2) and the right part of the separating plate (feature 3) are clearly visible. The left part of the separating plate is not imaged in the KPSDM result since the incident wave energy is completely reflected at the crack and does not reach this part of the plate. However, feature 5 in the RTM image shows a weak reflection below the crack which may be the result of waves being reflected at the salt concrete–halite transitions and thus propagating around the crack. Thereby, the separating plate can be illuminated by a weak signal. Such arrivals can be handled properly by the RTM method, so that the weak image of the separating plate in the RTM result is in principle possible.

Fig. 5

Comparison of KPSDM (left) and RTM (right) for the synthetic data set. The phase of the signals is indicated by colors (red: positive; blue: negative)

The most obvious difference between both images concerns the left part of the crack (feature 1). It is reconstructed correctly by the RTM algorithm, while in the KPSDM result the left part of the crack (feature 1a in Fig. 5) is imaged incorrectly inside the halite and an artificial gap between the two parts of the reflector is created. Since the crack is positioned relatively deep inside the model and its left part is dipping outwards, the reflected wave energy from this part of the reflector propagates towards the left edge of the model and does not reach the receivers directly. Instead, a part of that energy is reflected again at the left salt concrete–halite transition (Fig. 3) towards the center of the model and is thus recorded by the receivers. KPSDM is not accounting for such multiple reflections. The recorded signal is therefore transmitted through the salt concrete–halite transition by KPSDM. This feature has been observed for the real data set as well and is described in detail below.

In addition, at least some parts of the steeply dipping transition between salt concrete and surrounding halite are visible in the RTM image (feature 4), although this boundary has already been a part of the velocity model used for the FD simulation within the RTM scheme. Steeply dipping reflectors are elements having a large angle to the source-receiver line. In this case, the salt-concrete halite transition is positioned at an angle of approx. 80° to the front face. These reflectors are challenging for imaging algorithms since reflected wave energy is mostly directed away from the receivers and therefore barely recorded.

5 Real Data

5.1 Data Acquisition

The real data set was acquired at a test structure in an underground nuclear repository using the novel measuring system LAUS (Large Aperture Ultrasonic System) [19]. This system has various advantages compared to other measuring devices. The primary fact distinguishing the LAUS from conventional ultrasonic measuring systems is the number of transceiver arrays, which may vary according to the requirements and which can be positioned independently. A LAUS transceiver unit consists of 32 directly coupled shear wave transducers in a 2.5 cm distance staggered 8 by 4 arrangement designed to improve the source amplitude when used as a transmitter as well as to increase sensitivity when used as a receiver. Depending on the intended function, the transducers are connected to a square wave (single period) source signal generator or an analog amplifier and analog–digital converter by an electronic, software-controlled switch. Transducers and all electronic items of a unit, including wireless communication electronics and battery, are built into a single, independent device. It is connected to the object under investigation by a vacuum suction pod (Fig. 6). More detailed information on the device, its application in the test site and preliminary results using the SAFT imaging technique have been published earlier [20]. For our survey, 12 transceiver arrays were used simultaneously and served as source and as receiver. That way, a large offset (aperture) between source and receiver can be realized. This is equivalent to acquisition schemes used in surface seismic surveys including their advantages for improved imaging of inclined reflectors [8]. The fixed combination of the transceiver units in a metal frame (Fig. 7) is referred to as array. However, the transducers can also be positioned arbitrarily to optimize the distance and arrangement of the units.

Fig. 6

Two LAUS transducer units [19]

Fig. 7

LAUS deployed at the front face of the underground engineered test-barrier. Pressurized air for the suction pods is delivered via the flexible red pipes visible in the right part. The measurement line is indicated by the blue arrow

In our case the unit spacing (pitch) was 11 cm and the whole array of units along the front face of the salt concrete block had a length (aperture) of 1.21 m from the midpoint of the first to the midpoint of the last unit (Figs. 7 and 8). The center frequency of the emitted wavelet was f_c = 25 kHz to provide a sufficient penetration depth. In addition, only SH waves were emitted, i.e. the direction of particle motion was perpendicular to the profile direction (the line in which the receivers are arranged at the front face). In a 2D medium this has the advantage that the records are essentially free from converted wave types.

Fig. 8

Array movement along the profile. The triangles mark the positions of the LAUS transceiver arrays

One LAUS cycle is complete when all transceiver units have acted as a source with all other ones acting as receivers. In our case, the data recorded during one LAUS cycle consists of 12 shot gathers (records, in which one of the transceiver units has acted as a source) with 11 traces (A-scans) each. Four cycles were recorded along the profile. After each cycle, the array was moved 0.6 m in the direction of the profile resulting in a total covered length of 3.01 m (Fig. 8).

5.2 Migration Results

In the same way as for the synthetic data set, data processing preceding the migration was reduced to a minimum. In addition to a top mute of the direct wave, a frequency band pass filter between 5 and 80 kHz was applied. For the RTM algorithm, the velocity model shown in Fig. 9 was used as input for the FD simulations. The approximate position of the boundary between the salt concrete block and the surrounding halite was taken from a priori knowledge about the engineered test-barrier. Information about existing cracks or built-in monitoring devices inside the salt concrete were assumed to be unknown and therefore are not part of the model. Furthermore, the separating plate is only shown for orientation but was not used in the velocity model, since the aim was to reconstruct this element and its position is not known accurately.

Fig. 9

Velocity model used as input for RTM (all units are in cm). The separating plate was added for orientation only, it is not included in the velocity model. The blue and red line represent the front face and the aperture width on the front face, respectively

Figure 10 shows the results for both migration algorithms. Damping and geometrical spreading effects cause the deeper reflectors to be weak in the raw migration images. To enhance the image of deep reflectors, automatic gain control (AGC) with a depth window of 1 m was applied to the migration images. The different reflectors appear at similar positions in both images. This applies to the very shallow reflector (2) as well as to the reflector groups (3) and (4). A part of these reflectors can be assigned to built-in monitoring devices (e.g. for stress or temperature measurements). A strong reflector is visible at z ≈ 8 m (5), which can be interpreted as the separating plate due to its position. At the position of the reflector group (3) cracks have been confirmed in drillholes, which seem to be represented in the migration images. However, a significant difference between both images can be seen for the most prominent reflectors (1) and (6). In Fig. 10a, the left part of the reflector (6) is positioned such that it lies inside the halite and a gap between the two parts of reflector (6) is evident. The position of this reflector could be interpreted as a crack that extends from the concrete structure into the halite. However, the existence of any open and for that reason reflective crack within the halite is unlikely because of the tendency of halite to flow and to close any cracks. In contrast, this part of the reflector is located almost completely within the salt concrete in the RTM image (Fig. 10b). The gap in this reflector is not present. In comparison with the results for the synthetic model and in particular for the mis-positioned crack, one can infer that the same feature is observed here for the real data set. In general, the RTM image has a noisier appearance compared to the KPSDM image. However, Fig. 10 shows that the same reflectors and reflector groups have been recovered by both migration procedures. The higher noise level likely results from up- and down going waves interfering during the cross-correlation process.

Fig. 10

Comparison of imaging results obtained from KPSDM (left) and RTM (right) for the real data set. The dashed frame marks the area directly beneath the measurement line (profile) along the upper boundary

6 Discussion and Conclusions

For the synthetic as well as the real data sets investigated in this study, both imaging algorithms (KPSDM and RTM) yield comparable and plausible results as shown by the synthetic experiments. Most reflectors are imaged at the correct position up to a depth of 8 m. Since the cracks are air-filled and the separating plate is a metal item, the corresponding reflectors should have opposite polarity. This would ideally result in an inverted color sequence at the corresponding reflectors in the migration images, i.e. red-blue-red vs. blue-red-blue, respectively. Unfortunately, this is not evident in either migration images which is possibly due to delamination and/or perforation at the separating plate as well as the influence of the stacking process. Since the reflectors are located relatively deep in the material, very small inaccuracies of their location within the migrated single shot gathers lead to an imperfect constructive interference during the stacking process.

Cracks were identified mostly parallel to the front face. This supports the finding that the engineered barrier has been watertight for the last years, as mentioned in the introductory part. However, longitudinal cracks (with an angle of approx. 90° to the front face) can only be resolved close to the front face due to the acquisition geometry and the ratio between source receiver offset and imaging depth. The detection of deeper longitudinal cracks is the subject of subsequent investigations using a borehole probe.

Since there is a vanishing shear modulus in fluids such as water and air, shear waves are not transmitted, and shadow zones form behind the cracks. Small reflectors or parts of larger reflectors within those shadow zones can be hardly imaged by both approaches, as shown with the separating plate in Fig. 5. However, the real data set was acquired at a 3D structure. If a crack is considered as a one-dimensional structure or at least not extending over the complete cross section of the barrier, waves can also pass to deeper regions. This can explain the sharp reflection of the separating plate (feature 5) in Fig. 10 below the prominent reflectors 1 and 6.

KPSDM using a constant velocity seems to misalign the reflectors dipping towards the lateral boundaries of the model. This behavior was observed for the crack in the synthetic data set and has been likewise observed for the separating plate in the real data set. For certain details, e.g. the deepest crack, the RTM image shows significant advantages compared to the KPSDM image.

However, computation time is about three orders of magnitude higher for RTM compared to KPSDM. The computation of the complete wavefield is time consuming. In addition, many snapshots of the source wavefield must be stored for the cross-correlation process which is the reason of the high memory demand. The long recording time caused by the large model size increases the memory demand additionally. The RTM computations were carried out on a 24-core workstation within 5 days. It must be mentioned that the snapshots of the wavefield were saved on hard disk since this machine did not have sufficient memory to keep the snapshots in RAM. Using a machine with more core memory or a larger computing cluster would have decreased the computation time considerably. In addition, implementations of RTM on GPUs or analytical approaches have been developed to decrease computation time additionally [21, 22]. In contrast, the calculation of the KPDSM result was accomplished in a few minutes, depending on the number of computing cores used. This is similar as in the computation of SAFT images.

Therefore, KPSDM can be considered as a fast and robust method for obtaining a good and overall impression of the structural features, but RTM should be considered as the final step after all data processing to obtain the best image with least artefacts.

Further improvement of the migration images may be obtained by more advanced data processing, e.g. deconvolution for removing the influence of the source wavelet or additional methods of noise attenuation for further improvement of the signal-to-noise-ratio. Advanced Kirchhoff-based focusing prestack depth migration techniques (e.g. Fresnel-volume-migration [23]) can also be taken into consideration. Focusing type PSDM use information about the direction of recorded wavefronts to reduce the lateral extent of reconstructed reflectors by limiting the smearing along the isochrones resulting in a sharper reconstruction image.