Abstract
XXL-Computed Tomography (XXL-CT) is able to produce large scale volume datasets of scanned objects such as crash tested cars, sea and aircraft containers or cultural heritage objects. The acquired image data consists of volumes of up to and above \(\hbox {10,000}^{3}\) voxels which can relate up to many terabytes in file size and can contain multiple 10,000 of different entities of depicted objects. In order to extract specific information about these entities from the scanned objects in such vast datasets, segmentation or delineation of these parts is necessary. Due to unknown and varying properties (shapes, densities, materials, compositions) of these objects, as well as interfering acquisition artefacts, classical (automatic) segmentation is usually not feasible. Contrarily, a complete manual delineation is error-prone and time-consuming, and can only be performed by trained and experienced personnel. Hence, an interactive and partial segmentation of so-called “chunks” into tightly coupled assemblies or sub-assemblies may help the assessment, exploration and understanding of such large scale volume data. In order to assist users with such an (possibly interactive) instance segmentation for the data exploration process, we propose to utilize delineation algorithms with an approach derived from flood filling networks. We present primary results of a flood filling network implementation adapted to non-destructive testing applications based on large scale CT from various test objects, as well as real data of an airplane and describe the adaptions to this domain. Furthermore, we address and discuss segmentation challenges due to acquisition artefacts such as scattered radiation or beam hardening resulting in reduced data quality, which can severely impair the interactive segmentation results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Volumetric datasets produced by computed tomography (CT) may yield huge amounts of image information of the scanned specimen which are used in the field of non-destructive testing (NDT). The acquired image data consist of volumes of up to and above 10,0003 voxels which can relate up to terabytes in file size and can depict a multiple of 10,000 of different entities of objects (see Fig. 1). As there are seldom similar objects of similar types in the data (the “lot-one” problem), one of the major obstacles in the NDT domain is the lack of solid reasonable and generic segmentations methods for such images. Existing algorithms are usually not sufficient to deal with this information density and therefore perform poorly or need a lot of parameter tuning.
This work deals with the task of interactive segmentation of this vast amount of data into individual segments and into sub-assemblies using the recently published Flood Filling Networks (FFN) suggested by Januszewski et al. [11,12,13]. The goal of our experiments is to evaluate FFNs for the challenging task of instance segmentation of sub-assemblies which are captured and depicted by XXL-Computer Tomography (XXL-CT) [31, 35]. After a brief introduction into the current state of instance segmentation we will describe our data acquisition process using XXL-CT as well as conventional CT systems. We will also provide an overview of our annotation pipeline, which will be used to obtain reference annotations for the training of the flood-filling networks as well as ground truth data. The used annotation pipeline incorporates both, manual annotation as well as conventional image processing steps. Furthermore, we will show the applicability of FFNs to our problem domain and describe next steps in order to realize a feasible segmentation approach for vast volumetric CT datasets in the field of NDT.
2 Principles and Methods
2.1 Related Work of XXL-CT Data Image Segmentation
There exist a multitude of established algorithms for large-scale image data segmentation. Many of these are domain specific (e.g. for specific purposes such as defect detection, segmentation of well-known metal castings or bulk seed analysis [4]) or generic approaches using classical image processing approaches. Recently, more and more machine learning, and more specifically, deep learning based approaches are being developed which are trying to overcome some shortcomings of the classical algorithms. Specifically, these shortcomings relate to thresholds and mask sizes of the various image processing modules, which have to be manually adjusted, in this possibly separately for multiple spatial distributed regions or volumes inside the dataset. Other shortcomings include the difficulty to find valid parameters over a wide range of input data under consideration of outliers or the need for domain experts which can configure and supervise such systems.
Hence, deep convolutional neural networks based segmentation approaches attempt to compensate these named disadvantages by deriving the needed required settings, configurations and parametrization of the processing pipeline from adequate training data collected directly in the problem domain. Users of such systems then only need to be trained for the preceding data annotation process and no longer need to be experts in the image processing chain itself.
2.1.1 Deep Neural Networks
Many of the machine learning and also deep learning based segmentation approaches can be grouped by the generalized task they try to accomplish. For example, object detection algorithms [6, 7, 10, 21, 22, 28,29,30, 32, 42] try to locate the position and dimension of one or multiple objects of interest inside an image. In some cases, like the Mask R-CNN [9] algorithm individual parts of objects can also be located and delineated.
For semantic segmentation [7, 14, 20, 24, 25, 33] the segmentation task consists of assigning each pixel (or voxel) to a specific target class with the same identifier, meaning that all pixels (or voxels) which are part of for example a screw should be labeled with the identifier ‘screw’. For instance segmentation [5], additionally each individual instance of a class should be assigned an individual identifier. Thus, for example all pixels (or voxels) of a screw should be labelled with the identifier ‘screw’ but also each detected and segmented screw should be assigned its individual identifier.
Many popular deep neural network-based algorithms make use of huge annotated datasets like [3, 10, 15, 17, 23, 36,37,38] depicting millions of objects and most often multiple instances of the same class, as e.g. many screws of the same type. The segmentation task addressed within our own research relates to large-scale volumetric image data where there often exists only one available instance for a specific specimen. For example the front window of a car or a single existing scan of a cultural heritage. So in principle, we are working with data related to a ‘lot size of one’.
Furthermore, the vast data size of the XXL-CT image data introduces the need to incorporate adequate hardware based parallelization or sequentialization mechanisms to deal with such volumes as they are difficult to process on off-the-shelf computer hardware. Methods which iteratively access only a small part of the data are particularly suitable for processing large volume data records. This can be done using attention mechanisms, e.g. described in [19, 39] or by sequential wandering over the input data as in [12] or [26]. Using such mechanisms it is possible to segment large datasets [18]. Those algorithms e.g. use temporary buffers to store areas that have already been segmented [8].
It is possible to interactively involve the user in the learning [41] or evaluation [34, 40] process. Clever modelling of the input masks for convolutional neural networks [1, 16, 17] allow the field of view of a filter layer to be expanded without significantly increasing the required amount of neurons [1, 2].
2.1.2 Flood Filling Networks (FFNs)
In this work we primarily use Flood Filling Networks (FFNs) introduced by Januszewski et al. [11, 13], which already incoperates various of the above mentioned techniques to deal with huge datasets. They showed their capability to perform instance segmentation on volumetric ‘Serial Blockface Scanning Electron Microscopy’ (SBEM) datasets.
One strength of these FFNs lies in the fact that they do not learn the classes of each object. Instead they try to detect the boundaries of an object. The segmentation itself is an iterative algorithm with two nested loops. The outer loop iterates over all seed points and the inner loop runs through all sub-volumes containing the same segment. So the algorithm finds all segments one after the other.
The outer loop begins at a manually selected or automatically detected seed point and segments the current object using the inner loop. After the inner loop has completed, the next seed point which does not belong to an already recognized segment is selected. The outer loop is executed until all seed points have been consumed.
The inner loop is executed for each segment. It first checks whether the seed point passed by the outer loop does not belong to an already segmented object. If the seed point voxel is not marked as belonging to an known segment a sub-volume (or ‘field of view’) is extracted from the input data.
The original authors chose a size of \(33\times 33\times 17\) voxels for the sub-volume. Due to the use of SBEM for data acquisition, the spatial resolution in the third dimension was coarser than in the other two dimensions. By choosing an anisotropic receptive field, however, their sub-volume retained a cubic region of the specimen. For our experiments we chose to start with a sub-volume size of \(33\times 33\times 33\) voxels to keep the sub-volume dimension constant between the bulk material and XXL-CT experiments (see Sect. 2.2). Otherwise we retained the settings from the original authors [12] and also used this adopted implementation for our test.
The sub-volume is added to the processing queue and the inner loop iterates over this queue. With each iteration of the inner loop, the current sub-volume is transferred to a convolutional network (see Fig. 2). This network consists of a series of 3D convolutions with relu activation function and skip connections. The input volume is zero padded prior to each convolution which keeps the volume size between the different layers constant. The output from this network is a new mask volume of the same size. Each voxel value indicates the probability that this voxel belongs to the same segment as the current seed point. By means of an threshold value, an intermediate segmentation of the current segment is created. The selected voxels will then be marked as ‘already segmented’.
Graph of the convolution network used by FFN to segment the given field of view of the input volume. Active voxels in the segmentation sub-volume are used as seed points to guide the segmentation. The network creates an updated version of the segmentation volume by activating voxels associated with the selected segment
If a segment extends beyond the boundaries of the current sub-volume, additional sub-volumes are added to the inner loop processing queue. The new sub-volumes are defined with a large overlap to the original sub-volume. The field of view moves iteratively in an adjustable increment across the input volume, as long as the current segments extends beyond the limit of the current sub-volume. The currently detected segments are merged with the already detected active segment and can thus create resulting segments that span several sub-volumes. If the inner loop queue is empty, the segment is initially considered to be fully segmented.
The next iteration of the outer loop selects a new seed point that is not part of an already detected segment. The corresponding sub-volume gets added to a new inner loop processing queue which than iterates over all sub-volumes of the new segments. The outer loop stops after all seed points have been consumed. Between and after these iterations, several checking and combining mechanisms are used to avoid over- and under-segmentation (splits and merges).
2.2 Data Acquisitionsec: Data
For our experiments (see Sect. 3) two types of datasets were used. Firstly, we performed CT scans of various bulk material samples which are visually closely related to the SBEM datasets originally used for the development of the FFNs [11].
The second dataset consists of two \(512{{}^3}\) voxel chunks of a XXL-CT scan of a Second World War era airplane. The image and content characteristics of this dataset are highly related to the future datasets for which we want to develop our image volume segmentation pipeline.
2.2.1 Bulk Material
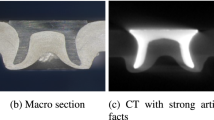
In order to transfer and evaluate the performance of the FFNs for NDT tasks, we performed multiple scans of corn, glass marbles, buttons, and pasta bulk material samples (see Fig. 3), which relate closely to the original SBEM data for which the FFNs have been developed. Similar to the SBEM data, the scanned bulk materials depict a higher foreground-to-background ratio and provide different segmentation challenges. For example, the corn sample (see Fig. 3a and e) consists of non-homogeneous, material, whereas the glass of marbles (see Figs. 3b, e and f) is highly affected by beam hardening artefacts which can be seen as broad dark spots and stripes inside the object.
For the bulk material measurements, the X-ray source was set to a acceleration voltage of 120 kV (175 kV for the marbles) and 4 mA current. The focal spot size was 400 µm. No prefilter was used. The object detector distance was set to 157.5 mm and the object source distance was set to 822.5 mm. The detector has a pixel size of 90 µm and a spatial resolution of \(3328\times 2777\) pixels. The resulting magnification of about 1.19 leads to a voxel size of equal spacing with \(75.53\text { mm}\times 75.53\text {mm}\times 75.53\text {mm}.\) The measurements were reconstructed in a 160 µm voxel grid.
As trade-off between resolution and performance, a complete scan consists of 1200 projections. In combination with an exposure time of 350 ms this leads to a measurement time of 7 minutes for one CT-scan. The bulk material samples have been placed into transparent plastic containers (see Fig. 3, top row). Between successive measurements the container was emptied and refilled with the same material to achieve a random mixture of positions and orientations of the bulk material for each measurement. To increase the scanning throughput some of the containers have been measured stacked onto another with a multi cm sheet of low density foam placed between them.
2.2.2 XXL-CT
The XXL-CT dataset of the airplane consists of two scans, related to the hull and wings of an airplane (see Fig. 4). Each of them is stitched together from two individual CT scans, namely the front and rear of the plane’s hull and the base and tips of the wings respectively. The task is to automatically detect and segment each individual semantic object (metals sheets, screws, rivets, ...) in this dataset.
The four CT scans of the airplane parts took about 17 days. The X-ray source was a 9 MeV linear accelerator set to 7.8 MeV. The source detector distance was set to approxmatly 12 m and the source object distance was set to aproxmatly 10 m. The line detector had a pixel pitch of 400 µm. One scan consists of 2300 projections with a resolution of \(9984\times 5286\) pixels. The resulting magnification of 1.2 lead to a voxel resolution of \(330\times 330\times 600\) µm within the reconstructed volume.
The obtained volumes of the hull (see Fig. 1) have an file size of \(6144\times 9600\times 5288\) voxels or 609 gigabytes for the front and \(6144\times 9600\times 5186\) voxels or 597 gigabyte for the rear.
As can be seen in Fig. 4c, most of the airplane’s interior of the reconstruction consist of empty space (as it is usually the case with airplanes). The main content of the CT volumes consists of thin metal sheets, which have poorly or barely visible edge transitions to the adjacent sheets.
For the many occurrences where two metal sheets bluntly meet semantic information has to be used to decide about the correct object boundaries. Also many volume regions are highly affected by data acquisition and reconstruction artefacts like beam hardening or scattered radiation especially near massive metal structures.
2.3 Annotation Pipeline
We used two approaches to generate training and validation data. A conventional image processing pipeline was used to annotate the bulk material datasets. The XXL-CT datasets have manually been segmentated by human annotators.
2.3.1 Conventional Image Processing Chain
Manual annotation or segmentation of volumetric image data is very time consuming and error-prone as the results are depending on human factors. Due to the homogeneity of bulk material, we used a conventional image processing chain to generate a segmentation baseline examples of for the bulk material of corn and marbles.
Our pipeline starts with a binarization using an threshold gained by Otsu’s method. This is followed by a 3D-distance transform which treats the voids between the specimens as foreground. The distance transform provides a height map with value ‘0’ in the voids between the specimens and increasing distance values inside the specimens. Afterwards we applied watershed transform with a pre-flooding depth of 3 on this output. We then iterated over every segment identifier in the volume and applied a label wise morphological closing using a spherical mask with diameter of 13 voxels to smoothen the edges. In the next step all the segments were recombined into one output volume. We used a connected component analysis with chessboard metric to find segments which might have been split during the process and assigned unique segment identifiers to such split segments. So optical disjunct segments would not have the same segment identifier and disturb the training process.
For the actual processing a 2563 voxel sub-volume has been extracted from each measurement in a way so that the whole sub-volume only consists of the bulk material and none of the transparent container which was used for the measurement was included (see Fig. 5).
While this approach of using a conventional image-processing pipeline is well suited for our needs to formulate a baseline algorithm, typical error cases arise in the form of over-segmentation, merged labels and boundary errors (see Fig. 6).
We corrected the over-segmentation for the marble dataset in the occurring three cases by manually unifying the respective segments. We did not correct the over-segmentation in the other datasets as the occurrence of over-segmentation was not as distinctive as in the marble cases with their large voxel count and iconic shapes. We also did not choose to correct the other error conditions in all the datasets as it would be a too costly and human-intensive process involving manual segmentation which we wanted to avoid for these datasets. Table 1 shows a overview over the bulk material instances and annotation error conditions. The resulting training and testing datasets therefore contained some of these inconsistencies.
Typical error cases for the classical segmentation pipeline: a and b are showing over-segmentation of the top left marble. c and d depict the merged labels of the two light green corns on the center of the left border. e and f show multiple boundary errors due to data artefacts at the border of center orange and grey marbles
2.3.2 Manual Segmented Ground Truth
For the XXL-CT dataset ground truth data was generated through manual annotation of individual segments using 3D Slicer [27]. For that task, two neighboring 5123 voxel sub-volumes have been extracted (see Fig. 4c). The lower block was used for the training process of the FFNs and was hence fully manually segmented. This process took about 350 hours for the segmentation of 7.2 million voxels into to 96 segments. The volume itself consists of approximately 18.5% object voxels, while remaining 81,5% of the voxels relate to background (air). Due to resource constraints only a subset of the test volume containing 62 segments have been manually segmented yet.
The actual training dataset used for the training of the flood filling network had a slightly higher segment count than the 96 annotated segments. This is based on the fact that not all components are fully embedded into the 5123 voxel sub-volume. Some components leave the field of view of the current sub-volume and reappear as disconnected segment at an different position (see Fig. 7). Semantic information is needed to establish that these segments belong in fact to the same object at a different position. This might possibly have confused the training process if it was presented with the request to connect multiple seemingly not connected segments. Therefore we stored the correct manually segmented training set with its 96 segments, but used a slightly modified version for the training, in which we compute a connected component analysis on the manually segmented data to relabel contacting components.
Example of one object not fully contained in the current sub-volume. The object, in this case a helical wire support structure (probably for a suction hose), is located in the corner of a sub-volume (see a for overview and b for closeup). Without semantic information the individual coils appear to be separate segments. c Show the result of human semantic segmentation. d Depicts the annotation which was used as training data for the neural network after applying a connected component analysis
The manual annotation process also incorporates a manual bandpass filter. The bandpass filter was iteratively set to highlight and select common grey values of the current target segment. Then a stylus was used to manually ‘paint in’ the segment. This step was repeated for multiple grey values and slices until the whole segment has been annotated. The use of a bandpass filter to select the segments by their grey values sometimes leads to grainy textures inside the segments (see Fig. 8). These grainy and splattered textures of the bandpass-threshold supported annotation might represent the visual representation of the raw input data, but the actual measured specimen does not reveal these textures. With the aim to achieve reasonable and visual pleasing segmentation results we opted for a postprocessing of these annotation with an \(3\times 3\times 3\) box mask morphological closing (see Fig. 8c).
In our annotation guidelines, we stipulated that the ‘human interpreted reality’ of the data set and not the ‘perceived visual representation’ should be segmented. For example, if we encountered scattered radiation artefacts, represented through bright or dark streaks through the volume or cupping artefacts from beam hardening, we tried to annotate the real specimen and not the distorted image.
Furthermore, we annotated each segment individually. This resulted in some cases where one voxel was annotated as belonging to multiple segments. For example, if the resolution of the reconstruction (approx. 0.33 mm3 per voxel) was not high enough to represent a thin sheet of metal, it was not possible to represent this reality in an annotation dataset with only voxel resolution. In such cases, the corresponding voxels were annotated as belonging to several segments. To create adequate training data for the FFN, we had to combine all annotated segments into one single volume which did not allow voxels to belonging to multiple segments.
Therefore, we manually sorted the annotated segments in a preprocessing step in such a way that we could just apply a voxelwise ‘greater than’ operation for each added segment to achieve a reasonable result. Other mechanisms to approach this issue shall be evaluated in the future. Figure 9 shows a slice of the fully segmented training dataset.
3 Results and Discussion
Within this work we trained three different FFN models, namely one for each of the corn and the marbles bulk datasets, and one of the XXL-CT dataset. For the training process the earlier described ground truth data was used. The training for the XXL-CT dataset was stopped after approximately 13 million iterations, which took about 30 days on one NVIDIA Tesla V100-SXM2-32GB GPU. The bulk material datasets have been trained for approximately 11 million iterations (or about 20 days) on the same hardware. Due to time and resource constraints the training was stopped.
3.1 Bulk Material
Figures 10 and 11 are showing the results of the segmentation of the corn and marbles bulk material datasets, respectively. Most of the instances are reasonably well segmented. Next to some slight oversegmentation two typical error cases can be observed.
The visible black horizontal and vertical stripes are likely an artefact of the FoV movement of the FFN segmentation process. These stripes are important in voxel wise instance segmentation, but have no influences to the original application of FFNs, where the connection of neuron was researched. A post-processing step based on morphological closing using a \(3\times 3\times 3\) box mask was used to remove these segmentation artefacts.
The second observed error relates to the existence of completely missing segments in the result. Their absence can be explained by the yet usage of the default unmodified FFN seeding algorithm which does not always create a seed for all instances connected to the sub-volume border. Also segments which have less than 1000 voxels are currently automatically discarded, which results in losing small objects at the boundary of the dataset.
As mentioned in Sect. 2.3.1 the usage of a classical image-processing pipeline for annotation leads to inconsistencies in some edge cases. A visual inspection of the FFN segmentation results did not provide evidence to assume that the network was strongly influenced by these incorrect annotations and tried to recreate them. The proportion of these inconsistencies in the training data was too low. However, an improvement in the annotation quality for subsequent investigations would certainly be advisable in order to minimize this influence and analyse its scope on the result.
3.1.1 Correlation Matrix
The ‘segment correlation figures’ (see Fig. 12) shows how well the results of two different segmentation algorithms match. In this case the ground truth data was generated by the classical image processing algorithm described in Sect. 2.3.1. It is depicted on the vertical axis and the result of the FFN segmentation is depicted on the horizontal axis.
Each row is assigned to one ‘reference segment’ \(S_{R}(i)\) and each column is assigned to a ‘detected segment’ \(S_{D}(j)\). Where ‘reference segment’ refers to the manually annotated segments of the ground truth and ‘detected segment’ refers to the resulting segmentation of the FFN algorithm. The value of each cell corresponds to the well-known “ Intersection over Union’ (IoU) score of two segments \(S_{R}(i)\) and \(S_{D}(j)\). If these two segments yield a complete overlap (meaning that their segmentations match completely) the value is equal to 1.0, otherwise if two compared segments do not share at least one common voxel the value will be 0.0.
The rows were sorted in descending order by the count of voxels of their corresponding segments. Consequently the top rows correspond to the largest segments. The columns have been sorted by searching for the best match for each reference row, i.e. the segment with the highest IoU value in this row which was not already assigned to a different reference segment. Detected segments unmatched to a reference segment have been sorted by their voxel count. We excluded segments with an voxel count of less than 100 voxels to reduce the size of the matrix.
Hence, a perfect segmentation in relation to the reference segmentation should be reflected by a quadratic correlation matrix which contains the same count of rows and columns, and thus the same amount of reference segments and detected segments. In addition, all correlation value outside the main diagonal should contain IoU values of 0.0. Values on the main diagonal should have IoU values of 1.0.
However, in realistic application examples investigated here the row and column count will differ. An over-segmentation will result in more columns than rows. Boundary errors will result in suboptimal correlation values. Rows with multiple horizontal values either denote an over-segmentation of the respective detected segment or a reference segment which has accidently been split into multiple segments. In contrast, vertical lines indicate segments spanning multiple reference or merged segments. Breaks in the diagonal line indicate reference segments without a good match in the segmentation result.
Figure 12b shows an example result of the segmentation of a marble test dataset compared with the model trained on the marble training dataset. The desired bright diagonal line is clearly visible, indicating that most of the reference segments have been well detected. The missing breaks and the premature ending of the diagonal line indicate that some tiny reference segments have not been detected at all.
It can also be seen that the reference segments are either almost completely segmented or remain completely undetected. The splitting of a reference segment by over-segmentation into areas of approximately the same size hardly occurs. This can be observed from the fact that there are little pronounced horizontal lines corresponding to a weak reference segment. This behavior can also be observed in the other measurements, as for example with the corn dataset (see Fig. 12a). The results are comparable in this regard.
3.1.2 Transferability of Models Trained on Bulk Material
As already mentioned, one of the beneficial properties of the investigated FFNs is that they do not explicitly contain any knowledge about the different classes of the elements to be segmented. Hence, we want to test this hypothesis by applying the models that have been trained on one dataset (e.g. the corn data) to another dataset (e.g. the marble data). In the case of simple transferability, the results should be of comparable quality. Thus, the FFN model previously trained on the corn examples and applied to the marble data yields acceptable segmentation results, as can exemplarily be seen in Fig. 13 (see Fig. 14 for corresponding correlation matrix).
Nevertheless, a transferability in the other direction, meaning to apply a model trained on the marble data used to segment corn, was not yet feasible for the current state of training (see Fig. 13d).
Another experiment (see Fig. 15) shows a similar result. Here we tried to segment the bulk material dataset of buttons (see Fig. 3d) with the FFN model trained on corn and marbles respectively. As can be seen, the resulting segmentation using the FFN model trained on corn (Fig. 15b) seems to be reasonable (as it is the case in the example of Fig. 13b using the same model). The segmentation result of the FFN model trained on the marble dataset (see Fig. 15c) lacks again with respect to transferability, an essential property that we originally expected from the FFN segmentation approaches. This should be taken into account when transferring pre-trained models for the segmentation of unrelated object types with different physical and geometrical properties.
However, our experiments were carried out on small datasets with varying feature shapes and instance counts. A fact which certainly had an influence on the segmentation quality, which we want to investigate in future experiments.
Segmentation results of FFN models trained on images of one dataset and then applied to images of another dataset. b shows reasonable results for the segmentation of the marble data using the corn model. On the other side the corn segmentation performed by a model trained on the marble dataset lacks in quality (d)
Correlation matrix of the segmentation result for the marble data run on a model trained with the corn training dataset (see Fig. 13b). The rows correspond to ‘reference segments’ sorted top to bottom by increasing voxel count of the segmentation. The columns correspond to ‘detected segments’ and are sorted by the maximum IoU
Results of FFN segmentation of the XXL-CT training dataset. a and e show orthogonal slices of the training dataset. The first layer in XY-orientation view provide a rough overview of the dataset, while the second view shows a particularly challenging layer in the YZ-orientation. The green lines mark the positions of the corresponding slice in the other orientation. b and f depict the annotation provided by a human. The result of the related FFN segmentation is shown in c and g. Finally, d and h show the segmented slices after a morphological closing step
Result of FFN segmentation of the XXL-CT testing dataset. a and e show slices of the training dataset. The first layer in XY-orientation gives a rough overview of the dataset, while the second view shows a particularly challenging layer in the YZ-orientation. The green lines mark the position of the slices in the other orientations. b and f depict the annotation provided by a human. The result of the FFN-based segmentation is shown in c and g. Finally, d and h show the segmented slices after a morphological closing step
3.2 XXL-CT
Figures 16a to f exemplarily depict the results of the FFN segmentation of the XXL-CT data based on the training manually annotated dataset, whereas Fig. 17a to h show results for the testing dataset (for which is no full manual segmentation available yet). As can be seen in Fig. 16h, in some regions the segmentation results mimics the manually segmented ground truth quite well, as especially in some tricky parts in which even a human expert needs semantic references to distinguish between different segments.
Figure 17g shows examples of over-segmentation in the testing dataset. The long streaks of segments have been also observed in segmentations of earlier training stages of the training dataset and are known faults from the original FFN implementation [12], but have not been relevant in that application. Some segments of visible objects are missing due to bad or missing seeds, or parameter settings which only keep segments with a minimum of 1000 voxels. Other segments, such as the bright circular pressure vessel on the border of the training and testing data (see Fig. 17d, bottom ) are over-segmented at the current state of training.
As can be seen in Fig. 17c, some of the thicker parts of the connecting struts have not been segmented by the FFN. This might be due to the fact that these kind of struts are either not included in the training dataset, or they have not been segmented due to missing or bad seed values. But as our transferability experiments suggest (see Sect. 3.1.2 and Fig. 15), the training process might interoperate some object structures implicitly into the network model, as it is common for convolution network layers which are the core of FFNs.
Figure 18a shows the correlation matrix of the results of the FFN based segmentation of the human annotated training dataset using the FFN model trained on the same dataset. In addition to a weakly pronounced main diagonal, indicating a lower segmentation quality, the horizontal bands on the left edge are particularly noticeable. These are relatively large reference segments which are broken down into smaller segments by over-segmentation. Examples of this over-segmentation can be seen in Fig. 16c in the pressure tank located at the top of the picture.
Figure 18b shows the correlation matrix of the testing dataset with the corresponding ground truth. Because the yet unfinished state of the testing dataset ground truth (currently there are only 62 segments annotated, see Sect. 2.3.2) many segments could not be related to a reference segment.
3.2.1 Transferability of XXL-CT Trained Model
Similar to the bulk material experiments (see Sect. 3.1.2) we performed some transferability experiments with the XXL-CT trained model. As can be seen in Fig. 19, the XXL-CT trained FFN-model struggles with the complete different task to segment the bulk material datasets. Beside the earlier mentioned reasons for the bulk material datasets another difficulty was observed in this experiment, namely the bulk material datasets and the XXL-CT datasets have been acquired on different CT systems. Thus, the corresponding differences in signal to noise ratio, the used reconstruction algorithm (cone beam filtered back-projection vs. stacked fan beam algebraic reconstruction), or the grey-value conversion might already be sufficient enough to disturb a successful segmentation.
The most challenging bulk material dataset consisting of extruded pasta depicting dinosaurs (see Fig. 3c) was used for this experiments. This dataset has proven to be quite challenging regarding the segmentation by the conventional image processing pipeline (see Sect. 2.3.1), thus it was not possible to generate training or ground truth data. In contrast to the other bulk material datasets, the pasta dataset depicts branching segments which are quite similar to the thin walled riveted metal sheets of the XXL-CT dataset. As can be seen in Fig. 19l, the segmentation quality of the pasta data set is quite insufficient. But compared to the other bulk material datasets it is the most plausible result. This supports the our assumption that the so-far trained FFN model somewhere implicitly contains the actual object structure.
Segmentation result of the corn, marbles, buttons and pasta bulk material, using a FFN-model trained on XXL-CT data. a, d, g and j Depict the achieved segmentation of corn, marbles buttons and pasta. b, e, h and k depict the input data. c, f, i and l Show the achieved segmentation overlayed onto input data in order to enhance the spatial findability
4 Conclusions
The following conclusions can be drawn from the experiments and results described in the previous sections: Flood filling networks (FFNs) are generally suitable for the segmentation of CT datasets, for both bulk material as well as ‘one-lot’ data, such as the parts of the airplane. Due to its architecture and structure of the underlaying convolutional neural networks, only minor modifications need to be addressed in order to segment large scale XXL-CT volume datasets. As it is common with most neural networks, FFNs also need a large count of ground truth records of suitable quality and quantity. The experiments we carried out with different types of bulk material data (corn, glass marbles, plastic buttons, pasta) and XXL-CT data indicate that for NDT a direct transfer from one type of test object to the next is possible in some cases, but not guaranteed.
Further tests and training with mixed data sets must prove this robustness. FFNs have a tendency to over-segment on small or unknown data sets. To join the resulting segments, suitable, possibly interactive, mechanisms must therefore be developed.
References
Chen, L., Papandreou, G., Kokkinos, I., Murphy, K., Yuille, A.L.: Deeplab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 40(4), 834–848 (2018)
Chen, L.C., Papandreou, G., Schroff, F., Adam, H.: Rethinking atrous convolution for semantic image segmentation. arXiv:1706.05587 (2017)
Chollet, F.: Xception: Deep learning with depthwise separable convolutions. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1800–1807 (2016)
Claußen, J., Woerlein, N., Uhlman, N., Gerth, S.: Quantification of seed performance: non-invasive determination of internal traits using computed tomography. In: 14th International Conference on Precision Agriculture (2018)
Dai, J., He, K., Sun, J.: Instance-aware semantic segmentation via multi-task network cascades. In: CVPR (2016)
Girshick, R.: Fast r-CNN. In: 2015 IEEE International Conference on Computer Vision (ICCV). IEEE (2015). https://doi.org/10.1109/iccv.2015.169
Girshick, R., Donahue, J., Darrell, T., Malik, J.: Rich feature hierarchies for accurate object detection and semantic segmentation. In: 2014 IEEE Conference on Computer Vision and Pattern Recognition. IEEE (2014). https://doi.org/10.1109/cvpr.2014.81
Gregor, K., Danihelka, I., Graves, A., Wierstra, D.: Draw: A recurrent neural network for image generation. arXiv:1502.04623 (2015)
He, K., Gkioxari, G., Dollár, P., Girshick, R.: Mask r-cnn. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 2961–2969 (2017)
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 770–778 (2016)
Januszewski, M., Kornfeld, J., Li, P.H., Pope, A., Blakely, T., Lindsey, L., Maitin-Shepard, J., Tyka, M., Denk, W., Jain, V.: High-precision automated reconstruction of neurons with flood-filling networks. bioRxiv (2017). https://doi.org/10.1101/200675
Januszewski, M., Kornfeld, J., Li, P.H., Pope, A., Blakely, T., Lindsey, L., Maitin-Shepard, J., Tyka, M., Denk, W., Jain, V.: High-precision automated reconstruction of neurons with flood-filling networks. Nat. Methods 15(8), 605–610 (2018)
Januszewski, M., Maitin-Shepard, J., Li, P., Kornfeld, J., Denk, W., Jain, V.: Flood-filling networks. arXiv:1611.00421 (2016)
Krähenbühl, P., Koltun, V.: Efficient inference in fully connected crfs with gaussian edge potentials. In: Proceedings of the 24th International Conference on Neural Information Processing Systems, NIPS’11, pp. 109–117. Curran Associates Inc., USA (2011)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. Commun. ACM 60(6), 84–90 (2017). https://doi.org/10.1145/3065386
LeCun, Y.: Generalization and network design strategies. Connect. Perspect. 19, 143–155 (1989)
LeCun, Y., Boser, B., Denker, J.S., Henderson, D., Howard, R.E., Hubbard, W., Jackel, L.D.: Backpropagation applied to handwritten zip code recognition. Neural Comput. 1(4), 541–551 (1989). https://doi.org/10.1162/neco.1989.1.4.541
Li, P.H., Lindsey, L.F., Januszewski, M., Zheng, Z., Bates, A.S., Taisz, I., Tyka, M., Nichols, M., Li, F., Perlman, E., Maitin-Shepard, J., Blakely, T., Leavitt, L., Jefferis, G.S., Bock, D., Jain, V.: Automated reconstruction of a serial-section EM drosophila brain with flood-filling networks and local realignment. bioRxiv (2019). https://doi.org/10.1101/605634
Li, Y., Kaiser, L., Bengio, S., Si, S.: Area attention. In: Proceedings of the 36th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 97, pp. 3846–3855. PMLR (2019)
Liang-Chieh, C., Papandreou, G., Kokkinos, I., murphy, k., Yuille, A.: Semantic image segmentation with deep convolutional nets and fully connected CRFs. In: International Conference on Learning Representations. Institute of Electrical and Electronics Engineers (IEEE), San Diego, United States (2015). https://doi.org/10.1109/tpami.2017.2699184
Lin, T.Y., Dollar, P., Girshick, R., He, K., Hariharan, B., Belongie, S.: Feature pyramid networks for object detection. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE (2017). https://doi.org/10.1109/cvpr.2017.106
Lin, T.Y., Goyal, P., Girshick, R., He, K., Dollar, P.: Focal loss for dense object detection. In: 2017 IEEE International Conference on Computer Vision (ICCV). IEEE (2017). https://doi.org/10.1109/iccv.2017.324
Lin, T.Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ramanan, D., Dollár, P., Zitnick, C.L.: Microsoft COCO: common objects in context. In: Computer Vision—ECCV 2014, pp. 740–755. Springer, Berlin (2014)
Liu, C., Chen, L.C., Schroff, F., Adam, H., Hua, W., Yuille, A.L., Fei-Fei, L.: Auto-deeplab: Hierarchical neural architecture search for semantic image segmentation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (2019). https://doi.org/10.1109/cvpr.2019.00017
Long, J., Shelhamer, E., Darrell, T.: Fully convolutional networks for semantic segmentation. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3431–3440 (2015)
Mnih, V., Heess, N., Graves, A., kavukcuoglu, K.: Recurrent models of visual attention. In: Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems, vol. 27, pp. 2204–2212. Curran Associates Inc., New York (2014)
Pieper, S., Halle, M., Kikinis, R.: 3d slicer. In: 2004 2nd IEEE International Symposium on Biomedical Imaging: Nano to Macro (IEEE Cat No. 04EX821), vol. 1, pp. 632–635 (2004). https://doi.org/10.1109/ISBI.2004.1398617
Redmon, J., Divvala, S., Girshick, R., Farhadi, A.: You only look once: unified, real-time object detection. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE (2016). https://doi.org/10.1109/cvpr.2016.91
Redmon, J., Farhadi, A.: Yolo9000: Better, faster, stronger. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 6517–6525 (2016)
Redmon, J., Farhadi, A.: Yolov3: an incremental improvement. arXiv:1804.02767 (2018)
Reims, N., Schulp, A., Böhnel, M., Larson, P., EZRT, F.E.R.: An XXL-CT-scan of an xxl tyrannosaurus rex skull. In: 19th World Conference on Non-destructive Testing (2016)
Ren, S., He, K., Girshick, R.B., Sun, J.: Faster r-cnn: towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1137–1149 (2015)
Ronneberger, O., Fischer, P., Brox, T.: U-net: convolutional networks for biomedical image segmentation. In: Lecture Notes in Computer Science, pp. 234–241. Springer, Berlin (2015)
Russakovsky, O., Li, L.J., Fei-Fei, L.: Best of both worlds: human-machine collaboration for object annotation. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE (2015). https://doi.org/10.1109/cvpr.2015.7298824
Salamon, M., Reims, N., Böhnel, M., Zerbe, K., Schmitt, M., Uhlmann, N., Hanke, R.: Xxl-ct capabilities for the inspection of modern electric vehicles. In: 19th World Conference on Non-Destructive Testing (2016)
Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. CoRR abs/1409.1556 (2014)
Szegedy, C., Ioffe, S., Vanhoucke, V., Alemi, A.A.: Inception-v4, inception-resnet and the impact of residual connections on learning. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, AAAI’17, pp. 4278–4284. AAAI Press (2017)
Szegedy, C., Wei Liu, Yangqing Jia, Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., Rabinovich, A.: Going deeper with convolutions. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1–9 (2015). https://doi.org/10.1109/CVPR.2015.7298594
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Lu, Polosukhin, I.: Attention is all you need. In: Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 30, pp. 5998–6008. Curran Associates Inc., New York (2017)
Wang, M., Hua, X.S.: Active learning in multimedia annotation and retrieval: a survey. ACM Trans. Intell. Syst. Technol. 2(2), 10:1–10:21 (2011)
Yang, Y., Loog, M.: Single shot active learning using pseudo annotators. Pattern Recogn. 89, 22–31 (2019). https://doi.org/10.1016/j.patcog.2018.12.027
Zoph, B., Vasudevan, V., Shlens, J., Le, Q.V.: Learning transferable architectures for scalable image recognition. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8697–8710 (2018)
Acknowledgements
This work was supported by the Bavarian Ministry for Economic Affairs, Infrastructure, Transport and Technology through the Center for Analytics Data Applications (ADA-Center) within the framework of “BAYERN DIGITAL II”
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gruber, R., Gerth, S., Claußen, J. et al. Exploring Flood Filling Networks for Instance Segmentation of XXL-Volumetric and Bulk Material CT Data. J Nondestruct Eval 40, 1 (2021). https://doi.org/10.1007/s10921-020-00734-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10921-020-00734-w