1 Introduction

The treatment of boundary-value problems in curved domains has been a subject of growing interest during the past decades in the numerical analysis community. Indeed, it is well-known that meshing curved domains with piecewise linear elements might lead to a drastic convergence order reduction, especially in the framework of very high-order accurate schemes, if no particular technique is employed to recover the optimal order. In the context of the discontinuous Galerkin (DG) method [22], several strategies developed initially for the finite element method (FEM) have been implemented. For example, the popular isoparametric elements method, introduced by Bassi and Rebay [4], requires the construction of a mesh with curved elements on the boundary using a local polynomial/spline representation together with non-constant Jacobian transformations from the reference element. In addition, extensions have been proposed using the so-called isogeometric analysis approach in the context of the FEM [23] with rational representations such as non-uniform rational B-splines (NURBS) [19], while isoparametric elements have also been used in the context of DG methods [5, 18]. However, these approaches suffer from significant drawbacks from a computational point of view. An inaccurate treatment of curved meshes causes accuracy degradation, which depends on the element shape, the mapping function, and the reference polynomial space [6, 28]. Moreover, meshing with curved element is a challenging geometric problem where ineligible cells can be produced (inverted cell, causing severe degradation of element quality, shrunk cell, curvature propagation further inwards, non-regular edge binding, for example) [1, 30, 34]. On the other hand, the computational effort to connect complex geometries with curved elements is considerable, eventually even more expensive than the solver itself due to non-linear mapping functions from the reference element. The direct reconstruction method (DRM), which uses curved elements, was proposed to improve efficiency by reducing computational costs [35, 36].

Alternative methods have been proposed in an attempt to circumvent the limitations caused by the use of curved elements [24, 32]. In the last reference, the authors propose a curvature based wall boundary condition for the Euler equation on unstructured grids in the context of the finite volume method. In [24] the authors present a technique based on a curvature boundary condition approach, in replacement of reflecting boundary conditions, for implementing solid wall boundary conditions on curved boundaries for the compressible Euler equations within the framework of the DG method. However, this method can only be formulated for slip-wall boundary conditions and the work is limited to 2D geometries.

In the last decade, a new paradigm has been proposed independently by two groups of researchers: the shifted boundary method (SBM) [26, 27] and the reconstruction for off-site data [11]. The main idea consists in definitively separating the real/physical domain to the numerical one with a surrogate/numerical boundary. Then a mechanism transforms the boundary condition prescribed on the physical boundary into an equivalent boundary condition on the surrogate boundary, up to a given degree of accuracy. The SBM has been developed within the framework of the classical finite element method and received very much attention from the computational fluid mechanics community [2, 7, 8, 10, 25, 29].

The alternative approach, the reconstruction for off-site data (ROD), has been recently proposed in the context of the finite volume method [12,13,14,15,16,17]. The method aims to overcome the difficulties of curved mesh approaches by discretising the physical domain with polygonal meshes constructed from the conventional meshing algorithms, where piecewise linear elements approximate the arbitrary curved boundary. To recover the optimal order of convergence, the ROD method employs specific polynomial reconstructions constrained for the prescribed boundary conditions on the physical boundary. Therefore, the method does not require the generation of curved meshes to fit the physical boundary or complex nonlinear transformations, while preserving the optimal order becomes simple and practical. The method has been later extended for the finite difference method on Cartesian grids [9]. The present work addresses the extension of the ROD method for the DG context, which is an important contribution to the numerical analysis community.

The remaining sections of the article are organised as follows. First, Sect. 2 presents the DG method considered in the present study, while Sect. 3 deals with the inclusion of the ROD method into the DG formulation. Then, the iterative procedure is present in Sect. 4, connecting the DG solver and the ROD procedure. Finally, the numerical experiments and results are reported in Sect. 5, and the article is completed with the conclusions in Sect. 6.

2 The Discontinuous Galerkin (DG) Method

Let \(\varOmega \subset {\mathbb {R}}^2\) be a bounded open set with a smooth boundary \(\partial \varOmega \) and \({\varvec{x}}=\left( x,y\right) \) denote a generic point in \(\mathbb R^2\). We seek function \(u = u({\varvec{x}})\), solution of the reaction–diffusion problem

$$\begin{aligned} {\mathcal {E}}\left[ u\right] \left( {\varvec{x}}\right)\equiv & {} -\nabla ^2 u\left( {\varvec{x}}\right) + c u\left( {\varvec{x}}\right) -f\left( {\varvec{x}}\right) = 0, \quad {\varvec{x}} \in \varOmega , \end{aligned}$$
(1)
$$\begin{aligned} {\mathcal {B}}\left[ u\right] \left( {\varvec{x}}\right)\equiv & {} \alpha \left( {\varvec{x}}\right) u\left( {\varvec{x}}\right) +\beta \left( {\varvec{x}}\right) \nabla u\left( {\varvec{x}}\right) \cdot {\varvec{n}}\left( {\varvec{x}}\right) -g\left( {\varvec{x}}\right) =0, \quad {\varvec{x}} \in \partial \varOmega , \end{aligned}$$
(2)

where c stands for a positive constant number, f is a source term, and \(\alpha ,\beta \) characterize the contribution of the boundary condition. In order to use a mixed formulation, consider the vector function \({\varvec{q}}= \left( q_x, q_y\right) ^\text {T}\) defined as the gradient of u, i.e. \({\varvec{q}}\left( {\varvec{x}}\right) = \nabla u\left( {\varvec{x}}\right) \). Thus, we may write \(\nabla ^2 u\left( {\varvec{x}}\right) = \nabla \cdot \nabla u\left( {\varvec{x}}\right) = \nabla \cdot {\varvec{q}} ({\varvec{x}} )\). Replacing this expression in (1), the solution is sought for the equivalent problem

$$\begin{aligned} - \nabla \cdot {\varvec{q}}\left( {\varvec{x}}\right) + c u\left( {\varvec{x}}\right)&= f\left( {\varvec{x}}\right) , \end{aligned}$$
(3)
$$\begin{aligned} {\varvec{q}}\left( {\varvec{x}}\right)&= \nabla u\left( {\varvec{x}}\right) . \end{aligned}$$
(4)

2.1 Discretisation

The physical domain \(\varOmega \) is meshed with K non-overlapping straight-sided triangles \(T^k, k=1,\ldots ,K\), leading to an approximate computational domain \(\varOmega _h\) given as

$$\begin{aligned} \varOmega \approx \varOmega _h= \bigcup _{k=1}^K T^k. \end{aligned}$$
(5)

The triangulation \({\mathcal {T}}_h = \left\{ T^k, k=1,\ldots ,K\right\} \) is assumed to be conformed where the intersection of two elements is either a complete edge, a vertex or the empty set. The space parameter h represents the maximum element diameter, namely

$$\begin{aligned} h= \max _{T^k \in {\mathcal {T}}_h } \{h_k\}, \qquad h_k= \sup _{P_1,P_2 \in T^k} \left\| P_1-P_2\right\| . \end{aligned}$$

The triangulation is also assumed to be regular [21] in the sense that the quotient between \(h_k\) and the maximum diameter of a ball inscribed in each element \(T^k \in {\mathcal {T}}_h\) has an upper bound. Given an element \(T^k\), denote as \(I^k\) the index set of the elements \(T^\ell \) that share a common edge \(e^{k\ell }\) and by \(I^B\) the index set of elements which have an edge on the boundary. Normal vector \({\varvec{n}}^{k\ell }\), \(\ell \in I^k\), is pointed outward of element \(T^k\) and \({\varvec{n}}^{\ell k}=-{\varvec{n}}^{k\ell }\).

To provide a numerical approximation \(u_h\) for problem (1)–(2), consider the following decomposition

$$\begin{aligned} u_h\left( {\varvec{x}}\right) = \bigoplus _{k=1}^K u_h^k\left( {\varvec{x}}\right) \in {\mathcal {V}}_h, \end{aligned}$$
(6)

where the discrete space is given by

$$\begin{aligned} {\mathcal {V}}_h = \{u_h \in L^2\left( \varOmega _h\right) : u_h^k = u_h|_{T^k} \in {\mathcal {P}}_N\left( T^k\right) , \forall T^k \in {\mathcal {T}}_h\}, \end{aligned}$$

with \({\mathcal {P}}_N\left( T^k\right) \) denoting the space of polynomials of degree less than or equal to N in element \(T^k\).

In each element \(T^k\), the local solution \(u_h^k\) has a polynomial decomposition with the two-dimensional Lagrange polynomials

$$\begin{aligned} {\varvec{x}} \in T^k \in {\mathcal {T}}_h: \quad u_h^k\left( {\varvec{x}}\right) = \sum _{i=1}^{N_p} u^k_i \ell _i^k\left( {\varvec{x}}\right) , \end{aligned}$$
(7)

where \(u^k_i=u_h^k\left( {\varvec{x}}_i^k\right) \) are the nodal values of the Lagrange polynomials basis \(\ell _i^k\left( {\varvec{x}}\right) \) at points \({\varvec{x}}_i^k\in T^k\), \(i=1,\ldots ,N_p\), with \(N_p=\left( N+1\right) \left( N+2\right) /2\). Moreover, vector \({\varvec{u}}^k = \left[ u^k_1,\ldots ,u^k_{N_p}\right] \) gathers the \(N_p\) nodal values. The location of points \({\varvec{x}}_i^k\) in element \(T^k\) is determined with an optimised explicit Warp & Blend construction procedure [33].

The DG discretisation of vector function \({\varvec{q}}\) is also introduced by taking \(q^k_{h,x},q^k_{h,y}\in \mathcal {V}_h\) and the auxiliary variable discretisation expressed as \({\varvec{q}}_h^k= \left( q_{h,x}^k, q_{h,y}^k\right) ^\text {T}\) with

$$\begin{aligned} {\varvec{x}} \in T^k \in {\mathcal {T}}_h: \quad q^k_{h,\zeta }\left( {\varvec{x}}\right) =\sum _{i=1}^{N_p} q^k_{i,\zeta }\ell _i^k\left( {\varvec{x}}\right) , \quad \zeta =x,y. \end{aligned}$$
(8)

Vectors \({\varvec{q}}^k_\zeta =\left[ q^{k}_{1,\zeta },\ldots ,q^{k}_{N_{p},\zeta }\right] \), \(\zeta =x,y\), gather the nodal values of polynomials \(q^k_{h,\zeta }\).

2.2 The Mixed Formulation

The numerical method is based on the principle that the local residuals of expressions

$$\begin{aligned} -\nabla \cdot {\varvec{q}}_h^k\left( {\varvec{x}}\right) + c u_h^k\left( {\varvec{x}}\right) - f\left( {\varvec{x}}\right) \qquad \text {and}\qquad {\varvec{q}}_h^k\left( {\varvec{x}}\right) - \nabla u_h^k\left( {\varvec{x}}\right) \end{aligned}$$

are orthogonal to the Lagrange polynomials with respect to the discrete \(L^2\) inner product on \({\mathcal {V}}_h\) given by

$$\begin{aligned} \left( u,v\right) _{L^2\left( \varOmega _h\right) } = \sum _{k=1}^K \left( u,v\right) _{L^2\left( T^k\right) }, \end{aligned}$$

where \(\left( u,v\right) _{L^2\left( T^k\right) }\) denotes the usual inner product on \(L^2\left( T^k\right) \). Therefore, a discrete solution \(\left( u_h,{\varvec{q}}_h\right) \) is sought for Equations (3) and (4) that satisfy

$$\begin{aligned} - \left( \nabla \cdot {\varvec{q}}^k_{h}, \ell _i^k \right) _{L^2\left( {T^k}\right) } +c \left( u_h^k , \ell _i^k\right) _{L^2\left( {T^k}\right) }&= \left( f, \ell _i^k \right) _{L^2\left( {T^k}\right) }, \end{aligned}$$
(9)
$$\begin{aligned} \left( {\varvec{q}}^k_{h}, \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix}\right) _{L^2\left( {T^k}\right) } - \left( \nabla u_h^k,\begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix}\right) _{L^2\left( {T^k}\right) }&= 0. \end{aligned}$$
(10)

2.2.1 Discretisation of Equation (9)

Integrating Eq. (9) by parts yields

$$\begin{aligned} - \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot {\varvec{q}}^{k\ell }_{h}\left( {\varvec{x}}\right) \ell _i^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} + \left( {\varvec{q}}^k_{h}, \nabla \ell _i^k \right) _{L^2\left( {T^k}\right) } + c \left( u_h^k, \ell _i^k \right) _{L^2\left( {T^k}\right) } = \left( f, \ell _i^k\right) _{L^2\left( {T^k}\right) }, \end{aligned}$$

where \({\varvec{q}}^{k\ell }_{h}\left( {\varvec{x}}\right) \) is the polynomial \({\varvec{q}}^{k}_{h}\left( {\varvec{x}}\right) \) defined on the edge \(e^{k\ell }\). At that stage, the normal outward flux needs to be computed using a numerical flux, for which the approximation

$$\begin{aligned} \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot {\varvec{q}}^{k\ell }_{h}\left( {\varvec{x}}\right) \ell _i^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} \approx \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot {\varvec{q}}^{*k\ell }_{h}\left( {\varvec{x}}\right) \ell _i^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} \end{aligned}$$

is considered, where \({\varvec{q}}^{*k\ell }_{h}\left( {\varvec{x}}\right) ={\varvec{q}}^{*\ell k}_{h}\left( {\varvec{x}}\right) \) is a symmetric numerical flux on the interface \(e^{k\ell }\), to be defined in the next section. The weak formulation then reads

$$\begin{aligned}&- \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot {\varvec{q}}^{ *k\ell }_{h}\left( {\varvec{x}}\right) \ell _i^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} + \left( {\varvec{q}}^k_{h}, \nabla \ell _i^k \right) _{L^2\left( {T^k}\right) } +c \left( u_h^k, \ell _i^k \right) _{L^2\left( {T^k}\right) } = \left( f, \ell _i^k \right) _{L^2\left( {T^k}\right) }. \end{aligned}$$

Integrating by parts again, the strong formulation is devised, given as

$$\begin{aligned}&- \left( \nabla \cdot {\varvec{q}}^k_{h}, \ell _i^k \right) _{L^2\left( {T^k}\right) } + \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \bigg ( {\varvec{q}}_{h}^{k\ell }\left( {\varvec{x}}\right) -{\varvec{q}}^{*k\ell }_{h}\left( {\varvec{x}}\right) \bigg ) \ell _i^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} +c \left( u_h^k, \ell _i^k \right) _{L^2\left( {T^k}\right) } = \left( f, \ell _i^k\right) _{L^2\left( {T^k}\right) }. \end{aligned}$$

Finally, the discrete formulation for Eq. (9) is given as

$$\begin{aligned}&S_{x}^k{\varvec{q}}^k_x + S_{y}^k{\varvec{q}}^k_y+ \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \bigg ( {\varvec{q}}_{h}^{k\ell }\left( {\varvec{x}}\right) -{\varvec{q}}^{ *k\ell }_{h}\left( {\varvec{x}}\right) \bigg ) \varvec{\ell }^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}} + c M^k {\varvec{u}}^k = M^k {\varvec{f}}^k, \end{aligned}$$

where

$$\begin{aligned} M_{ij}^k&= \left( \ell _i^k,\ell _j^k \right) _{L^2\left( T^k\right) },\quad S_{x,ij}^k = \left( \ell _i^k,\partial \ell _j^k /\partial x \right) _{L^2\left( T^k\right) },\\ S_{y,ij}^k&= \left( \ell _i^k,\partial \ell _j^k /\partial y \right) _{L^2\left( T^k\right) }, \quad \varvec{\ell }^k\left( {\varvec{x}}\right) = \left[ \ell _1^k\left( {\varvec{x}}\right) ,\ldots ,\ell _{N_{p}}^k\left( {\varvec{x}}\right) \right] , \end{aligned}$$

with \(i,j=1, \ldots , N_p\).

2.2.2 Discretisation of Equation (10)

Integrating Eq. (10) by parts yields

$$\begin{aligned} \left( {\varvec{q}}^k_{h}, \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} \right) _{L^2\left( {T^k}\right) } = \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} u_h^{k\ell } \mathop {}\!\text {d}{\varvec{x}} -\left( u^k_{h}, \nabla \cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix}\right) _{L^2\left( {T^k}\right) }, \end{aligned}$$

where \(u^{k\ell }_{h}\left( {\varvec{x}}\right) \) is the polynomial \(u^{k}_{h}\left( {\varvec{x}}\right) \) defined on the edge \(e^{k\ell }\). At that stage, the normal outward flux needs to be computed using a numerical flux, for which the approximation

$$\begin{aligned} \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} u_h^{k\ell } \mathop {}\!\text {d}{\varvec{x}} \approx \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} u_h^{*k\ell } \mathop {}\!\text {d}{\varvec{x}} \end{aligned}$$

is considered, where \(u^{*k\ell }_{h}\left( {\varvec{x}}\right) =u^{*\ell k}_{h}\left( {\varvec{x}}\right) \) is a symmetric numerical flux defined on the interface \(e^{k\ell }\), to be defined in the next section. The weak formulation then reads

$$\begin{aligned} \left( {\varvec{q}}^k_{h}, \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix}\right) _{L^2\left( {T^k}\right) } = \sum _{\ell \in I^k} \int _{e^{k\ell }} {\varvec{n}}^{k\ell }\cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} u_h^{*k\ell } \mathop {}\!\text {d}{\varvec{x}}-\left( u^k_{h}, \nabla \cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} \right) _{L^2\left( {T^k}\right) }. \end{aligned}$$

Integrating by parts again, the strong formulation is devised, given as

$$\begin{aligned} \left( {\varvec{q}}^k_{h}, \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix}\right) _{L^2\left( {T^k}\right) } = \left( \nabla u^k_{h}, \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} \right) _{L^2\left( {T^k}\right) } - \sum _{\ell \in I^k} \int _{e^{k\ell }}{\varvec{n}}^{k\ell }\cdot \begin{bmatrix}\ell _i^k\\ \ell _i^k\end{bmatrix} \left( u_h^{k\ell } - u_h^{*k\ell }\right) \mathop {}\!\text {d}{\varvec{x}}. \end{aligned}$$

Finally, the discrete formulation for Eq. (10) is given as

$$\begin{aligned} M^k {\varvec{q}}^k_{x}= & {} S_x^k {\varvec{u}}^k -\sum _{\ell \in I^k} \int _{e^{k\ell }} n^{k\ell }_x \left( {\varvec{u}}^{k\ell }_{h}\left( {\varvec{x}}\right) - {\varvec{u}}^{*k\ell }_{h}\left( {\varvec{x}}\right) \right) \varvec{\ell }^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}}, \\ M^k {\varvec{q}}^k_{y}= & {} S_y^k {\varvec{u}}^k - \sum _{\ell \in I^k} \int _{e^{k\ell }} n^{k\ell }_y \left( {\varvec{u}}^{k\ell }_{h}\left( {\varvec{x}}\right) - {\varvec{u}}^{*k\ell }_{h}\left( {\varvec{x}}\right) \right) \varvec{\ell }^k\left( {\varvec{x}}\right) \mathop {}\!\text {d}{\varvec{x}}. \end{aligned}$$

2.3 Numerical Fluxes

The numerical flux across edge \(e^{k\ell }\) requires the evaluation of \({\varvec{q}}^{*k\ell }_h\) and \(u^{*k\ell }_h\). Consider the internal penalty fluxes given by (see [22])

$$\begin{aligned} {\varvec{q}}^{*k\ell }_{h} = \{\{{\varvec{q}}_h\}\}^{k\ell } - \tau \llbracket u_h\rrbracket ^{k\ell }, \quad u^{*k\ell }_{h} = \{\{u_h\}\}^{k\ell }, \end{aligned}$$
(11)

with

$$\begin{aligned}&\{\{{\varvec{q}}_h\}\}^{ k\ell } = \frac{{\varvec{q}}_h^k + {\varvec{q}}_h^\ell }{2}, \qquad \{\{ u_h\}\}^{ k\ell } = \frac{ u_h^k + u_h^\ell }{2}, \qquad \text {and} \\&\llbracket u_h\rrbracket ^{k\ell } = {\varvec{n}}^{k\ell } u_h^{k} + {\varvec{n}}^{\ell k} u_h^\ell = {\varvec{n}}^{k\ell } \left( u_h^{k} -u_h^\ell \right) , \end{aligned}$$

where \(\ell \) corresponds to the index of an adjacent element in the case of an inner interface case, and \(\ell =B\) for a boundary element. Parameter \(\tau \) is a real number that depends on the domain characteristics and the polynomial degree associated with the triangle. For \(\tau = 0\), Eq. (11) reduces to the central flux while a positive value introduces a local numerical diffusion to stabilise the solution.

For an inner interface \(e^{k\ell }\) with adjacent elements \(T^k\) and \(T^\ell \), polynomials \(u^k_h\) and \(u^\ell _h\) are well-defined. For a boundary edge \(e^{kB}\), we consider a ghost state \(\left( u_h^{B}, {\varvec{q}}_h^{B}\right) \). If Dirichlet boundary conditions are prescribed, we define the ghost state as \(u_h^{B}= -u_h^k + 2g\) and \({\varvec{q}}_h^{B}= {\varvec{q}}_h^{k}\). Therefore, the numerical fluxes \({\varvec{q}}^{*k\ell }_h\) and \(u^{*k\ell }_h\) are defined as

$$\begin{aligned} {\varvec{q}}^{*kB}_h = {\varvec{q}}_h^k - 2 \tau {\varvec{n}}^{kB}(u_h^k - g) \quad \text{ and } \quad u^{*kB}_h = g. \end{aligned}$$

On the other hand, if Neumann boundary conditions are prescribed, we define the ghost state as \( u_h^{B}= u_h^k\) and \({\varvec{q}}_h^{B}= - {\varvec{q}}_h^{k} +2g\). Thus, the numerical fluxes are defined as

$$\begin{aligned} {\varvec{q}}^{*kB}_h = g \quad \text{ and } \quad u^{*kB}_h = u_h^k. \end{aligned}$$

The ghost state enables the weak enforcement of the boundary conditions. Since we are considering straight-sided triangles, the ghost state is defined in the same way either if we consider a convex or a concave domain.

All the unknowns are gathered in vector \({\varvec{U}}_{DG} = [{\varvec{u}}^k]_{k \in {\mathcal {T}}_h}\). Moreover, consider that the boundary condition values associated with element \(T^k, k \in I^B,\) are gathered in vector \({\varvec{U}}^{k}_{B}\) and \({\varvec{U}}_{B} = \left[ U^{k}_{B}\right] _{k \in I^B}\) assembles all the boundary condition values. To sum up, for a given vector \({\varvec{U}}_{B}\) of boundary condition values prescribed on the computational boundary \(\partial \varOmega _h\), the DG solution \({\varvec{U}}_{DG}\) is computed by solving a system of linear equations \(\left( -{\varvec{A}}+c{\varvec{B}}\right) {\varvec{U}} = {\varvec{F}}\), where \({\varvec{A}}\) is the stiffness matrix in \({\mathbb {R}}^{N_pK \times N_pK}\), \({\varvec{B}}\) is the standard block-diagonal mass matrix in \({\mathbb {R}}^{N_pK \times N_pK}\), and \({\varvec{F}}\) stands for the source term with the contribution of the boundary conditions.

3 The Reconstruction for Off-Site Data (ROD) Method

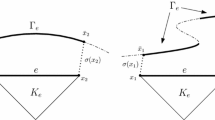
The ROD method is employed to exactly impose the boundary conditions prescribed on the curved physical boundary for each element \(T^k\) with an edge on the polygonal computational boundary. For that purpose, we consider a set of \(R^k\) points, \({\varvec{P}}^k = \left( P_r^k\right) _{r=1,\ldots , R^k}\), belonging to the physical boundary, for each element \(T^k, k \in I^B\). Assuming that the boundary parametrisation is known, to determine the points for the element \(T^k\), \(R^k\) equally spaced points \(p_r^k\), with \(r=1,\ldots , R^k\), are first chosen on the associated boundary edge, \(e^{kB}\), and then projected onto the physical boundary (see Fig. 1). It is worth mentioning that the choice of equidistant points is not mandatory, and other distributions of the points located on the computational boundary can be considered. The set of all points \({\varvec{P}}^k\), for all \(k \in I^B\), is called the collar and it is denoted by \({\mathcal {C}}_h\).

Fig. 1
figure 1

Example of an element \(T^k\) with an edge \(e^{kB}\) on the computational boundary \(\partial \varOmega _h\) and the corresponding points \(P^k_r \in {\mathcal {C}}_h, r=1, \ldots , R^k\)

Full size image

For each element \(T^k\), \(k \in I^{B}\), with a boundary edge \(e^{kB}\) on the computational boundary, \(\partial \varOmega _h\), consider the polynomial

$$\begin{aligned} u_h^{\star k}\left( {\varvec{x}}\right) =\sum _{i=1}^{N_p} u^{\star k}_i \ell _i^k\left( {\varvec{x}}\right) , \end{aligned}$$

that better approximates the local solution over element \(T^k\), \(u_h^k\), and exactly satisfies the boundary conditions at a set of points \({\varvec{P}}^k\) located on the physical boundary. All the nodal values of polynomial \(u_h^{\star k}\) are stored in vector \({\varvec{u}}^{\star k}=\left[ u^{\star k}_1,\cdots ,u^{\star k}_{N_p}\right] ^\text {T}\).

A generic polynomial in element \(T^k\), \(k \in I^{B}\), reads

$$\begin{aligned} \pi \left( {\varvec{x}};{\varvec{a}}\right) =\sum _{i=1}^{N_p} a_i\ell _i^k\left( {\varvec{x}}\right) , \end{aligned}$$

where vector \({\varvec{a}} = \left[ a_1,\ldots ,a_{N_p}\right] \) gathers the \(N_p\) nodal values, \(a_i=a_i\left( {\varvec{x}}_i^k\right) \). Moreover, consider the functional

$$\begin{aligned} {\varvec{a}}\rightarrow {\mathcal {E}}^k\left( {\varvec{a}};{\varvec{u}}^k\right) = \frac{1}{2} \sum \limits _{i=1}^{N_p} \left( a_i-u^k_i\right) ^2, \end{aligned}$$
(12)

subjected to the linear constraints

$$\begin{aligned} {\mathcal {B}}^k_r\left( {\varvec{a}}\right) = \alpha ^k_r \pi \left( P_r^k;{\varvec{a}}\right) + \beta ^k_r \nabla \pi \left( P_r^k;{\varvec{a}}\right) \cdot {\varvec{n}}^k_r-g_r^k=0,\quad r=1,\ldots ,R^k, \end{aligned}$$
(13)

where \({\varvec{n}}^k_r\) is the outward normal vector associated with \(P_r^k\), \( \alpha ^k_r = \alpha \left( P_r^k\right) \), \(\beta ^k_r = \beta \left( P_r^k\right) \), and \(g_r^k = g\left( P_r^k\right) \), with \(r=1, \ldots , R^k\). Finally, \({\varvec{u}}^{\star k}\) is sought as a minimisation of functional (12) under linear constraints (13).

From a practical viewpoint, the minimisation with constraints is computed with the Lagrange multipliers method. In element \(T^k\), \(k\in I^{B}\), the Lagrangian functional

$$\begin{aligned} \mathfrak {L}^k \left( {\varvec{a}},\varvec{\lambda }\right) ={\mathcal {E}}^k\left( {\varvec{a}};{\varvec{u}}^k\right) +\sum _{r=1}^{R^k} \lambda _r {\mathcal {B}}^k_r\left( {\varvec{a}}\right) \end{aligned}$$

is introduced, where \(\varvec{\lambda } = \left[ \lambda _1, \ldots , \lambda _{R^k}\right] ^\text {T}\) is the vector of Lagrange multipliers. Then, the solution \({\varvec{u}}^{\star k}\) and \(\varvec{\lambda }^{\star k}\) of problems \(\displaystyle \nabla _{{\varvec{a}}} {\mathfrak {L}}\left( {\varvec{a}},\varvec{\lambda }\right) = {\varvec{0}}\) and \(\displaystyle \nabla _{\varvec{\lambda }} {\mathfrak {L}}\left( {\varvec{a}},\varvec{\lambda }\right) = {\varvec{0}}\) is sought, that read component-wise

$$\begin{aligned} \partial _{a_j} \mathfrak {L} \left( {\varvec{a}},\varvec{\lambda }\right)= & {} \partial _{a_j} {\mathcal {E}}^k\left( {\varvec{a}};{\varvec{u}}^k\right) + \sum _{r=1}^{R^k} \lambda _r \partial _{a_j} {\mathcal {B}}^k_r\left( {\varvec{a}}\right) ,\quad j=1,\ldots ,N_p,\\ \partial _{\lambda _r} \mathfrak {L} \left( {\varvec{a}},\varvec{\lambda }\right)= & {} {\mathcal {B}}^k_r\left( {\varvec{a}}\right) , \quad r=1,\ldots ,R^k. \end{aligned}$$

From the definition of operator \({\mathcal {B}}^k_r\), one has

$$\begin{aligned} \partial _{a_j} {\mathcal {B}}^k_r\left( {\varvec{a}}\right)&= \partial _{a_j}\left( \alpha _r^k \sum _{i=1}^{N_p} a_i \ell _i^k\left( P_r^k\right) + \beta _r^k \sum _{i=1}^{N_p} a_i \nabla \ell _i^k\left( P_r^k\right) \cdot {\varvec{n}}^k_r - g_r^k \right) \\&= \alpha _r^k \ell _j^k\left( P_r^k\right) + \beta _r^k \nabla \ell _j^k\left( P_r^k\right) \cdot {\varvec{n}}_r^k, \quad j=1,\ldots ,N_p, \\ {\mathcal {B}}^k_r\left( {\varvec{a}}\right)&= \alpha _r^k \sum _{i=1}^{N_p} a_i \ell _i^k\left( P_r^k\right) + \beta _r^k \sum _{i=1}^{N_p} a_i \nabla \ell _i^k\left( P_r^k\right) \cdot {\varvec{n}}^k_r -g_r^k, \quad r=1,\ldots ,R^k. \end{aligned}$$

Introducing the column vectors

$$\begin{aligned} \left( {\varvec{B}}^k_r\right) ^\text {T}=\Big [ \alpha _r^k \ell _j^k\left( P_r^k\right) +\beta _r^k \nabla \ell _j^k\left( P_r^k\right) \cdot {\varvec{n}}_r^k \Big ]_{j=1}^{N_p}, \end{aligned}$$

for \(r= 1,\ldots , R^k\), and matrix \({\varvec{B}}^k=\left[ {\varvec{B}}^k_1,\ldots ,{\varvec{B}}^k_{R^k}\right] \) in \({\mathbb {R}}^{N_p\times R^k}\), the minimisation problem is stated under the matrix form

$$\begin{aligned} {} \begin{bmatrix} {\varvec{I}}_{N_p} &{} {\varvec{B}}^k\\ \left( {\varvec{B}}^k\right) ^\text {T} &{} {\varvec{0}} \end{bmatrix} \begin{bmatrix} {\varvec{a}} \\ \varvec{\lambda } \end{bmatrix}= \begin{bmatrix} {\varvec{u}}^k \\ g\left( {\varvec{P}}^k\right) \end{bmatrix}, \end{aligned}$$
(14)

where \({\varvec{I}}_{N_p}\) is the identity matrix in \({\mathbb {R}}^{N_p \times N_p}\) and \({\varvec{0}}\) is the null matrix in \({\mathbb {R}}^{R^k \times R^k}\).

The computed polynomials, \(u_h^{\star k}\), \(k\in I^{B}\), provide the boundary condition values \({\varvec{U}}^{\star k}_{B}\), \(k \in I^B\), which are gathered in \({\varvec{U}}^\star _{B}\). If Dirichlet boundary conditions are prescribed, the computed polynomials, \(u_h^{\star k}\), \(k\in I^{B}\), are evaluated at the nodes of the corresponding boundary edges, \(e^{kB}\). On the other hand, if Neumann boundary conditions are prescribed, we compute \(\nabla u_h^{\star k} \cdot {\varvec{n}}^{k B} \), \(k\in I^{B}\), where \(\nabla u_h^{\star k}\) is the gradient of the computed polynomial evaluated at each node of the boundary edge \(e^{kB}\) and \({\varvec{n}}^{k B}\) is the corresponding outward normal vector.

4 The Overall Method

As described in Sect. 2, the solution \(u_h\) is determined from the prescribed boundary condition values on the computational boundary and the source term. It then provides a linear operator tagged “DG solver”, defined as

$$\begin{aligned} {\varvec{U}}_{B}\rightarrow {\varvec{U}}_{DG}=\mathcal {S}\left( {\varvec{U}}_{B},f\right) \end{aligned}$$
(15)

for any vector \({\varvec{U}}_B\) defined for the computational boundary. On the other side, as described in Sect. 3, the vector \({\varvec{U}}^\star _{B}\) for boundary condition values is determined from the solution \(u_h\) represented by vector \({\varvec{U}}_{DG}\). It then provides a linear operator tagged “ROD operator”, defined as

$$\begin{aligned} {\varvec{U}}_{DG} \rightarrow {\varvec{U}}^\star _{B}=\mathcal {R}\left( {\varvec{U}}_{DG},g\right) . \end{aligned}$$
(16)

Then, the solution corresponds to the fixed point of the composed operators (15) and (16), namely

$$\begin{aligned} {\varvec{U}}_{B}\rightarrow {\varvec{U}}^\star _{B}=\mathcal {R}\Big (\mathcal {S}\left( {\varvec{U}}_{B},f\right) ,g\Big ). \end{aligned}$$

In practice, to compute an approximation, the succession \(\left( {\varvec{U}}_{B}^{\left( it\right) },{\varvec{U}}_{DG}^{\left( it\right) }\right) \) is defined by the two affine operators

$$\begin{aligned} {\varvec{U}}_{B}^{\left( it\right) }\rightarrow {\varvec{U}}_{DG}^{\left( it+1\right) }=\mathcal {S}\Big ({\varvec{U}}_{B}^{\left( it\right) },f\Big ),\qquad {\varvec{U}}_{DG}^{\left( it+1\right) }\rightarrow {\varvec{U}}_{B}^{\left( it+1\right) }=\mathcal {R}\Big ({\varvec{U}}_{DG}^{\left( it+1\right) },g\Big ). \end{aligned}$$

The procedure, presented in Algorithm 1, is performed until either the residual reaches a given tolerance \(\varepsilon \) or a given maximum number of iterations \(N_{\text {max}}\) is reached. Nevertheless, the procedure is performed at least once to compare the solutions obtained with the polynomial reconstructions.

Algorithm 1
figure a

DG–ROD method.

Full size image

5 Numerical Benchmark

Let denote by \(u_{h}\) an approximation of the solution u for a given mesh \(\mathcal {T}_h\) and \(\left\| u-u_h\right\| \) the norm of the error. The method is of convergence order p if one has asymptotically

$$\begin{aligned} \left\| u-u_h\right\| \le C h^p, \end{aligned}$$

with C a real constant independent of h. The errors are assessed at the node points of the elements, \(T^k\in \mathcal {T}_h\), \(k=1,\ldots ,K\), for which two discrete norms are defined, namely

$$\begin{aligned} E_1\left( \mathcal {T}_h\right)&= \sum _{k=1}^{K}\left| T^k\right| \left( \frac{1}{N_p} \sum _{i=1}^{N_p} \left| u\left( {\varvec{x}}^k_i\right) -u_h\left( {\varvec{x}}^k_i\right) \right| \right) , \quad \text {and} \\ \quad E_{\infty }\left( \mathcal {T}_h\right)&= \max _{T^k \in {\mathcal {T}}_h}\left( \max _{\varvec{x_i}^k \in T^k}\left| u\left( \varvec{x_i}^k\right) -u_h\left( \varvec{x_i}^k\right) \right| \right) . \end{aligned}$$

Consider two different meshes, denoted as \(\mathcal {T}_{h_1}\) and \(\mathcal {T}_{h_2}\), whose the corresponding numerical solutions are denoted as \(u_{h_1}\) and \(u_{h_2}\), respectively. Then, the convergence order between two successively finer meshes is determined as

$$\begin{aligned} \mathcal {O}_\gamma \left( \mathcal {T}_{h_1},\mathcal {T}_{h_2}\right) = \frac{\log \Big (E_{\gamma }\left( \mathcal {T}_{h_1}\right) /E_{\gamma }\left( \mathcal {T}_{h_2}\right) \Big )}{\log \left( h_1/h_2\right) }, \quad \gamma \in \{1, \infty \}. \end{aligned}$$

For the numerical flux (11), in [22], authors considered \( \tau \ge C \left. \left( N+1\right) ^2 \bigg / h\right. \), \(C \ge 1\), and, in the present study, \(\tau = 200\left. \left( N+1\right) ^2 \bigg / h\right. \) is taken. Finally, \(c=1\) is considered for Eq. (1) in the following benchmark test cases.

5.1 Disk Domain

The first benchmark test case concerns the reaction–diffusion equation on a disk of radius \(R=1\) with a non-constant Dirichlet boundary condition. An analytical solution is manufactured for problem (1)–(2) and is given as \(u\left( x,y\right) = \exp \left( x-2y\right) \), from which the corresponding source term is deduced. Simulations are carried out with successively finer meshes generated by Gmsh (version 4.6.0) [20] (see Fig. 2). The iterative procedure for the DG–ROD method is performed considering a residual criterion with a tolerance of \(\varepsilon =1\text {E}-13\) and a maximum number of \(N_{\text {max}}=20\) iterations. To determine the collar points, we consider an orthogonal projection of equidistant points located on the computational boundary onto the physical boundary.

Fig. 2
figure 2

Unstructured meshes generated for the disk domain

Full size image

Simulations are firstly performed for the classical DG method prescribing the non-constant Dirichlet boundary condition at the nodes of the computational boundary (the edges of the mesh). More precisely, each node of the computational boundary has a corresponding node on the real boundary where the Dirichlet boundary condition is prescribed. For the classical DG method, the value evaluated at the physical boundary point is used at the corresponding node on the computational boundary. The results, reported in Table 1, demonstrate the accuracy deterioration from such a geometrical mismatch without any specific treatment for curved boundaries, and the error convergence is limited to the second-order.

Table 1 Errors and convergence orders for the classical DG method in the disk domain prescribed with a non-constant Dirichlet boundary condition
Full size table

Table 2 reports the errors and convergence orders for the DG–ROD method. As observed, the optimal convergence orders are recovered according to the polynomial degree, N, and the number of collar points associated with the element \(T^k\), \(R^k\), to define the ROD operator in each element with a boundary edge. More precisely, the optimal convergence orders are achieved when the relation \(R^k = N+1\) is satisfied. In that case, the second-, third-, fourth-, and fifth-orders of convergence are achieved with \(N=1,2,3,4\), respectively. Note that the relation \(R^k \le N+1\) must be satisfied to ensure that the least squares minimisation procedure results in a well–conditioned problem. At last, a ratio of 1/10 between the \(L^1\)- and \(L^\infty \)-norm errors is observed, which indicates an even distribution of the error, in contrast to the classical DG method where the largest errors are concentrated in the vicinity of the boundary.

Table 2 Errors and convergence orders for the DG–ROD method in the disk domain prescribed with a non-constant Dirichlet boundary condition
Full size table

Moreover, the results demonstrate the capability of the DG–ROD method to improve the numerical solution even for the coarsest mesh. The polynomial reconstructions of the boundary condition correct the error from approximating the curved boundary with a polygonal boundary even for a mesh with \(K=14\), where the corresponding h has the same order of magnitude as the radius of the disk.

In Fig. 3, we report the condition number of the DG matrix as a function of the mesh size, h, and the polynomial degree N, in the disk domain prescribed with Dirichlet boundary conditions. The average of the condition number of the ROD matrix as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, is reported in Fig. 4. The condition number of the DG matrix increases when we consider a higher polynomial degree or a finer mesh. We also note a slight increase in the condition number of the ROD matrix when considering \(R^k= 2\) for \(N=1,2\). The distance between the points \({\varvec{P}}^k\) for each element \(T^k, k \in I^B,\) when considering two points is less than the distance between the points \({\varvec{P}}^k\) when considering one or three points (see Fig. 1). Consequently, for \(N=R^k= 2\), we are dealing with two constraints that provide two lines in the linear system with similar coefficients (almost co-linear), which is reflected in the condition number of the ROD operator.

Fig. 3
figure 3

Condition number of the solver operator \(\mathcal {S}\), \(\kappa (\mathcal {S})\), as a function of the mesh size, h, and the polynomial degree, N, in the disk domain with Dirichlet boundary conditions

Full size image
Fig. 4
figure 4

Average of the condition number of the operator \(\mathcal {R}\), \(\kappa (\mathcal {R})\), as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree N, in the disk domain with Dirichlet boundary conditions

Full size image

Figure 5 plots the errors between the approximate and exact solutions (first row) and the error between two successive approximate solutions within the fixed point iterative procedure. In both cases, a fast convergence towards a plateau is observed, where the error stalls at a level that depends on the method’s accuracy and mesh size.

Fig. 5
figure 5

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the disk domain prescribed with a non-constant Dirichlet boundary condition

Full size image

The convergence order of the fixed point iterative procedure is also assessed. Denoting the fixed point as \(\overline{{\varvec{U}}}_{B}\) and taking advantage that both the DG solver and the ROD operator are affine, then

$$\begin{aligned} {\varvec{U}}^{\left( it+1\right) }_{B}-\overline{{\varvec{U}}}_{B}=\mathcal {R}\Big (\mathcal {S}\left( {\varvec{U}}^{\left( it\right) }_{B}-\overline{{\varvec{U}}}_{B},f\right) ,g\Big ). \end{aligned}$$

Assume that, asymptotically, the error behaviour reads as

$$\begin{aligned} \left\| {\varvec{U}}^{\left( it+1\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| \approx C \left\| {\varvec{U}}^{\left( it\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| ^\theta \end{aligned}$$

or equivalently

$$\begin{aligned} \log \left( \left\| {\varvec{U}}^{\left( it+1\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| \right) \approx \log \left( C\right) +\theta \log \left( \left\| {\varvec{U}}^{\left( it\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| \right) , \end{aligned}$$

with \(C\ge 0\), \(\theta >0\). Considering the parameterized curve \(\left( X\left( it\right) ,Y\left( it\right) \right) \), given as

$$\begin{aligned} it \rightarrow \Big (X\left( it\right) =\log \left( \left\| {\varvec{U}}^{\left( it\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| \right) ,Y\left( it\right) =\log \left( \left\| {\varvec{U}}^{\left( it+1\right) }_{B}-\overline{{\varvec{U}}}_{B}\right\| \right) \Big ), \end{aligned}$$
(17)

the convergence order of the fixed point can be evaluated numerically.

To estimate the convergence order given by relation (17), Fig. 6 plots the parametric curve with respect to it for the DG–ROD method using the finest mesh. The linear approximation of the curve provides \(C=4.80\text {E}-06\) and \(\theta =0.05\) with \(R^k=3\) and \(N=2\), \(C=3.75\text {E}-02\) and \(\theta =1.00\) with \(R^k=4\) and \(N=3\), and \(C=7.10\text {E}-02\) and \(\theta =1.00\) with \(R^k=5\) and \(N=4\).

Fig. 6
figure 6

Fixed point convergence curve for the DG–ROD method in the disk domain prescribed with the non-constant Dirichlet boundary condition

Full size image

We tested the DG-ROD method in a physical application by considering the vanishing wave for the Schrödinger equation on a disk of radius R. The 2D Schrödinger equation with a constant potential V is given as

$$\begin{aligned} i \hslash \partial _t \psi ({\varvec{x}},t)=-\frac{ \hslash ^2}{2m}\nabla ^2 \psi ({\varvec{x}},t)+V\psi ({\varvec{x}},t), \end{aligned}$$

where i is the imaginary unit, \(\hslash \) is the reduced Plank constant, \(\psi \) is the wave function and m is the mass of the particle. Assuming \(\displaystyle \psi ({\varvec{x}},t)=\exp \left( -i\frac{E}{h}t\right) u({\varvec{x}})\) and \(V>E\), whith E the total energy, provides

$$\begin{aligned} \nabla ^2 u({\varvec{x}})-a^2u({\varvec{x}})=0, \end{aligned}$$

with \(a^2=\frac{2m(V-E)}{\hslash ^2}\). Moreover, if the solution is invariant by rotation, and considering \(a=1\), the solution in polar coordinates is given by the modified Bessel function \(u(r) = \sum _{k=0}^{\infty } \frac{\left( \frac{r}{2}\right) ^{2k}}{k! \varGamma (k+1)}\).

In the numerical tests, we considered a disk of radius \(R=1\) with a constant Dirichlet boundary condition. We observed that the optimal convergence orders are recovered, and the method behaves similarly to the previous test case.

5.2 Rose–Shaped Domain

Consider a geometry generated by applying a diffeomorphic transformation to an annular domain, denoted as \(\varOmega ^{\prime }\), with interior and exterior physical boundaries with radius \(r_{I}\) and \(r_{E} \), respectively. The diffeomorphic transformation corresponds to the mapping \(\varOmega ^{\prime } \rightarrow \varOmega \), where \(\varOmega \) is the rose–shaped domain, given in polar coordinates

$$\begin{aligned} \varOmega ^{\prime } \rightarrow \varOmega : \begin{bmatrix} r^{\prime } \\ \theta ^{\prime } \end{bmatrix} \rightarrow \begin{bmatrix} r \\ \theta \end{bmatrix} = \begin{bmatrix} R(r^{\prime }, \theta ^{\prime }; \alpha , \beta ) \\ \theta \end{bmatrix}, \end{aligned}$$
(18)

where \(\alpha \) is the number of petals and function \(R(r^{\prime }, \theta ^{\prime }):= R(r^{\prime }, \theta ^{\prime }; \alpha , \beta )\) corresponds to a periodic radius perturbation of magnitude in \([-\beta , \beta ]\), with \(\beta \in {\mathbb {R}}\), given as

$$\begin{aligned} R(r^{\prime }, \theta ^{\prime }; \alpha , \beta ) = r^{\prime }\left( 1 - \beta + \beta \cos (\alpha \theta ^{\prime }) \right) . \end{aligned}$$
(19)

Thus, the interior and exterior physical boundaries parametrisation are given as \(R_{I}: = R(r_{I}, \theta )\) and \(R_{E}: = R(r_{E}, \theta )\), respectively. The analytic solution corresponds to the manufactured solution \(u\left( x,y\right) =\log \left( x^2+y^2\right) \). The interior and exterior boundaries are prescribed with a non–constant Dirichlet boundary condition.

In this benchmark, we consider \(r_{I} = 0.5\), \(r_{E} = 1\), the number of petals is \(\alpha = 8\), and the perturbation magnitude is \(\beta = 0.1\). The rose–shaped domain is meshed with triangular elements (see Fig. 7). The reaction–diffusion equation is solved and the approximate solution is compared with the exact solution. The numerical simulations are carried out with successively finer meshes generated by Gmsh and the fixed point iterative procedure for the DG–ROD method stops when either the tolerance for the residual (\(\varepsilon =1\text {E}-13\)) or the maximum number of iterations is reached (\(N_{\text {max}}=30\)). To determine the collar points, we consider a radial projection of equidistant points located on the computational boundary onto the physical boundary.

Fig. 7
figure 7

Unstructured meshes generated for the rose-shaped domain

Full size image

The errors and convergence orders for the classical DG method, reported in Table 3, show that the error convergence is limited to the second–order. On the other hand, Table 4 reports the errors and convergence orders for the DG–ROD method. As observed, even in such a complex curved physical domain, the optimal convergence orders are recovered, and the method behaves similarly to the previous test case with Dirichlet boundary conditions.

Table 3 Errors and convergence orders for the classical DG method in the rose–shaped domain with the Dirichlet boundary conditions
Full size table
Table 4 Errors and convergence orders for the DG–ROD method in the rose–shaped domain with Dirichlet boundary conditions
Full size table

In Fig. 8 we report the condition number of the DG matrix as a function of the mesh size, h, and the polynomial degree N in the rose–shaped domain with Dirichlet boundary conditions. The average of the condition number of the ROD matrix as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, is reported in Fig. 9. The condition number of the DG matrix increases when we consider a higher polynomial degree or a finer mesh. Similarly to the previous test-case, for \(N=2\) the DG-ROD method improves the convergence order with \(R^k =1\), but not with \(R^k = 2\). This result may be related to the condition number of the ROD operator. We note a slight increase in the condition number of the ROD matrix when considering \(R^k= 2\) for \(N=1,2\).

Fig. 8
figure 8

Condition number of the solver operator \(\mathcal {S}\), \(\kappa (\mathcal {S})\), as a function of the mesh size, h, and the polynomial degree, N, in the rose–shaped domain with Dirichlet boundary conditions

Full size image
Fig. 9
figure 9

Average of the condition number of the operator \(\mathcal {R}\), \(\kappa (\mathcal {R})\), as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree N, in the rose–shaped domain with Dirichlet boundary conditions

Full size image

Figure 10 plots the errors between the approximate and exact solutions and the error between two successive approximate solutions within the fixed point iterative procedure. In both cases, we observe a convergence towards a plateau.

Fig. 10
figure 10

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the rose–shaped domain with Dirichlet boundary conditions

Full size image

Figure 11 plots the parametric curve with respect to it for the DG–ROD method using the finest mesh. The linear approximation of the curve provides \(C=5.48\text {E}-02\) and \(\theta =0.98\) for \(R^k=3\) and \(N=2\), \(C=1.79\text {E}-01\) and \(\theta =1.00\) for \(R^k=4\) and \(N=3\), and \(C=3.50\text {E}-01\) and \(\theta =1.00\) for \(R^k=5\) and \(N=4\), which again confirms the linear convergence of the fixed point iterative procedure. Note that for \(R^k=5\) and \(N=4\), the number of iterations performed by the DG-ROD method is significantly greater than in the other cases.

Fig. 11
figure 11

Fixed point convergence curve for the DG–ROD method in the rose–shaped domain prescribed with the non-constant Dirichlet boundary condition

Full size image

5.3 Annulus Domain

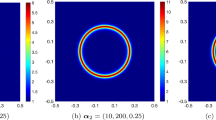
An annulus domain with inner radius \(R_{I}=0.5\) (interior boundary \(\partial \varOmega _{I}\)) and outer radius \(R_{E}=1\) (exterior boundary \(\partial \varOmega _{E}\)) is meshed with triangular elements (see Fig. 12). In this test case, three types of boundary conditions are compared by prescribing either a Dirichlet or a Neumann condition on the exterior and interior boundary. The analytic solution corresponds to the manufactured solution \(u\left( x,y\right) =\log \left( x^2+y^2\right) \). The boundaries are prescribed according to the following cases:

  • Dirichlet–Dirichlet case: the interior and exterior boundaries are prescribed with constant Dirichlet boundary conditions having \(g\left( {\varvec{x}}\right) = \log \left( R^2_{I}\right) , \; {\varvec{x}} \in \partial \varOmega _{I}\) and \(g\left( {\varvec{x}}\right) = \log \left( R^2_{E}\right) , \; {\varvec{x}} \in \partial \varOmega _{E}\), respectively (see Fig. 12a);

  • Dirichlet–Neumann case: the interior boundary is prescribed with a constant Dirichlet boundary condition having \(g\left( {\varvec{x}}\right) = \log \left( R^2_{I}\right) , \; {\varvec{x}} \in \partial \varOmega _{I}\), whereas the exterior boundary is prescribed with a non-constant Neumann boundary condition having \(g\left( {\varvec{x}}\right) = 2 {\varvec{x}}\cdot {\varvec{n}}, \; {\varvec{x}} \in \partial \varOmega _{E}\) (see Fig. 12b).

  • Neumann–Dirichlet case: the interior boundary is prescribed a non-constant Neumann boundary condition having \(g\left( {\varvec{x}}\right) = 8 {\varvec{x}}\cdot {\varvec{n}}, \; {\varvec{x}} \in \partial \varOmega _{I}\), whereas the exterior boundary is prescribed with a constant Dirichlet boundary condition having \(g\left( {\varvec{x}}\right) = \log \left( R^2_{E}\right) = 0, \; {\varvec{x}} \in \partial \varOmega _{E}\) (see Fig. 12c).

Fig. 12
figure 12

Unstructured meshes generated for the annulus domain with \(K = 608\) and \(h = 1.31\text {E}-01\) with Dirichlet (blue solid line) and Neumann boundary conditions (green dashed line) (Color figure online)

Full size image

The reaction–diffusion equation is solved for each case, and the approximate solution is compared with the exact solution. The numerical simulations are carried out with successively finer meshes generated by Gmsh (version 4.6.0) [20], and the fixed point iterative procedure for the DG–ROD method stops when either the tolerance for the residual or the maximum number of iterations is reached. To determine the collar points, we consider an orthogonal projection of equidistant points located on the computational boundary onto the physical boundary.

As for the previous test cases, simulations are firstly performed for the classical DG method prescribing the boundary conditions at the nodes of the interior and exterior computational boundaries (the edges of the mesh). The results for the Dirichlet–Dirichlet case, reported in Table 5, unequivocally confirm the accuracy deterioration resulting from such a geometrical mismatch without any specific treatment for curved boundaries, where the error convergence is limited to the second-order. Moreover, the results reported in Table 6 and Table 7 reveal a similar behaviour for the Dirichlet–Neumann case and for the Neumann–Dirichlet case, respectively, although slightly higher errors are obtained than in the Dirichlet–Dirichlet case.

Table 5 Errors and convergence orders for the classical DG method in the annulus domain with the Dirichlet–Dirichlet case
Full size table
Table 6 Errors and convergence orders for the classical DG method in the annulus domain with the Dirichlet–Neumann case
Full size table
Table 7 Errors and convergence orders for the classical DG method in the annulus domain with the Neumann–Dirichlet case
Full size table

Table 8 reports the errors and convergence orders for the DG–ROD method with the Dirichlet–Dirichlet case. As observed, the optimal convergence orders are recovered, and the method behaves similarly to the previous test case for the disk domain (Sect. 5.1).

Table 8 Errors and convergence orders for the DG–ROD method in the annulus domain with the Dirichlet–Dirichlet case
Full size table

The results for the DG–ROD method with the Dirichlet–Neumann case and with Neumann–Dirichlet are reported in Tables 9 and 10, respectively, and substantial differences are noticed. The optimal convergence orders are not always achieved. More specifically, with \(N=2\), the method is bounded by a second-order of convergence, regardless of the number of collar points. With \(N=3\), the results are more favourable, since the fourth-order of convergence is achieved if \(R^k \ge 3\) is satisfied. Finally, the accuracy with \(N=4\) seems limited to the fourth-order of convergence. These results emphasise that dealing with Neumann boundary conditions is more challenging. Nevertheless, the DG–ROD method manages to substantially improve the quality of the solution in comparison with the classical DG method.

Table 9 Errors and convergence orders for the DG–ROD method in the annulus domain with the Dirichlet–Neumann case
Full size table
Table 10 Errors and convergence orders for the DG–ROD method in the annulus domain with the Neumann–Dirichlet case
Full size table

In Fig. 13, we report the condition number of the DG matrix as a function of the mesh size, h, and the polynomial degree, N, for the Dirichlet-Dirichlet, Dirichlet-Neumann and Neumann–Dirichlet cases. The condition number of the DG matrix increases when we consider a higher polynomial degree or a finer mesh. Moreover, we note an increase in the condition number of the DG matrix when considering Neumann boundary conditions compared to the Dirichlet-Dirichlet case.

Fig. 13
figure 13

Condition number of the solver operator \(\mathcal {S}\), \(\kappa (\mathcal {S})\), as a function of the mesh size, h, and the polynomial degree, N, in the annulus domain

Full size image

In Fig. 14, we report the average of the condition number of the ROD matrix as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, for the Dirichlet-Dirichlet, Dirichlet-Neumann and Neumann–Dirichlet cases. We note that the condition number is almost constant in the Dirichlet-Dirichlet case, for each pair \((R^k, N)\). On the other hand, when considering Neumann boundary conditions, there is a slight increase in the condition number as we refine the mesh.

Fig. 14
figure 14

Average of the condition number of the operator \(\mathcal {R}\), \(\kappa (\mathcal {R})\), as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, in the annulus domain

Full size image

Another interesting point concerns the convergence of the fixed point iterative procedure. In Figs. 15, 16 and 17 we report the errors between the approximate and exact solutions (first row) and the error between two successive approximate solutions, for the Dirichlet–Dirichlet, Dirichlet–Neumann, and Neumann–Dirichlet cases. In the last two cases, the errors between two successive iterations reach similar plateaus to the Dirichlet–Dirichlet case, whereas the error between the approximate and exact solutions is generally almost two magnitudes higher. Such behaviour indicates that the conditioning of the global system of linear equations is a hundred times higher than with the Dirichlet–Dirichlet case. Consequently, the DG–ROD method suffers from accuracy deterioration due to the high condition number resulting from the imposition of the Neumann boundary condition. Despite this behavior, note that the number of iterations performed by the DG–ROD method does not increase with Neumann boundary conditions.

Fig. 15
figure 15

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the annulus domain with the Dirichlet–Dirichlet case

Full size image

The convergence of the fixed point iterative procedure for the Dirichlet–Dirichlet, Dirichlet–Neumann and Neumann–Dirichlet cases is plotted in Fig. 18. For the Dirichlet–Dirichlet case the linear approximation of the curve provides \(C=6.45\text {E}-07\) and \(\theta =0.04\) with \(R^k=3\) and \(N=2\), \(C=5.77\text {E}-03\) and \(\theta =0.85\) with \(R^k=4\) and \(N=3\), and \(C=4.80\text {E}-02\) and \(\theta =0.99\) with \(R^k=5\) and \(N=4\) (see Fig. 18a). For the Dirichlet–Neumann case the linear approximation of the curve provides \(C=6.07\text {E}-06\) and \(\theta =0.06\) with \(R^k=3\) and \(N=2\), \(C=1.91\text {E}-03\) and \(\theta =0.75\) with \(R^k=4\) and \(N=3\), and \(C=1.40\text {E}-02\) and \(\theta =0.90\) with \(R^k=5\) and \(N=4\) (see Fig. 18b). For the Neumann–Dirichlet case the linear approximation of the curve provides \(C= 3.99\text {E}-06\) and \(\theta =0.19 \) with \(R^k=4\) and \(N=3\), and \(C= 3.46\) and \(\theta =1.32\) with \(R^k=5\) and \(N=4\) (see Fig. 18c). The limitation resulting from the Neumann boundary condition is noticeable for \(R^k=5\) and \(N=4\) since the associated residual is stalled after two or three iterations, while the residual with the Dirichlet–Dirichlet case still decreases for one additional iteration.

Fig. 16
figure 16

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the annulus domain with the Dirichlet–Neumann case

Full size image
Fig. 17
figure 17

Error evolution as a function of the number of fixed point iterations of the DG–ROD method in the annulus domain with the Neumann–Dirichlet case

Full size image
Fig. 18
figure 18

Fixed point convergence curve for the DG–ROD method in the annulus domain with the Dirichlet–Dirichlet, Dirichlet–Neumann and Neumann Dirichlet cases

Full size image

5.4 Nozzle–Like Domains

Consider a nozzle–like domain given by

$$\begin{aligned} \varOmega = \{(x, y): x_l< x< x_r , -h(x)< y < h(x)\} \end{aligned}$$
(20)

such that the solution satisfies the homogeneous Neumann condition on the upper and lower bound \(\partial \varOmega _{u}\) and \(\partial \varOmega _{d}\) and Dirichlet condition on the left and right border \(\partial \varOmega _{l}\), \(\partial \varOmega _{r}\).

In this benchmark, we consider a convex domain \( \varOmega _1 = \{(x, y): 1<x<2, -h_1(x)<y <h_1(x)\} \) with \(h_1(x) = \sqrt{2(9 -x^2)}\) (see Fig. 19a) and a concave domain \( \varOmega _2 = \{(x, y): -1<x< 1, -h_2(x)<y <h_2(x)\} \) with \(h_2(x) = \sqrt{1+ 2\log (\cosh {x})}\) (see Fig. 19b). The analytic solutions corresponds to the manufactured solutions \(u_1\left( x,y\right) =\frac{y^4}{x^2}\) and \(u_2\left( x,y\right) =y \sinh {x}\), respectively. The nozzle–like domains are meshed with triangular elements. The reaction–diffusion equation is solved for each case, and the approximate solution is compared with the exact solution. The numerical simulations are carried out with successively finer meshes generated by Gmsh and the fixed point iterative procedure for the DG–ROD method stops when either the tolerance for the residual (\(\varepsilon =1\text {E}-13\)) or the maximum number of iterations is reached (\(N_{\text {max}}=30\)). In this benchmark, to determine the collar points, we consider a vertical projection of equidistant points located on the Neumann computational boundary onto the physical boundary.

Fig. 19
figure 19

Unstructured meshes generated for the nozzle-like domains with Dirichlet (blue solid line) and Neumann boundary conditions (green dashed line) (Color figure online)

Full size image

The errors and convergence orders for the classical DG method are provided in Table 11 and in Table 12 for the convex case and for the concave case, respectively. As expected, the accuracy is limited to the second–order of convergence, since there is a geometrical mismatch between the physical and the computational boundaries.

Table 11 Errors and convergence orders for the classical DG method in the convex domain with the Dirichlet and Neumann boundary conditions
Full size table
Table 12 Errors and convergence orders for the classical DG method in the concave domain with the Dirichlet and Neumann boundary conditions
Full size table

Table 13 reports the results for the DG-ROD method for the convex case. The method behaves similarly to the previous Dirichlet–Neumann case in the annulus domain. With \(N \in \{2,4\}\), the accuracy seems limited to the degree of the polynomial and with \(N=3\), the method achieves the fourth–order of convergence. Table 14 reports the results for the concave case which are more favorable since the method achieves the fifth–order of convergence with \(N=4\).

Table 13 Errors and convergence orders for the DG–ROD method in the convex domain with Dirichlet and Neumann boundary conditions
Full size table
Table 14 Errors and convergence orders for the DG–ROD method in the concave domain with Dirichlet and Neumann boundary conditions
Full size table

In Fig. 20, we report the condition number of the DG matrix as a function of the mesh size, h, and the polynomial degree, N, for the convex case (left panel) and for the concave case (right panel). The condition number of the DG matrix increases when we consider a higher polynomial degree or a finer mesh. Moreover, we note a slight increase in the condition number of the DG matrix in the concave case compared to the convex case.

Fig. 20
figure 20

Condition number of the solver operator \(\mathcal {S}\), \(\kappa (\mathcal {S})\), as a function of the mesh size, h, and the polynomial degree, N, in the nozzle-like domains

Full size image

In Fig. 21, we report the average of the condition number of the ROD matrix as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, for the convex case (left panel) and for the concave case (right panel). In the nozzle-like domains with Neumann boundary conditions, we observe larger condition number of the ROD matrix compared to the cases with only Dirichlet boundary conditions.

Fig. 21
figure 21

Average of the condition number of the operator \(\mathcal {R}\), \(\kappa (\mathcal {R})\), as a function of the mesh size, h, and the number of collar points associated with the element \(T^k\), \(R^k\), for each polynomial degree, N, in the nozzle-like domains

Full size image

The errors between the approximate and exact solutions and the error between two successive approximate solutions within the fixed point iterative procedure are plotted in Fig. 22 for the convex case and in Fig. 23 for the concave case. Analogously to the previous test cases, we observe a fast convergence towards a plateau.

Fig. 22
figure 22

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the convex domain with Dirichlet and Neumann boundary conditions

Full size image
Fig. 23
figure 23

Error evolution as a function of the number of fixed point iterations for the DG–ROD method in the concave domain with Dirichlet and Neumann boundary conditions

Full size image

The convergence of the fixed point iterative procedure for both the convex and concave cases is plotted in Fig. 24. For the convex case the linear approximation of the curve provides \(C=6.66\text {E}-03\) and \(\theta =0.01\) with \(R^k=3\) and \(N=2\), \(C=4.96\text {E}-05\) and \(\theta =0.14\) with \(R^k=4\) and \(N=3\), and \(C=1.63\text {E}-03\) and \(\theta =0.71\) with \(R^k=5\) and \(N=4\) (see Fig. 24a). For the concave case the linear approximation of the curve provides \(C=6.49\text {E}-06\) and \(\theta =0.01\) with \(R^k=3\) and \(N=2\), \(C=3.28\text {E}-04\) and \(\theta =0.65\) with \(R^k=4\) and \(N=3\), and \(C=3.71\text {E}-02\) and \(\theta =0.99\) with \(R^k=5\) and \(N=4\) (see Fig. 24b).

Fig. 24
figure 24

Fixed point convergence curve for the DG–ROD method in the nozzle–like domain with convex and concave cases

Full size image

6 Conclusions

The results in the benchmark test cases unequivocally demonstrate that the classical DG method has a second-order limitation for the error convergence in curved domains discretised with piecewise linear elements. Indeed, the method achieves a second-order convergence, regardless of the polynomial degree employed, since there is a geometrical mismatch of the same magnitude order between the physical boundary (where the boundary conditions are prescribed) and the computational boundary (where the boundary conditions are numerically imposed). Moreover, local errors on the boundary propagate to the whole domain, yielding a second-order of convergence for the global errors [4]. In particular, DG solutions are highly sensitive to the accuracy of the approximations to the boundaries [3, 4], and it has been shown that if homogeneous Dirichlet boundary conditions prescribed on a curved physical boundary are numerically imposed on a polygonal computational boundary, any finite element method will be at most second-order accurate [31]. These findings clearly highlight the importance of supplementing the DG method with an appropriate boundary treatment, especially to achieve a high-order of convergence.

The proposed DG–ROD method is based on polynomial reconstructions in the computational domain, where the associated coefficients are determined such that the same polynomial reconstructions adequately satisfy the boundary conditions prescribed on the physical boundary. In this way, these polynomial reconstructions are close to the numerical solution on the associated elements but correct the error from approximating the curved boundary with a polygonal boundary. Moreover, this polynomial reconstruction procedure is based on an iterative method that comprises two independent black boxes: the solution of the differential equation by the DG method (where the boundary conditions are defined on the computational boundary) and the ROD method for the elements with an edge on the computational boundary.

The results in the benchmark test cases demonstrate that the proposed DG–ROD method distinctively recovers the optimal convergence orders for polynomials degrees \(N=1,2,3,4\) in curved domains solely discretised with piecewise linear elements. Moreover, the numerical results suggest a relation between the number of points, \(R^k\), for each element \(T^k\) with an edge on the computational boundary and the polynomial degree, N, employed. More specifically, to increase the convergence order to \(N+1\) when employing a polynomial degree of N, at least \(R^k = N+1\) points need to be considered on the boundary for each element \(T^k\). Finally, Neumann boundary conditions do not always lead to the same optimal behaviour observed for Dirichlet boundary conditions. Indeed, there is greater difficulty in achieving the optimal convergence orders when Neumann boundary conditions are imposed, possibly due to the higher conditioning of the global system of linear equations, as the numerical experiments suggest.