Fourth-Order Accurate Compact Scheme for First-Order Maxwell’s Equations

Abstract

We construct a compact fourth-order scheme, in space and time, for the time-dependent Maxwell’s equations given as a first-order system on a staggered (Yee) grid. At each time step, we update the fields by solving positive definite second-order elliptic equations. We develop compatible boundary conditions for these elliptic equations while maintaining a compact stencil. The proposed scheme is compared computationally with a non-compact scheme and with a convolutional dispersion relation preserving (DRP) scheme.

1 Introduction

Time-dependent Maxwell’s equations have been established over 125 years as the theoretical representation of electromagnetic phenomena [9, 10]. However, the accuracy requirement of high-frequency simulations remains a challenge due to the pollution effect. This was investigated first for the convection equation [8] and later for the Helmholtz equation [1, 5].

We consider a uniform discretization of $\Omega =[0,1]^3$, $\Delta x \!=\! \Delta y \!=\! \Delta z \!=\! h = \frac{L}{N}$ where L is the length of the domain in a direction and N is the number of grid points in that direction. The wavenumber is given by $\omega = \frac{f}{v}$ where f is the frequency of the wave and v is its velocity. The pollution effect states that, for a p-order time accurate scheme, the quantity $\omega ^{p+1}h_{t}^p$ should remain constant for the error to remain constant as the wave number varies. A similar phenomenon applies also to spatial errors [1, 5]. This effect motivates the need for higher-order schemes, i.e., larger p. Using straightforward central differences, higher-order accuracy requires a larger stencil. This has two disadvantages. Firstly, the larger the stencil, the more work may be needed to invert a matrix with a larger bandwidth and more non-zero entries. Even more serious are the difficulties near boundaries. A large stencil requires some modification near the boundaries where all the points needed in the stencil are not available. This raises questions about the efficiency and stability of such schemes. In addition, higher-order compact methods can achieve the same error while using fewer grid nodes, making them more efficient in terms of both storage and CPU time than non-compact or low-order methods (see e.g., [3] for the wave equation, [13] for Helmholtz equation, [17, 18] for Maxwell’s equations, and references therein). The Yee scheme (also known as finite-difference time-domain, or FDTD) was introduced by Yee [16] and remains the common numerical method used for electromagnetic simulations [15]. Although it is only a second-order method, it is still preferred for many applications because it preserves important structural features of Maxwell’s equations that other methods fail to capture. One of the main novelties presented by Yee was the staggered-grid approach, where the electric field $\textbf{E}$ and magnetic field $\textbf{H}$ do not live at the same discrete space or time locations but at separate nodes on a staggered lattice. From the perspective of differential forms in space-time, it becomes clear that the staggered-grid approach is more faithful to the structure of Maxwell’s equations that are dual to one another and hence $\textbf{E}, \textbf{H}$ naturally live on two staggered, dual meshes [14]. The question of staggered versus non-staggered high-order schemes has been studied in [6] (see also [15, pp. 63–109]), where it has been shown that, for a given order of accuracy, a staggered scheme is more accurate and efficient than a non-staggered scheme.

In this paper, we present a new compact fourth-order accurate scheme, in both space and time, for Maxwell’s equations in three dimensions using an equation-based method on a staggered grid. At each time step, we update the solution by solving uncoupled (positive definite) second-order elliptic equations using the conjugate gradient method. This procedure involves a non-trivial treatment at the boundaries on which boundary conditions are not given explicitly but have to be deduced by the equation itself while maintaining the compact stencil. While the development of the scheme is done in 3D, the simulations are only two-dimensional.

1.1 Maxwell’s Equations

Let $\textbf{E},\textbf{H},\textbf{D},\textbf{B}$, and $\textbf{j}$ be (real-valued) vector fields, defined for $(t,\textbf{x})\in [0,\infty )\times \Omega$, which take values in $\mathbb {R}^3$. $\textbf{E}$ and $\textbf{H}$ are the electric and magnetic field strength, respectively, $\textbf{D}$ is the displacement, $\textbf{B}$ is the magnetic flux density. In addition $\rho$ and $\textbf{j}$ are the densities of the extraneous electric charges and currents, c is the speed of light in vacuum, and $\varepsilon$ and $\mu$ are the electric permittivity and magnetic permeability, respectively. The Maxwell equations on $\Omega$, in first-order differential vector form, are given by

$$\begin{aligned} \frac{1}{c}\frac{\partial \textbf{D}}{\partial t}&= \nabla \!\times \! \textbf{H}- \frac{4\pi }{c}\textbf{j},&\frac{1}{c}\frac{\partial \textbf{B}}{\partial t}&=-\nabla \times \textbf{E}\nonumber \\ \nabla \cdot \textbf{D}&= 4\pi \rho&\nabla \cdot \textbf{B}&=0 \nonumber \\ \textbf{D}&= \varepsilon \textbf{E}&\textbf{B}&= \mu \textbf{H}\end{aligned}$$

(1)

where $\nabla \times$ denotes the curl operator and $\nabla \cdot$ denotes the divergence operator with respect to $\textbf{x}$. The first pair of equations (1) represents the Ampére law (law of magnetic circulation) and Faraday law (law of electromagnetic induction). The second pair of equations (1) represent the Gauss laws of electricity and magnetism, respectively. The third pair of equations (1) is the constitutive relations, where we are assuming that the permittivity $\varepsilon$ and permeability $\mu$ are positive scalar constants which corresponds to a homogeneous and isotropic dielectric medium that fills the region $\Omega$. The constitutive relations in (1) are the same as they would have been in the case of static fields. Hence, the equations (1) are considered only for the range of frequencies below the threshold values where the dispersion of material characteristics starts to manifest itself. For many actual materials, these threshold frequencies are high and this limitation presents little to no loss of generality. For further detail on the derivation and interpretation of Maxwell’s equations (1) we refer the reader to [10, Chapter IX].

By taking the divergence of the Ampére law and substituting the Gauss law of electricity, we arrive at the continuity equation for the charges and currents:

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot \textbf{j} = 0. \end{aligned}$$

This equation represents the physical property of the conservation of the electric charge. At the same time, as it is derived from Maxwell’s equations, we conclude that it provides a necessary solvability condition for the system (1). Also, by taking the divergence of the Faraday law we obtain $\frac{\partial }{\partial t}\left( \nabla \cdot \textbf{B}\right) =0$, which implies that as long as the magnetic field is solenoidal at the initial moment, it will remain solenoidal at all subsequent times as well. At $t=0$, we assume that smooth initial conditions are given for $\textbf{D}$ and $\textbf{B}$. In addition, we assume that $\Omega =[0,1]^3$ and $\textbf{n} \times \textbf{E}=0$ on $\partial \Omega$ (see [11, Section 8]).

By differentiating the Ampére law in (1) with respect to time t, substituting $\frac{\partial }{\partial t}\nabla \times \textbf{B}=\mu \frac{\partial }{\partial t}\nabla \times \textbf{H}$ from the Faraday law, and employing the identity $\nabla \times \nabla \times \textbf{E}=-\Delta \textbf{E}+\nabla (\nabla \cdot \textbf{E})$ along with the Gauss law of electricity and the constitutive relations, we obtain the (inhomogeneous) wave equation for the electric field:

$$\begin{aligned} \begin{aligned} \frac{\varepsilon \mu }{c^2}\frac{\partial ^2\textbf{E}}{\partial t^2}=&\> \Delta \textbf{E}-\nabla (\nabla \cdot \textbf{E})-\frac{4\pi \mu }{c^2}\frac{\partial \textbf{j}}{\partial t}\\ =&\> \Delta \textbf{E}-\frac{4\pi }{\varepsilon }\nabla \rho -\frac{4\pi \mu }{c^2}\frac{\partial \textbf{j}}{\partial t}. \end{aligned} \end{aligned}$$

(2)

A similar argument yields the wave equation for the magnetic field:

$$\begin{aligned} \frac{\varepsilon \mu }{c^2}\frac{\partial ^2\textbf{H}}{\partial t^2}= \Delta \textbf{H}+\frac{4\pi }{c}\nabla \times \textbf{j}. \end{aligned}$$

(3)

From Eqs. (2) and (3) we conclude, in particular, that the propagation speed of electromagnetic waves in a homogeneous isotropic dielectric is equal to $\frac{c}{\sqrt{\varepsilon \mu }}$.

For convenience, we introduce a simplified setup with simplified notation and rescale Maxwell’s equations accordingly. Namely, from here on we assume that the propagation speed in the material is equal to one so that $c=\sqrt{\varepsilon \mu }$. Let us also denote $\textbf{J}=\frac{4\pi }{c}\textbf{j}$, absorb the coefficient of $4\pi$ into $\rho$: $\rho \mapsto 4\pi \rho$, and define $Z=\sqrt{\frac{\mu }{\varepsilon }}$. Then, the Maxwell’s system of Eq. (1) is recast as

$$\begin{aligned} \frac{\partial \textbf{E}}{\partial t}=Z(\nabla \times \textbf{H}-\textbf{J}) \quad \textrm{in} \quad (0,\infty )\times \Omega&\end{aligned}$$

(4a)

$$\begin{aligned} \frac{\partial \textbf{H}}{\partial t}=-\frac{1}{Z}\nabla \times \textbf{E}\quad \textrm{in} \quad (0,\infty )\times \Omega&\end{aligned}$$

(4b)

$$\begin{aligned} \nabla \cdot \textbf{H}(t,x,y,z) = 0&\end{aligned}$$

(4c)

$$\begin{aligned} \nabla \cdot \textbf{E}(t,x,y,z) =\frac{\rho }{\varepsilon }&\end{aligned}$$

(4d)

Equation (4) are to be supplemented with the initial conditions at $t=0$:

$$\begin{aligned} \textbf{E}(0,x,y,z)=\textbf{E}_0, \quad \textbf{H}(0,x,y,z)=\textbf{H}_0, \end{aligned}$$

and boundary conditions $\textbf{n}\times \textbf{E}=0$ on $\partial \Omega$.

Moreover, the second order wave Eqs. (2) and (3) reduce to

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \textbf{E}}{\partial t^2} =&\>\Delta \textbf{E}-\nabla (\nabla \cdot \textbf{E}) -Z\frac{\partial \textbf{J}}{\partial t}\\ =&\>\Delta \textbf{E}-\frac{1}{\varepsilon }\nabla \rho -Z\frac{\partial \textbf{J}}{\partial t} \end{aligned} \end{aligned}$$

(5)

and

$$\begin{aligned} \frac{ \partial ^2 \textbf{H}}{\partial t^2}= \Delta \textbf{H}-\nabla \times \textbf{J}, \end{aligned}$$

(6)

respectively.

To determine the number of imposed boundary conditions, we need to examine the eigenvalues for the reduced one-dimensional equations at that boundary. A positive eigenvalue indicates a variable that enters from outside the domain and so needs to be specified. A negative eigenvalue indicates the variable is determined from the inside and so cannot be imposed and instead is determined by the interior equations. A zero eigenvalue is more ambiguous.

Remark 1

An imposed boundary condition must contain only derivatives of a lower order than the differential equation. Thus, for a first-order system, all boundary conditions must be of Dirichlet type. A Neumann condition is not considered an imposed boundary condition.

To derive the boundary conditions for $\textbf{E}$ and $\textbf{H}$, we analyze the characteristics of the homogeneous counterpart to system (1), $\rho =0$ and $\textbf{J}=0$, in the direction normal to the boundary (cf. [7, Section 9.1]). The two divergence equations can be considered as constraints on the initial data and do not affect the characteristics. Let w be the vector $(E_x,E_y,E_z,H_x,H_y,H_z)^{t}$. Then, considering only the x space derivatives (without loss of generality) we arrive at

$$\begin{aligned} \frac{\partial w}{\partial t} = A w_x \end{aligned}$$

where

$$\begin{aligned} A = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{\epsilon } \\ 0 &{} 0 &{} 0 &{} 0 &{} -\frac{1}{\epsilon } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{1}{\mu } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -\frac{1}{\mu } &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

The eigenvalues of A are $c \!=\pm \! \frac{1}{\epsilon \mu }$ (twice) and 0 (twice). Thus, two boundary conditions need to be imposed, two are determined from the interior and two are not clear. We shall see that we impose $\textbf{E}_{\parallel } = 0$ (two conditions) and $\textbf{H}_{\perp } = 0$ (one condition).

The structure of the paper is as follows: In Sect. 2 we define all the necessary quantities with a detailed description of the grid placement. We then describe the type of the given boundary conditions, In Sect. 3 we present our scheme in space and time and then discuss. in more detail. the Neumann boundary conditions. Section 4 is devoted to the stability analysis of the scheme. Finally, Sect. 5 gives numerical confirmation of the theoretical results.

2 Preliminaries

We consider a uniform discretization of $\Omega =[0,1]^3$, $\Delta x \!=\! \Delta y \!=\! \Delta z \!=\! h$ and $h_{t}$ is the time-step. We introduce the following notations:

• $\textbf{x}=(x,y,z)\in \mathbb {R}^3$.

• $r=\frac{h_{t}}{h}$ is the Courant-Friedrichs-Lewy (CFL) number.

• $\textbf{E}(t,\textbf{x})=(E_x(t,\textbf{x}),E_y(t,\textbf{x}),E_z(t,\textbf{x}))$, $\textbf{H}(t,\textbf{x})=(H_x(t,\textbf{x}),H_y(t,\textbf{x}),H_z(t,\textbf{x}))$.

• $\Delta$ denotes the Laplacian with respect to $\textbf{x}$.

• $\Delta \textbf{E}=(\Delta E_x, \Delta E_y, \Delta E_z)$, $\Delta \textbf{H}=(\Delta H_x, \Delta H_y, \Delta H_z)$.

• $\textbf{E}^n$ (resp. $\textbf{H}^{n+1/2}$) denotes $\textbf{E}(t=nh_{t})$ (resp. $\textbf{H}(t=(n+1/2)h_{t})$).

• For $i,j,k\in \mathbb {N}\cup \{0\}$, $x_{i}=i h,y_{j}=j h,z_{k}=k h$.

• $x_{i+\frac{1}{2}}=\left( i+\frac{1}{2}\right) h, y_{j+\frac{1}{2}}=\left( j+\frac{1}{2}\right) h, z_{k+\frac{1}{2}}=\left( k+\frac{1}{2}\right) h$.

• $[N]=\{0,1,..,N\},\quad N\in \mathbb {N}.$

• $[k,m]=\{k,k+1,..m\},\quad k<m\in \mathbb {N}.$

• 1 denotes the identity operator.

• For any operator $T:\mathbb {R}^M\rightarrow \mathbb {R}^N$, $\Vert T\Vert :=\sup \limits _{0\ne x\in \mathbb {R}^N}\frac{|Tx|}{|x|}$.

• $\partial _{t}:=\frac{\partial }{\partial t}$ and $\partial _{t}^2:=\frac{\partial ^2}{\partial ^2 t}$.

• $\delta _{t} U^{n+\frac{1}{2}}:=\frac{U^{n+1}-U^{n}}{h_{t}}$.

To discretize the equations, we introduce a staggered mesh in both space and time as in the Yee scheme [16]. With this arrangement, all space derivatives are spread over a single mesh width, and the central time and space derivatives are centered at the same point, similar to that of the Yee scheme. $\textbf{E}$ is evaluated at time $nh_{t}$ while $\textbf{H}$ and $\textbf{J}$ are evaluated at time $(n\!+\! \frac{1}{2})h_{t}$. For the spatial discretization, we define the following meshes:

$$\begin{aligned}&\Omega _h^{E_z}:=\{(x_i,y_j,z_{k+\frac{1}{2}}),\quad (i,j,k)\in [N]^2 \times [N-1]\}\end{aligned}$$

(7)

$$\begin{aligned}&\Omega _h^{E_y}:=\{(x_i,y_{j+\frac{1}{2}},z_{k}), \quad (i,j,k)\in [N]\times [N-1] \times [N] \}\nonumber \\&\Omega _h^{E_x}:=\{ (x_{i+\frac{1}{2}},y_{j},z_{k}),\quad (i,j,k) \in [N-1]\times [N]^2 \} \nonumber \\&\Omega _h^{H_z}:=\{ (x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},z_{k}),\quad (i,j,k)\in [N-1]^2\times [N] \}\nonumber \\&\Omega _h^{H_y}:=\{ (x_{i+\frac{1}{2}},y_j,z_{k+\frac{1}{2}}),\quad (i,j,k) \in [N-1]\times [N] \times [N-1] \} \\&\Omega _h^{H_x}:=\{ (x_i,y_{j+\frac{1}{2}},z_{k+\frac{1}{2}}), \quad (i,j,k) \in [N]\times [N-1]^2\}.\nonumber \end{aligned}$$

(8)

For each $s=x,y,z$ we define the interior meshes:

$$\begin{aligned} \textrm{int}(\Omega _h^{E_s}):=(0,1)^3\cap \Omega _h^{E_s}, \qquad \textrm{int}(\Omega _h^{H_s}):=(0,1)^3\cap \Omega _h^{H_s}. \end{aligned}$$

Fig. 1

The grid points of $\Omega _h^{E_z}, \Omega _h^{H_x}, \Omega _h^{H_y}$ projected on the (x, y) plane in the case $N=5$

By convention, $x_0=y_0=z_0=0$ and $x_N=y_N=z_N=1$. We denote

$$\begin{aligned} \Omega _h^{\textbf{E}}:=\Omega _h^{E_x}\times \Omega _h^{E_y}\times \Omega _h^{E_z}, \qquad \Omega _h^\textbf{H}:= \Omega _h^{H_x}\times \Omega _h^{H_y}\times \Omega _h^{H_z}, \end{aligned}$$

and

$$\begin{aligned}{} & {} \textrm{int}(\Omega _h^{{\textbf{E}}}):=\textrm{int}(\Omega _h^{E_x})\times \textrm{int}(\Omega _h^{E_y})\times \textrm{int}(\Omega _h^{E_z}), \quad \partial \Omega _h^\textbf{E}:=\Omega _h^\textbf{E}\setminus \textrm{int}(\Omega _h^{\textbf{E}}) \\{} & {} \textrm{int}(\Omega _h^{\textbf{H}}):= \textrm{int}(\Omega _h^{H_x})\times \textrm{int}(\Omega ^{H_y})\times \textrm{int}(\Omega _h^{H_z}), \quad \partial \Omega _h^\textbf{H}:=\Omega _h^\textbf{H}\setminus \textrm{int}(\Omega ^{\textbf{H}}). \end{aligned}$$

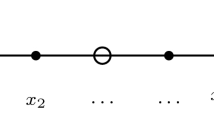
See Fig. 1 for an illustration of the sets $\Omega _h^{E_z}, \Omega _h^{H_x},\Omega _h^{H_y}$ projected on the x, y plane. The discretized functions $\textbf{E}_h, \textbf{H}_h$ are then defined as:

$$\begin{aligned} \textbf{E}_h^n:=\textbf{E}(nh_{t},\Omega _h^\textbf{E}),\quad \textbf{H}_h^{n+\frac{1}{2}}:=\textbf{H}\left( (n+\frac{1}{2})h_{t},\Omega _h^\textbf{H}\right) . \end{aligned}$$

With this arrangement, the boundary condition $\textbf{n}\times \textbf{E}=0$ on $\partial \Omega _h^{\textbf{E}}$ implies that

$$\begin{aligned}&E_x(x_{i+\frac{1}{2}},0,z_j)=E_x(x_{i+\frac{1}{2}},N,z_j)= E_x(x_{i+\frac{1}{2}},y_j,0)=E_x(x_{i+\frac{1}{2}},y_j, N)=0, \nonumber \\&E_y(0,y_{j+\frac{1}{2}},z_j)=E_y(N,y_{j+\frac{1}{2}},z_j)= E_y(x_i,y_{j+\frac{1}{2}},0)=E_y(x_i, y_{j+\frac{1}{2}}, N)=0, \nonumber \\&E_z(0,y_j,z_{k+\frac{1}{2}})=E_x(N,y_j,z_{k+\frac{1}{2}})= E_z(x_i,0,z_{k+\frac{1}{2}})=E_z(x_i,N,z_{k+\frac{1}{2}})=0.&\end{aligned}$$

(9)

In short, $E_x\!=\!0$ when $y\!=\!0,1$ and $z\!=\!0,1$; $E_y\!=\!0$ when $x\!=\!0,1$ and $z\!=\!0,1$;$E_z\!=\!0$ when $x\!=\!0,1$ and $y\!=\!0,1$.

2.1 Boundary Conditions for Time Derivatives

We will now derive the boundary conditions for the time derivatives of the fields $\textbf{E}$ and $\textbf{H}$ rather than the fields themselves. We do so since time marching with our compact scheme derived in Sect. 3 involves solving elliptic equations for the time derivatives of the fields (see Eqs. (12a) and (12b)).

By (9), we have the following Dirichlet-type boundary conditions:

$$\begin{aligned} \begin{gathered} \partial _tE_x\!=\!0 \ \text {if} \ y\!=\!0,1 \ \text {and} \ z\!=\!0,1,\\ \partial _tE_y\!=\!0 \ \text {if} \ x\!=\!0,1 \ \text {and} \ z\!=\!0,1,\\ \partial _tE_z\!=\!0 \ \text {if} \ x\!=\!0,1 \ \text {and} \ y\!=\!0,1. \end{gathered} \end{aligned}$$

(10)

Moreover, differentiating the Gauss law of electricity $\nabla \cdot \textbf{E}=\frac{\rho }{\varepsilon }$ with respect to time and using (9) we see that, for the remaining variables, the Neumann-type conditions hold:

$$\begin{aligned} \partial _x\partial _{t}E_x= \dfrac{\partial _t\rho }{\varepsilon } \ \text {if} \ x=0,1,\\ \partial _y\partial _{t}E_y= \dfrac{\partial _t\rho }{\varepsilon } \ \text {if} \ y=0,1,\\ \partial _z\partial _{t}E_z= \dfrac{\partial _t\rho }{\varepsilon } \ \text {if} \ z=0,1. \end{aligned}$$

The Faraday law $\partial _{t}\textbf{H}=-\frac{1}{Z}\nabla \times \textbf{E}$ yields the following Dirichlet-type boundary conditions:

$$\begin{aligned} \begin{aligned} \partial _tH_x=0 \ \text {if} \ x=0,1,\\ \partial _tH_y=0 \ \text {if} \ y=0,1,\\ \partial _tH_z=0 \ \text {if} \ z=0,1. \end{aligned} \end{aligned}$$

(11)

In Table 1, we provide the values of the second-order derivatives at the boundaries of $\Omega$ that we need for subsequent analysis and that can be derived from Eqs. (10) and (11) by differentiation.

Table 1 Second-order derivatives in time and mixed space-time derivatives at the boundaries of $\Omega$

The Ampère law $\partial _{t}\textbf{E}=Z(\nabla \times \textbf{H}-\textbf{J})$ implies that

$$\begin{aligned}&\partial _t^2E_x=Z\left( \frac{\partial H_z}{\partial _y\partial _t}-\frac{\partial ^2 H_y}{\partial _z\partial _t}-\partial _t\textbf{J}_x \right) , \\&\partial _t^2E_y=Z\left( \frac{\partial H_x}{\partial _z\partial _t}-\frac{\partial ^2 H_z}{\partial _x\partial _t}-\partial _t\textbf{J}_y \right) , \\&\partial _t^2E_z=Z\left( \frac{\partial H_y}{\partial _x\partial _t}-\frac{\partial ^2 H_x}{\partial _y\partial _t}-\partial _t\textbf{J}_z \right) . \end{aligned}$$

Substituting the values from Table 1 into these equations, we obtain the following six Neumann-type boundary conditions:

$$\begin{aligned} \partial _y\partial _tH_x=-\partial _t\textbf{J}_z \ \text {if} \ y=0,1 \quad \partial _z\partial _tH_x=\partial _t\textbf{J}_y \ \text {if} \ z=0,1,\\ \partial _x\partial _tH_y=\partial _t\textbf{J}_z \ \text {if} \ x=0,1 \quad \partial _z\partial _tH_y=-\partial _t\textbf{J}_x \ \text {if} \ z=0,1,\\ \partial _x\partial _tH_z=-\partial _t\textbf{J}_y \ \text {if} \ x=0,1 \quad \partial _y\partial _tH_z=\partial _t\textbf{J}_x \ \text {if} \ y=0,1. \end{aligned}$$

With these arrangements, the derivatives $\partial _{t}\textbf{E}$ and $\partial _{t}\textbf{H}$ are supplied with well-defined boundary conditions, as summarized in Table 2. In short, on $\partial \Omega$ we have $\partial _{t}{} \textbf{E}_{\parallel } = \partial _{t}{} \textbf{H}_{\perp } = 0$, while $\partial _{t}\textbf{E}_{\perp }$ and $\partial _{t}{} \textbf{H}_{\parallel }$ obey a Neumann condition. As discussed earlier, Dirichlet conditions are true boundary conditions while Neumann conditions are derived from the interior equations.

Table 2 Boundary conditions for the time derivatives of the Cartesian components of $\textbf{E}$ and $\textbf{H}$

3 The Scheme

3.1 Equation Based Derivation

We now extend the second-order accurate Yee scheme to a fourth-order accurate scheme, in both space and time, while maintaining the compact Yee stencil. Using Maxwell’s equations, the idea is to use a Taylor expansion in time to the next order and then replace the resulting third-order time derivatives with space derivatives.

The fourth-order Taylor expansion applied to (4) and combined with Eqs. (5) and (6) yields:

$$\begin{aligned}&Z(\nabla \times \textbf{H}^{n+1/2}-\textbf{J}^{n+1/2})= \left( \frac{\partial \textbf{E}}{\partial t} \right) ^{n+1/2}= \frac{\textbf{E}^{n+1} -\textbf{E}^n}{h_{t}}-\frac{h_{t}^2}{24}\frac{\partial ^3 \textbf{E}^{n+1/2}}{\partial t^3}+O(h_{t}^4)=\\&\delta _{t}\textbf{E}^{n+1/2}-\frac{h_{t}^2}{24}\partial _{t} \left( -Z\partial _t\textbf{J}^{n+1/2}-\nabla (\nabla \cdot \textbf{E}^{n+1/2})+\Delta \textbf{E}^{n+1/2} \right) +O(h_{t}^4)=\\&\delta _{t}\textbf{E}^{n+1/2}-\frac{h_{t}^2}{24} \left( -Z\partial _{t}^2\textbf{J}^{n+1/2} -\nabla (\nabla \cdot \partial _t\textbf{E}^{n+1/2})+\Delta \partial _{t}\textbf{E}^{n+1/2} \right) +O(h_{t}^4)=\\&\delta _{t}\textbf{E}^{n+1/2}-\frac{h_{t}^2}{24} \left( -Z\partial _{t}^2\textbf{J}^{n+1/2} +Z\nabla (\nabla \cdot \textbf{J}^{n+1/2})+\Delta \partial _{t}\textbf{E}^{n+1/2} \right) +O(h_{t}^4). \end{aligned}$$

Since $\Delta \partial _{t}\textbf{E}^{n+1/2}=\Delta \delta _{t} \textbf{E}^{n+1/2}+O(h_{t}^2)$, we have that

$$\begin{aligned}&Z(\nabla \times \textbf{H}^{n+1/2}-\textbf{J}^{n+1/2})=\\&\quad \delta _{t}\textbf{E}^{n+1/2}-\frac{h_{t}^2}{24} \left( -Z\partial _{t}^2\textbf{J}^{n+1/2} +Z\nabla (\nabla \cdot \textbf{J}^{n+1/2})+\Delta \delta _{t}\textbf{E}^{n+1/2} \right) +O(h_{t}^4). \end{aligned}$$

Similarly, we have for $\textbf{H}$:

$$\begin{aligned}&-\frac{1}{Z}\nabla \times \textbf{E}^{n+1}=\frac{\partial \textbf{H}^{n+1}}{\partial t}=\\&\quad \delta _t\textbf{H}^{n+1}-\frac{h_{t}^2}{24}\partial _{t}\left( \Delta \textbf{H}^{n+1}-\nabla \times \textbf{J}^{n+1} \right) +O(h_{t}^4)=\\&\quad \delta _t\textbf{H}^{n+1}-\frac{h_{t}^2}{24}\left( \delta _{t}\Delta \textbf{H}^{n+1}-\nabla \times \partial _{t}\textbf{J}^{n+1} \right) +O(h_{t}^4). \end{aligned}$$

Thus, at each time step, we obtain several uncoupled modified Helmholtz equations which are positive definite. Note: the equations might be coupled at the boundary for more complicated situations.

$$\begin{aligned} -\Delta \delta _{t} \textbf{E}^{n+\frac{1}{2}}+\frac{24}{h_{t}^2}\delta _{t}\textbf{E}^{n+\frac{1}{2}}&= Z\frac{24}{h_{t}^2}\nabla \times \textbf{H}^{n+\frac{1}{2}}+P(\textbf{J})^{n+\frac{1}{2}}+ O(h_{t}^4+h^4) \quad \textrm{in} \quad (0,1)^3, \end{aligned}$$

(12a)

$$\begin{aligned} -\Delta \delta _{t}\textbf{H}^{n+1}+\frac{24}{h_{t}^2}\delta _{t}\textbf{H}^{n+1}&= -\frac{1}{Z}\frac{24}{h_{t}^2}\nabla \times \textbf{E}^{n+1} -\nabla \times \partial _{t}\textbf{J}^{n+1}+ O(h_{t}^4+h^4) \quad \textrm{in} \quad (0,1)^3, \end{aligned}$$

(12b)

where

$$\begin{aligned} P(\textbf{J})^{n+\frac{1}{2}}{\mathop {=}\limits ^{\text {def}}}Z\left( -\textbf{J}^{n+\frac{1}{2}}-\nabla (\nabla \cdot \textbf{J}^{n+\frac{1}{2}})+\frac{\partial ^2\textbf{J}^{n+\frac{1}{2}}}{\partial t^2}\right) . \end{aligned}$$

(13)

Equation (12) are supplemented by the boundary conditions for the functions $\delta _{t}\textbf{E}$ and $\delta _{t}\textbf{H}$, as discussed in Sect. 2.

3.2 Modified Helmholtz Equation

In a Cartesian coordinate system, each of the Eqs. (12a) and (12b) gets split into three scalar modified-Helmholtz equations:

$$\begin{aligned} -\Delta \phi +\kappa ^2\phi =\kappa ^2F, \ \kappa ^2>0. \end{aligned}$$

(14)

We use the fourth-order accurate compact finite-difference scheme [13] for solving elliptic equations of the type (14).

Consider an equally-spaced mesh of dimension $N_x\times N_y\times N_z$ and size h in each direction. We denote by $D_{xx}$, $D_{yy}$, and $D_{zz}$ the standard second-order central-difference operators and define

$$\begin{aligned} \Delta _h{\mathop {=}\limits ^{\text {def}}}D_{xx}+D_{yy}+D_{zz}, \quad \varUpsilon _h{\mathop {=}\limits ^{\text {def}}} D_{zz}D_{xx}+D_{yy}D_{zz}+D_{xx}D_{yy}. \end{aligned}$$

Then, the fourth-order accurate scheme for (14) is given by [13]:

$$\begin{aligned} -\left( \Delta _h+\frac{h^2}{6}\varUpsilon _h\right) \phi +\kappa ^2\left( 1+\frac{\kappa ^2h^2}{12}\right) \phi = \kappa ^2\left( 1+\frac{\kappa ^2h^2}{12}+\frac{h^2}{12}\Delta _h \right) F. \end{aligned}$$

(15)

If $\Delta F$ is known at the grid nodes to fourth-order accuracy, then (14) can be simplified further to

$$\begin{aligned} -\left( \Delta _h+\frac{h^2}{6}\varUpsilon _h\right) \phi +\kappa ^2\left( 1+\frac{\kappa ^2h^2}{12}\right) \phi = \kappa ^2\left( 1+\frac{\kappa ^2h^2}{12} \right) F+ \frac{\kappa ^2h^2}{12}\Delta F. \end{aligned}$$

(16)

Letting $\kappa ^2 \!=\! \dfrac{24}{h_{t}^2}$ in (12) and (15) gives rise to six elliptic equations of type (14) with $\phi$ and F specified in Table 3. Once the discretization in space has been applied (Sect. 3.4), Eq. (12) lead to six positive definite linear systems to be solved independently by conjugate gradients. Note: it is difficult to use multigrid since the grid dimension for various equations is not the same and hence not all equations can have $2^n$ grid nodes in every direction.

Table 3 The expressions for $\phi$ and F in (14) ($P(\textbf{J})$ is given by (13))

3.3 Neumann Boundary Conditions

We reemphasize that Neumann conditions for a first-order system are not imposed boundary conditions. They are rather an implication of the PDEs in the interior. Let $\Omega =[0,1]^3$. We define ghost nodes outside the numerical grid so that the Neumann conditions are satisfied with fourth-order accuracy (see Fig. 2).

Fig. 2

Left: The grid nodes for $H_x$ projected onto the (x, y) plane in the case $N_x=N_y=5$. The unit square is bounded by the dashed line. Solid circles show the mesh points of $\Omega _h^{H_x}$. Hollow circles denote the ghost points induced by the Neumann boundary conditions at $y=0,1$. Right: The grid nodes for $H_y$ projected onto the (x, y) plane in the case $N_x=N_y=5$. The unit square is bounded by the dashed frame. Solid stars show the mesh points of $\Omega _h^{H_y}$. Hollow stars denote ghost points induced by the Neumann boundary conditions at $x=0,1$

We propose two methods for the implementation of the Neumann boundary conditions.

Method 1 (equation-based) Consider, without loss of generality, Eq. (14) with the Neumann boundary condition $\partial _x \phi (0,y,z)=g(y,z)$. Differentiating (14) with respect to x (cf. [13]), we have:

$$\begin{aligned} \phi _x(0,x,z)=\frac{\phi (\frac{1}{2}h,y,z)-\phi (-\frac{1}{2}h,y,z)}{h}+\frac{h^2}{24} \left( \phi _{xyy}+\phi _{xzz}-\kappa ^2\phi _x-\kappa ^2F_x \right) +O(h^4).\nonumber \\ \end{aligned}$$

(17)

Assume that $\phi _{xyy}+\phi _{xzz}$ is known for $x=0$. Setting $x\!=\!0$ in (17), we define the ghost value $\phi (-\frac{1}{2}h,y,z)$ such that the Neumann boundary condition $\partial _x \phi \!=\!=g(y,z)$ is satisfied to fourth-order.

Method 2 (Taylor based) By Taylor’s expansion

$$\begin{aligned} \phi _x(0,y,z)=\frac{\phi (\frac{1}{2}h,y,z)-\phi (-\frac{1}{2}h,y,z)}{h}-\frac{h^2}{24}\partial _{xxx}\phi (0,y,z)+O(h^4). \end{aligned}$$

(18)

Hence, knowing $\partial _x\phi$ and $\partial _{xxx}\phi$ at $x\!=\!0$ enables one to obtain the ghost variable $\phi (-\frac{1}{2}h,y,z)$ using (18).

Next, we show how to approximate the Neumann-type boundary conditions to fourth-order accuracy for $\partial _{t}\textbf{E}$ using Method 1 and for $\partial _{t}\textbf{H}$ using Method 2.

Lemma 1

Let $\phi (x,y,z)=\partial _tE_x$ be evaluated at some fixed $t_0$. Then, the quantities

$$\begin{aligned} \phi _{xyy}(0,y,z),\ \phi _{xzz}(0,y,z),\ \phi _x(0,y,z),\ \text {and}\ F_x \end{aligned}$$

are known to fourth-order accuracy. (Recall that, F contains the terms involving only $\partial _zH_y-\partial _y H_z$ and $\textbf{J}$.) If, in addition, $\textbf{J}=0$ and $\rho =0$, then $\phi _{xyy}(0,y,z)=\phi _{xzz}(0,y,z)=\phi _x(0,y,z)=F_x(0,y,z)=0$.

Proof

$\phi _x(0,y,z)$ equals to $\partial _tE_x$ at $x=0$, which has already been specified. Moreover, we have

$$\begin{aligned} \partial _x E_x+\partial _y E_y+\partial _z E_z=\frac{\rho }{\varepsilon }. \end{aligned}$$

(19)

Differentiating (19) twice with respect to y and once with respect to $t$, we arrive at

$$\begin{aligned} -\partial _{xyy}\phi +\partial _{tyy}(\rho /\varepsilon )= \partial _{yyy}\phi +\partial _{zyy}\phi . \end{aligned}$$

If $x=0$, then $\partial _{tyyy}E_x=\partial _{tzyy}E_x=0$, and hence if $x=0$, then $\partial _{xyy}\phi =\partial _{tyy}(\rho /\varepsilon )$. Differentiating (19) twice with respect to z and once with respect to $t$, we get

$$\begin{aligned} -\partial _{xzz}\phi +\partial _{tzz}(\rho /\varepsilon )= \partial _{yzz}\phi +\partial _{zzz}\phi . \end{aligned}$$

If $x=0$, then $\partial _{tzzz}E_x=\partial _{tyzz}E_x=0$, and hence at $x=0$ we have $\partial _{xzz}\phi =\partial _{tzz}(\rho /\varepsilon )$.

To obtain $F_x$ at $x=0$, it is sufficient to evaluate $\partial _x (\partial _z H_y- \partial _y H_z )$. This quantity, in turn, can be derived via the Ampère law $\partial _t\textbf{E}=Z(\nabla \times \textbf{H}-\textbf{J})$ if $\partial _{xt}E_x$ is available. And the latter is known through the Neumann boundary condition for $\partial _{t}\textbf{E}$ at $x=0$.

The second assertion follows immediately by the same argument. $\square$

By repeating the previous proof for the remaining faces of the cube $\Omega =[0,\,1]^3$ and field components $E_y$ and $E_z$, we obtain the following

Corollary 1

Neumann boundary conditions for Eq. (12a) admit a compact fourth-order accurate discretization using Method 1.

Next, we will show how to use Method 2 to build a compact discretization of the Neumann boundary conditions for $\partial _t\textbf{H}$.

Lemma 2

Let $\phi (x,y,z)=\partial _tH_y$ be evaluated at some fixed $t_0$. Then, the term $\phi _{xxx}$ at $x=0,1$ can be approximated to fourth-order accuracy.

Proof

Assume without loss of generality that $Z=1$. The equation

$$\begin{aligned} \partial _tE_z=\partial _{x}H_y-\partial _y H_x-\textbf{J}_z \end{aligned}$$

(20)

(cf. (4a)) and boundary conditions $\partial _{t}E_z=0$ at $x=0,1$ imply that at $x=0,1$

$$\begin{aligned} \partial _{txxx}H_y=\partial _{tyxx}H_x+\partial _{txx}\textbf{J}_z. \end{aligned}$$

Then, we use $\partial _t\nabla \cdot \textbf{H}=0$ and replace $\partial _x H_x$ with $-\partial _{ty} H_y-\partial _{tz} H_z$. This yields:

$$\begin{aligned} \partial _{tyxx}H_x=-\partial _{tyyx}H_y-\partial _{txyz}H_z. \end{aligned}$$

To complete the proof, we have to approximate $\partial _{tyyx}H_y$ and $\partial _{txyz}H_z$. This is done as follows. We use (20) again to obtain

$$\begin{aligned} \partial _{tyyx}H_y=\partial _{tyyy}H_x+\partial _{tyy}\textbf{J}_z. \end{aligned}$$

At $x=0,1$, the first equation of (11) implies that $\partial _{ty y y}H_x=0$.

To approximate $\partial _{tx y z}H_z$, we use the y-component of the Ampère law (4a):

$$\begin{aligned} \partial _tE_y=\partial _{z}H_x-\partial _{x}H_z-\textbf{J}_y. \end{aligned}$$

Therefore, at $x=0,1$ we have:

$$\begin{aligned} \partial _{x}H_z=\textbf{J}_y+\partial _z H_x \end{aligned}$$

and

$$\begin{aligned} \partial _{tx y z}H_z=\partial _{tyz }\textbf{J}_y+ \partial _{tyzz }H_x. \end{aligned}$$

Since $\partial _{t}H_x=0$ at $x=0,1$, we finally derive:

$$\begin{aligned} \partial _{ty zz}H_x=0. \end{aligned}$$

This completes the proof. $\square$

By repeating the previous procedure for $H_x$ and $H_z$, we obtain the following corollaries.

Corollary 2

Neumann boundary conditions for Eq. (12b) admit a compact fourth-order accurate discretization using Method 2.

Corollary 3

Assume that $\rho =0$ and $\textbf{J}=0$. Then, all Neumann boundary conditions obtained for $\partial _t\textbf{E}$ and $\partial _t\textbf{H}$ are homogeneous and all the derivatives in (17), (18) vanish. In particular, $\phi (\tilde{x}-\frac{1}{2})=\phi (\tilde{x}+\frac{1}{2})$ is a fourth-order accurate approximation to the homogeneous Neumann condition at the boundary point $\tilde{x}$ (see also Sect. 5).

We emphasize that the right-hand side, F, needs to be approximated with fourth-order accuracy. This is done using a fourth-order Padé approximation for the curl operator (see details in “Appendix A.1”). Then, we solve Eqs. 1, 2, and 3 from Table 3 using the scheme (15), and subsequently solve Eqs. 4, 5, and 6 from Table 3 using the scheme (16).

We define the following operators, given Eqs. (15) and (16).

Definition 4

For any $s=x,y,z$ and $G= H_s, E_s,$ let

$$\begin{aligned} P_{1}^{G}, P_{2}^{G}:\textrm{int}(\Omega _h)^{G}\rightarrow \textrm{int}(\Omega _h)^{G} \end{aligned}$$

be the symmetric operators given by

$$\begin{aligned}{} & {} P_{1}^{G}:=-\left( \Delta _h+\frac{h^2}{6}\varUpsilon _h\right) +\frac{24}{h_{t}^2}\left( 1+\frac{2}{r^2} \right) , \\{} & {} P_{2}^{G}:=\frac{24}{h_{t}^2}\left( -1-\frac{2}{r^2}-\frac{h^2}{12}\Delta _h \right) . \end{aligned}$$

We omit the superscript G whenever it does not lead to any ambiguity.

Hereafter, $r=\frac{h_{t}}{h}$ will denote the CFL number. As shown in “Appendix A.2”, if $r<\sqrt{3+\sqrt{21}}$, then $P_2^G$ and $P_1^G$ are symmetric positive definite matrices and the following estimates hold:

$$\begin{aligned}&0<\frac{2}{r^2}\le \Vert \frac{h_{t}^2}{24}P_2^G\Vert \le 1+\frac{2}{r^2}, \end{aligned}$$

(21)

$$\begin{aligned}&1<1+\frac{2}{r^2}-\frac{r^2}{6}\le \Vert \frac{h_{t}^2}{24}P_1^G\Vert \le 1+\frac{2}{r^2}+\frac{r^2}{2}. \end{aligned}$$

(22)

In particular,

$$\begin{aligned} \Vert \left( P_{1}^{G}\right) ^{-1}P_{2}^{G}\Vert \ge \frac{\frac{2}{r^2}}{1+\frac{2}{r^2}+\frac{r^2}{2}}. \end{aligned}$$

3.4 The Numerical Scheme

Let

$$\begin{aligned} \textbf{curl}_h{\mathop {=}\limits ^{\text {def}}} \begin{pmatrix} 0&{} -\delta _z &{} \delta _y\\ \delta _z&{}0&{}-\delta _x\\ -\delta _y&{}\delta _x&{}0\\ \end{pmatrix} \end{aligned}$$

be the block matrix representing a spatial Padé fourth-order finite-difference approximation of the curl operator.

See “Appendix A.1” for the full definition of the matrix $\textbf{curl}_h$.

Let $\textbf{E}^n_h$ and $\Delta \textbf{E}^n_h$ be given on $\Omega _h^{\textbf{E}}$ and let $\textbf{H}^{n+\frac{1}{2}}_h$ be given on $\Omega _h^{\textbf{H}}$. To advance in time, we take two steps.

Step 1:

$$\begin{aligned} {\textbf{E}}_h^{n+1}= \begin{pmatrix} E_x^n+h_{t} E_x^{*}\\ E_y^n+h_{t} E_y^{*}\\ E_y^n+h_{t} E_y^{*} \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned}&\underbrace{ \begin{pmatrix} P_1^{E_x} &{} 0&{}0 \\ 0 &{} P_1^{E_y} &{}\\ 0&{}0&{}P_1^{E_z} \end{pmatrix} }_{P_1^\textbf{E}} \begin{pmatrix} E_x^{*}\\ E_y^{*} \\ E_z^{*} \end{pmatrix}=ZP(\textbf{J}^{n+1/2})+\\ {}&\kappa ^2Z \begin{pmatrix} 0&{} -\delta _z &{} \delta _y\\ \delta _z&{}0&{}-\delta _x\\ -\delta _y&{}\delta _x&{}0 \end{pmatrix} \left[ \left( 1+\frac{\kappa ^2 h^2}{12} \right) \begin{pmatrix} H_x^{n+\frac{1}{2}}\\ H_y^{n+\frac{1}{2}}\\ H_z^{n+\frac{1}{2}} \end{pmatrix}+ \frac{h^2}{12} \begin{pmatrix} \Delta _h H_x^{n+\frac{1}{2}}\\ \Delta _h H_y^{n+\frac{1}{2}}\\ \Delta _h H_z^{n+\frac{1}{2}} \end{pmatrix} \right] \end{aligned}$$

(cf. Sect. 3.2). Extend ${\textbf{E}}_h^{n+1}$ to $\Omega _h^\textbf{E}$ using the boundary conditions.

Define

$$\begin{aligned} \Delta \textbf{E}_h^{n+1} =\Delta \textbf{E}_h^n+\kappa ^2(\textbf{E}_h^{n+1}-\textbf{E}_h^n)-Z\frac{24}{h_{t}} \begin{pmatrix} 0&{} -\delta _z &{} \delta _y\\ \delta _z&{}0&{}-\delta _x\\ -\delta _y&{}\delta _x&{}0 \end{pmatrix} \begin{pmatrix} H_x^{n+\frac{1}{2}}\\ H_y^{n+\frac{1}{2}}\\ H_z^{n+\frac{1}{2}} \end{pmatrix}-h_{t} P(\textbf{J})^{n+\frac{1}{2}} \end{aligned}$$

on $\Omega _h^\textbf{E}$ (see (12))

Step 2:

$$\begin{aligned} {\textbf{H}}_h^{n+\frac{3}{2}}= \begin{pmatrix} H_x^{n+\frac{1}{2}}+h_{t} H_x^{*}\\ H_y^{n+\frac{1}{2}}+h_{t} H_y^{*}\\ H_y^{n+\frac{1}{2}}+h_{t} H_y^{*} \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned}&\underbrace{ \begin{pmatrix} P_1^{H_x} &{} 0&{}0 \\ 0 &{} P_1^{H_y} &{}\\ 0&{}0&{} P_1^{H_z} \end{pmatrix} }_{P_1^\textbf{H}} \begin{pmatrix} H_x^{*}\\ H_y^{*} \\ H_z^{*} \end{pmatrix}-\frac{1}{Z}\nabla \times \partial _{t}^2\textbf{J}^{n+1} =\\&-\frac{\kappa ^2}{Z} \begin{pmatrix} 0&{} -\delta _z &{} \delta _y\\ \delta _z&{}0&{}-\delta _x\\ -\delta _y&{}\delta _x&{}0 \end{pmatrix} \left[ \left( 1+\frac{\kappa ^2h^2}{12} \right) \begin{pmatrix} E_x^{n+1}\\ E_y^{n+1}\\ E_z^{n+1} \end{pmatrix}+ \frac{h^2}{12} \begin{pmatrix} \Delta E_x^{n+1}\\ \Delta E_y^{n+1}\\ \Delta E_z^{n+1} \end{pmatrix} \right] , \end{aligned}$$

(cf. Sect. 3.2). Extend $\textbf{H}_h^{n+3/2}$ to $\Omega _h^\textbf{H}$ using the appropriate boundary condition.

4 Stability Analysis

We assume, with no loss of generality, that $\rho \!=\!0$, $\textbf{J}\!=\! 0$, and $Z \!=\! 1$. The scheme can therefore be written compactly:

$$\begin{aligned} \textbf{E}_h^{n+1} -\textbf{E}_h^{n}&= h_{t} P_1^{-1} \textbf{curl}_h \left( \kappa ^2\left( 1+\frac{\kappa ^2h^2}{12}\right) \textbf{H}_h^{n+1/2}+\frac{\kappa ^2h^2}{12}\Delta \textbf{H}_h^{n+1/2}\right) , \end{aligned}$$

(23a)

$$\begin{aligned} \textbf{H}_h^{n+3/2} -\textbf{H}_h^{n+1/2}&= -h_{t} P_1^{-1} \textbf{curl}_h \left( \kappa ^2\left( 1+\frac{\kappa ^2h^2}{12}\right) \textbf{E}_h^{n+1}+\frac{\kappa ^2h^2}{12}\Delta \textbf{E}_h^{n+1} \right) . \end{aligned}$$

(23b)

We approximate $\Delta$ in Eqs. (23a) and (23b) using the standard second-order difference Laplacian $\Delta _h$ (same as in (15)). Then, we recast (23a), (23b) as:

$$\begin{aligned}&\left( \textbf{1}- h_{t} \begin{pmatrix} 0&{}0\\ -P_1^{-1}P_2\textbf{curl}_h&{} 0 \end{pmatrix} \right) \begin{pmatrix} \textbf{E}^{n+1} \\ \textbf{H}^{n+3/2} \end{pmatrix}= \nonumber \\&\left( \textbf{1}-h_{t} \begin{pmatrix} 0 &{}-P_1^{-1}P_2\textbf{curl}_h\\ 0&{} 0 \end{pmatrix} \right) \begin{pmatrix} \textbf{E}^{n} \\ \textbf{H}^{n+1/2} \end{pmatrix}, \end{aligned}$$

(24)

where the operators $P_1$ and $P_2$ are introduced in Definition 4. Next, assume the solution is in the form of a plane wave:

$$\begin{aligned} \begin{pmatrix} \textbf{E}^{n}\\ \textbf{H}^{n+1/2} \end{pmatrix}_{i,j,k}= \sigma ^n (\exp (-\sqrt{-1}(\xi _xih+\xi _yjh+\xi _zkh))) \begin{pmatrix} \textbf{E}_0\\ \textbf{H}_0 \end{pmatrix}. \end{aligned}$$

Let $Q=-P_1^{-1} P_2 \textbf{curl}_h$ and let $\lambda$ denote an eigenvalue of Q. We substitute the plane wave solution into (24) and derive

$$\begin{aligned} \begin{pmatrix} \sigma -1&{} \lambda h_{t}\\ -\sigma h_{t} \lambda &{} \sigma -1 \end{pmatrix} \begin{pmatrix} \textbf{E}_0\\ \textbf{H}_0 \end{pmatrix}= \begin{pmatrix} 0\\ 0 \end{pmatrix}. \end{aligned}$$

Therefore,

$$\begin{aligned} \sigma ^2-\sigma (2-\lambda ^2h_{t}^2)+1=0. \end{aligned}$$

In particular, $|h_{t}\lambda |\le 2$ implies that $|\sigma |\le 1$. Then, using the definition of the matrix A given by Eq. (35) and Remark 2 (see “Appendix A.1”), we can derive the stability condition in the following form:

$$\begin{aligned} r2\sqrt{3}\Vert A^{-1}\Vert \Vert -P_1^{-1}P_2\Vert \le 2 \Leftrightarrow r\le \frac{1}{\sqrt{3}\Vert A^{-1}\Vert \cdot \Vert -P_1^{-1}P_2\Vert }. \end{aligned}$$

(25)

By (21), $r<\sqrt{3+\sqrt{21}}$ implies that $\Vert -P_1^{-1}P_2\Vert \ge \frac{\frac{2}{r^2}}{1+\frac{2}{r^2}+\frac{r^2}{2}}$ (see “Appendix A.2” for detail). Therefore, the scheme is stable provided that

$$\begin{aligned} r\le \min \left\{ \sqrt{3+\sqrt{21}}, \frac{1+\frac{2}{r^2}+\frac{r^2}{2}}{\sqrt{3}\Vert A^{-1}\Vert \frac{2}{r^2}} \right\} . \end{aligned}$$

The inequality

$$\begin{aligned} \frac{1+\frac{2}{r^2}+\frac{r^2}{2}}{\frac{2}{r^2}}\ge 1, \quad r\in (0,\infty ) \end{aligned}$$

gives rise to a sufficient stability condition

$$\begin{aligned} 0<r\le \frac{1}{\sqrt{3}\Vert A^{-1}\Vert }\sim \frac{5}{6\sqrt{3}}. \end{aligned}$$

(26)

In the following section, we will examine a two-dimensional reduction of Maxwell’s equation. A modification of Remark 2 readily implies the stability condition

$$\begin{aligned} 0<r\le \frac{1}{\sqrt{3}\Vert A^{-1}\Vert }\sim \frac{5}{6\sqrt{2}} \end{aligned}$$

(27)

(cf. [18]). The numerical results summarized in Table 5 corroborate the stability estimate (27).

5 Example: Transverse Magnetic Waves in $[0,1]^2$

5.1 Numerical Simulations Data

For the computations, we consider the scaled two-dimensional TM system without any current or charges. Thus, the equations are reduced to

$$\begin{aligned} \frac{\partial E_z}{\partial t}&= Z \left( -\frac{\partial H_x}{\partial y} + \frac{\partial H_y}{\partial x} \right) , \end{aligned}$$

(28a)

$$\begin{aligned} \frac{\partial H_x}{\partial t}&= - \frac{1}{Z} \frac{\partial E_z}{\partial y}, \end{aligned}$$

(28b)

$$\begin{aligned} \frac{\partial H_y}{\partial t}&= \frac{1}{Z} \frac{\partial E_z}{\partial x}. \end{aligned}$$

(28c)

Since $\textbf{H}$ is given at time moments $n+1/2$ we need to specify its initial condition at the time $t\!=\! \frac{\Delta _t}{2}$. By Taylor series,

$$\begin{aligned} \textbf{H}\left( \frac{h_{t}}{2}\right) \!=\! \textbf{H}(0) \!+\! \left( \frac{h_{t}}{2}\right) \textbf{H}_{t} (0) \!+\! \frac{1}{2} \left( \frac{h_{t}}{2}\right) ^2 \textbf{H}_{tt} (0) \!+\! \frac{1}{6} \left( \frac{h_{t}}{2}\right) ^3 \textbf{H}_{ttt}(0) \!+\! \frac{1}{24} \left( \frac{h_{t}}{2}\right) ^4 \textbf{H}_{tttt} (0).\nonumber \\ \end{aligned}$$

(29)

$\textbf{H}_{t} (0)$ is given by (4b) and $\textbf{H}_{tt} (0)$ is given by (6). Differentiating (6) yields:

$$\begin{aligned} \frac{ \partial ^3 \textbf{H}}{\partial t^3}=-\nabla \times \nabla \times \textbf{H}_{t}-\nabla \times \partial _{tt}\textbf{J}= \Delta \textbf{H}_{t}-\nabla \times \partial _{tt}\textbf{J}, \end{aligned}$$

where, again, $\textbf{H}_{t}$ is given by (4b). Similarly,

$$\begin{aligned} \frac{ \partial ^4 \textbf{H}}{\partial t^4}=-\nabla \times \nabla \times \textbf{H}_{tt}-\nabla \times \partial _{t^3}\textbf{J}= \Delta \textbf{H}_{tt}-\nabla \times \partial _{ttt}\textbf{J}, \end{aligned}$$

where $\textbf{H}_{tt}$ is given by (6). At the nodes on or next to a boundary, we have either Dirichlet or Neumann conditions as given in Table 2. For (28), we have assumed $\textbf{J}\!=\! 0$. For the computations, we further assume $Z \!=\! 1$.

Let $k_x,k_y\in \mathbb {N}$ and let $\omega :=Z\pi \sqrt{k_x^2+k_y^2}$. We consider the analytical solutions

$$\begin{aligned} E_z(x,y)&=\cos (\omega t) \sin {\left( Z \pi k_x x\right) } \sin {\left( Z \pi k_y y\right) }, \end{aligned}$$

(30a)

$$\begin{aligned} H_x(x,y)&=-\frac{\sin ( \omega t)}{\omega } \pi k_y \sin (Z \pi k_x x) \cos {\left( Z \pi k_y y\right) }, \end{aligned}$$

(30b)

$$\begin{aligned} H_y(x,y)&=\frac{\sin \left( \omega t\right) }{\omega } \pi k_x \cos {\left( Z \pi k_x x\right) } \sin {\left( Z\pi k_y y\right) }. \end{aligned}$$

(30c)

We use the mean absolute error

$$\begin{aligned} \frac{1}{3N_{t}\cdot N^2}\sum _{i,j,n=0}^{N,N,N_{t}}&\left| {E_z}^n_{\mathrm {numer.}}(i,j)-{E_z}_{\textrm{true}}^n(i,j) \right| + \left| {H_x}^n_{\mathrm {numer.}}(i,j)-{H_x}_{\textrm{true}}^n(i,j) \right| +\\&\left| {H_y}^n_{\mathrm {numer.}}(i,j)-{H_y}_{\textrm{true}}^n(i,j) \right| , \end{aligned}$$

where the subscripts “$\mathrm {numer.}$” and “$\textrm{true}$” refer to the numerical and analytical solution, respectively. The ghost nodes are easily defined using Corollary 3. The ghost points for $H_x$ (see Fig. 2) are defined similarly.

5.2 Comparable Schemes: $C4, NC, AI^h$

We compare our proposed scheme, denoted by C4, with the following two schemes, which are second-order accurate in time. These schemes are obtained according to the Yee updating rules:

$$\begin{aligned}&E_z^{n+1}=E_z^n+h_{t} (D_x H_y^{n+1/2}-D_yH_x^{n+1/2}),\\ {}&H_x^{n+3/2}=H_x^{n+1/2}-h_{t} D_y E_z^{n+1}, \\ {}&H_y^{n+3/2}=H_y^{n+1/2}+h_{t} D_x E_z^{n+1}, \end{aligned}$$

where $D_x$ and $D_y$ are finite difference operators that approximate the first derivative on different stencils. For the derivatives in the x direction, we consider a general stencil

$$\begin{aligned} S= \frac{1}{h} \begin{pmatrix} -b &{} -a &{} a &{} b \\ -d &{} -c&{} c &{}d \\ -b &{} -a &{} a &{} b \end{pmatrix}, \end{aligned}$$

whereas for the derivatives in the y direction we use the transposed stencil $S^t$. In particular,

$$\begin{aligned}&\partial _x u_{ij}\sim \frac{c(u_{i+\frac{1}{2},j}-u_{i-\frac{1}{2},j})+ d(u_{i+\frac{3}{2},j}-u_{i-\frac{3}{2},j})}{h}+\\&\frac{ a(u_{i+\frac{1}{2},j+1}+u_{i+\frac{1}{2},j-1}-u_{i-\frac{1}{2},j+1}-u_{i-\frac{1}{2},j-1})+ b(u_{i+\frac{3}{2},j+1}+u_{i+\frac{3}{2},j-1}-u_{i-\frac{3}{2},j+1}-u_{i-\frac{3}{2},j-1})}{h}. \end{aligned}$$

For grid nodes near the boundary, we use the standard fourth-order accurate one-sided finite-difference approximation of the first derivatives.

By a Taylor expansion, we obtain second-order accuracy provided that

$$\begin{aligned} c+3d+2a+6b=1, \end{aligned}$$

and fourth-order accuracy if the additional constraints hold:

$$\begin{aligned} c+27d+2a+54b&=0, \end{aligned}$$

(31a)

$$\begin{aligned} a+3b&=0. \end{aligned}$$

(31b)

We define the following stencils:

$$\begin{aligned}{} & {} K_2= \frac{1}{\Delta x} \begin{pmatrix} -b &{} -a &{} a &{} b \\ -d &{} -1+3d+2a+6b&{} 1-3d-2a-6b &{}d \\ -b &{} -a &{} a &{} b \end{pmatrix}, \end{aligned}$$

(32)

$$\begin{aligned}{} & {} K_4= \frac{1}{\Delta x} \begin{pmatrix} \frac{a}{3} &{}-a&{}a&{}-\frac{a}{3} \\ -\frac{16a-1}{24}&{} - \frac{9-16a}{8}&{} \frac{9-16a}{8} &{}\frac{16a-1}{24} \\ \frac{a}{3} &{} - a&{} a &{} -\frac{a}{3} \end{pmatrix}. \end{aligned}$$

(33)

The non-compact fourth-order accurate scheme, denoted by NC, exploits the stencil $K_4$ with $a\!=\!0$. Its order of accuracy is $O(h^4)+O(h_{t}^2)$.

Our last comparable scheme is a data-driven scheme, $AI^h$. We consider this approach since it has been recently shown to reduce the numerical dispersion for the wave equation [12]. The general framework for a data-driven scheme is described as follows. Let $\{(X^n,Y^n)\}_{n}$ be n-tuples of data-points such that for any n, $X^n\in \mathbb {R}^m$ and $Y^n\in \mathbb {R}^l$. We define a network $\mathcal {N}_{\textbf{a}}$ as a function from $\mathbb {R}^m\rightarrow \mathbb {R}^l$ which depends on parameters $\textbf{a}$. We define a loss function of the form $\mathcal {L}_{\textbf{a}}:=\sum _n |\mathcal {N}_{\textbf{a}}(X^n)-Y^n|$ where $|\cdot |$ is a given norm in $\mathbb {R}^l$. We solve the problem

$$\begin{aligned} \underset{\textbf{a}}{\textrm{argmin}} \ \mathcal {L}_{\textbf{a}} \end{aligned}$$

and obtain the optimal parameters $\textbf{a}$ and the corresponding optimal network $\mathcal {N}_{\textbf{a}}$. The minimization process can be done using variations of the gradient descent method. The data-driven scheme $AI^h$ uses the stencil $K_2$, where the free parameters are obtained by a minimization process over the given training data. This scheme is of order $O(h^2)+O(h_{t}^2)$. The details of the minimization process and the selected training data are given in “Appendix A.3”.

Table 4 Grid convergence for the three schemes we have chosen. N is the grid dimension

Table 5 The error for different CFL numbers r

5.3 Observations

In Table 4, we verify the fourth-order accuracy of our scheme C4 and provide the rates of grid convergence for the other two (NC, $AI^h$) schemes as well.

In Table 5, we examine the effect of the CFL number on the mean error and verify the results of our stability analysis (Sect. 4). For the points-per-wavelength (PPW) ratio of 64 ($k_x=k_y=2$), the mean error is smaller for scheme C4, as expected. Moreover, the NC scheme is more accurate than AI since it is of a higher spatial order, For the PPW ratio of approximately 6.4, the AI scheme shows a similar error to that of C4 even though it is of only second order. This is because the AI scheme was trained on coarse grids with a small number of points per wavelength.

In Fig. 3, we examine the mean error as a function of the wave number. As expected, as the PPW ratio decreases, the C4 scheme no longer outperforms the other schemes. This is consistent with the Taylor approximation where the local truncation error depends on higher-order derivatives that increase for shorter wavelengths (larger wavenumbers $\sqrt{k_x^2+k_y^2}$).

Fig. 3

In both panels $k_y=k_x$, $T=\frac{4}{\sqrt{2}}$, $Z=1$, and $h=\frac{1}{64}$. The points-per-wavelength ratio ranges from 64 ($\sqrt{k_x^2+k_y^2}=2$) to $\sim 2.5$ ($\sqrt{k_x^2+k_y^2}=50$)

In Figs. 4 and 5, we examine how the error behaves as a function of the time step. As expected, scheme C4 is more accurate when the wave number is low ($\sqrt{k_x^2+k_y^2}=2$) and the local truncation errors are relatively small. However, we see that for $k_x=k_y=11$ the non-compact scheme is more accurate for $r=\frac{1}{6\sqrt{2}}$ while C4 is more accurate for $r=\frac{5}{6\sqrt{2}}$ when the time step increases and as a result the temporal error is larger.

Fig. 4

The numerical error for different wavenumbers. $h=\frac{1}{64}, r=\frac{1}{6\sqrt{2}}$, $Z=1$

Fig. 5

The numerical error for different wavenumbers. $h=\frac{1}{64}, r=\frac{5}{6\sqrt{2}}$, $Z=1$

Moreover, we see that for $r=\frac{1}{6\sqrt{2}}$, the scheme NC is more accurate than AI while the situation is the opposite for $r=\frac{5}{6\sqrt{2}}$. This is not a surprise since the dispersion effects may grow as the time step increases [2].

For higher wave numbers ($\sqrt{k_x^2+k_y^2}=29$ and $\sqrt{k_x^2+k_y^2}=51$), the fourth-order accuracy of C4 and the spatial fourth-order accuracy of NC lose their advantage due to the pollution effect, and as the wave number increases the AI scheme demonstrates a similar accuracy even though it is only second-order accurate in both time and space.

6 Conclusions

We have constructed a compact implicit scheme for the 3D Maxwell’s equations. The scheme is fourth-order accurate in both space and time and can be useful for long-time simulations, including scenarios where the PPW ratio is not very high. The scheme is compact and maintains its accuracy near the boundaries using equation-based approximations. The temporal grid is staggered, which allows us to solve 3 scalar uncoupled elliptic equations at each half-time step. That can be done in parallel using the conjugate gradient method. The elliptic equations are strictly positive definite, which yields rapid convergence of the iterative scheme. With a fixed CFL number, approximately three iterations of the conjugate gradient are required for convergence regardless of the grid size. This is likely explained by the fact that the amount of positivity in Eq. (12) increases as the grid length decreases because the quantity $\frac{24}{h_t^2}$ becomes larger as h decrease and the CFL number remains fixed. Overall, the method is efficient in both CPU and memory requirements. Although we have tested numerically only 2D examples, the implementation in 3D is straightforward.

Since the method we have presented is a finite-difference scheme, the pollution effect cannot be avoided completely. For higher wavenumbers, lower-order methods obtained by minimizing a certain loss function over the stencil parameters (such as data-driven) can outperform higher-order schemes.

A Appendix

1.1 A.1 Operator Details

Let $\otimes$ denote the Kronecker product of matrices and let I, J, K be index sets. Let

$$\begin{aligned} D_1= \frac{1}{h} \begin{pmatrix} -1 &{} 1 &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} -1 &{} 1 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} 0 &{} -1 &{} 1 &{} 0 &{} \dots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 0 &{} -1 &{} 1 &{} 0 \\ 0 &{} 0 &{} \dots &{} 0 &{} 0 &{} -1 &{} 1 \end{pmatrix} \end{aligned}$$

(34)

denote the standard central finite-difference matrix with grid size h/2 whose dimension equals $(m-1)\times m$, where $m\in \{|I|, |J|,|K|\}$. We define the following operators from $I\times J\times K$ to $I\times J\times K$.

$$\begin{aligned}&D_x:=D_1\otimes \textbf{1}_J\otimes \textbf{1}_K,\\&D_y:= \textbf{1}_I\otimes D_1\otimes \textbf{1}_K, \\&D_z:= \textbf{1}_I\otimes \textbf{1}_J\otimes D_1. \end{aligned}$$

Next, we consider a fourth-order accurate approximation for the first derivatives: Assume that f(x) is known at N points $x_0,x_1,..,x_{N-1}$. Then, one estimates $f'(x+h/2)$ at the $N-1$ points $x_{\frac{1}{2}},..,x_{N-3/2}$ to fourth order as:

$$\begin{aligned} \underbrace{ \frac{1}{24} \begin{pmatrix} 26 &{} -5 &{} 4 &{} -1 &{} 0 &{} \dots &{} 0 \\ 1 &{} 22 &{} 1 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} 1 &{} 22 &{} 1 &{} 0 &{} \dots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 1 &{} 22 &{} 1 &{} 0 \\ 0 &{} 0 &{} \dots &{} 0 &{} 1 &{} 22 &{} 1 \\ 0 &{} 0 &{} \dots &{} -1 &{} 4 &{} -5 &{} 26 \end{pmatrix}}_{A} \begin{pmatrix} f'(x_{\frac{1}{2}}) \\ f'(x_{3/2}) \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ f'(x_{N-3/2}) \end{pmatrix}= \frac{1}{h} \begin{pmatrix} f(x_{1})-f(x_0) \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ f(x_{N-1)}-f(x_{N-2}) \end{pmatrix}+O(h^4).\quad \end{aligned}$$

(35)

We define the following operators from $I\times J\times K$ to $I\times J\times K$.

$$\begin{aligned}&a_x^{-1}:=A^{-1}\otimes \textbf{1}_J\otimes \textbf{1}_K,\\&a_y^{-1}:= \textbf{1}_I\otimes A^{-1}\otimes \textbf{1}_K, \\&a_z^{-1}:= \textbf{1}_I\otimes \textbf{1}_J\otimes A^{-1}, \end{aligned}$$

and

$$\begin{aligned}&\delta _x:=a_x^{-1}D_x,\\ {}&\delta _y:=a_y^{-1}D_y, \\&\delta _z:=a_z^{-1}D_z. \end{aligned}$$

Finally, we define a fourth-order approximation of the curl operator as a matrix that operates on the vectorized tensor of dimension $|I|\cdot |J| \cdot |K|\times 1$:

$$\begin{aligned} \textbf{curl}_h:= \begin{pmatrix} 0&{} -\delta _z &{} \delta _y\\ \delta _z&{}0&{}-\delta _x\\ -\delta _y&{}\delta _x&{}0\\ \end{pmatrix}. \end{aligned}$$

Remark 2

By [7, section 11], $\Vert \textbf{curl}_h\Vert \le \frac{2\Vert A^{-1}\Vert \sqrt{3}}{h}$ and by [18], $\Vert A^{-1}\Vert \sim \frac{6}{5}$.

We recall the standard second-order finite difference matrices for the second derivative. We define the operators $D_{xx},D_{yy},D_{zz}$ from $I\times J\times K$ to $I\times J\times K$ using the square matrix

$$\begin{aligned} D_2= \frac{1}{h^2} \begin{pmatrix} -2 &{} 1 &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ 1 &{} -2 &{} 1 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} 1 &{} -2 &{} 1 &{} 0 &{} \dots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 1 &{} -2 &{} 1 &{} 0 \\ 0 &{} 0 &{} \dots &{} 0 &{} 1 &{} -2 &{} 1 \\ 0 &{} 0 &{} \dots &{} 0 &{} 0 &{} 1 &{} -2 \end{pmatrix}, \\&D_{xx}:=D_2\otimes \textbf{1}_J\otimes \textbf{1}_K,\\ {}&D_{yy}:= \textbf{1}_I\otimes D_2\otimes \textbf{1}_K, \\ {}&D_{zz}:= \textbf{1}_I\otimes \textbf{1}_J\otimes D_2. \end{aligned}$$

1.2 A.2 Operator Estimates

Let $r=\frac{h_{t}}{h}$ be the CFL number. Consider the finite-difference operators

$$\begin{aligned} P_1:=-\left( \Delta _h+\frac{h^2}{6}\varUpsilon _h\right) +\frac{24}{h_{t}^2}\left( 1+\frac{2}{r^2} \right) , \end{aligned}$$

and

$$\begin{aligned} P_2:=\frac{24}{h_{t}^2}\left( -1-\frac{2}{r^2}-\frac{h^2}{12}\Delta _h \right) , \end{aligned}$$

where

$$\begin{aligned} \Delta _h{\mathop {=}\limits ^{\text {def}}}D_{xx}+D_{yy}+D_{zz}, \quad \varUpsilon _h{\mathop {=}\limits ^{\text {def}}} D_{zz}D_{xx}+D_{yy}D_{zz}+D_{xx}D_{yy}. \end{aligned}$$

Let $\sigma (\cdot )$ denote the spectrum of a given operator. The inclusion

$$\begin{aligned} \sigma (h^2\Delta _h)\subset [-12,0] \end{aligned}$$

implies that

$$\begin{aligned} \frac{h_{t}^2}{24}\sigma (-P_{2})\subset [1+2/r^2-1, 1+2/r^2]. \end{aligned}$$

The operator $\frac{h_{t}^2}{24}\left( -\Delta _h-\frac{h^2}{6}\varUpsilon _h \right) +1+\frac{2}{r^2}$ operates on a Fourier ansatz $\exp (\sqrt{-1}(i\theta _x+j\theta _y+k\theta _z)$ by

$$\begin{aligned}&1+\frac{2}{r^2}+\frac{r^2}{24}\underbrace{\left( 6-2(\cos \theta _x+\cos \theta _y+\cos \theta _z) -\frac{4T}{6} \right) }_{S}, \end{aligned}$$

where

$$\begin{aligned} T= (\cos (\theta _z)-1)(\cos (\theta _x)-1)+ (\cos (\theta _x)-1)(\cos (\theta _y)-1)+ (\cos (\theta _z)-1)(\cos (\theta _y)-1), \end{aligned}$$

and $-4\le S\le 12$. Hence,

$$\begin{aligned} \begin{aligned} \frac{h_{t}^2}{24}\sigma (P_{1})\subset [1+2/r^2-r^2/6, 1+2/r^2+r^2/2] , \\ \frac{h_{t}^2}{24} \sigma (- P_2)\in [1+\frac{2}{r^2}-1, 1+\frac{2}{r^2}]. \end{aligned} \end{aligned}$$

(36)

As a result, $r<\sqrt{3+\sqrt{21}}$ implies that $-P_2, P_1$ are positive definite and

$$\begin{aligned} 0<\frac{2}{r^2}\le \Vert \frac{h_{t}^2}{24}P_{2}\Vert \le 1+\frac{2}{r^2}, \end{aligned}$$

and

$$\begin{aligned} 0<1+\frac{2}{r^2}-\frac{r^2}{6}\le \Vert \frac{h_{t}^2}{24}P_1\Vert \le 1+\frac{2}{r^2}+\frac{r^2}{2}. \end{aligned}$$

1.3 A.3 The Data-Driven Scheme $AI^h$

We follow the approach of [12]. We wish to find the optimal parameters a, b, d for evaluation of the first derivative using the stencil

$$\begin{aligned} K_2= \frac{1}{\Delta x} \begin{pmatrix} -b &{} -a &{} a &{} b \\ -d &{} -1+3d+2a+6b&{} 1-3d-2a-6b &{}d \\ -b &{} -a &{} a &{} b \end{pmatrix} \end{aligned}$$

in Yee updating rules (see Sect. 5.2). The network will be a function that takes a solution $\textbf{E}^n, \textbf{H}^{n+1/2}$ and returns $\textbf{E}^{n+1},\textbf{H}^{n+3/2}$ using Yee updating rules. We generate a data set of analytical solutions using (30a) as follows. We fix $h=\frac{1}{16}$, CFL number r and the corresponding $h_{t}$. We also fix the final time T. The number of spatial grid points is then denoted by N and the number of times steps is denoted by $N_{t}$. For any $(k_x,k_y)$ in $\{12,13,14,15\}^2$ we generate analytical solutions $E_z,H_x,H_y$ defined by (30a). For any $0\le n \le N_{t}$ we let ${E_z}^n_{k_x,k_y,\textrm{true}},{H_x}^n_{k_x,k_y\textrm{true}},{H_y}^n_{k_x,k_y,\textrm{true}}$ be the corresponding values of the analytical solutions evaluated at the time $t=nh_{t}$. We let

$$\begin{aligned} X^{n,k_x,k_y}:=({E_z}^n_{k_x,k_y,\textrm{true}},{H_x}^n_{k_x,k_y\textrm{true}},{H_y}^n_{k_x,k_y,\textrm{true}}). \end{aligned}$$

Next, we build the network, $\mathcal {N}_{a,b,d}$, which takes a numerical solution at time step n and outputs the solution at time $n+1$ evaluated using Yee updating rules with the stencil $K_2$.

A single data point in our data set is then defined by $(\textrm{input}^{n,k_x.k_y}, \textrm{output}^{n,k_x,k_y})$ where

$$\begin{aligned} \textrm{input}^{n,k_x,k_y}=X^{n,k_x,k_y} \end{aligned}$$

and

$$\begin{aligned} \textrm{output}^{n,k_x,k_y}=(X^{n+1,k_x,k_y}, X^{n+2,k_x,k_y}, X^{n+3,k_x,k_y}). \end{aligned}$$

We omit the superscripts $k_x,k_y$ from now on.

The loss function is then defined over all data points as follows:

$$\begin{aligned} \mathcal {L}_{a,b,d}=\sum _n|X^{n+1}-\mathcal {N}(X^n)|+|X^{n+2}-\mathcal {N}(\mathcal {N}(X^n))|+ |X^{n+3}-\mathcal {N}(\mathcal {N}(\mathcal {N}(X^n)))|\nonumber \\ \end{aligned}$$

(37)

where $|\cdot |$ in (37) is taken to be the mean absolute error between two vectors. The loss function is minimized using Adam optimizer and Keras [4] over the data points with the usual splitting routine of train, test, and validation sets.