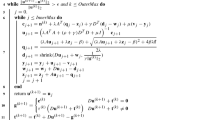1 Introduction

In the field of image processing, recovering clear images from blurred and noisy observations is a fundamental task. Image degradation occurs when acquisition equipment or lighting affects the image. Therefore, images obtained from devices or machines can be corrupted by various types of ‘pollution’, such as noise and blur. Hence, image denoising and deblurring have received significant attention in applied mathematics over the years. Noise is a useless signal, and two types of noise have been widely studied: additive noise [23, 26, 28] and multiplication noise [24, 25, 27].

Additive noise is a random process independent of the signal. If vector b is the additive Gaussian noise with standard variance \(\sigma \) and mean 0, the degraded image f is formulated as

$$\begin{aligned} f=Hw+b, \end{aligned}$$
(1)

where w represents the original image, and H is a linear operator. Many methods have been developed to recover w from f, such as variational-based methods [12, 20], nonlocal methods [13, 26], wavelet-based methods [23, 28], and so on. Among these methods, the regularization methods based on total variation (TV) and the wavelet frame were widely used to handle the additive noise with deblurring simultaneously. For instance, the Rudin-Osher-Fatemi (ROF) model [31] based on TV has been widely used. Differing from the TV-based regularization, wavelet frame based approaches have also been widely used due to their multi-resolution structure, sparse representations, and high redundancy [23].

On the other hand, multiplicative noise is proportional to the signal, and the noise model with blur can be formulated as

$$\begin{aligned} f=Hw\eta , \end{aligned}$$
(2)

where \(\eta \) denotes multiplicative noise, which follows standard distributions such as Gamma distributions. The probability density function of multiplicative Gamma noise [2] is defined as

$$\begin{aligned} p(\eta ;K)=\frac{K^K}{(K)}\eta ^{K-1}e^{-K\eta }\textbf{1}_{\{\eta \ge 0\}}, \end{aligned}$$
(3)

where \(\textbf{1}_{\{\eta \ge 0\}}\) represents the indicator function of the subset \(\{\eta |\eta \ge 0\}\), \(\varGamma (\cdot )\) is the classical Gamma function, \(\eta \) follows a gamma law with mean 1, and the variance of \(\eta \) is 1/K. The integer K determines the level of the Gamma noise.

Methods employed in literature for multiplicative noise and blur removal include diffusion equation methods [32, 38], nonlocal low-rank based methods [15, 24], and variational-based methods [4, 40]. In these methods, Rudin, Lions and Osher [30] introduced TV regularization to multiplicative noise and proposed the first variational model, known as the RLO model. However, the RLO model cannot produce effective results in restoring Gamma noise. Aubert and Aujol [2] introduced a second variational model, referred to as the AA model, which employed Bayesian Maximum A Posteriori (MAP) probability estimation. The authors in [2] expanded the denoising model to handle the deblurring problem, in which the gradient projection-based algorithm was used in their model. Because of the nonconvexity of the AA model, the resulting optimization problem is not easy to solve. To overcome this difficulty, Dong and Zeng [11] proposed two models for image restoration. The first model, denoted as the DZ model, is a generalized model that modifies the data fidelity term by adding a quadratic penalty term. This modification guarantees the convexity of the objective function under mild conditions. The second model is a strictly convex model that guarantees the uniqueness of the solution. Dong and Zeng achieved this by using the I-divergence technique. To solve the convex models, they used the split Bregman algorithm. Through the use of the logarithm to transform the multiplicative noise and blur removal problem into the additive noise and blur removal problem, Shi and Osher [33] proposed an SO model with a quadratic term, which is globally convex. The experimental results demonstrate that these TV regularization-based models have good performance in image restoration, such as effectively preserving edges and details in images, whereas stair-casing artifacts would be inevitable with TV.

The wavelet frames-based regularization method is a typical sparsity-based method for image restoration. There are three different types of wavelet models, i.e., analysis-based models [1, 5], synthesis-based models [6, 10], and balance models [3, 7]. In the analysis-based approach, assuming that the wavelet tight frame coefficient W of the natural image w is sparse, the size of Ww can adaptively represent the regularity of the underlying image. Due to the redundancy and multi-resolution structure of the wavelet tight frame, the wavelet-based approach can significantly improve the quality of the recovered image.

In reality, however, the type of noise may be neither additive nor multiplicative. Instead, it might be a mixture of the same type [16, 36] or a mixture of these two types [18, 35]. However, the previously mentioned methods can not deal with this problem directly. Recently, many methods have been proposed to solve mixed noise. Thanh et al. [34] proposed a model based on TV to deal with a mixture of Poisson-Gaussian noise. Wang et al. [36] proposed an adaptive algorithm based on CNN deep learning, namely EM-CNN. It combined traditional variational methods and deep learning-based algorithms to remove Gaussian-Gaussian noise or Gaussian-impulse noise. Some works also have been proposed for removing mixed Gaussian-Gamma noise. Ullah et al. [35] proposed a new model using a linear combination of the fractional total variation, image priors, and the data fidelity term in [31]. They used an empirical selection of the parameters to balance the above three items. Huang et al. [14] focused on variational approaches to obtain restorations. Since the model was non-convex, a convex relaxation model was proposed. Although those methods present competitive performance in handling mixture noise removal task, they perform mediocrely in deblurring tasks, such as the boundaries are still blurred.

In this paper, the restoration of blurred images corrupted by a mixture of additive Gaussian noise and multiplicative Gamma noise is studied. The mathematical expression of the degraded image f is formulated as follows:

$$\begin{aligned} f=(Hw+b)\eta . \end{aligned}$$
(4)

To address this issue, we propose a novel model that uses regularizer based on wavelet tight frame. Specifically, our model incorporates a convexity-preserving term, which ensures that the objective function is convex under mild conditions. By using wavelet tight frame as a regularization term, our model is able to preserve image details while removing noise and blurring. Then, we develop an inexact symmetric Gauss–Seidel-based majorized semi-proximal alternating direction method of multipliers (sGS-imsPADMM) with relative error control for solving the proposed model. The experiments demonstrate that the proposed method is well suited to mixed noise and blur removal simultaneously. The main contributions of this work are three-fold:

  • We propose a novel convex model to deal with degraded images corrupted by mixed Gaussian-Gamma noise and blur. We utilize the convexity preserving term and wavelet tight frame regularization into the non-convex model to obtain a solvable convex model.

  • We develop an inexact sGS-imsPADMM with relative error control for solving the proposed model because it can reduce the cost of solving subproblems and achieve appropriate accuracy. Although sGS-imsPADMM has not been widely considered in imaging science, it is a nice example explaining the excellent performance of the algorithm that can be applied to image processing problems.

  • The extensive experiments demonstrated that the proposed model surpasses state-of-the-art models in removing mixed Gaussian-Gamma noise as well as blur. Moreover, the proposed inexact sGS-imsPADMM approach with relative error control can achieve a better solution in terms of restoration quality while also being faster than other methods like ADMM.

The rest of the paper is organized as follows. In Sect. 2, the related models for restoring blurred images with mixed noise are briefly reviewed, and we propose a novel model for mixed noise and blur removal. Section 3 presents an iterative algorithm for solving corresponding convex optimization problems and gives the convergence analysis. In Sect. 4, some numerical experiments are conducted to demonstrate the efficiency and superiority of the proposed model and solving method. Section 5 concludes this paper.

2 A Novel Model for Denoising and Deblurring

In this section, we give a review of some related models in image restoration. Then, we propose a novel model by using a regularizer based on wavelet tight frame and a convexity-preserving term, to restore blurred images with Gaussian-Gamma noise.

As mentioned before, Huang et al. [14] introduced an intermediate image \(u=Hw+b\) to derive a variational model from (4), in which u can be regarded as a convolution image with additive Gaussian noise b. In this approach, it is assumed that b is small. Moreover, it can be further assumed that \(\text{ inf } f >0\), then suppose that \(0<\sigma \le 2\text{ inf } f\). The variational model [14] can be described as follows:

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu A(w), \end{aligned}$$
(5)

where \(\mu \) is a positive parameter. The last term A(w) is a convex regularization term to prevent the model from over-fitting. Due to the non-convexity of the term \(\log u\), the above model is non-convex and difficult to handle. To this end, they proposed to approximate the above model by a convex relaxation model.

Inspired by the convex relaxation model, we introduce a quadratic convex term to ensure that the model is component-wise convex on u. From this, a convex model for denoising and deblurring is proposed:

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| \sqrt{u}-\sqrt{f}\right\| _2^2+\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu A(w), \end{aligned}$$
(6)

where \(\alpha \) is a positive parameter. The preservation of convexity in the model not only guarantees its convexity but also enhances the overall effectiveness of image restoration to a certain degree. Further details on this matter will be discussed in the experimental section.

An important property of the image recovery process is the sparse representation of the image. The use of wavelet tight frame to represent an image is beneficial in ensuring the existence of sparsity. To demonstrate the advantages of the model’s flexibility, we consider a model with wavelet tight frame regularization that can improve the performance of both deblurring and denoising of mixed noise, especially for Gaussian-Gamma noise. Generally, we propose the following model:

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| \sqrt{u}-\sqrt{f}\right\| _2^2+\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu \Vert Ww\Vert _1, \end{aligned}$$
(7)

where W is the framelet transform satisfying \(W^{T}W=I\) with the identity matrix I.

We demonstrate the convexity of the proposed model (7) under certain mild conditions in the following, as discussed in [11].

Proposition 1

If \(\alpha \ge \frac{(3-\inf f)\sqrt{6}}{9\sup \sqrt{f}}\), the model (7) is component-wise convex on u.

Proof

Let \(E(u) = \langle \log u+\frac{f}{u},1\rangle +\alpha \Vert \sqrt{u}-\sqrt{f}\Vert _2^2\). With \(t\in \mathbb {R}^{+}\) and parameter \(\alpha \), we define a function g as

$$\begin{aligned} g(t):= \log t+\frac{f}{t}+\alpha (\sqrt{t}-\sqrt{f})^2. \end{aligned}$$

We can get the second-order derivative differentiation of g as

$$\begin{aligned} g''(t)=-t^{-2}+2ft^{-3}+\frac{\alpha \sqrt{f}}{2}t^{-\frac{3}{2}}. \end{aligned}$$

Thus, when \(\alpha \ge \frac{(3-\inf f)\sqrt{6}}{9\sup \sqrt{f}}\), we have \(g''(t)\ge 0\), i.e., g is convex. Furthermore, since function g has only one minimizer, g is strictly convex when \(\alpha =\frac{(3-\inf f)\sqrt{6}}{9\sup \sqrt{f}}\). Therefore, the function \(\langle \log u+\frac{f}{u},1\rangle +\alpha \Vert \sqrt{u}-\sqrt{f}\Vert ^2_2+\frac{\Vert Hw-u\Vert ^2_2}{2\sigma ^2}\) is strictly convex. Based on the convexity of the wavelet tight frame regularization, we conclude that the model (7) is convex. \(\square \)

3 Algorithm and Convergence Analysis

This section proposes an iterative algorithm to solve the proposed model (7). The objective function in (7) is convex, and there are various optimization algorithms that can be applied to this problem, such as classical ADMM. Although the objective function of the proposed model can be split into two-block convex functions, solving the ADMM subproblems with high accuracy can be computationally expensive. To reduce the computational burden, one strategy is to divide the variables in (7) into three or more blocks based on their composite structures and solve the resulting problems using a multi-block ADMM type that directly extends the 2-block ADMM to a multi-block setup. However, this method of direct scaling may not converge, which can be a potential issue. Therefore, we propose an inexact sGS-imsPADMM algorithm to solve (7). This algorithm can reduce the cost of solving subproblems while ensuring theoretical convergence.

3.1 An Inexact sGS-imsPADMM with Relative Error Control for Solving (7)

By introducing an auxiliary variable x, we first reformulate the minimization problem (7) into an equivalent one as follows:

$$\begin{aligned} \begin{aligned}&\min _{u,w,x}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| \sqrt{u}-\sqrt{f}\right\| _2^2+\frac{\Vert Hw-u\Vert ^2_2}{2\sigma ^2}+\mu \Vert x\Vert _1,\\&~\text{ s.t. }\quad x-Ww=0. \end{aligned} \end{aligned}$$
(8)

Define \(y_1=u\), \(y_2=w\) and \(y=(y_1, y_2)\), \(x\in \mathcal {X}\) and \(y\in \mathcal {Y}\), then problem (8) falls within the following general convex composite programming:

$$\begin{aligned} \begin{aligned}&\min _{x\in \mathcal {X},y\in \mathcal {Y}}\mu \Vert x\Vert _1+\frac{\Vert Hy_2-y_1\Vert ^2_2}{2\sigma ^2}+\left\langle \log y_1+\frac{f}{y_1},1\right\rangle +\alpha \left\| \sqrt{y_1}-\sqrt{f}\right\| ^2_2, \\&\quad \text{ s.t. }\quad x-Wy_2=0. \end{aligned} \end{aligned}$$
(9)

Let us define \(g(y)=g(y_1,y_2):= \frac{\Vert Hy_2-y_1\Vert ^2_2}{2\sigma ^2}\). Then it is a continuously differentiable and convex function, and its gradient is Lipschitz continuous. Therefore, there exists a positive semidefinite matrix \(\varSigma _g\) such that for any \(y,~y'\in \mathcal {Y}\),

$$\begin{aligned} g(y)\le \widehat{g}(y;y'):= g(y')+\left\langle \nabla g(y'),y-y'\right\rangle +\frac{1}{2}\left\| y-y'\right\| ^2_{\varSigma _g}. \end{aligned}$$
(10)

Define \(p(x):= \mu \Vert x\Vert _1\) and \(q(y):= \left\langle \log y_1+\frac{f}{y_1},1\right\rangle +\alpha \left\| \sqrt{y_1}-\sqrt{f}\right\| ^2_2\), and it follows from Proposition 1 that both of them are closed proper convex functions when \(\alpha \ge \frac{(3-\inf f)\sqrt{6}}{9\sup \sqrt{f}}\). For any \(z:=(x,y,l)\in \mathcal {X}\times \mathcal {Y}\times \mathcal {L}\) and \((x',y')\in \mathcal {X}\times \mathcal {Y}\), the majorized augmented Lagrangian function associated with (9) is

$$\begin{aligned} L_{\beta }(x,y;(x',y',l))=p(x)+q(y)+\widehat{g}(y;y') +\left\langle l,x-Wy_2\right\rangle +\frac{\beta }{2}\left\| x-Wy_2\right\| ^2_2, \end{aligned}$$
(11)

where \(\beta \) is the penalty parameter and l is the Lagrangian multiplier.

We say that the Slater constraint qualifying (CQ) holds for problem (9), if it satisfies

$$\begin{aligned} \{(x, y)\mid x\in \text{ ri }(\text{ dom }~p),~y\in \text{ ri }(\text{ dom }~q),~ x-Wy_2=0\} \ne \emptyset , \end{aligned}$$
(12)

where ‘dom’ represents the domain of definition, and ‘ri’ represents taking the open set of the domain of definition. When the Slater CQ is satisfied, according to Corollaries 28.2.2 and 28.3.1 in [29], the solution set of (9) is non-empty.

In the following, we propose an inexact sGS-imsPADMM with relative error control for solving the proposed model (7). The concrete algorithm framework is summarized in Algorithm 1.

Algorithm 1
figure a

An inexact sGS-imsPADMM with relative error control for solving (7).

Full size image

Next, we explain how to solve these subproblems in Algorithm 1, respectively. For x-subproblem in Step 1, we have

$$\begin{aligned} \begin{aligned} x^{k+1}=\arg \min _{x}L_{\beta }(x,y_1^k,y_2^k;z^k)+\frac{1}{2}\left\| x-x^k\right\| ^2_{\mathcal {P}}. \end{aligned} \end{aligned}$$
(13)

The above problem is equivalent to evaluating the proximal operator of the \(\ell _1\)-norm function, which has a closed-form solution as follows:

$$\begin{aligned} x^{k+1}=\mathcal {T}_{\mu /(\beta +\lambda _{\max }(\mathcal {P}))}\left( \frac{\beta Wy^k_1-l^k+\mathcal {P}x^k}{\beta +\lambda _{\max }(\mathcal {P})}\right) , \end{aligned}$$
(14)

where \(\lambda _{\max }(\mathcal {P})\) denotes the largest eigenvalue of the matrix \(\mathcal {P}\) and the operator \(\mathcal {T}_\sigma \) is a soft-thresholding operator defined as

$$\begin{aligned} (\mathcal {T}_{\sigma }(x))_i=\text{ sgn }(x_i)[|x_i|-\sigma ]_{+}, \end{aligned}$$
(15)

with sgn(\(\cdot \)) being a signum function and \([x_i]_{+}\) means max\((x_i,0)\).

The \(y_1\)-subproblem in Step 2b of Algorithm 1 can be read as

$$\begin{aligned} y_1^{k+1}\approx \arg \min _{y_1}L_{\beta }\left( x^{k+1},y_1,\widetilde{y}_2^{k+1};z^k\right) +\frac{1}{2}\left\| y_1-y_1^k\right\| ^2_{{\mathcal {{\widetilde{Q}}}}_1}, \end{aligned}$$
(16)

which can be computed inexactly by Newton iterative method and then the corresponding error vector \(\gamma _1^{k+1}\) can be obtained.

The \(y_2\)-subproblem in Step 2b is equivalent to solving the following linear system:

$$\begin{aligned} \gamma _2^{k+1}\in \frac{H^T(Hy_2-y_1^{k+1})}{\sigma ^2}-\beta W^T\left( x^{k+1}-Wy_2+\frac{l^k}{\beta }\right) +(\varSigma _g+\widetilde{\mathcal {Q}}_2)(y_2-y_2^k). \end{aligned}$$
(17)

Under the periodic boundary condition (BC) for \(y_1\), and since \(W^TW = I\), where I is identity matrix. We can use Fourier transform to compute the solution of (17).

3.2 Convergence Analysis

In this section, we first give the Karush-Kuhn-Tucker (KKT) condition, and prove the convergence of the simplified algorithm under the premise that the solution exists.

It follows from [29] that \((\bar{x}, \bar{y})\in \mathcal {X}\times \mathcal {Y}\) is the solution of problem (9) if and only if there is a Lagrangian multiplier \(\bar{l}\in \mathcal {L}\) of the augmented Lagrangian function for (9), such that \((\bar{x}, \bar{y}, \bar{l})\in \mathcal {X}\times \mathcal {Y}\times \mathcal {L}\) is the solution of the following KKT conditions

$$\begin{aligned} 0\in \partial p(x)+l,\quad 0\in \partial q(y)+\nabla g(y)-W^Tl,\quad 0=x-Wy_2. \end{aligned}$$
(18)

We denote \(z:= (x, y, l)\) and \(\mathcal {Z}:=\mathcal {X}\times \mathcal {Y}\times \mathcal {L}\), then the solution set of KKT system (18) for problem (9) is denoted by \(\bar{\mathcal {Z}}\).

Let \(\theta :\mathcal {V}\rightarrow (-\infty ,+\infty ]\) be a closed convex function, then the Moreau-Yosida proximal mapping \(\varPi _{\theta }(v)\) related to \(\theta \) is defined as

$$\begin{aligned} \varPi _{\theta }(v):=\mathop {\arg \min }_{v'\in \mathcal {V}} \left\{ \theta (v')+\frac{1}{2}\Vert v'-v\Vert ^2 \right\} ,\quad \forall v\in \mathcal {V}. \end{aligned}$$
(19)

The Moreau-Yosida proximal map [17] is a globally Lipschitz, that is,

$$\begin{aligned} \Vert \varPi _{\theta }(v)-\varPi _{\theta }(v')\Vert ^2\le \langle v-v',\varPi _{\theta }(v)-\varPi _{\theta }(v')\rangle . \end{aligned}$$
(20)

We define the KKT mapping \(e(\cdot ):\mathcal {Z}\rightarrow \mathcal {Z}\) as

$$\begin{aligned} e(z) :=\left( \begin{array}{c} x-\varPi _{p}(x-Il) \\ y-\varPi _{q}(y-(\nabla g(y)-W^Tl)) \\ -x+Wy_2 \end{array} \right) , \quad \forall z\in \mathcal {Z}. \end{aligned}$$
(21)

Note that there exists \(z^*\in \bar{\mathcal {Z}}\) if and only if \(e(z^*)=0\).

Next, for the positive semidefinite matrix \(\varSigma _g\), we use the following decomposition:

$$\begin{aligned} \left( \begin{array}{cc} (\varSigma _g)_{11} &{} (\varSigma _g)_{12} \\ (\varSigma _g)^{T}_{12} &{} (\varSigma _g)_{22} \end{array} \right) , \end{aligned}$$
(22)

and define the matrices \(\mathcal {M}\) and \(\widetilde{\mathcal {N}}\) as follows:

$$\begin{aligned} \mathcal {M}:=\mathcal {P}+\beta I^TI=\mathcal {P}+\beta I\quad \text{ and }\quad \widetilde{\mathcal {N}}:=\varSigma _g+\widetilde{\mathcal {Q}} +\beta W^TW=\varSigma _g+\widetilde{\mathcal {Q}} +\beta I. \end{aligned}$$
(23)

Accordingly, we further define \(\mathcal {N}_d:=\text{ Diag }(\mathcal {N}_{11},\mathcal {N}_{22})\), where \(\mathcal {N}_{11}:= \widetilde{\mathcal {Q}}_1+(\varSigma _g)_{11}\) and \(\mathcal {N}_{22}:= \widetilde{\mathcal {Q}}_2+(\varSigma _g)_{22}+\beta I\).

From the above definitions, we have

$$\begin{aligned} \widetilde{\mathcal {N}}=\left( \begin{array}{cc} \mathcal {N}_{11} &{} \frac{1}{2}(\varSigma _g)_{12} \\ \frac{1}{2}(\varSigma _g)^{T}_{12} &{} \mathcal {N}_{22} \end{array} \right) =\mathcal {N}_d+\mathcal {N}_r+\mathcal {N}_r^T, \end{aligned}$$
(24)

where \(\mathcal {N}_r\) is the strictly upper triangular part of \(\widetilde{\mathcal {N}}\). Moreover, we define the following matrices:

$$\begin{aligned} \begin{aligned} \mathcal {Q}&:= \widetilde{\mathcal {Q}}+\text{ sGS }(\widetilde{\mathcal {N}}),\quad \mathcal {N}:=\varSigma _g+\mathcal {Q} +\beta I=\widetilde{\mathcal {N}}+\text{ sGS }(\widetilde{\mathcal {N}}), \end{aligned} \end{aligned}$$
(25)

where \(\text{ sGS }(\mathcal {N}):=\mathcal {N}_r\mathcal {N}_d^{-1}\mathcal {N}_r^T\). Denote \(d^{k+1}_y:= \gamma ^{k+1}+\mathcal {N}_r\mathcal {N}_d^{-1}(\gamma ^{k+1}-\widetilde{\gamma }^{k+1})\). Then we have the following proposition.

Proposition 2

The sequences \(\{(x^k, y^k, l^k)\}\), \(\{\gamma ^k\}\) and \(\{\widetilde{\gamma }^k\}\) generated by the sGS-imsPADMM are well-defined. For any \(k \ge 0\), \(d^{k+1}_y\) satisfy

$$\begin{aligned} \left\| d^{k+1}_y\right\| ^2_{\mathcal {N}^{-1}}\le c' \varepsilon ^2_k \left( \left\| y^{k}-y^{k-1}\right\| ^2_{\mathcal {N}}+\left\| y^{k+1}-y^{k}\right\| ^2_{\mathcal {N}}\right) , \end{aligned}$$
(26)

where \(c'\) is defined as

$$\begin{aligned} \begin{aligned} c':= \left( 4\left\| \mathcal {N}_d^{-\frac{1}{2}} \right\| ^2+2\left\| \mathcal {N}_d^{-\frac{1}{2}}(\mathcal {N}_d+\mathcal {N}_r)^{-1}\right\| ^2\right) \bigg /\lambda ^2_{\min }\mathcal {N}>0. \\ \end{aligned} \end{aligned}$$
(27)

Proof

According to the sGS decomposition theorem ( [8], Proposition 4.1 and [21], Theorem 1), Proposition 4.1 [9] and Proposition 2 [19], we can readily show that the sequences are well-defined and that (26) holds. \(\square \)

We define the mapping \(\mathcal {R}: \mathcal {X}\times \mathcal {Y}\) by \(\mathcal {R}(x, y):=x- Wy_1\), \(\forall (x, y)\in \mathcal {X}\times \mathcal {Y}\), and introduce some notations in the following, for \(k\ge 0\),

$$\begin{aligned} \varDelta ^k_x:= x^k-x^{k+1},\quad \varDelta ^k_y :=y^k-y^{k+1},\quad r^k:= \mathcal {R}\left( x^k, y^k\right) ,\quad \tilde{l}^{k+1}:= l^k+\beta r^{k+1}, \end{aligned}$$
(28)

with the convention that \(\bar{y}^0 = y^0\).

Lemma 1

[8, Lemma 5.1] Let \(\{a_k\}_{k\ge 0}\) be a nonnegative sequence satisfying \(a_{k+1}\le a_k+\varepsilon _k\) for all \(k\ge 0\), where \(\{\varepsilon _k\}_{k\ge 0}\) is a nonnegative and summable sequence of real numbers. Then the quasi-Fejér monotone sequence \(\{a_k\}\) converges to a unique limit point.

In order to illustrate the relationship between the terms \(\left\Vert z^{k+1}-z^{k}\right\Vert ,\) \( \left\Vert z^{k}-z^{k-1}\right\Vert \) and \(\left\Vert e(z^{k+1})\right\Vert \), we give the following two lemmas, whose proofs are similar to those in [9, 19] and [39], respectively.

Lemma 2

Let \(\{z^k\}\) be the sequence generated by the sGS-imsPADMM. For any \(k\ge 1\), we have

$$\begin{aligned} \left\Vert e(z^{k+1})\right\Vert ^2 \le \left\Vert z^{k+1}-z^{k}\right\Vert ^2_{\mathcal {K}_1}+ \left\Vert z^{k}-z^{k-1}\right\Vert ^2_{\mathcal {K}_2}, \end{aligned}$$
(29)

where

$$\begin{aligned}{} & {} {\mathcal {K}_1}:=c_1 \textrm{Diag} (I,I+\beta I,(\vartheta ^2\beta )^{-1}I),\qquad {\mathcal {K}_2}:=c_2\textrm{Diag}(I,I,0),\\{} & {} \quad \left\{ \begin{aligned}&c_1:=\max \{c_1^1,c_1^2,c_1^3 \},\\&c_1^1:=8\left( \lambda _{\max }(\mathcal {P}+\beta I)\right) ^2,\\&c_1^2:=\max \left\{ 6\left( \lambda _{\max }\left( \frac{1}{2}\varSigma _g+\mathcal {Q}+\beta I\right) +\frac{1}{2}\lambda _{\max }(\varSigma _g)\right) ^2, 4\beta I\right\} , \\&c_1^3:={\beta }^{-1}+7(1-\vartheta )^{2}\beta I,\\ \end{aligned}\right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{aligned}&c_2:=\max \{c_2^1,c_2^2 \},\\&c_2^1:=4\max _k\{\epsilon ^2_k\}\left( \lambda _{\max }(\mathcal {P}+\beta I)\right) ^2,\\&c_2^2:=3\max _k\{\epsilon ^2_k\}\left( \lambda _{\max }\left( \frac{1}{2}\varSigma _g+\mathcal {Q}+\beta I\right) +\frac{1}{2}\lambda _{\max }(\varSigma _g)\right) ^2. \end{aligned}\right. \end{aligned}$$

Lemma 3

Let \(e:\mathcal {X}\rightarrow (-\infty ,+\infty )\) be a smooth convex function and assume that there exists a self-adjoint positive semidefinite linear operator \(\mathcal {P}\) such that, for any given \(x'\in \mathcal {X}\),

$$\begin{aligned} e(x)\le e(x')+\left\langle \nabla e(x'),x-x'\right\rangle +\frac{1}{2}\left\Vert x-x'\right\Vert ^2_{\mathcal {P}}. \end{aligned}$$
(30)

Then, for any \(x_1,x_2\in \mathcal {X}\), we obtain

$$\begin{aligned} \left\langle \nabla e(x_1)-\nabla e(x'),x_2-x'\right\rangle \ge -\frac{1}{4}\left\Vert x_1-x_2\right\Vert ^2_{\mathcal {P}}. \end{aligned}$$
(31)

For any \(k\ge 1\), we define for any \(z\in \mathcal {Z}\) and \(k\ge 0\),

$$\begin{aligned} \begin{aligned} \phi _{k}\left( z\right) :=&\frac{1}{\vartheta \beta }\left\| l-l^{k}\right\| ^{2}+\left\| x-x^{k}\right\| _{\mathcal {P}}^{2}+\left\| y-y^{k}\right\| _{\mathcal {N}}^{2} \\&+(1+\nu )\left\| y^k-{y}^{k-1}\right\| _{\varSigma _{g}+\mathcal {Q}+\frac{\nu \beta }{1+\nu }I}^{2}. \end{aligned} \end{aligned}$$
(32)

The following proposition is essential for establishing the convergence.

Proposition 3

Suppose that the solution set \(\bar{\mathcal {Z}}\) to the KKT system of problem (9) is nonempty. Let \(\{z_k\}\) be the sequence generated by the sGS-imsPADMM with relative error control. Then, for any \(\bar{z}:= (\bar{x}, \bar{y}, \bar{l})\in \bar{\mathcal {Z}}\), \(k\ge 1\) and \(\nu >0\),

$$\begin{aligned} \begin{aligned}&\left\| \triangle ^k_x\right\| ^2_{\mathcal {P}}+\left\| \triangle ^k_y\right\| ^2_{ \mathcal {O}}-2\nu \left( \left\| \triangle ^k_x\right\| ^2_{\mathcal {M}}+\left\| \triangle ^k_y\right\| ^2_{\mathcal {N}} \right) +\widehat{\omega }\left\| r^{k+1}\right\| ^2\\&\quad \le \phi _k(\bar{z})-\left( 1-\frac{\epsilon ^2_k}{\nu }\right) \phi _{k+1}(\bar{z})+\omega \left\| r^{k}\right\| ^2-\left( 1-\frac{\epsilon ^2_k}{\nu }\right) \omega \left\| r^{k+1}\right\| ^2\\&\qquad -\frac{\epsilon ^2_k}{\nu } \left\| x^{k+1}-\bar{x}\right\| ^2_{\mathcal {P}}, \end{aligned} \end{aligned}$$
(33)

where \(\omega :=\beta (1-\min \{\vartheta ,\vartheta ^{-1}\})\), \(\widehat{\omega }:=\beta (1-\vartheta +\min \{\vartheta ,\vartheta ^{-1}\})\) and \(\mathcal {O}:=\frac{1}{2}\varSigma _g+\mathcal {Q}+\widehat{\omega }\vartheta I\).

Proof

The proof of Proposition 3 is detailed in the Appendix A.1. \(\square \)

Now we present the convergence result of the proposed sGS-imsPADMM in the following.

Theorem 1

Suppose that the solution set \(\bar{\mathcal {Z}}\) to the KKT system of problem (7) is nonempty and \(\{z_k\}\) is generated by the sGS-imsPADMM. Assume that

$$\begin{aligned} \mathcal {M}=\mathcal {P}+\beta I> 0\quad and\quad \mathcal {G}:=\varSigma _{g}+\mathcal {Q}+\frac{\nu \beta }{1+\nu }I> 0. \end{aligned}$$
(34)

Then, we get the sequence \(\{z_k\}\) converges to a point in \(\bar{\mathcal {Z}}\).

Proof

The proof of Theorem 1 is detailed in the Appendix 1. \(\square \)

4 Numerical Experiments

In this section, to demonstrate the effectiveness of the proposed model/method, we compared our model/method with other models/methods: the DZ model [11], the HNZ model [14], the FL model [18], the EM-CNN method [36], and the PARM model [24]. All the experiments have been successfully tested in MATLAB R2019b (Windows 10) and were run on a PC with Intel(R) Core(TM) i5-6200U CPU @2.30 GHz and 8 GB of RAM.

In our experiments, the quality of the recovered images is measured quantitatively by the peak signal noise ratio (PSNR) and the structural similarity index measure (SSIM) [37]. Note that larger PSNR and larger SSIM values mean better restored results. If the image size is \(m\times n\), then PSNR is defined as follows:

$$\begin{aligned} \text{ PSNR }=10\log {\frac{mn\max (\max (\hat{y_2}),\max (y_2))^2}{\Vert \hat{y_2}-y_2\Vert ^2}}, \end{aligned}$$
(35)

where \(\hat{y_2}\) and \(y_2\) are the restored image and the original image, respectively. Based on the KKT mapping (21), the iteration for our models is terminated when the following condition is met [8]:

$$\begin{aligned} \Vert e(z^{k+1})\Vert < 10^{-4}. \end{aligned}$$
(36)

4.1 Parameter Setting

For all these methods, we adjust the parameters within a specific range to achieve the best PSNR values and visually the best-restored images. For our model, we select the regularization parameter \(\alpha \) in the range [3, 9], \(\lambda \) in the range [0.01, 0.04] and \(\mu \) in the range [1, 1.8]. In addition, Fig. 2 displays the restoration results obtained by our model under the MB1 (the symbol is presented in Table 1) with different values of parameters. The step-length \(\vartheta \) is set to be \(\vartheta =1.618\in (0, (1+\sqrt{5})/2)\) for guaranteed convergence, and the sequence \(\{\varepsilon _{k}\}\) that we used is chosen such that \(\varepsilon _{k}\le 1/k\).

In this experiment, six images (all of the size 256 \(\times \) 256) are given in Fig. 1 to test the performance of the proposed model. To generate the observed images, the test images are contaminated with different blurring motion blur (MB) and Gaussian blur (GB), different standard deviations \(\sigma \)=1, 5 and 10 for Gaussian noise and different shape parameters K=30, 50 and 100 for Gamma noise. The larger \(\sigma \) is, the more serious the additive Gaussian noise is. On the contrary, the smaller K is, the more serious the multiplicative Gamma noise is. For MB, we use len = 9, 10 and 15 with an angle of 30, 60 and 120, where len represents the motion translation length of motion blur, angle represents the angle of motion rotation. As for GB, the blurring kernels to be tested are of size \(5\times 5\) and \(9\times 9\). Then, the standard deviations in GB are set as 2 and 4. Furthermore, we use the notation of MB(9,30) to denote the case of motion blur of len = 9 with an angle of 30. Similarly, GB(5,2) will be set for a Gaussian kernel of size \(5\times 5\) and a standard deviation of 2. Specifically, we define the symbol MB1 to be MB(9,30) with additive Gaussian noise of standard deviation of \(\sigma = 1\) and multiplicative Gamma noise of \(K=100\). In the same way, we define the symbol GB2 to be GB(9,4) with additive Gaussian noise of standard deviation of \(\sigma = 5\) and multiplicative Gamma noise of \(K=50\). All the symbols are presented in Table 1.

Table 1 Explanation of symbols for blur with mixed noise
Full size table
Fig. 1
figure 1

Standard test images

Full size image
Fig. 2
figure 2

Plots of PSNR(dB) value versus every parameter in our model for different test images at MB1

Full size image

4.2 Comparison with Other Models

In order to reflect the role of the quadratic penalty in the proposed model, we first compare the results without the penalty. The model without quadratic penalty is reduced to

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu \Vert W w\Vert _1. \end{aligned}$$
(37)

Figure 3 shows the comparison results of the simplified model and the proposed model. It can be observed from the image that the model without penalty term performs poorly in denoising. This example demonstrates the importance of penalty.

Next, we compare the recovery results of the simple approach with a common least-square term \(\Vert u-f\Vert _2^2\) (denoted as Mod. 1). The model can be formulated as

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| u-f\right\| _2^2+\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu \Vert W w\Vert _1. \end{aligned}$$
(38)

According to Proposition 1, we can conclude, if \(\alpha \ge \frac{1}{54f^2}\), the model (38) is component-wise convex on u. In addition, the image restoration effect is shown in Sect. 4.3. It can be found from the numerical results in Table 2 and Table 3 that the image degradation becomes more serious, the restoration effect of the Mod. 1 decreases more. The Mod. 1 is less robust.

Fig. 3
figure 3

Comparison of simplified model for image restoration effect and PSNR(dB)/SSIM values, respectively. a and e are ground truth; b and f are the images degraded with GB1 and MB1, respectively; c and g are the images degradation results of the simplified model; d and h are the images degradation results of ours

Full size image
Table 2 PSNR (dB), SSIM for motion blur with different noise levels
Full size table
Table 3 PSNR (dB), SSIM for Gaussian blur with different noise levels
Full size table

To demonstrate that our tightframe-based model is influential, we present the comparison with the TV-based model (denoted as TV model). The TV-based model can be formulated as

$$\begin{aligned} \min _{u>0,w}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| \sqrt{u}-\sqrt{f}\right\| _2^2+\frac{\Vert Hw-u\Vert _2^2}{2\sigma ^2}+\mu _1\Vert \nabla w\Vert _1. \end{aligned}$$
(39)

We use the sGS-imsPADMM method to solve (39). In order to apply sGS-imsPADMM, we express the minimization problem (39) as an equivalent form:

$$\begin{aligned} \begin{aligned}&\min _{u,w,c}\left\langle \log u+\frac{f}{u},1\right\rangle +\alpha \left\| \sqrt{u}-\sqrt{f}\right\| _2^2+\frac{\Vert Hw-u\Vert ^2_2}{2\sigma ^2}+\mu _1\Vert c\Vert _1,\\&\quad \text{ s.t. }\quad c-\nabla w=0. \end{aligned} \end{aligned}$$
(40)

Let \(y_1=u\), \(y_2=w\) and \(y=(y_1, y_2)\), \(c\in \mathcal {C}\) and \(y\in \mathcal {Y}\), when \(\alpha \ge \frac{(3-\inf f)\sqrt{6}}{9\sup \sqrt{f}}\), according to Sect. 3, for any \(h:=(c,y,p)\in \mathcal {C}\times \mathcal {Y}\times \mathcal {P}\) and \((c',y')\in \mathcal {C}\times \mathcal {Y}\). There exists a positive semidefinite matrix \(\varSigma _h\) such that for \(y,y'\in \mathcal {Y}\),

$$\begin{aligned} g(y)\le \widehat{g}(y;y'):= g(y')+\left\langle \nabla g(y'),y-y'\right\rangle +\frac{1}{2}\left\| y-y'\right\| ^2_{\varSigma _h}. \end{aligned}$$
(41)

The majorized augmented Lagrangian function is given by

$$\begin{aligned} \begin{aligned} L_{\tau }(c,y;(c',y',p))=\mu \Vert c\Vert _1+q(y)+\widehat{g}(y;y')+\left\langle p,c-\nabla w\right\rangle +\frac{\tau }{2}\left\| c-\nabla w\right\| ^2_2, \end{aligned} \end{aligned}$$
(42)

where \(\tau \) is the penalty parameter and p is the Lagrangian multiplier. The sGS-imsADMM algorithm with a relative error criterion for solving (42) is presented in Algorithm 2. The image restoration effect is shown in Subsection 4.3.

Algorithm 2
figure b

Inexact sGS-imsPADMM for solving (39).

Full size image
Fig. 4
figure 4

Images degradation results and PSNR(dB)/SSIM values. a and e are the images degraded by Gaussian noise \(\sigma \)=5 and 10, respectively; b and f are the images degraded by Gamma noise K=50 and 30, respectively; c and g are the images degraded by blurring MB(15, 60) and GB(9, 4), respectively; d and h are the images degraded by MB2, GB3, respectively

Full size image

4.3 Image Restoration Results Under Mixed Noise with Motion Blur

Figure 4 presents the visual effects of image degradation by additive noise, multiplicative noise, Gaussian blur, motion blur, and mixed noise with blur. It can be seen that multiplicative noise destroys the amount of image information, so the destruction of image information with blur and mixed noise is more serious. Therefore, we compare our models with some multiplicative noise models to show the superiority of the proposed models in removing mixed noise and blur. In Fig. 4, “Test 1" is degraded by Gaussian noise, Gamma noise and motion blur, respectively. (a)–(c) show the visual effects of different degraded images, (d) shows the image degraded by MB2. Similarly, (e)–(g) show the degradation of “Test 2" by Gaussian noise, Gamma noise and Gaussian blur, respectively. (h) shows the image degraded by GB3, and image degradation in (d) and (h) are the most serious. Image restoration in this case is even more difficult.

Table 2 shows the numerical results of the restored images by different methods. The best results in each case are highlighted in bold. It can be seen that our model achieves best data results in most cases under different degradation levels. In addition, our model gets a satisfactory result in terms of average values of SSIM and PSNR.

In order to more clearly demonstrate the advantages of our model, we present the visual effects of image restoration at a lower level of image degradation. We also display the zoomed regions of the restoration results in Figs. 5 and 6. It can be seen that the images recovered by our methods achieve the best quality concerning mixed noise removal and deblurring simultaneously. In Fig. 5, we observe that the DZ method [11], the HNZ model [14], the EM-CNN method [36], and the PARM method [24] can not completely remove the blur. Note that the FL method [18] and TV method results still have some motion blur in the red and green zoomed areas. There is still a lot of noise in the recovery results of the Mod. 1. The results of our model in these two aspects are satisfactory. A similar situation is shown in Fig. 6, the restoration results of the FL method and TV method in red enlarged areas can not remove the blur completely, where the number “96" is indistinct in the middle as if linked together. Moreover, it seems that the TV method results in stair-casing artifacts. Essentially, the traditional TV regularization will cause the stair-casing effect in the smooth area of the reconstructed image, and the texture information of the image can not be retained well.

Fig. 5
figure 5

The restoration results on “Test 1” with zoomed region and PSNR(dB)/SSIM values. a Ground truth. b Images degraded by MB(15, 60) with \(\sigma \)=1 and K=600. The denoising and deblurring results of: c DZ, d HNZ, e FL, f EM-CNN, g PARM, h TV model, i Mod. 1 and j ours, respectively

Full size image
Fig. 6
figure 6

The restoration results on “Test 5" with zoomed region and PSNR(dB)/SSIM values. a Ground truth. b Images degraded by MB(9, 30) with \(\sigma \)=1 and K=600. The denoising and deblurring results of: c DZ, d HNZ, e FL, f EM-CNN, g PARM, h TV model, i Mod. 1 and j ours, respectively

Full size image

4.4 Image Restoration Results Under Mixed Noise with Gaussian Blur

In this experiment, we degrade the standard test images Fig. 1 by mixed noise with Gaussian blur at GB1, GB2, and GB3. Table 3 shows the numerical results of the restored images by different methods and the better results are marked in black. Consequently, our method has the best numerical results at the average values of PSNR and SSIM.

Figures 7 and 8 show the image restoration results under mixed noise with Gaussian blur. As illustrated in Fig. 7, the recovery results of the DZ method, the HNZ method, the EM-CNN method, and the PARM method are too smooth and the texture details are blurred.

Specifically, the reconstructed images of the FL method and TV method have staircase effects, and we observe that the TV method and Mod. 1 are not completely denoised. However, our method yields the best visual effects in keeping the image sharp and removing noises. The situation in Fig. 8 is similar, we can see a significant step-up effect in the “shadows" of the red magnification areas in (e) and (f). Consequently, our method has the best image quality in terms of preserving edges and removing mixed noises.

Figure 9 shows the denoised and deblurred results of residue on the “Test 1" image. In this sense, the noise residue of ours contains less useful information than the other models, and the solution contains more textures and structure [38].

Fig. 7
figure 7

The restoration results on “Test 2" with zoomed region and PSNR(dB)/SSIM values. a Ground truth. b Images degraded by GB(5, 2) with \(\sigma \)=5 and K=600. The denoising and deblurring results of: c DZ, d HNZ, e FL, f EM-CNN, g PARM, h TV model, i Mod. 1 and j ours, respectively

Full size image
Fig. 8
figure 8

The restoration results on “Test 1" with zoomed region and PSNR(dB)/SSIM values. a Ground truth. b Images degraded by GB(5, 2) with \(\sigma \)=5 and K=300. The denoising and deblurring results of: c DZ, d HNZ, e FL, f EM-CNN, g PARM, h TV model, i Mod. 1 and j ours, respectively

Full size image
Fig. 9
figure 9

The restoration results and the corresponding residual results. a The degraded images restored from “Test 1" at GB3 by different methods. b Gamma noise component. c Gaussian noise component. d Gaussian blur component. 1st row through 8th row: the restoration results of DZ, HNZ, FL, EM-CNN, PARM, TV model, Mod. 1 and ours, respectively

Full size image
Fig. 10
figure 10

1st, 2nd column: The plots of relative error, PSNR with CPU-time. Blue line: ADMM. Red line: sGS-imsPADMM. 3rd, 4th column: The restoration results of ADMM, sGS-imsPADMM with PSNR(dB)/SSIM. c–d, g–h Images “Test 1, Test 3" are degraded by GB1. k–l, o–(p) Images “Test 5, Test 6" are degraded by MB1

Full size image
Table 4 The values of PSNR, SSIM, CPU-time in seconds and number of internal and external iteration steps
Full size table

4.5 Comparison of ADMM and sGS-imsPADMM Algorithm

In order to demonstrate the advantages of the sGS-imsPADMM algorithm, we compared the difference between the sGS-imsPADMM algorithm and the ADMM algorithm in terms of image restoration effect, CPU-time, and number of iterations. Numerical results are shown in Table 4. It can be seen that the ADMM algorithm requires more iterations and more time, and the sGS-imsPADMM is nearly 2 times faster than the ADMM algorithm. To visually demonstrate the advantages of sGS-imsPADMM algorithm compared with the ADMM algorithm, we compared the plots of PSNR and relative error with CPU-time of sGS-imsPADMM algorithm and ADMM algorithm in Fig. 10. For convenience, we discussed the result of the image restoration on the “Test 1, Test 3" degraded by GB1 and the “Test 5, Test 6" degraded by MB1. Next, we compared the effects of two algorithms, ADMM and sGS-imsPADMM. Compared with the ADMM algorithm, the sGS-imsPADMM algorithm shows faster convergence effect.

5 Conclusion

In this paper, we presented a novel model for restoring blurred images with mixed noise, which incorporates wavelet tight frame regularization. The convexity of the model is ensured by a convexity-preserving term introduced in the model. Using sGS-imsPADMM with relative error control, we have effectively solved our proposed model and proved the convergence of the algorithm to a stationary point of the objective function. Our experiments have demonstrated that the proposed method outperforms several advanced methods and achieves the best image quality. Furthermore, the sGS-imsPADMM algorithm is nearly 2 times faster than ADMM. We have also successfully applied sGS-imsPADMM with relative error control for removing mixed noise and blur. In future work, we plan to explore the application of this algorithm to other problems, such as unknown types of noise with blur.