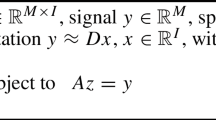Abstract
This work focuses on recovering images from various forms of corruption, for which a challenging non-smooth, non-convex optimization model is proposed. The model consists of a concave truncated data fidelity functional and a convex total-variational term. We introduce and study various novel equivalent mathematical models from the perspective of duality, leading to two new optimization frameworks in terms of two-stage and single-stage. The two-stage optimization approach follows a classical convex-concave optimization framework with an inner loop of convex optimization and an outer loop of concave optimization. In contrast, the single-stage optimization approach follows the proposed novel convex model, which boils down to the global optimization of all variables simultaneously. Moreover, the key step of both optimization frameworks can be formulated as linearly constrained convex optimization and efficiently solved by the augmented Lagrangian method. For this, two different implementations by projected-gradient and indefinite-linearization are proposed to build up their numerical solvers. The extensive experiments show that the proposed single-stage optimization algorithms, particularly with indefinite linearization implementation, outperform the multi-stage methods in numerical efficiency, stability, and recovery quality.







Similar content being viewed by others
Data Availability
The codes generated during the current study are available from the corresponding author on reasonable request.
Notes
For instance, for the random-valued impulse noise, \( \text { O} = \varvec{1}\,\); and for the salt-and-pepper impulse noise, \({\text {O}_i} = \left\{ {\begin{aligned}&{0, \quad {{f}_i} = {u_{\text {max}}} \;\text {or}\; {{u_{\text {min}}}},}\\&{1, \quad \text {otherwise.}} \end{aligned}} \right. \).
References
Bai, L.: A new nonconvex approach for image restoration with gamma noise. Comput. Math. Appl. 77(10), 2627–2639 (2019)
Bi, S., Liu, X., Pan, S.: Exact penalty decomposition method for zero-norm minimization based on MPEC formulation. SIAM J. Sci. Comput. 36(4), A1451–A1477 (2014)
Blake, A., Zisserman, A.: The Graduated Non-Convexity Algorithm, pp. 131–166 (2003)
Candès, E.J., Tao, T.: The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inform. Theory 56(5), 2053–2080 (2010)
Chambolle, A.: An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 20(1), 89–97 (2004)
Chambolle, A., Caselles, V., Cremers, D., Novaga, M., Pock, T.: An introduction to total variation for image analysis. Theor. Found. Numer. Methods Sparse Recov. 9(263–340), 227 (2010)
Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numer. 25, 161–319 (2016)
Chan, R., Lanza, A., Morigi, S., Sgallari, F.: Convex non-convex image segmentation. Numer. Math. 138(3), 635–680 (2018)
Clason, C., Jin, B., Kunisch, K.: A duality-based splitting method for l1-tv image restoration with automatic regularization parameter choice. SIAM J. Sci. Comput. 32(3), 1484–1505 (2010)
Cui, Z.X., Fan, Q.: A nonconvex+ nonconvex approach for image restoration with impulse noise removal. Appl. Math. Model. 62, 254–271 (2018)
Gu, G., Jiang, S., Yang, J.: A TVSCAD approach for image deblurring with impulsive noise. Inverse Probl. 33(12), 125008 (2017)
Guo, X., Li, F., Ng, M.K.: A fast \(\ell \)1-tv algorithm for image restoration. SIAM J. Sci. Comput. 31(3), 2322–2341 (2009)
He, B., Ma, F., Yuan, X.: Optimal proximal augmented Lagrangian method and its application to full Jacobian splitting for multi-block separable convex minimization problems. IMA J. Numer. Anal. 40(2), 1188–1216 (2020)
He, B., Xu, S., Yuan, X.: Extensions of ADMM for separable convex optimization problems with linear equality or inequality constraints. arXiv:2107.01897 (2021)
Hong, B.W., Koo, J., Burger, M., Soatto, S.: Adaptive regularization of some inverse problems in image analysis. IEEE Trans. Image Process. 29, 2507–2521 (2019)
Kang, M., Jung, M.: Simultaneous image enhancement and restoration with non-convex total variation. J. Sci. Comput. 87(3), 1–46 (2021)
Keinert, F., Lazzaro, D., Morigi, S.: A robust group-sparse representation variational method with applications to face recognition. IEEE Trans. Image Process. 28(6), 2785–2798 (2019)
Lai, M.J., Xu, Y., Yin, W.: Improved iteratively reweighted least squares for unconstrained smoothed \(l_q\) minimization. SIAM J. Numer. Anal. 51(2), 927–957 (2013)
Lanza, A., Morigi, S., Selesnick, I., Sgallari, F.: Nonconvex nonsmooth optimization via convex-nonconvex majorization-minimization. Numer. Math. 136, 343–381 (2017)
Lanza, A., Morigi, S., Selesnick, I.W., Sgallari, F.: Sparsity-inducing nonconvex nonseparable regularization for convex image processing. SIAM J. Imaging Sci. 12(2), 1099–1134 (2019)
Lanza, A., Morigi, S., Sgallari, F.: Convex image denoising via non-convex regularization with parameter selection. J. Math. Imaging Vis. 56, 195–220 (2016)
Lerman, G., McCoy, M.B., Tropp, J.A., Zhang, T.: Robust computation of linear models by convex relaxation. Found. Comput. Math. 15(2), 363–410 (2015)
Lu, Z., Zhang, Y.: Sparse approximation via penalty decomposition methods. SIAM J. Optim. 23(4), 2448–2478 (2013)
Nikolova, M.: Minimizers of cost-functions involving nonsmooth data-fidelity terms. Application to the processing of outliers. SIAM J. Numer. Anal. 40(3), 965–994 (2002)
Nikolova, M., Ng, M.K., Tam, C.P.: On \(\ell _1\) data fitting and concave regularization for image recovery. SIAM J. Sci. Comput. 35(1), A397–A430 (2013)
Peng, G.J.: Adaptive ADMM for dictionary learning in convolutional sparse representation. IEEE Trans. Image Process. 28(7), 3408–3422 (2019)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (2015)
Rudin, L.I., Osher, S.: Total variation based image restoration with free local constraints. In: Proceedings of 1st International Conference on Image Processing, vol. 1, pp. 31–35. IEEE (1994)
Selesnick, I.W., Bayram, I.: Sparse signal estimation by maximally sparse convex optimization. IEEE Trans. Signal Process. 62(5), 1078–1092 (2014)
Swoboda, P., Mokarian, A., Theobalt, C., Bernard, F., et al.: A convex relaxation for multi-graph matching. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 11156–11165 (2019)
Tao, M.: Minimization of \(l_1\) over \(l_2\) for sparse signal recovery with convergence guarantee. SIAM J. Sci. Comput. 44(2), A770–A797 (2022)
Tao, P.D., An, L.H.: Convex analysis approach to DC programming: theory, algorithms and applications. Acta Math. Vietnam 22(1), 289–355 (1997)
Tao, P.D., Souad, E.B.: Duality in DC (difference of convex functions) optimization. subgradient methods. In: Trends in Mathematical Optimization: 4th French-German Conference on Optimization, pp. 277–293. Springer (1988)
Tao, P.D., et al.: Algorithms for solving a class of nonconvex optimization problems. methods of subgradients. In: North-Holland Mathematics Studies, vol. 129, pp. 249–271. Elsevier (1986)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B. 58(1), 267–288 (1996)
Tikhonov, A.N., Arsenin, V.I.: Solutions of Ill-Posed Problems, vol. 14. V.H. Winston, Washington (1977)
Vongkulbhisal, J., De la Torre, F., Costeira, J.P.: Discriminative optimization: theory and applications to computer vision. IEEE Trans. Pattern Anal. 41(4), 829–843 (2018)
Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1(3), 248–272 (2008)
Wu, T., Shao, J., Gu, X., Ng, M.K., Zeng, T.: Two-stage image segmentation based on nonconvex \(l_2-l_p\) approximation and thresholding. Appl. Math. Comput. 403, 126168 (2021)
Yang, H., Antonante, P., Tzoumas, V., Carlone, L.: Graduated non-convexity for robust spatial perception: From non-minimal solvers to global outlier rejection. IEEE Robot. Autom. Lett. 5(2), 1127–1134 (2020)
Yang, J., Yuan, X.: Linearized augmented Lagrangian and alternating direction methods for nuclear norm minimization. Math. Comput. 82(281), 301–329 (2013)
Yang, J., Zhang, Y., Yin, W.: An efficient tvl1 algorithm for deblurring multichannel images corrupted by impulsive noise. SIAM J. Sci. Comput. 31(4), 2842–2865 (2009)
You, J., Jiao, Y., Lu, X., Zeng, T.: A nonconvex model with minimax concave penalty for image restoration. J. Sci. Comput. 78(2), 1063–1086 (2019)
Yuan, G., Ghanem, B.: \(\ell _0\)tv: a sparse optimization method for impulse noise image restoration. IEEE Trans. Pattern Anal. 41(2), 352–364 (2017)
Zhang, B., Zhu, G., Zhu, Z.: A tv-log nonconvex approach for image deblurring with impulsive noise. Signal Process. 174, 107631 (2020)
Zhang, T.: Analysis of multi-stage convex relaxation for sparse regularization. J. Mach. Learn. Res. 11(3), 1081–1107 (2010)
Zhang, X., Bai, M., Ng, M.K.: Nonconvex-tv based image restoration with impulse noise removal. SIAM J. Imaging Sci. 10(3), 1627–1667 (2017)
Zhou, Q.Y., Park, J., Koltun, V.: Fast global registration. In: Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11–14, 2016, Proceedings, Part II 14, pp. 766–782. Springer (2016)
Zhu, W.: Image denoising using \(l^{p}\)-norm of mean curvature of image surface. J. Sci. Comput. 83(2), 1–26 (2020)
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 12271419, 61877046, 61877047, 11801430, and 62106186), in part by the RG(R)-RC/17-18/02-MATH, HKBU 12300819, NSF/RGC Grant N-HKBU214-19, ANR/RGC Joint Research Scheme (A-HKBU203-19) and RC-FNRA-IG/19-20/SCI/01.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 12271419, 61877046, 61877047, 11801430, and 62106186), in part by the RG(R)-RC/17-18/02-MATH, HKBU 12300819, NSF/RGC Grant N-HKBU214-19, ANR/RGC Joint Research Scheme (A-HKBU203-19) and RC-FNRA-IG/19-20/SCI/01
JY: Contributed equally as joint first author.
Appendices
Appendix A: Close-form Solver for Sub-problem (13)
When function g to be the truncated-\({l_1}\) function with any \(\alpha > 0\), its dual form is \({g^*}\left( q \right) = \alpha \left( { - 1 + q} \right) I\left( {q \in \left[ {0,1} \right] } \right) \,\). Thus, the optimization problem (13) can be reformulated as:
so, in this case, the straightforward close form solution for q is
Appendix B: Numerical Implementation of (18) and (19)
In this part, we list two different implementations for solving problems (18) and (19): the first one is implemented using the classical projected gradient-ascent method (PG), while the second one employs a indefinite linearized method (IDL) recently published in [13].
1.1 Appendix B.1: Solver by Projected Gradient-Ascent Method (PG)
Clearly, the maximization problem (18) over w results in:
which can be easily tackled by the following projection gradient-ascent scheme:
where \(\mu > 0\) is the step-size of gradient-ascent and the associate gradient is
As we observed in practice, the total number of projection gradient ascent iterations (41) has no obvious influence on its numerical performance; so we take one iteration (41) in this work to decrease computational complexity.
The maximization problem (19) over \(\varvec{p}\) is reduced as:
which can be solved by the following projection gradient-ascent scheme:
where \(\sigma > 0\) is the step-size of gradient-ascent, \(\nabla = - \textrm{Div}^T\,\), and \({\prod }_\lambda \) is the projection onto the convex set \({C_\lambda } = \left\{ {\eta |\left| \eta \right| \le \lambda } \right\} \,\).
1.2 Appendix B.2: Solver by Indefinite Linearized Method (IDL)
A proximal linearization strategy, which adds a positive-definite proximal term to linearize the studied optimization problem and derives their closed-form solutions, was introduced in [41]. Recently, He et al. [13] showed that such positive definiteness of the added proximal term for linearization is not required for convergence, they proposed an efficient indefinite linearized algorithmic that permits a larger step-size to speed up convergence.
For problem (18), the indefinite linearized w-subproblem is
We can easily compute its closed-form solution:
where \(c_1 > \beta \rho \left( {H{H^T}} \right) \) and \(\tau \in \left( {0.75,1} \right) \,\).
The indefinite linearized \(\varvec{p}\)-subproblem for problem (19) is
So, we have its closed-form solution:
where \(c_2 > \beta \rho \left( \textrm{Div}^T \textrm{Div}\right) \) and \(\tau \in \left( {0.75,1} \right) \,\).
Appendix C: Numerical Implementation of (28) and (29)
Just as the previous “Appendix B”, we can implement two different numerical solvers for (28) and (29), by the classical projected gradient-ascent method (PG) and the indefinite linearized method (IDL).
1.1 Appendix C.1: Solver by Projected Gradient-Descent Method (PG)
The projection gradient-descent scheme for solving (28) is
where \(\nu > 0\) is the step-size of gradient-descent, and the associate gradient is
In essence, recall the definition of \(\varvec{x}\,\), the iterative formulas for updating variables w and \(\varvec{p}\) are as follows:
and
where \(\mu > 0\) is the step-size for updating \(w\,\), \(\sigma >0\) is the step-size for updating \(\varvec{p}\,\), \({\prod }_\lambda \) is the projection onto the convex set \({C_\lambda } = \left\{ {\eta \, | \, \left| \eta \right| \le \lambda } \right\} \,\), and
For the truncated-\(l_1\) function, its dual function is \({g^*}\left( q \right) = \alpha \left( { - 1 + q} \right) I\left( {q \in \left[ {0,1} \right] } \right) \,\), and the optimization problem (29) can then be reformulated as:
Since \(B = \left( \varvec{0} ,\, {\hat{I}} ,\, {\hat{I}}\right) ^{T}\,\) is a variant of the identity matrix I, the above problem (52) has a closed-form solution
where \({\prod }_{[\varvec{0},\varvec{1}]}\) is the projection onto the convex set \({C_{[\varvec{0},\varvec{1}]} } = \left\{ {\eta \, | \, \varvec{0} \le \eta \le \varvec{1} } \right\} \,\), \(A\varvec{x}^k_2\) and \(A\varvec{x}^k_3\) are as shown in ().
1.2 Appendix C.2: Solver by Indefinite Linearized Method (IDL)
We now implement the indefinite linearized method (IDL) to solve sub-problem (28). Its corresponding indefinite linearized version is
where the indefinite matrix M in (54) is taken as
So, the proximal optimization problem (54) can be reduced to
whose closed-form solution is
Thus, the iterative formula for updating the variables w and \(\varvec{p}\) are
and
where \(c_1 > \beta \rho \left( {H{H^T}} \right) \,\), \(c_2 > \beta \rho \left( \textrm{Div}^T \textrm{Div}\right) \,\), and \(\tau \in \left( {0.75,1} \right) \,\).
Clearly, the coefficient matrix B in the optimization problem (29) is indeed a rearrangement of the identity matrix. Hence, the optimization of q using the indefinite linearized technique is the same as (53).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, X., Yuan, J., Tai, XC. et al. Efficient Convex Optimization for Non-convex Non-smooth Image Restoration. J Sci Comput 99, 57 (2024). https://doi.org/10.1007/s10915-024-02504-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02504-6