Abstract
In this work, we consider space-time goal-oriented a posteriori error estimation for parabolic problems. Temporal and spatial discretizations are based on Galerkin finite elements of continuous and discontinuous type. The main objectives are the development and analysis of space-time estimators, in which the localization is based on a weak form employing a partition-of-unity. The resulting error indicators are used for temporal and spatial adaptivity. Our developments are substantiated with several numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Space-time methods for solving differential equations with Galerkin-type finite element methods go back to [50] and a recent state-of-the-art summary was compiled in [40]. Space-time methods can be divided into two categories: the numerical solution and error estimation. In this work, we are primarily interested in the latter. After the previously mentioned early work, various problems have been considered in space-time formulations such as incompressible flow [61], first-order hyperbolic systems [15], elastic wave equation [31, 32, 34], visco-acoustic/visco-elastic wave equations [16], financial mathematics [28], the Biot equations in poroelasticity [6], and fluid–structure interaction [26, 30, 60, 62,63,64]. Advancements for the numerical solution by means of space-time methods, such as for example multigrid methods, were undertaken in [27, 49, 55] and with space-time domain decomposition [58].
Classical norm-based a posteriori error estimation was done for parabolic problems in [21, 22, 37, 39, 59, 68]. Goal-oriented error estimation of space-time problems was performed in [10, 43, 56, 57]. Therein, space-time formulations may serve three purposes: spatial error estimation, temporal error estimation [26, 28, 45, 46] or both simultaneously [4, 10, 15, 16, 56, 57]. Decoupling space and time for rate-dependent problems in elasto-plasticity was considered in [51]. Moreover, we mention space-time developments in PDE-based optimization with and without a posteriori error control [7, 24, 25, 33, 38, 41,42,43, 47, 48]. A brief review of space-time concepts for goal-oriented a posteriori error estimation in fluid–structure interaction for deriving the adjoint in goal-oriented error estimation and optimization was conducted in [69].
Employing the dual-weighted residual method [8, 9] for space-time goal-oriented error estimation comes with the challenge that the adjoint problem is running backwards-in-time. For nonlinear problems, this means that the primal solution must be available at the respective time points. This can be done by simply storing all primal solutions in the RAM (random access memory) or hard disk, or by using checkpointing techniques [43, 56].
The main objective in this work is to combine space-time concepts from [57] with an easy-to-implement partition-of-unity localization proposed in [53]. The latter was established for stationary problems, which is extended in this study to space-time error estimation. Two error estimators are proposed: joint and split. Because of Galerkin orthogonality, we need higher-order information in the adjoint problem for calculation of the primal residual estimator. There are different ways to achieve this. For stationary problems a mixed order approach is often used. There, we discretize the primal problem with the low order cG(s)dG(r) elements and the adjoint problem with high order \(cG(s+1)dG(r+1)\) elements. The notation was proposed in [20, 23] and means that spatial discretization is based on cG(s) or \(cG(s+1)\) continuous Galerkin finite elements respectively, where \(s\in {\mathbb {N}}\) indicates the polynomial degree, while temporal discretization is based on dG(r), discontinuous Galerkin finite elements, where \(r\in {\mathbb {N}}_0\) indicates the temporal polynomial degree.
This approach needs interpolation operators to calculate the low order adjoint solution. In the equal low order approach both problems are discretized with low order elements and the high order solutions are obtained by a suitable patch wise reconstruction operator. For the adjoint estimator higher-order information in the primal problem is needed as well. For the two earlier approaches this can again be calculated by patch wise reconstruction. Alternatively, in the equal high order approach both problems can be discretized with high order elements. Then, only interpolation operators are needed but the whole solution becomes more expensive. Additionally, these approaches can be mixed by using different approaches for temporal and spatial discretization. From the resulting a posteriori error estimates, local error indicators are extracted to establish adaptive algorithms for both temporal and spatial mesh refinement. For verification, error reductions and effectivity indices are observed. Some preliminary results were published in the conference proceedings papers [66] (heat equation) and [67] (low Mach number combustion). Moreover, the successfull application to incompressible flow is documented in [54] and a summary of all developments appeared in [65]. However, technical derivations and the theory have not been worked out therein. Moreover, the current work provides (for the first time) detailed computational comparisons of the joint and split error estimators in terms of effectivity indices as well as thorough investigations of the PU-DWR method in a space-time context.
The outline of this paper is as follows: In Sect. 2, the primal problem statements are provided including their space-time discretizations. Next, in Sect. 3, the dual-weighed residual method is recapitulated. Afterward in Sect. 4, partition-of-unity DWR space-time goal-oriented a posteriori error estimators are proposed. In Sect. 5, three numerical examples are studied in order to substantiate our algorithmic developments. We summarize our work in Sect. 6.
2 Space-Time Notation and Problem Formulations
In this section, we introduce notation and space-time spaces. Then, abstract forms on the continuous level, semi-discrete in time level, and fully discrete level are introduced. These are subsequently realized with specific problem statements, namely the heat equation and a combustion problem, respectively. The road map of our developments is first based on abstract derivations as we believe that with this knowledge our results can be more easily applied to other problem statements such as incompressible flow, e.g., as already done in [54], and further nonstationary, nonlinear, coupled problems.
2.1 Notation and Spaces
The space time domain is denoted by \(\Sigma \subset {\mathbb {R}}^{d+1}\) with \(\Sigma = \{\Omega (t)\subset {\mathbb {R}}^d:t \in I \}\), with the temporal interval \(I=(0,T)\) and spatial domain \(\Omega \). In this paper, we consider time-independent domains \(\Omega \), resulting in \(\Sigma = \Omega \times I\).
Using \(V=V(\Omega )= H^1_D(\Omega ) = \{v\in H^1(\Omega ); v|_{\Gamma _D}=0\} \) and \(H = H(\Omega )= L^2(\Omega )\) we can define our space-time Hilbert space as
where \(L^2(I,V(\Omega ))\) is the Bochner space of \(L^2\) functions over I with values in \(V(\Omega )\).
Here, \(\Gamma _D\subseteq \partial \Omega \) denotes the Dirichlet boundary with condition \(v(t)=0\text { on }\Gamma _D\). For inhomogeneous conditions i.e. \(v(t)=g(t)\text { on }\Gamma _D\) the ansatz space is \(X(I,V)+g\), we will however limit derivations to the homogeneous case for the sake of brevity. On X(I, V) we can use the \(L^2(I,L^2(\Omega ))\) scalar product
Since we want to use discontinuous Galerkin discretizations in time we have to define an infinite dimensional space \({\widetilde{X}}({\mathcal {T}}_k,V(\Omega ))\) that allows for jumps at the grid points of the temporal mesh \({\mathcal {T}}_k\).
To obtain \({\mathcal {T}}_k\) we decompose the temporal interval I into M open subintervals \(I_m{:}{=}(t_{m-1},t_m)\) of length \(k_m=t_m-t_{m-1}\), with the condition that
hold. Then, \({\mathcal {T}}_k\) is the collection of all intervals from \(I_1\) to \(I_M\).
Following the nomenclature of [14] we can define the broken Bochner space
For each local space the continuous embedding \(W(I_m,V(\Omega ))\subset C({\bar{I}}_m,H(\Omega ))\) holds such that the limits from above and below, i.e. \(v_m^\pm {:}{=}\lim \limits _{\varepsilon \rightarrow 0} v(t_m\pm \varepsilon )\) are well defined.
Using these we can define the jump across temporal intervals as
for all inner temporal grid points \(t_m\in {\mathcal {T}}_k\).
Additionally, we introduce \([v]_0\) as a shorthand for the weakly imposed initial conditions, i.e.
Finally, let \(A:X\times X\rightarrow {\mathbb {R}}\) be a semi-linear form representing the PDE (partial differential equation) in weak form, being nonlinear in the first argument and linear in the second argument. Let \(F:X\rightarrow {\mathbb {R}}\) be a linear form representing given right hand side data. Then, the abstract problem reads:
Problem 2.1
(Abstract form on the continuous level) Find \(u\in X\) such that
We provide strong forms and the respective weak forms in terms of (7) for the heat equation and a combustion problem in Sects. 2.3 and 2.4, respectively.
2.2 Discretization
In principle, the discretization steps are the same for all parabolic problems. Since we want to be able to have different trial functions in time and space, we split the discretization, starting with the temporal basis functions.
2.2.1 Semi-discretization in Time
Given the temporal triangulation \({\mathcal {T}}_k\) as defined above we can obtain the semidiscrete space by discretization of the temporal functions into piecewise polynomials of degree \(r\in {\mathbb {N}}_0\):
with \(A(u_k)(\varphi )\) and \(F(\varphi )\) depending on the actual problem, the general time-discrete weak dG(r) formulations reads:
Problem 2.2
[(Abstract form semi-discrete in time) Find \(u_k\in {\widetilde{X}}_k^r({\mathcal {T}}_k,V)\), where \(r\ge 0\), such that
2.2.2 Fully Discrete Abstract Problem
For the spatial discretization we use triangulations \({\mathcal {T}}_h^m\) of \(\Omega \), where \(m=1,\ldots , M\) indicates each temporal subinterval \(I_m\). These are decomposed into quadrilateral/hexagonal elements K and we use continuous test and trial functions of degree s resulting in \(V_h^s \left( {\mathcal {T}}_h^m \right) \subset V(\Omega )\) defined as
We notice that we can have different triangulations on different subintervals, resulting in time-dependent or dynamic meshes. Using this, we can define the fully discrete function space:
With these definitions, we obtain the fully discrete cG(s)dG(r) formulation:
Problem 2.3
(Abstract form fully discrete level) Find \(u_{kh}\in {\widetilde{X}}_{k,h}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M})\), such that
Specific realizations are provided in the following two subsections, Sects. 2.3 and 2.4, respectively, by setting
2.3 Heat Equation
Having the abstract formulations on the continuous, semi-discrete (in time) and fully discrete levels at hand, we now proceed and provide two specific realizations. First, the heat equation is considered in this subsection and then a combustion problem is introduced in the next subsection. Let \(u:\Sigma \rightarrow {\mathbb {R}}\) be the solution of the heat equation
for a given initial condition \(u^0\in H\) and right hand side function \(f\in L^2(0,T;V^*)\). Using the discretization steps as described above, we obtain the following equations
2.4 Combustion
The following coupled nonlinear PDE describes the temperature dependent reaction and diffusion of a combustible substance without the influence of an additional fluid flow (\(v\equiv 0\)); see [36]. Therefore, the low Mach number hypothesis holds and the fluid flow is not influenced by the reaction and can be ignored. The resulting equations for the dimensionless temperature \(\theta :\Sigma \rightarrow {\mathbb {R}}\) and the species concentration \(Y:\Sigma \rightarrow {\mathbb {R}}\) are
with the combustion reaction described by Arrhenius law
The Arrhenius law is parametrized by the Lewis number \(Le>0\), the gas expansion \(\alpha >0\) and the dimensionless activation energy \(\beta >0\). We want to be able to allow all three common types of boundary conditions i.e. those of Dirichlet, Neumann and Robin type. For this we split the boundary \(\partial \Omega \) into three non-overlapping parts \(\Gamma _D\), \(\Gamma _N\) and \(\Gamma _R\). The Dirichlet boundary conditions are built into the function spaces, which is the usual approach. The Neumann and Robin boundary conditions are given by
It remains to state the initial conditions:
By following the typical steps for the derivation of a weak formulation, integration by parts in space, and subsequent summation, we obtain
Splitting the boundary integrals and considering homogeneous Dirichlet conditions on some parts, i.e., \(\varphi ^\theta |_{\Gamma _D}=\varphi ^Y|_{\Gamma _D}=0\), we get
By introducing jump terms as described earlier, we obtain the following semi-linear and linear forms, respectively:
with \(u_{kh} = (\theta _{kh},Y_{kh})\) and \(\varphi _{kh} = (\varphi _{kh}^\theta ,\varphi _{kh}^Y)\).
2.5 General Formulation of Parabolic Problems
A general parabolic weak formulation that includes the previous problem statements can be stated by
with an elliptic operator \(a(u,\varphi ){:}{=}\int \limits _0^T {\bar{a}}(u(t),\varphi (t))\textrm{d}t\). Then, (non-)linearity of A solely depends on the (non-)linearity of \({\bar{a}}\).
Remark 2.4
We notice that additional terms due to Neumann or Robin boundary conditions would appear inside \({\bar{a}}(u(t),\varphi (t))\) and/or \(F(\cdot )\).
2.6 Numerical Solution
In the algorithmic realization, we notice that the choice of trial and test spaces allow for a decoupling of the temporal discretization into slabs, i.e. slices of the space-time cylinder. In the simplest case a slice just encompasses a single temporal interval, resulting in a sequential time-stepping scheme due to the dG(r) test functions, and therefore effectively yielding classical time discretization schemes. For dG(0) an implicit Euler-type scheme is recovered. At each time slab, the spatial problems are solved as described in the following.
For the basic implementation of the (linear) heat equation with a classical DWR error estimator, we refer to the dwr-diffusion package [35] and the solvers implemented therein. There, the sparse direct solver UMFPACK [13] is used for the linear equation systems.
For the nonlinear combustion equation we employ a classical Newton-type solver as briefly described in the following. In the space-time setting we have to solve
where \(u_{kh}\) is the complete space-time solution over all intervals. Given an initial guess \(u_{kh}^{0}\), find the update \(\delta u\in {\widetilde{X}}_{kh}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M})\) of the linear defect-correction problem for \(j=0,1,2, \ldots \)
Remark 2.5
As we have discontinuous test functions the nonlinear problem can be decoupled into one subproblem per time interval. Then, we obtain a time-stepping scheme with one Newton loop per interval.
The defect-correction problems are solved using the parallel sparse direct solver MUMPS [1]. The Jacobian \(A'(\cdot )(\cdot ,\cdot )\) is derived by using analytical expressions, e.g., [70, Chapter 13], in order to maintain superlinear (or quadratic) convergence. However, for \(j>0\) reassembly of the matrix is omitted if the relative reduction of the residual is below a certain threshold. This simplified Newton approach saves a lot of computational time as the factorization only needs to be done after a reassembly step. This approach also benefits from preconditioned Krylow methods as the preconditioner is only recomputed after reassembly. The step size \(\alpha \) is determined by a damping line-search after solving the defect-correction problem.
3 The Dual Weighted Residual Method in a Space-Time Setting
In this section, we review the general ideas of the DWR method. We then derive joint and split error identities and corresponding error estimators.
3.1 Error Representation and Estimation
Let \(J:X\rightarrow {\mathbb {R}}\) be some goal functional representing some quantity of interest (QoI). The general form reads
where \(T_1,T_2\in I\), e.g., \(T_1 = 0\) and \(T_2 = T\) and T is the end time value. We are interested in the discretization error \(J(u) - J(u_{kh})\) and more specifically to minimize this error for a reasonable computational cost:
This becomes a constrained optimization problem since the solutions \(u\in X\) and \(u_{kh} \in {\tilde{X}}_{k,h}^{r,s}\) are obtained as PDE solutions from (7) to (11), respectively. These PDE problem statements are seen as constraint in terms of the optimization problem. Consequently, for a given goal functional J(u) we want to solve the following optimization problem
This problem setting is the same in [9, Sect. 2.2, (2.13)]. Clearly, after the discretization, we can then measure the discretization error \(J(u) - J(u_{kh})\). We notice that from an optimization viewpoint \(J(u_{kh})\) is a constant in (29) and therefore implicitly contained therein modulo the constant shift.
We apply the method of Lagrange multipliers for this constrained optimization problem (see e.g., [9]) and introduce the dual variable \(z\in X(I,V)\). To account for the discontinuities in the primal problem we define a discontinuous Lagrange functional \(\widetilde{{\mathcal {L}}}(u,z):{\widetilde{X}}({\mathcal {T}}_k,V)\times {\widetilde{X}}({\mathcal {T}}_k,V)\rightarrow {\mathbb {R}}\), such that
Note that A(u)(z) and F(z) contain the jump terms and weakly imposed initial conditions.
For stationary points \((u,z)\in X(I,V)\times X(I,V)\) all jump terms vanish and the initial conditions are met exactly, such that \(\widetilde{{\mathcal {L}}}(u,z)\) is consistent with the continuous functional \({\mathcal {L}}(u,z)\). The first order optimality conditions yield the original primal problem \(A(u)(\varphi )=F(\varphi )\) as well as the adjoint problem:
Find \(z\in {\widetilde{X}}({\mathcal {T}}_k,V)\) such that
Remark 3.1
Note that the test and trial functions are switched in (31). Accordingly, the temporal derivative is now applied to the test function \(\psi \). To rectify this, we apply integration by parts to the corresponding scalar product, obtaining:
The negative sign of the temporal derivative means the adjoint problem has to be solved backwards in time, with an initial value \(z^M\) depending on the goal functional.
For functionals evaluated on the whole temporal domain \(z^M=0\) holds and for functionals defined only at T \(J_u'(u(T),\psi (T))\) can be reinterpreted as an initial value \(z^M\) for details see e.g. [43].
For linear PDEs and linear goal functionals we obtain the exact error representations (see [9]):
In the following, we focus on the primal error representation. As we can see we would need both the exact dual solution z and the discrete dual solution \(z_{kh}\). As this is infeasible for complicated problems we use a discrete solution of higher order for z. In the equal low order approach both primal and adjoint problem are discretized using the same low order elements. The higher order adjoint solution is then obtained by a patch wise reconstruction. This reconstruction is described in detail in [57]. In the mixed order approach the adjoint problem is discretized by higher order elements and the solution is used as the representation of the exact solution. The fully discrete solution is then obtained by interpolation into the lower order space. It is also possible to use different approaches in time and space e.g. discretizing the primal problem with cG(1)dG(0) and the adjoint problem with cG(2)dG(0).
Additionally, (33) can be split into a temporal and a spatial part by introducing the semidiscrete adjoint solution \(z_k\) such that
where temporal and spatial errors are given by, respectively,
That way (36) can be used for temporal refinement and (37) for spatial refinement.
3.2 DWR for Nonlinear Time Dependent Problems
3.2.1 Adjoint Problem Statements
For \(A_{\text {gen.}}\) the left hand side of the adjoint problem (31) in the space-time context explicitly reads as
As an example, for the combustion problem described in the Sect. 2.4 we obtain \(F = F_{\text {comb.}}\) as well as the operator of the semi-linear form and its directional derivative, respectively,
Therein \(\omega '(u)(\psi )\) is the directional derivative of \(\omega (u)\) into the direction \(\psi \).
3.2.2 Goal-Oriented Error Representations
As there are two ways to separate the full estimator into parts, we want to use a clear and precise terminology to distinguish between those two.
Firstly, we can separate by the problem residuals we compute. This gives the primal and adjoint/dual estimators. Oftentimes, the average of those two parts is also called mixed estimator instead of full estimator.
Secondly, we can split the difference between the exact and the fully discrete solution by introducing the time-discrete solution. Not doing so we will call the resulting estimator the joint estimator. If we calculate both the temporal and spatial error estimator, we will call the sum of both the split error estimator. As both seperations can be done simultaneously, combined expressions like split primal estimator or joint dual estimator are possible.
For nonlinear problems we obtain the following error representation [9]:
Theorem 3.2
(Joint error identity) Let the primal problem and adjoint problem be given. Let \((u,z)\in {\widetilde{X}}({\mathcal {T}}_k,V)\times {\widetilde{X}}({\mathcal {T}}_k,V)\), \((u_k,z_k)\in {\widetilde{X}}_k^r({\mathcal {T}}_k,V) \times {\widetilde{X}}_k^r({\mathcal {T}}_k,V)\) and \((u_{kh},z_{kh})\in {{\widetilde{X}}}_{k,h}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M}) \times \widetilde{X}_{k,h}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M})\). Then, we have the space-time joint error identity
with the primal error estimator \(\rho \) and the adjoint error estimator \(\rho ^*\)
as well as a remainder term \({\mathcal {R}}_{kh}\) of higher order.
Proof
With \(\widetilde{X}_{k,h}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M}) \subset {\widetilde{X}}({\mathcal {T}}_k,V)\) and \(J(u_{kh})=\widetilde{{\mathcal {L}}}(u_{kh},z_{kh})\) the assumptions of [57][Proposition 3.1] hold, proving the representation. \(\square \)
Theorem 3.3
(Split error identity) With the previous assumptions, we have the split error identity
with
Proof
The proof follows the same ideas as before but with \(\widetilde{X}_{k,h}^{r,s}({\mathcal {T}}_k,{\mathcal {T}}_h^{1,\dots ,M}) \subset {\widetilde{X}}_k^r({\mathcal {T}}_k,V) \subset {\widetilde{X}}({\mathcal {T}}_k,V)\) as well as \(J(u_{kh})=\widetilde{{\mathcal {L}}}_k(u_{kh},z_{kh})\) and \(J(u_k) = \widetilde{{\mathcal {L}}}(u_k,z_k)\). \(\square \)
3.2.3 Error Estimators
From the previous error identities, we obtain error estimators in four variants. First, we have the full error estimator
However, the unknown solutions u and z still enter. This is already an error estimator, because for cases where u and z are known, we can already estimate (discretization) errors in goal functionals. Of course, for most problems in practice, this first version does not play a role.
To this end, higher-order approximations \({{\widetilde{u}}}\in {\widetilde{X}}\) and \({{\widetilde{z}}}\in {\widetilde{X}}\) are introduced [9]. Examples of such approximations are \({{\widetilde{u}}}:= u_{kh}^{r+1,s+1}\) and \({{\widetilde{z}}}:= z_{kh}^{r+1,s+1}\) such that we obtain the computable error estimator
If the remainder term is omitted (which is indeed usually done in practice) we obtain the practical error estimator
Finally, we also introduce the primal-based error estimator:
As we also need higher order information of the primal problem for (43) and (44) to calculate the adjoint estimator we now have three possible approaches. In addition to the two previous discretization approaches the equal high order approach uses a higher order element discretization for both the primal and adjoint problem. Then, interpolation into a lower order element space yields both \(u_{kh}\) and \(z_{kh}\). However, inserting the interpolated \(u_{kh}\) into the goal functional yields worse results compared to a native low order solution, so ideally the primal problem should also be solved in low order to calculate the functional values. Various algorithmic realizations with corresponding theoretical results, and performance analyses for stationary problems were recently established in [19].
4 Error Localization
In this section, we address our key development, namely the construction of a space-time partition-of-unity (PU) localization of goal-oriented a posteriori error estimators. In the published literature as mentioned in the introduction, so far only stationary cases have been addressed with the PU localization. Here, we first extend the idea to time-dependent problems. Since we want to use the DWR error estimator for grid refinement, we need to split the estimator into element- or DoF-wise error contributions. Three known approaches are the classical integration by parts [5, 9], a variational filtering operator over patches of elements [11] and a variational partition-of-unity localization [53]. For stationary problems, the effectivity of these localizations was established and numerically substantiated in [53].
First, in Sect. 4.1, we exemplarily derive the variational partition of unity approach for our space-time estimator of the heat equation. Second, Sect. 4.3 focuses on details of the actual evaluation including the needed interpolation operations. Next, we list in Sect. 4.4 the resulting error indicators, finally followed by the adaptive algorithms designed in Sect. 4.5.
4.1 The Partition-of-Unity Approach for the Heat Equation
In this key section, we extend the ideas from [53] and apply a partition-of-unity (PU) localization to a space-time error estimator. To this end, we first design the PU space. The simplest choice is \(V_{PU} = {\widetilde{X}}_{k,h}^{0,1}\), i.e. a cG(1)dG(0) discretization. Effectively, this yields one spatial partition of unity \((\chi _{i,m})_{i=1}^{\#DoFs({\mathcal {T}}_h^m)}\in Q_1({\mathcal {T}}_h^m)\) per time interval \(I_m\) for \(m=1,\ldots , M\). As this is a Lagrangian finite element, we have
Proposition 4.1
For a function \(\chi \in V_{PU}\), it holds
Proof
Follows immediately from the properties of the finite element functions. \(\square \)
Remark 4.2
Another common choice for the PU space is \(V_{PU} = X_{kh}^{1,1}\), i.e. a cG(1)cG(1) discretization, for example in native \(d+1\)-dimensional discretizations [17]. In general this ensures a coupling between neighboring temporal elements to address the problem shown in [12]. However, for discontinuous Galerkin discretizations the dominating edge residuals, i.e. jump terms, are explicitly included in the estimator.
Remark 4.3
Clearly, using a dG discretization in time yields a natural decoupling for which the space-time PU reduces effectively to a PU in space. Nonetheless, we formulated our concepts using a space-time PU as the methodology applies (see again [17]) to a larger class of problems. As our work is one of the first into this direction in the literature, our aim is to provide the full methodology in order to have a starting point for further future work.
In the following, \(\tilde{u}\in {\widetilde{X}}\) and \(\tilde{z}\in {\widetilde{X}}\) denote approximations of the exact solutions. In principle the joint and split estimators only differ in the interpolation difference i.e \(\tilde{z}-z_{kh}\) or \(\tilde{z}-z_k\) and \(z_k-z_{kh}\) respectively.
For the joint estimator the local contributions are summed over all DoFs of a fixed interval to obtain the corresponding temporal estimator. Subsequent summation over all time intervals yields the global estimator. For the split estimators the spatial estimator is summed over all space-time DoFs and the temporal estimator is summed over all time intervals. The total error estimator is then the sum of these two error parts.
Proposition 4.4
(Primal joint error estimator for the heat equation) For the space-time formulation of the heat equation, we have the following a posteriori joint error estimator with partition-of-unity localization:
with the error indicators
Proof
We start from Theorem 3.2 with
which yields
Considering the primal part only (see (45)), gives us
Inserting the PU (46) yields
Then, employing the definition of the primal residual leads to
Here, we employ the left hand side and right hand side of the heat equation, namely (13) and (14), respectively, by replacing the test function \(\varphi _{kh}\) by the PU-weighted adjoint sensitivity measure \((z-z_{kh})\chi _{i,m}\). Finally, the (unknown) solution z is approximated by some higher order representation \({\tilde{z}}\) from which we obtain the assertion. \(\square \)
Definition 4.5
(Effectivity and indicator indices) We notice that the effectivity index is defined as
Applying the triangle inequality on \(\eta _{joint}\) yields a more strict criterion, i.e., here
from which the so-called indicator index
can be defined.
Remark 4.6
Note that we only use the temporal part for marking time steps and calculating the global estimator. Since the indicators for each time step are obtained by summing over all elements in said time step the spatial PU \(\chi _{i,m}\) effectively cancels due to the PU property. As a consequence, the spatial PU can be omitted directly in the computation of the temporal indicators.
Proposition 4.7
(Primal split error estimator for the heat equation) For the space-time formulation of the heat equation, we have the following a posteriori split error estimator with partition-of-unity localization:
with the temporal error indicators
and the spatial error indicators
Proof
For the primal split error estimator we start with Theorem 3.3. Then, we proceed for both parts with the primal estimator:
Combining the left hand sides to the full error estimator and utilizing the PU in a similar way as the proof of Proposition 4.4 yields
Here the error indicators are obtained as in the proof of Proposition 4.4, which yields the assertion. \(\square \)
Remark 4.8
Note that the basis functions are globally defined, so the DoF-wise errors contain an implicit sum over all elements in practice. However, calculating element based estimators by constraining the spatial integrals to each element K yields the unlocalized estimator, as the sum over all \(\chi _{i,m}\) on a single element is 1 and effectively cancels out. To use well-known element based marking strategies the DoF-estimators have to be calculated globally. Afterwards element wise estimators can be calculated by summing all estimators belonging to the DoFs of the corresponding element:
where \(\bullet \) stands for h or kh.
Proposition 4.9
(Adjoint joint error estimator for the heat equation) For the space-time formulation of the heat equation, we have the following a posteriori joint error estimator with partition-of-unity localization:
with the error indicators
Proof
We start from Theorem 3.2 with
which yields
Considering the adjoint part only, gives us
Utilizing the PU as in the proof of Proposition 4.4 and the respective definition of J in (28) and the adjoint \(A'_u\) of the heat equation by again approximating u by some higher-order approximation \({\tilde{u}}\) yields the assertion. \(\square \)
Proposition 4.10
(Adjoint split error estimator for the heat equation) For the space-time formulation of the heat equation, we have the following a posteriori split error estimator with partition-of-unity localization:
with the temporal error indicators
and the spatial error indicators
Proof
The proof starts as in Proposition 4.7, but now taking the adjoint residual. The rest is then a combination of the previous three propositions and follows conceptionally the same lines. \(\square \)
Remark 4.11
We emphasize that in this work, we estimate discretization errors only. The space-time extension of stationary PU-DWR versions such as [18, 44, 52] to linear or nonlinear iteration errors in our current space-time setting is part of future work.
4.2 The Partition-of-Unity Approach for the Combustion Problem
In this section, we state the error estimator of the combustion problem:
Proposition 4.12
(Primal split error estimator for combustion) Let us assume homogeneous boundary conditions on \(\Gamma _N\) as well as for the species concentration on \(\Gamma _R\). For the temperature we have the cooling conditions \(\kappa \theta +\partial _n\theta =0\) on the Robin boundary, such that \(g_N^\theta = g_N^Y = g_R^\theta = g_R^Y \equiv 0\), \(a_R^\theta = \kappa \), \(b_R^\theta =1\) and \(a_R^Y=b_R^Y=0\) hold. Then, we have the following a posteriori primal split error estimator with partition-of-unity localization for the space-time formulation of the time-dependent combustion problem:
with the temporal error indicators
and the spatial error indicators
Proof
We start as in Proposition 4.7 and employ for the primal residual and the right hand side the weak form of the combustion problem, i.e., (24) and (25), respectively. \(\square \)
Proposition 4.13
(Adjoint split error estimator for combustion) Using the same boundary conditions, we have the following a posteriori adjoint split error estimator with partition-of-unity localization for the space-time formulation of the time-dependent combustion problem:
with the temporal error indicators
and the spatial indicators
Proof
We start as in Proposition 4.10 and the respective definition of J in (28). In contrast, the adjoint \(A'_u\) is now derived from the combustion system by approximating \(u=(\theta ,Y)\) by some higher-order approximation \({\tilde{u}} = ({\tilde{\theta }},{\tilde{Y}})\) yields the assertion. \(\square \)
4.3 Evaluation of the Space-Time PU-DWR
For the practical evaluation we need to properly define the interpolation differences. Depending on the approach, we need interpolations from a high order space into a low order space and reconstructions the other way around. In space we denote them as
In time we use
In the following, we take a closer look at the interpolation difference for a higher order solution as used in the mixed and equal high order approach, i.e. the interpolations \(i_h^{(s+1)}\) and \(i_k^{(r+1)}\). After that we write down the resulting localized error estimators for each PU-DoF. For good visual representations of the high order reconstructions based on a low order solution see [53, 57] for the spatial part \(i_{2h}^{(s+1)}\) and temporal part \(i_{2k}^{(r+1)}\) respectively.
For our visualization the high order space \({\widetilde{X}}_{k,h}^{1,2}\) and the low order space \({\widetilde{X}}_{k,h}^{0,1}\) are used. Then, \(u_k\) and \(z_k\) are elements of \({\widetilde{X}}_{k,h}^{0,2}\). Furthermore, we notice that in this specific case of piecewise constant discrete solutions the identities \(u_{k}^{-}(t_{m})=u_{k}^{+}(t_{m-1})\) and \(u_{kh}^{-}(t_{m})=u_{kh}^{+}(t_{m-1})\) hold. With this, we obtain the following operators:
Definition 4.14
(Temporal interpolation operators for \(r=0\))
The interpolation operator from piecewise linear elements to piecewise constant elements reads as
The reconstruction of the high order solution, i. e. the other way around, is obtained by linear interpolation
For the spatial interpolation operator \(i_h^2\) we use a linear finite element ansatz with the vertex DoFs of the spatial triangulation. Using \(i_h^2\) on the temporally interpolated solution \(i_k \tilde{z}\) yields \(i_{kh}\tilde{z}\) and vice versa. To illustrate this, Fig. 1 shows the different interpolation levels for a single 1\(+\)1D finite element.
Definition 4.15
(Application of operators depending on the choice of solution spaces) Let \({\hat{u}}\) and \({\hat{z}}\) denote the approximated solutions of the primal and adjoint problems, depending on the choice of finite elements for each problem. Then, we obtain our terms by the following evaluations:
For \(z_{kh}^{-}(t_m)\) we have the same interpolations on \({\hat{z}}\) as for \(u_{kh}^{-}(t_m)\) on \({\hat{u}}\).
For these finite element spaces we can use the midpoint rule with \(t_0 = (t_{m+1}-t_m)/2\) for all temporal integrals when the resulting terms are linear in time. For temporal nonlinearities and higher-order right hand side functions f, higher-order quadrature rules, usually Gauss quadratures, have to be used.
Remark 4.16
(Reconstructions for the adjoint estimator) For the adjoint estimator we additionally need \(u_k\) and u. The semi-discrete \(u_k\) can be obtained the same way as \(z_k\), but for u we need to change the interpolation direction, which results in
Remark 4.17
Finally, we comment on the treatment of pointwise evaluations such as in Proposition 4.10 and Proposition 4.13 in the terms \(u_k^-(t_m)-u_{kh}^-(t_m)\) and \(Y_{k}^-(t_m)-Y_{kh}^-(t_m)\), respectively. As an example, we explain more details for the heat equation. Due to the reverse construction into a higher order space using \(i_{2k}^{(r+1)}\), it holds \(u^-(t_m) = u_k^{-}(t_{m+1})\) for which we deal with a jump at \(t_m\), which in general is not identically equal to zero. Moreover, we note that these jump terms include a spatial integration which is done by Gauss-Legendre quadrature, i.e. with quadrature points that do not lie on the boundaries of the spatial elements. Therefore, \(((u_k^{-}(t_m)-u_{kh}^{-}(t_m))\chi _{i,m},[z_{kh}]_m)\) and corresponding terms will in general be nonzero as well, irrespective of the spatial interpolation. Conversely, if the difference is zero then the low order solution is an exact representation of the high order solution such that no refinement is needed.
4.4 Error Indicators in Space and Time
With the previous evaluations, we can now define the respective indicators in space and time for the heat equation and the combustion problem. Note that the temporal derivative \(\partial _t u_{kh}\) vanishes for \(u_{kh}\in {\widetilde{X}}_{k,h}^{0,s}\), i.e. piecewise constant elements in time.
4.4.1 Natural PU cG(1)dG(0)
Employing the previously introduced PU, namely cG(1)dG(0) yields to the following results for the error indicators.
Proposition 4.18
(Joint primal error indicator for the heat equation) We have the following joint error indicator for the heat equation
with the time step size \(k_m=t_m-t_{m-1}\).
Proof
Starting from Proposition 4.4 and the representations of \(\eta _{kh}^{i,m}\), we evaluate the temporal integrals and employ the interpolation operators derived in Sect. 4.3 and obtain the joint error indicator \(\eta _{kh,\text {heat}}^{i,m}\). \(\square \)
Accordingly, we have
Proposition 4.19
(Split primal error indicators for the heat equation) The split indicators \(\eta _{k,\text {heat}}^{m}\) and \(\eta _{h,\text {heat}}^{i,m}\) for the heat equation are given by
and
Proof
Starting from Proposition 4.7 and the representations of \(\eta _{k}^{m}\) and \(\eta _{h}^{i,m}\), we evaluate the temporal integrals and employ the interpolation operators derived in Sect. 4.3 and obtain the error indicators \(\eta _{k,\text {heat}}^{m}\) and \(\eta _{h,\text {heat}}^{i,m}\). \(\square \)
Using the same interpolations we obtain
Proposition 4.20
(Split primal error indicators for combustion) For the combustion problem we have the following primal error indicators
and
Proof
Starting from Proposition 4.12 and the representations of \(\eta _{k}^{m}\) and \(\eta _{h}^{i,m}\), we evaluate the temporal integrals and employ the interpolation operators derived in Sect. 4.3 and obtain the error indicators \(\eta _{k,\text {combustion}}^{m}\) and \(\eta _{h,\text {combustion}}^{i,m}\). \(\square \)
Remark 4.21
(Identity of the indicator variants) Since \(\sum \limits _{i\in {\mathcal {T}}_h^m} \chi _{i,m} \equiv 1\) in Proposition 4.1 holds, we have
such that the choice between the two indicator variants is only important for adaptive refinement. If one is only interested in estimating the error then both variants are identical.
4.4.2 Alternative PU cG(1)cG(1)
To investigate the impact of the choice of the PU space we derive the split primal indicators for the heat equation based on a cG(1)cG(1) PU. Now, the right hand side integration might need even higher order quadrature rules. Apart from that, the highest temporal order in the temporal indicators is quadratic (constant primal solution, linear adjoint solution and PU) so we apply Simpsons rule instead. Additionally, we obtain two sets of spatial and temporal indicators per interval \(I_m\), i.e.
The temporal indicators for refinement of \(I_m\) are then obtained by
For the spatial element indicators we first have to interpolate the indicator vectors \((\eta _{h,m-1,\text {heat}}^{i,m-1})_{i\in V_h^1({\mathcal {T}}_h^{m-1})}\) and \((\eta _{h,m+1,\text {heat}}^{i,m})_{i\in V_h^1({\mathcal {T}}_h^{m+1})}\) to \({\mathcal {T}}_h^m\). Then, the element indicator for \(K\in {\mathcal {T}}_h^m\) is calculated as
Employing these derivations for the new choice of the PU, Simpson’s rule for quadrature in time, and then proceeding as in Sect. 4.4.1, we obtain the following results.
Proposition 4.22
(Split primal error indicators for the heat equation with cG(1)cG(1) PU) The split indicators for the heat equation are given by
and
as well as
and
For the general adjoint estimator we also need \(z_{kh}\) and \(u_k\) from \(I_{m+1}\) which can be obtained by the interpolations described in (63) and (64) respectively. Additionally we only look at goal functionals of the types
which are essentially interchangeable in the following formulas. Therefore, we only write down the indicators for \(J_1\).
Proposition 4.23
(Joint adjoint error indicator for the heat equation) We have the following joint error indicator for the heat equation
Proposition 4.24
(Split adjoint error indicators for the heat equation) The split indicators \(\eta _k^{m,*}\) and \(\eta _{h,i}^{m,*}\) for the heat equation are given by
and
All functionals we want to examine for the combustion equation are only dependent on \(u_{kh}\) and the primal weight, which is at most linear in time. Therefore, we can simplify the estimator by also applying the midpoint rule to the functional.
Proposition 4.25
(Split adjoint error indicators for combustion) For the combustion problem we have the following adjoint error indicators
and
4.5 Adaptive Algorithm
There are multiple options for solving the primal and adjoint problems, i.e. time-stepping, time-slabbing and fully simultaneous space-time, which all need adjustments to marking and refinement. However, all simulations shown here are time-stepping based so we limit ourselves to this approach. Again, we note that in a space-time context the adjoint problem runs backward in time. Then, all information is collected to evaluate the error estimators.
Since one of the error components might dominate, we employ an equilibration for time-stepping as proposed in [57]. This will sometimes restrict refinement to space or time. The overall procedure follows the typical loop: solve, estimate, mark, and refine.
For error estimation in time-stepping we obtain Algorithm 1. There, the main choice is in whether to use the split or joint estimators. Note that in the case of the joint estimator, the indicators \(\eta _{kh}^m\) and \(\eta _{kh}^{m,*}\) are calculated by summation of the spatial indicators.
Having calculated the estimators we mark and refine elements by following Algorithm 2. There, the equilibration is done by first calculating the global estimators. Note that these coincide in the joint case, such that no equilibration is performed.
5 Numerical Tests
In this final section, we substantiate our space-time error estimators and algorithms with the help of three numerical experiments. In the first configuration, a \(2+1D\) heat equation with manufactured solution is considered. This allows us to investigate in detail effectivity indices. Next, in Configuration 2, again a \(2+1D\) heat equation is utilized, but with a dynamic manufactured solution inspired by Hartmann [29]. In our final configuration, we consider a nonlinear coupled problem, namely nonlinear combustion. Therein, very detailed comparisons of different polynomial degrees, primal, adjoint and full estimators are undertaken. The computations are based on extensions of the DTM package dwr-diffusion [35], which itself is based on deal.II [3]. The programming codes are open-source can be found on https://github.com/jpthiele/pu-dwr-diffusion and https://github.com/jpthiele/pu-dwr-combustion respectively, and follow good practices of sustainable research software developments [2].
5.1 Configuration 1: 2 + 1D Heat Equation with a Simple Manufactured Solution
5.1.1 Problem Statement
To test the 2 + 1D implementation and the derived estimators we prescribe the following solution for the heat equation introduced in Sect. 2.3
Inserting the solution into the PDE yields the right hand side function
5.1.2 Configuration
The PDE is solved on the unit square and the temporal interval (0, 1), i.e. \(T=1\). Inserting \(x=0\), \(y=0\) or \(t=0\) yields \(u = 0\), resulting in homogeneous Dirichlet boundary conditions and an initial condition of \(u^0 \equiv 0\).
5.1.3 Goal Functionals
To test whether the error identity holds, we need a linear goal functional. A simple choice is the averaged solution
Inserting the analytical solution for an arbitrary T we obtain
as reference value.
5.1.4 Discussion of Findings
We expect (33) and (34) to hold, which is identical to \(I_{\text {eff}}= 1\). We observe the effectivity indices for all three approaches in space defined as
with \(\eta _{kh}^{s/{\widetilde{s}}}\) as the general estimator for \({\hat{u}}_{kh}\in {\widetilde{X}}_{k,h}^{0,s}\) and \({\hat{z}}_{kh}\in {\widetilde{X}}_{k,h}^{0,{\widetilde{s}}}\) as defined in Propositions 4.19 and 4.24 for the primal and adjoint estimators respectively. All estimators are computed using Algorithm 1.
Table 1 shows that all approaches yield effectivity indices very close to 1. We also notice, that the biggest difference between primal and adjoint estimator is obtained for the mixed order approach.
However, this is not surprising as the approach is tailored to the primal estimator and calculating the adjoint estimator could be seen as questionable for the two following reasons. When interpolating the higher order solution for the adjoint problem for \(z_{kh}\) we do not obtain the optimal \(z_{kh}\) compared to solving with bilinear elements directly. Additionally, reconstructing the higher order primal solution yields a worse approximation compared to solving directly with biquadratic finite elements.
Furthermore, we notice that we use a lot more elements in time than in space. In space-time, the estimator is dependent on a good balance between space and time discretization. For the sake of brevity we investigate this further in the following configuration as the solution is much more interesting.
5.2 Configuration 2: 2 + 1D Heat Equation with a Dynamic Manufactured Solution
5.2.1 Problem Statement
This test case was designed in [29]. We again solve the heat equation. The manufactured solution is a rotating hill on a unit-square spatial domain \(\Omega = (0,1)^2\) in the time interval \((0,T),\;T=1\).
The manufactured solution is given as
The right hand side of the problem is obtained as in Sect. 5.1 by inserting this solution into the heat equation. Additionally, all definitions for \(\eta _{kh}^{s/{\widetilde{s}}}\) and \(I_{\text {eff}}^{s/{\widetilde{s}}}\) are the same using again Algorithm 1 to compute the indicators.
5.2.2 Goal Functional
Since we are interested in capturing the local behaviour of the solution, we choose the \(L_2\)-error as functional of interest, i.e.
5.2.3 Comparison of the Different Spatial Approaches
We start by looking at the exact error and the resulting estimators for different choices of \(M_{\text {initial}}\). We see that the estimators in Tables 2, 3, 4 and 5 are converging to relatively stable values with rising \(M_{\text {initial}}\). We can also see that since the temporal elements are only doubled while the spatial elements are quadrupled, the initial number of temporal elements has to be large enough for uniform refinement. In adaptive simulations we can control this better as we can choose different fractions of spatial and temporal elements to be marked for refinement.
The equal low order estimators (Table 3) are underestimating the error with an effectivity of roughly \(0.34-0.40\) for the coarsest mesh. This gets much better after the two refinements where the estimator is close to the exact \(L_2\)-error. However, as the reconstruction effectively works on an even coarser mesh this is not surprising.
The mixed order estimators (Table 4) are less dependent on the spatial mesh size but overestimate the error with an effectivity of \(1.20-1.48\). We can also see that the overestimation gets smaller with rising \(M_{\text {initial}}\) but this is of course an additional cost factor.
The equal high order estimators (Table 5) are also less dependent on the spatial mesh size, but they also use double the amount of degrees of freedom for the primal problem. They also overestimate the error but for large enough \(M_{\text {initial}}\) the effectivity is less than 1.10. However, Table 6 shows that solving the primal problem with biquadratic elements and using a bilinear interpolation between the vertices does not recover the best approximation \(u_{kh}\). In practice this means that the primal problem should be solved natively with bilinear elements to obtain the solution for which the error is actually estimated, which leads to additional costs. This gets especially expensive for nonlinear problems. Note that in this particular case the resulting adjoint solution and consequently the estimators would also be different as the \(L_2\) error itself factors into \(J'_u\), so the accuracy of the estimator could be better.
In conclusion, both reconstructing a higher order solution and natively solving the primal or adjoint problem with higher order elements in space work well for linear problems, but the reconstruction is cheaper and leads to a better estimator for fine enough meshes.
How the low and mixed order approach perform for higher order finite elements and corresponding errors could be subject of further studies.
5.2.4 Comparison of Adaptive Refinement to the Original Computations
For this configuration we want to compare our results to those described by Hartmann [29], where the manufactured solution was first formulated. To our knowledge this configuration was not reproduced and published so far, so the original thesis is the only point of comparison. There, the classical estimator is used, which is obtained by partial integration to obtain a strong form with jump terms in space. There, \(Q_1\) elements in space and dG(0) elements in time are used as well, but it is unknown which quadrature formula was used in time for the nonlinear f. We used the right box rule as this is what corresponds to the implicit Euler scheme and got our error (\(1.92e-02\)) closest to the error of the original results (\(1.75e-02\)). Table 7 shows our results with the split and joint estimators. These perform very well in comparison to the original Hartmann results from [29, Table 3.4].
Even though the marking strategy used by Hartmann is unknown, we got close to the number of temporal elements and the maximum number of spatial elements with fixed rate marking in Algorithm 2. In comparison, our estimators better localize the error as we get comparable errors with one less loop that additionally has a smaller maximum number of spatial elements. This can be seen in Fig. 2, where the original results are only performing roughly as well as our computation with uniform refinement, while both PU-DWR estimators yield better convergence. We plotted the \(L_2\) error against \(M*N_{\max }\) which is an upper bound for the actual number of space-time elements as no further information was available from the original computations. However, Table 8 shows that at least for our simulations the actual number is not too far from the upper bound. Additionally, we can see that, as expected, the split estimator outperforms the joint estimator.
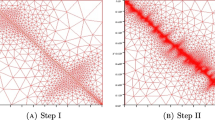
Finally, Fig. 3 shows that the local refinement nicely matches the corresponding solution of Fig. 4 and that the meshes are indeed changing over time.
Section 5.2: Error convergence of the Hartmann testcase
Section 5.2: Grid after 4 refinement loops with the split PU-DWR estimator at \(t=i/4\), \(i\in \{1,2,3,4\}\)
Section 5.2: Solution after 4 refinement loops with the split PU-DWR estimator at \(t=i/4\), \(i\in \{1,2,3,4\}\)
5.2.5 Comparison of PU Spaces
Here, we want to examine whether the additional coupling with a cG(1) partition-of-unity in time is beneficial for adaptive refinement. For this, we performed multiple adaptive simulations with the corresponding low, mixed and high order estimators. Figures 5, 6 and 7 show the exemplary results with an initial temporal mesh of 1600 elements with fixed rate marking of \(60\%\) in time and \(40\%\) in space. In all three cases the dG(0) PU performs better than the cG(1) PU, with the lowest difference for the equal high order estimator. For the equal high order case the \(L^2\)-error is calculated on the interpolated primal solution, which does not recover the actual best approximation solution of directly solving the primal solution in the low order space, such that the initial error is higher than for uniform refinement. Finally, Fig. 8 shows the results for the mixed order estimator with a finer initial temporal mesh, which are qualitatively the same as for Fig. 6.
Overall we conclude that for discontinuous Galerkin discretizations in time the dG(0) partition-of-unity is completely sufficient in addition to being cheaper to compute and easier to implement.
Section 5.2: Error convergence of the Hartmann testcase for \(\eta ^{1/1}\) and \(M_\text {init} = 1600\)
Section 5.2: Error convergence of the Hartmann testcase for \(\eta ^{1/2}\) and \(M_\text {init} = 1600\)
Section 5.2: Error convergence of the Hartmann testcase for \(\eta ^{2/2}\) and \(M_\text {init} = 1600\)
Section 5.2: Error convergence of the Hartmann testcase for \(\eta ^{1/2}\) and \(M_\text {init} = 3200\)
5.3 Configuration 3: Nonlinear Combustion
5.3.1 Problem Statement
The final test case is as described in [57] (originally based on [36]) and some preliminary results were published in our prior work [67]. Here, we solve the nonlinear combustion equations described in Sect. 2.4.
5.3.2 Configuration
The reaction is simulated in a rectangular channel of length \(L=60\) and height \(H=16\) in which two cooled rods of length L/4 and height H/4 are inserted into both channel walls at L/4. The reaction is solved for a total of \(T=60\) with 256 time and 896 space DoFs initially.
The cooling of \(\Gamma _R\) is described by the Robin boundary condition \(\partial _n\theta = -0.1\theta \), with homogeneous Neumann conditions for the species concentration. The left wall \(\Gamma _D\) is kept at a constant temperature of \(\theta _D = 1\) without any combustible species \(Y_D = 0\). All other walls \(\Gamma _N\) are described by homogeneous Neumann boundary conditions. An initial flame front is described by
5.3.3 Parameters
The reaction parameters are a Lewis number of \(Le = 1\), a gas expension of \(\alpha = 0.8\) and a dimensionless energy of \(\beta = 10\).
5.3.4 Goal Functionals
The first functional we investigate is the average reaction rate i.e.
This nonlinear functional is defined on the whole space-time domain. For the second functional we calculate the average species concentration on the cooled rods \(\Gamma _R\) i.e.
This is a linear functional, but it is only defined on part of the boundary.
5.3.5 Discussion of Findings for \(J_1\)
For both functionals the indicators for \(\eta _{kh}^{{s/{\widetilde{s}}}}\) are computed using Propositions 4.20 and 4.25 and Algorithm 1 with \({{\widetilde{u}}}\), \(u_k\), \(u_{kh}\) and \({{\widetilde{z}}}\), \(z_k\), \(z_{kh}\) following from (63) to (64) with \({\hat{u}}_{kh}\in {\widetilde{X}}^{0,s}_{k,h}\) and \({\hat{z}}_{kh}\in {\widetilde{X}}^{0,{{\widetilde{s}}}}_{k,h}\). Then, the full estimators are computed by taking the averages of the primal and adjoint indicators at each space-time Dof and summing over all DoFs.
Tables 9, 10 and 11 show the behaviour of the primal, adjoint and full estimators for \(J_1\) respectively. We can see that all estimators with the mixed order and equal high order approach behave similarly. For both, the adjoint estimator and the resulting full estimator are overestimating the error by about two orders of magnitude. However, the primal estimators are not too far off. The equal low order approach yields the best results on the finest level, and the primal and adjoint estimators are comparable. It can be inferred that there is no benefit from calculating the full estimator in this case. Therefore, we use Algorithm 2 with fixed rate marking refining \(50\%\) of all temporal elements and on each interval \(30\%\) of all spatial elements based only on the primal indicators.
Figure 9 shows the error convergence under adaptive refinement when using only the primal estimator. When only counting the primal unknowns for both estimators, our findings for equal low order and mixed order are comparable, and both perform better than global refinement. However, when both the number of Dofs of the adjoint and the PU are additionally taken into account, the low order approach clearly outperforms the mixed order approach. We can also see that the starting disadvantage of having the same error on the coarsest mesh with more DoFs is rectified by the first adaptive refinement step.
Section 5.3: Error convergence for the reaction rate functional. On the left only the number of unknowns for the primal problem and on the right all unknowns are taken into account
Figure 10 shows the reaction rate and the corresponding grids for two different time points. We can see that the grid evolves nicely and follows the combustion reaction. This shows that our localization works well in capturing the physics and refining accordingly.
Section 5.3: reaction rate and grid at \(t=20\) (left) and \(t=60\) (right)
5.3.6 Discussion of Findings for \(J_2\)
Tables 12, 13 and 14 show the behaviour of the primal, adjoint and full estimators for \(J_2\) respectively. The equal low order approach shows a similar behaviour to the previous functional. However, the overestimation of the adjoint estimators for the mixed order and high order approach is not as bad as for the nonlinear functional. On the other hand their respective primal estimators are underestimating the error by quite a bit. In the full estimators these over- and underestimations are cancelling out quite nicely such that this estimator would be more useful here. For this reason the simulations for Fig. 11 were done by using the full estimator for adaptivity in Algorithm 2 with the same marking strategy as before. As with the first functional we see that both approaches yield comparable results when only counting the memory cost for solving the primal problem. We also see that both approaches eventually outperform uniform refinement when taking the total cost into account. But the equal low order approach is again and still the best choice.
Section 5.3: Error convergence for the species concentration functional. On the left only the number of unknowns for the primal problem and on the right all unknowns are taken into account
Figure 12 shows the species concentration and the refined grids based on \(J_2\) at different time steps. We see that along the cooled rods the grid again follows the combustion reaction. As that is the area where we have changes in the concentration this fits well. We also see that the mesh is refined around the cooled rod once the reaction moved past them. Together with the convergence behaviour we see again that the novel localization works well.
Section 5.3: Rod species concentration and corresponding grid at \(t=20\) (left) and \(t=60\) (right)
6 Conclusions
In this work, we proposed partition-of-unity (PU) dual-weighted residual a posteriori error estimators and space-time adaptivity for linear and nonlinear partial differential equations. From the algorithmic side, the main novelties are the extension of the PU localization to space-time Galerkin finite element discretizations and the realization of split and joint error estimators. From the implementation side, despite starting from pre-implementations in the DTM package dwr-diffusion [35] and deal.II [3], extensive code developments and debugging was necessary, which greatly exceed existing implementations, specifically for the nonlinear features such as the nonlinear combustion PDE as well as nonlinear goal functionals. In three numerical examples, we studied in the detail the computational performance for the linear heat equation and also for a nonlinear low Mach number combustion problem. We also found that the equal low order approach yielded the best estimation and adaptive performance across the board and that a cG(1)dG(0) PU is sufficient for cG(s)dG(r) discretizations of the primal problem. Furthermore, an example of an immediate practical application of our framework can be found within the excellence cluster PhoenixDFootnote 1 in which space-time methods and goal-oriented error estimation are of interest for the efficient solution of multiphysics problems and where the heat equation and the Navier–Stokes equations are needed.
Data availability
The algorithms and numerical results are implemented open source and can be found on https://github.com/jpthiele/pu-dwr-diffusion and https://github.com/jpthiele/pu-dwr-combustion respectively, and follow good practices of sustainable research software developments [2]. Moreover, the reproducibility codes can be found on zenodo via https://zenodo.org/records/10641104 and https://zenodo.org/records/10641119.
References
Amestoy, P., Duff, I.S., Koster, J., L’Excellent, J.-Y.: A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Appl. 23(1), 15–41 (2001)
Anzt, H., Bach, F., Druskat, S., Löffler, F., Loewe, A., Renard, B., Seemann, G., Struck, A., Achhammer, E., Aggarwal, P., Appel, F., Bader, M., Brusch, L., Busse, C., Chourdakis, G., Dabrowski, P., Ebert, P., Flemisch, B., Friedl, S., Fritzsch, B., Funk, M., Gast, V., Goth, F., Grad, J., Hermann, S., Hohmann, F., Janosch, S., Kutra, D., Linxweiler, J., Muth, T., Peters-Kottig, W., Rack, F., Raters, F., Rave, S., Reina, G., Reißig, M., Ropinski, T., Schaarschmidt, J., Seibold, H., Thiele, J., Uekerman, B., Unger, S., Weeber, R.: An environment for sustainable research software in germany and beyond: current state, open challenges, and call for action [version 1; peer review: awaiting peer review]. F1000Research 9(295) (2020)
Arndt, D., Bangerth, W., Blais, B., Clevenger, T.C., Fehling, M., Grayver, A.V., Heister, T., Heltai, L., Kronbichler, M., Maier, M., Munch, P., Pelteret, J.-P., Rastak, R., Tomas, I., Turcksin, B., Wang, Z., Wells, D.: The deal.II library, Version 9.2. J. Numer. Math. 28(3), 131–146 (2020)
Bangerth, W., Geiger, M., Rannacher, R.: Adaptive Galerkin finite element methods for the wave equation. Comput. Methods Appl. Math. 10(1), 3–48 (2010)
Bangerth, W., Rannacher, R.: Adaptive Finite Element Methods for Differential Equations. Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, Boston (2003)
Bause, M., Radu, F.A., Köcher, U.: Space-time finite element approximation of the Biot poroelasticity system with iterative coupling. Comput. Methods Appl. Mech. Eng. 320, 745–768 (2017)
Becker, R., Meidner, D., Vexler, B.: Efficient numerical solution of parabolic optimization problems by finite element methods. Optim. Methods Softw. 22(5), 813–833 (2007). https://doi.org/10.1080/10556780701228532
Becker, R., Rannacher, R.: Weighted a posteriori error control in FE methods. In: Bock, H.G., Kanschat, G., Rannacher, R., Brezzi, F., Glowinski, R., Kuznetsov, Y.A., Périaux J. (eds.) 2nd European Conference on Numerical Mathematics and Advanced Applications, ENUMATH 1997, World Scientific (1995)
Becker, R., Rannacher, R.: An optimal control approach to a posteriori error estimation in finite element methods. Acta Numer. 10, 1–102 (2001)
Besier, M., Rannacher, R.: Goal-oriented space-time adaptivity in the finite element Galerkin method for the computation of nonstationary incompressible flow. Int. J. Numer. Methods Fluids 70(9), 1139–1166 (2012). https://doi.org/10.1002/fld.2735
Braack, M., Ern, A.: A posteriori control of modeling errors and discretization errors. Multiscale Model. Simul. 1(2), 221–238 (2003)
Carstensen, C., Verfürth, R.: Edge residuals dominate a posteriori error estimates for low order finite element methods. SIAM J. Numer. Anal. 36(5), 1571–1587 (1999)
Davis, T.A.: Algorithm 832: UMFPACK V4.3–An unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw. 30(2), 196–199 (2004)
Di Pietro, D.A., Ern, A.: Mathematical Aspects of Discontinuous Galerkin Methods, vol. 69. Springer, New York (2011)
Dörfler, W., Findeisen, S., Wieners, C.: Space-time discontinuous Galerkin Discretizations for linear first-order hyperbolic evolution systems. Comput. Methods Appl. Math. 16(3), 409–428 (2016)
Dörfler, W., Wieners, C., Ziegler, D.: Parallel space-time solutions for the linear visco-acoustic and visco-elastic wave equation. In: Nagel, W.E., Kröner, D.H., Resch, M.M. (eds.) High Performance Computing in Science and Engineering ’19, pp. 589–599. Springer, Cham (2021)
Endtmayer, B., Langer, U., Schafelner, A.: Goal-oriented adaptive space-time finite element methods for regularized parabolic p-laplace problems. arXiv:2306.07167, (2023)
Endtmayer, B., Langer, U., Wick, T.: Multigoal-oriented error estimates for non-linear problems. J. Numer. Math. 27(4), 215–236 (2019)
Endtmayer, B., Langer, U., Wick, T.: Reliability and efficiency of DWR-type a posteriori error estimates with smart sensitivity weight recovering. Comput. Methods Appl. Math. 21(2), 351–371 (2021)
Eriksson, K., Estep, D., Hansbo, P., Johnson, C.: Computational Differential Equations. Cambridge University Press, Cambridge (2009)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems I: a linear model problem. SIAM J. Numer. Anal. 28(1), 43–77 (1991)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems II: optimal error estimates in Linfty L2 and Linfty Linfty. SIAM J. Numer. Anal. 32(3), 706–740 (1995)
Eriksson, K., Johnson, C., Logg, A.: Adaptive Computational Methods for Parabolic Problems. American Cancer Society, Atlanta (2004)
Failer, L.: Optimal Control of Time-Dependent Nonlinear Fluid-Structure Interaction. PhD thesis, Technical University Munich (2017)
Failer, L., Meidner, D., Vexler, B.: Optimal control of a linear unsteady fluid-structure interaction problem. J. Optim. Theory Appl. 170(1), 1–27 (2016)
Failer, L., Wick, T.: Adaptive time-step control for nonlinear fluid-structure interaction. J. Comput. Phys. 366, 448–477 (2018)
Gander, M.J., Neumüller, M.: Analysis of a new space-time parallel multigrid algorithm for parabolic problems. SIAM J. Sci. Comput. 38(4), A2173–A2208 (2016)
Goll, C., Rannacher, R., Wollner, W.: The Damped Crank-Nicolson Time-Marching Scheme for the Adaptive Solution of the Black-Scholes Equation. SSRN Scholarly Paper ID 2795622, Social Science Research Network, Rochester, NY (2015)
Hartmann, R.: A-posteriori Fehlerschätzung und adaptive Schrittweitein- und Ortsgittersteuerung bei Galerkin-Verfahren für die Wärmeleitungsgleichung. Diplomarbeit, University of Heidelberg, Heidelberg (1998)
Hübner, B., Walhorn, E., Dinkler, D.: A monolithic approach to fluid-structure interaction using space-time finite elements. Comput. Methods Appl. Mech. Eng. 193(23), 2087–2104 (2004)
Hughes, T.J.R., Hulbert, G.M.: Space-time finite element methods for Elastodynamics: formulations and error estimates. Comput. Methods Appl. Mech. Eng. 66(3), 339–363 (1988)
Hulbert, G.M., Hughes, T.J.: Space-time finite element methods for second-order hyperbolic equations. Comput. Methods Appl. Mech. Eng. 84(3), 327–348 (1990)
Khimin, D., Steinbach, M., Wick, T.: Space-time formulation, discretization, and computational performance studies for phase-field fracture optimal control problems. J. Comput. Phys. 470, 111554 (2022)
Köcher, U.: Variational Space-Time Methods for the Elastic Wave Equation and the Diffusion Equation. PhD thesis, Helmut-Schmidt-Universität (2015)
Köcher, U., Bruchhäuser, M.P., Bause, M.: Efficient and scalable data structures and algorithms for goal-oriented adaptivity of space-time FEM codes. SoftwareX 10, 100239 (2019)
Lang, J.: Adaptive Multilevel Solution of Nonlinear Parabolic PDE Systems. Lecture Notes in Computational Science and Engineering Book Series, Springer, New York (2001)
Langer, U., Schafelner, A.: Adaptive space-time finite element methods for non-autonomous parabolic problems with distributional sources. Comput. Methods Appl. Math. 20(4), 677–693 (2020)
Langer, U., Schafelner, A.: Adaptive space-time finite element methods for parabolic optimal control problems. J. Numer. Math. 30(4), 247–266 (2021)
Langer, U., Schafelner, A.: Space-time hexahedral finite element methods for parabolic evolution problems. DK Report 2021-05 (2021)
Langer, U., Steinbach, O.: Space-Time Methods: Application to Partial Differential Equations. Volume 25 of Radon Series on Computational and Applied Mathematics, de Gruyter, Berlin (2019)
Langer, U., Steinbach, O., Tröltzsch, F., Yang, H.: Space-time finite element discretization of parabolic optimal control problems with energy regularization. SIAM J. Numer. Anal. 59(2), 675–695 (2021)
Langer, U., Steinbach, O., Tröltzsch, F., Yang, H.: Unstructured space-time finite element methods for optimal control of parabolic equations. SIAM J. Sci. Comput. 43(2), A744–A771 (2021)
Meidner, D.: Adaptive Space-Time Finite Element Methods for Optimization Problems Governed by Nonlinear Parabolic Systems. Dissertation (2007)
Meidner, D., Rannacher, R., Vihharev, J.: Goal-oriented error control of the iterative solution of finite element equations. J. Numer. Math. 17, 143–172 (2009)
Meidner, D., Richter, T.: Goal-oriented error estimation for the fractional step theta scheme. Comput. Methods Appl. Math. 14(2), 203–230 (2014)
Meidner, D., Richter, T.: A posteriori error estimation for the fractional step theta discretization of the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 288, 45–59 (2015)
Meidner, D., Vexler, B.: Adaptive space-time finite element methods for parabolic optimization problems. SIAM J. Control Optim. 46(1), 116–142 (2007)
Neitzel, I., Vexler, B.: A priori error estimates for space-time finite element discretization of semilinear parabolic optimal control problems. Numer. Math. 120(2), 345–386 (2012)
Neumüller, M.: Space-Time Methods Fast Solvers and Applications. PhD thesis, TU Graz (2013)
Oden, J.: A general theory of finite elements. II. Applications. Int. J. Numer. Methods Eng. 1, 247–259 (1969)
Rannacher, R., Suttmeier, F.-T.: A posteriori error estimation and mesh adaptation for finite element models in elasto-plasticity. Comput. Methods Appl. Mech. Eng. 176(1), 333–361 (1999)
Rannacher, R., Vihharev, J.: Adaptive finite element analysis of nonlinear problems: balancing of discretization and iteration errors. J. Numer. Math. 21(1), 23–61 (2013)
Richter, T., Wick, T.: Variational localizations of the dual weighted residual estimator. J. Comput. Appl. Math. 279, 192–208 (2015)
Roth, J., Thiele, J.P., Köcher, U., Wick, T.: Tensor-product space-time goal-oriented error control and adaptivity with partition-of-unity dual-weighted residuals for nonstationary flow problems. Comput. Methods Appl. Math. 24(1), 185–214 (2024)
Schafelner, A.: Space-Time Finite Element Methods. PhD thesis, Johannes Kepler University Linz (2022)
Schmich, M.: Adaptive Finite Element Methods for Computing Nonstationary Incompressible Flows. PhD thesis (2009)
Schmich, M., Vexler, B.: Adaptivity with dynamic meshes for space-time finite element discretizations of parabolic equations. SIAM J. Sci. Comput. 30(1), 369–393 (2008)
Singh, G., Wheeler, M.F.: A space-time domain decomposition approach using enhanced velocity mixed finite element method. J. Comput. Phys. 374, 893–911 (2018)
Steinbach, O., Yang, H.: Comparison of algebraic multigrid methods for an adaptive space-time finite-element discretization of the heat equation in 3D and 4D. Numer. Linear Algebra Appl. 25(3), e2143 (2018)
Takizawa, K., Tezduyar, T.: Multiscale space-time fluid-structure interaction techniques. Comput. Mech. 48, 247–267 (2011)
Tezduyar, T.E., Behr, M., Mittal, S., Liou, J.: A new strategy for finite element computations involving moving boundaries and interfaces–The deforming-spatial-domain/space-time procedure: II. Computation of free-surface flows, two-liquid flows, and flows with drifting cylinders. Comput. Methods Appl. Mech. Eng. 94(3), 353–371 (1992)
Tezduyar, T.E., Sathe, S.: Modelling of fluid-structure interactions with the space-time finite elements: solution techniques. Int. J. Numer. Meth. Fluids 54(6–8), 855–900 (2007)
Tezduyar, T.E., Sathe, S., Keedy, R., Stein, K.: Space-time finite element techniques for computation of fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 195(17), 2002–2027 (2006)
Tezduyar, T.E., Sathe, S., Stein, K.: Solution techniques for the fully discretized equations in computation of fluid-structure interactions with the space-time formulations. Comput. Methods Appl. Mech. Eng. 195(41), 5743–5753 (2006)
Thiele, J.: Error-Controlled Space-Time Finite Elements, Algorithms, and Implementations for Nonstationary Problems. PhD thesis, Leibniz University Hannover (2023)
Thiele, J.P., Wick, T.: Space-time pu-dwr error control and adaptivity for the heat equation. PAMM 21(1), e202100174 (2021)
Thiele, J.P., Wick, T.: Space-time error control using a partition-of-unity dual-weighted residual method applied to low mach number combustion. In: Melenk, J.M., Perugia, I., Schöberl, J., Schwab, C. (eds.) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2020+1, pp. 509–520. Springer, Cham (2023)
Verfürth, R.: A posteriori error estimates for finite element discretizations of the heat equation. Calcolo 40, 195–212 (2003)
Wick, T.: On the Adjoint Equation in Fluid-Structure Interaction. WCCM-ECCOMAS2020 (2021)
Wick, T.: Numerical Methods for Partial Differential Equations. Institutionelles Repositorium der Leibniz Universität Hannover, Hannover (2022). https://doi.org/10.15488/11709
Acknowledgements
The authors thank Uwe Köcher (Hamburg), Julian Roth (IfAM), Johannes Lankeit (IfAM), and Bernhard Endtmayer (IfAM) for fruitful discussions. Moreover, we thank the anonymous referee for excellent questions that helped to improve the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work is funded by the Deutsche Forschungsgemeinschaft (DFG) under Germany’s Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thiele, J.P., Wick, T. Numerical Modeling and Open-Source Implementation of Variational Partition-of-Unity Localizations of Space-Time Dual-Weighted Residual Estimators for Parabolic Problems. J Sci Comput 99, 25 (2024). https://doi.org/10.1007/s10915-024-02485-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02485-6