Abstract
An auxiliary optimal control problem is formulated that provides with its unique solution, a continuous representation of the global error of a numerical approximation to the solution of a linear quadratic optimal control problem. The resulting error functions are characterized as the unique solutions to an optimality system that is reformulated as a boundary value problem. With this formulation, reliable pointwise error estimates can be generated utilizing well-established techniques of defect control. A novel algorithm based on defect correction and defect control is presented that generates pointwise approximations to the global error of numerical optimal control solutions on a uniform grid. It is proven and numerically validated that this algorithm can generate pointwise estimates that approximate the true global error with a prescribed accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper is devoted to the pointwise quantification of errors of discrete-time approximations to solutions of certain classes of linear quadratic optimal control (LQOC) problems. We extend for the first time the approach initiated by Zadunaisky [1, 2] for continuous-in-time estimates of errors in numerical approximations of Cauchy and boundary value problems with ordinary differential equations (ODE) to the field of optimal control problems governed by linear ODE models. Our purpose is to derive a continuous representation of the discretization errors of the numerical state and control functions approximating the solution to optimal control problems of the form
where \(\alpha \ge 0\), \(c\in {\mathbb R}^n\), \(A\in {\mathbb R}^{n\times n}\), \(B\in {\mathbb R}^{n\times m}\), \(x^0 \in {\mathbb R}^n\), \(x(t) \in {\mathbb R}^n\) for all \(t\in [t_0,T]\), and \(|\cdot |\) denotes the standard euclidean norm. For the weight matrices, it is supposed that \(R\in {\mathbb R}^{m\times m}\) is symmetric positive definite and \(Q\in {\mathbb R}^{n\times n}\) is symmetric positive semi-definite.
This work considers two cases for \(U_{ad}\). If the set of admissible controls for (1) is bounded and given by
where \({{\mathcal {U}}}:= [ \underline{u}, \overline{u} ]^m\), \(\underline{u} \le 0 \le \overline{u}\); we refer to (1)–(2) as the LQOC problem.
In the case without control constraints, that is, if the optimal control is sought in the set
we refer to (1) with (3) as the linear quadratic regulator (LQR) problem.
In both cases, \(U_{ad}\) is closed and convex in \(L^2(t_0,T;{\mathbb R}^m)\) and the optimal control problems (1)–(2) and (1) with (3) admit unique solutions which are denoted with (x, u).
Since the fundamental works by Kalman [3, 4], linear quadratic control problems play an important role in optimal control theory and see extensive use in engineering applications. This is also because the LQR setting allows for the analysis of optimal control problems with nonlinear dynamics by providing a local approximation of the optimal control solution. In some cases, non-linear control problems can be solved directly using a linear model [5]. Applications of LQR problems involve the construction of trajectory controllers by linearization around the desired trajectory of a nonlinear system or for deriving feedback controls for the stabilization of nonlinear systems in equilibrium points. The input-constrained case (1)–(2) is a natural extension of LQR problems and the constraints on the inputs can model limitations of the hardware implementing the controller. However, despite its simple form, in general, no exact solution to (1) is available except for a few cases. Hence, in practice, (1) must be solved using computational methods that involve time-discretization of some form. A prominent approach is the so-called direct approach of optimal control, where the optimal control problem is recast into a finite-dimensional optimization problem by time-discretization of the system dynamics and the objective functional J. Another approach for finding approximations to the optimal control is the indirect approach, where an approximate solution to the system of necessary conditions arising from the Pontryagin maximum principle (PMP) [6] is sought. The PMP states that given an optimal control \(u \in U_{ad}\) and the corresponding state x, there exists an adjoint state p such that
where \(H(x,u,p) = p^T(Ax + Bu) - \frac{1}{2} (x^T Q x + u^T R u )\) is the Hamilton-Pontryagin (HP) function and it holds:
In the case of LQR problems, from (4) the relation \(u(t) = R^{-1}B^T p(t)\) follows and the optimality system described by the PMP can be reduced to an initial-terminal-value problem of the form
with the initial and terminal conditions given by
where
and \(\mathbb {1}_n \in {\mathbb R}^{n\times n}\) denoted the unit matrix. In the following, we refer to initial-terminal-value problems as boundary-value problems (BVP).
Computational methods for solving LQR problems mostly make use of the fact that the optimal control is given in the form of the feedback law \(u(t) = R^{-1}B^T Y(t) x(t)\) [7]. The construction of such a feedback law requires the solution Y(t) of a matrix Riccati differential equation which needs to be solved numerically using a suitable integration scheme [8,9,10,11]. Alternatively, in the unconstrained case, finding an approximation to the optimal control solution involves solving the BVP (7)–(8) directly using appropriate solvers [12, 13].
For our investigation, independently of the underlying solution method, we assume that the resulting numerical approximations to x, u, and p are available and defined on the uniform grid given by
with mesh width \(h = \frac{T-t_0}{L}\) and \(L \in {\mathbb N}\). Moreover, we suppose that these approximations are represented by well-defined grid functions as follows
where \(x_l:= x_h(t_l) \approx x(t_l)\), \(u_l:= u_h(t_l) \approx u(t_l)\) and \(p_l:= p_h(t_l) \approx p(t_l)\) hold for \(l = 0,\ldots ,L\). Certainly, \(x_h\), \(u_h\) and \(p_h\) are only relevant if they provide a reliable representation of the true solution to the problem (1) on the grid \(\varDelta _h\). That is if the norm of the global error vectors with components
for all \(l = 0,\ldots , L\), is sufficiently small. For this reason, a substantial amount of research has been devoted to the question of convergence and convergence rates of numerical approximations to the continuous solutions of (1); see, e.g., [14,15,16,17]. In particular, considering the class of Runge–Kutta (RK) methods for time-discretization in optimal control, Hager and Dontchev [18, 19] proved, for a large class of optimal control problems with and without control constraints, that for all \(h>0\) sufficiently small, a constant \(C>0\) exists, such that the following holds:
where \(u_l = {{\,\mathrm{arg\,max}\,}}_{v \in {{\mathcal {U}}}} H(x_{l},v,p_{l})\) is supposed for all \(l = 0,\ldots , L\) and the order k depends on both, the smoothness of the solution to (1) and the order-of-accuracy of the Runge–Kutta scheme used for the discretization of the state equation.
In [18, 19], the pair \((x_{h},u_{h})\) is the strict local minimizer of a discrete counterpart to the optimal control problem corresponding to (1), where integration is replaced by a numerical quadrature consistent with the RK scheme applied to the state equation. Hager proved [19] that, in the case of unconstrained optimal control problems, the usual order conditions for RK discretization of ODEs lead to (10) at least for \(k = 1\) and \(k = 2\). For the cases \(k = 3\) and \(k = 4\) and if control constraints are active additional conditions on the RK coefficients are necessary; we refer to the original papers [18] and [19] for a detailed discussion. These results ensure convergence of the approximations to the solution of (1) as \(h \rightarrow 0\). However, for any fixed grid \(\varDelta _h\), the estimate (10) does not give insight into the distribution of the global error over the entire interval of integration.
In this paper, a continuous representation of the global error is developed, which is new to the field of optimal control, allowing the quantification of pointwise errors in the approximation \((x_{h},u_{h})\) to the solution of our control problems where the admissible sets are defined by either (2) or (3). Therefore, on the interval \([t_0,T]\), continuous error functions are defined by \(e_x\) and \(e_u\), such that their evaluation on the grid \(\varDelta _h\) exactly gives the global error of the underlying numerical solutions \(x_h\) and \(u_h\), respectively. To construct these error functions, we extend the strategy of Zadunaisky [1, 2] originally applied to BVPs and initial value problems (IVP) to the framework of optimal control problems.
In the next section, our extension of Zadunaisky’s strategy to the framework of optimal control is discussed. An auxiliary optimal control problem is derived that has as its unique solution the error functions \(e_x\) and \(e_u\) which in turn are characterized by the solution of a BVP derived from the PMP. To construct the auxiliary problem, appropriate interpolation operators are defined, to achieve continuous extensions for \(x_h\) and \(u_h\) to the interval \([t_0,T]\). Assuming that the global errors of \(x_h\) and \(u_h\) are of a certain order in the sense of (10), we provide conditions for the interpolation operator that guarantee that the uniform convergence of \(e_x\) and \(e_u\) to zero is of the same order as the convergence of the underlying approximations on \(\varDelta _h\) to x and u as \(h \rightarrow 0\). Section 3 is devoted to the discussion of numerical procedures for generating reliable approximations of the desired error functions. Therein, a novel iterative procedure for generating error estimates in the LQR setting is proposed. This method successively generates improved error estimates using the symplectic Euler method and is inspired by the iterated defect correction (IDeC) schemes of Stetter [20, 21] and Frank et. al. [22,23,24]. To ensure the reliability of the approximations to \(e_x\) and \(e_u\), a defect control-based strategy is utilized similar to [12, 13]. It is proved that with this algorithm a continuous approximation to the error functions \(e_x\) and \(e_u\) can be computed that is arbitrarily close to the global error of \(x_h\) and \(u_h\) on the grid \(\varDelta _h\). The findings of this work are supported with results of numerical experiments presented in Sect. 4, where a numerical order analysis of numerical approximations to \(e_x\) and \(e_u\) is discussed. In particular, an application of the proposed methodology to LQR problems arising from a Petrov-Galerkin approximation of controlled convection-diffusion problems is presented, together with a discussion of the resulting computational complexity. Moreover, in the Appendix we present a cyclic reduction-based direct method that takes advantage of the special structure of the linear systems arising from the application of the symplectic Euler method to the auxiliary optimality systems. A section of conclusion completes this work.
2 The Construction of Continuous Error Functions
The strategy of Zadunaisky was initially developed to construct global error estimates of a given approximation to solutions of BVPs and IVPs [1, 2]. Notice, that, in the case of LQR problems, the optimal pair (x, u) is uniquely defined by the solution of the BVP (7)–(8), together with the relation \(u = R^{-1}B^T p\). Hence, by assuming that the approximations \((x_h,p_h)\) to the solution of (7)–(8) are available, the method of Zadunaisky can be readily extended to the optimal control framework. That is, first an auxiliary BVP problem is constructed having as its unique solution the error functions
where \({{\mathcal {I}}}\) is an appropriate interpolating polynomial. An error functions for the controls can be constructed similarly as
In the second step, the solution to the auxiliary problem is approximated using an appropriate solver returning the estimates \(e_{x,h}\), \(e_{p,h}\). Then, if \(u_h = R^{-1}B^T p_h\) holds, the error of the control approximation is given by \(e_{x,h} = R^{-1}B^T e_{p,h}\). While this approach is applicable in the LQR setting, the general LQOC case (1)–(2), where control bounds are active, does not allow a direct application of Zadunaiskys approach to the optimality system. Instead, it is more advantageous to directly elaborate our methodology with the cost function and the system dynamics. In this way, an auxiliary optimal control problem can be constructed which has as its unique solution the error functions \((e_x,e_u)\) and can be constructed using the approximations \((x_h,u_h)\). This approach makes it possible to extend Zadunaisky’s strategy to a large range of numerical optimal control settings.
For the construction of the auxiliary optimal control problem, we define the vector space
together with the corresponding subsets
and
If LQR problems are considered and thus \((x_h,u_h)\) is an approximate solution to (1) with (3), we will always assume that \(U^h_{ad} = Z^{h,m}\). Moreover, we define the restriction operator \( {{\mathcal {R}}}^h: W^{1,\infty }(t_0,T;{\mathbb R}^r) \rightarrow Z^{h,1} \) with \({{\mathcal {R}}}^h(z)(t_l) = z(t_l)\), for all \(t_l \in \varDelta _h\) and any \(z \in W^{1,\infty }(t_0,T;{\mathbb R}^r)\). Restrictions of the above-defined error functions to the global errors of \((x_h,u_h)\in X^h \times U_{ad}^h\) are then given by
To extend the definition of the error functions \(e_x\) and \(e_u\) to the framework of LQOC problems, appropriate requirements for the interpolation operators applied to \(x_h\) and \(u_h\) are necessary. We make the following Remark about the regularity of solutions to (1):
Remark 1
In the unconstrained case where we have (1) with (3), the optimal control and the corresponding state share the same regularity class. In particular, one can prove by using a bootstrap argument on the optimality system (4)–(6), that \(x \in C^{\infty }(t_0,T;{\mathbb R}^n)\) and \(u \in C^{\infty }(t_0,T;{\mathbb R}^m)\).
On the other hand, in the case of active box constraints (2), and since R is symmetric and positive definite, the component functions \(u_i\), with \(i = 1,\ldots ,m\), of the optimal control have an explicit form:
where \(w_i\) denotes the i-th component of \(w(t) = R^{-1}B^T p(t)\) [5]. Since \(u\in L^2(t_0,T;{\mathbb R}^m)\), the optimal state x is absolutely continuous and, in turn, the solution to the adjoint system (6) is continuously differentiable. With respect to \(w_i\) we have that \(\min \{w_i,\overline{u}\} \in W^{1,\infty }({\mathbb R})\). Then Lemma 7.6 in [25] guarantees that with \(w_i \in C^1([t_0,T])\) it holds \(\min (w_i(\cdot ),\overline{u}) \in W^{1,\infty }([t_0,T])\). A repeated application of this reasoning applied to the maximum function guarantees that the functions (13) are bounded Lipschitz functions and hence \(u \in W^{1,\infty }(t_0,T;{\mathbb R}^m)\), such that \(x \in W^{2,\infty }(t_0,T;{\mathbb R}^n)\).
By the above remark, we have that the continuous extensions of \(u_h\) and \(x_h\) are best chosen from the class of bounded and Lipschitz functions or a suitable subset. The following definition makes use of this fact.
Definition 1
(Interpolation operator) Let \(\alpha _i: Z^{h,1} \mapsto {\mathbb R}\) define a linear form for all \(i = 1,\ldots , N \), and choose \(\{\beta _i\}_{i = 1, \ldots N}\) as the basis of a finite-dimensional subspace \(W_N \subset W^{1,\infty }(t_0,T)\). Then the mapping
is called interpolation operator if \({{\mathcal {I}}}(z_h)(t_l) = z_h(t_l)\) holds for all \(l = 0,\ldots ,L\).
An interpolation operator is accurate of order \(k_z>0\) with respect to some function \(z \in W^{1,\infty }(t_0,T)\), if there exists some constant \(C>0\), such that for all \(h>0\) sufficiently small, it holds
In the case of an unconstrained control variable, where the optimal state and control are members of the same regularity class, one can use the same interpolation operator to generate both the continuous extension to \(x_h\) and to \(u_h\). However, if control bounds are active a further distinction between the interpolation operators for the discrete states and discrete controls is necessary. For generalization and in line with Definition 1, the following assumptions are made for an arbitrary function \(z \in W^{1,\infty }(t_0,T)\) with corresponding approximation \(z_h \in Z^{h,1}\), where \(z_h(t_l) \approx z(t_l)\) for all \(t_l \in \varDelta _h\). We have
-
(A1)
Assume \(z(t)\in [\underline{u},\overline{u}]\), holds for all \(t \in [t_0,T]\) and \( z_h(t_l)\in [\underline{u},\overline{u}]\), holds for all \(t_l \in \varDelta _h\), then \({{\mathcal {I}}}(z_h)(t)\in [\underline{u},\overline{u}]\) must be satisfied for all \(t \in [t_0,T]\).
-
(A2)
If \(z \in W^{2,\infty }(t_0,T)\), then it must hold \({{\mathcal {I}}}(z_{h}) \in W^{2,\infty }(t_0,T)\).
-
(A3)
Assume that there exists a \(k \in {\mathbb N}\) and a constant \(C>0\), such that \(\max _{l = 0, \ldots L} | z(t_l) - z_h(t_l) | \le C h^k\) holds for all \(h>0\) sufficiently small. Then there exists another constant \(\tilde{C}>0\), such that \(\Vert ({{\mathcal {I}}}\circ {{\mathcal {R}}}^h)(z) - {{\mathcal {I}}}(z_h) \Vert _{\infty } \le \tilde{C}h^k\) is satisfied for all \(h>0\) sufficiently small.
Assumption (A3) guarantees that an interpolating function \({{\mathcal {I}}}(z_h)\) does reflect the behaviour of the global error in \(z_h\) at least asymptotically as \(h \rightarrow 0\). That is, any sequence of interpolating functions \(({{\mathcal {I}}}(z_h))_{h>0}\) converging pointwise on the interval \([t_0, T]\) with order k, due to the convergence properties of the sequence \((z_h)_{h>0}\), convergences uniformly to z with the same order. A well-known example of an interpolation operator satisfying this assumption together with Assumption (A2), is the cubic spline interpolation operator with not-a-knot boundary conditions.
Remark 2
The Assumption (A2) is satisfied by construction since for cubic splines it holds \({{\mathcal {I}}}(z_h) \in C^2(t_0,T)\). We show the validity of (A3) in the case of cubic splines with not-a-knot boundary conditions. Therefore, we define \(z_l:= z_h(t_l)\) for all \(l = 1,\ldots ,L \), and require for all \(h>0\) sufficiently small there exists a \(C>0\), such that it holds
For each \(t \in [t_l,t_{l+1}]\) a cubic spline is defined by
with the coefficients
Together with the not-a-knot end conditions for the interpolatory cubic polynomial, the coefficients \(\mu _0,\ldots ,\mu _L\) are uniquely determined by the linear equations
for \(l = 1,\ldots ,L-1\) as well as
for \(l =0 \) and \(l = L\). As a result, each coefficient \(\mu _l\) is given as the linear combination of divided differences
and using the requirement (15), it holds
for some \(C_1,C_2,C_3 > 0\) and \(h>0\) sufficiently small. Together with this result, there exists a \(\tilde{C} > 0\) such that
holds for a sufficiently small \(h>0\). Since this estimate holds on any subinterval \([t_l,t_{l+1}]\), the interpolating function \({{\mathcal {I}}}({{\mathcal {R}}}^h(z) - z_h )\) converges uniformly to zero with order k on the whole interval \([t_0,T]\) as \(h\rightarrow 0\). The validity of (A3) now is a direct consequence of the linearity of the spline interpolation with respect to the interpolation nodes.
When interpolation of discrete controls \(u_h \in U^h_{ad}\) is desired, and control bounds are active, a restriction to a smaller class of interpolation operators is necessary to guarantee (A1). This is tied to the fact that the possible oscillatory behaviour of higher-degree polynomials like cubic splines can lead to a violation of requirement (A1). The following remark proves that the linear spline interpolation operator is a suitable choice for the interpolation of \(u_h \in U^h_{ad}\) as it not only satisfies (A3) but also (A1).
Remark 3
To construct a linear spline interpolation operator for an approximation \(u_h \in U^h_{ad}\) in the case \(m = 1\), the basis functions are chosen to be the hat functions:
with \(\beta _l \in W^{1,\infty }(t_0,T)\), for all \(l = 0,1,\ldots ,L\). The linear forms within (14) are defined such that
Hence, due to the property of the basis functions \(\{\beta _l\}_{l = 0,\ldots ,L}\) as a partition of unity it follows
A similar reasoning is applied when proving that the lower bound is satisfied for \({{\mathcal {I}}}(u_h)\). As a result, assumption (A1) is satisfied for the linear spline interpolation operator. The assumption (A3) is easily verified for a linear spline by using the linearity of \(\alpha _l\) and the property of the basis functions \(\{\beta _l\}_{l = 0,\ldots ,L}\) as a partition of unity.
For the entirety of the upcoming discussion, we will use the following convention: For any \(z_h \in Z^{h,r}\) with \(r \in {\mathbb N}\), the corresponding interpolating function, defined using an interpolation operator \({{\mathcal {I}}}\), will be given by
where \(z_{h,i}\in Z^{h,1}\) denotes the i-th component function of \(z_h\). With this, the definition of interpolation operators and the requirements (A1) - (A3) in mind, we define continuous extensions of the global errors (11)–(12) as follows.
Definition 2
(Continous error extensions) Let (x, u) denote the unique solution to the optimal control problem (1) and \((x_h,u_h) \in X_{x^0}^h \times U^h_{ad}\) its corresponding approximate solution on the grid \(\varDelta _h\). Moreover, define
as appropriate interpolation operators satisfying Assumptions (A1) - (A3). Then continuous extensions for the global errors of \(x_h\) and \(u_h\) are defined as follows:
and
respectively. A continuous error extension will be called consistent with the global error of the underlying approximation if it is uniformly convergent to zero in the same order as the global error of the underlying approximation.
The choice of the interpolation operator has a decisive influence on the quality of the continuous error extension. In particular, it is a reasonable prerequisite to aim for a continuous error representation that reflects the convergence behaviour of the global error not only at the interpolation nodes but on the entirety of \([t_0,T]\). The following Lemma provides possible criteria for the choice of interpolation operators, such that the functions \(e_x\) and \(e_u\) are consistent with the global error of the approximations \(x_h\) and \(u_h\).
Lemma 1
Let \(z\in W^{1,\infty }(t_0,T)\), with corresponding approximation \(z_h \in Z^{h,1}\). Assume, there exists a constant \(C>0\) for all \(h>0\) sufficiently small such that
holds for a fixed \(k \in {\mathbb N}\) and define \(e_{z} = z - {{\mathcal {I}}}(z_h)\). Moreover, let \({{\mathcal {I}}}\) denote an interpolation operator which is accurate of order \(k_z\) with respect to z and satisfies (A3). Then, there exists a constant \(\tilde{C}>0\) such that
is satisfied for all \(h>0\) sufficiently small.
Proof
It appears that the size of \( \Vert z - {{\mathcal {I}}}(z_h) \Vert _{\infty } \) is governed by two sources, the error of interpolation itself and an error due to the interpolation with approximate rather than exact values. Moreover, since \({{\mathcal {I}}}\) is an interpolation operator that is accurate of order \(k_z\) and due to Assumption (A3), there exist constants \(C_1,C_2>0\) such that
Thus the interpolating function \({{\mathcal {I}}}(z_h)\) is uniformly convergent to z of order \(\min \{k,k_u\}\) as \(h \rightarrow 0\), and the Lemma is proved. \(\square \)
Corollary 1
Assume that \({{\mathcal {I}}}_x\) and \({{\mathcal {I}}}_u\) are interpolation operators that fulfil assumption (A3) and are accurate of order \(k_x\) and \(k_u\) with respect to x and u respectively. Then if the estimate (10) is satisfied for all \(h>0\) sufficiently small, there exists a constant \(\tilde{C}>0\) such that
holds for all \(h>0\) sufficiently small.
To obtain continuous extensions \(e_u\) and \(e_x\) that reflect the convergence behaviour of their discrete counterparts (11)–(12), interpolation operators must be selected that have at least the same order of accuracy as the underlying method for generating \(x_h\) and \(u_h\). If the control bounds are not active, both the control and the corresponding state are arbitrarily smooth. Therefore, in this case, and by a restriction to piecewise polynomial interpolation operators, the continuous extensions \(e_u\) and \(e_x\) are consistent with the underlying global error if one chooses polynomial pieces with a sufficiently high polynomial degree [26, 27]. However, if the control bounds are active, the consistency of the global extensions in the sense of the definition 2 is not always easy to achieve. In the following remark, the consistency of \(e_u\) and \(e_x\) with respect to the underlying global error for cubic and linear spline interpolation polynomials is discussed.
Remark 4
The cubic spline interpolation operator, as described in Remark 2, defines an interpolation operator that is exactly of order four, with respect to any function \(z \in C^4(t_0,T)\) [28, 29]. Thus, if no control constraints are active, the continuous error extensions \(e_x\) and \(e_u\) with cubic splines are consistent in the sense of Definition 2 as long as the size of the global errors in \(x_h\) and \(u_h\) is of order \(O(h^k)\) with \(k\le 4\). If the control constraints are active, only a weaker result is possible, since both the control u and the associated state x are not arbitrarily smooth, see Remark 1. In this case, the cubic spline interpolation to the state x in \(W^{2,\infty }(t_0,T)\) defines an interpolation operator that is exactly of order two [30]. On the other hand, the linear spline interpolation operator of the Remark 3 with respect to the control \(u\in W^{1,\infty }(t_0,T)\) is only exact of order one. The continuous error extensions \(e_x\) and \(e_u\) are therefore only consistent in the sense of Definition 2 if the size of the global error in \(x_h\) is \(O(h^k)\) with \(k\le 2\) and the size of the global error in \(u_h\) is equal to O(h).
The definition of continuous error extensions \(e_x\) and \(e_u\) allows to represent the unique solution to (1) as the sum of the continuous error estimate which is unknown and a known part represented by the continuous approximations \({{\mathcal {I}}}_x(x_h)\) and \({{\mathcal {I}}}_u(u_h)\). Utilizing this representation of the optimal solution to (1)–(2), we can construct an auxiliary problem having as its solution exactly the continuous error extensions given in Definition 2.
Lemma 2
Let \((x_h,u_h) \in X_{x^0}^h \times U^h_{ad}\), with corresponding interpolating functions \({{\mathcal {I}}}_x(x_h)\) and \({{\mathcal {I}}}_u(u_h)\). The tuple \((e_x,e_u)\) of continuous error extensions in the sense of Definition 2, where (x, u) solves (1)–(2), is the unique solution to the following optimal control problem
where
and the set of admissible controls is given by
where \({{\mathcal {E}}}_t = [ \underline{u} - {{\mathcal {I}}}_{u}(u_h)(t), \overline{u} - {{\mathcal {I}}}_{u}(u_h)(t)]^m\).
Proof
It is first proved that (18) admits a unique solution in \(E_{ad}\). By Definition 1 it follows \(D_{xu} \in L^1(t_0,T;{\mathbb R}^n)\). Now, as \(\upsilon \in L^2(t_0,T;{\mathbb R}^m)\), the Carathéodory theorem guarantees the existence and uniqueness of a solution to \(\dot{\xi } = A \xi + B \upsilon - D_{xu}\) with \(\xi (t_0) = 0\). This solution takes the form
where \(X(t) = e^{At}\). As a result of the boundedness of X(t) on \([t_0,T]\), and assuming \(\upsilon \in E_{ad}\) it follows that \(\xi \in AC(t_0,T;{\mathbb R}^n)\). Hence, (20) defines a control-to-state map for the control system involved in (18). This map is given by \({{\mathcal {C}}}: E_{ad} \rightarrow AC(t_0,T;{\mathbb R}^n)\), \(\upsilon \mapsto {{\mathcal {C}}}(\upsilon )\), which is a linear affine function.
Now, define \(\hat{{{\mathcal {J}}}}(\upsilon ):= {{\mathcal {J}}}({{\mathcal {C}}}(\upsilon ),\upsilon )\) as the reduced cost functional of \({{\mathcal {J}}}\), which results strictly convex. Since \({{\mathcal {E}}}_t\) is compact if both \(\underline{u}\) and \(\overline{u}\) are finite, the set \(E_{ad}\) is convex, closed, and bounded, such that in this case (18) admits a unique solution. In the LQR case where \(U_{ad} = L^2(t_0,T;{\mathbb R}^m)\), we have \(E_{ad}= L^2(t_0,T;{\mathbb R}^m)\) and the existence of a unique solution to (18) follows directly from the positive definiteness of R and the fact that \(\hat{{{\mathcal {J}}}}\) is coercive. To show that this solution is given by the tuple \((e_x,e_u)\), we first prove that \(e_u\) is an admissible control and \(e_x\) its corresponding state, i.e. \({{\mathcal {C}}}(e_u) = e_x\). Define by \( C: U_{ad} \rightarrow AC(t_0,T;{\mathbb R}^n)\), the control-to-state map for (1) (see [31]). By Definition 2, \(e_u \in E_{ad}\), using the relation \(C(u) = x\) and the fact that the function \({{\mathcal {I}}}_x(x_h)\) is the unique solution to an ODE problem of the form
it follows:
for all \(t \in [t_0,T]\). In order to see that \(e_u\) is a minimizer for \(\hat{{{\mathcal {J}}}}\) on \(E_{ad}\), consider the correspondence
for all \(u \in U_{ad}\) and \(\upsilon \in E_{ad}\) such that \(u(t) = \upsilon (t) + {{\mathcal {I}}}_u(u_h)(t)\) a.e. in \((t_0,T)\). This fact at hand, the minimizing property of \(e_u\) is an immediate consequence of Definition 2 and the optimality of u. Thus the tuple \((e_x,e_u)\) is the unique solution to the optimal control problem (18). \(\square \)
Due to the formulation of the continuous error extension as a unique solution of an optimal control problem, the PMP [6] is applied to obtain \(e_x\) and \(e_u\) from the solution of a BVP.
Theorem 1
Let \((x_h,u_h) \in X_{x^0}^h \times U^h_{ad}\), with corresponding interpolating functions \({{\mathcal {I}}}_x(x_h)\) and \({{\mathcal {I}}}_u(u_h)\). Moreover, define \(y:= (e_x,p)^T\) with the error extension \(e_x\) given as in Lemma 2, p characterized by (6) and let
with each component of \(\pi \) defined by
where \(i = 1,\ldots ,m\). Then y is the unique solution to the non-linear BVP
where \(b = (0,\alpha (c-{{\mathcal {I}}}_x(x_h)(T)))^T\). Moreover, the continuous error extension \(e_u\) for the global errors in \(u_h\), is uniquely determined by \(e_u = \pi (p)\).
Proof
By Lemma 2 the functions \((e_x,e_u)\) are the unique solution to the optimal control problem (18). Since \({{\mathcal {I}}}_x(x_h) \in W^{2,\infty }(t_0,T;{\mathbb R}^n)\) and \({{\mathcal {I}}}_u(u_h) \in W^{1,\infty }(t_0,T;{\mathbb R}^m)\), the PMP can be applied in that case as well. We define the following HP function
corresponding to (18). The PMP guarantees that, for \(e_u\) and the corresponding trajectory \(e_x\), there exists an associated function \(q\in W^{2,\infty }(t_0,T;{\mathbb R}^n)\), such that \(e_x, e_u\) and q satisfy the optimality system
together with
for all \(v\in {{\mathcal {E}}}_t\) and any \(t\in [t_0,T]\). Due to Definition 2 and (26), one can identify q with the adjoint state of the original problem (1)–(2) and set \(q = p\). In the following let
Then (27) is equivalent to
where \(\langle \cdot ,\cdot \rangle \) denotes the standard inner product over \({\mathbb R}\). Since R is symmetric and positive definite, there exists an orthogonal matrix \(P\in {\mathbb R}^{m\times m}\) such that \(P^TRP\) is a diagonal matrix with the eigenvalues of R and it holds
By (28) the function \(\varphi \) attains its minimum at \(e_u\) and since the eigenvalues of R are all positive, for any \(t\in [t_0,T]\) one obtains
where \({{\mathcal {E}}}_{t,i}:= [\underline{u} - {{\mathcal {I}}}_{u,i}(u_h)(t), \overline{u} - {{\mathcal {I}}}_{u,i}(u_h)(t)]\). As a result, the continuous error extension for the control is uniquely defined by \(e_u = \pi (p)\) with its components given as (22). Due to the positive definiteness requirements on R and Q, the HP function \({{\mathcal {H}}}\) is jointly concave in z and v. Together with the convexity of \(\varPhi \) and \({{\mathcal {E}}}_t\) for all \(t \in [t_0,T]\) we have that the conditions of the PMP are also sufficient [32]. A consequence of this fact and of the unique solvability of (18) is that \(e_x\) and p are the unique solutions to the HP system (23) \(\square \)
Corollary 2
Assume that (x, u) is the unique solution to (1) with (3) and p is defined by (6). Moreover, let \((x_h,u_h) \in X_{x^0}^h \times U^h_{ad}\), define approximations to (x, u) with corresponding interpolating functions \({{\mathcal {I}}}_x(x_h)\) and \({{\mathcal {I}}}_u(u_h)\). Then \(y = (e_x,p)^T\), with \(e_x\) as the continuous extension of the global errors of \(x_h\), is the unique solution to the ODE
with forcing function \(F = (-D_x,Q{{\mathcal {I}}}_x(x_h))^T\), \(D_x = \frac{d}{dt}{{\mathcal {I}}}_x(x_h) - A {{\mathcal {I}}}_x(x_h)\) and boundary conditions as in (23). Moreover, the continuous error extension \(e_u\) for the global errors of \(u_h\) is uniquely determined by
When considering error extensions \(e_x\) and \(e_u\) as solutions to (18) with \(E_{ad} = L^2(t_0,T;{\mathbb R}^m)\), a feedback control can be derived. Notice that (18) can be interpreted as a general linear tracking problem, where a feedback law is easily constructed just as in the classical setting of LQR problems. Thus the error functions \(e_x\) and \(e_u\) are related through the following equation
where \(G(t) = R^{-1}B^T Y(t)\) is the gain feedback matrix for the original problem (1) and \(V(t) = R^{-1}B^T v(t) - {{\mathcal {I}}}_u(u_h)(t)\) is a new command signal arising from the presence of \({{\mathcal {I}}}_u(u_h)\) and \({{\mathcal {I}}}_x(x_h)\) in (18). The functions Y and v are solutions to the following differential equations
and
As a result, the function \(e_x\) is obtained, given v and Y, by integrating forward in time the matrix IVP as follows:
Then \(e_u\) is obtained by substituting \(e_x\) into the feedback law (30).
3 Numerical Approximation of Continuous Error Functions
The main result of the last section is that the continuous extensions \(e_x\) and \(e_u\), defined in Definition 2, are characterized by the auxiliary problem (18). Theorem 1 guarantees that the solution to this auxiliary control problem is uniquely identified by the following optimality system
This system renders not only necessary but sufficient conditions that need to be satisfied by the functions defined in Definition 2. Hence, solving (31) numerically with an appropriate method will provide pointwise estimates for the global error functions \(e_x\) and \(e_u\) and in turn estimates for the global errors (11)–(12). As the auxiliary problem (18) defines a new optimal control problem it can be solved independently of the initial method or grid used to solve (1). In fact, in general, the grid used for solving (18) can be chosen to be much denser than that used for the approximation of x and u. In this case, for solving (18) numerically, a stepsize \(\eta > 0\) is chosen such that \(\varDelta _{h} \subseteq \varDelta _{\eta }\) holds, where \(\varDelta _{\eta }\) defines a new grid in the sense of (9). For the following discussion on the choice of appropriate numerical methods to generate pointwise approximations to continuous error functions \(e_x\) and \(e_u\), the main focus is on LQR problems, where the resulting auxiliary problem is given by (18) with \(E_{ad} = L^2(t_0,T;{\mathbb R}^m)\). In this framework, the linear algebraic system (31) is equivalent to the BVP formulated in Corollary 2.
The method, we present in the following, is a novelty to the field of optimal control and arises from combining, for the first time, IDeC with a symplectic Euler method. Thus, this algorithm is closely related to the concept of acceleration methods, but in contrast to methods like Richardson extrapolation, only requires a single mesh to improve the rate of convergence of an underlying grid function. The original form of IDeC goes back to Stetter [20, 21] and was later theoretically investigated by Frank, Ueberhuber, and others [24, 33]. A recent review of existing defect correction methods for ODEs can be found in [34].
Before going into further detail, the general idea of the upcoming method is described. In the first step, an appropriate one-step method is applied to the ODE (29) with boundary conditions as in (23), to generate approximations \(e_{x,l}\approx e_x(t_l)\) and \(p_{l} \approx p(t_l)\) for all \(l = 0,\ldots ,L\). With these approximations at hand, one can achieve an estimate for the error in the controls on the grid \(\varDelta _{h}\) by extracting the appropriate values and setting \(e_{u,l} = \pi (p_l) \approx e_u(t_l)\) for all \(l = 0,\ldots ,L\) [35]. Similar to before, we represent the generated approximations using the grid functions \(e_{x,\eta }\in X_0^{\eta }\), \(p_{\eta }\in Z^{\eta ,n}\) and \(e_{u,\eta }\in Z^{\eta ,m}\), where we define \(e_{x,l}:=e_{x,\eta }(t_l)\), \(p_{l}:=p_{\eta }(t_l)\) and \(e_{u,l}:=e_{u,\eta }(t_l)\) for all \(t_l \in \varDelta _{\eta }\). The accuracy of these pointwise error estimates is then evaluated utilizing ideas of defect control [12, 13] that are transferred to the framework of optimal control. Until a desired level of accuracy for \(e_{x,\eta }\) and \(e_{u,\eta }\) with respect to \(e_x\) and \(e_u\) is achieved, the initial approximations are corrected successively. Therefore in the second step, and with similar reasoning as in Sect. 2, an auxiliary problem is constructed and solved to estimate the deviation of \(e_{x,\eta }\) and \(e_{u,\eta }\) from \(e_x\) and \(e_u\), respectively. The process is stopped as soon as a desired level of accuracy for the approximations to \(e_x\) and \(e_u\) is achieved.
To determine a suitable method for determining \(e_{x,\eta }\) and \(e_{u,\eta }\), it must be taken into account that the system (29) is a canonical Hamiltonian system. This property becomes apparent by introducing the Hamiltonian \(\hat{{{\mathcal {H}}}}(t,e_x,p):= {{\mathcal {H}}}(t,e_x,p,\pi (p))\), where \({{\mathcal {H}}}\) is defined by (24). With this in mind, the system (29) with boundary conditions given as in (23) is equivalent to the following system
Thus, the solution \(y:=(e_x,p)\) is characterized by a symplecticity property [35] and it is reasonable to discretize the involved equations using a symplectic integrator. According to the results of [36], for non-autonomous Hamiltonian systems, the symplectic Euler method is appropriate. For the given Hamiltonian system an application of this method leads to the following equations
for each \(l = 0,\ldots ,L-1\), where \(F_1 = -D_x\) and \(F_2 = Q \, {{\mathcal {I}}}_x(x_h)\). We associate the solution to (32)–(33) with the grid function \(y_{\eta }:= (e_{x,\eta },p_{\eta })\) and define the corresponding realizations by \(y_l:= (e_{x,\eta }(t_l),p_{\eta }(t_l))^T\) for any \(t_l \in \varDelta _\eta \).
Remark 5
According to results in [37], the symplectic Euler scheme is a consistent and convergent first-order, one-step method if \(e_x,p \in C^{2}(t_0,T;{\mathbb R}^n)\). The regularity requirements for this method are fulfilled if at least a cubic spline, as defined in Remark 2, is chosen for the interpolation of \(x_h\).
Once we have pointwise estimates \(e_{x,\eta }\) and \(e_{u,\eta } = \pi (p_{\eta })\) for the continuous error extension \(e_x\) and \(e_u\) on a given grid \(\varDelta _{\eta }\), we need to ensure that these estimates adequately reflect the global errors of the approximations \(x_h\) and \(u_h\). Therefore, a reliable and computable bound for the global error of \(e_{x,\eta }\) and \(e_{u,\eta }\) is necessary. For this reason, similar to Sect. 2, a suitably accurate interpolation operator in the sense of the Definition 1 is chosen so that assumptions (A2) and (A3) are fulfilled. This interpolation operator, denoted \({{\mathcal {I}}}_{y}\), is then applied to the solution of (48) to determine the continuous extension \({{\mathcal {I}}}_y(y_{\eta }):=({{\mathcal {I}}}(e_{x,\eta }), {{\mathcal {I}}}(p_{\eta }))^T\). Following the idea of Zadunaisky [1, 2], a natural measure of the quality of this continuous approximation to y is available through the defect, given by
In fact, the interpolating function \({{\mathcal {I}}}_y(y_{\eta })\) satisfies a perturbed problem given by
together with the boundary conditions in (23). This perturbed BVP is close to the original (23) if the norm of (34) is small. In this case, and if the underlying BVP is sufficiently well conditioned, the solution of the neighbouring problem (35) is also close to that of (23). In turn, the norm of the global errors
is of small size as well. This fact suggests that the norm of (34) establishes a computable quantity for evaluating the quality of \(e_{x,\eta }\) and \(p_{\eta }\).
For the following, we define the continuous error extensions of the global errors of \(e_{\eta }\), \(p_{\eta }\) and \(e_{u,\eta }\) by
and
respectively, where in (38) it is taken into account that the relations \(e_u = \pi (p)\) and \(e_{u,\eta } = \pi (p_\eta )\) hold. The definitions (36)–(38) at hand, the defect is established as a computable upper bound for the global errors of the approximation \(e_{u,\eta }\) and \(e_{x,\eta }\).
Theorem 2
Let the Assumptions of Corollary 2 hold and assume that the interpolation operator \({{\mathcal {I}}}\) used to define (36)–(38) satisfies (A2). Moreover, suppose that the approximate solutions \(e_{x,\eta }\) and \(p_{\eta }\), to the linear algebraic system (31) satisfy the conditions
Then for every \(r\in {\mathbb N}\cup \{\infty \}\), there exists a \(C >0\) such that
where D is given by (34), with \({{\mathcal {I}}}_y(y_{\eta })=({{\mathcal {I}}}(e_{x,\eta }), {{\mathcal {I}}}(p_{\eta }))^T\).
Proof
By Corollary 2, the function \(y = (e_x,p)^T\) is the unique solution to the linear ODE
with boundary conditions as in (23) and \(F \in W^{1,\infty }(t_0,T;{\mathbb R}^{2n})\). The defect of this ODE, with respect to the interpolated approximation \({{\mathcal {I}}}_y(y_{\eta })\) is given by (34), and due to the assumptions (39), this interpolating function satisfies the boundary conditions in (23). By Assumption (A2) we have that \( D \in W^{1,\infty }(t_0,T;{\mathbb R}^{2n})\), such that together with (39), the function \({{\mathcal {I}}}_y(y_{\eta })\) uniquely satisfies
with the boundary conditions in (23). As a result, the error function \(\delta _y:= (\delta _x, \delta _p)^T\) uniquely satisfies
By standard results [38], the solution \(\delta _y\) can be represented in terms of an appropriately chosen Green’s function \(G(t,\tau )\) such that
Hence, the maximum of \(\delta _y\) can be explicitly bounded by the defect. Therefore the Hölder inequality is applied to the above integral representation of \(\delta _y\) to obtain:
for an appropriate r and s such that \(\frac{1}{r} + \frac{1}{s} = 1\), where for \(r = \infty \), we set \(s = 1\). Due to this result and since \(\Vert \delta _y \Vert _{\infty } = \max _{t \in [t_0,T]} ( | \delta _x(t) | + | \delta _p(t) |)\) we obtain
Since \(e_u = \pi (p)\) holds due Corollary 2, we have
where \(\Vert \cdot \Vert \) denotes an appropriate matrix norm. Taking this fact into account, we obtain the estimate
where \(C = \kappa (1 + \Vert R^{-1}B^T\Vert )\). \(\square \)
Corollary 3
Let the assumptions of Theorem 2 be satisfied and \( e_{u,\eta } = \pi (p_{\eta })\). Then for each \(r \in {\mathbb N}\cup \{\infty \}\) there exists a \(C >0\) such that
where D denotes the defect (34).
According to Corollary 3, the defect provides in particular an upper bound for the global error of the approximation, provided by (32)–(33). Due to the Remark 5, the error of the approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) is of the size \(O(\eta )\). To establish the defect (34) not only as an upper bound for the global error but also as a reliable estimate for the size of the global error, at least asymptotically, we need \(D = O(\eta )\). The following lemma guarantees that this property is fulfilled for the symplectic Euler method if a suitable interpolation operator for \(x_h\) and \(y_{\eta }\) is chosen.
Lemma 3
Let the interpolation operator \({{\mathcal {I}}}_x\) in Definition 2, chosen such that \(e_x \in C^{2}(t_0,T;{\mathbb R}^n)\). Moreover, choose \({{\mathcal {I}}}_y\) in (34), such that \({{\mathcal {I}}}_y(y_{\eta }) \in C^{2}(t_0,T;{\mathbb R}^{2n})\), where \(y_{\eta }\) is uniquely defined by the solution of (48). Then for the defect (34), it holds \(\Vert D\Vert _{\infty } = O(\eta )\).
Proof
One integration step of the symplectic Euler method applied to the BVP (23) is given by
with
Since \(e_x,p \in C^{2}(t_0,T;{\mathbb R}^n)\) and due to Remark 5 it holds:
and hence
The application of Taylor’s formula allows for the substitution
such that
The latter equation is equivalent to
Due to the regularity of \({{\mathcal {I}}}_y(y_\eta )\) it must hold \(\Vert \dot{y}-\frac{d}{dt}{{\mathcal {I}}}_y(y_\eta )\Vert _{\infty } = O(1)\) and thus it follows \(|D(t_l)| = O(\eta )\). Moreover, for each \(t \in [t_l,t_{l+1}]\) it holds
Hence, we obtain
Together with the boundedness of \(\Vert \dot{D}\Vert _{\infty }\), due to \(\dot{D}\in C^0(t_0,T;{\mathbb R}^{2n})\), it then follows \(|D(t)| = O(\eta )\) for any \(t \in [t_l,t_{l+1}]\). Since the choice of the sub-interval was arbitrary, the theorem is proved. \(\square \)
If highly accurate approximations for \(e_x\) and \(e_u\) are desired, the determination of a solution of (32)–(33) is associated with high computational costs since \(\eta > 0\) must be chosen sufficiently small. These costs increase considerably if the variables x(t) and u(t) are high-dimensional. It, therefore, makes sense to strive for an improvement in the convergence rate of the approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) before refining the grid \(\varDelta _{\eta }\). To achieve an improvement in the convergence rate of the initial approximations, the deviations \(\delta _x\) and \(\delta _u\) must be investigated. By the reasoning applied in Theorem 2, these functions are related to \(\delta _y\), which is the unique solution to the BVP
By applying similar reasoning as initially for (31) an estimate for the solution to (42) can be determined with the symplectic Euler method. The resulting approximation on the grid \(\varDelta _{\eta }\) is defined by the grid function
and the boundary conditions in (42). Here and in the following, \(\delta _{x,\eta }\) and \(\delta _{p,\eta }\) denote the approximations of \(\delta _x\) and \(\delta _p\) on \(\varDelta _{\eta }\) using the symplectic Euler scheme (32)–(33), where the defect D assumes the role of the forcing term.
With the estimate of \(\delta _y\) on a sufficiently dense grid at hand, an improvement of the initial approximations to \(e_x\) and p is obtained by setting
The corrected approximations satisfy (39) and are thus approximations to the solution of the linear ODE (29) with boundary conditions in (23). Hence, Theorem 2 applies, when defining \(y^{(1)}_{\eta }:= (e^{(1)}_{x,\eta },p^{(1)}_{\eta })^T\) and \(e^{(1)}_{u,\eta } = \pi (p^{(1)}_{\eta })\), together with the defect
To achieve a further improvement of the initial approximation, this correction procedure can be continued iteratively by starting with the grid function \(y^{(1)}_{\eta }\). For each improved iteration, generated by this procedure, the following corollary of Theorem 2 applies.
Corollary 4
Let the assumptions of Theorem 2 hold and assume that \(\delta ^{(j)}_{x,\eta }\) and \(\delta ^{(j)}_{p,\eta }\), for all \(j \in {\mathbb N}_0\) are defined such that
Moreover, define
and for \(j = 0,1,\ldots \) set
such that the function
is the unique solution to \(\dot{\delta }^{(j)}_y = M \delta ^{(j)}_y - D^{(j)}\) with boundary conditions given in (42) and forcing term
Then, there exists a constant \(C>0\) independent of the current iteration j, such that it holds
with \( \delta ^{(j)}_u = e_u -\pi ( p -\delta ^{(j)}_p)\).
Remark 6
For each iteration, we have \(C = \kappa (1+\Vert R^{-1}B^{T}\Vert )\), where the constant \(\kappa >0\) is referred to as the conditioning number of the underlying BVP. Its magnitude depends on the fundamental solution of the homogeneous BVP corresponding to (42) and the boundary condition matrices \(b_{t_0}\) and \(b_{T}\). The size of this constant, in particular, affects the reliability of the defect as a measure of the quality of an approximation. It is therefore advantageous to estimate the conditioning number of the original BVP (7) - (8) from the LQR problem (1) a priori. A discussion on the estimation of condition numbers can be found in [38] and [39].
By (46), the norm of the defect \(D^{(j)}\) provides an upper bound for the size of the global error for each corrected approximation. Thus, to monitor whether a correction step of the form (45) leads to an improvement of the original approximation, the norms of two consecutive defects \(D^{(j)}\) and \(D^{(j-1)}\) are compared based on the results of the following Lemma.
Lemma 4
Assume that the interpolation operator \({{\mathcal {I}}}_y\) is accurate of order k with respect to the solution y of the ODE (29) with the boundary conditions in (23). Suppose that there exists a constant \(C_0>0\) such that it holds
for all \(\eta >0\) sufficiently small. Moreover, in addition to (A3), assume that for \(y^{(j)}_{\eta }\) and \({{\mathcal {I}}}_y\) there exist \(C_1,C_2>0\) for all \(\eta >0\) sufficiently small such that the following implication holds
Then there exists \(C>0\) for all \(\eta >0\) sufficiently small such that the following relation holds:
Proof
Due to the linearity of \(D^{(j)}\) with respect to the interpolating function \({{\mathcal {I}}}_y\) and the fact that y satisfies \(\dot{y} = M y + F\), the following result holds for all \(\eta >0\) sufficiently small:
\(\square \)
Remark 7
The assumptions of Lemma 4 are rather natural for interpolation operators utilizing piecewise interpolating polynomials. The cubic spline defined in Remark 2 is an example of an interpolation operator satisfying these prerequisites.
Lemma 4 provides two pieces of information for the construction of a reliable and efficient algorithm with correction iterations of the form (45). First, it allows the definition of a criterion to check whether a correction step leads to an improvement of the initial approximation \(y_{\eta }\), and second, it provides an upper bound for the maximum number of correction steps. For the first case, it should be noted that for a sufficiently small step size \(\eta > 0\) and a suitable interpolation operator, the condition \(\Vert D^{(j)}\Vert _{L^r} \le \Vert D^{(j-1)} \Vert _{L^r}\) must be fulfilled if the correction (45) provides an improvement in the order of convergence of \(y_{\eta }\). Thus, if \(\Vert D^{(j)}\Vert _{L^r} > \Vert D^{(j-1)}\Vert _{L^r}\) holds, the grid \(\varDelta _{\eta }\) might be too coarse and needs to be refined for the correction procedure to work. The second conclusion of Lemma 4, is related to Remark 4 and the regularity of the function y one wishes to approximate. The maximum achievable order of accuracy depends not only on the choice of \({{\mathcal {I}}}_y\), but also on the choice of the interpolation operator used to interpolate the approximation state \(x_h\) of the original LQR problem given by (1) with (3). In general, the maximum number of corrections is defined by \(j_{max} = k-1\), see Lemma 4.
Remark 8
Using the cubic spline interpolation operator defined in Remark 2, we obtain \(y \in W^{3,\infty }(t_0,T;{\mathbb R}^{2n})\) and thus \(k=3\) for Lemma 4 according to the results in [30]. Consequently, the defect would not be able to adequately reflect the accuracy order of \(y_{\eta }\) if \(j>2\), which suggests setting the maximum number of correction steps to \(j_{max} = 2\).
It remains to determine a suitable criterion so that the algorithm stops automatically as soon as the generated approximations to the global errors are sufficiently accurate. Based on the results of Lemma 3, Corollary 4 and Lemma 4, a suitable criterion is defined by adding the condition \(\Vert D^{(j)}\Vert _{L^r} \le \theta \). The above results guarantee that there is a step size \(\eta >0\), so that this condition is fulfilled. To find the required step size, the grid \(\varDelta _{\eta }\) is refined and a new correction cycle is initialized when the maximum number of corrections \(j_{max}\) is reached and the desired tolerance has not yet been obtained. As soon as the specified tolerance or a desired number of correction cycles is reached, the process is stopped and an estimate of the continuous error extension \(e_u\) is provided by \(\pi ({{\mathcal {I}}}(p^{(j)}_{\eta }))\). The pseudocode for the described method is given in Algorithm 1. The following theorem guarantees the well-definedness of the integrated termination criterion for the algorithm. Since it is a direct conclusion from the above findings, this result is stated without proof.
Theorem 3
Let the conditions of Theorem 2 and Lemma 3 be satisfied. Then for any tolerance \(\theta > 0\) and a sufficiently accurate interpolation operator \({{\mathcal {I}}}\), there exists an iteration \(0 \le j\le j_{max}\) with stepsize \(\eta > 0\), such that for the error estimates \(e^{(j)}_{x,\eta }\) and \(e^{(j)}_{u,\eta }\) in Corollary 4, it holds:
An important computational aspect of Algorithm 1 is the choice of the procedure for determining the approximations \(y^{(0)}_{\eta }\) and each \( \delta ^{(j)}_{y} \). Since every correction cycle requires the solution of multiple systems like (32)–(33), it is important to aim for a method that allows for efficient execution of the correction steps. To achieve this goal, we exploit the linearity of the involved differential equation and represent the solution to (32)–(33) equivalently as the solution to the linear system of equations
with \(\vec {y}_{\eta } = \left( p_{\eta }(t_0), y_{\eta }(t_1),\ldots , y_{\eta }(t_{L-1}), e_{x,\eta }(t_L)\right) ^T \in {\mathbb R}^{2nL}\), where
and
with \( b_2 = \alpha (c-{{\mathcal {I}}}_x(x_h)(T))\). The involved system matrix has the advantageous structure of a block tridiagonal, Toeplitz matrix as follows
where
Together with the involutory property of \({\textbf{M}}_0\), the system (48) is especially well-suited for the application of a one-step block cyclic reduction approach [40]. As a consequence of this approach only a reduced system of equations needs to be solved, which is half the size of the original one. A variety of methods can be invoked to determine a solution to the reduced system. For medium-sized problems a block LU factorization-based algorithm [41] is appropriate, also known as block Thomas algorithm, which is a variation of block Gaussian elimination without pivoting and takes advantage of the block tridiagonal structure of \({\textbf{M}}_{\eta }\). In its non-block form, this algorithm was first presented in [42]. At each correction step the approximates \(\delta ^{(j)}_{y,\eta }\) are determined using the linear system (48) with the righthand side updated to
and resulting in the solution vector
Consequently, at each correction step (45) with \(\eta > 0\) fixed, a linear system with system matrix \({\textbf{M}}_{\eta }\) is solved, suggesting that cyclic reduction and a required LU decomposition or suitable preconditioning for an iterative method must be determined only once for each choice of \(\eta > 0\). This, in turn, allows for an efficient execution of each correction step. A detailed description of a direct method, combining one-step cyclic reduction and LU decomposition for determining \( y^{(0)}_{\eta } \) and each \(\delta ^{(j)}_{y,\eta }\) is provided in the Appendix. Besides solving the linear system (48) for determining the desired grid functions another crucial part of Algorithm 1 is the construction of each defect and thus the interpolating functions \({{\mathcal {I}}}(y^{(j)}_{{\eta }})\). In particular, when piecewise polynomials like splines are used, the required interpolating functions are determined by solving several linear systems equal to the spatial dimension 2n of the function y. Since there exists no coupling between the component function of \(y^{(j)}_{{\eta }}\), parallelization of the interpolation process is possible, which has an advantageous effect on computational cost. In Sect. 4, a numerical investigation of Algorithm 1 and its time complexity is provided. Moreover, the experiments described in Sect. 4 reveal that by a successive correction with (45) the order of convergence of the approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) is improved by a whole number. This fact is consistent with the results of IDeC given in, e.g., [24]. The convergence analysis for these methods, however, is not straightforward and usually requires the existence of asymptotic expansions to the global error of the underlying scheme [33]. It is well known that these expansions exist for RK-methods with constant step-size [37], providing evidence that a similar result can be achieved for our symplectic Euler method presented. An extensive discussion of this matter is out of the scope of this paper and will thus not be given within this work.
So far, the numerical error estimates for LQR problems have been discussed. To complete this section, the estimation of continuous error functions with active control constraints is discussed below. For this case, a solution of the optimal control problem (18)–(19) is sought, where the mapping \(\pi \) defined by (22) is a projection of the linear affine transformed co-state p onto the set of feasible control values. Therefore, the BVP (23), which results from the linear algebraic system (31), is nonlinear, so that the algorithm (1) is not readily applicable. However, since the HP system (31) is uniquely solvable and the associated maximization of the Hamiltonian function (4) can be solved analytically, the use of a forward-backwards iteration is suitable for the approximation of \(e_x\) and \(e_u\). Prominent examples of these methods are the projected gradient approach [43], as well as methods of successive approximation [44,45,46]. Having at disposal estimates for the continuous error extension on the grid \(\varDelta _{\eta }\), an estimate for the quality of the approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) is desired. Therefore, similar to before the quantities (36)–(38) are defined. Since \(\pi \), as defined by (22), is a projection of p(t) onto the compact set \({{\mathcal {E}}}_t\) and hence Lischitz continuous, it holds:
Consequently, the investigation of the error in the approximation \(e_{u,\eta }\) to the function \(e_u\) can also be reduced to an investigation of the error function \(\delta _p\) in the case of active control constraints. According to Theorem 1, the functions \(e_x\) and p are solutions to the BVP (23). We suppose that the numerical solution to the system (31) satisfies
Then, just as in the case of LQR problems, the resulting interpolated approximations \({{\mathcal {I}}}_y = ({{\mathcal {I}}}(e_{x,\eta }), {{\mathcal {I}}}(p_{\eta }))\) satisfies the perturbed problem
with boundary conditions as in (23), the defect (34) and \({{\mathcal {L}}}\) given by (21). Intuitively, one expects that the same reasoning as applied in the unconstrained setting holds for the defect. That is, if the maximum norm of the defect is sufficiently small, the perturbed and the original BVP (23) are closely related, and thus the approximations \(e_{x,\eta }\), \(p_{\eta }\), on the given grid \(\varDelta _{\eta }\), sufficiently close to \(e_x\) and p. In turn by (50) \(e_{u,\eta }\) should as well represent a suitable approximation to \(e_u\). However, in contrast to the LQR case an exact bound as stated in Theorem 2 does not hold. Instead, the defect rather serves as an asymptotically correct upper bound for the maximum norm of the function \(\delta _y\). To substantiate this statement a reasoning similar to [13] is applied. Therefore we assume that the approximations \(e_{x,\eta }\) and \(p_{\eta }\) are accurate of order k in the sense of (10) and the interpolation operator \({{\mathcal {I}}}_y\) satisfies (A3) and is chosen such that \(\Vert \delta _y\Vert _{\infty } = O(\eta ^k)\). We rewrite the defect as follows:
Then integration over the sub-interval \([t_l,t]\) with \(t \in (t_l,t_{l+1}]\), results in
Due to the Lipschitz properties of \(\pi \) and the assumption \(\Vert \delta _y\Vert _{\infty } = O(\eta ^k)\), we have
for all \(t \in (t_l,t_{l+1}]\). This correspondence provides essentially two pieces of information about the asymptotic behaviour of the defect. First, in the worst case, for the defect it holds \(D(t) = O(\eta ^{k-1})\) and, secondly, for \(\eta \) sufficiently small the quantity \(\eta \Vert D\Vert _{\infty }\) can serve as an upper bound for the global error of our approximations \(e_{x,\eta }\) and \(p_{\eta }\). In turn, \(\eta \Vert R^{-1}B^T\Vert \; \Vert D\Vert _{\infty }\) can at least asymptotically be seen as an upper bound for the global error of the approximation \(e_{u,\eta }\). However, since this relation holds only asymptotically, the defect in the control-constrained case is a less reliable measure for the quality of our approximations \({{\mathcal {I}}}(e_{x,\eta })\) and \(\pi ({{\mathcal {I}}}(p_{\eta }))\) than it is in the unconstrained case.
4 Numerical Experiments
To demonstrate the findings of our work, results of numerical experiments are presented. For validation purposes, in the first subsection, small problems with known analytical solutions are considered. In the second subsection an application of Algorithm 1 to an LQR problem is presented that arises from the finite element Petrov-Galerkin approximation of a controlled convection-diffusion equation.
4.1 Numerical Validation with Small LQR and LQOC Problems
As a first example, an LQR problem is considered. Therefore, we use the specifications \(Q = 0\), \(R = 0.005\), \(\alpha = 10\), and \(c = (-2,-2)^T\). The governing ODE model is given by
where \(t \in [0,10]\). The true solution (x, u) is achieved by solving the corresponding BVP (7)–(8) using the Matlab ’Symbolic Math’ toolbox and setting \(u = R^{-1}B^T p\). To generate the approximations \((x_h,u_h)\) on the equidistant grid with step-size \(h = 0.5\), a direct method of optimal control is applied. Here, we chose a coarse grid for the initial approximation to better visualize the error functions and approximations. The system dynamics (53) are approximated using the second-order accurate Crank-Nicolson method. Consistent with this choice, the integral in the cost functional (1) is approximated using the trapezoidal rule. The resulting nonlinear programming problem is then given by
where we suppose \(x_l:= x_h(t_l)\) and \(u_l:= u_h(t_l)\) for all \(l = 0,\ldots ,L\). The finite-dimensional optimization problem (54) is solved numerically using a second-order interior point optimization technique [47]. For constructing the continuous extensions in the sense of Definition 2, the interpolation operator \({{\mathcal {I}}}\) is chosen to be the cubic spline interpolation with not-a-knot boundary condition, as described in Remark 2. For constructing approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) to the continuous error functions \(e_x\) and \(e_u\), we apply Algorithm 1 with the tolerance \(\theta = 1e-03\), maximum number of corrections \(j_{\max } = 2\), initial step-size \(\eta = 0.05\) and \(\gamma = 0.5\). The \(L^{\infty }\)-error for the approximations \(e^{(j)}_{x,\eta }\) and \(e^{(j)}_{u,\eta }\), in the form of the maximum norm of the functions \(\delta _x^{(j)}\) and \(\delta _u^{(j)}\) respectively is provided in the Table 1. For the corresponding estimated upper bounds \(\Vert D^{(j)}\Vert _{L^r}\) we set \(r = \infty \) and report them in Table 3. By comparing the results given in Table 1 and 3 the maximum norm of the defect provides an upper bound for the error of approximation with respect to the error functions \(e_x\) and \(e_u\). This aligns with the results of Theorem 2 when choosing \(r = \infty \) and for the given problem, the defect is an appropriate indicator for the reliability of the continuous error estimates \({{\mathcal {I}}}(e_{x,\eta })\) and \({{\mathcal {I}}}(e_{u,\eta })\). The resulting trajectories of the continuous error estimates and the continuous extensions of the numerical approximations are represented in Fig. 1. Due to the use of the trapezoidal rule when constructing the discrete-time problem (54), less weight is put on the optimization of the discrete controls at the boundaries of \([t_0,T]\). Thus, the global error in \(u_h\) and \(x_h\) is the largest, close to \(t_0\) and T. As visible in Fig. 1, this behaviour is perfectly reflected by the error functions \(e_x\) and \(e_u\) as well as their approximations generated by Algorithm 1. For a numerical order analysis, we additionally investigate for each iteration \(j = 0,1,2\) the asymptotic behaviour of the defect \(D^{(j)}\) as well as that of the continuous error estimates \({{\mathcal {I}}}(e^{(j)}_{x,\eta })\) and \({{\mathcal {I}}}(e^{(j)}_{u,\eta })\). Therefore, multiple approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) using Algorithm 1, with the specification \(\theta = 2\textrm{e}{-06}\) and \(\eta = 0.0625\) are generated. Having at disposal those approximations for each iterate of Algorithm 1 and the corresponding defect values, least-squares fit of the generated value to a function of the form \(C\eta ^k\) is applied. The corresponding log-log plot for the results is provided in Fig. 2, the estimated orders of \(\delta _{\eta }^{(j)}\) for \(j = 0,1,2\) are given in Table 2. The estimated orders of \(D^{(j)}\) for \(j = 0,1,2\) are presented in Table 4. Consistent with the framework of IDeC [24], Table 2 shows that for each iteration \(j = 0,1,2\) of Algorithm 1 the corrections defined by (45) lead to an improvement in the order of accuracy of the initial estimates \({{\mathcal {I}}}(e_{x,\eta })\) and \({{\mathcal {I}}}(e_{u,\eta })\). This is strongly connected with the ability of the defect to reflect the asymptotic behaviour of the underlying global error. From Table 4 it is apparent that the defect is asymptotically equivalent to the global error of the corrected approximations \(e^{(j)}_{x,\eta }\) and \(e^{(j)}_{u,\eta }\) for \(j < 2\). However, for the last approximation with \(j = 2\), an order reduction appears in the defect \( D^{(2)} \). While a cubic spline interpolation polynomial satisfies Assumption (A3) as shown in Remark 2 its derivative is not able to reflect the asymptotic behaviour of the underlying approximation \(e_{x,\eta }\). More precisely in the given case, it can be proved that \(\frac{d}{dt}{{\mathcal {I}}}(e^{(2)}_{x,\eta }) = O(\eta ^{2})\), holds. Taking into account the relation (47), it appears that in the given case the size of the defect cannot be improved beyond this worst-case bound. To overcome this order reduction effect in the defect, we apply Lemma 4 and chose an interpolation operator with a higher order of accuracy. By the use of a quartic, instead of a cubic spline for the interpolation operator \({{\mathcal {I}}}\) we obtain the results presented in Table 5 and 6. It is apparent that by the choice of a higher-order spline, the order reduction effect in the defect of the last iterate no longer occurs.
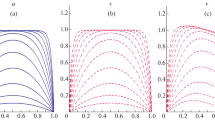
Trajectories of the true solution and the continuous extensions of the corresponding numerical approximations to the first test problem based on (54), together with the corresponding continuous error estimates
LogLog-plot for the \(L^{\infty }\)-error of the estimates \({{\mathcal {I}}}(e_{x,\eta })\) for \(x_h\) (a) and \({{\mathcal {I}}}(e_{u,\eta })\) for \(u_h\) (b) with respect to the step-size \(\eta \). The corresponding estimated orders are reported in Table 2
Our next test problem is taken from [18] and specified by the parameters \(Q = 2\), \(R = 2\), \(\alpha = 0\). In this case, the Cauchy problem is given by
where \(t \in [0,1]\). Moreover, it is required that \(u(t) \in {{\mathcal {U}}}= (-\infty ,1]\) for all \(t \in [0,1]\). The exact optimal solution (x, u) is given by
and
To generate an approximation \((x_h,u_h)\) to the above functions, the indirect approach of optimal control is applied. Therefore the HP system (4)–(6) is solved by successive iteration. The symplectic Euler method with step size \(h = 0.1\) is used to construct a discrete HP system which is then solved using the projected gradient method. To determine \(e_{x,\eta }\) and \(e_{u,\eta }\) the auxiliary HP system (31) discretized using the symplectic Euler method on a uniform grid with step size \(\eta = 0.01\). The resulting system, then is solved using the sequential quadratic Hamiltonian algorithm [46]. The continuous extensions for \(x_h\) and \(e_{x,\eta }\), are constructed using the cubic spline of Remark 2. For the interpolation of \(u_h\) and \(e_{u,\eta }\) the linear spline described in Remark 3 is utilized. The resulting trajectories, together with those of the true solutions \(x,u,e_x\) and \(e_u\) are shown in Fig. 3. As long as the control bounds are active for both the discrete control \(u_h\) and the optimal control u, the approximation of the state is exact by construction. This is perfectly in line with the behaviour of the error function \(e_x\) and its continuous approximation \({{\mathcal {I}}}_x(e_{x,\eta })\). As soon as the control constraints are inactive the global error of the approximation \(p_h\) to the co-state impacts the global error of \(u_h\). In Fig. 3b one can see that the global error of the discrete control is at its maximum, where the control constraints on u turn from active to inactive. Even though the global error in \(u_h\) decays linearly, the construction of the forward Euler method causes the global error in the controls and thus in \(x_h\) to add up linearly what complies with the trajectory of \(e_x\) and its continuous approximation \({{\mathcal {I}}}_x(e_{x,\eta })\), see Fig. 3a. Figure 3b illustrates the impact of the choice of a linear interpolation operator on the regularity of the continuous error function \(e_u\). Due to the non-linearity of (57), non-differentiable points occur at the grid points for \(0.5\le t \le 1\). Nevertheless, as noted in Remark 4 the continuous error function \(e_u\) is consistent with the global error of \(u_h\). Therefore notice that \(\Vert e_u\Vert _{\infty }\) has an estimated order of uniform convergence of \(k \approx 1.01113\) for \(h \rightarrow 0\). Moreover, it is well known that the Euler method as applied to the system (4)–(6) is first-order accurate. Taking those facts together the consistency of the continuous error estimate \(e_u\) follows. A similar result is provided for \(e_x\), where the estimated order of uniform convergence as \(h \mapsto 0\) is \( k\approx 0.99262 \).
4.2 An Application to a PDE Optimal Control Problem
In the following, we apply Algorithm 1 to derive continuous error extensions for numerical solutions of LQR problems governed by a convection-diffusion equation approximated using the finite element Petrov-Galerkin scheme [48]. For the sake of completeness and to make this investigation within the paper self-contained, we provide a derivation of the relationship between LQR problems and numerical approximations to finite-time horizon regulator problems of the form
where \(\varOmega = (0,1)\) denotes the domain of the space variable, \(\mu > 0\), \(\nu > 0\) and \(b \in L^2(\varOmega )\) as well as \({{\mathcal {Q}}}: L^2(\varOmega ) \rightarrow L^2(\varOmega )\) are suitably chosen bounded linear operators. Here and in the following \(\langle \cdot , \cdot \rangle \) denotes the standard \(L^2\)-inner product on \(L^2(\varOmega )\) and we suppose \(\nu = 1\). The basic idea of the Petrov-Galerkin approximation applied to (59)–(61) relies on the weak formulation of the convection-diffusion equation. For this purpose, we multiply (59) by a test function \(\varphi \in W_0^{1,2}(\varOmega )\) and then integrate over the domain \(\varOmega \). After functional manipulation, we obtain
for any \(t \in (0,T]\) and \(u \in L^2(0,T)\). The problem (59)–(61) in its weak formulation now is to find for any \(t \in (0,T]\) and \(u \in L^2(0,T)\) fixed, a so-called weak solution w(t, s) that satisfies the variational Eq. (62) for all test functions \(\varphi \in W_0^{1,2}(\varOmega )\) together with \(w(0,s) = w_0(s)\) almost everywhere on \(\varOmega \). The Petrov-Galerkin approach now aims to construct an approximation to this weak solution by projecting the weak formulation onto a suitable subspace of \(W_0^{1,2}(\varOmega )\).
Now, let \(\varOmega \) be equally partitioned by the gridpoints \(s_i = \frac{i}{n+1}\) where \(i = 0,\ldots , n+1\). For the resulting grid, a suitable basis of piecewise trial functions \(\{\beta _i\}_{i = 1,\ldots , n}\) is chosen from a finite element space \(W_n \subset W_0^{1,2}(\varOmega )\) to approximate w(t, s) using the ansatz
Additionally, restricting the choice of test functions to a set \(\{\phi _j\}_{j = 1,\ldots ,n}\) of appropriate basis functions selected from a possibly different finite element space \(V_n \subset W_0^{1,2}(\varOmega )\), the weak formulation (62) is reduced to a problem in a finite-dimensional vector subspace and called the Petrov–Galerkin formulation of (59)–(61): Given \(u \in L^2(0,T)\) and for any \(t \in (0,T]\) find \(w^n(t,\cdot ) \in W_n\) such that
holds for all \(j = 1,\ldots ,n\) and \(w^n(0,s) = w^n_0(s)\), where \(w^n_0(s)\) is a suitable projection of \(w_0(s)\) onto \(W_n\). For the following, we suppose that this projection is achieved by pointwise interpolation at the gridpoints \(s_i\) and thus define \(x_i(0) = w_0(s_i)\) for all \(i = 1,\ldots ,n \). With this in mind and substituting \(w^n(t,s)\) into the Petrov-Galerkin formulation (64), it appears that the coefficient functions \(x_1(t), \ldots , x_n(t)\) for (63) are characterized by a first-order system of linear ordinary differential equations with respect to time and the initial condition \(x^0:= (w_0(s_1),\ldots ,w_0(s_n))^T\). That is, we have
where \(x(t):= (x_1(t),\ldots ,x_n(t))^T\), \(b^n:= (\langle b, \phi _1 \rangle , \ldots , \langle b, \phi _n \rangle )^T\) and the matrices
are the mass and stiffness matrices of the underlying Petrov-Galerkin approximation. By the above derivation, controlling the approximate solution \(w^n(x,t)\) using the control function u(t) with respect to the time variable is equivalent to controlling the coefficient functions x(t) using the correspondence (65). Thus by substituting the finite element formulation (63) into (58) one can see that determining an optimal control for the Petrov-Galerkin formulation of the controlled convection-diffusion equation in the finite element space \(V_n\) reduces to an LQR problem of the form (1). That is, an approximate solution to (58) can be determined by first solving numerically the problem
where we set
followed by substitution of the results into the ansatz function (63).
Notice that the quality of the approximation to w(t, s) and its corresponding optimal control, depends upon two factors, the choice of the trial space \(V_n\) and the test space \(W_n\) as well as the choice of the method to solve (66). As a result, two error sources occur, the first corresponding to the Petrov-Galerkin approximation and the second one due to the accuracy of the method used to solve (66). Our investigation within this section is devoted to the quantification of errors due to the latter source and the application of Algorithm 1 to numerical solutions of (66). Thus all continuous error estimates are related to approximations to \(w^n(t,s)\) and the corresponding optimal control, in the following denoted with \(u^n(t)\). A discussion of continuous error representations with respect to the true solution w(t, s) to (58) and its corresponding optimal control will be omitted here, as this would be beyond the scope of this paper. Instead, we utilize a well-tested Petrov-Galerkin method for the controlled convection-diffusion equation to generate A, B, and Q, such that the effect of numerical instabilities occurring due to the discretization with respect to the space variable are mitigated. In the case of finite element methods, the functions \(\{\beta _i\}_{i = 1\ldots ,n}\) and \(\{\phi _i\}_{i = 1\ldots ,n}\) are commonly selected from piecewise polynomial spaces [49]. A standard choice for \(V_n\) and \(W_n\) is the space of piecewise linear functions, where a basis can be constructed choosing appropriate hat-functions as defined in Remark 3. Specifically, we choose
Using these basis functions in the construction of (63) and setting \(\phi _j = \beta _j\) for all \(j = 1, \ldots , n\), one arrives at the standard linear finite element Galerkin approximation of the convection-diffusion equation. While this choice is easily accessible, it has been observed that this basic approach may introduce instabilities to the numerical approximation of problems like (58)–(61), see [48]. Thus, to improve the accuracy of the finite element approximation, we utilize the upwinding scheme proposed in [48]. That is, for our numerical experiments, we set
where
and \(\epsilon > 0\) is a stabilization parameter. This parameter depends on the grid used to generate the finite element solution and serves as a control mechanism for the error with respect to the space variable. As specifications for the optimal control problem (58)–(61) we set
To ensure convergence of the previously described upwinding scheme, we choose \(\epsilon = \frac{1}{6(n+1)}\) as proposed in [48]. For our first experiment and to make the numerical error analysis of the results more accessible, we choose \(\mu = \frac{1}{20}\) and construct the finite element approximation (63) using a number of \(n = 30\) basis functions. In practice, usually a larger number of basis functions is required to make the spatial error of the Petrov-Galerkin solution negligible, therefor when analyzing the time complexity of Algorithm 1, we provide an example with \(n = 512\) basis functions. In either case, an approximation to the solution to (66) in the time domain, denoted with \((x_h,u_h)\), is generated using a direct method of optimal control. Therefore the system dynamics (65) are discretized using the first-order accurate Backward Euler scheme with a step-size \(h = 5e-02\). The resulting quadratic programming problem is then given by
This finite-dimensional problem is solved numerically using the second-order interior point optimization technique described in [47]. The resulting solutions are represented in the form of grid functions \((x_{h},u_h)\in X^{h}_{x^0} \times Z^{h,1}\), with \(x_{h}(t_l) = x_l\) and \(u_{h}(t_l) = u_l\) for all \(l = 0,\ldots , L\). For the construction of the corresponding continuous extensions and their continuous error functions in the sense of Definition 2, a fifth-order accurate quartic spline interpolation operator is utilized. Using the same interpolation operator a continuous approximation to \(w^n(t,x)\) is defined by
where we suppose that for each component of the grid function \(x_{h}\), it holds \(x_{h,i}(t_l) \approx x_i(t_l)\) for \(t_l \in \varDelta _{\eta }\) and \(i = 1,\ldots ,n\). The continuous extension for the global error of the approximation to the Petrov-Galerkin solution (63) is then defined as follows
Here, \(e_{x_i}(t)\) denotes the i-th component function of \(e_x(t)\) and thus the continuous error extension of the global errors corresponding to the coefficient function \(x_i(t)\) in the sense of Definition 2. Since no closed-form solution is available for (66), we generate a reference solution for visualization. Therefore a second-order accurate Crank-Nicolson scheme with step-size \(h = 2.5e-04\) is used. Approximations \(e_{x,\eta }\) and \(e_{u,\eta }\) to the continuous error functions \(e_x\) and \(e_u\), are generated by Algorithm 1 with the tolerance \(\theta = 1e-05\) and a maximum number of corrections \(j_{\max } = 3\), initial step-size \(\eta = 5e-04\), \(\gamma = 0.5\) and \(r = 2\). We estimate the norm of the defect \(D^{(j)}\) required in our algorithm using the discrete \(L^2\)-norm on the grid \(\varDelta _{\eta }\), i.e.
At each correction cycle of Algorithm 1, the linear system of Eq. (48) is solved with a direct method combining one-step cyclic reduction and LU-factorization, see the Appendix.
After the approximations \((e_{x,\eta },e_{u,\eta })\) are generated, a continuous approximation to (69) is defined by
The trajectories of the resulting continuous error estimates for the global errors of the approximations \((x_h,u_h)\), together with their continuous extensions are presented in Fig. 5. In Fig. 4, based on the generated approximations, the continuous extensions (68) and (69) are given in the space-time plane. To allow for a better interpretation of the results, we remark that by the construction of the discrete-time problem (67) and due to the use of the backward Euler scheme there are no active constraints on \(u_0\). As a result, the choice \(u_0 = 0\) is optimal for (67) and convergence of \(u_h\) to u can only be guaranteed at the gridpoints corresponding to \(l = 1, \ldots , L-1\). In turn, the global errors in \(u_h\) and \(x_h\) are expected to be large, close to the initial time \(t_0\). As clearly visible from Fig. 5, the approximations to \(e_x\) and \(e_u\), generated with Algorithm 1, can properly reflect this behaviour of the global errors. Similarly due to the construction of the Petrov-Galerkin solution (63) and the corresponding continuous approximation (68), large error quantities are to be expected close to the coordinate origin. As one can see in Fig. 4b, the error function (69) constructed from the approximations generated with Algorithm 1 is perfectly able to reflect this behaviour. To numerically validate the quality of the generated continuous error extension, the norm of the defect for each iteration of Algorithm 1 is reported in Table 7. An estimate for the order of approximation k of the error estimate \(e_{x,\eta }\) is generated using the ratio
which is based on Richardson’s extrapolation technique. For \(e_{u,\eta }\) an estimate for the order of approximation is derived correspondingly and the results are reported in Table 8.
a Petrov-Galerkin solution \(w^n(t,s)\), generated by solving (67). b Continuous error extension \(e^{n}_{w,\eta }(t,s)\) generated by Algorithm 1
Trajectories of the interpolated reference solution and the continuous extensions of the numerical approximations \((x_h,u_h)\) to the LQR problem (66), together with the corresponding continuous error estimates
For each iteration, we provide the estimated orders of magnitude for the defect in Table 9, which are determined with the same Richardson extrapolation-based technique. By comparing the results given in Table 8 and 9, for the given problem, the defect is asymptotically equivalent to the global error of the corrected approximations \(e^{(j)}_{x,\eta }\) and \(e^{(j)}_{u,\eta }\) for all iterations. Opposed to the first test problem no order reduction effect occurs with respect to the defect, such that its order can be improved beyond the worst-case bound provided in Lemma 4.
To conclude our discussion of Algorithm 1, we consider the computational cost of our methodology and substantiate our findings with a numerical experiment applied to the PDE control problem (58). Therefore, a convection-dominated problem with \(\mu = 1/1500\) is chosen. To stabilize the numerical solution of the convection-diffusion optimal control problem, the stabilization parameter for the upwind scheme is set to \(\alpha = 200 / n\). To reduce the spatial error for the Petrov-Galerkin scheme, a number of \( n = 512 \) basis functions is used. For Algorithm 1 the same specifications are used as earlier in this section, only changing the tolerance to \(\theta = 1e-04\). All results are generated on an ’Intel Xeon CPU E5-2695 v3 @ 2.30GHz’ machine with a total of 28 cores, where for the parallel construction of each component function of \({{\mathcal {I}}}(y^{(j)}_{\eta })\), a total number of 12 cores is utilized. At each correction cycle in Algorithm 1, the corresponding grid functions are determined using the procedure described in the Appendix. All upcoming CPU times are averaged over multiple runs and rounded to the nearest integer. The mean total CPU time (\(CPU_{SE}\)) required to execute Algorithm 1, together with mean CPU time required for constructing each defect \(D^{(j)}\) (\(CPU_{{{\mathcal {I}}}}\)) and determining \(y^{(j)}_{\eta }\) (\(CPU_{{\textbf{M}}}\)) is presented in Table 10. The mean CPU time required to solve the remaining tasks like constructing \(F_{\eta }\) and evaluating \(\Vert D^{(j)}\Vert _{\eta }\) are therein denoted with \(CPU_{R}\). Furthermore, for each correction cycle the size of \(\Vert D^{(j)} \Vert _{\eta }\) is reported. For reference, the mean total CPU time, required to solve the original quadratic programming problem (67) on the specified initial grid with \(h = 5e-02\) is given as \(CPU_{QP}\). It is set in relation to the CPU-time required to execute Algorithm 1 and the resulting ratio, together with the ratios for the CPU times given in Table 10 are reported in Table 11.
For our theoretical investigation of the time complexity, it is sufficient to restrict ourselves to a single correction cycle. We analyze the process of constructing each of the defect functions \(D^{(j)}\) when using spline interpolation. At each iteration of Algorithm 1, 2n spline functions are constructed, each with \(L+1\) interpolation points. Every spline requires the solution of a linear system with a banded tridiagonal matrix, which is solved in linear time with respect to the number of grid points L. The resulting time complexity of \(CPU_{{{\mathcal {I}}}}\) is O(nL), which is in line with the results reported in Table 10. Next, we discuss the computational complexity required to solve the linear system (48). This part strongly depends on the solution method chosen and it is not surprising that constructing the grid functions accounts for most of the computing time. Here, we consider the approach presented in the Appendix. This method uses one step of cyclic reduction, which requires multiple matrix multiplications that can be executed using the Strassen algorithm which has a time complexity of \(O(n^{2.8})\) [50]. For the construction of the block-LU factorization, L matrix-matrix multiplications are required and L linear systems of size \(2n \times 2n\) need to be solved, where each system has a \(2n \times 2n\) matrix as right-hand side. Using either matrix inversion or a suitably fast convergent iterative method for solving each subsystem, the time complexity is dominated by the number of necessary matrix multiplications and thus amounts to \(O(L n^{2.8})\) [51]. After the LU decomposition is constructed, at each correction step a grid function is determined with a time-complexity of \(O(Ln^2)\). This number follows from solving L linear systems of size \(2n \times 2n\), for example by an iterative method and the required matrix–vector multiplications which have the time complexity \(O(n^2)\). Thus, the overall computational complexity of Algorithm 1 is \(O(L n^{2.8})\), when using the direct approach presented in the Appendix. In this framework a further speed-up of Algorithm 1 is possible by using optimized fast LU decomposition subroutines [52] and further parallelization [53]. The direct method presented in the Appendix has a memory requirement of \(O(L n^2)\) which is dominated by the required LU decomposition. Here, the application of cyclic reduction and by taking advantage of the sparsity structures of the involved block matrices, the actual memory requirement is less than a quarter of that required to solve the original system (48) directly. The memory requirement and computational complexity might be further improved by applying block iterative solvers, developed for solving block tridiagonal matrix systems [54, 55]. In conclusion and agreement with the results given in Tables 10 and 11, respectively, we can state that Algorithm 1 has a linear computational complexity concerning the number of grid points. The time complexity with respect to the dimension of the underlying ODE system strongly depends on the method chosen to solve the involved linear system and can be further optimized by applying appropriate solvers.
5 Conclusion
The purpose of this work was to construct and analyze functions \((e_x,e_u)\) that provide continuous representations of global errors of the numerical solutions \((x_h,u_h)\) to linear quadratic optimal control problems. It is shown that the pair \((e_x,e_u)\) is the unique solution to an auxiliary optimal control problem. This solution was characterized by an optimality system that was reformulated as a boundary value problem. To generate reliable numerical approximations to the functions \(e_x\) and \(e_u\) and thus to the global error of \((x_h,u_h)\) an algorithm based on defect control as well as defect correction techniques was introduced. With this algorithm, an approximation to the constructed error functions was computed that was arbitrarily close to the global error. The proposed algorithm was validated with numerical experiments with ODE and PDE linear quadratic optimal control problems obtaining results that were in agreement with the theoretical findings of this work.
We hope that this work contributes to the foundation of theoretical and numerical methodologies for estimating error functions of optimal control problems governed by differential models. We believe that these estimates are essential in applications where highly accurate controls are required, and in improving uncertainty quantification by providing pointwise estimates of discretization errors.
Data Availability
The code and datasets generated during the current study will be available from the corresponding author upon request after publication.
References
Zadunaisky, P.E.: A method for the estimation of errors propagated in the numerical solution of a system of ordinary differential equations. In: Kontopoulos, G.I.: (ed.) The Theory of Orbits in the Solar System and in Stellar Systems, 25, 281 (1966)
Zadunaisky, P.: On the estimation of errors propagated in the numerical integration of ordinary differential equations. Numer. Math. 27, 21–39 (1976). https://doi.org/10.1007/BF01399082
Kalman, R.E., et al.: Contributions to the theory of optimal control. Bol. Soc. Mat. Mexicana 5(2), 102–119 (1960)
Kalman, R.E., Bucy, R.S.: New results in linear filtering and prediction theory. J. Basic Eng. 83(1), 95–108 (1961). https://doi.org/10.1115/1.3658902
Athans, M.: Optimal Control: An Introduction to the Theory and Its Applications. Dover Books on Engineering. Dover Publications, Mineola (2013)
Boltyanskiť, V.G., Gamkrelidze, R.V., Pontryagin, L.S.: On the theory of optimal processes. Dokl. Akad. Nauk SSSR (N.S.) 110, 7–10 (1956)
Sima, V.: Algorithms for Linear-Quadratic Optimization. CRC Press, Boca Raton (1996). https://doi.org/10.1201/9781003067450
Kenney, C., Leipnik, R.: Numerical integration of the differential matrix Riccati equation. IEEE Trans. Autom. Control 30(10), 962–970 (1985). https://doi.org/10.1109/TAC.1985.1103822
Lasiecka, I., Triggiani, R. (eds.): 9. Numerical approximations of the solution to the abstract differential and algebraic Riccati equations, pp. 107–126. Springer, Berlin (1991). https://doi.org/10.1007/BFb0006889
Dieci, L.: Numerical integration of the differential Riccati equation and some related issues. SIAM J. Numer. Anal. 29(3), 781–815 (1992). https://doi.org/10.1137/0729049
Kirsten, G., Simoncini, V.: Order reduction methods for solving large-scale differential matrix Riccati equations. SIAM J. Sci. Comput. 42(4), A2182–A2205 (2020). https://doi.org/10.1137/19M1264217
Kierzenka, J., Shampine, L.F.: A bvp solver based on residual control and the maltab PSE. ACM Trans. Math. Softw. 27(3), 299–316 (2001). https://doi.org/10.1145/502800.502801
Kierzenka, J., Shampine, L.: A BVP solver that controls residual and error. European Society of Computational Methods in Sciences and Engineering (ESCMSE). J. Numer. Anal. Ind. Appl. Math. 3, 27–41 (2008)
Budak, B.M., Berkovich, E.M., Solov’eva, E.N.: Difference approximations in optimal control problems. SIAM J. Control 7(1), 18–31 (1969). https://doi.org/10.1137/0307002
Bosarge, W.E., Jr., Johnson, O.G.: Error bounds of high order accuracy for the state regulator problem via piecewise polynomial approximations. SIAM J. Control 9(1), 15–28 (1971). https://doi.org/10.1137/0309003
Hager, W.W.: Rates of convergence for discrete approximations to unconstrained control problems. SIAM J. Numer. Anal. 13(4), 449–472 (1976). https://doi.org/10.1137/0713040
Dontchev, A.L.: Error estimates for a discrete approximation to constrained control problems. SIAM J. Numer. Anal. 18(3), 500–514 (1981). https://doi.org/10.1137/0718032
Dontchev, A.L., Hager, W.W., Veliov, V.M.: Second-order Runge–Kutta approximations in control constrained optimal control. SIAM J. Numer. Anal. 38(1), 202–226 (2000). https://doi.org/10.1137/S0036142999351765
Hager, W.W.: Runge–Kutta methods in optimal control and the transformed adjoint system. Numer. Math. 87, 247–282 (2000). https://doi.org/10.1007/s002110000178
Stetter, H.J.: Economical global error estimation. In: R.A. Willoughby (ed.) Stiff Differential Systems, pp. 245–258. Springer, Boston, MA (1974). https://doi.org/10.1007/978-1-4684-2100-2_19
Stetter, H.J.: The defect correction principle and discretization methods. Numer. Math. 29, 425–443 (1978). https://doi.org/10.1007/BF01432879
Frank, R.: The method of iterated defect-correction and its application to two-point boundary value problems part 1. Numer. Math. 25, 409–419 (1976). https://doi.org/10.1007/BF01396337
Frank, R.: The method of iterated defect-correction and its application to two-point boundary value problems part 2. Numer. Math. 27, 407–420 (1976). https://doi.org/10.1007/BF01399604
Frank, R., Ueberhuber, C.W.: Iterated defect correction for differential equations part i: theoretical results. Computing 20(3), 207–228 (1978). https://doi.org/10.1007/bf02251946
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2001). https://doi.org/10.1007/978-3-642-61798-0
Swartz, B.K., Varga, R.S.: Error bounds for spline and L-spline interpolation. J. Approx. Theory 6(1), 6–49 (1972). https://doi.org/10.1016/0021-9045(72)90079-2
Schwarz, H.R., Köckler, N.: Interpolation und Approximation, pp. 91–182. Vieweg+Teubner, Wiesbaden (2011). https://doi.org/10.1007/978-3-8348-8166-3_4
de Boor, C.: A Practical Guide to Splines, vol. 27. Springer, New York (1978). https://doi.org/10.2307/2006241
Beheforooz, G.H., Papamichael, N.: End conditions for cubic spline interpolation. IMA J. Appl. Math. 23(3), 355–366 (1979). https://doi.org/10.1093/imamat/23.3.355
Beatson, R.K.: On the convergence of some cubic spline interpolation schemes. SIAM J. Numer. Anal. 23(4), 903–912 (1986). https://doi.org/10.1137/0723058
Borzì, A.: Modelling with Ordinary Differential Equations: A Comprehensive Approach. Numerical Analysis and Scientific Computing Series. Chapman & Hall, Abingdon (2020). https://doi.org/10.1201/9781351190398
Seierstad, A., Sydsaeter, K.: Sufficient conditions in optimal control theory. Int. Econ. Rev. 18(2), 367–391 (1977). https://doi.org/10.2307/2525753
Frank, R., Macsek, F., Ueberhuber, C.W.: Asymptotic error expansions for defect correction iterates. Computing 32(2), 115–125 (1984). https://doi.org/10.1007/BF02253686
Ong, B.W., Spiteri, R.J.: Deferred correction methods for ordinary differential equations. J. Sci. Comput. 83, 1–29 (2020). https://doi.org/10.1007/s10915-020-01235-8
Sanz-Serna, J.M.: Symplectic Runge–Kutta schemes for adjoint equations, automatic differentiation, optimal control, and more. SIAM Rev. 58(1), 3–33 (2016). https://doi.org/10.1137/151002769
Jay, L.O.: Symplecticness conditions of some low order partitioned methods for non-autonomous Hamiltonian systems. Numer. Algorithms 86(2), 495–514 (2021). https://doi.org/10.1007/s11075-020-00898-6
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I—Nonstiff Problems. Springer, Berlin (2009)
Ascher, U.M., Mattheij, R.M.M., Russell, R.D.: Numerical Solution of Boundary Value Problems for Ordinary Differential Equations. Soc. Ind. Appl. Math. (1995). https://doi.org/10.1137/1.9781611971231
Shampine, L., Muir, P.: Estimating conditioning of BVPs for ODEs. Math. Comput. Model. 40(11), 1309–1321 (2004). https://doi.org/10.1016/j.mcm.2005.01.021
Bini, D., Meini, B.: The cyclic reduction algorithm. Numer. Algorithms 51, 23–60 (2009). https://doi.org/10.1007/s11075-008-9253-0
Golub, G.H., van Loan, C.F.: Matrix Computations, 4th edn. JHU Press, Baltimore (2013)
Thomas, L.: Elliptic Problems in Linear Difference Equations over a Network. Tech. rep., Watson Sc. Comp. Lab. Rep. Columbia University, New York (1949)
Pulova, N.: A pointwise projected gradient method applied to an optimal control problem. J. Comput. Appl. Math. 226(2), 331–335 (2009). https://doi.org/10.1016/j.cam.2008.08.007. (Special Issue: Large scale scientific computations)
Krylov, I., Chernous’ko, F.: On a method of successive approximations for the solution of problems of optimal control. USSR Comput. Math. Math. Phys. 2(6), 1371–1382 (1963). https://doi.org/10.1016/0041-5553(63)90353-7
Shindo, Y., Sakawa, Y.: Local convergence of an algorithm for solving optimal control problems. J. Optim. Theory Appl. 46(3), 265–293 (1985). https://doi.org/10.1007/BF00939285
Hofmann, S., Borzì, A.: A sequential quadratic Hamiltonian algorithm for training explicit RK neural networks. J. Comput. Appl. Math. 405, 113943 (2022). https://doi.org/10.1016/j.cam.2021.113943
Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106, 25–57 (2006). https://api.semanticscholar.org/CorpusID:14183894
Burns, J., Zietsman, L.: Upwind approximations and mesh independence for lqr control of convection diffusion equations. In: Proceedings of the IEEE Conference on Decision and Control, pp. 219 – 224 (2008). https://doi.org/10.1109/CDC.2007.4434454
Mitchell, A., Griffiths, D., Meiring, A.: Finite element galerkin methods for convection-diffusion and reaction-diffusion. In: Axelsson, O., Frank, L., Van Der Sluis, A. (Eds.) Analytical and Numerical Approaches to Asymptotic Problems in Analysis, North-Holland Mathematics Studies, 47, 157–177. North-Holland (1981). https://doi.org/10.1016/S0304-0208(08)71108-3. https://www.sciencedirect.com/science/article/pii/S0304020808711083
Strassen, V.: Gaussian elimination is not optimal. Numer. Math. 13, 354–356 (1969)
Bailey, D., Ferguson, H.: A strassen-newton algorithm for high-speed parallelizable matrixinversion, pp. 419–424 (1988). https://doi.org/10.1109/SUPERC.1988.44680
Li, S., Gu, M., Cheng, L.: Fast structured lu factorization for nonsymmetric matrices. Numerische Mathematik 127 (2014). https://doi.org/10.1007/s00211-013-0582-0
Yang, W., Li, K., Li, K.C.: A parallel solving method for block-tridiagonal equations on cpu–gpu heterogeneous computing systems. J. Supercomput. 73, 1760–1781 (2017)
Amodio, P., Mazzia, F.: A parallel gauss-seidel method for block tridiagonal linear systems. SIAM J. Sci. Comput. 16(6), 1451–1461 (1995)
Chan, R.H.F., Jin, X.Q.: An Introduction to Iterative Toeplitz Solvers. Society for Industrial and Applied Mathematics (2007)
Varah, B.J.M.: On the solution of block-tridiagonal systems arising from certain finite-difference equations*. Math. Comput. 26, 859–868 (1972). https://api.semanticscholar.org/CorpusID:122267226
Heller, D.: Some aspects of the cyclic reduction algorithm for block tridiagonal linear systems. SIAM J. Numer. Anal. 13(4), 484–496 (1976)
Wu, C.Y., Huang, T.Z.: Stability of block lu factorization for block tridiagonal matrices. Comput. Math. Appl. 57(3), 339–347 (2009)
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was partially supported by the BMBF-Project iDeLIVER: Intelligent MR Diagnosis of the Liver by Linking Model and Data-driven Processes.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In the following, we describe a direct method for solving the linear system of equations in Algorithm 1. The upcoming procedure consists of a block cyclic reduction (CR) step [40], followed by the solution of the reduced system using block LU decomposition. In particular, we discuss the main computational aspects of the approach and its numerical stability in our framework. Our algorithm starts by applying one step of CR to the system
where we set \(\tilde{y}_l = (e_{x,l+1},p_l)^T\), if \(f_l = F_{\eta ,l}\) holds for all \(l = 1,\ldots , L\) and \(\tilde{y}_l = (\delta ^{(j)}_{x,l+1},\delta ^{(j)}_{p,l})^T\), if \(f_l = D^{(j)}_{\eta ,l}\) holds for all \(l = 1,\ldots , L\). The involved block matrices are defined as in (49) and we assume for simplicity that L is even. To obtain a reduced system with CR, first, an even-odd permutation is applied to reformulate (72) equivalently as
where
and
together with
Next, block Gaussian elimination is applied to the permuted system (73), resulting in the following two reduced systems
and
For the following, we denote the right-hand side of (75) with \(\tilde{f}:= f_{e} -{{\mathcal {M}}}_{21}\,{{\mathcal {M}}}_{11}\,f_{o} \in {\mathbb R}^{ n L}\).
Since \({{\mathcal {M}}}_{11}\) is an involutory matrix, the solution to (76) is explicitly determined as follows:
with \(\tilde{L}: = L/2 \). Hence, as (77) depends on the vector \(\tilde{y}_e\) it is only necessary to solve the reduced system (72) utilizing an appropriate solver, which is a notable improvement to directly solving (72). One can show by direct calculation that the Schur-complement of \({{\mathcal {M}}}_{11}\), defining the system matrix of (75), admits the same block tridiagonal structure as the original system (72). We have
where the \(2n \times 2n\)-matrix blocks are given by
with \({\textbf{M}}^{(1)}_{1}\) and \({\textbf{M}}^{(1)}_{2}\) possessing the same sparsity pattern as \({\textbf{M}}_{1}\) and \({\textbf{M}}_{2}\). For the resulting reduced system (75), a direct solver in the form of block-Gaussian elimination is applied, namely the block Thomas algorithm. The resulting block LU factorization \({\textbf{M}}^{(1)}_{\eta } = {\varvec{\Lambda }}\,{\varvec{\Upsilon }}\), is specified by the following matrices
The \(2n \times 2n\)-matrix blocks \({\varvec{\Lambda }}_i \) and \({\varvec{\Upsilon }}_i\) are constructed iteratively with Algorithm 2. For this approach, we remark that due to the sparsity pattern of \({\textbf{M}}^{(1)}_{1}\) and \({\textbf{M}}^{(1)}_{2}\), each block matrix determined with Algorithm 2 can be partitioned as follows
where \({\varvec{\Lambda }}_{i,1}, {\varvec{\Upsilon }}_{i,1}, {\textbf{M}}^{(1)}_{0,2} \in {\mathbb R}^{2n \times n } \) are non-sparse matrices and
As a result, after building the LU-decomposition of \( {\textbf{M}}^{(1)}_{\eta } \) only the submatrices \({\varvec{\Lambda }}_{i,1}\) and \({\varvec{\Upsilon }}_{i,1}\), for \( i = 1,\ldots ,\tilde{L}-1\) need to be stored in memory. In the next step, the solution to the reduced system (75) is determined by invoking Algorithm 3 which successively solves the two systems
With the solution to (75) determined, \(\tilde{y}_o\) is constructed using (77). The solution to the original system (72) is then put together by an appropriate permutation of \((\tilde{y}_o, \tilde{y}_e)^T\). In turn, the grid function \(y_{\eta }\) is defined by setting
with boundary values
For the construction of each \(\delta ^{(j)}_{y,\eta }\) in Algorithm 1, similar reasoning is applied by taking into account (44). The resulting procedure of Algorithm 1, for determining \(y_{\eta }\) and each \(\delta ^{(j)}_{y,\eta }\) respectively, is summarized in Algorithm 4.
It is apparent that, compared to solving (72) directly, the one-step cyclic reduction approach, together with the involutory property of the matrix \({\textbf{M}}_0\) enables us to considerably reduce the computational effort and memory requirement for determining the desired grid functions. Moreover, since the reduced problem (75) admits the same block tridiagonal Toeplitz structure, the LU decomposition can be determined straightforwardly, in the manner of the block Thomas algorithm. In addition, the memory requirement for storing the LU decomposition is further reduced by exploiting the advantageous sparsity patterns of the involved block matrices. Since in Algorithm 1, for any fixed \(\eta > 0\), only the forcing term, i.e. the righthand side of the system (72) differs in between iterations, the LU decomposition must only be determined once per correction cycle, that is when determining \(y^{(0)}_{\eta }\). As a result, in every remaining iteration of each correction cycle, dedicated to determining \(\delta ^{(j)}_{\eta }\), solely the two systems (78) need to be solved.
To conclude, we briefly discuss the numerical stability of the proposed procedure. It is known that a sufficient condition for the block Gaussian elimination to be numerically stable is the block diagonal dominance of the involved system matrix [56]. Since the block diagonal dominance of the original system matrix is preserved during cyclic reduction, this criterion can be verified for the matrix \({\textbf{M}}_{\eta }\) [57, 58]. Recalling the block structure of the system matrix and examining the matrix blocks defined in (49), it can be seen by applying the Gelfand spectral radius theorem that diagonal dominance and thus numerical stability can be guaranteed by choosing \(\eta > 0\) sufficiently small, depending on the spectral radii of Q and \(BR^{-1}B^{T}\). Moreover, under a row permutation of the matrix blocks (49) and if A is a negative definite matrix, the LU decomposition of the resulting permuted system is numerically stable if the stability condition for the involved Euler discretization of the state and costate equation (32)–(33) is satisfied.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hofmann, S., Borzì, A. Pointwise Error Estimates of Numerical Solutions to Linear Quadratic Optimal Control Problems. J Sci Comput 99, 21 (2024). https://doi.org/10.1007/s10915-024-02484-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02484-7