Abstract
Discrete wavelet methods, originally formulated in the setting of regularly sampled signals, can be adapted to data defined on a point cloud if some multiresolution structure is imposed on the cloud. A wide variety of hierarchical clustering algorithms can be used for this purpose, and the multiresolution structure obtained can be encoded by a hierarchical tree of subsets of the cloud. Prior work introduced the use of Haar-like bases defined with respect to such trees for approximation and learning tasks on unstructured data. This paper builds on that work in two directions. First, we present an algorithm for constructing Haar-like bases on general discrete hierarchical trees. Second, with an eye towards data compression, we present thresholding techniques for data defined on a point cloud with error controlled in the \(L^{\infty }\) norm and in a Hölder-type norm. In a concluding trio of numerical examples, we apply our methods to compress a point cloud dataset, study the tightness of the \(L^{\infty }\) error bound, and use thresholding to identify MNIST classifiers with good generalizability.









Similar content being viewed by others
Data Availability
The MNIST dataset used in Sect. 4.3 is available at Yann LeCun’s website (http://yann.lecun.com/exdb/mnist/). The datasets used in Sect. 4.1 and 4.2 are available from the corresponding author upon request.
Notes
The stipulation that the bound depend only on \({\underline{B}}\) and \({\overline{B}}\), and not on size of the tree, is essential, and in fact a bound in terms of \({\underline{B}}\) and the size of the tree always holds (take \(a_{i} = 1\) in Theorem 3).
We sample \([{20\,\mathrm{\%}}, {100\,\mathrm{\%}}]\) with lower resolution because we observe very little change in the behavior of the classifiers between the 20 % and 100 % (unthresholded) coefficient retention levels.
References
Robinson, A.H., Cherry, C.: Results of a prototype television bandwidth compression scheme. Proc. IEEE 55(3), 356–364 (1967)
Bradley, Stevan D.: Optimizing a scheme for run length encoding. Proc. IEEE 57(1), 108–109 (1969)
Hauck, Edward L.: Data compression using run length encoding and statistical encoding, December 2 (1986). US Patent 4,626,829
Ziv, J., Lempel, A.: A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 23(3), 337–343 (1977)
Pavlov, Igor: LZMA specification (draft), (June 2015)
Nevill-Manning, C.G., Witten, I.H.: Identifying hierarchical structure in sequences: a linear-time algorithm. J. Artif. Intell. Res. 7, 67–82 (1997)
Mandagere, N., Zhou, P., Smith, MA., Uttamchandani, S.: Demystifying data deduplication. In: Proceedings of the ACM/IFIP/USENIX Middleware ’08 Conference Companion, pp. 12–17, (2008)
Manber, U.: Finding similar files in a large file system. In: USENIX Winter 1994 Technical Conference Proceedings, vol. 94, pp. 1–10, (1994)
Xia, Wen, J., Hong, F., Dan, H., Yu: S.: A similarity-locality based near-exact deduplication scheme with low ram overhead and high throughput. In: Proceedings of the 2011 USENIX Annual Technical Conference, pp. 26–30, (2011)
Wallace, G.K.: The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 38(1), 18–34 (1992)
Grgic, S., Kers, K., Grgic, M.: Image compression using wavelets. In: Proceedings of the IEEE International Symposium on Industrial Electronics. ISIE ‘99, vol. 1, pp. 99–104, (1999)
Marcellin, M.W., Gormish, M.J., Bilgin, A., Boliek, M.P.: An overview of JPEG-2000. In: Proceedings DCC 2000. Data Compression Conference, pp. 523–541, (2000)
Tang, Xiaoli, Pearlman, William A: Lossy-to-lossless block-based compression of hyperspectral volumetric data. In: 2004 International Conference on Image Processing. ICIP ’04., vol. 5, pp. 3283–3286. IEEE, (2004)
Lindstrom, Peter: Fixed-rate compressed floating-point arrays. IEEE Trans. Visual Comput. Gr. 20(12), 2674–2683 (2014)
Li, Shaomeng, Jaroszynski, Stanislaw, Pearse, Scott, Orf, Leigh, Clyne, John: VAPOR: a visualization package tailored to analyze simulation data in earth system science. Atmosphere 10(9), 488 (2019)
Ainsworth, Mark, Tugluk, Ozan, Whitney, Ben, Klasky, Scott: Multilevel techniques for compression and reduction of scientific data–quantitative control of accuracy in derived quantities. SIAM J. Sci. Comput. 41(4), A2146–A2171 (2019)
Austin, W., Ballard, G., Kolda, T.G.: Parallel tensor compression for large-scale scientific data. In: 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS), pp. 912–922, (2016)
Ballester-Ripoll, Rafael, Lindstrom, Peter, Pajarola, Renato: TTHRESH: tensor compression for multidimensional visual data. IEEE Trans. Visual Comput. Gr. 26(9), 2891–2903 (2020)
Wu, Qing, Xia, Tian, Yu, Yizhou: Hierarchical tensor approximation of multidimensional images. In: 2007 IEEE International Conference on Image Processing, vol. 4, pp. 49–52. IEEE, (2007)
Jiang, W.W., Kiang, S.Z., Hakim, N.Z., Meadows, H.E.: Lossless compression for medical imaging systems using linear/nonlinear prediction and arithmetic coding. In: ISCAS ‘93, IEEE International Symposium on Circuits and Systems, vol. 1, pp. 283–286, (1993)
Lindstrom, Peter, Isenburg, Martin: Fast and efficient compression of floating-point data. IEEE Trans. Visual Comput. Gr. 12(5), 1245–1250 (2006)
Roelofs, Greg: PNG: The Definitive Guide. O’Reilly Media, Sebastopol (1999)
Bautista Gomez, LA., Cappello, F: Improving floating point compression through binary masks. In: 2013 IEEE International Conference on Big Data, pp. 326–331, (2013)
Di, S., Cappello, F.: Fast error-bounded lossy HPC data compression with SZ. In: 2016 IEEE 30th International Parallel and Distributed Processing Symposium, Chicago, IL, USA, pp. 730–739 (2016). IEEE
Tao, D., Di, S., Chen, Z., Cappello, F.: Significantly improving lossy compression for scientific data sets based on multidimensional prediction and error-controlled quantization. In: 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), pp. 1129–1139, Orlando, FL, USA, (2017). IEEE
Ainsworth, Mark, Tugluk, Ozan, Whitney, Ben, Klasky, Scott: Multilevel techniques for compression and reduction of scientific data–the unstructured case. SIAM J. Sci. Comput. 42(2), A1402–A1427 (2020)
Shuman, D.I., Narang, S.K., Frossard, P., Ortega, A., Vandergheynst, P.: The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 30(3), 83–98 (2013)
Avena, Luca, Castell, Fabienne, Gaudillière, Alexandre, Mélot, Clothilde: Intertwining wavelets or multiresolution analysis on graphs through random forests. Appl. Comput. Harmon. Anal. 48(3), 949–992 (2020)
Coifman, Ronald R., Maggioni, M.: Diffusion wavelets. Appl. Comput. Harmonic Anal. 21(1), 53–94 (2006)
Hammond, David K., Vandergheynst, Pierre, Gribonval, Rémi.: Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 30(2), 129–150 (2011)
Murtagh, Fionn: The Haar wavelet transform of a dendrogram. J. Classif. 24(1), 3–32 (2007)
Lee, Ann B., Nadler, Boaz, Wasserman, Larry: Treelets–an adaptive multi-scale basis for sparse unordered data. Ann. Appl. Stat. 2(2), 435–471 (2008)
Elisha, Oren, Dekel, Shai: Wavelet decompositions of random forests: smoothness analysis, sparse approximation and applications. J. Mach. Learn. Res. 17(1), 6952–6989 (2016)
Salloum, Maher, Fabian, Nathan D., Hensinger, David M., Lee, Jina, Allendorf, Elizabeth M., Bhagatwala, Ankit, Blaylock, Myra L., Chen, Jacqueline H., Templeton, Jeremy A., Tezaur, Irina: Optimal compressed sensing and reconstruction of unstructured mesh datasets. Data Sci. Eng. 3(1), 1–23 (2018)
Bender, EA., Williamson, SG: Lists, decisions and graphs. S. Gill Williamson, (2010)
Gavish, Matan, Nadler, Boaz, Coifman, Ronald R: Multiscale wavelets on trees, graphs and high dimensional data: theory and applications to semi supervised learning. In: ICML, pp. 367–374, (2010)
Shapiro, Jerome M.: Embedded image coding using Zerotrees of wavelet coefficients. IEEE Trans. Signal Process. 41(12), 3445–3462 (1993)
Jarlskog, Cecilia: A recursive parametrization of unitary matrices. J. Math. Phys. 46(10), 103508 (2005)
Shilov, Georgi E., Silverman, Richard A., et al.: Elementary real and complex analysis. Courier Corporation, Chelmsford (1996)
Bentley, Jon Louis: Multidimensional binary search trees used for associative searching. Commun. ACM 18(9), 509–517 (1975)
LeCun, Yann, Bottou, Léon., Bengio, Yoshua, Haffner, Patrick: Gradient-based learning applied to document recognition. Proc. IEEE 86(11), 2278–2324 (1998)
Lepelaars, Carlo: 97% on MNIST with a single decision tree (+ t-SNE). https://www.kaggle.com/code/carlolepelaars/97-on-mnist-with-a-single-decision-tree-t-sne, (November 2019). Version 26
Halko, Nathan, Martinsson, Per-Gunnar., Tropp, Joel A.: Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53(2), 217–288 (2011)
Pedregosa, Fabian, Varoquaux, Gaël., Gramfort, Alexandre, Michel, Vincent, Thirion, Bertrand, Grisel, Olivier, Blondel, Mathieu, Prettenhofer, Peter, Weiss, Ron, Dubourg, Vincent, Vanderplas, Jake, Passos, Alexandre, Cournapeau, David, Brucher, Matthieu, Perrot, Matthieu, Duchesnay, Edouard: Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830 (2011)
Linderman, George C., Rachh, Manas, Hoskins, Jeremy G., Steinerberger, Stefan, Kluger, Yuval: Fast interpolation-based t-SNE for improved visualization of single-cell RNA-seq data. Nat. Methods 16(3), 243–245 (2019)
Poličar, Pavlin G., Stražar, Martin, Zupan, Blaž: openTSNE: a modular Python library for t-SNE dimensionality reduction and embedding. bioRxiv, (2019)
Sattath, Shmuel, Tversky, Amos: Additive similarity trees. Psychometrika 42(3), 319–345 (1977)
Bertsekas, Dimitri: Nonlinear Programming, 2nd edn. Athena Scientific, Belmont (1999)
Funding
This material is based upon work supported by the US Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Scientific Discovery through Advanced Computing (SciDAC) program under the FASTMath institute and the scientific data compression project.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Hierarchical Trees
Lemma 5
Let \((N, E, n_{\texttt {root}})\) be a rooted tree. Define a relation \(\preceq \) on \(N\) by \(n \preceq m\) iff the path from \(n_{\texttt {root}}\) to \(m\) goes through \(n\). \(\preceq \) is a partial order on \(N\).
Proof
We must show that, for \(n, m, o \in N\), (a) \(n \preceq n\), (b) \(n = m\) if \(n \preceq m\) and \(n \succeq m\), and (c) \(n \preceq o\) if \(n \preceq m\) and \(m \preceq o\).
-
(a)
The path from \(n_{\texttt {root}}\) to \(n\) necessarily includes \(n\), so \(n \preceq n\).
-
(b)
Suppose \(n \ne m\). The path from \(n_{\texttt {root}}\) to \(m\) includes \(n\), since \(n \preceq m\). In particular, it contains as a subset a path from \(n_{\texttt {root}}\) to \(n\) not including \(m\). On the other hand, the path from \(n_{\texttt {root}}\) to \(n\) includes \(m\), since \(m \preceq n\). There are therefore two distinct paths from \(n_{\texttt {root}}\) to \(n\), one including \(m\) and one not. This contradicts the definition of a tree.
-
(c)
The path from \(n_{\texttt {root}}\) to \(o\) includes \(m\), since \(m \preceq o\). This path contains a path from \(n_{\texttt {root}}\) to \(m\), which must include \(n\), since \(n \preceq m\). So, the path from \(n_{\texttt {root}}\) to \(o\) also includes \(n\), and so \(n \preceq o\).
\(\square \)
Lemma 6
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. For \(j, j' \in I\), \(\texttt {lca}(j, j')\) is well-defined by Definition 3.
Proof
Let \(C\) be the collection of indices \(\{i \in I: i \preceq j, j'\}\). We claim that \(C\) has a unique element of maximal depth. First, note that \(C\) can have only one element at a particular depth, because \(j\) (or, equally well, \(j'\)) can have only one ancestor at a particular depth. So, it suffices to show the existence of some element of maximal depth.
\(\{\texttt {depth}(i): i \in C\}\) is bounded: if \(i \in C\), then \(\texttt {depth}(i) \le \texttt {depth}(j), \texttt {depth}(j')\), since \(i \preceq j, j'\). Furthermore, \(C\) is nonempty, because \(\texttt {root}\preceq j, j'\) by definition. There therefore exists some element of maximal depth. \(\square \)
Given \(i, i' \in I\), write \(i \parallel i'\) if \(i \npreceq i'\) and \(i' \npreceq i\).
Lemma 7
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. Let \(i, i' \in I\).
-
(a)
\(i \preceq i'\) iff \(\varOmega _{i} \supseteq \varOmega _{i'}\).
-
(b)
\(i \parallel i'\) iff \(\varOmega _{i} \cap \varOmega _{i'} = \emptyset \).
Proof
We begin with a useful intermediate result. Assume the forward direction of (a). Let \(i^{*} = \texttt {lca}(i, i')\). We claim that if \(i^{*} \ne i, i'\), then \(\varOmega _{i} \cap \varOmega _{i'} = \emptyset \). Let \(n = \texttt {depth}(i) - \texttt {depth}(i^{*})\) and \(n' = \texttt {depth}(i') - \texttt {depth}(i^{*})\). As \(i^{*} \prec i, i'\), \(n, n' \ge 1\). \(\texttt {parent}^{n - 1}(\varOmega _{i})\) and \(\texttt {parent}^{n' - 1}(\varOmega _{i'})\) are then well-defined. These sets are children of \(\varOmega _{i^{*}} = \texttt {parent}^{n}(\varOmega _{i}) = \texttt {parent}^{n'}(\varOmega _{i'})\). By the definition of the lowest common ancestor, they must be distinct. By Definition 1 (b), then, they must be disjoint. \(\texttt {parent}^{n - 1}(\varOmega _{i}) \supseteq \varOmega _{i}\) and \(\texttt {parent}^{n' - 1}(\varOmega _{i'}) \supseteq \varOmega _{i'}\) by the forward direction of (a). So, \(\varOmega _{i} \cap \varOmega _{i'}\) is a subset of \(\texttt {parent}^{n - 1}(\varOmega _{i}) \cap \texttt {parent}^{n' - 1}(\varOmega _{i'})\). The latter is empty, so the former must be empty.
-
(a)
Note that the forward direction does not depend on the intermediate result, which assumes it.
 If \(i \preceq i'\), then \(i = \texttt {parent}^{n}(i')\) with \(n = \texttt {depth}(i') - \texttt {depth}(i)\). Definition 1 (b) dictates that each parent contain its children. Applying repeatedly, we have $$\begin{aligned} \varOmega _{i} = \texttt {parent}^{n}(\varOmega _{i'}) \supseteq \cdots \supseteq \texttt {parent}^{1}(\varOmega _{i'}) \supseteq \varOmega _{i'} . \end{aligned}$$
If \(i \preceq i'\), then \(i = \texttt {parent}^{n}(i')\) with \(n = \texttt {depth}(i') - \texttt {depth}(i)\). Definition 1 (b) dictates that each parent contain its children. Applying repeatedly, we have $$\begin{aligned} \varOmega _{i} = \texttt {parent}^{n}(\varOmega _{i'}) \supseteq \cdots \supseteq \texttt {parent}^{1}(\varOmega _{i'}) \supseteq \varOmega _{i'} . \end{aligned}$$ Let \(i^{*} = \texttt {lca}(i, i')\).
Let \(i^{*} = \texttt {lca}(i, i')\).\(i^{*} \preceq i'\), so we are done if \(i = i^{*}\).
So, suppose \(i \ne i^{*}\).
Suppose \(i' = i^{*}\). \(\varOmega _{i^{*}} \supseteq \varOmega _{i}\) by the forward direction. \(\varOmega _{i} \supseteq \varOmega _{i'} = \varOmega _{i^{*}}\) by assumption, so we have \(\varOmega _{i} = \varOmega _{i^{*}}\). This is a violation of Definition 1 (b), which dictates that descendants be strict subsets of their ancestors.
So, suppose \(i' \ne i^{*}\). \(i^{*} \ne i, i'\), so by the intermediate result \(\varOmega _{i} \cap \varOmega _{i'} = \varOmega _{i'} = \emptyset \). By the definition of a hierarchical tree, though, \(\varOmega _{i'}\) must be nonempty.
-
(b)
 Let \(i^{*} = \texttt {lca}(i, i')\). Since \(i \parallel i'\), \(i^{*} \ne i, i'\). The conclusion then follows from the intermediate result.
Let \(i^{*} = \texttt {lca}(i, i')\). Since \(i \parallel i'\), \(i^{*} \ne i, i'\). The conclusion then follows from the intermediate result. Since \(\varOmega _{i'}\) is nonempty by the definition of a hierarchical tree, \(\varOmega _{i} \nsupseteq \varOmega _{i'}\), and so \(i \npreceq i'\) by the forward direction of (a). By the same argument, \(i \nsucceq i'\).
Since \(\varOmega _{i'}\) is nonempty by the definition of a hierarchical tree, \(\varOmega _{i} \nsupseteq \varOmega _{i'}\), and so \(i \npreceq i'\) by the forward direction of (a). By the same argument, \(i \nsucceq i'\).
\(\square \)
Corollary 1
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. Let \(i, i' \in I\). If \(\varOmega _{i} \cap \varOmega _{i'} \ne \emptyset \) and \(\varOmega _{i} \nsubseteq \varOmega _{i'}\), then \(i \preceq i'\).
Proof
\(\varOmega _{i} \cap \varOmega _{i'} \ne \emptyset \) implies \(i \preceq i'\) or \(i \succeq i'\) by Lemma 7(b). \(\varOmega _{i} \nsubseteq \varOmega _{i'}\) implies \(i \nsucceq i'\) by Lemma 7(a). Therefore \(i \preceq i'\). \(\square \)
Lemma 8
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. For \(x, y \in \varOmega \) distinct, \(\texttt {lca}(x, y)\) is well-defined by Definition 3.
Proof
Let \(C\) be the collection of sets \(\{\varOmega _{i}: i \in I \text { and } x, y \in \varOmega _{i}\}\). We claim that \(C\) has a unique element of maximal depth.
We begin with existence. First, note that \(C\) is nonempty: \(\varOmega _{\texttt {root}} \in C\) by Definition 1 (a). By Definition 1 (c), there exists some \(i' \in I\) such that \(\varOmega _{i'} \ni x\) but \(\varOmega _{i'} \not \ni y\). Let \(\varOmega _{i}\) be an element of \(C\). \(\varOmega _{i} \cap \varOmega _{i'} \ne \emptyset \), since both \(\varOmega _{i}\) and \(\varOmega _{i'}\) contain \(x\). On the other hand, since \(\varOmega _{i'}\) does not contain \(y\), \(\varOmega _{i} \not \subseteq \varOmega _{i'}\). By Corollary 1, then, \(i \preceq i'\). In particular, \(\texttt {depth}(i) \le \texttt {depth}(i')\), and so \(\{\texttt {depth}(\varOmega _{i}): \varOmega _{i} \in C\}\) is bounded. As a result, there exists at least one element of maximal depth.
To show uniqueness, suppose there exist two elements of maximal depth, \(\varOmega _{i}\) and \(\varOmega _{i'}\). \(\varOmega _{i} \cap \varOmega _{i'} \ne \emptyset \), since both \(\varOmega _{i}\) and \(\varOmega _{i'}\) contain \(x\) (and \(y\)). By Lemma 7(b), then, \(i \preceq i'\) or \(i' \preceq i\). In either case, since \(\texttt {depth}(i) = \texttt {depth}(i')\), \(i = i'\). The element of maximal depth is therefore unique. \(\square \)
Corollary 2
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. Let \(x, y \in \varOmega \) be distinct, and let \(i \in I\). If \(\varOmega _{i} \ni x, y\), then \(\varOmega _{i} \preceq \texttt {lca}(x, y)\).
Proof
Write \(\varOmega _{i^{*}} = \texttt {lca}(x, y)\). By definition, \(\varOmega _{i^{*}} \ni x, y\). As \(\varOmega _{i} \ni x, y\) by assumption, \(\varOmega _{i}\) and \(\varOmega _{i'}\) intersect, and so \(i \preceq i^{*}\) or \(i^{*} \preceq i\) by Lemma 7(b). If \(i^{*} \prec i\), then \(\texttt {depth}(i^{*}) < \texttt {depth}(i)\), contradicting the definition of the lowest common ancestor. Therefore \(i \preceq i^{*}\). \(\square \)
Lemma 9
Let \(\{\varOmega _{i}: i \in I\}\) be a hierarchical tree. \(d\) is an ultrametric on \(\varOmega \). i.e., for \(x, y, z \in \varOmega \), then \(d(x, z) \le \max {\{d(x, y), d(y, z)\}}\).
One approach to proving Lemma 9 is to realize the hierarchical tree as an ultrametric tree [47] where the edge between \(\varOmega _{i}\) and its child \(\varOmega _{j}\) has weight \([\nu (\varOmega _{i}) - \nu (\varOmega _{j})] / 2\) if \(j \in \texttt {branches}\) and \(\nu (\varOmega _{i}) / 2\) if \(j \in \texttt {leaves}\). \(d\) is then the metric induced by the edge weights. A proof which relies instead on the structure of hierarchical trees follows.
Proof
Let \(x, y, z \in \varOmega \). We must show that (a) \(d\) is nonnegative, (b) \(d\) is symmetric, (c) \(d(x, y) = 0\) iff \(x = y\), and (d) the ultrametric inequality \(d(x, z) \le \max {\{d(x, y), d(y, z)\}}\) holds.
-
(a)
Nonnegativity follows from the nonnegativity of \(\nu \).
-
(b)
Symmetry follows from the symmetry of \(\texttt {lca}\).
-
(c)
If \(x = y\), then \(d(x, y) = 0\) by definition. If \(x \ne y\), then \(d(x, y) = \nu (\texttt {lca}(x, y))\). In the discrete case, \(\texttt {lca}(x, y)\) is nonempty and \(\nu \) is a rescaling of the counting measure, so \(\nu (\texttt {lca}(x, y)) \ne 0\). In the continuous case, \(\texttt {lca}(x, y)\) has nonzero Lebesgue measure and \(\nu \) is a rescaling of the Lebesgue measure, so again \(\nu (\texttt {lca}(x, y)) \ne 0\).
-
(d)
If the points are not distinct or if \(d(x, z) \le d(x, y)\), then the inequality holds automatically. So, suppose the points are distinct and \(d(x, z) > d(x, y)\). Write \(\varOmega _{i^{*}_{xy}} = \texttt {lca}(x, y)\), \(\varOmega _{i^{*}_{xz}} = \texttt {lca}(x, z)\), and \(\varOmega _{i^{*}_{yz}} = \texttt {lca}(y, z)\). We aim to show that \(d(x, z)\) is equal to \(d(y, z)\). As \(d(x, z) = \nu (\varOmega _{i^{*}_{xz}})\) and \(d(y, z) = \nu (\varOmega _{i^{*}_{yz}})\), it suffices to show that \(i^{*}_{xz} = i^{*}_{yz}\).
We claim that \(i^{*}_{xz} \preceq i^{*}_{xy}\). \(\varOmega _{i^{*}_{xz}}\) and \(\varOmega _{i^{*}_{xy}}\) intersect, since both contain \(x\). Because \(\nu \) is a measure, \(\nu (\varOmega _{i^{*}_{xz}}) \le \nu (\varOmega _{i^{*}_{xy}})\) if \(\varOmega _{i^{*}_{xz}} \subseteq \varOmega _{i^{*}_{xy}}\). By assumption, though, \(d(x, z) = \nu (\varOmega _{i^{*}_{xz}}) > \nu (\varOmega _{i^{*}_{xy}}) = d(x, y)\). Therefore \(\varOmega _{i^{*}_{xz}} \nsubseteq \varOmega _{i^{*}_{xy}}\). By Corollary 1, then, \(i^{*}_{xz} \preceq i^{*}_{xy}\). In particular, since \(i^{*}_{xz} \ne i^{*}_{xy}\), \(i^{*}_{xz} \prec i^{*}_{xy}\).
We claim that \(i^{*}_{xz} \preceq i^{*}_{yz}\). \(\varOmega _{i^{*}_{xz}} \ni z\) and \(\varOmega _{i^{*}_{yz}} \ni y\) automatically. Using Lemma 7(a), since \(i^{*}_{xz} \preceq i^{*}_{yz}\), \(\varOmega _{i^{*}_{xz}} \supseteq \varOmega _{i^{*}_{yz}}\), As a result, \(\varOmega _{i^{*}_{xz}} \ni y, z\), and so \(i^{*}_{xz} \preceq i^{*}_{yz}\) by Corollary 2.
We claim that \(\varOmega _{i^{*}_{xy}} \not \ni z\). \(\varOmega _{i^{*}_{xy}} \ni x\); if in addition \(\varOmega _{i^{*}_{xy}} \ni z\), then \(i^{*}_{xy} \preceq i^{*}_{xz}\) by Corollary 2. But we know that \(i^{*}_{xz} \prec i^{*}_{xy}\), so in fact \(\varOmega _{i^{*}_{xy}} \not \ni z\).
We claim that \(i^{*}_{yz} \preceq i^{*}_{xy}\). \(\varOmega _{i^{*}_{yz}}\) and \(\varOmega _{i^{*}_{xy}}\) intersect, since both contain \(y\). \(\varOmega _{i^{*}_{yz}} \ni z\), but \(\varOmega _{i^{*}_{xy}} \not \ni z\), as shown in the previous paragraph. That is, \(\varOmega _{i^{*}_{yz}} \nsubseteq \varOmega _{i^{*}_{xy}}\). By Corollary 1, then, \(i^{*}_{yz} \preceq i^{*}_{xy}\).
We claim that \(i^{*}_{yz} \preceq i^{*}_{xz}\). \(\varOmega _{i^{*}_{yz}} \ni y\) automatically. Because \(i^{*}_{yz} \preceq i^{*}_{xy}\) and \(\varOmega _{i^{*}_{xy}} \ni x\), \(\varOmega _{i^{*}_{yz}} \ni x\). By Corollary 2, then, \(i^{*}_{yz} \preceq i^{*}_{xz}\).
We conclude that \(i^{*}_{xz} = i^{*}_{yz}\), so that the ultrametric inequality holds.
\(\square \)
Discrete Hierarchical Trees
Lemma 10
Let \(\{\varOmega _{i}: i \in I\}\) be a discrete hierarchical tree. \(\left| \varOmega _{i}\right| = 1\) for all \(i \in \texttt {leaves}\).
Proof
Let \(i \in \texttt {leaves}\), and suppose \(\left| \varOmega _{i}\right| \ne 1\). \(\varOmega _{i}\) is nonempty, so \(\left| \varOmega _{i}\right| > 1\). In particular, there exist distinct \(x, y \in \varOmega _{i}\). By Definition 1 (c), there exists some \(i' \in I\) with \(x \in \varOmega _{i'}\) and \(y \not \in \varOmega _{i'}\). \(\varOmega _{i}\) and \(\varOmega _{i'}\) have nonempty intersection, since both contain \(x\). On the other hand, \(\varOmega _{i'}\) is not a superset of \(\varOmega _{i}\), since the latter contains \(y\) and the former does not. So, by Corollary 1, \(i \preceq i'\). In particular, \(\texttt {children}(i)\) is not empty. This contradicts the inclusion of \(i\) in \(\texttt {leaves}\). \(\square \)
Lemma 11
Let \(\{\varOmega _{i}: i \in I\}\) be a discrete hierarchical tree. For all \(x \in \varOmega \), there exists some \(i \in \texttt {leaves}\) such that \(\varOmega _{i} \ni x\).
Proof
Suppose there exists some \(x \in \varOmega \) such that there exists no \(i \in \texttt {leaves}\) with \(\varOmega _{i} \ni x\). If \(i \in I\) satisfies \(\varOmega _{i} \ni x\), then, \(i \not \in \texttt {leaves}\), and so \(\texttt {children}(i)\) is nonempty. In particular, there exists \(j \in \texttt {children}(i)\) with \(\varOmega _{j} \ni x\), by Definition 1 (b). Observe that \(\texttt {depth}(\varOmega _{j}) = \texttt {depth}(\varOmega _{i}) + 1\). That is, for all \(i \in I\) with \(\varOmega _{i} \ni x\), there exists some \(j \in I\) with \(\varOmega _{j} \ni x\) and \(\texttt {depth}(\varOmega _{j}) = \texttt {depth}(\varOmega _{i}) + 1\). Furthermore, there does exist at least one \(i \in I\) (namely, \(\texttt {root}\)) with \(\varOmega _{i} \ni x\), by Definition 1 (a). The set \(\{\texttt {depth}(\varOmega _{i}): i \in I \text { and } \varOmega _{i} \ni x\}\) is therefore unbounded.
We now show that \(\{\texttt {depth}(\varOmega _{i}): i \in I\}\) is in fact bounded, so that no such \(x \in \varOmega \) exists. We claim that \(\texttt {depth}(\varOmega _{i}) \le \left| \varOmega \right| - \left| \varOmega _{i}\right| \) for all \(i \in I\). If \(i = \texttt {root}\), then
since \(\varOmega _{\texttt {root}} = \varOmega \) by Definition 1 (a). Otherwise, observe that \(\left| \varOmega _{i}\right| \le \left| \texttt {parent}(\varOmega _{i})\right| - 1\) by Definition 1 (b). Applying this inequality repeatedly, we have
for \(n \le \texttt {depth}(\varOmega _{i})\). Setting \(n = \texttt {depth}(\varOmega _{i})\), we obtain \(\left| \varOmega _{i}\right| \le \left| \varOmega \right| - \texttt {depth}(\varOmega _{i})\) (i.e., \(\texttt {depth}(\varOmega _{i}) \le \left| \varOmega \right| - \left| \varOmega _{i}\right| \)), since then \(\texttt {parent}^{n}(\varOmega _{i}) = \varOmega _{\texttt {root}} = \varOmega \). As a result, \(\{\texttt {depth}(\varOmega _{i}): i \in I\}\) is bounded, and so there exists some \(i \in \texttt {leaves}\) with \(\varOmega _{i} \ni x\) for any \(x \in \varOmega \). \(\square \)
Lemmas for Remark 4
Lemma 12
Let \(\{\varOmega _{i}: i \in I\}\) be a discrete hierarchical tree. Let \(i \in \texttt {branches}\). \(\texttt {nc}(i) = {\underline{B}}^{-1}\) iff \(\nu (\varOmega _{j}) = {\underline{B}} \nu (\varOmega _{i})\) for all \(j \in \texttt {children}(i)\).
Proof
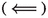 :
:-
Because \(\nu \) is a measure and \(\varOmega _{i}\) is the disjoint union of its children,
$$\begin{aligned} \nu (\varOmega _{i}) = \sum _{j = 1}^{\texttt {nc}(i)} \nu (\varOmega _{j}) = \sum _{j = 1}^{\texttt {nc}(i)} {\underline{B}} \nu (\varOmega _{i}) = {\underline{B}} \hspace{0.83328pt}\texttt {nc}(i) \hspace{0.83328pt}\nu (\varOmega _{i}) . \end{aligned}$$Therefore, \(\texttt {nc}(i) = {\underline{B}}^{-1}\).
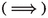 :
:-
By the definition of \({\underline{B}}\), \(\nu (\varOmega _{j}) \ge {\underline{B}} \nu (\varOmega _{i})\) for all \(j \in \texttt {children}(i)\). The reverse inequality also holds: taking \(\varOmega _{1}\) as an example,
$$\begin{aligned} \nu (\varOmega _{1})= & {} \nu (\varOmega _{i}) - \sum _{j = 2}^{\texttt {nc}(i)} \nu (\varOmega _{j})\\\le & {} \nu (\varOmega _{i}) - {\underline{B}} \hspace{0.83328pt}[\texttt {nc}(i) - 1] \hspace{0.83328pt}\nu (\varOmega _{i})\\ = {\underline{B}} \nu (\varOmega _{i}). \end{aligned}$$since \(\texttt {nc}(i) = {\underline{B}}^{-1}\). As a result, \(\nu (\varOmega _{1}) = {\underline{B}} \nu (\varOmega _{i})\), and the same holds for the other children of \(\varOmega _{i}\).
\(\square \)
Lemma 13
Let \(\{\varOmega _{i}: i \in I\}\) be a discrete hierarchical tree. If \(\psi _{i, m}\) is a wavelet of a Haar-like basis for \(V\), then
Furthermore, this bound is tight.
Proof
For \(i \in \texttt {branches}\), denote by \(V_{i}\) the linear span of \(\{{\textbf {1}}_{\varOmega _{j}}: j \in \texttt {children}(i)\}\) and by \(W_{i}\) the space \(V_{i} \cap {\textbf {1}}_{\varOmega _{i}}^{\perp }\). By Definition 2, if \(\psi _{i, m}\) is a wavelet of a Haar-like basis, then \(\psi _{i, m}\) has norm \(1\) and \(\psi _{i, m} \in W_{i}\). So, it suffices to show that Eq. 5 holds for unit norm functions in \(W_{i}\), that the Eq. 5 is tight for such functions, and that given such a function we can construct a Haar-like basis containing it.
The third claim is straightforward to prove. Take \(i^{*} \in \texttt {branches}\) and let \(\psi \in W_{i^{*}}\) have norm \(1\). For \(i \in \texttt {branches}{\setminus } \{i^{*}\}\), construct an orthonormal basis \(\mathcal {B}_{i}\) for \(W_{i}\). Similarly, construct for \(W_{i^{*}}\) an orthonormal basis \(\mathcal {B}_{i^{*}}\) containing \(\psi \). This can be done because \(\psi \) has norm \(1\) and is contained in \(W_{i^{*}}\). Let \(\mathcal {B}\) denote the collection \(\{{\textbf {1}}_{\varOmega }\} \cup \bigcup _{i \in \texttt {branches}} \mathcal {B}_{i}\). We claim that \(\mathcal {B}\) is a Haar-like basis for \(V\). The only condition of Definition 2 that isn’t immediate is the orthogonality of \(\mathcal {B}\). Let \(\psi _{i} \in \mathcal {B}_{i} \subset \mathcal {B}\). We claim that \(\psi _{i}\) is orthogonal to every other function in \(\mathcal {B}\). This holds automatically for \({\textbf {1}}_{\varOmega }\) (by the definition of \(W_{i}\)) and the other members of \(\mathcal {B}_{i}\) (since \(\mathcal {B}_{i}\) is orthogonal). The remaining case is \(\psi _{i'} \in \mathcal {B}_{i'} \subset \mathcal {B}\) with \(i \ne i'\). If \(i \parallel i'\), then \(\varOmega _{i}\) and \(\varOmega _{i'}\) are disjoint by Lemma 7(b). \(\varOmega _{i} \supseteq {{\,\textrm{supp}\,}}(\psi _{i})\) and \(\varOmega _{i'} \supseteq {{\,\textrm{supp}\,}}(\psi _{i'})\), so \(\psi _{i}\) and \(\psi _{i'}\) are then orthogonal. Otherwise, without loss of generality, \(i \preceq i'\). \(i \ne i'\), so in fact \(i \prec i'\). In particular, there exists some \(j \in \texttt {children}(i)\) such that \(j \preceq i'\). \(\psi _{i}\) is constant on \(\varOmega _{j}\) by Definition 1 (b) and the definition of \(V_{i}\), and \(\psi _{i'} \perp {\textbf {1}}_{\varOmega _{i'}}\) by the definition of \(W_{i'}\). \(\varOmega _{j} \supseteq \varOmega _{i'}\) by Lemma 7(a), so again \(\psi _{i} \perp \psi _{i'}\).
We now return to the claim that Eq. 5 holds and is tight for unit norm functions in \(W_{i}\). We begin by bounding the value taken by such functions on a single child of \(\varOmega _{i}\). Let \(i^{*} \in \texttt {branches}\), and let \(\varOmega _{1}, \dotsc , \varOmega _{k}\) be an enumeration of \(\texttt {children}(\varOmega _{i^{*}})\). We seek a solution to the *

\(V_{i^{*}}\) is in bijection with \(\mathbb {R}^{k}\), so * can be reformulated as a constrained optimization problem over Euclidean space. Define \(T :V_{i^{*}} \rightarrow \mathbb {R}^{k}\) by \(T(\phi ) = (\phi (\varOmega _{1}), \dotsc , \phi (\varOmega _{k}))\). Observe that \(T\) is a bijection. Let the objective function \(f :\mathbb {R}^{k} \rightarrow \mathbb {R}\) be given by \(f(x) = -x_{1}\), so that \(f(T(\psi )) = -\psi (\varOmega _{1})\). Next we must translate each constraint on \(\psi \in V_{i^{*}}\) to a constraint on \(T(\psi ) \in \mathbb {R}^{k}\). Define \(h_{1}, h_{2} :R^{k} \rightarrow \mathbb {R}\) by \(h_{1}(x) = \sum _{i = 1}^{k} A_{i} x_{i}\) and \(h_{2}(x) = -1 + \sum _{i = 1}^{k} A_{i} x_{i}^{2}\).
- *.1:
-
Trivially, *.1 holds iff \(T(\psi ) \in \mathbb {R}^{k}\).
- *.2:
-
Write \(A_{1}, \dotsc , A_{k}\) for the measures \(\nu (\varOmega _{1}), \dotsc , \nu (\varOmega _{k})\) and \(A\) for the sum \(A_{1} + \cdots + A_{k}\). The inner product of \(\psi \) and \({\textbf {1}}_{\varOmega _{i^{*}}}\) is given by
$$\begin{aligned} \langle \psi , {\textbf {1}}_{\varOmega _{i^{*}}}\rangle = \sum _{i = 1}^{k} \nu (\varOmega _{i}) \hspace{0.83328pt}\psi (\varOmega _{i}) = \sum _{i = 1}^{k} A_{i} T(\psi )_{i} = h_{1}(T(\psi )) . \end{aligned}$$*.2 then holds iff \(h_{1}(T(\psi )) = 0\).
- *.3:
-
The inner product of \(\psi \) with itself is given by
$$\begin{aligned} \langle \psi , \psi \rangle = \sum _{i = 1}^{k} \nu (\varOmega _{i}) \hspace{0.83328pt}\psi (\varOmega _{i}) \hspace{0.83328pt}\psi (\varOmega _{i}) = \sum _{i = 1}^{k} A_{i} T(\psi )_{i}^{2} = h_{2}(T(\psi )) - 1 . \end{aligned}$$*.3 then holds iff \(h_{2}(T(\psi )) = 0\).
* can therefore be rewritten

The Lagrangian function \(L_{f} :\mathbb {R}^{k} \times \mathbb {R}^{2} \rightarrow \mathbb {R}\) is given by
Its gradient with respect to \(x\) is given by
We will use the method of Lagrange multipliers to find the global minimum of \(\dagger \). First, we will apply a necessary condition to find two candidate local minima. Then, we will apply a sufficient condition to show that one of the two is the global minimum.
The gradients of the feasibility constraints are given by
Let \(\Im \) denote the feasible set of \(\dagger \). We claim that \(\nabla h_{1}\) and \(\nabla h_{2}\) are linearly independent on \(\Im \). Let \(x \in \Im \). Each of \(A_{1}, \dotsc , A_{k}\) is positive. So, in order for \(h_{1}(x)\) to be zero, \(x\) must either be \({\textbf {0}}\) or have at least one positive and at least one negative component. \(h_{2}({\textbf {0}}) = -1\), so \(x\) cannot be \({\textbf {0}}\). \(x\) therefore has at least one positive and at least one negative component. \(\nabla h_{2} (x)\) therefore likewise has at least one positive and at least one negative component. All the components of \(\nabla h_{1} (x)\), though, are positive. In particular, \(\nabla h_{1} (x)\) and \(\nabla h_{2} (x)\) are linearly independent.
Suppose that \(x^{*}\) is a local minimum of \(\dagger \). Because \(f\), \(h_{1}\), and \(h_{2}\) are continuously differentiable and \(\nabla h_{1}\) and \(\nabla h_{2}\) are linearly independent on \(\Im \), there exist Lagrange multipliers \(\lambda ^{*} \in \mathbb {R}^{2}\) such that the gradient with respect to \(x\) of the Lagrangian at \((x^{*}, \lambda ^{*})\) is zero [48, Proposition 3.1.1]. That is,
If \(\lambda ^{*}_{2} = 0\), then \(\lambda ^{*}_{1} = 0\) by Eq. 7, contradicting Eq. 6. \(\lambda ^{*}_{2}\) is therefore nonzero and so Eq. 7 can be simplified to \(x^{*}_{i} = -\lambda ^{*}_{1} / {2 \lambda ^{*}_{2}}\) for all \(2 \le i \le k\). Substituting into \(\dagger \).2, we obtain an expression for \(x^{*}_{1}\):
We next solve for \(\lambda ^{*}_{1}\) using Eq. 6:
Next, apply \(\dagger \).3.
We will write \(\lambda ^{*}_{+, 2}\) for the positive square root and \(\lambda ^{*}_{-, 2}\) for the negative square root. \(x^{*}_{+}\) and \(x^{*}_{-}\) will denote the corresponding candidate local minima. Equations 7 and 10 together yield an expression for \(x^{*}_{\pm , i}\): for \(2 \le i \le k\),
Similarly, Eqs. 8, 9, and 10 yield an expression for \(x^{*}_{\pm , 1}\):
The candidate local minima of \(\dagger \) are then
We claim that \(x^{*}_{+}\) is a local minimum with Lagrange multipliers \((\lambda ^{*}_{1}, \lambda ^{*}_{+, 2})\). Observe that \(f\), \(h_{1}\), and \(h_{2}\) are twice continuously differentiable. As shown above, \(\nabla _{x} L_{f} (x^{*}_{+}, (\lambda ^{*}_{1}, \lambda ^{*}_{+, 2}))= 0\). Because \(x^{*}_{+} \in \),
The Hessian with respect to \(x\) of the Lagrangian is given by
Each of \(A_{1}, \dotsc , A_{k}\) is positive, so \(\nabla ^{2}_{x x} L_{f}\) is symmetric positive definite at \((x, \lambda )\) if \(\lambda _{2} > 0\). \(\lambda ^{*}_{+, 2} > 0\), so \(x^{*}_{+}\) is a local minimum of \(\dagger \) [48, Proposition 3.2.1].
Denote by (\(\ddagger \)) the problem of minimizing \(-f\) with the constraints of \(\dagger \). We claim that \(x^{*}_{-}\) is a local minimum of (\(\ddagger \)) with Lagrange multipliers \((-\lambda ^{*}_{1}, -\lambda ^{*}_{-, 2})\). \(-f\), \(h_{1}\), and \(h_{2}\) are twice continuously differentiable. Let \(L_{-f} :\mathbb {R}^{k} \times \mathbb {R}^{2} \rightarrow \mathbb {R}\) be the Lagrangian function:
\(L_{-f}\) is related to the Lagrangian \(L_{f}\) of \(\dagger \) as follows:
As a result,
Since \(x^{*}_{-} \in \Im \),
Because \(\nabla _{x} L_{-f} (x, \lambda ) = -\nabla _{x} L_{f} (x, -\lambda )\), \(\nabla ^{2}_{x x} L_{-f} (x, \lambda ) = -\nabla ^{2}_{x x} L_{f} (x, -\lambda )\). Referring to Eq. 11, we see that \(\nabla ^{2}_{x x} L_{f}\) is symmetric negative definite at \((x^{*}_{-}, (\lambda ^{*}_{1}, \lambda ^{*}_{-, 2}))\), since \(\lambda ^{*}_{-, 2} < 0\). \(\nabla ^{2}_{x x} L_{-f}\) is then symmetric positive definite at \((x^{*}_{-}, (-\lambda ^{*}_{1}, -\lambda ^{*}_{-, 2}))\). We conclude that \(x^{*}_{-}\) is a local minimum of (\(\ddagger \))[48, Proposition 3.2.1].
As a local minimum of (\(\ddagger \)), \(x^{*}_{-}\) is a local maximum of \(\dagger \). In particular, \(x^{*}_{+}\) is the only local minimum of the latter \(\dagger \). \(\Im \) is compact, so \(x^{*}_{+}\) must be the global minimum. The global minimum of * is therefore the function \(\psi ^{*} \in V_{i^{*}}\) defined by
If \(A_{1} \le A / 2\), then
Eq. 5 is therefore respected in this case. The Eq. 5 is tight if \(A_{1}\) is minimal. If instead \(A_{1} \ge A / 2\), then
\(A - A_{1} \ge \min _{1 \le i \le k} A_{i}\), so the Eq. 5 again holds. The Eq. 5 is tight if \(\varOmega _{i^{*}}\) has two children, of which \(\varOmega _{1}\) is the larger, so that \(A - A_{1} = A_{2} = \min _{1 \le i \le k} A_{i}\). \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Archibald, R., Whitney, B. Haar-Like Wavelets on Hierarchical Trees. J Sci Comput 99, 3 (2024). https://doi.org/10.1007/s10915-024-02466-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02466-9





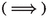 If
If 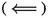 Let
Let  Let
Let  Since
Since  :
: :
: