Transferable Neural Networks for Partial Differential Equations

Abstract

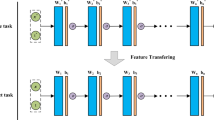
Transfer learning for partial differential equations (PDEs) is to develop a pre-trained neural network that can be used to solve a wide class of PDEs. Existing transfer learning approaches require much information about the target PDEs such as its formulation and/or data of its solution for pre-training. In this work, we propose to design transferable neural feature spaces for the shallow neural networks from purely function approximation perspectives without using PDE information. The construction of the feature space involves the re-parameterization of the hidden neurons and uses auxiliary functions to tune the resulting feature space. Theoretical analysis shows the high quality of the produced feature space, i.e., uniformly distributed neurons. We use the proposed feature space as the pre-determined feature space of a random feature model, and use existing least squares solvers to obtain the weights of the output layer. Extensive numerical experiments verify the outstanding performance of our method, including significantly improved transferability, e.g., using the same feature space for various PDEs with different domains and boundary conditions, and the superior accuracy, e.g., several orders of magnitude smaller mean squared error than the state of the art methods.

Appendices

Appendix

Definitions of the PDEs in Sect. 3.2

The definitions of the PDEs considered in Sect. 3.2 are given below.

The Poisson’s equation considered in case $(C_1)$–$(C_5)$ is defined by

$$\begin{aligned} \varDelta u(\varvec{x}) = f(\varvec{x}), \end{aligned}$$

(21)

where the exact solution for the 2D settings, i.e., $(C_1)$–$(C_4)$, is $u(\varvec{x}) = \sin (2\pi x_1)\sin (2\pi x_2)\sin (2\pi x_3)$, and the exact solution for the 3D setting, i.e., $(C_5)$, is $u(\varvec{x}) = \sin (2\pi x_1)\sin (2\pi x_2)$. The forcing term $f(\varvec{x})$ can be obtained by applying the Laplacian operator to the exact solution. The domains of computation for $(C_1)$–$(C_5)$ are given below:

($C_1$):

A 2D rectangular domain: $\varOmega = [-1,1]^2$;

($C_2$):

A 2D circular domain: $\varOmega = B_1(\varvec{0})$;

($C_3$):

A 2D L-shaped domain: $\varOmega = [-1,1]^2 \backslash [0,1]^2$;

($C_4$):

A 2D annulus domain: $\varOmega = B_1(\varvec{0}) \backslash B_{0.5}(\varvec{0})$;

($C_5$):

A 3D box domain $\varOmega = [-1,1]^3$.

We consider the Dirichlet boundary condition in the experiments, where the boundary condition $g(\varvec{x})$ in Eq. (1) can be obtained by restricting the exact solution on the boundary of $\varOmega$. Figure 7 illustrates how to place the domains of computation into the unit ball for the test cases $(C_1)$ – $(C_4)$ to use the transferable feature space.

Fig. 7

Illustration of how to place the domains of computation for the test cases $(C_1)$ – $(C_4)$ in Sect. 3.2 into the unit ball to use the transferable feature space to solve the Poisson’s equation in different domains

The steady-state Navier–Stokes equation considered in case $(C_6)$ is defined by:

$$\begin{aligned} \begin{aligned} {\varvec{u}} \cdot \nabla {\varvec{u}} + \nabla p - \nu \varDelta {\varvec{u}}&= 0\\ \nabla \cdot {\varvec{u}}&= 0 \end{aligned} \end{aligned}$$

where $\varvec{u} = (v_1, v_2)$ represents the velocity, p is the pressure, $\nu$ is the viscosity and $Re = 1/\nu$ is the Reynold’s number. The domain of computation is $\varOmega = [-0.5,1]\times [-0.5,1.5]$ with Direchilet boundary condition. We consider the Kovasznay flow problem that has the exact solution, i.e.,

$$\begin{aligned} v_1(x_1, x_2)&= 1 - e^{\lambda x_1} \cos (2 \pi x_2)\end{aligned}$$

(22)

$$\begin{aligned} v_2(x_1, x_2)&= \frac{\lambda }{2 \pi } e^{\lambda x_1} \sin (2 \pi x_2)\end{aligned}$$

(23)

$$\begin{aligned} p(x_1, x_2)&= \frac{1}{2} (1 - e^{2 \pi x_1} ) \end{aligned}$$

(24)

where $\lambda = \frac{1}{2\nu } - \sqrt{\frac{1}{4\nu ^2} + 4\pi ^2}$ and the Reynold’s number is set to 40. The Dirichlet boundary condition can be obtained by restricting the exact solution on the boundary of $\varOmega$.

The Fokker-Planck equation considered in case $(C_7)$ and $(C_8)$ is defined by

$$\begin{aligned} \begin{aligned} \frac{\partial u(t,{\varvec{x}})}{\partial t} + b(t, \varvec{x})\sum _{i=1}^{d}\frac{\partial u}{\partial x_{i}}(t,{\varvec{x}}) + \frac{\sigma ^2}{2}\sum _{i,j=1}^{d} \frac{\partial ^2 u}{\partial x_{i}x_{j}}(t,{\varvec{x}})&= 0,\\ u(0,\varvec{x})&= g(\varvec{x}), \end{aligned} \end{aligned}$$

(25)

where the coefficients $b(t,\varvec{x})$, $\sigma$, $g(\varvec{x})$ and the exact solutions are

• $(C_7)$: $b(x,t) = 2 \cos {(3 t)}$, $\sigma =0.3$, $u(x,0) = p(x; 0, 0.4^2)$ and $u(x,t) = p(x; \frac{2\sin { (3t)}}{3}, 0.4^2 + t 0.3^2)$, where $p(x; \mu , \varSigma )$ denote the Gaussian density with mean $\mu$ and variance $\varSigma$.

• $(C_8)$: $b(x_1, x_2, t) = [\sin (2\pi t), \cos (2\pi t)]^T$, $\sigma =0.3$, $u(x_1, x_2, 0) = p(x; [0,0], 0.4^2 \textbf{I}_2)$, and $u(x_1, x_2, t) = p(x; [-\frac{\cos (2\pi t)-1}{2\pi }, \frac{\sin (2\pi t)}{2\pi } ], (0.4^2 + t 0.3^2)\textbf{I}_2)$, where $p(x; \mu , \varSigma )$ is the Gaussian density with mean $\mu$ and variance $\varSigma$.

The wave equation considered in case $(C_9)$ is defined by

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 u}{\partial t^2} = c\frac{\partial ^2 u}{\partial x^2},\;\; x \in [0,1], t\in [0,2] \\&u(x,0) = \sin (4\pi x)\\&u(0,t) = u(1,t) \end{aligned} \end{aligned}$$

where $c = 1/(16\pi ^2)$. The domain of computation is $\varOmega = [0,1] \times [0,2]$; the exact solution is

$$\begin{aligned} u(x,t) = \frac{1}{2} \left( \sin (4\pi x + t) + \sin (4\pi x - t)\right) . \end{aligned}$$

Setup of the Experiments in Sect. 3.2

We specify the setup for the test cases $(C_1)$ to $(C_9)$ as follows:

• $(C_1)$: We evaluate the loss function in Eq. (19) on a $50 \times 50$ uniform mesh in $\varOmega = [-1,1]^2$, i.e., $J_1 = 2500$ in Eq. (19), and on 200 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 200$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_2)$: We evaluate the loss function in Eq. (19) on a $50 \times 50$ uniform mesh in $\varOmega = [-1,1]^2$ and mask off the grid points outside the domain $\varOmega = B_1(\varvec{0})$, i.e., $J_1 = 1876$, and evaluate the boundary loss on 200 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 200$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_3)$: We evaluate the loss function in Eq. (19) on a $50 \times 50$ uniform mesh in $\varOmega = [-1,1]^2$ and mask off the grid points outside the domain $\varOmega = [-1,1]^2 \backslash [0,1]^2$, i.e., $J_1 = 1875$, and evaluate the boundary loss on 200 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 200$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_4)$: We evaluate the loss function in Eq. (19) on a $50 \times 50$ uniform mesh in $\varOmega = [-1,1]^2$ and mask off the grid points outside the domain $\varOmega = B_1(\varvec{0}) \backslash B_{0.5}(\varvec{0})$, i.e., $J_1 = 1408$, and evaluate the boundary loss on 200 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 200$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_5)$: We evaluate the loss function in Eq. (19) on a 10,000 uniformly distributed random locations in $\varOmega = [-1,1]^3$, i.e., $J_1 = 10000$, and evaluate the boundary loss on 2400 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 2400$, 400 points on each side of $\varOmega$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_6)$: We evaluate the loss function in Eq. (19) on a $50 \times 50$ uniform mesh in $\varOmega = [-0.5,1]\times [-0.5,1.5]$, i.e., $J_1 = 2500$ in Eq. (19), and on 200 uniformly distributed points on $\partial \varOmega$ (50 points on each side of the box), i.e., $J_2 = 200$. We use Pichard iteration to handle the nonlinearity. Specifically, the residual loss is defined by

  $$\begin{aligned} loss = {\varvec{u}_\text {NN}^{k-1}} \cdot \nabla {\varvec{u}_\text {NN}^{k}} + \nabla p_\text {NN}^k - \nu \varDelta {\varvec{u}_\text {NN}^{k}}, \end{aligned}$$

  where k is the Picard iteration number. In the k-th iteration, the nonlinear term ${\varvec{u}_\text {NN}^{k-1}} \cdot \nabla {\varvec{u}_\text {NN}^{k}}$ becomes linear due to the use of ${\varvec{u}_\text {NN}^{k-1}}$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_7)$: The domain of computation is $(t,x) \in [0,1]\times [-2,2]$. We evaluate the loss function on a 50 (time) $\times$ 200 (space) = 10,000 grid points in the domain $\varOmega$. We use the absorbing boundary condition in the spatial domain. We have a total of 3000 samples on the boundary of $\varOmega$, i.e., 1000 samples for each of u(x, 0), u(2, t) and $u(-2,t)$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_8)$: The domain of computation is $t \in [0,1]$ and $(x_1,x_2) \in [-2,2]^2$. We evaluate the loss function on 10,000 uniformly selected random points in the domain $\varOmega$. We use the absorbing boundary condition in the spatial domain. In terms of samples on the boundary, we have $50 \times 50 = 2500$ grid points for the initial condition $u(x_1, x_2, 0)$, $20(\text {time}) \times 50(\text {space}) = 1000$ grid points for each of $u(\pm 2, x_2, t)$ and $u(x_1,\pm 2, t)$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

• $(C_9)$: We evaluate the loss function in Eq. (19) on $50\text {(time)} \times 100\text {(space)} = 2500$ grid points in domain, i.e., $J_1 = 10,000$, and evaluate the boundary loss on 1000 uniformly distributed points on $\partial \varOmega$, i.e., $J_2 = 1500$, 500 points on each side of $\varOmega$. After solving the least squares problem, we compute the error, i.e., the results shown in Fig. 5 on a test set of 10,000 uniformly distributed random locations in $\varOmega$.

We use the standard least squares solver torch.linalg.lstsq in Pytorch to solve all the least squares problems. Our code is implemented using Pytorch on a workstation with an NVIDIA Tesla V100 GPU.

Setup for PINN. The code for PINN is included in the supplementary material. For each test case, PINN uses exactly the same setting as TransNet, including network architecture, loss function, and data, to ensure a fair comparison. In terms of training, we set the learning rate to 0.001 with a decrease factor of 0.7 every 1000 epochs. We first use Adam optimizer to train the neural networks for 5000 epochs, which gives us the results in Fig. 5 labeled by “PINN:Adam”. Then we continue training the network using LBFGS for another 200 iterations, which gives us the results in Fig. 5 labeled by “PINN:Adam+BFGS”.

Setup for the random feature models. The random feature model uses exactly the same setting as TransNet, including network architecture, loss function, and data, to ensure a fair comparison. The parameters $\{\varvec{w}_m, b_m\}_{m=1}^M$ are determined by the default initialization methods in Pytorch, and the parameters in the output layer are obtained by the least squares solver torch.linalg.lstsq in Pytorch.