Pricing Discretely Monitored Asian Options Under Regime-Switching and Stochastic Volatility Models with Jumps

Abstract

This paper proposes a unified approach for pricing discretely monitored floating and fixed strike Asian options under a broad class of regime-switching and stochastic volatility models with jumps. The randomness in volatility can be either characterized by regime switching among discrete market states, a diffusive stochastic variance process correlated with the underlying asset price, or a random time change applied to a background process. Our approach can be applied to price financial derivatives with exotic averaging type payoffs, which goes beyond most of the existing frameworks in terms of versatility. Our success relies on the adoption of the change-of-measure approach and a dimension reduction technique. Specifically, we construct new backward recursions for Asian options that include floating and fixed strike payoffs under a wide range of regime-switching and stochastic volatility models with jumps. The Fourier-cosine series expansion and Gauss quadrature rule are applied to solve the backward recursions. The exponential convergence rate of our approach is proven theoretically and verified numerically via comprehensive error analysis. Extensive numerical experiments demonstrate that our approach is reliable, accurate, and efficient.

Appendices

Proof of Proposition 3.1

To prove Proposition 3.1, we need an extension of Lemma 3.1, the details of which are stated as follows:

Lemma A.1

Under regime-switching Lévy models, SV models with Lévy jumps, and time-changed Lévy models considered in Sect. 2, for any $n\in {\mathbb {N}}$ and $0\le s_0<\cdots <s_n$, under the probability measure $\overline{{\mathbb {Q}}}$ specified in Eq. (3.3), the joint distribution of $(Y_{s_1}-Y_{s_0},\ldots ,Y_{s_n}-Y_{s_0})$ given $(Y_{s_0},v_{s_0})$ depends only on $v_{s_0}$.

Proof

Under $\overline{{\mathbb {Q}}}$, the joint characteristic function of $(Y_{s_1}-Y_{s_0},\ldots ,Y_{s_n}-Y_{s_0})$ conditional on $(Y_{s_0},v_{s_0})$ satisfies

$$\begin{aligned} \overline{{\mathbb {E}}}\big [e^{\textrm{i}\sum _{k=1}^{n}w_k(Y_{s_k}-Y_{s_0})}\,\big |\,Y_{s_0}, v_{s_0}\big ]&=~e^{-(r-q)(s_n-s_0)}{\mathbb {E}}\big [e^{Y_{s_n}-Y_{s_0}+\textrm{i}\sum _{k=1}^{n}w_k(Y_{s_k}-Y_{s_0})}\,\big |\,Y_{s_0}, v_{s_0}\big ]\nonumber \\&=~e^{-(r-q)(s_n-s_0)}{\mathbb {E}}\big [e^{\textrm{i}\sum _{k=1}^{n}{\overline{w}}_k(Y_{s_{k}}-Y_{s_{0}})}\,\big |\,Y_{s_0}, v_{s_0}\big ], \end{aligned}$$

(A.1)

where ${\overline{w}}_n=w_n-\textrm{i}$ and ${\overline{w}}_k=w_k$ for $k=1,\ldots ,n-1$ when $n\ge 2$. Applying Lemma 3.1, we can conclude that under $\overline{{\mathbb {Q}}}$, the joint characteristic function of $(Y_{s_1}-Y_{s_0},\ldots ,Y_{s_n}-Y_{s_0})$ conditional on $(Y_{s_0},v_{s_0})$ depends only on $v_{s_0}$. This completes the proof. $\square$

According to Eq. (3.4), the value function ${\mathcal {V}}_{flo,c}(R,y,\nu ;t)$ can be deduced as follows:

$$\begin{aligned}&~{\mathcal {V}}_{flo,c}(R,y,\nu ;t)\nonumber \\&\quad = \frac{e^ye^{-q(T-t)}}{N+1}\overline{{\mathbb {E}}}\bigg [\Big ((N+1)K-\frac{1+\sum _{k=l_t}^{N}e^{Y_{t_k}-\ln R}}{e^{Y_{t_N}-\ln R}}\Big )^+\,\Big |\,R_t=R,Y_t=y, v_t=\nu \bigg ]\nonumber \\&\quad = \frac{e^ye^{-q(T-t)}}{N+1}\overline{{\mathbb {E}}}\bigg [\Big ((N+1)K-\frac{1+\sum _{k=l_t}^{N}e^{Y_{t_k}-\ln R}}{e^{Y_{t_N}-\ln R}}\Big )^+\,\Big |\,Y_t=y, v_t=\nu \bigg ]\nonumber \\&\quad = \frac{e^ye^{-q(T-t)}}{N+1}\overline{{\mathbb {E}}}\bigg [\Big ((N+1)K-\frac{1+\sum _{k=l_t}^{N}e^{Y_{t_k}-Y_t+y-\ln R}}{e^{Y_{t_N}-Y_t+y-\ln R}}\Big )^+\,\Big |\,Y_t=y, v_t=\nu \bigg ]\nonumber \\&\quad = \frac{e^ye^{-q(T-t)}}{N+1}\overline{{\mathbb {E}}}\bigg [\Big ((N+1)K-\frac{1+\sum _{k=l_t}^{N}e^{Y_{t_k}-Y_t+y-\ln R}}{e^{Y_{t_N}-Y_t+y-\ln R}}\Big )^+\,\Big |\,Y_t=y-\ln R,v_t=\nu \bigg ]\nonumber \\&\quad =~\frac{e^ye^{-q(T-t)}}{N+1}\overline{{\mathbb {E}}}\bigg [\Big ((N+1)K-\frac{1+\sum _{k=l_t}^{N}e^{Y_{t_k}}}{e^{Y_{t_N}}}\Big )^+\,\Big |\,Y_t=y-\ln R, v_t=\nu \bigg ]\nonumber \\&\quad = \frac{e^{y}e^{-q(T-t)}}{N+1}V(y-\ln R,\nu ;t), \end{aligned}$$

(A.2)

where the second equality follows from the Markovian property of (Y, v), and the fourth equality holds owing to Lemma A.1.

Proof of Theorem 3.1

The definition Eq. (3.6) leads to the terminal condition Eq. (3.8). Between two consecutive monitoring dates,

$$\begin{aligned} V_{k}\left( y,\nu \right)&=~\overline{{\mathbb {E}}}\bigg [ \Big ( (N+1)K-\frac{1+\sum _{i=k+1}^{N}e^{Y_{t_i}}}{e^{Y_{t_N}}}\Big ) ^{+}\,\bigg |\, Y_{t_{k}}=y, v_{t_{k}}=\nu \bigg ] \nonumber \\&=~\overline{{\mathbb {E}}}\bigg [ \overline{{\mathbb {E}}}\bigg [\Big ( (N+1)K-\frac{1+\sum _{i=k+1}^{N}e^{Y_{t_i}}}{e^{Y_{t_N}}}\Big ) ^{+}\,\Big |\,{\mathcal {F}}_{t_{k+1}}\bigg ]\,\bigg |\, Y_{t_{k}}=y, v_{t_{k}}=\nu \bigg ]\nonumber \\&=~\overline{{\mathbb {E}}}\bigg [ \overline{{\mathbb {E}}}\bigg [ \Big ((N+1)K-\frac{1+e^{Y_{t_{k+1}}}+\sum _{i=k+2}^{N}e^{Y_{t_i}}}{e^{Y_{t_N}}}\Big ) ^{+}\,\Big |\, Y_{t_{k+1}}, v_{t_{k+1}}\bigg ]\,\bigg |\,Y_{t_{k}}=y, v_{t_{k}}=\nu \bigg ],\nonumber \\ \end{aligned}$$

(B.1)

where the second and last equalities are attributed to the tower property and Markovian property of (Y, v), respectively. Consider the following inner expectation:

$$\begin{aligned}&~\overline{{\mathbb {E}}}\bigg [ \Big ((N+1)K-\frac{1+e^{Y_{t_{k+1}}}+\sum _{i=k+2}^{N}e^{Y_{t_i}}}{e^{Y_{t_N}}}\Big ) ^{+}\,\Big |\, Y_{t_{k+1}}=y', v_{t_{k+1}}\bigg ]\nonumber \\&\quad =~\overline{{\mathbb {E}}}\bigg [ \Big ((N+1)K-\frac{1+\sum _{i=k+2}^{N}e^{Y_{t_i}-\ln (1+e^{y'})}}{e^{Y_{t_N}-\ln (1+e^{y'})}}\Big ) ^{+}\,\Big |\, Y_{t_{k+1}}=y', v_{t_{k+1}}\bigg ]\nonumber \\&\quad =~\overline{{\mathbb {E}}}\bigg [ \Big ( (N+1)K-\frac{1+\sum _{i=k+2}^{N}e^{Y_{t_i}-Y_{t_{k+1}}+y'-\ln (1+e^{y'})}}{e^{Y_{t_N}-Y_{t_{k+1}}+y'-\ln (1+e^{y'})}}\Big ) ^{+}\,\Big |\, Y_{t_{k+1}}=y', v_{t_{k+1}}\bigg ]\nonumber \\&\quad =~\overline{{\mathbb {E}}}\bigg [ \Big ((N+1)K-\frac{1+\sum _{i=k+2}^{N}e^{Y_{t_i}}}{e^{Y_{t_N}}}\Big ) ^{+}\,\Big |\, Y_{t_{k+1}}=y'-\ln (1+e^{y'}), v_{t_{k+1}}\bigg ]\nonumber \\&\quad =~V_{k+1}(y'-\ln (1+e^{y'}), v_{t_{k+1}}). \end{aligned}$$

(B.2)

The derivations are analogous to Eq. (A.2). The combination of Eqs. (B.1) and (B.2) yields Eq. (3.7). Finally, Eq. (3.9) follows from Eq. (3.5).

Proof of Eq. (4.4)

It suffices to evaluate the Fourier transform of the density function ${\overline{p}}_{Y,v}(\Delta , y',\nu '\,|\, y,\nu )$ with respect to $y'$, which can be derived as follows:

$$\begin{aligned} \widehat{{\overline{p}}}_{Y,v}(\Delta , \omega ,\nu '\,|\,y,\nu )&=~\int _{-\infty }^{\infty } e^{\textrm{i}\omega y'} {\overline{p}}_{Y,v}(\Delta , y',\nu '\,|\,y,\nu ) \,\textrm{d}y'\\&=~\int _{-\infty }^{\infty } e^{\textrm{i}\omega y'} e^{-(r-q)\Delta +y'-y}p_{Y,v}(\Delta , y',\nu '\,|\,y,\nu ) \,\textrm{d}y'\\&=~ e^{-(r-q)\Delta -y} \int _{-\infty }^{\infty } e^{(1+\textrm{i}\omega ) y'} p_{Y,v}(\Delta , y',\nu '\,|\,y,\nu )\,\textrm{d}y' \\&=~e^{-(r-q)\Delta }e^{\textrm{i}\omega y}\Psi _{\Delta }(\omega -\textrm{i};\nu ,\nu ') =e^{\textrm{i}\omega y}\overline{\Psi }_{\Delta }(\omega ;\nu ,\nu '). \end{aligned}$$

The second and the fourth equalities are attributed to Eqs. (3.3) and (4.2), respectively.

Derivation of the Greeks

Based on eqs. (3.9) and (4.8), the delta $\varDelta _{flo,c}$ and gamma $\varGamma _{flo,c}$ of floating strike Asian call options can be derived as follows:

$$\begin{aligned} \left\{ \begin{aligned} \varDelta _{flo,c}&=\frac{e^{-qT}}{N+1}V_0(0,v_0)\approx \frac{e^{-qT}}{N+1}\Re \bigg \{\sum _{m=0}^{M-1}\!'\beta _{0}^{(m)}(v_{0})e^{-\textrm{i}m\pi \frac{a}{b-a}}\bigg \},\\ \varGamma _{flo,c}&\end{aligned}\right. \end{aligned}$$

Similarly, based on eqs. (3.15) and (4.12), we can approximate the delta $\varDelta _{fix,p}$ and gamma $\varGamma _{fix,p}$ of fixed strike Asian put options as follows:

$$\begin{aligned} \left\{ \begin{aligned} \varDelta _{fix,p}&=-\frac{e^{-rT}}{N+1}V_0\left( \ln \frac{S_0}{(N+1)K-S_0},v_0\right) +\frac{e^{-rT}((N+1)K-S_0)}{N+1}\frac{\partial V_0\left( \ln \frac{S_0}{(N+1)K-S_0},v_0\right) }{\partial S_0}\\&\approx -\frac{e^{-rT}}{N+1}\Re \bigg \{\sum _{m=0}^{M-1}\!'\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}\\&\quad +e^{-rT}\Re \bigg \{\sum _{m=0}^{M-1}\!'\frac{\textrm{i}m\pi }{b-a}\frac{K}{S_0}\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}\\&= e^{-rT}\Re \bigg \{\sum _{m=0}^{M-1}\!'\Big (\frac{K}{S_0}\frac{\textrm{i}m\pi }{b-a}-\frac{1}{N+1}\Big )\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \},\\ \varGamma _{fix,p}&=-2\frac{e^{-rT}}{N+1}\frac{\partial V_0\left( \ln \frac{S_0}{(N+1)K-S_0},v_0\right) }{\partial S_0}+\frac{e^{-rT}((N+1)K-S_0)}{N+1}\frac{\partial ^2 V_0\left( \ln \frac{S_0}{(N+1)K-S_0},v_0\right) }{\partial S_0^2}\\&\approx -e^{-rT}\Re \bigg \{\sum _{m=0}^{M-1}\!'\frac{\textrm{i}m\pi }{b-a}\frac{2K}{S_0((N+1)K-S_0)}\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}\\&\quad -e^{-rT}\Re \bigg \{\sum _{m=0}^{M-1}\!'\frac{\textrm{i}m\pi }{b-a}\frac{K((N+1)K-2S_0)}{S_0^2((N+1)K-S_0)}\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}\\&\quad -e^{-rT}\Re \bigg \{\sum _{m=0}^{M-1}\!'\frac{ m^2\pi ^2}{(b-a)^2}\frac{(N+1)K^2}{S_0^2((N+1)K-S_0)}\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}\\&\approx -\frac{e^{-rT}(N+1)K^2}{S_0^2((N+1)K-S_0)}\Re \bigg \{\sum _{m=0}^{M-1}\!'\Big (\frac{\textrm{i}m\pi }{b-a}+\frac{m^2\pi ^2}{(b-a)^2}\Big )\beta _{0}^{(m)}(v_{0})e^{\textrm{i}m\pi \frac{\ln (S_0/((N+1)K-S_0))-a}{b-a}}\bigg \}. \end{aligned}\right. \end{aligned}$$

Analysis of Errors $\mathbb {III}_{k}$ and $\epsilon ({\widetilde{V}}_0)$

Denote the inner summation of $\mathbb {III}_{k}$ by $\mathbb {III}_{k}^{in}$. Application of the triangle inequality yields

$$\begin{aligned} \begin{aligned} |\mathbb {III}_{k}^{in}|:&=\bigg |\sum _{m=0}^{M-1}\!'\Re \Big \{\overline{\Psi }_\Delta \Big (\frac{m\pi }{b-a};\nu ,\zeta _{j}\Big )e^{\textrm{i}m\pi \frac{y-a}{b-a}}\Big \}\\&\quad \times \int _{a}^{b}[{\widetilde{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})-{\check{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})]\\ {}&\quad \cos (m\pi \frac{y'-a}{b-a})\,\textrm{d}y'\bigg |\\&\le \sum _{m=0}^{M-1}\!'\Big |\Re \Big \{\overline{\Psi }_\Delta \Big (\frac{m\pi }{b-a};\nu ,\zeta _{j}\Big )e^{\textrm{i}m\pi \frac{y-a}{b-a}}\Big \}\Big |\\&\quad \times \int _{a}^{b}\big |{\widetilde{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})-{\check{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})\big | \,\textrm{d}y'\\&\le [(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^{a})]\sum _{m=0}^{M-1}\!'\Big |\Re \Big \{\overline{\Psi }_\Delta \Big (\frac{m\pi }{b-a};\nu ,\zeta _{j}\Big )e^{\textrm{i}m\pi \frac{y-a}{b-a}}\Big \}\Big |. \end{aligned} \end{aligned}$$

The last inequality holds because

$$\begin{aligned} \begin{aligned}&~\int _{a}^{b}|{\widetilde{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})-{\check{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})| \,\textrm{d}y'\\&\quad \le ~\int _{a^*}^{b}|{\widetilde{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})-{\check{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})| \,\textrm{d}y'\\&\qquad +\int _{a}^{a^*} |{\widetilde{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})-{\check{V}}_{k+1}(y'-\ln (1+e^{y'}),\zeta _{j})| \,\textrm{d}y'\\&\quad \le ~(b-a)\epsilon ({\widetilde{V}}_{k+1})+U_V(a^*-a)=(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^a), \end{aligned} \end{aligned}$$

where the last inequality is attributed to the fact that ${\widetilde{V}}_{k+1}\le U_V$, and the last equality follows from $a^*=a-\ln (1-e^a)$. For brevity, we introduce $P_m:=\Re \left\{ \overline{\Psi }_\Delta \Big (\frac{m\pi }{b-a};\nu ,\zeta _{j}\Big )e^{\textrm{i}m\pi \frac{y-a}{b-a}}\right\}$ that can be alternatively expressed as $P_m=\int _{{\mathbb {R}}} {\overline{p}}_{Y,v}(\Delta ,y',\zeta _{j}\,|\,y,\nu )\cos \Big (m\pi \frac{y'-a}{b-a}\Big )\,\textrm{d}y'.$ Under assumption 5.1, by [15, Proposition 4.1], $P_m$ vanishes exponentially as $m \rightarrow \infty$. Hence, $\sum _{m=0}^{M-1}\!'|P_m|$ is bounded, and there exists a constant $C_1>0$ such that $\sum _{m=0}^{M-1}\!'|P_m|\le C_1.$ It then follows that

$$\begin{aligned} |\mathbb {III}_{k}^{in}|\le & {} [(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^a)]\sum _{m=0}^{M-1}\!'|P_m|\\ {}\le & {} [(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^a)]C_1. \end{aligned}$$

We calculate the outer summation of $\mathbb {III}_{k}$:

$$\begin{aligned} |\mathbb {III}_{k}|&= \Big |\sum _{j=1}^{J}\frac{2w_{j}}{b-a}\mathbb {III}_{k}^{in}\Big |\nonumber \\&\le \sum _{j=1}^{J}\frac{2w_{j}}{b-a}[(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^a)]C_1\nonumber \\&\le \frac{2(b_v-a_v)}{b-a}[(b-a)\epsilon ({\widetilde{V}}_{k+1})-U_V\ln (1-e^a)]C_1\nonumber \\ {}&=C_2\epsilon ({\widetilde{V}}_{k+1})-C_{3}\ln (1-e^a), \end{aligned}$$

(E.1)

where $C_{2}=2(b_v-a_v)C_1$ and $C_{3}=2(b_v-a_v)U_VC_1/(b-a)$.

Next, we show that

$$\begin{aligned} \epsilon ({\widetilde{V}}_{k})\le \epsilon _{k}(M,J)-{\mathcal {C}}_{k}\ln (1-e^{a}) \end{aligned}$$

(E.2)

for $k=N-1,\ldots , 0$. Here, $\epsilon _{k}(M,J)$ is a quantity that converges exponentially with respect to M and J, and ${\mathcal {C}}_{k}>0$ is a constant independent of M and J. An upper bound for $\epsilon ({\widetilde{V}}_{0})$ follows immediately. In the following, we establish the proof by mathematical induction.

Clearly, Eq. (E.2) with $k=N-1$ holds because of Eq. (5.5). Suppose that $\epsilon ({\widetilde{V}}_{k+1})\le \epsilon _{k+1}(M,J)-{\mathcal {C}}_{k+1}\ln (1-e^{a})$. Combining Eqs. (5.6) and (E.1), we obtain the following expression:

$$\begin{aligned} \epsilon ({\widetilde{V}}_{k})&\le \epsilon _{k}^{(loc)}+C_2\epsilon ({\widetilde{V}}_{k+1})-C_{3}\ln (1-e^a)\\&\le \epsilon _{k}^{(loc)}+C_2(\epsilon _{k+1}(M,J)-{\mathcal {C}}_{k+1}\ln (1-e^{a}))-C_{3}\ln (1-e^a)\\&=\epsilon _{k}^{(loc)}+C_2\epsilon _{k+1}(M,J)-(C_2{\mathcal {C}}_{k+1}+C_3)\ln (1-e^{a})=\epsilon _k(M,J)-{\mathcal {C}}_{k}\ln (1-e^a), \end{aligned}$$

where $\epsilon _k(M,J):=\epsilon _{k}^{(loc)}+C_2\epsilon _{k+1}(M,J)$ converges exponentially with respect to M and J, and ${\mathcal {C}}_{k}:=C_2{\mathcal {C}}_{k+1}+C_3>0$ is a constant independent of M and J. The proof is completed by mathematical induction.

Table 7 Australian and New Zealander option prices

Australian and New Zealander Option Prices

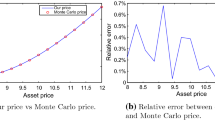
Table 7 presents Australian and New Zealander option prices under three types of models. The Monte Carlo (MC) simulation results with $8\times 10^6$ sample paths serve as benchmarks. Our approach remains to achieve remarkable accuracy and efficiency.