A Novel Boundary Integral Formulation for the Biharmonic Wave Scattering Problem

Abstract

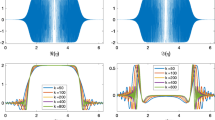
This paper is concerned with the cavity scattering problem in an infinite thin plate, where the out-of-plane displacement is governed by the two-dimensional biharmonic wave equation. Based on an operator splitting, the scattering problem is recast into a coupled boundary value problem for the Helmholtz and modified Helmholtz equations. A novel boundary integral formulation is proposed for the coupled problem. By introducing an appropriate regularizer, the well-posedness is established for the system of boundary integral equations. Moreover, the convergence analysis is carried out for the semi- and full-discrete schemes of the boundary integral system by using the collocation method. Numerical results show that the proposed method is highly accurate for both smooth and nonsmooth examples.

Appendices

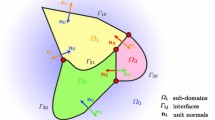
A Representations and splittings of the kernels

The integral kernels of the operators L, S, K, R, H are given by

$$\begin{aligned} l(t,\zeta )&=\frac{\textrm{i}\kappa }{2}n(\zeta )\cdot [\gamma (t)-\gamma (\zeta )] \frac{H_1^{(1)}(\kappa |\gamma (t)-\gamma (\zeta )|)}{|\gamma (t)-\gamma (\zeta )|},\\ s(t,\zeta )&=\frac{\textrm{i}}{2}H_0^{(1)}(\textrm{i}\kappa |\gamma (t)-\gamma (\zeta )|),\\ k(t,\zeta )&=\frac{\kappa }{2}n(t)\cdot [\gamma (t)-\gamma (\zeta )] \frac{H_1^{(1)}(\textrm{i}\kappa |\gamma (t)-\gamma (\zeta )|)}{|\gamma (t)-\gamma (\zeta )|},\\ r(t,\zeta )&=\frac{\textrm{i}\kappa ^2}{2}H_0^{(1)}(\kappa |\gamma (t)-\gamma (\zeta )|)n(t)\cdot n(\zeta ),\\ h(t,\zeta )&=\frac{\textrm{i}}{2}\tilde{h}(t,\zeta )\Big \{\kappa ^2H_0^{(1)}(\kappa |\gamma (t)-\gamma (\zeta )|)- \frac{2\kappa H_1^{(1)}(\kappa |\gamma (t)-\gamma (\zeta )|)}{|\gamma (t)-\gamma (\zeta )|}\Big \}\\&\qquad +\frac{\textrm{i}\kappa \gamma '(t)\cdot \gamma '(\zeta )}{2|\gamma (t)-\gamma (\zeta )|}H_1^{(1)}(\kappa |\gamma (t)-\gamma (\zeta )|) +\frac{1}{4\pi }\frac{1}{\sin ^2\frac{1}{2}(t-\zeta )}. \end{aligned}$$

Here $n(t):=\big (\gamma '_2(t), -\gamma '_1(t)\big )^\top$, $n^\perp (t):=\gamma '(t)=\big (\gamma '_1(t), \gamma '_2(t)\big )^\top$, and

$$\begin{aligned} \tilde{h}(t,\zeta )=\frac{\big [\gamma '(t)\cdot (\gamma (t)-\gamma (\zeta ))\big ]\big [\gamma '(\zeta )\cdot (\gamma (t) -\gamma (\zeta ))\big ]}{|\gamma (t)-\gamma (\zeta )|^2}. \end{aligned}$$

For the splitting (17), we have

$$\begin{aligned} l_1(t,\zeta )&= \frac{\kappa }{2\pi }n(\zeta )\cdot \big [ \gamma (\zeta )-\gamma (t)\big ]\frac{J_1(\kappa |\gamma (t)-\gamma (\zeta )|)}{ |\gamma (t)-\gamma (\zeta )|}, \\ s_1(t,\zeta )&= -\frac{1}{2\pi }J_0(\textrm{i}\kappa |\gamma (t)-\gamma (\zeta )|), \\ k_1(t,\zeta )&= \frac{\textrm{i}\kappa }{2\pi }n(t)\cdot \big [ \gamma (t)-\gamma (\zeta )\big ]\frac{J_1(\textrm{i}\kappa |\gamma (t)-\gamma (\zeta )|)}{ |\gamma (t)-\gamma (\zeta )|}, \\ r_1(t,\zeta )&= -\frac{\kappa ^2}{2\pi }J_0(\kappa |\gamma (t)-\gamma (\zeta )|)n(t)\cdot n(\zeta ), \\ h_1(t,\zeta )&=-\frac{1}{2\pi }\tilde{h}(t,\zeta )\Bigg (\kappa ^2J_0(\kappa |\gamma (t)-\gamma (\zeta )|)-\frac{2\kappa J_1(\kappa |\gamma (t)-\gamma (\zeta )|)}{ |\gamma (t)-\gamma (\zeta )|}\Bigg )\\&\qquad -\frac{\kappa \gamma '(t)\cdot \gamma '(\zeta )}{2\pi |\gamma (t)-\gamma (\zeta )|}J_1(\kappa |\gamma (t)-\gamma (\zeta )|), \end{aligned}$$

where $J_0$ and $J_1$ are the Bessel functions of the first kind with order zero and one, respectively. The diagonal entries are given by

$$\begin{aligned} l_1(t,t)&=0, \quad l_2(t,t)= \frac{1}{2\pi }\frac{{n}(t)\cdot \gamma ''(t)}{|\gamma '(t)|^2},\\ s_1(t,t)&=-\frac{1}{2\pi }, \quad s_2(t,t)= \frac{\textrm{i}}{2}-\frac{C}{\pi }-\frac{1}{\pi }\ln \big (\frac{\textrm{i}\kappa }{2}|\gamma '(t)|\big ),\\ r_1(t,t)&=-\frac{\kappa ^2}{2\pi }|\gamma '(t)|^2, \quad r_2(t,t)=\kappa ^2|\gamma '(t)|^2 \Big \{\frac{\textrm{i}}{2}-\frac{C}{\pi }-\frac{1}{\pi }\ln \big (\frac{\kappa }{2}|\gamma '(t)|\big )\Big \},\\ k_1(t,t)&=0, \quad k_2(t,t)= \frac{1}{2\pi }\frac{{n}(t)\cdot \gamma ''(t)}{|\gamma '(t)|^2},\quad h_1(t,t)=-\frac{\kappa ^2|\gamma '(t)|^2}{4\pi }, \\ h_2(t,t)&=\Big (\pi \textrm{i}-1-2C-2\ln \frac{\kappa |\gamma '(t)|}{2}\Big ) \frac{\kappa ^2|\gamma '(t)|^2}{4\pi }+\frac{1}{12\pi }\\&\qquad +\frac{[\gamma '(t)\cdot \gamma ''(t)]^2}{2\pi |\gamma '(t)|^4}-\frac{|\gamma ''(t)|^2}{4\pi |\gamma '(t)|^2}-\frac{\gamma '(t)\cdot \gamma '''(t)}{6\pi |\gamma '(t)|^2}, \end{aligned}$$

where C denotes Euler’s constant. We refer to [2, 13] for the details of the decomposition.

B Proofs for Theorems 6 and 7

1.1 B.1 Proof of Theorem 6

The function ${\mathcal {D}}\psi$ can be split into the following two parts:

$$\begin{aligned} ({\mathcal {D}}\psi )(t)=\int _0^{2\pi }\ln \Big (4\sin ^2\frac{t-\zeta }{2} \Big )\alpha (t,\zeta )\psi (\zeta )\,\textrm{d}\zeta +\int _0^{2\pi }\beta (t, \zeta )\psi (\zeta )\,\textrm{d}\zeta , \end{aligned}$$

where

$$\begin{aligned} \alpha (t,\zeta )=\left[ \begin{array}{cc} \alpha _1(t,\zeta )&{} \alpha _2(t,\zeta )\\ \alpha _3(t,\zeta )&{} \alpha _4(t,\zeta ) \end{array} \right] , \quad \beta (t,\zeta )=\left[ \begin{array}{cc} \beta _1(t,\zeta )&{} \beta _2(t,\zeta )\\ \beta _3(t,\zeta )&{} \beta _4(t,\zeta ) \end{array} \right] \end{aligned}$$

with $\alpha _j(t,t)=\partial _t \alpha _j(t,t)=\partial ^2_{tt} \alpha _j(t,t)=0, j=1,2,3,4$ and $\alpha _j, \beta _j$ being analytic. We write the derivative $\frac{{\textrm{d}}^{2}}{{\textrm{d}}t^{2}}({\mathcal {D}}\psi )$ in form of

$$\begin{aligned}&({\mathcal {D}}''\psi )(t)P{:}{=}\frac{{\text {d}}^{2}}{{\text {d}}t^{2}}({\mathcal {D}}\psi )(t)\\ {}&=\int _0^{2\pi }\ln \Big (4\sin ^2\frac{t-\zeta }{2} \Big ){\widetilde{\alpha } (t,\zeta )} \psi (\zeta )\,{\text {d}}\zeta +\int _0^{2\pi }{\widetilde{\beta } (t,\zeta )} \psi (\zeta )\,{\text {d}}\zeta , \end{aligned}$$

where

$$\begin{aligned} {\widetilde{\alpha }}(t,\zeta )&=\partial ^2_{tt}\alpha (t,\zeta ),\\ {\widetilde{\beta }}(t,\zeta )&=2\cot \frac{t-\zeta }{2}\partial _t\alpha (t,\zeta )-\alpha (t,\zeta ) \frac{1}{2\sin ^2\frac{t-\zeta }{2}}+\partial ^2_{tt}\beta (t,\zeta ). \end{aligned}$$

By the interpolatory quadrature, the full discretization of ${\mathcal {D}}''$ can be written as

$$\begin{aligned} ({\mathcal {D}}''_n\psi )(t)=\int _0^{2\pi }\ln \Big (4\sin ^2\frac{t-\zeta }{2}\Big ){\mathcal {P}}_n\Big \{{\widetilde{\alpha } (t,\cdot )} \psi \Big \}(\zeta )\,{\text {d}}\zeta +\int _0^{2\pi }{\mathcal {P}}_n\Big \{{\widetilde{\beta } (t,\cdot )} \psi \Big \}(\zeta )\,{\text {d}}\zeta . \end{aligned}$$

Noting $p>1/2, 0\le q\le p, {\widetilde{\alpha }}(t,t)=0$, and the analyticity of the elements in ${\widetilde{\alpha }}(t,\zeta )$ and ${\widetilde{\beta }}(t,\zeta )$, we have from [15, Lemma 13.21 and Theorem 12.18] that

$$\begin{aligned} \Vert {\mathcal {D}}''_n\psi -{\mathcal {D}}''\psi \Vert _{q+1}\le C_1\frac{1}{n^{p+1-q}}\Vert \psi \Vert _{p},\quad \Vert {\mathcal {D}}''_n\chi -{\mathcal {D}}''\chi \Vert _{q+1}\le {\widetilde{C}}_1\frac{1}{n^{p-q}}\Vert \chi \Vert _{p} \end{aligned}$$

for any $\psi \in X_n^2$ and $\chi \in H^p[0,2\pi ]^2$, where the positive constants $C_1$ and ${\widetilde{C}}_1$ depend on p and q. Since ${\mathcal {D}}''_n\psi =\frac{{\textrm{d}}^{2}}{{\textrm{d}}t^{2}}({\mathcal {D}}_n\psi )$, the above inequalities reduce to

$$\begin{aligned} \Vert {\mathcal {D}}_n\psi -{\mathcal {D}}\psi \Vert _{q+3}\le C_2\frac{1}{n^{p+1-q}}\Vert \psi \Vert _{p}, \quad \Vert {\mathcal {D}}_n\chi -{\mathcal {D}}\chi \Vert _{q+3}\le {\widetilde{C}}_2\frac{1}{n^{p-q}}\Vert \chi \Vert _{p}, \end{aligned}$$

where $C_2$ and ${\widetilde{C}}_2$ are positive constants depending on p and q. By [15, Theorem 8.13], the proof is completed since the above inequalities hold for any q satisfying $0\le q\le p$ and $p>1/2$.

1.2 B.2 Proof of Theorem 7

Recalling the boundedness of ${\mathcal {N}}: H^{p}[0,2\pi ]^2\rightarrow H^{p-1}[0,2\pi ]^2$ and using (27), we have for any $\chi \in H^p[0,2\pi ]^2, 0\le q\le p, p>1/2$ that

$$\begin{aligned} \Vert ({\mathcal {N}}_n-{\mathcal {N}})\chi \Vert _{q-1}=\Vert {\mathcal {N}}({\mathcal {P}}_n\chi -\chi )\Vert _{q-1}\le C_1\Vert ({\mathcal {P}}_n\chi -\chi )\Vert _{q}\le \frac{C_2}{n^{p-q}}\Vert \chi \Vert _{p}, \end{aligned}$$

where $C_1$ and $C_2$ are positive constants depending on q and p, q, respectively. For any $p>1/2$, it is clear to note that ${\mathcal {N}}_n$ and ${\mathcal {N}}_n-{\mathcal {N}}$ are uniformly bounded from $H^p[0,2\pi ]^2$ to $H^{p-1}[0,2\pi ]^2$.

For any $\psi \in X_n^2$, it follows from Theorem 6 and ${\mathcal {N}}_n\psi ={\mathcal {N}}\psi$ that

$$\begin{aligned}&\Vert {\mathcal {N}}_n{\mathcal {D}}_n\psi -{\mathcal {N}}{\mathcal {D}}\psi \Vert _{p+2}\\&\le \Vert {\mathcal {N}}_n({\mathcal {D}}_n-{\mathcal {D}})\psi \Vert _{p+2}+\Vert ({\mathcal {N}} _n-{\mathcal {N}})({\mathcal {D}}\psi -{\mathcal {P}}_n{\mathcal {D}}\psi )\Vert _{p+2} +\Vert ({\mathcal {N}}_n-{\mathcal {N}}){\mathcal {P}}_n{\mathcal {D}}\psi \Vert _{p+2}\\&\preceq \Vert ({\mathcal {D}}_n-{\mathcal {D}})\psi \Vert _{p+3}+\Vert {\mathcal {D}} \psi -{\mathcal {P}} _n{\mathcal {D}}\psi \Vert _{p+3}\\&\preceq 1/n\Vert \psi \Vert _{p}+1/n\Vert {\mathcal {D}}\psi \Vert _{p+4} \preceq 1/n\Vert \psi \Vert _{p}. \end{aligned}$$

Moreover, by Theorem 6, we have for any $p>1/2$ that ${\mathcal {D}}_n$ and ${\mathcal {D}}_n-{\mathcal {D}}$ are uniformly bounded from $H^p[0,2\pi ]^2$ to $H^{p+3}[0,2\pi ]^2$. Combining (27) and (31), and noting the boundedness of ${\mathcal {D}}: H^p[0,2\pi ]^2\rightarrow H^{p+4}[0,2\pi ]^2$ and the uniform boundedness of ${\mathcal {P}}_n: H^{p+2}[0,2\pi ]^2\rightarrow H^{p+2}[0,2\pi ]^2$, we obtain

$$\begin{aligned}&\Vert {\mathcal {D}}^2_n\psi -{\mathcal {D}}^2\psi \Vert _{p+2} \le \Vert {\mathcal {D}}^2_n\psi -{\mathcal {D}}^2\psi \Vert _{p+6}\\&\le \Vert {\mathcal {D}}_n({\mathcal {D}}_n-{\mathcal {D}})\psi \Vert _{p+6} +\Vert ({\mathcal {D}}_n-{\mathcal {D}})({\mathcal {D}}\psi -{\mathcal {P}}_n{\mathcal {D}}\psi )\Vert _{p+6} +\Vert ({\mathcal {D}}_n-{\mathcal {D}}){\mathcal {P}}_n{\mathcal {D}}\psi \Vert _{p+6}\\&\preceq \Vert ({\mathcal {D}}_n-{\mathcal {D}})\psi \Vert _{p+3}+\Vert ({\mathcal {D}}\psi -{\mathcal {P}}_n{\mathcal {D}}\psi )\Vert _{p+3}+1/n\Vert {\mathcal {P}}_n{\mathcal {D}}\psi \Vert _{p+3}\\&\preceq 1/n\Vert \psi \Vert _{p}+1/n\Vert {\mathcal {D}}\psi \Vert _{p+4}+1/n\Vert {\mathcal {D}}\psi \Vert _{p+3} \preceq 1/n\Vert \psi \Vert _{p}. \end{aligned}$$

With the help of ${\mathcal {N}}_1\psi \in X_n^2$, the boundedness of ${\mathcal {N}}_2: H^{p}[0,2\pi ]^2\rightarrow H^{p+1}[0,2\pi ]^2$ and the uniform boundedness of ${\mathcal {D}}_n-{\mathcal {D}}: H^{p-1}[0,2\pi ]^2$ to $H^{p+2}[0,2\pi ]^2$ and ${\mathcal {P}}_n: H^{p-1}[0,2\pi ]^2\rightarrow H^{p-1}[0,2\pi ]^2$ for $p>\frac{3}{2}$, we deduce

$$\begin{aligned}&\Vert {\mathcal {D}}_n{\mathcal {N}}_n\psi -{\mathcal {D}}{\mathcal {N}}\psi \Vert _{p+2} =\Vert ({\mathcal {D}}_n-{\mathcal {D}}){\mathcal {N}}\psi \Vert _{p+2}\\&\le \Vert ({\mathcal {D}}_n-{\mathcal {D}})({\mathcal {N}}\psi -{\mathcal {P}}_n{\mathcal {N}}\psi )\Vert _{p+2} +\Vert ({\mathcal {D}}_n-{\mathcal {D}}){\mathcal {P}}_n{\mathcal {N}}\psi \Vert _{p+2}\\&\preceq \Vert {\mathcal {N}}\psi -{\mathcal {P}}_n{\mathcal {N}}\psi \Vert _{p-1}+1/n\Vert {\mathcal {P}}_n{\mathcal {N}}\psi \Vert _{p-1}\\&\le \Vert {\mathcal {N}}_1\psi -{\mathcal {P}}_n{\mathcal {N}}_1\psi \Vert _{p-1}+\Vert {\mathcal {N}}_2\psi -{\mathcal {P}}_n{\mathcal {N}}_2\psi \Vert _{p-1}+1/n\Vert {\mathcal {P}}_n{\mathcal {N}}\psi \Vert _{p-1}\\&\preceq 1/n^2\Vert {\mathcal {N}}_2\psi \Vert _{p+1}+1/n\Vert {\mathcal {N}}\psi \Vert _{p-1} \preceq 1/n\Vert \psi \Vert _{p}. \end{aligned}$$

Combining the above estimates yields

$$\begin{aligned} \Vert {\mathcal {V}}_n\psi -{\mathcal {V}}\psi \Vert _{p+2}&\le \Vert {\mathcal {N}}_n{\mathcal {D}}_n\psi -{\mathcal {N}}{\mathcal {D}}\psi \Vert _{p+2} +\Vert {\mathcal {D}}_n{\mathcal {N}}_n\psi -{\mathcal {D}}{\mathcal {N}}\psi \Vert _{p+2}\\&\quad +\Vert {\mathcal {D}}_n^2\psi -{\mathcal {D}}^2\psi \Vert _{p+2} \\&\preceq 1/n\Vert \psi \Vert _{p}, \end{aligned}$$

which completes the proof by noting that the operators ${\mathcal {E}}^{-1},{\mathcal {P}}_n: H^{p+2}[0,2\pi ]^2\rightarrow H^{p+2}[0,2\pi ]^2$ are uniformly bounded.