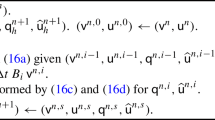Recovery Type a Posteriori Error Estimation of an Adaptive Finite Element Method for Cahn–Hilliard Equation

Abstract

In this paper, we derive a novel recovery type a posteriori error estimation of the Crank–Nicolson finite element method for the Cahn–Hilliard equation. To achieve this, we employ both the elliptic reconstruction technique and a time reconstruction technique based on three time-level approximations, resulting in an optimal a posteriori error estimator. We propose a time-space adaptive algorithm that utilizes the derived a posteriori error estimator as error indicators. Numerical experiments are presented to validate the theoretical findings, including comparing with an adaptive finite element method based on a residual type a posteriori error estimator.

Appendix A. Proof of Theorem 3.2

In this section, we present the proof of the Theorem 3.2. To begin with, we recall the following results.

Lemma A.1

[3] Let $\dot{V}:=\left\{ \phi \in H^{1}(\Omega ),\bar{\phi }:=\frac{1}{|\Omega |}\int _{\Omega }\phi dx=0\right\} ,$ there exists $C_{I}>0$ such that for all $\phi \in \dot{V}$ if $d=2$ and for all $\phi \in \dot{V}\cap L^{\infty }(\Omega )$ if $d=3$, we have

$$\begin{aligned} \Vert \phi \Vert _{L^{3}(\Omega )}^{3}\le C_{I}\Vert \phi \Vert _{L^{\infty }(\Omega )}^{1-\sigma }\Vert \nabla \Delta ^{-1}\phi \Vert ^{\sigma }\Vert \nabla \phi \Vert ^{2}, \end{aligned}$$

(A.1)

where $\sigma =1$ if $d=2$ and $\sigma =\frac{4}{5}$ if $d=3$.

Lemma A.2

[5] (Generalized Gronwall’s Lemma) Suppose that the nonnegative functions $y_{1}\in C([0,T])$, $y_{2},\,y_{3}\in L^{1}(0,T)$, $a\in L^{\infty }(0,T)$, and the real number $A\ge 0$ satisfy

$$\begin{aligned} y_{1}(t)+\int _{0}^{t}y_{2}(s)ds\le A+\int _{0}^{t}a(s)y_{1}(s)ds+\int _{0}^{t}y_{3}(s)ds \end{aligned}$$

for all $t\in [0,T]$. Assume that for $B\ge 0$, $\beta \ge 0$ and every $t\in [0,T]$, we have

$$\begin{aligned} \int _{0}^{t}y_{3}(s)ds\le B\sup _{s\in [0,t]}y_{1}^{\beta }(s)\int _{0}^{t}\left( y_{1}(s)+y_{2}(s)\right) ds. \end{aligned}$$

Setting $E:=exp\left( \int _{0}^{T}a(s)ds\right)$ and assume that $8AE\le \left( 8B(1+T)E\right) ^{-1/\beta }$, then we obtain

$$\begin{aligned} \sup _{t\in [0,T]}y_{1}(t)+\int _{0}^{T}y_{2}(s)ds\le 8Aexp\left( \int _{0}^{T}a(s)ds\right) . \end{aligned}$$

To prove Theorem 3.2, we introduce the $L^{2}$ lifting property for the nonlinear elliptic problem (2.10b). This is inspired by the $L^{2}$ lifting property for a similar nonlinear elliptic problem discussed in [26]:

$$\begin{aligned} \left\{ \begin{aligned} -\Delta z+b(x,z)&=0,\qquad \text {in}\ \Omega \times (0,T],\\ u&=0, \qquad \text {on}\ \partial \Omega \times [0,T], \end{aligned} \right. \end{aligned}$$

(A.2)

where the nonlinear term b satisfies

$$\begin{aligned} \begin{aligned}{}&{} \sup _{x\in \bar{\Omega }}\left| b(x,z)-b(x,z_{0})+\frac{\partial b}{\partial z}(x,z_{0})(z_{0}-z) \right| \lesssim (1+\max \{|z|^{s},|z_{0}|^{s}\})|z-z_{0}|^{q}, \\ {}&\forall z,\ z_{0}\in R, \end{aligned}\qquad \end{aligned}$$

(A.3)

for $q\in (1,2],\ s\in [0,5-q]$.

Lemma A.3

($L^{2}$ lifting property) Given $h_{0}\ll 1$. For the nonlinear elliptic problem (2.10b), if $h=\max \{h_{K},K\in \mathcal {T}_{h}\}\in (0,h_{0}]$, then

$$\begin{aligned} \begin{aligned} \Vert \mu -\mu _{h}\Vert&\le \kappa (h) \Vert \mu -\mu _{h}\Vert _{1,\Omega }, \end{aligned} \end{aligned}$$

(A.4)

where $\kappa (h)= C_IC_R h^s +\frac{1}{\varepsilon ^2} \hat{C_I}C_R h^s$, here $C_R,\, C_I,\,\hat{C_I}$ are constants independent of $\varepsilon$ and h.

Proof

Let $\omega \in H^{1+s}(\Omega )$ for some $0<s\le 1$ be the solution to the dual problem of (2.10b): Find $\omega \in H^{1}(\Omega )$, such that

$$\begin{aligned} \varepsilon a( \omega , v)+\langle \mathfrak {B}(\mu ,\mu _h) \omega ,v\rangle =\langle \mu -\mu _h,v\rangle ,\qquad \forall v\in H^{1}(\Omega ), \end{aligned}$$

(A.5)

where the operator

$$\begin{aligned} \mathfrak {B}(\mu ,\mu _h)=\frac{1}{\varepsilon }\int _{0}^{1}3[\mu _h+\xi (\mu -\mu _h)^2]d\xi . \end{aligned}$$

Obviously, it holds that

$$\begin{aligned} \frac{1}{\varepsilon }\left( \mu ^3-\mu _h^3\right) =\mathfrak {B}(\mu ,\mu _h)(\mu -\mu _h). \end{aligned}$$

(A.6)

By the regularity estimate [23, 24, 35] for the dual problem (A.5),

$$\begin{aligned} |\omega |_{H^{1+s}(\Omega )}\le \frac{1}{\varepsilon }C_R\Vert \mu -\mu _h\Vert _{0,\Omega }. \end{aligned}$$

(A.7)

Let $I^h: H^1(\Omega )\rightarrow V_h$ be a quasi-interpolator, satisfying

$$\begin{aligned} \Vert \omega -I^h\omega \Vert _{1,\Omega }\le C_I h^s |\omega |_{H^{1+s}}, \end{aligned}$$

(A.8)

$$\begin{aligned} \Vert \omega -I^h\omega \Vert _{0,\Omega }\le \hat{C_I} h^s |\omega |_{H^{1+s}}. \end{aligned}$$

(A.9)

Consider the linearized dual problem (A.5) with $v=\mu -\mu _h\in H^{1}(\Omega )$, we obtain

$$\begin{aligned} \varepsilon a( \mu -\mu _h,\omega )+\langle \mathfrak {B}(\mu ,\mu _h)(\mu -\mu _h),\omega \rangle =\Vert \mu -\mu _h\Vert ^2. \end{aligned}$$

(A.10)

By Galerkin orthogonality, for $I^h\omega \in V_h$,

$$\begin{aligned} \varepsilon a( \mu -\mu _h,I^h\omega )+\langle \mathfrak {B}(\mu ,\mu _h)(\mu -\mu _h),I^h\omega \rangle =0. \end{aligned}$$

(A.11)

Subtracting (A.11) from (A.10) and using (A.6), we have

$$\begin{aligned} \varepsilon a( \mu -\mu _h,\omega -I^h\omega )+ \frac{1}{\varepsilon }\langle \mu ^3-\mu _h^3,\omega -I^h\omega \rangle =\Vert \mu -\mu _h\Vert ^2. \end{aligned}$$

(A.12)

By using the Cauchy-Schwarz inequality, interpolation estimate (A.8) and regularity (A.7) for the first term on the left hand side (LHS) of (A.12), it holds

$$\begin{aligned} \begin{aligned} \left| \varepsilon a( \mu -\mu _h,\omega -I^h\omega )\right|&=\left| \varepsilon \left( ( \nabla (\mu -\mu _h),\nabla (\omega -I^h\omega )\right) \right| \\&\le \varepsilon \Vert \nabla (\mu -\mu _h)\Vert \cdot \Vert \nabla (\omega -I^h\omega )\Vert \\&\le \varepsilon \Vert \mu -\mu _h\Vert _{1,\Omega }\cdot \Vert \omega -I^h\omega \Vert _{1,\Omega }\\&\le \varepsilon C_I h^s \Vert \mu -\mu _h\Vert _{1,\Omega }\cdot |\omega |_{H^{1+s}}\\&\le C_I h^sC_R \Vert \mu -\mu _h\Vert _{1,\Omega }\cdot \Vert \mu -\mu _h\Vert _{0,\Omega }. \end{aligned} \end{aligned}$$

(A.13)

For the second term on LHS of (A.12), applying the Cauchy-Schwarz inequality, we have

$$\begin{aligned} \begin{aligned} \left| \frac{1}{\varepsilon }\left\langle \mu ^3-\mu _h^3,\omega -I^h\omega \right\rangle \right|&=\left| \frac{1}{\varepsilon }\left\langle (\mu -\mu _h)(\mu ^2+\mu \mu _h+\mu _h^2),\omega -I^h\omega \right\rangle \right| \\&\le \frac{1}{\varepsilon }\Vert \mu -\mu _h\Vert _{0,p,\Omega }\cdot \Vert \mu ^2+\mu \mu _h +\mu _h^2\Vert _{0,q,\Omega }\cdot \Vert \omega -I^h\omega \Vert _{0,k,\Omega } \end{aligned}\nonumber \\ \end{aligned}$$

(A.14)

with $\frac{1}{p}+\frac{1}{q}+\frac{1}{k}=1$. Taking $p=q=4,\ k=2$ in (A.14), and using embedding theorem, interpolation estimate (A.9) and regularity (A.7) give

$$\begin{aligned} \begin{aligned} \left| \frac{1}{\varepsilon }\left\langle \mu ^3-\mu _h^3,\omega -I^h\omega \right\rangle \right|&\le \frac{1}{\varepsilon }\Vert \mu -\mu _h\Vert _{0,4,\Omega }\cdot \Vert \mu ^2+\mu \mu _h +\mu _h^2\Vert _{0,4,\Omega }\cdot \Vert \omega -I^h\omega \Vert _{0,2,\Omega }\\&\le \frac{1}{\varepsilon }\Vert \mu -\mu _h\Vert _{1,\Omega }\cdot \Vert \mu ^2+\mu \mu _h +\mu _h^2\Vert _{1,\Omega }\cdot \Vert \omega -I^h\omega \Vert _{0,\Omega }\\&\le \frac{1}{\varepsilon }\hat{C_I} h^s\Vert \mu -\mu _h\Vert _{1,\Omega }\cdot |\omega |_{H^{1+s}}\\&\le \frac{1}{\varepsilon ^2}\hat{C_I}C_R h^s\Vert \mu -\mu _h\Vert _{1,\Omega }\cdot \Vert \mu -\mu _h\Vert _{0,\Omega }. \end{aligned} \end{aligned}$$

(A.15)

Plugging (A.13) and (A.15) into (A.12) gives

$$\begin{aligned} \begin{aligned} \Vert \mu -\mu _h\Vert ^2&\le C_I h^sC_R \Vert \mu -\mu _h\Vert _{1,\Omega }\cdot \Vert \mu -\mu _h\Vert _{0,\Omega }+\frac{1}{\varepsilon ^2}\hat{C_I}C_R h^s\Vert \mu \\&-\mu _h\Vert _{1,\Omega }\cdot \Vert \mu -\mu _h\Vert _{0,\Omega }. \end{aligned} \end{aligned}$$

Thus, the result of (A.4) is obtained by simplification. $\square$

Now, we are ready to present the proof of Theorem 3.2.

Proof

According to (3.7), we have that

$$\begin{aligned} \partial _{t}e_u+\mathcal {A}e_{w} =&-\mathcal {A}\epsilon _{w}+\frac{Aw_{h}^{n}-A w_{h}^{n-1}}{2}+\mathcal {A}(q(t) -q^{n})+w_{h}^{n}-Rw_{h}^{n}+(t-t_{n-\frac{1}{2}})\partial _{n}^{2}u_{h}, \end{aligned}$$

(A.16)

$$\begin{aligned} \varepsilon \mathcal {A}e_{u}-e_{w} =&-\varepsilon \mathcal {A}\epsilon _{u}+\epsilon _{w}+\varepsilon \frac{Au_{h}^{n}-Au_{h}^{n-1}}{2} +\frac{Pf(u_{h}^{n})-Pf(u_{h}^{n-1})}{2\varepsilon }-\frac{w_{h}^{n}-w_{h}^{n-1}}{2}\nonumber \\&+\varepsilon \mathcal {A}(p(t)-p^{n})-(q(t)-q^{n})+\frac{f(u)-f(p^{n})}{\varepsilon } +\frac{1}{\varepsilon }\left( u_{h}^{n}-p^{n}\right) . \end{aligned}$$

(A.17)

To make the conclusion clean, we separate the remaining of this proof into eleven steps.

Step 1: Multiplying both sides of (A.16) by $-\Delta ^{-1}e_{u}$ and (A.17) by $e_{u}$, respectively, then adding the resulting equations, we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}&\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}+\varepsilon \Vert \nabla e_{u}\Vert ^{2} =\left( \frac{Aw_{h}^{n}-Aw_{h}^{n-1}}{2},-\Delta ^{-1}e_{u}\right) +\left( \mathcal {A}(q(t)-q^{n}),-\Delta ^{-1}e_{u}\right) \\&+\left( w_{h}^{n}-Rw_{h}^{n},-\Delta ^{-1}e_{u}\right) +\left( (t-t_{n-\frac{1}{2}}) \partial _{n}^{2}u_{h},-\Delta ^{-1}e_{u}\right) \\&-\varepsilon a\left( \epsilon _{u},e_{u}\right) +\varepsilon \left( \frac{Au_{h}^{n}-A u_{h}^{n-1}}{2},e_{u}\right) +\frac{1}{\varepsilon }\left( u_{h}^{n}-p^{n},e_{u}\right) \\&+\left( \frac{Pf(u_{h}^{n}) -Pf(u_{h}^{n-1})}{2\varepsilon },e_{u}\right) +\left( -\frac{w_{h}^{n}-w_{h}^{n-1}}{2},e_{u}\right) \\&+\left( \left( \varepsilon \mathcal {A}\left( p(t)-p^{n}\right) -\frac{1}{\varepsilon } \left( f(p^{n})\frac{t_{n}-t}{\tau _{n}}-f(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\right) -(q(t)-q^{n})\right) ,e_{u}\right) \\&{+}\left( \frac{1}{\varepsilon }\left( f(u_{h}^{n})\frac{t{-}t_{n{-}1}}{\tau _{n}}{+}f(u_{h}^{n-1}) \frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n}){+}f(p^{n})\frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n{-}1}) \frac{t_{n}{-}t}{\tau _{n}}\right) ,e_{u}\right) \\&{+}\left( \frac{1}{\varepsilon }\left( f(u_{h}){-}f(u_{h}^{n})\frac{t{-}t_{n-1}}{\tau _{n}}{-}f(u_{h}^{n-1}) \frac{t_{n}{-}t}{\tau _{n}})\right) ,e_{u}\right) {+}\left( \frac{1}{\varepsilon }\left( f(u){-}f(u_{h})\right) ,e_{u}\right) , \end{aligned}$$

for all $t\in (t_{n-1},t_{n}]$ and each $n=1,2,\ldots ,N$. Then integrate with respect to t, we get

$$\begin{aligned}&\frac{1}{2}\Vert \nabla \Delta ^{-1}e_{u}^{N}\Vert ^{2}+\int _{0}^{T}\varepsilon \Vert \nabla e_{u}\Vert ^{2}dt \nonumber \\=&\frac{1}{2}\Vert \nabla \Delta ^{-1}e_{u}^{0}\Vert ^{2}+\int _{0}^{T}\left( \frac{Aw_{h}^{n}-A w_{h}^{n-1}}{2}, -\Delta ^{-1}e_{u}\right) dt\nonumber \\ {}&+\int _{0}^{T}\left( w_{h}^{n}-Rw_{h}^{n},-\Delta ^{-1}e_{u}\right) dt +\int _{0}^{T} \left( (t-t_{n-\frac{1}{2}})\partial _{n}^{2}u_{h},-\Delta ^{-1}e_{u}\right) dt \nonumber \\&+\int _{0}^{T}\left( \mathcal {A}(q(t)-q^{n})+q(t)-q^{n},-\Delta ^{-1}e_{u}\right) dt+\int _{0}^{T} -\varepsilon a\left( \epsilon _{u},e_{u}\right) dt\nonumber \\&+\int _{0}^{T}\left( q^{n}-q(t)-(w_{h}^{n}-w_{h}),-\Delta ^{-1}e_{u}\right) dt+\int _{0}^{T} \left( w_{h}^{n}-w_{h},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&+\int _{0}^{T}\varepsilon \left( \frac{Au_{h}^{n}-Au_{h}^{n-1}}{2},e_{u}\right) dt +\int _{0}^{T}\frac{1}{\varepsilon }\left( u_{h}^{n}-p^{n},e_{u}\right) dt\nonumber \\&+\int _{0}^{T}\left( \frac{Pf(u_{h}^{n})-Pf(u_{h}^{n-1})}{2\varepsilon },e_{u}\right) dt +\int _{0}^{T}\left( -\frac{w_{h}^{n}-w_{h}^{n-1}}{2},e_{u}\right) dt\nonumber \\&+\int _{0}^{T}\Big (\Big (\varepsilon \mathcal {A}\Big (p(t)-p^{n}\Big )-\frac{1}{\varepsilon } \Big (h(p^{n})\frac{t_{n}-t}{\tau _{n}}-h(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\nonumber \\&-\frac{1}{2}(t-t_{n-1})(t-t_{n}) \frac{\frac{h(p^{n})-h(p^{n-1})}{\tau _{n}}-\frac{h(p^{n-1})-h(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n} +\tau _{n-1}}{2}}\Big )-\Big (q(t)-q^{n}\Big )\Big ),e_{u}\Big ) dt\nonumber \\&+\int _{0}^{T}\Big (\frac{1}{\varepsilon }\left( p^{n}-p^{n-1}-\left( u_{h}^{n}-u_{h}^{n-1}\right) \right) \frac{t_{n}-t}{\tau _{n}}+\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\nonumber \\&\quad \Big (\frac{\frac{p^{n}-p^{n-1}}{\tau _{n}}-\frac{p^{n-1}-p^{n-2}}{\tau _{n-1}}}{\frac{\tau _{n} +\tau _{n-1}}{2}}-\frac{\frac{u_{h}^{n}-u_{h}^{n-1}}{\tau _{n}} -\frac{u_{h}^{n-1}-u_{h}^{n-2}}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ),e_{u}\Big ) dt \nonumber \\&+\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( u_{h}^{n}-u_{h}^{n-1}\right) \frac{t_{n}-t}{\tau _{n}},e_{u}\right) dt\nonumber \\&{+}\int _{0}^{T}\Big (\frac{1}{\varepsilon }\left( f(u_{h}^{n})\frac{t{-}t_{n{-}1}}{\tau _{n}}{+}f(u_{h}^{n{-}1}) \frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n}){+}f(p^{n})\frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\right) \nonumber \\&+\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\nonumber \\&\left( \frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1}) -f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}-\frac{\frac{f(p^{n}) -f(p^{n-1})}{\tau _{n}}-\frac{f(p^{n-1})-f(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\right) ,e_{u}\Big ) dt\nonumber \\&\quad \int _{0}^{T}\Big (\frac{1}{\varepsilon }\Big (f(u_{h})-f(u_{h}^{n})\frac{t-t_{n-1}}{\tau _{n}} -f(u_{h}^{n-1})\frac{t_{n}-t}{\tau _{n}}-\frac{1}{2}(t-t_{n-1})(t-t_{n})\nonumber \\&\quad \frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1}) -f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ),e_{u}\Big ) dt +\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( f(u)-f(u_{h})\right) ,e_{u}\right) dt\nonumber \\ :=&\frac{1}{2}\Vert \nabla \Delta ^{-1}e_{u}^{0}\Vert ^{2}+\mathcal {B}_{1}+\cdots +\mathcal {B}_{17}, \end{aligned}$$

(A.18)

where

$$\begin{aligned} \mathcal {B}_{1}&:=\int _{0}^{T}\left( w_{h}^{n}-Rw_{h}^{n},-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{2}&:=\int _{0}^{T}\left( \frac{Aw_{h}^{n}-A w_{h}^{n-1}}{2},-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{3}&:=\int _{0}^{T} \left( (t-t_{n-\frac{1}{2}})\partial _{n}^{2}u_{h},-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{4}&:=\int _{0}^{T}\left( \mathcal {A}(q(t)-q^{n})+q(t)-q^{n},-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{5}&:=\int _{0}^{T}-\varepsilon a\left( \epsilon _{u},e_{u}\right) dt;\\ \mathcal {B}_{6}&:=\int _{0}^{T}\left( q^{n}-q(t)-(w_{h}^{n}-w_{h}),-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{7}&:=\int _{0}^{T}\left( w_{h}^{n}-w_{h},-\Delta ^{-1}e_{u}\right) dt;\\ \mathcal {B}_{8}&:=\int _{0}^{T}\varepsilon \left( \frac{Au_{h}^{n}-A u_{h}^{n-1}}{2},e_{u}\right) dt;\\ \mathcal {B}_{9}&:=\int _{0}^{T}\frac{1}{\varepsilon }\left( u_{h}^{n}-p^{n},e_{u}\right) dt;\\ \mathcal {B}_{10}&:=\int _{0}^{T}\left( \frac{Pf(u_{h}^{n})-Pf(u_{h}^{n-1})}{2\varepsilon },e_{u}\right) dt;\\ \mathcal {B}_{11}&:=-\int _{0}^{T}\left( \frac{ w_{h}^{n}-w_{h}^{n-1}}{2},e_{u}\right) dt;\\ \mathcal {B}_{12}&:=\int _{0}^{T}\Big (\Big (\varepsilon \mathcal {A}\Big (p(t)-p^{n}\Big ) -\frac{1}{\varepsilon }\Big (h(p^{n})\frac{t_{n}-t}{\tau _{n}}-h(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\\&\quad -\frac{1}{2}(t-t_{n-1})(t-t_{n}) \frac{\frac{h(p^{n})-h(p^{n-1})}{\tau _{n}}-\frac{h(p^{n-1})-h(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n} +\tau _{n-1}}{2}}\Big )-\Big (q(t)-q^{n}\Big )\Big ),e_{u}\Big ) dt;\\ \mathcal {B}_{13}&:=\int _{0}^{T}\Big (\frac{1}{\varepsilon }\left( p^{n}-p^{n-1} -\left( u_{h}^{n}-u_{h}^{n-1}\right) \right) \frac{t_{n}-t}{\tau _{n}}+\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\\&\quad \Big (\frac{\frac{p^{n}-p^{n-1}}{\tau _{n}}-\frac{p^{n-1} -p^{n-2}}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}-\frac{\frac{u_{h}^{n}-u_{h}^{n-1}}{\tau _{n}} -\frac{u_{h}^{n-1}-u_{h}^{n-2}}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ),e_{u}\Big ) dt;\\ \mathcal {B}_{14}&:=\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( u_{h}^{n}-u_{h}^{n-1}\right) \frac{t_{n}-t}{\tau _{n}},e_{u}\right) dt;\\ \mathcal {B}_{15}&:{=}\int _{0}^{T}\Big (\frac{1}{\varepsilon }\left( f(u_{h}^{n}) \frac{t{-}t_{n{-}1}}{\tau _{n}}{+}f(u_{h}^{n{-}1})\frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n}) {+}f(p^{n})\frac{t_{n}-t}{\tau _{n}}{-}f(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\right) \\&\quad +\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\\&\left( \frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1})-f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}-\frac{\frac{f(p^{n})-f(p^{n-1})}{\tau _{n}} -\frac{f(p^{n-1})-f(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\right) ,e_{u}\Big ) dt;\\ \mathcal {B}_{16}&:=\int _{0}^{T}\Big (\frac{1}{\varepsilon }\Big (f(u_{h})-f(u_{h}^{n}) \frac{t-t_{n-1}}{\tau _{n}}-f(u_{h}^{n-1})\frac{t_{n}-t}{\tau _{n}}\\&\quad -\frac{1}{2}(t-t_{n-1})(t-t_{n})\frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}} -\frac{f(u_{h}^{n-1})-f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ),e_{u}\Big ) dt;\\ \mathcal {B}_{17}&:=\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( f(u)-f(u_{h})\right) ,e_{u}\right) dt. \end{aligned}$$

Next we estimate each of the terms $\{\mathcal {B}_{j}\}_{j=1,\ldots ,17}$, separately.

Step 2: First, the term $\mathcal {B}_{1}$, which contains a spatial discretization error term, is bounded by using Schwarz inequality, the Nitche technique and interpolation error estimation

$$\begin{aligned} \mathcal {B}_{1}=&\int _{0}^{T}\left( w_{h}^{n}-Rw_{h}^{n},-\Delta ^{-1}e_{u}\right) dt\nonumber \\ =&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( w_{h}^{n}-Rw_{h}^{n},-\Delta ^{-1}e_{u}\right) dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| w_{h}^{n} -Rw_{h}^{n}\right\| \cdot \left\| \Delta ^{-1}e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}C_{3}h\left\| w_{h}^{n} -Rw_{h}^{n}\right\| _{1,\Omega }\left\| \Delta ^{-1}e_{u}\right\| dt. \end{aligned}$$

(A.19)

While h is small enough, it can be ignored. In the same way, the term $\mathcal {B}_{6}$ can be also ignored.

Similarly, the time discretization terms $\mathcal {B}_{2}$ and $\mathcal {B}_{3}$ can be estimated as

$$\begin{aligned} \mathcal {B}_{2}&=\int _{0}^{T}\left( \frac{Aw_{h}^{n}-Aw_{h}^{n-1}}{2},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{Aw_{h}^{n}-A w_{h}^{n-1}}{2} \right\| _{-1}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\&:=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\gamma _{w}^{n}\left\| \nabla \Delta ^{-1}e_{u}\right\| dt.\end{aligned}$$

(A.20)

$$\begin{aligned} \mathcal {B}_{3}&=\int _{0}^{T} \left( (t-t_{n-\frac{1}{2}}) \partial _{n}^{2}u_{h},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{\tau _{n}^{2}}{8} \cdot \partial _{n}^{2}u_{h}\right\| _{-1}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\&:=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\beta _{u}^{n}\left\| \nabla \Delta ^{-1}e_{u}\right\| dt. \end{aligned}$$

(A.21)

Step 3: For the term $\mathcal {B}_{4}$, based on the definition of elliptic reconstruction, we have

$$\begin{aligned} \mathcal {B}_{4}&=\int _{0}^{T}\left( \mathcal {A}(q(t)-q^{n})+q(t)-q^{n},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\Big (\mathcal {A}\Big (\frac{t-t_{n-1}}{\tau _{n}}q^{n} +\frac{t_{n}-t}{\tau _{n}}q^{n-1}+\frac{1}{2}(t-t_{n-1})(t-t_{n})\partial _{n}^{2}q-q^{n}\Big )\nonumber \\&\quad +\Big (\frac{t-t_{n-1}}{\tau _{n}}q^{n}+\frac{t_{n}-t}{\tau _{n}}q^{n-1} +\frac{1}{2}(t-t_{n-1})(t-t_{n})\partial _{n}^{2}q-q^{n}\Big ),-\Delta ^{-1}e_{u}\Big ) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\Big ((((\mathcal {A}Rw_{h}^{n-1}+Rw_{h}^{n-1}) -(\mathcal {A}Rw_{h}^{n}+Rw_{h}^{n}))\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad +\frac{1}{2}(t-t_{n-1})(t-t_{n})(\partial _{n}^{2}\mathcal {A}q+\partial _{n}^{2}q)), -\Delta ^{-1}e_{u}\Big ) dt\nonumber \\&{\le }\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| (\mathcal {A}Rw_{h}^{n-1}+Rw_{h}^{n-1} {-}(\mathcal {A}Rw_{h}^{n}{+}Rw_{h}^{n}))\frac{t_{n}-t}{\tau _{n}} {+}\frac{\tau _{n}^{2}}{8}\partial _{n}^{2}(\mathcal {A}Rw_{h}{+}Rw_{h})\right\| _{-1}\cdot \nonumber \\&\quad \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\Big (\left\| Aw_{h}^{n-1}+w_{h}^{n-1} -(Aw_{h}^{n}+w_{h}^{n})\right\| _{-1}+\left\| \frac{\tau _{n}^{2}}{8} \partial _{n}^{2}(Aw_{h}+w_{h})\right\| _{-1}\Big )\cdot \nonumber \\&\quad \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\ :&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\eta _{w}^{n}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt. \end{aligned}$$

(A.22)

Step 4: The term $\mathcal {B}_{5}$ yields the spatial discretization error, which is bounded as follows

$$\begin{aligned} \mathcal {B}_{5}&=-\int _{0}^{T}\varepsilon a(\epsilon _{u},e_{u})dt\nonumber \\&=-\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\varepsilon a(\epsilon _{u},e_{u})dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\varepsilon \Vert \nabla \epsilon _{u}\Vert \cdot \Vert \nabla e_{u}\Vert dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( 2\varepsilon ^{-2}\Vert \nabla \epsilon _{u}\Vert ^{2} +\frac{\varepsilon ^{4}}{8}\Vert \nabla e_{u}\Vert ^{2}\right) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} 2\varepsilon ^{-2}\left\| \nabla \epsilon _{u}\right\| ^{2}dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{\varepsilon ^{4}}{8}\left\| \nabla e_{u}\right\| ^{2}dt, \end{aligned}$$

(A.23)

and in view of the triangle inequality and the linearity of the operators G and $\nabla$, we get

$$\begin{aligned} \int _{t_{n-1}}^{t_{n}}\Vert \nabla \epsilon _{u}\Vert ^{2}dt&=\int _{t_{n-1}}^{t_{n}}\Vert \nabla (p-u_{h})\Vert ^{2}dt\nonumber \\&=\int _{t_{n-1}}^{t_{n}}\Big \Vert \nabla \Big (\Big (Ru_{h}^{n}-u_{h}^{n}\Big )\frac{t-t_{n-1}}{\tau _{n}} +\Big (Ru_{h}^{n-1}-u_{h}^{n-1}\Big )\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad +\frac{1}{2}(t-t_{n-1})(t-t_{n})(\partial _{n}^{2}p-\partial _{n}^{2}u_{h})\Big )\Big \Vert ^{2}dt\nonumber \\&\le \int _{t_{n-1}}^{t_{n}}\bigg (\big \Vert \nabla \big (Ru_{h}^{n}-u_{h}^{n}\big )\big \Vert ^{2} \Big (\frac{t-t_{n-1}}{\tau _{n}}\Big )^{2}+\big \Vert \nabla \big (Ru_{h}^{n-1}-u_{h}^{n-1}\big ) \big \Vert ^{2}\Big (\frac{t_{n}-t}{\tau _{n}}\Big )^{2}\nonumber \\&\quad +\frac{(t-t_{n-1})^{2}(t-t_{n})^{2}}{4}\Vert \partial _{n}^{2}\nabla p -\partial _{n}^{2}\nabla u_{h}\Vert ^{2}\nonumber \\&\quad +2\big \Vert \nabla \big (Ru_{h}^{n}-u_{h}^{n}\big )\big \Vert \cdot \big \Vert \nabla \big (Ru_{h}^{n-1} -u_{h}^{n-1}\big )\big \Vert \frac{(t-t_{n-1})(t_{n}-t)}{\tau _{n}^{2}}\nonumber \\&\quad +2\big \Vert \nabla \big (Ru_{h}^{n}-u_{h}^{n}\big )\big \Vert \cdot \Vert \partial _{n}^{2}\nabla p-\partial _{n}^{2}\nabla u_{h}\Vert \frac{(t-t_{n-1})^{2}(t-t_{n})}{2\tau _{n}}\nonumber \\&\quad +2\big \Vert \nabla \big (Ru_{h}^{n-1}-u_{h}^{n-1}\big )\big \Vert \cdot \Vert \partial _{n}^{2}\nabla p -\partial _{n}^{2}\nabla u_{h}\Vert \frac{(t-t_{n-1})(t-t_{n})^{2}}{2\tau _{n}} \bigg )dt\nonumber \\&\le C_{0}^{2}\left( (\mathcal {E}_{u}^{n})^{2}\frac{(t-t_{n-1})^{3}}{3(t_{n} -t_{n-1})^{2}}\left. \right| _{t_{n-1}}^{t_{n}}-(\mathcal {E}_{u}^{n-1})^{2}\frac{(t_{n}-t)^{3}}{3(t_{n}-t_{n-1})^{2}}\left. \right| _{t_{n-1}}^{t_{n}}\right. \nonumber \\&\quad \left. +2\mathcal {E}_{u}^{n}\mathcal {E}_{u}^{n-1}\frac{\frac{1}{2}(t_{n}+t_{n-1})t^{2} -\frac{1}{3}t^{3}-t_{n}t_{n-1}\cdot t}{(t_{n}-t_{n-1})^{2}}\left. \right| _{t_{n-1}}^{t_{n}}\right) \nonumber \\&\quad +\frac{\tau _{n}^{3}}{12}C_{0}\Vert \partial _{n}^{2}\nabla p-\partial _{n}^{2}\nabla u_{h}\Vert \Big (\mathcal {E}_{u}^{n}+\mathcal {E}_{u}^{n-1}\Big )+\frac{\tau _{n}^{5}}{120}\Vert \partial _{n}^{2}\nabla p-\partial _{n}^{2}\nabla u_{h}\Vert ^{2}\nonumber \\&\le \frac{C_{0}^{2}}{3}\tau _{n}\left( (\mathcal {E}_{u}^{n})^{2}+(\mathcal {E}_{u}^{n-1})^{2} +\mathcal {E}_{u}^{n}\mathcal {E}_{u}^{n-1}\right) \nonumber \\&\quad +C_{0}^{2}\frac{\tau _{n}^{2}\tau _{n-1}\Big (\mathcal {E}_{u}^{n}+\mathcal {E}_{u}^{n-1}\Big ) +\tau _{n}^{3}\Big (\mathcal {E}_{u-1}^{n}+\mathcal {E}_{u}^{n-2}\Big )}{6\tau _{n-1}(\tau _{n}+\tau _{n-1})} \Big (\mathcal {E}_{u}^{n}+\mathcal {E}_{u}^{n-1}\Big )\nonumber \\&\quad +C_{0}^{2}\tau _{n}^{3}\frac{\Big (\tau _{n-1}\Big (\mathcal {E}_{u}^{n}+\mathcal {E}_{u}^{n-1}\Big ) +\tau _{n}\Big (\mathcal {E}_{u-1}^{n}+\mathcal {E}_{u}^{n-2}\Big )\Big )^{2}}{30\tau _{n-1}^{2}(\tau _{n}+\tau _{n-1})^{2}}\nonumber \\&:= \widetilde{\mathcal {E}_{u}^{n}}^{2}, \end{aligned}$$

(A.24)

then taking (A.24) into (A.23), we get

$$\begin{aligned} \begin{aligned} \mathcal {B}_{5}\le \sum _{n=1}^{N}2\varepsilon ^{-2}\widetilde{\mathcal {E}_{u}^{n}}^{2} +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{\varepsilon ^{4}}{8}\left\| \nabla e_{u}\right\| ^{2}dt. \end{aligned} \end{aligned}$$

(A.25)

Similarly, the spatial discretization error term $\mathcal {B}_{9}$ is estimated as follows

$$\begin{aligned} \mathcal {B}_{9}=&\int _{0}^{T}\frac{1}{\varepsilon }\left( u_{h}^{n}-p^{n},e_{u}\right) dt\nonumber \\ =&\sum _{n=1}^{N}\frac{1}{\varepsilon }\int _{t_{n-1}}^{t_{n}}\left( u_{h}^{n}-Ru_{h}^{n},e_{u}\right) dt\nonumber \\ \le&\sum _{n=1}^{N}\frac{1}{\varepsilon }\int _{t_{n-1}}^{t_{n}} \left\| u_{h}^{n}-Ru_{h}^{n}\right\| \cdot \left\| e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\frac{1}{\varepsilon }\int _{t_{n-1}}^{t_{n}}\kappa (h) \left\| u_{h}^{n}-Ru_{h}^{n}\right\| _{1,\Omega }\left\| e_{u}\right\| dt, \end{aligned}$$

(A.26)

where we have used Lemma A.3 in the last inequality. Since h could be small enough, the term $B_9$ can be ignored. With a similar argument, the term $\mathcal {B}_{13}$ can be also ignored.

Step 5: The time discretization term $\mathcal {B}_{7}$ is bounded as follows

$$\begin{aligned} \mathcal {B}_{7}&=\int _{0}^{T}\left( w_{h}^{n}-w_{h},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( (w_{h}^{n}-w_{h}^{n-1})\frac{t_{n}-t}{\tau _{n}} -\frac{1}{2}(t-t_{n-1})(t-t_{n})\partial _{n}^{2}w_{h},-\Delta ^{-1}e_{u}\right) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \left\| w_{h}^{n}-w_{h}^{n-1}\right\| _{-1} +\left\| \frac{\tau _{n}^{2}}{8}\partial _{n}^{2}w_{h}\right\| _{-1}\right) \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\&:=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\delta _{w}^{n}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt. \end{aligned}$$

(A.27)

Similarly, the terms $\mathcal {B}_{8}$, $\mathcal {B}_{10}$, $\mathcal {B}_{11}$, $\mathcal {B}_{14}$ are also the time discretization terms, and they are estimated as follows

$$\begin{aligned} \mathcal {B}_{8}&=\int _{0}^{T}\varepsilon \left( \frac{Au_{h}^{n}-Au_{h}^{n-1}}{2},e_{u}\right) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\varepsilon \left\| \frac{Au_{h}^{n}-A u_{h}^{n-1}}{2}\right\| \cdot \left\| e_{u}\right\| dt\nonumber \\ :&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\gamma _{u}^{n}\left\| e_{u}\right\| dt, \end{aligned}$$

(A.28)

$$\begin{aligned} \mathcal {B}_{10}=&\int _{0}^{T}\left( \frac{Pf(u_{h}^{n})-Pf(u_{h}^{n-1})}{2\varepsilon },e_{u}\right) dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{Pf(u_{h}^{n}) -Pf(u_{h}^{n-1})}{2\varepsilon }\right\| \left\| e_{u}\right\| dt\nonumber \\ :=&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\xi _{u}^{n}\cdot \left\| e_{u}\right\| dt, \end{aligned}$$

(A.29)

$$\begin{aligned} \mathcal {B}_{11}=&-\int _{0}^{T}\left( \frac{w_{h}^{n}-w_{h}^{n-1}}{2},e_{u}\right) dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{w_{h}^{n}-w_{h}^{n-1}}{2}\right\| \left\| e_{u}\right\| dt\nonumber \\ :=&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\beta _{w}^{n}\cdot \left\| e_{u}\right\| dt,\end{aligned}$$

(A.30)

$$\begin{aligned} \mathcal {B}_{14}&=\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( u_{h}^{n}-u_{h}^{n-1}\right) \frac{t_{n}-t}{\tau _{n}},e_{u}\right) \nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{u_{h}^{n}-u_{h}^{n-1}}{\varepsilon }\right\| \left\| e_{u}\right\| dt\nonumber \\&:=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\delta _{u}^{n}\cdot \left\| e_{u}\right\| dt. \end{aligned}$$

(A.31)

Step 6: The term $\mathcal {B}_{12}$, which also contains a time discretization term, is estimated by using the definitions of $w^{n}$, w and $R^{n}$.

$$\begin{aligned} \mathcal {B}_{12}&=\int _{0}^{T}\Big (\Big (\varepsilon \mathcal {A}\Big (p(t)-p^{n}\Big ) -\frac{1}{\varepsilon }\Big (h(p^{n})\frac{t_{n}-t}{\tau _{n}}-h(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad -\frac{1}{2}(t-t_{n-1})(t-t_{n}) \frac{\frac{h(p^{n})-h(p^{n-1})}{\tau _{n}}-\frac{h(p^{n-1})-h(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big )-\Big (q(t)-q^{n}\Big )\Big ),e_{u}\Big ) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\Big (\Big (\varepsilon \mathcal {A}\Big (p^{n} \frac{t-t_{n-1}}{\tau _{n}}+p^{n-1}\frac{t_{n}-t}{\tau _{n}}+\frac{1}{2}(t-t_{n-1})(t-t_{n})\partial _{n}^{2}p-p^{n}\Big )\nonumber \\&\quad -\frac{1}{\varepsilon }\Big (h(p^{n})-h(p^{n-1})\Big )\frac{t_{n}-t}{\tau _{n}} +\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\frac{\frac{h(p^{n})-h(p^{n-1})}{\tau _{n}} -\frac{h(p^{n-1})-h(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\nonumber \\&\quad -\Big (q^{n}\frac{t-t_{n-1}}{\tau _{n}}+q^{n-1}\frac{t_{n}-t}{\tau _{n}} +\frac{1}{2}(t-t_{n-1})(t-t_{n})\partial _{n}^{2}q-q^{n}\Big )\Big ),e_{u}\Big ) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\Big (\Big (\big (\varepsilon \mathcal {A}Ru_{h}^{n-1} +\frac{1}{\varepsilon }h(Ru_{h}^{n-1})-q^{n-1}\big )-\big (\varepsilon \mathcal {A}Ru_{h}^{n} +\frac{1}{\varepsilon }h(Ru_{h}^{n})-q^{n}\big )\Big )\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad +\frac{\frac{(\varepsilon \mathcal {A}p^{n}+\frac{ h(p^{n})}{\varepsilon }-q^{n}) -(\varepsilon \mathcal {A}p^{n-1}+\frac{ h(p^{n-1})}{\varepsilon }-q^{n-1})}{\tau _{n}} -\frac{(\varepsilon \mathcal {A}p^{n-1}+\frac{ h(p^{n-1})}{\varepsilon }-q^{n-1}) -(\varepsilon \mathcal {A}p^{n-2}+\frac{ h(p^{n-2})}{\varepsilon }-q^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\nonumber \\&\quad \frac{(t-t_{n-1})(t-t_{n})}{2},e_{u}\Big ) dt\nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} \Big (2\Big \Vert \Big (\varepsilon Au_{h}^{n-1} +\frac{1}{\varepsilon }h(u_{h}^{n-1})-w_{h}^{n-1}\Big )-\Big (\varepsilon Au_{h}^{n} +\frac{1}{\varepsilon }h(u_{h}^{n})-w_{h}^{n}\Big )\Big \Vert \nonumber \\&\quad +\Big \Vert \Big (\varepsilon Au_{h}^{n-1}+\frac{1}{\varepsilon }h(u_{h}^{n-1}) -w_{h}^{n-1}\Big )-\Big (\varepsilon Au_{h}^{n-2}+\frac{1}{\varepsilon }h(u_{h}^{n-2}) -w_{h}^{n-2}\Big ) \Big \Vert \Big )\cdot \Vert e_{u}\Vert dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} \theta _{u}^{n}\cdot \Vert e_{u}\Vert dt. \end{aligned}$$

(A.32)

Step 7: The term $\mathcal {B}_{15}$ also yields a time discretization error, which is estimated by using Lagrange mean value theorem and embedding theorem.

$$\begin{aligned} \mathcal {B}_{15}{=}&\int _{0}^{T}\Big (\frac{1}{\varepsilon }\left( f(u_{h}^{n}) \frac{t{-}t_{n{-}1}}{\tau _{n}}{+}f(u_{h}^{n-1})\frac{t_{n}{-}t}{\tau _{n}}{-}f(p^{n}) {+}f(p^{n})\frac{t_{n}-t}{\tau _{n}}{-}f(p^{n-1})\frac{t_{n}-t}{\tau _{n}}\right) \nonumber \\&+\frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n})\nonumber \\&\left( \frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1}) -f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}-\frac{\frac{f(p^{n}) -f(p^{n-1})}{\tau _{n}}-\frac{f(p^{n-1})-f(p^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n} +\tau _{n-1}}{2}}\right) ,e_{u}\Big ) dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \frac{t-t_{n-1}}{\tau _{n}\varepsilon } \left( f(u_{h}^{n})-f(p^{n})\right) ,e_{u}\right) dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} \left( \frac{t_{n}-t}{\tau _{n}\varepsilon }\left( f(u_{h}^{n-1})-f(p^{n-1})\right) ,e_{u}\right) dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n}) \frac{\frac{f(u_{h}^{n})-f(p^{n})}{\tau _{n}}}{\frac{\tau _{n}+\tau _{n-1}}{2}},e_{u}\right) dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \frac{1}{\varepsilon }(t-t_{n-1})(t-t_{n}) \frac{\frac{f(u_{h}^{n-1})-f(p^{n-1})}{\tau _{n}}}{\frac{\tau _{n}+\tau _{n-1}}{2}},e_{u}\right) dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \frac{1}{2\varepsilon }(t-t_{n-1})(t-t_{n}) \frac{\frac{f(u_{h}^{n-2})-f(p^{n-2})}{\tau _{n}}}{\frac{\tau _{n}+\tau _{n-1}}{2}},e_{u}\right) dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{3}{2\varepsilon }\left\| f'(\xi _{1})\right\| _{0,3,\Omega } \cdot \left\| u_{h}^{n}-p^{n}\right\| _{0,6,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{2}{\varepsilon }\left\| f'(\xi _{2})\right\| _{0,3,\Omega } \cdot \left\| u_{h}^{n-1}-p^{n-1}\right\| _{0,6,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2\varepsilon }\left\| f'(\xi _{3})\right\| _{0,3,\Omega } \cdot \left\| u_{h}^{n-2}-p^{n-2}\right\| _{0,6,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{3}{2\varepsilon }\left\| f'(\xi _{1})\right\| _{1,\Omega } \cdot \left\| u_{h}^{n}-p^{n}\right\| _{1,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{2}{\varepsilon }\left\| f'(\xi _{2})\right\| _{1,\Omega } \cdot \left\| u_{h}^{n-1}-p^{n-1}\right\| _{1,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2\varepsilon }\left\| f'(\xi _{3})\right\| _{1,3,\Omega } \cdot \left\| u_{h}^{n-2}-p^{n-2}\right\| _{1,6,\Omega }\cdot \left\| e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{\varepsilon }C\mathcal {E}_{u}^{n}\left\| e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{\varepsilon }C\mathcal {E}_{u}^{n-1}\left\| e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{\varepsilon }C\mathcal {E}_{u}^{n-2}\left\| e_{u}\right\| dt\nonumber \\ :=&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\alpha _{u}^{n}\left\| e_{u}\right\| dt. \end{aligned}$$

(A.33)

Step 8: In order to estimate the term $\mathcal {B}_{16}$, which also yields a time discretization error, we first simplify the following formula

$$\begin{aligned}&f(u_{h})-f(u_{h}^{n})\frac{t-t_{n-1}}{\tau _{n}}-f(u_{h}^{n-1})\frac{t_{n}-t}{\tau _{n}} -\frac{1}{2}(t-t_{n-1})(t-t_{n})\nonumber \\&\frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1}) -f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\nonumber \\&\quad =\big [3(u_{h}^{n})^{2}u_{h}^{n-1}-2(u_{h}^{n})^{3}-(u_{h}^{n-1})^{3}\big ]\cdot \left( \frac{t-t_{n-1}}{\tau _{n}}\right) ^{2}\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad +\big [3u_{h}^{n}(u_{h}^{n-1})^{2}-(u_{h}^{n})^{3}-2(u_{h}^{n-1})^{3}\big ]\cdot \frac{t-t_{n-1}}{\tau _{n}}\left( \frac{t_{n}-t}{\tau _{n}}\right) ^{2}\nonumber \\&\quad +\big [3(u_{h}^{n})^{2}\partial _{n}^{2}u_{h}-3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\big ] \cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\left( \frac{t-t_{n-1}}{\tau _{n}}\right) ^{2}\nonumber \\&\quad +\big [3(u_{h}^{n-1})^{2}\partial _{n}^{2}u_{h}-3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\big ] \cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\left( \frac{t_{n}-t}{\tau _{n}}\right) ^{2}\nonumber \\&\quad +\big [3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}-\frac{\frac{(u_{h}^{n})^{3} -(u_{h}^{n-1})^{3}}{\tau _{n}}-\frac{(u_{h}^{n-1})^{3}-(u_{h}^{n-2})^{3}}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\big ]\cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\nonumber \\&\quad +\Big [\big (3u_{h}^{n}(\partial _{n}^{2}u_{h})^{2}-3u_{h}^{n-1}(\partial _{n}^{2}u_{h})^{2}\big ) \cdot \left( \frac{t-t_{n-1}}{\tau _{n}}\right) +3u_{h}^{n-1}(\partial _{n}^{2}u_{h})^{2}\Big ]\nonumber \\&\quad \cdot \Big (\frac{1}{2}(t-t_{n-1})(t-t_{n})\Big )^{2}+\Big [\Big (\frac{1}{2}(t-t_{n-1})(t-t_{n})\Big )^{3}(\partial _{n}^{2}u_{h})^{3}\Big ], \end{aligned}$$

(A.34)

thus we have

$$\begin{aligned} \mathcal {B}_{16}&=\int _{0}^{T}\Big (\frac{1}{\varepsilon }\Big (f(u_{h})-f(u_{h}^{n})\frac{t-t_{n-1}}{\tau _{n}}-f(u_{h}^{n-1}) \frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad -\frac{1}{2}(t-t_{n-1})(t-t_{n}) \frac{\frac{f(u_{h}^{n})-f(u_{h}^{n-1})}{\tau _{n}}-\frac{f(u_{h}^{n-1})-f(u_{h}^{n-2})}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ),e_{u}\Big ) dt\nonumber \\&=\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{\varepsilon } \Big ( \Big [3(u_{h}^{n})^{2}u_{h}^{n-1} -2(u_{h}^{n})^{3}-(u_{h}^{n-1})^{3}\Big ]\cdot \Big (\frac{t-t_{n-1}}{\tau _{n}}\Big )^{2}\frac{t_{n}-t}{\tau _{n}}\nonumber \\&\quad +\Big [3u_{h}^{n}(u_{h}^{n-1})^{2}-(u_{h}^{n})^{3}-2(u_{h}^{n-1})^{3}\Big ]\cdot \frac{t-t_{n-1}}{\tau _{n}}\Big (\frac{t_{n}-t}{\tau _{n}}\Big )^{2}\nonumber \\&\quad +\Big [3(u_{h}^{n})^{2}\partial _{n}^{2}u_{h}-3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\Big ] \cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\left( \frac{t-t_{n-1}}{\tau _{n}}\right) ^{2}\nonumber \\&\quad +\Big [3(u_{h}^{n-1})^{2}\partial _{n}^{2}u_{h}-3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\Big ] \cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\left( \frac{t_{n}-t}{\tau _{n}}\right) ^{2}\nonumber \\&\quad +\Big [3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}--\frac{\frac{(u_{h}^{n})^{3} -(u_{h}^{n-1})^{3}}{\tau _{n}}-\frac{(u_{h}^{n-1})^{3}-(u_{h}^{n-2})^{3}}{\tau _{n-1}}}{\frac{\tau _{n}+\tau _{n-1}}{2}}\Big ]\cdot \frac{1}{2}(t-t_{n-1})(t-t_{n})\nonumber \\&\quad +\Big [\big (3u_{h}^{n}(\partial _{n}^{2}u_{h})^{2}-3u_{h}^{n-1}(\partial _{n}^{2}u_{h})^{2}\big ) \cdot \left( \frac{t-t_{n-1}}{\tau _{n}}\right) +3u_{h}^{n-1}(\partial _{n}^{2}u_{h})^{2}\Big ] \cdot \Big (\frac{1}{2}(t-t_{n-1})(t-t_{n})\Big )^{2}\nonumber \\&\quad +\Big [\Big (\frac{1}{2}(t-t_{n-1})(t-t_{n})\Big )^{3}(\partial _{n}^{2}u_{h})^{3}\Big ] ,e_{u}\Big ) dt \nonumber \\&\le \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{3(u_{h}^{n})^{2}u_{h}^{n-1}-2(u_{h}^{n})^{3} -(u_{h}^{n-1})^{3}}{\varepsilon }\right\| \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad + \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{3u_{h}^{n}(u_{h}^{n-1})^{2}-2(u_{h}^{n-1})^{3} -(u_{h}^{n})^{3}}{\varepsilon } \right\| \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{\big (3(u_{h}^{n})^{2}\partial _{n}^{2}u_{h} -3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\big )\tau _{n}^{2}}{8\varepsilon } \right\| \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{\big (3(u_{h}^{n-1})^{2}\partial _{n}^{2}u_{h} -3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h}\big )\tau _{n}^{2}}{8\varepsilon } \right\| \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left\| \frac{\big (3u_{h}^{n}u_{h}^{n-1}\partial _{n}^{2}u_{h} -\frac{\frac{(u_{h}^{n})^{3}-(u_{h}^{n-1})^{3}}{\tau _{n}}-\frac{(u_{h}^{n-1})^{3} -(u_{h}^{n-2})^{3}}{\tau _{n-1}}}{\frac{\tau _{n} +\tau _{n-1}}{2}}\big )\tau _{n}^{2}}{8\varepsilon } \right\| \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} \left( \left\| \frac{\big (3u_{h}^{n}(\partial _{n}^{2}u_{h})^{2}-3u_{h}^{n-1} (\partial _{n}^{2}u_{h})^{2}\big )\tau _{n}^{4}}{64\varepsilon } \right\| +\left\| \frac{\big (3u_{h}^{n-1}(\partial _{n}^{2}u_{h})^{2}\big )\tau _{n}^{4}}{64\varepsilon }\right\| \right) \cdot \left\| e_{u}\right\| dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\left( \left\| \frac{(\partial _{n}^{2}u_{h})^{3}\tau _{n}^{6}}{512\varepsilon } \right\| \right) \cdot \left\| e_{u}\right\| dt\nonumber \\&:= \sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\zeta _{u}^{n}\left\| e_{u}\right\| dt. \end{aligned}$$

(A.35)

Step 9: Grouping together (A.19)–(A.22), (A.26) and (A.27), we have

$$\begin{aligned} \mathcal {B}_{1}+\cdots&+\mathcal {B}_{4}+\mathcal {B}_{6}+\mathcal {B}_{7}\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\gamma _{w}^{n}\left\| \nabla \Delta ^{-1}e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\beta _{u}^{n}\left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\delta _{w}^{n}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\eta _{w}^{n}\cdot \left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\ :=&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\eta _{0}\left\| \nabla \Delta ^{-1}e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2}\eta _{0}^{2}dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2}\left\| \nabla \Delta ^{-1}e_{u}\right\| ^{2}dt. \end{aligned}$$

(A.36)

Summing up (A.28)–(A.33) and (A.35), it holds that

$$\begin{aligned} \mathcal {B}_{8}+\cdots +\mathcal {B}_{16}\le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\gamma _{u}^{n}\left\| e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\xi _{u}^{n}\left\| e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\beta _{w}^{n}\left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}} \theta _{u}^{n}\cdot \Vert e_{u}\Vert dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\delta _{u}^{n}\cdot \left\| e_{u}\right\| dt\nonumber \\&+\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\alpha _{u}^{n}\left\| e_{u}\right\| dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\zeta _{u}^{n}\left\| e_{u}\right\| dt\nonumber \\ :=&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\eta _{1}\left\| e_{u}\right\| dt\nonumber \\ \le&\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2\varepsilon ^2}\eta _{1}^{2}dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{\varepsilon ^2}{2}\left\| e_{u}\right\| ^{2}dt. \end{aligned}$$

(A.37)

Step 10: Notice that [4]

$$\begin{aligned} f(a_1)-f(a_2)-f'(a_2)(a_1-a_2)= 3a_2(a_1-a_2)^2+(a_1-a_2)^3, \end{aligned}$$

then

$$\begin{aligned} \left( f(a_1)-f(a_2)-f'(a_2)(a_1-a_2)\right) \left( a_1-a_2\right)&=3a_2(a_1-a_2)^3+(a_1-a_2)^4\nonumber \\&\ge -\tilde{f}(a_2)\mid a_1-a_2\mid ^{3} \end{aligned}$$

(A.38)

with $\tilde{f}(a_2)=3|a_2|$. Therefore, according to (A.38) and the spectrum estimate [1, 9], we obtain the following estimation for the term $\mathcal {B}_{17}$

$$\begin{aligned} \mathcal {B}_{17}=&\int _{0}^{T}\left( \frac{1}{\varepsilon }\left( f(u)-f(u_{h})\right) ,e_{u}\right) dt\nonumber \\ \le&\int _{0}^{T}\left( -\frac{1}{\varepsilon }\left( f'(u_{h})e_{u},e_{u}\right) +\frac{1}{\varepsilon }\left( \tilde{f}(u_{h}),|u-u_{h}|^{3}\right) \right) dt\nonumber \\ \le&\int _{0}^{T}\left( -\frac{1-\varepsilon ^3}{\varepsilon }\left( f'(u_{h})e_{u},e_{u}\right) -\varepsilon ^2\left( f'(u_{h})e_{u},e_{u}\right) +\frac{1}{\varepsilon } \left( \tilde{f}(u_{h}),|u-u_{h}|^{3}\right) \right) dt\nonumber \\ {\le }&\int _{0}^{T}\left( \left( 1{-}\varepsilon ^3\right) \overline{\Lambda }_{h}(t)\Vert \nabla \Delta ^{{-}1} e_{u}\Vert ^{2} {+}\varepsilon \left( 1-\varepsilon ^3\right) \Vert \nabla e_{u}\Vert ^{2}{+}2\varepsilon ^2\Vert e_{u}\Vert ^{2} {+}\frac{1}{\varepsilon }\mu _{g}\Vert e_{u}\Vert _{L^{3}}^{3}\right) dt, \end{aligned}$$

(A.39)

here $\mu _{g}:=\sup \limits _{t\in (0,T)}\Vert \tilde{f}(u_{h})\Vert _{L^{\infty }(\Omega )}$.

Step 11: Taking (A.25), (A.36) and (A.39) into (A.18), we have

$$\begin{aligned} \frac{1}{2}\Vert \nabla \Delta ^{-1}e_{u}^{N}\Vert ^{2}{+}\int _{0}^{T}\varepsilon \Vert \nabla e_{u}\Vert ^{2}dt&{\le } \frac{1}{2}\Vert \nabla \Delta ^{-1}e_{u}^{0}\Vert ^{2}{+}\sum _{n=1}^{N}2\varepsilon ^{{-}2} \widetilde{\mathcal {E}_{u}^{n}}^{2}{+}\sum _{n=1}^{N}\int _{t_{n{-}1}}^{t_{n}} \frac{\varepsilon ^{4}}{8}\left\| \nabla e_{u}\right\| ^{2}dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2}\eta _{0}^{2}dt+\sum _{n=1}^{N} \int _{t_{n-1}}^{t_{n}}\frac{1}{2}\left\| \nabla \Delta ^{-1}e_{u}\right\| ^{2}dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{1}{2\varepsilon ^2}\eta _{1}^{2}dt +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}\frac{\varepsilon ^2}{2}\left\| e_{u}\right\| ^{2}dt\nonumber \\&\quad +\int _{0}^{T}\left( 1-\varepsilon ^3\right) \overline{\Lambda }_{h}(t)\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}dt\nonumber \\&\quad +\sum _{n=1}^{N}\int _{t_{n-1}}^{t_{n}}2\varepsilon ^2\left\| e_{u}\right\| ^{2}dt +\int _{0}^{T}\varepsilon \left( 1-\varepsilon ^3\right) \Vert \nabla e_{u}\Vert ^{2}dt\nonumber \\&\quad +\int _{0}^{T}\frac{1}{\varepsilon }\mu _{g}\Vert e_{u}\Vert _{L^{3}}^{3}dt. \end{aligned}$$

(A.40)

Note that

$$\begin{aligned} \frac{5\varepsilon ^2}{2}\left\| e_{u}\right\| ^{2}&=\frac{5\varepsilon ^2}{2} \left( \nabla (-\Delta ^{-1}e_{u}),\nabla e_{u}\right) \nonumber \\&\le \sqrt{5}\Vert \nabla \Delta ^{-1}e_{u}\Vert \cdot \frac{\sqrt{5}\varepsilon ^2}{2}\Vert \nabla e_{u}\Vert \nonumber \\&\le \frac{5}{2}\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}+\frac{5\varepsilon ^{4}{8}}{\Vert }\nabla e_{u}\Vert ^{2}, \end{aligned}$$

(A.41)

plugging (A.41) into (A.40), and further simplification, then we obtain

$$\begin{aligned}&\Vert \nabla \Delta ^{-1}e_{u}^{N}\Vert ^{2}+\int _{0}^{T}\frac{\varepsilon ^{4}}{2}\Vert \nabla e_{u}\Vert ^{2}dt \nonumber \\&\quad \le \Vert \nabla \Delta ^{-1}e_{u}^{0}\Vert ^{2}+\sum _{n=1}^{N}4\varepsilon ^{-2} \widetilde{\mathcal {E}_{u}^{n}}^{2}+\sum _{n=1}^{N}\left( \eta _{0}^{2} +\varepsilon ^{-2}\eta _{1}^{2}\right) \tau _{n}\nonumber \\&\qquad +\int _{0}^{T}\left( 6+2\left( 1-\varepsilon ^3\right) \overline{\Lambda }_{h}(t)\right) \Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}dt\nonumber \\&\qquad +\int _{0}^{T}\frac{2}{\varepsilon }\mu _{g}\Vert e_{u}\Vert _{L^{3}}^{3}dt. \end{aligned}$$

(A.42)

Let

$$\begin{aligned} y_{1}(t)&:=\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}, \qquad y_{2}(t):=\frac{\varepsilon ^{4}}{2}\Vert \nabla e_{u}\Vert ^{2},\qquad y_{3}(t):=2\varepsilon ^{-1}\mu _{g}\Vert e_{u}\Vert _{L^{3}}^{3},\\ \eta ^2&:=\Vert \nabla \Delta ^{-1}e_{u}^{0}\Vert ^{2}+\sum _{n=1}^{N}4\varepsilon ^{-2} \widetilde{\mathcal {E}_{u}^{n}}^{2}+\sum _{n=1}^{N}\left( \eta _{0}^{2}+\varepsilon ^{-2}\eta _{1}^{2}\right) \tau _{n}. \end{aligned}$$

According to Lemma A.1 and assume that $\Vert e_{u}\Vert _{L^{\infty }}\le C$, it holds that

$$\begin{aligned} \int _{0}^{T}2\varepsilon ^{-1}\mu _{g}\Vert e_{u}\Vert _{L^{3}}^{3}dt&\le \int _{0}^{T}2\varepsilon ^{-1} \mu _{g}C_{I}\Vert e_{u}\Vert _{L^{\infty }(\Omega )}^{1-\sigma }\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{\sigma }\Vert \nabla e_{u}\Vert ^{2}dt\\&\le \int _{0}^{T}2\varepsilon ^{-1}\mu _{g}C_{I}\Vert e_{u}\Vert _{L^{\infty } (\Omega )}^{1-\sigma }\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{\sigma }\Vert \nabla e_{u}\Vert ^{2}dt\\&\le 2\varepsilon ^{-1}\mu _{g}C_{S}\left( \sup _{t\in (0,T)}\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{\sigma }\right) \int _{0}^{T}\Vert \nabla e_{u}\Vert ^{2}dt\\&\le B\left( \sup _{t\in (0,T)}\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{\sigma }\right) \int _{0}^{T}\left( \Vert \nabla e_{u}\Vert ^{2}+ \Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}\right) dt, \end{aligned}$$

with $B:=2\varepsilon ^{-1}\mu _{g}C_{S}$. Setting

$$\begin{aligned} E:=\exp \left( \int _{0}^{T}a(t)dt\right) ,\qquad \qquad \beta :=\sigma ,\qquad \qquad A=\eta ^2, \end{aligned}$$

and based on the assumption on A shown in Lemma A.2, we have

$$\begin{aligned} \eta ^{2}\le \frac{\varepsilon ^{1/\sigma }}{(2\mu _{g}C_{S}(1+T))^{1/\sigma }} \left( 8\exp \left( \int _{0}^{T}a(t)dt\right) \right) ^{-1-\frac{1}{\sigma }}. \end{aligned}$$

Therefore, by using Lemma A.2, we obtain

$$\begin{aligned} \sup _{t\in [0,T]}\Vert \nabla \Delta ^{-1}e_{u}\Vert ^{2}+\int _{0}^{T} \frac{\varepsilon ^{4}}{2}\Vert \nabla e_{u}\Vert ^{2}dt\le 8\eta ^{2}\exp \left( \int _{0}^{T}a(t)dt\right) . \end{aligned}$$

$\square$