Abstract
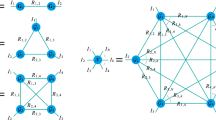
The fully-connected tensor network (FCTN) decomposition is an emerging method for processing and analyzing higher-order tensors. For an Nth-order tensor, the standard deterministic algorithms, such as alternating least squares (FCTN-ALS) algorithm, need to store large coefficient matrices formed by contracting \(N-1\) FCTN factor tensors. The memory cost of coefficient matrices grows exponentially with the size of the original tensor, which makes the algorithms memory-prohibitive for handling large-scale tensors. To enable FCTN decomposition to handle large-scale tensors effectively, we propose a stochastic gradient descent (FCTN-SGD) algorithm without sacrificing accuracy. The memory cost of FCTN-SGD algorithm grows linearly with the size of the original tensor and is significantly lower than that of the FCTN-ALS algorithm. The success of the FCTN-SGD algorithm lies in the suggested factor sampling operator, which cleverly avoids storing large coefficient matrices in the algorithm. By using the suggested operator, sampling on small factor tensors is equal to sampling on large coefficient matrices with a theoretical guarantee. Furthermore, we present an FCTN-VRSGD algorithm by introducing variance reduction into the FCTN-SGD algorithm, and theoretically prove the convergence of the FCTN-VRSGD algorithm under a mild assumption. Numerical experiments demonstrate the efficiency and accuracy of the proposed FCTN-SGD and FCTN-VRSGD algorithms, especially for real-world large-scale tensors.







Similar content being viewed by others
Data Availibility Statement
The datasets generated during and analysed during the current study are available from the corresponding author on reasonable request.
Notes
Given a parameter \(\epsilon >0\), a solution \(\{\mathcal {G}_1^s, \mathcal {G}_2^s, \ldots , \mathcal {G}_N^s\}\) is defined as a stochastic \(\epsilon \)-stationary solution of \(f(\mathcal {G})\) if \(\mathbb {E}[||\nabla _{\mathcal {G}_{n}}f(\mathcal {G}^{k})||_F]\le \epsilon \) for \(n=1,2, \ldots ,N\).
References
Wang, Y., Meng, D., Yuan, M.: Sparse recovery: from vectors to tensors. Natl. Sci. Rev. 5(5), 756–767 (2017)
Bro, R.: PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst. 38(2), 149–171 (1997)
Yokota, T., Zhao, Q., Cichocki, A.: Smooth PARAFAC decomposition for tensor completion. IEEE Trans. Signal Process. 64(20), 5423–5436 (2016)
Zeng, C.: Rank properties and computational methods for orthogonal tensor decompositions. J. Sci. Comput. 94(1), 6 (2023)
Pan, J., Ng, M.K., Liu, Y., Zhang, X., Yan, H.: Orthogonal nonnegative Tucker decomposition. SIAM J. Sci. Comput. 43(1), B55–B81 (2021)
Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31(3), 279–311 (1966)
Zhou, G., Cichocki, A., Xie, S.: Fast nonnegative matrix/tensor factorization based on low-rank approximation. IEEE Trans. Signal Process. 60(6), 2928–2940 (2012)
Che, M., Wei, Y., Yan, H.: An efficient randomized algorithm for computing the approximate Tucker decomposition. J. Sci. Comput. 88(2), 32 (2021)
Kilmer, M.E., Braman, K., Hao, N., Hoover, R.C.: Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 34(1), 148–172 (2013)
Zhang, Z., Aeron, S.: Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 65(6), 1511–1526 (2017)
Qiu, D., Bai, M., Ng, M.K., Zhang, X.: Robust low transformed multi-rank tensor methods for image alignment. J. Sci. Comput. 87, 1–40 (2021)
De Lathauwer, L.: Decompositions of a higher-order tensor in block terms-part i: lemmas for partitioned matrices. SIAM J. Matrix Anal. Appl. 30(3), 1022–1032 (2008)
Yokota, T., Lee, N., Cichocki, A.: Robust multilinear tensor rank estimation using higher order singular value decomposition and information criteria. IEEE Trans. Signal Process. 65(5), 1196–1206 (2017)
Onunwor, E., Reichel, L.: On the computation of a truncated SVD of a large linear discrete ill-posed problem. Numer. Algorithms 75(2), 359–380 (2017)
Li, J.-F., Li, W., Vong, S.-W., Luo, Q.-L., Xiao, M.: A Riemannian optimization approach for solving the generalized eigenvalue problem for nonsquare matrix pencils. J. Sci. Comput. 82, 1–43 (2020)
Jia, Z., Wei, M.: A new TV-stokes model for image deblurring and denoising with fast algorithms. J. Sci. Comput. 72, 522–541 (2017)
Li, M., Li, W., Chen, Y., Xiao, M.: The nonconvex tensor robust principal component analysis approximation model via the weighted \(\ell \) p-norm regularization. J. Sci. Comput. 89(3), 67 (2021)
Maruhashi, K., Guo, F., Faloutsos, C.: Multiaspectforensics: pattern mining on large-scale heterogeneous networks with tensor analysis. In: 2011 International Conference on Advances in Social Networks Analysis and Mining, pp. 203–210 (2011)
Che, M., Wei, Y.: Multiplicative algorithms for symmetric nonnegative tensor factorizations and its applications. J. Sci. Comput. 83(3), 1–31 (2020)
Zhao, X., Bai, M., Ng, M.K.: Nonconvex optimization for robust tensor completion from grossly sparse observations. J. Sci. Comput. 85(2), 46 (2020)
Zheng, W.-J., Zhao, X.-L., Zheng, Y.-B., Lin, J., Zhuang, L., Huang, T.-Z.: Spatial–spectral–temporal connective tensor network decomposition for thick cloud removal. ISPRS J. Photogramm. Remote Sens. 199, 182–194 (2023)
Bengua, J.A., Phien, H.N., Tuan, H.D., Do, M.N.: Efficient tensor completion for color image and video recovery: low-rank tensor train. IEEE Trans. Image Process. 26(5), 2466–2479 (2017)
Yuan, L., Li, C., Mandic, D., Cao, J., Zhao, Q.: Tensor ring decomposition with rank minimization on latent space: an efficient approach for tensor completion. Proc. AAAI Conf. Artif. Intell. 33(01), 9151–9158 (2019)
Oseledets, I.V.: Tensor-train decomposition. SIAM J. Sci. Comput. 33(5), 2295–2317 (2011)
Garnerone, S., de Oliveira, T.R., Zanardi, P.: Typicality in random matrix product states. Rev. Mod. Phys. 81, 032336 (2010)
Zhao, Q., Zhou, G., Xie, S., Zhang, L., Cichocki, A.: Tensor ring decomposition, arXiv preprint arXiv:1606.05535 (2016)
Cirac, J.I., Pérez-García, D., Schuch, N., Verstraete, F.: Matrix product states and projected entangled pair states: concepts, symmetries, theorems. Rev. Mod. Phys. 93, 045003 (2021)
Marti, K.H., Bauer, B., Reiher, M., Troyer, M., Verstraete, F.: Complete-graph tensor network states: a new fermionic wave function ansatz for molecules. New J. Phys. 12(10), 103008 (2010)
Zheng, Y.-B., Huang, T.-Z., Zhao, X.-L., Zhao, Q., Jiang, T.-X.: Fully-connected tensor network decomposition and its application to higher-order tensor completion. Proc. AAAI 35(12), 11071–11078 (2021)
Sidiropoulos, N.D., De Lathauwer, L., Fu, X., Huang, K., Papalexakis, E.E., Faloutsos, C.: Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 65(13), 3551–3582 (2017)
Martin, D.R., Reichel, L.: Projected Tikhonov regularization of large-scale discrete ill-posed problems. J. Sci. Comput. 56(3), 471–493 (2013)
Zhang, X., Ng, M.K., Bai, M.: A fast algorithm for deconvolution and Poisson noise removal. J. Sci. Comput. 75(3), 1535–1554 (2018)
Shi, C., Huang, Z., Wan, L., Xiong, T.: Low-rank tensor completion based on log-det rank approximation and matrix factorization. J. Sci. Comput. 80(3), 1888–1912 (2019)
Jia, Z., Jin, Q., Ng, M.K., Zhao, X.-L.: Non-local robust quaternion matrix completion for large-scale color image and video inpainting. IEEE Trans. Image Process. 31, 3868–3883 (2022)
Comon, P., Luciani, X., de Almeida, A.L.F.: Tensor decompositions, alternating least squares and other tales. J. Chemom. 23(7–8), 393–405 (2009)
De Lathauwer, L., Nion, D.: Decompositions of a higher-order tensor in block terms-part iii: alternating least squares algorithms. SIAM J. Matrix Anal. Appl. 30(3), 1067–1083 (2008)
Che, M., Wei, Y., Yan, H.: Randomized algorithms for the low multilinear rank approximations of tensors. J. Comput. Appl. Math. 390, 113380 (2021)
Che, M., Wei, Y., Yan, H.: The computation of low multilinear rank approximations of tensors via power scheme and random projection. SIAM J. Matrix Anal. Appl. 41(2), 605–636 (2020)
Battaglino, C., Ballard, G., Kolda, T.G.: A practical randomized CP tensor decomposition. SIAM J. Matrix Anal. Appl. 39(2), 876–901 (2018)
Kolda, T.G., Hong, D.: Stochastic gradients for large-scale tensor decomposition. SIAM J. Math. Data Sci. 2(4), 1066–1095 (2020)
Cheng, D., Peng, R., Liu, Y., Perros, I.: SPALS: fast alternating least squares via implicit leverage scores sampling. Adv. Neural Inf. Process. Syst. 29 (2016)
Fu, X., Ibrahim, S., Wai, H.-T., Gao, C., Huang, K.: Block-randomized stochastic proximal gradient for low-rank tensor factorization. IEEE Trans. Signal Process. 68, 2170–2185 (2020)
Minster, R., Saibaba, A.K., Kilmer, M.E.: Randomized algorithms for low-rank tensor decompositions in the Tucker format. SIAM J. Math. Data Sci. 2(1), 189–215 (2020)
Dong, H., Tong, T., Ma, C., Chi, Y.: Fast and provable tensor robust principal component analysis via scaled gradient descent, arXiv preprint arXiv:2206.09109 (2022)
Zhang, J., Saibaba, A.K., Kilmer, M.E., Aeron, S.: A randomized tensor singular value decomposition based on the t-product. Numer. Linear Algebra Appl. 25(5), e2179 (2018)
Yuan, L., Zhao, Q., Gui, L., Cao, J.: High-order tensor completion via gradient-based optimization under tensor train format. Signal Process. Image Commun. 73, 53–61 (2019)
Malik, O.A., Becker, S.: A sampling-based method for tensor ring decomposition. In: Proceedings of the 38th International Conference on Machine Learning, vol. 139, pp. 7400–7411 (2021)
Khoo, Y., Lu, J., Ying, L.: Efficient construction of tensor ring representations from sampling. Multiscale Model. Simul. 19(3), 1261–1284 (2021)
Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51(3), 455–500 (2009)
Cutkosky, A., Orabona, F.: Momentum-based variance reduction in non-convex sgd. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R. (Eds.) Advances in Neural Information Processing Systems, vol. 32 (2019)
Fu, X., Ma, W.-K., Huang, K., Sidiropoulos, N.D.: Blind separation of quasi-stationary sources: exploiting convex geometry in covariance domain. IEEE Trans. Signal Process. 63(9), 2306–2320 (2015)
De Lathauwer, L., Castaing, J.: Blind identification of underdetermined mixtures by simultaneous matrix diagonalization. IEEE Trans. Signal Process. 56(3), 1096–1105 (2008)
Vergara, A., Fonollosa, J., Mahiques, J., Trincavelli, M., Rulkov, N., Huerta, R.: On the performance of gas sensor arrays in open sampling systems using inhibitory support vector machines. Sens. Actuators B Chem. 185, 462–477 (2013)
Vervliet, N., De Lathauwer, L.: A randomized block sampling approach to canonical polyadic decomposition of large-scale tensors. IEEE J. Sel. Top. Signal Process. 10(2), 284–295 (2016)
Wang, Q., Cui, C., Han, D.: Accelerated doubly stochastic gradient descent for tensor CP decomposition. J. Optim. Theory Appl. 197(2), 665–704 (2023)
Funding
The research of Xi-Le Zhao was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 12371456, 12171072, 62131005, the Sichuan Science and Technology Program under Grant No. 23ZYZYTS0042, and the National Key Research and Development Program of China under Grant No. 2020YFA0714001. The research of Yu-Bang Zheng was supported by NSFC under Grant No. 62301456. The research of Ting-Zhu Huang was supported by NSFC under Grant No. 12171072.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A. Proof of Lemma 1
Lemma 1
Under Assumptions 1.1–1.3, suppose parameters \(\{\alpha ^s\}_{s\in \mathbb {N}}\) and \(\{\gamma ^s\}_{s\in \mathbb {N}}\) satisfy the following:
Then the FCTN-VRSGD algorithm satisfies
where \(w_k=\frac{\beta ^s}{4}(\frac{3}{4}-\beta ^sL)-\frac{2(\beta ^s(1-\gamma ^s))^2}{15\beta ^{s+1}}\).
Proof of Lemma 1
Before showing (A.2), let us introduce two inequalities as follows:
and
where \(\mathcal {D}_n^s=\mathcal {R}_n^s-\nabla _{\mathcal {G}_n}f(\mathcal {G}^s)\).
The detailed proof of (A.3) is as follows. For a given \(\xi ^s\), the update of \(\mathcal {G}_{\xi ^s}\) in Algorithm 1 can be rewritten as
Let \(\mathcal {G}_{\xi ^s}=\mathcal {G}_{\xi ^s}^s\) and \(\mathcal {G}_{\xi ^s}=\mathcal {G}_{\xi ^s}^{s+1}\) in (A.5) respectively, we have
By the block Lipschitz continuity of the quadratic function \(f(\mathcal {G})\) [42], we can obtain
where \(L>0\) is a Lipschitz constant. The combination of (A.6) and (A.7) gives
where \(\mathcal {D}_{\xi ^s}^{s}=\mathcal {R}_{\xi ^s}^{s}-\nabla _{\mathcal {G}_{\xi ^{s}}}f(\mathcal {G}^{s})\) and \(\mathcal {P}_{\xi ^s}^{s}=\frac{1}{\beta ^s}(\mathcal {G}_{\xi ^s}^{s}-\mathcal {G}_{\xi ^s}^{s+1})\). (a) is obtained form \(<\!\!\!A,B\!\!\!>\le 2||A||_F^2+\frac{1}{8}||B||_F^2\). When \(0<\beta ^s\le \frac{3}{4L}\), (b) holds because
The detailed proof of (A.4) is as follows.
(a) is obtained from \(\mathbb {E}_{\zeta ^s}\big [\mathcal {Q}_{\xi ^s}^{s}|\mathcal {B}^s,\xi ^s\big ]=\nabla _{\mathcal {G}_{\xi ^{s}}}f(\mathcal {G}^{s})\), that is, the stochastic gradient \(\mathcal {Q}_{\xi ^s}^{s}\) is an unbiased estimate for the full gradient for \(\mathcal {G}_{\xi ^s}^{s}\), and thus \(\mathbb {E}_{\zeta ^s}\big [<\mathcal {Q}_{\xi ^s}^{s}\!-\!\nabla _{\mathcal {G}_{\xi ^{s}}}f(\mathcal {G}^{s}),\mathcal {D}_{\xi ^s}^{s}>|\mathcal {B}^s,\xi ^s\big ]=0\). (b) is obtained from
Taking the total expectation of (A.10), we have the following inequality
Now, we show that (A.2) holds. By setting \(\phi (\mathcal {G}^s)=f(\mathcal {G}^s)+\frac{N}{30\beta ^sL^2}||\mathcal {D}_{\xi ^s}^s||_F^2\), we can obtain
where (a) holds when the second inequality of (A.1) is satisfied. Thus, we have
where \(w_s=\frac{\beta ^s}{4}(\frac{3}{4}-\beta ^sL)-\frac{4((1-\gamma ^{s})\beta ^{s})^2}{30\beta ^{s+\!1}}\). (A.16) can be rewritten as
Summing up inequality (A.17) from \(s=0\) to \(s=S-1\), we have
\(\square \)
B. Proof of Lemma 2
Lemma 2
Under Assumptions 1.1–1.3, suppose parameters \(\{\beta ^s\}_{s\in \mathbb {N}}\) and \(\{\gamma ^s\}_{s\in \mathbb {N}}\) satisfy the following:
where \(0<m\le \frac{3^{\frac{1}{3}}}{9L}\). Then the condition (A.1) in Lemma 1 holds.
Proof of Lemma 2
From \(0<m\le \frac{3^{\frac{1}{3}}}{9L}\), we can obtain
and
The first inequality of (A.1) is equivalently expressed as
Combining (B.2) and (B.3), we can obtain that (B.4) holds by following:
where \(\gamma ^s\in (0,1)\). The second inequality of (A.1) is equivalently expressed as
If
then (B.6) holds since \((1-\gamma ^s)^2\big (1+4(\beta ^sL)^2\big )\le (1-\gamma ^s)\big (1+4(\beta ^sL)^2\big )\). From (B.7), we have
\(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zheng, WJ., Zhao, XL., Zheng, YB. et al. Provable Stochastic Algorithm for Large-Scale Fully-Connected Tensor Network Decomposition. J Sci Comput 98, 16 (2024). https://doi.org/10.1007/s10915-023-02404-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02404-1